水下无线传感器网络(underwater wireless sensor networks, UWSNs)以其能耗低、灵活性大、部署区间广的特点, 在海洋环境的监控及目标跟踪中显示了巨大的应用价值.
在水下环境中, 节点随水流移动, 其位置信息对环境信息获取更加重要.而信号的衰减影响网络通信及拓扑稳定性, 给水下节点定位带来严峻挑战.现有UWSNs定位方法的研究主要集中在静态网络定位和动态网络定位[1].针对静态UWSNs, 文献[2]提出借助水下自主航行器(autonomous underwater vehicle, AUV)辅助节点实现较高精度的定位, 但AUV航行速度受限, 适用于小规模UWSNs.考虑大规模静止UWSNs, 文献[3]提出分层定位策略.但大量节点周期性通信, 增加了网络的通信开销.考虑节点的移动性, 文献[4]提出了适用于动态UWSNs的DNRL(the dive and rise localization)方法.由于DNR(dive and rise)节点下潜速度缓慢, 深水处节点的定位时间延迟, 定位误差增大.文献[5]将DNR节点定位后的普通节点转化为参考节点参与定位, 降低了定位时延;但参考节点的增加导致网络通信能耗增加.考虑到水下节点的运动特性, 文献[6-7]提出了预测定位方法.文献[6]以AR模型预测锚节点速度.由于锚节点数量较少且速度更新频率较低, 降低了网络的通信能耗.文献[7]采用遗传算法优化SLMP方法(scalable localization with mobility prediction), 提高了复杂水下环境中节点的定位精度.文献[8]提出了MP-PSO方法(localization method based on mobility prediction and partial swarm optimization algorithms), 采用粒子群算法优化锚节点位置坐标进而降低网络定位误差, 但锚节点周期性优化坐标信息增加网络通信能耗.
综合考虑通信能耗和定位精度, 本文根据节点运动模型实现预测定位.建立了节点在海洋环境中的运动方程, 以K-medoids方法和扩展卡尔曼算法预测方程中的参数, 进而预测锚节点速度;定位过程中, 利用锚节点预测的运动模型信息, 实现普通节点的位置信息预测.以MITgcm模型[9]获得的东经117.25°—132.2°, 北纬24°—43.45°区域的研究环境为基础, 对该区域内的UWSNs定位方法进行仿真分析, 结果显示定位覆盖度、平均定位误差和平均通信能耗均优于SLMP算法和MP-PSO算法.
1 节点运动模型考虑近海监控的UWSNs网络, 潮汐是影响网络节点运动的主要因素, 由于节点质量、体积较小, 与近海洋流运动轨迹又有所不同.本文以简单的潮汐运动模型为基础, 通过空间基函数的选择及模型参数的优化获得精度和实时性较高的节点运动模型.
1.1 洋流运动基础模型潮汐是海水在太阳及月球引力作用下周期性的运动, 节点的基础运动模型采用包含一系列潮汐成分频率的时间和空间基函数构成, 其一维数学表达式[10]为
| $ \begin{array}{l} y\left( {x, t} \right) = {y_0}\left( x \right) + \mathop \sum \limits_{i = 1}^N \left[ {{g_i}\left( x \right)\cos \;{\omega _i}t} \right] + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathop \sum \limits_{i = 1}^N \left[ {{h_i}\left( x \right)\sin \;{\omega _i}t} \right]. \end{array} $ | (1) |
式中:x为位置点, y为x点处的速度(一般南北方向记为v, 东西方向记为u), N为潮汐成分的个数, cos ωit、sin ωit为频率为ωi的潮汐成分的时间基函数, y0(x)表示在观察采样时间区间内洋流速度的平均值, y0(x), gi(x), hi(x)为与位置相关的函数.
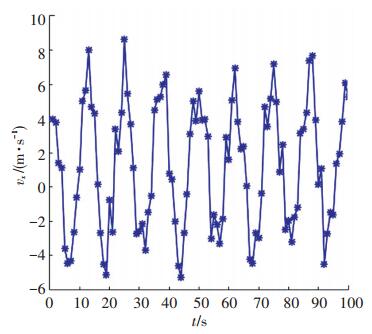
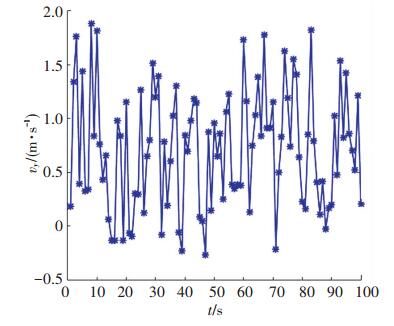
1.2 节点运动模型近海环境下的速度由均匀振荡的潮汐场和顺时针及逆时针交替构成无穷序列的剩余场组成, 呈现确定的半周期性, 运动特征如图 1、2所示[11].
|
图 1 x方向速度 Figure 1 Velocity in x direction |
|
图 2 y方向速度 Figure 2 Velocity in y direction |
在潮汐作用下, 节点的运动为非线性运动, 垂直于水流方向的运动为有限的阻尼运动[12], 故本文采用近似误差小、平滑度高的高斯径向基函数[13]作为空间基函数构造节点运动模型, 则式(1)中的y0(x), gi(x), hi(x)可分别表示为
| $ \begin{array}{l} {\varphi _j}\left( x \right) = \exp (\frac{{ - ||x - {c_j}|{|^2}}}{{2{\sigma ^2}}}), \\ \;\;\;\;\;\;\;{y_0}\left( x \right) = \mathop \sum \limits_{j = 1}^M {\theta _{1, j}}{\varphi _j}\left( x \right), \\ \;\;\;\;\;\;\;{g_i}\left( x \right) = \mathop \sum \limits_{j = 1}^M {\theta _{2i, j}}{\varphi _j}\left( x \right), \\ \;\;\;\;\;\;\;{h_i}\left( x \right) = \mathop \sum \limits_{j = 1}^M {\theta _{2i + 1, j}}{\varphi _j}\left( x \right). \end{array} $ |
式中:M为高斯径向基函数的个数, cj为第j个高斯径向基函数的中心, σ为径向基函数的宽度, θi, j为高斯径向基函数的系数.将上述公式代入式(1)得到节点运动模型y(x, t)为
| $ y\left( {x, t} \right) = \mathop \sum \limits_{j = 1}^M {\lambda _j}\left( t \right){\varphi _j}\left( x \right), $ | (2) |
| $ {\lambda _j}\left( t \right) = {\theta _{1, j}} + \mathop \sum \limits_{i = 1}^N {\theta _{2i, j}}\cos \;{\omega _i}t + \mathop \sum \limits_{i = 1}^N {\theta _{2i + 1, j}}\sin \;{\omega _i}t. $ | (3) |
该运动模型与高斯径向基函数的中心cj及其系数θi, j密切相关.因此, 通过优化高斯径向基函数的中心cj和系数θi, j得到实时的、精确的节点运动模型.
2 节点运动模型的优化模型中的高斯径向基函数的中心cj和系数θi, j与节点的位置密切相关, 综合考虑通信能耗、模型的精度, 利用K-mediods聚类方法对高斯径向基函数中心的选择进行了优化;并利用扩展卡尔曼方法对模型系数θi, j进行预测, 保证模型的实时性.
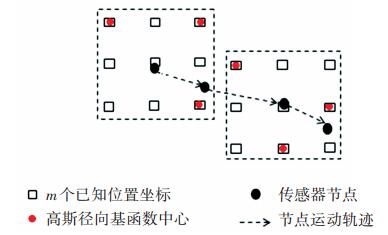
2.1 高斯径向基函数的聚类优化由式(2)、(3)可知, 某一时刻节点的位置和速度与高斯径向基函数组的选择有关, 也即和高斯径向基函数的中心的选择有关.节点与高斯径向基函数中心的距离在一定程度上决定了该函数对模型精度的影响作用.如图 3所示, t1时刻节点的高斯径向基函数空间内有m个已知的位置坐标, 假设需要在该区域内选择M(M < m)个高斯径向基函数来描述节点的运动, 则需要对已知的m个位置坐标进行聚类分簇, 最终确定M个高斯径向基函数的中心.综合考虑通信消耗、模型的精度, 本文选择K-mediods聚类方法[14]确定高斯径向基函数.
|
图 3 节点运动模型 Figure 3 Mobility pattern of node |
定义簇内平均相异度的代价函数为
| $ E = \mathop \sum \limits_{j = 1}^M \mathop \sum \limits_{p \in {C_j}} (||p - {C_j}|{|^2}), $ |
式中Cj为第j个簇中的高斯径向基函数的中心坐标, p为第j个簇中除中心之外的剩余位置坐标.
以簇内平均相异度的代价函数E最小为优化目标, 通过K-mediods聚类方法获得高斯径向基函数组, 其中心在该空间内分布分散, 能够在满足描述节点信息精度的基础上, 减少节点运动过程中的更新次数, 即减少了通信及计算能量消耗.
2.2 基于扩展卡尔曼滤波的模型系数预测为节约通信能量消耗, 减少系数的更新频率, 在模型中引入系数预测机制, 在误差允许范围内使用预测系数.考虑到式(3)为非线性方程, 采用计算量小的扩展卡尔曼算法完成模型系数的预测与优化.
为建立式(3)离散的状态方程和观测方程, 设算法中定位周期为T1, 则对于tk=k×T1时刻离散化后的运动模型系数公式为
| $ \begin{array}{l} {\lambda _j}({\rm{k}}{T_1}) = {\theta _{1, j}} + \mathop \sum \limits_{i = 1}^N {\theta _{2i, j}}\cos ({\omega _i}k{T_1}) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathop \sum \limits_{i = 1}^N {\theta _{2i + 1, j}}\sin ({\omega _i}k{T_1}). \end{array} $ | (4) |
对sin(ωkT1)和cos(ωkT1)采用泰勒一次式展开并代入式(4), 可得到
| $ \begin{array}{l} {\lambda _j}(k{T_1}) = {\lambda _{\rm{j}}}(\left( {k - 1} \right){T_1}) + \\ \;\;\;\;\;\mathop \sum \limits_{i = 1}^N {\omega _i}{T_1}[{\theta _{2i, j}}{\theta _{2i + 1, j}}]\left[ \begin{array}{l} - \sin ({\omega _i}\left( {k - 1} \right){T_1})\\ \cos ({\omega _i}\left( {k - 1} \right){T_1}) \end{array} \right]. \end{array} $ |
令λ(kT)1=[λ1(kT1), λ2(kT1), …, λM(kT1)]T记为λ(k), 则得到扩展卡尔曼状态方程为
| $ \begin{array}{l} \lambda \left( k \right) = \lambda \left( {k - 1} \right) + \mathop \sum \limits_{i = 1}^N {\omega _i}{T_1}\left[ {\begin{array}{*{20}{c}} {{\theta _{2i, 1}}}&{{\theta _{2i + 1, 1}}}\\ \vdots&\vdots \\ {{\theta _{2i, M}}}&{{\theta _{2i + 1, M}}} \end{array}} \right] \cdot \\ \;\;\;\;\;\;\;\;\;\;\left[ \begin{array}{l} - \sin ({\omega _i}\left( {k - 1} \right){T_1})\\ \cos ({\omega _i}\left( {k - 1} \right){T_1}) \end{array} \right] + w\left( {k - 1} \right), \end{array} $ |
式中w(k-1)为第tk-1时刻的过程噪声,
| $ w\left( {k - 1} \right) = {\left[ {{w_1}\left( {k - 1} \right), {w_2}\left( {k - 1} \right), \cdots {w_M}\left( {k - 1} \right)} \right]^{\rm{{\rm T}}}}. $ |
节点运动模型的扩展卡尔曼观测方程为
y(k-1)=H(k-1)λ(k-1)+v(k-1),
式中H(k-1)=[φ1(x), φ2(x), …, φM(x)], v(k-1)为观测噪声, y(k-1)为锚节点的运动速度.
故扩展卡尔曼算法的状态空间模型为
| $ \left\{ \begin{array}{l} \lambda \left( k \right) = \lambda \left( {k - 1} \right) + \mathop \sum \limits_{i = 1}^N {\omega _i}{T_1}\\ \left[ {\begin{array}{*{20}{c}} {{\theta _{2i, 1}}}&{{\theta _{2i + 1, 1}}}\\ \vdots&\vdots \\ {{\theta _{2i, M}}}&{{\theta _{2i + 1, M}}} \end{array}} \right]\left[ \begin{array}{l} - \sin ({\omega _i}\left( {k - 1} \right){T_1})\\ \cos ({\omega _i}\left( {k - 1} \right){T_1}) \end{array} \right] + w\left( {k - 1} \right), \\ y\left( {k - 1} \right) = H\left( {k - 1} \right)\lambda \left( {k - 1} \right) + v\left( {k - 1} \right). \end{array} \right. $ | (5) |
将式(5)代入扩展卡尔曼递推方程组后可得式(6)~(10), 进而获得矩阵λ(k)的最优矩阵
| $ \begin{array}{l} \mathit{\boldsymbol{\hat \lambda }}\left( {k|k - 1} \right) = \mathit{\boldsymbol{\lambda }}\left( {k - 1|k - 1} \right) + \mathop \sum \limits_{i = 1}^N {\omega _i}{T_1} \cdot \\ \;\;\left[ {\begin{array}{*{20}{c}} {{\theta _{2i + 1}}}&{{\theta _{2i, M}}}\\ \vdots&\vdots \\ {{\theta _{2i + 1, 1}}}&{{\theta _{2i + 1, M}}} \end{array}} \right]\left[ \begin{array}{l} - \sin ({\omega _i}\left( {k - 1} \right){T_1})\\ \cos ({\omega _i}\left( {k - 1} \right){T_1}) \end{array} \right], \end{array} $ | (6) |
| $ P\left( {k|k - 1} \right) = P\left( {k - 1|k - 1} \right) + Q\left( k \right), $ | (7) |
| $ \begin{array}{l} K\left( k \right) = P\left( {k|k - 1} \right){\mathit{\boldsymbol{H}}^{\rm{T}}}\left( k \right)[\mathit{\boldsymbol{H}}\left( k \right)\mathit{\boldsymbol{P}}\left( {k|k - 1} \right){\mathit{\boldsymbol{H}}^{\rm{T}}}\left( k \right) + \\ \;\;\;\;\;\;\;\;\;\;\;R\left( k \right){]^{ - 1}}, \end{array} $ | (8) |
| $ \begin{array}{l} \hat \lambda \left( {k|k} \right) = \hat \lambda \left( {k|k - 1} \right) + K\left( k \right)[y\left( {k - 1} \right) - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{H}}\left( {k - 1} \right)\mathit{\boldsymbol{\hat \lambda }}\left( {k|k - 1} \right)], \end{array} $ | (9) |
| $ P\left( k \right) = [I - K\left( k \right)\mathit{\boldsymbol{H}}\left( k \right)]\mathit{\boldsymbol{P}}\left( {k|k - 1} \right). $ | (10) |
式中Q(k)、R(k)分别为过程噪声w(k)和观测噪声v(k)的均值和方差.
由式(3)可得, 在
| $ \mathit{\boldsymbol{\hat \theta }}\left( k \right) = {[{\mathit{\boldsymbol{\alpha }}^{\rm{{\rm T}}}}\left( k \right)\mathit{\boldsymbol{\alpha }}\left( k \right)]^{ - 1}}{\mathit{\boldsymbol{\alpha }}^{\rm{{\rm T}}}}\left( k \right)\hat \lambda {\left( k \right)^{\rm{T}}}. $ |
式中α(k)=(1, cos(ω1kT1), sin(ω1kT1), …, cos(ωNkT1), sin(ωNkT1)], θ(k)=[θ1(k), …, θj(k), …, θM(k)], 并且θj(k)=[θ1, j(k), θ2, j(k), …, θ2N+1, j(k)]T.
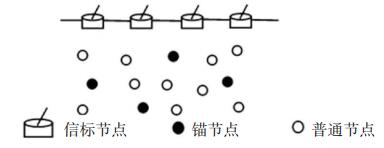
3 节点的预测定位本文考虑如图 4所示的监控网络结构, 其中信标节点浮于水面, 具备GPS定位功能, 节点的通信、计算、能量不受限;锚节点的通信、计算、能量不受限, 可以通过与信标节点的通信实现自定位;普通节点的通信、能量有限, 可以与通信范围内的锚节点进行通信.
|
图 4 网络结构 Figure 4 Network structure diagram |
定位过程中锚节点与信标节点通信并完成定位;普通节点与锚节点通信实现定位.受应用环境和节点自身限制, 普通节点很难实时与锚节点通信, 获得完整的定位信息.考虑到水下节点的运动特征与邻居节点的运动特征有关[15], 即普通节点与邻居锚节点的运动轨迹接近, 本文提出基于UWSNs运动模型的节点预测定位方法.锚节点通过与信标节点通信获得位置信息, 采用K-medoids聚类方法和扩展卡尔曼方法获得相应的高斯径向基函数及系数, 并预测某一时间窗口Tw(Tw=K×T1, K为整数)内的锚节点位置、速度和模型参数信息;普通节点与锚节点通信, 依据距离相近原则, 利用锚节点传递的模型参数完成预测定位.算法包括锚节点运动信息预测和普通节点定位.
3.1 锚节点运动信息预测在任意时刻tk=k×T1, 锚节点利用信标节点的信息, 计算自身位置和速度, 并获得当前时刻的高斯径向基函数和相应的模型系数θ.根据扩展卡尔曼方法预测tk+1时刻的模型系数θ和速度, 根据式(11)预测tk+1时刻的位置, 则位置为
| $ {L_{{\rm{est}}}}({t_{k + 1}}) = {L_{{\rm{real}}}}({t_k}) + \mathop \sum \limits_{t = {t_k}}^{t = {t_k}} \hat v\left( t \right) \times {T_1}. $ | (11) |
式中:Lreal(tk)为tk时刻锚节点的实际位置, Lest(tk+1)为tk+1时刻的预测位置,
考虑到普通节点能量受限, 锚节点会预测Tw时间段内的位置及模型信息, 并发送给普通节点.出于定位精度的考虑, 定位过程中, 锚节点会将ti时刻的位置信息与预测信息比较, 如果误差超出阈值, 锚节点会重新预测Tw内的运动信息并发送给普通节点.锚节点发送给普通节点的数据包结构如图 5所示.

|
图 5 数据包结构 Figure 5 Structure of data packet |
普通节点定期接收锚节点的广播信息, 受水流环境的影响, 到锚节点的距离不同, 其与锚节点运动的相近程度不同, 定义锚节点信息的信任权重为
| $ {\xi _{an}} = \frac{{{d_{an}}^{ - 1}}}{{\mathop \sum \limits_{a = 1}^{{\rm{Sum}}} {d_{an}}^{ - 1}}}, $ | (12) |
式中dan为锚节点a到普通节点n之间的距离.
并根据式(12)获得的信任权重计算普通节点运动模型中的系数θn(i)为
| $ {\theta _n}\left( i \right) = \mathop \sum \limits_{a = 1}^S {\xi _{an}}{\theta _a}\left( i \right). $ | (13) |
式中:θn(i)为普通节点n第i个节点运动模型系数, θa(i)为锚节点a第i个节点运动模型系数, S为锚节点的总数量.
为减少预测过程中的累积误差, 当普通节点在同一时刻接收到3个及以上锚节点信息时, 利用三边法[16]完成定位;否则, 利用式(12)、(13)及节点运动模型式(2)、(3)完成Tw时间段内的节点速度预测, 并根据式(14)实现Tw时间段内的位置预测;如果在Tw时间内有锚节点信息的更新, 则重新更新普通节点的位置预测信息.
| $ {L_n}({t_{k + 1}}) = {L_n}({t_k}) + {{\hat v}_n}({t_k}) \times {T_1}. $ | (14) |
式中:Ln(tk)为普通节点n在tk时刻位置, Ln(tk+1)为估计的tk+1时刻位置,
本文以东经117.25°—132.2°, 北纬24°—43.45°区域的数据为基础, 对该区域内的UWSN定位方法进行了仿真分析, 并与SLMP方法和MP-PSO方法进行了比较.实验过程中节点的部署区域为100 m×100 m×100 m, 节点数量为500个, 浮标节点、锚节点、普通节点比例分别为10%、10%、80%, 预测窗口长度为Tw=30 s, 定位周期T1=1 s, 通信距离R=20 m, 误差阈值为0.05R.
4.2 性能评价指标及相关参数1) 节点密度:节点通信范围内的邻居节点的数量.本文通过改变通信范围从而改变节点密度.
2) 定位覆盖度:定位误差小于50%通信距离的已定位节点占网络中所有节点的比例, 即c=nest/n, 其中nest为定位误差小于50%通信距离的节点数目, n为网络中所有节点的数目.
3) 平均定位误差:定位误差小于50%通信距离的节点的平均定位误差与通信距离的比值, 即
| $ e = \frac{{\mathop \sum \limits_{t = {t_{{\rm{start}}}}}^{{t_{{\rm{end}}}}} \mathop \sum \limits_{i = 1}^{{n_{{\rm{est}}}}} \sqrt {{{({x_i} - {{\hat x}_i})}^2} + {{({y_i} - {{\hat y}_i})}^2}} }}{{{n_{{\rm{est}}}} \times ({t_{{\rm{end}}}} - {t_{{\rm{start}}}}) \times R}}, $ |
其中(xi, yi)为节点的实际坐标,
4) 平均通信能耗:不考虑数据包的大小, 定位误差小于50%通信距离的节点平均每秒每个节点交换信息的次数, 即
| $ n = \frac{{\mathop \sum \limits_{t = {t_{{\rm{start}}}}}^{{t_{{\rm{end}}}}} ({n_{{\rm{anchor}}}} + {n_{{\rm{ordinary}}}})}}{{{n_{{\rm{est}}}} \times ({t_{{\rm{end}}}} - {t_{{\rm{start}}}})}}, $ |
其中nanchor为每秒锚节点发送信息的次数, nordinary为每秒已定位普通节点接收信息的次数.
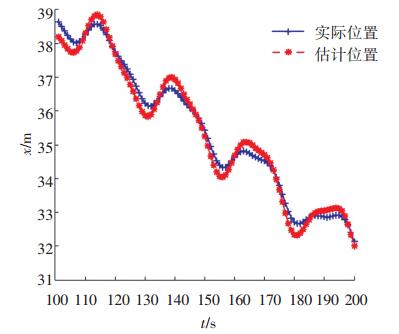
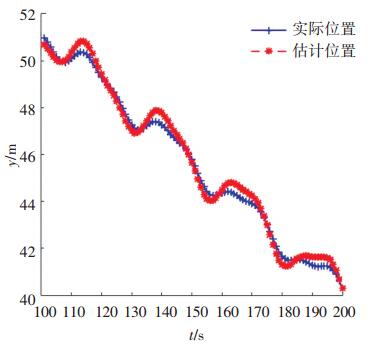
4.3 锚节点定位结果图 6、7显示, 锚节点的定位误差较小, 并且没有随时间的增加而增大.因为PLM-MP算法采用K-medoids方法和扩展卡尔曼算法得到实时的节点运动模型, 减小预测的速度误差, 增加定位精度.并且锚节点与信标节点通信, 更正位置信息, 故定位精度较高.
|
图 6 锚节点x方向实际位置和估计位置坐标随时间变化曲线 Figure 6 Curve of real position and estimated position of anchor node in x coordinate changing with time |
|
图 7 锚节点y方向实际位置和估计位置坐标随时间变化曲线 Figure 7 Curve of real position and estimated position of anchor node in y coordinate changing with time |
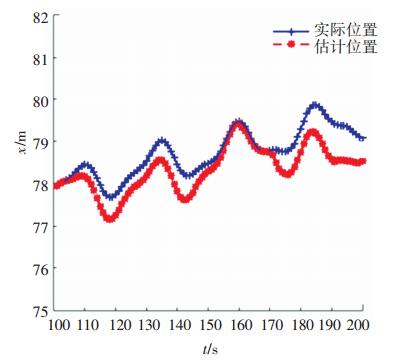
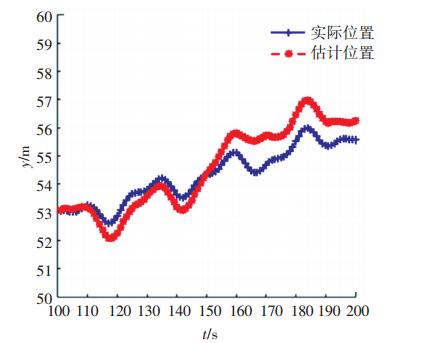
通过对比图 6~9表明, 普通节点的定位误差稍大于锚节点, 普通节点的运动模型依赖于锚节点的位置及运动模型参数预测, 锚节点的定位误差会累积到普通节点的定位中.
|
图 8 普通节点x方向实际位置和估计位置坐标随时间变化曲线 Figure 8 Curve of real position and estimated position of ordinary node in x coordinate changing with time |
|
图 9 普通节点y方向实际位置和估计位置坐标随时间变化曲线 Figure 9 Curve of real position and estimated position of ordinary node in y coordinate changing with time |
定位覆盖度是衡量能否定位大规模水下无线传感器网络的重要指标. 图 10显示了定位覆盖度与节点密度的关系.随着节点密度或锚节点比例的增加, 定位覆盖度均增加.节点密度或锚节点比例的增加, 使得普通节点通信范围内的参考节点增加, 进而实现定位的普通节点数量增加, 定位覆盖度增大.
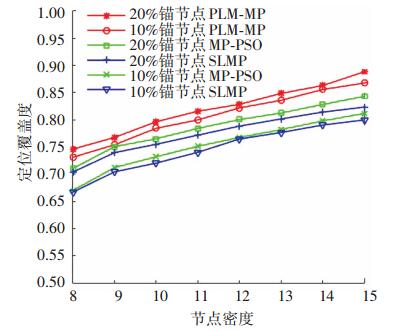
|
图 10 定位覆盖度与节点密度关系 Figure 10 Variation of coverage with node density |
相同节点密度或锚节点比例下, PLM-MP算法的定位覆盖度高于SLMP算法和MP-PSO算法. SLMP算法和MP-PSO算法中参考信息为速度, 当普通节点无法接收到参考节点信息时, 将不能实现定位.而PLM-MP算法中普通节点参考的为预测窗口时间内的模型系数, 即使普通节点未接收到参考节点信息, 仍可根据存储的模型系数估计其速度, 并根据上一时刻位置实现定位.
平均定位误差是衡量节点定位准确度的性能指标. 图 11显示, 随着节点密度或锚节点比例的增加, 平均定位误差减小.随着节点密度或锚节点比例的增加, 普通节点通信范围内的参考节点数量增加, 故可选择精度更高的参考节点信息实现定位, 从而降低定位误差.
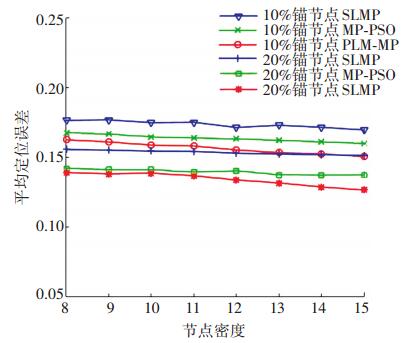
|
图 11 节点平均定位误差与节点密度关系 Figure 11 Variation of average location error with node density |
相同节点密度或锚节点比例下, PLM-MP算法的平均定位误差小于SLMP算法和MP-PSO算法.平均定位误差由普通节点定位误差和锚节点定位误差组成.由图 12、13可知, PLM-MP算法中锚节点的平均速度误差和平均位置误差均小于SLMP算法, 因为PLM-MP算法中节点的运动模型以海水运动情况为基础, 考虑了水下运动的多种因素, 更适合于复杂的水下环境.而锚节点较高精度的速度和位置信息, 使得普通节点的位置精度增加, 故PLM-MP算法的平均定位误差小于SLMP算法.
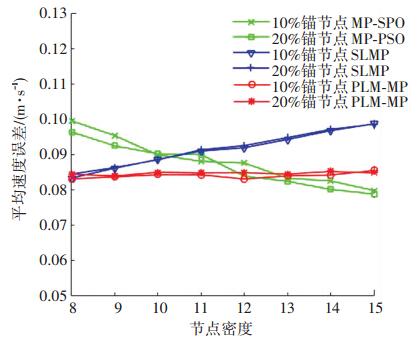
|
图 12 锚节点平均速度误差与节点密度关系 Figure 12 Variation of average velocity error of anchor nodes with node density |
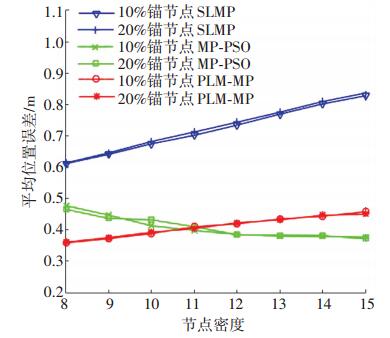
|
图 13 锚节点平均位置误差与节点密度关系 Figure 13 Variation of average location error of anchor nodes with node density |
MP-PSO算法中, 普通节点作为参考节点时, 未考虑其定位精度, 从而引入定位误差较大的普通节点参与定位;而PLM-MP算法普通节点参考信息仅由锚节点提供, 并且存在三边法修正过程, 降低了普通节点的累积误差, 故PLM-MP算法中普通节点的位置误差较小, 从而降低了平均定位误差.
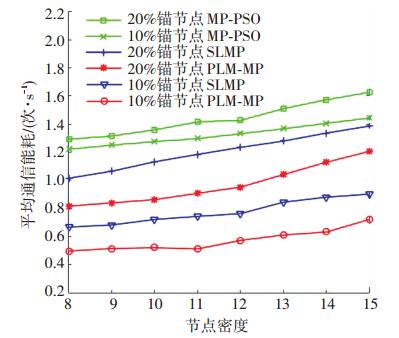
4.7 平均通信能耗与节点密度关系平均通信能耗是衡量网络通信开销的重要指标, 平均通信能耗越小, 网络使用寿命越长. 图 14显示, 随着节点密度或锚节点比例的增加, 平均通信能耗增加.节点密度增加, 普通节点通信范围内的参考节点增加, 通信次数增加, 进而通信能耗增加.锚节点比例增加, 信息发送次数增加, 网络通信能耗增加.
|
图 14 平均通信能耗与节点密度的关系 Figure 14 Variation of average communication cost with node density |
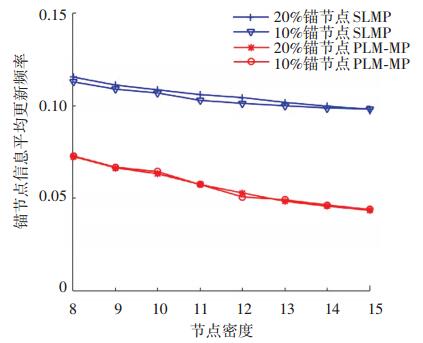
相同节点密度或锚节点比例下, PLM-MP算法的平均通信能耗小于SLMP算法和MP-PSO算法.平均通信能耗与锚节点的信息更新频率密切相关. 图 15显示, PLM-MP算法中锚节点信息的更新频率远小于SLMP算法. PLM-MP算法中节点的运动模型更为精确, 使用时间更长, 从而降低锚节点信息更新频率. MP-PSO算法中, 锚节点周期性优化位置信息以获得速度, 故其更新频率远大于PLM-MP算法和SLMP算法, 所以通信能耗较高.
|
图 15 锚节点平均信息更新频率与节点密度关系 Figure 15 Variation of update frequency of anchor nodes' information with node density |
1) 建立了近海监控UWSNs的节点运动模型, 采用K-medoids聚类方法和扩展卡尔曼算法优化节点运动模型中的参数, 提高了模型的精度和实时性,
2) 采用分层定位策略实现了节点定位, 锚节点通过与信标节点通信实现定位并预测运动模型;依据普通节点与锚节点运动的空间相关性, 普通节点利用锚节点运动模型信息优化自身运动模型系数, 并实现定位.
3) 对东经117.25°—132.2°, 北纬24°—43.45°海域的UWSNs节点定位的仿真分析结果表明, PLM-MP算法的定位覆盖度、平均定位误差和平均通信能耗均优于SLMP算法和MP-PSO算法.
致谢: 感谢国家海洋局第二研究所周锋研究员课题组提供的海洋相关数据.| [1] |
HAN Guangjie, JIANG Jinfang, SHU Lei, et al. Localization algorithms of underwater wireless sensor networks: a survey[J]. Sensors, 2012, 12(2): 2026. DOI:10.1007/s11235-011-9564-7 |
| [2] |
LUO Hanjiang, ZHAO Yiyang, GUO Zhongwen, et al. UDB: using directional beacons for localization in underwater sensor networks[C]//Proceedings of the 2008 14th International Conference on Parallel and Distributed Systems. Washington DC : IEEE Computer Society, 2008: 551 http://www.researchgate.net/publication/203039428_Udb_using_directional_beacons_for_localization_in_underwater_sensor_networks
|
| [3] |
ZHOU Zhong, CUI Junhong, ZHOU Shengli. Efficient localization for large-scale underwater sensor networks[J]. Ad Hoc Networks, 2010, 8(3): 267. DOI:10.1016/j.adhoc.2009.08005 |
| [4] |
EROL M, VIEIRA L F M, GERLA M. Localization with Dive'N' Rise (DNR) beacons for underwater acoustic sensor networks[C]//Proceedings of the Second Workshop on Underwater Networks. New York: Association for Computing Machinery, 2007: 97 http://www.researchgate.net/publication/220926384_Localization_with_Dive'N'Rise_(DNR)_beacons_for_underwater_acoustic_sensor_networks
|
| [5] |
EROL M, VIEIRA L F M, CARUSO A, et al. Multi stage underwater sensor localization using mobile beacons[C]//Proceedings of the 2008 Second International Conference on Sensor Technologies and Applications. Washington DC: IEEE Computer Society, 2008: 710 http://dl.acm.org/citation.cfm?id=1446592
|
| [6] |
ZHOU Zhong, CUI Junhong, SHI Zhijie, et al. Scalable localization with mobility prediction for underwater sensor networks[J]. IEEE Transactions on Mobile Computing, 2011, 10(3): 335. DOI:10.1109/tmc.2010.158 |
| [7] |
刘禹.基于运动模型的水下无线传感器网络节点定位算法的研究[D].长春: 吉林大学, 2015 LIU Yu. The research of localization algorithm for underwater wireless sensor networks based on mobility model[D]. Changchun: Jilin University, 2015 http://cdmd.cnki.com.cn/Article/CDMD-10183-1015600536.htm |
| [8] |
ZHANG Ying, LIANG Jixing, JIANG Shengming, et al. A localization method for underwater wireless sensor networks based on mobility prediction and particle swarm optimization algorithms[J]. Sensors, 2016, 16(2): 212. DOI:10.3390/s16020212 |
| [9] |
MARSHALL J, ADCRORT A, HILL C, et al. A finite-volume incompressible Navier Stokes model for studies of the ocean on parallel computers[J]. Journal of Geophysical Research, 1997, 102(C3): 5753. DOI:10.1029/96JC02775 |
| [10] |
PAWLOWICA R, BEARDALEY B, LENTZ S. Classical tidal harmonic analysis including error estimates in MATLAB using T-TIDE[J]. Computers & Geosciences, 2002, 28(8): 929. DOI:10.1016/S0098-3004(02)0013-4 |
| [11] |
BEERENS S P, RIDDERINKHOF H, ZIMMERMAN J T F. An analytical study of chaotic stirring in tidal areas[J]. Chaos, Solitons and Fractals, 1994, 4(6): 1011. DOI:10.1016/0960-0779(94)90136-8 |
| [12] |
ANDERSON T R, FOLLOWS M J. Representing plankton functional types in ocean general circulation models: competition, tradeoffs and self-organizing architecture[C]//Proceedings of the 2010 15th IEEE International Conference on Engineering of Complex Computer Systems. Washington DC: IEEE Computer Society, 2010: 291 https://www.researchgate.net/publication/221473896_Representing_Plankton_Functional_Types_in_Ocean_General_Circulation_Models_Competition_Tradeoffs_and_Self-Organizing_Architecture
|
| [13] |
BISHOP C M. Review: neural networks for pattern recognition[J]. Journal of the American Statistical Association, 1997, 92(440): 1642. DOI:10.1016/S0065-2458(08)60404-0 |
| [14] |
周涛, 陆惠玲. 数据挖掘中聚类算法研究进展[J]. 计算机工程与应用, 2012, 48(12): 100. ZHOU Tao, LU Huiling. Clustering algorithm research advances on datamining[J]. Computer Engineering and Applications, 2012, 48(12): 100. DOI:10.3778/j.issn.1002-8331.2012.12.021 |
| [15] |
BAGTZOGLOU A C, NOVIKOV A. Chaotic behavior and pollution dispersion characteristics in engineered tidal embayments: a numerical investigation[J]. Jawra Journal of the American Water Resources Association, 2007, 43(1): 207. DOI:10.1111/j.1752-1688.2007.0017.x |
| [16] |
许毅, 陈立家, 甘浪雄, 等. 无线传感器网络技术原理及应用[M]. 北京: 清华大学出版社, 2015: 178. XU Yi, CHEN Lijia, GAN Langxiong, et al. Principle and application of wireless sensor network[M]. Beijing: Tsinghua University Press, 2015: 178. |
 2018, Vol. 50
2018, Vol. 50


