2. 中国空气动力研究与发展中心 高速所,四川 绵阳 621000
2. High Speed Aerodynamic Institute, China Aerodynamics Research and Development Center, Mianyang 621000, Sichuan, China
水陆两栖平台能够提高水上与陆地交通方式转换的效率,减少出行的时间成本.推进装置是两栖平台的核心部件,但是水面平台的螺旋桨和喷水推进装置,输出一维推力,无法应用于陆上行驶;陆上平台以轮式车辆为主,车轮水中旋转推进无法满足效率要求[1].因此,两栖平台研究需革新推进装置,提高其驱动性能.
两栖平台探索过程中,水陆差异式推进是重要方向,以陆上轮式驱动,水面螺旋桨和喷水推进为主.其中,英国Gibbs公司设计的Humingda水陆两栖汽车,采用轮胎收放技术减小了水上航行阻力;美国Dobbertin公司设计了两栖汽车Hydrocar,通过对应环境下车船结构整体转变提高了性能[2-3].但是,差异式推进使用两套装置,占用了平台空间,复杂了传动结构;且平台底面型状已向船舶发展,方形系数减小,降低了陆上行驶性能和外观要求.
近年来,对动物运动行为的研究不断推进,其中水陆通用式推进运动经过自然进化适应了环境,为两栖平台通用式推进的发展提供了灵感.以河蟹为生物原型,王立权研制了一种八足仿生蟹,实现了0.2 m/s速度的横行运动,并可以跨越0.3 m宽度的障碍[4-5];郁树梅设计了一种由9个万向运动单元组成的蛇形机器人,在陆地和水中均能灵活运动,并拓展了蜿蜒和翻滚运动步态研究[6-7].通用式推进通过一套装置满足了两栖运动要求,简化了装置结构,但速度仍需进一步提高.
蛇怪蜥蜴踏水奔跑最高可达1.5 m/s,在同质量等级生物中水上运动较快[8].针对这种踏水运动行为,FLOYD S,徐林森等设计了四连杆往复踏水机构,通过脚掌单点轨迹拟合,初步实现了装置水面低速踏水前进,正进一步提高稳定性和速度[9-11].为简化结构并提高性能,课题组模仿踏水运动,已提出了水面矢量推进器,实现了三维驱动输出和初步的驱动分析[12].
本文将深入分析矢量推进器的仿生机理,结合脚掌位置设计水面平台和两栖平台,开展样机试验总结仿生效果;通过平台动力学研究获取可控参量,进一步建立平板旋转绕流模型,分析参量对驱动性能的影响,并进行试验验证,为驱动控制提供参照.
1 结构设计及分析 1.1 结构设计与仿生机理分析蛇怪蜥蜴通过脚掌踏水实现了快速的水面奔跑,每个脚掌踏水周期分为3个阶段:下踏,后划和恢复,如图 1(a)所示.

|
图 1 蛇怪蜥蜴踏水过程和脚踝轨迹[13] Figure 1 Basilisk lizard treading process and ankle trajectory |
由图 1(a)可看出,脚掌在水下绕脚踝转动,脚掌平面相对于水平面转动角近180°.同时,脚踝相对臀部的运动轨迹为椭圆形,如图 1(b)中带圈红实线所示,实心段固液作用剧烈;将红实线标示的出水恢复阶段的脚踝向前收转变为向后收,则水下运动轨迹近似为半圆型,如图 1(b)中红虚线所示.上述脚掌水下180°角度转动和半圆型轨迹则可同时由旋转运动实现.
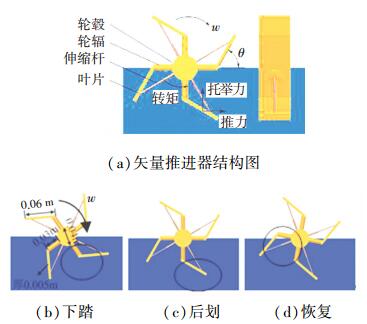
因此,以旋转击水模式代替往复踏水,基于平板模拟脚掌,设计了水面矢量推进器,如图 2(a)所示,由轮毂、轮辐、伸缩杆和叶片组成.运动方面:通过叶片与轮辐基准夹角60°设置,匹配图 1(a)中脚掌踏水的三阶段划分,叶片的下踏、后划和恢复阶段分别如图 2(b)~2(d)所示,且伸缩杆可微调叶片与轮辐夹角θ.驱动输出方面:模仿蛇怪蜥蜴踏水支撑体重、推动前行和维持平衡,推进器通过平板旋转绕流输出托举力、推力和转矩.结构参数:叶片尺寸0.06 m×0.005 m×0.05 m,轮辐长度0.03 m,轮毂直径0.04 m,如图 2(b)所示.
|
图 2 矢量推进器结构和运动原理图 Figure 2 Vector propeller structure and motion schematic diagram |
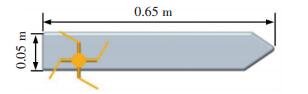
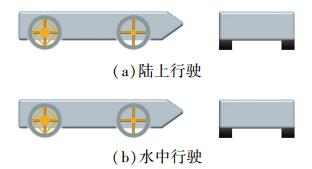
进一步模仿图 1(a)所示蛇怪蜥蜴质心在前、脚掌在后的运动姿态,针对大方形系数平台,将单轴矢量推进器置于后部,设计了水面平台,如图 3所示平台主体参数:0.65 m×0.25 m×0.05 m推进器的水面平台位置以及垂直于转轴的推力输出方式,均与陆面车轮相同.于是,融合车轮和推进器结构特性,基于水面平台设计了一种两栖平台,如图 4所示.其中,后车轮与推进器一体式设计,推进器叶片可收缩折叠,路面行驶时位于轮辋内;水上航行时,推进器向外移出并展开,旋转驱动;后轮采用轮叶复合的通用式设计,实现了陆上与水中行驶,简化了平台结构.
|
图 3 水面平台结构示意图 Figure 3 Structure of water-surface platform |
|
图 4 两栖平台结构 Figure 4 Structure of amphibious platform |
为获取推进器和平台的仿生效果和航行性能,开展了样机试验,航行过程中推进器叶片与水流的固液作用,如图 5所示,平台和推进器样机参数同上.由图 5可看出,叶片的拍击入水位置高于水平面,出水位置低于水平面,在出水位置形成了气穴凹面,如同蛇怪蜥蜴脚掌在气穴中出水减阻,实现了对脚掌气穴式踏水的模仿.同时,相对于初始水平面,水流的高低变化增加了入水行程,减小了出水行程;基于下压和上提运动分别与驱动力和阻力输出相对应,可得:增大了竖直入水驱动力,减小了竖直出水阻力.

|
图 5 推进器转动流场 Figure 5 Flow field of propeller rotation |
样机实现了如蛇怪蜥蜴前倾式的滑水航行,如图 6(a)所示.通过陀螺仪和加速度计测得了攻角曲线,并由NEO-6m GPS模块测得了样机航速,分别如图 6(b)和6(c)所示,在3.9~6.3 s的稳态滑水航行阶段,攻角平均值为10.6°,速度平均值为1.24 m/s;滑水航行是水面平台的高速运动航态[14],矢量推进器实现了样机由排水至滑水航态转变,克服了“兴波阻力墙”问题,为平台减阻提速提供了新思路.

|
图 6 平台航行试验 Figure 6 Navigation experiment on the platform |
通过仿生设计,实现了蛇怪蜥蜴式的推进器和平台运动,采用通用式推进转变两栖平台的航态为滑水,为简化结构和提高航速提供了新思路,随后将开展矢量推进器驱动输出的优化控制研究.
2 平台和推进器动力学分析蛇怪蜥蜴通过脚掌踏水深度和频率灵活地调节身体的水面奔跑状态.为控制平台的航行状态,首先,开展平台航行动力学研究获取影响性能的推进器可控参量;然后,建立矢量推进器的流体动力学模型,数值计算参量对驱动性能的影响规律.
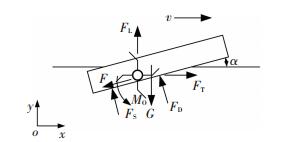
2.1 平台航行动力学研究将大方形系数平台侧视图简化为平板[15],忽略平台的空气动力,滑水航行过程中平台受到了动升力FD、静压力FS、重力G、摩擦阻力F、以及推进器输出的托举力FL、推力FT和转矩Mo的作用,如图 7所示.基于ЦАГИ方法,各作用力及力臂表达如下[15].
|
图 7 平台滑水航行受力图 Figure 7 Mechanical analysis of amphibious vehicle in the hydroplaning state |
平台所受动升力FD和静压力FS分别为
| $ {F_{\rm{D}}} = \frac{{0.7{\rm{ \mathsf{ π} }}\lambda \alpha }}{{1 + 1.4\lambda }} \cdot \frac{1}{2}\rho {v^2}B_u^2, $ | (1) |
| $ {F_{\rm{S}}} = \frac{{\lambda - 0.4}}{{\lambda + 0.4}} \cdot \frac{{{\lambda ^2}\alpha }}{{F_{\rm{B}}^2}} \cdot \frac{1}{2}\frac{{\rho {v^2}}}{{B_u^2}}. $ | (2) |
式中:
动升力作用位置至轮轴的距离lD和静压力作用位置至轮轴的距离lS分别为
| $ {l_{\rm{D}}} = {l_{\rm{i}}} - (0.75 + 0.08\frac{{{\lambda ^{0.865}}}}{{\sqrt {{F_B}} }})l, $ | (3) |
| $ {l_{\rm{S}}} = {l_{\rm{i}}} - \frac{{\lambda - 0.8}}{{3\lambda - 1.2}}l. $ | (4) |
式中li为轮轴到平台尾部的距离.
摩擦阻力F主要作用于平台底部[16], 表达式为
| $ F = fA{v^{1.8}}. $ | (5) |
式中A为湿面积,f为摩擦系数.
将两栖平台受到的各作用力进行水平和竖直分解,可得
| $ {F_x} = {F_{\rm{T}}} - ({F_{\rm{D}}} + {F_{\rm{S}}})\sin \alpha - F\cos \alpha , $ | (6) |
| $ {F_y} = {F_{\rm{L}}} + ({F_{\rm{D}}} + {F_{\rm{S}}})\cos \alpha - G - F\sin \alpha . $ | (7) |
进一步得到相对于轮轴的力矩为
| $ {M_i} = {M_{\rm{o}}} + F{l_{\rm{F}}} + {F_D}{l_{\rm{D}}} - {F_S}{l_{\rm{S}}} - G{l_{\rm{G}}}\cos \alpha . $ | (8) |
式中lF为F相对于轮轴的力臂.
水平分力Fx是平台推进的动力;竖直分力Fy可减小吃水深度降低前行阻力;转矩Mi通过维持平台前倾实现排水至滑水的航态转变.航行中,在平台的Fx、Fy和Mi输出里,推进器驱动是唯一的主动调节因素;而轮轴高度和转速是推进器的可控参量.
2.2 推进器流体动力学模型将推进器固液作用简化为平板旋转绕流的科学问题,建立流体动力学模型,分析轮轴高度和航行中航速与转速协调变化对推进器驱动输出的影响,如图 8(a)所示.

|
图 8 数值计算模型 Figure 8 Numerical calculation model |
其中,网格划分如图 8(b)所示,主要设置:计算域3 m×1 m×1 m,推进器参数同上,采用四面体单元,推进器表面网格长度为0.005 m,并向边界以1.1的比例放大.边界条件设置:推进器轮轴固定于水面,右下侧为速度入口,左侧为压力出口,剩余边界面均为壁面.
基于k-ε RNG湍流模型,结合PISO算法和流体体积法跟踪叶片平板的固液作用,求解连续方程和动量方程,获取推进器的流体动力参数.在三维不可压非定常流动假定下,任一单元的连续方程、动量方程分别为
| $ \frac{{\partial \rho }}{{\partial t}} + \frac{\partial }{{\partial {x_i}}}(\rho {u_i}) = 0, $ | (9) |
| $ \frac{\partial }{{\partial t}}(\rho {u_i}) + \frac{\partial }{{\partial {x_j}}}(\rho {u_i}{u_j}) = - \frac{{\partial p}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}(\mu \frac{{\partial {u_i}}}{{\partial {x_j}}}) + {S_i}. $ | (10) |
式中:xi为方向标量(i=1, 2, 3),ui, uj为速度分量均值(i, j=1, 2, 3),p为压力均值,ρ为流体密度,μ为流体粘性系数,Si为广义源项.
k-ε方程为
| $ \frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + \frac{{\partial (\rho k{u_i})}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}[{\alpha _k}{\mu _{{\rm{eff}}}}\frac{{\partial k}}{{\partial {x_j}}}] + {G_k} + \rho \varepsilon , $ | (11) |
| $ \frac{{\partial \left( {\rho \varepsilon } \right)}}{{\partial t}} + \frac{{\partial (\rho \varepsilon {u_i})}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}[{\alpha _\varepsilon }{\mu _{{\rm{eff}}}}\frac{{\partial \varepsilon }}{{\partial {x_j}}}] + \frac{{C_{1\varepsilon }^*}}{k}{G_\kappa } - {C_{2\varepsilon }}\rho \frac{{{\varepsilon ^2}}}{k}. $ | (12) |
式中:μeff为等效粘度,Gk为湍动能产生项,αk、αε、C1ε*、C2ε为模型系数,取值分别为1.39、1.39、1.42、1.68.
3 驱动性能分析基于数值计算的力学参数特性曲线,分析单叶片输出的仿生效果及其与整体驱动的对应规律;提取特征值,分析轮轴高度和航速与转速协同变化对推进器驱动性能的影响.可控参量初始设置:结构尺寸同1.1节,推进器转速1 r/s,轮轴高度距水面0 m,航速0 m/s.
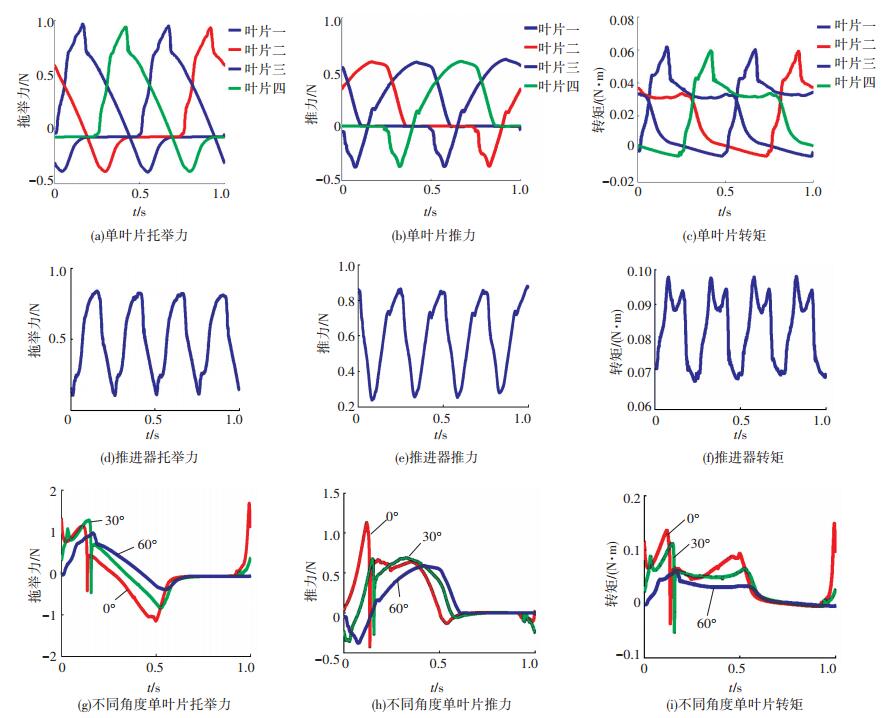
3.1 单叶片输出与驱动合成分析推进器从轮辐水平的位置开始转动,4个叶片依次入水,叶片的力学特性曲线按入水顺序如图 9(a)~9(c)所示,单叶片输出频率为1 Hz,与转速值相同.由图 9(a)~9(c)可看出:4个叶片的力学特性曲线变化相同,输出时间依次相差0.25 s,对应相位角差值为90°;由第一个叶片在转角α时的输出F1(α),可得推进器总驱动输出
|
图 9 力学特性曲线 Figure 9 Mechanical properties curves |
| $ \begin{array}{l} F = {F_1}\left( \alpha \right) + {F_1}\left( {\alpha + 90^\circ } \right) + {F_1}\left( {\alpha + 180^\circ } \right) + \\ \;\;\;\;\;\;{F_1}\left( {\alpha + 270^\circ } \right). \end{array} $ | (13) |
推进器合成输出如图 9(d)~9(f)所示,可看出:周期性的叶片平板旋转绕流,产生了周期性的叶片输出,合成了周期性的推进器三维驱动输出,频率为4 Hz.
进一步研究叶片的固液作用,由图 9(a)~9(c)蓝线可看出,叶片一入水后首先在0.17 s产生了托举力峰值0.96 N,如脚掌下踏阶段;然后在0.42 s产生了推力峰值0.59 N,伴随着托举力降低,如脚掌后划阶段;转矩与托举力的峰值时间相同,均对应叶片拍击液面完全入水时刻;转矩先增大至完全入水时0.062 N·m后减小表明,叶片入水作用强度大且出水作用强度小,与蛇怪蜥蜴脚掌的出入水强度变化模式相同.
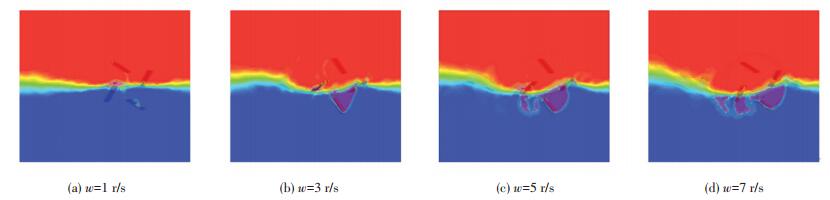
在转速增大后,叶片出水时的气穴空间逐渐增加,在1 m/s航速下的气穴变化如图 10所示,叶片在气穴中出水,与图 6中叶片拍击试验的流场相对应;叶片入水时固液作用充分,出水时在气穴中减阻,实现了对力学输出模式和气穴空间形式的双重仿生.
|
图 10 1 m/s航速时不同转速下的两相分布 Figure 10 Two-phase distribution at different speeds at 1 m/s speed |
同时,叶片角度设定影响着驱动输出,单叶片θ取0°、30°和60°时的力学特性曲线,如图 9(g)~9(i)所示.由图 9(g)~9(i)可看出:θ取0°时托举力、推力和转矩峰值来得最早;出水时托举力为数值较大的负值阻力,经30°过渡后,取60°时三维驱动的入水强度得到了明显的缓冲,托举力振幅减小了52%,均值由-0.02 N增加至0.12 N;减小了出水阻力,如图 9(g)~9(i)中出水时刻的转矩所示.
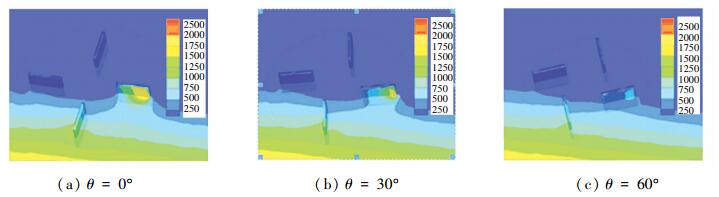
叶片角度引起的入水作用强度变化可由托举力峰值时叶片拍击水面的三维压力反映出,由0°夹角时的大部分1 250 Pa减小至60°夹角时的大部分500 Pa,如图 11所示. θ取60°时叶片三维驱动的均衡输出验证了角度设置的合理性.
|
图 11 不同夹角时的叶片压力图 Figure 11 Blade pressure at different angles |
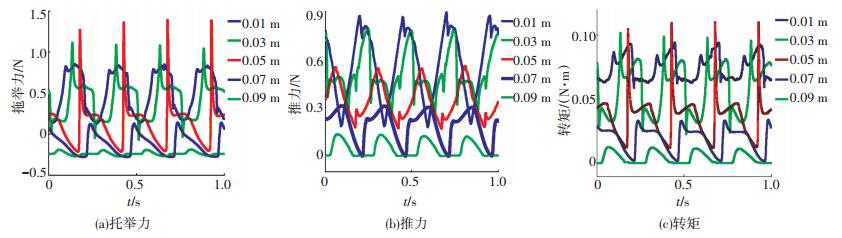
轮轴距水面的高度既是推进器的主要控制参量,同时面临着波浪起伏等被动变化.不同轮轴高度下的推进器力学特性曲线如图 12所示.由图 12可看出:随着轮轴在水面上提升,驱动输出的波峰时间推后;托举力和转矩的振幅先增大后减小,在0.05 m时取得极大值1.57 N和0.092 N·m,在0.09 m时取得极小值0.08 N和0.013 N·m;推力振幅由0.68 N至0.13 N单调递减.
|
图 12 不同高度下的力学特性曲线 Figure 12 Mechanical properties curves at different heights |
进一步分析振幅变化可得,托举力和转矩振幅与入水时刻作用脉冲大小的变化趋势相同.这是因为随轮轴高度从0.01 m增加,叶片入水逐渐趋近于平行拍击液面,无缓冲,在0.05 m时入水作用脉冲达到最大,进一步增加后,叶片前侧先入水,缓冲增加,作用脉冲和振幅减小,如图 13所示.同时,推力振幅和水平后划的行程相关,随轮轴高度从0.01 m增加,后划行程逐渐减少而强度减弱,致使振幅单调递减.

|
图 13 不同高度下的两相分布图 Figure 13 Water volume contour at different heights |
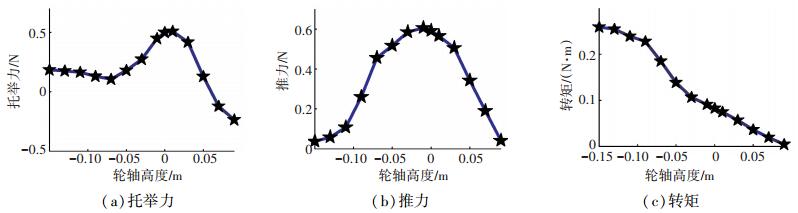
提取1 s时间内驱动输出的平均值为特征值,进行力学性能分析,轮轴高度由-0.15 m(浸没水下)至0.09 m(即将移出水面)变化,力学性能如图 14所示.由图 14可看出,推力在h=-0.01 m时取得最大值0.61 N,托举力在h=0.01 m时取得最大值0.51 N;转矩由0.259 N·m至0.004 N·m单调递减.
|
图 14 力学性能随轮轴高度的变化图 Figure 14 Driving properties changing with axle height |
其中,推力和转矩变化是因为在h=0附近,产生推力的后划行程最大,随着轮轴降低致使前划行程增加而产生了阻力,随着轮轴升高则减少了后划行程而减小了推力,如图 13所示;浸没水中时叶片与水流的作用面积最大,阻力矩随面积增大而增大,所以转矩最大.
3.3 航速与转速的协同变化转速是平台任意航速下进行加减速控制最直接的参量,转速与航速相互联系又相对独立,因此视为协同变化.
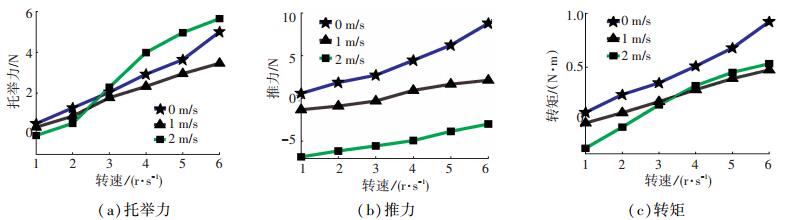
航速恒定条件下,得到了0 m/s,1 m/s和2 m/s航速时转速由1 r/s至6 r/s变化的力学性能曲线,如图 15所示.由图 15可看出,同航速下,三维驱动输出随着转速的提高而增加,其中在1 m/s时,托举力、推力和转矩分别由1 r/s时的0.322 N、-1.30 N和-0.015 N·m增加至6 r/s时的3.26 N、2.14 N和0.476 N·m.
|
图 15 3种航速下不同转速的力学性能曲线 Figure 15 Mechanical properties changing with rotation velocity at constant navigation velocity |
转速恒定条件下,取w=2 r/s,航速由0 m/s至2 m/s变化的力学特性曲线如图 16所示.由图 16可看出,推进器三维输出具有较好的周期性,频率为8 Hz;推力和转矩随航速的增大而减小,曲线起伏明显,由0 m/s时均值1.81 N和0.244 N·m减小至2 m/s时-5.95 N和-0.040 N·m;托举力由0 m/s时均值1.28 N振荡至2 m/s时0.50 N,变化相对较小.

|
图 16 不同航速下的力学特性曲线 Figure 16 Mechanical properties curves at different navigation velocities |
为获取航速和转速的协同变化影响,进一步由0 m/s,0.5 m/s,1 m/s,1.5 m/s和2 m/s航速下转速由1 r/s至6 r/s变化的力学性能绘制三维图,如图 17所示.

|
图 17 力学性能随航速和转速三维变化图 Figure 17 Driving properties changing with navigation velocity and rotation velocity |
由图 17可看出,推力随航速增加而减小,随转速增加而增大,这是因为叶片击水的相对水平速度随航速增加而减小,减弱了水平作用强度;而作用频率随转速增加而增加.托举力随转速增加而增大,低转速下随航速增加变化不大,高转速下有来流时随航速增加而增大,这是因为竖直方向的相对速度起伏较小,低转速时作用模式变化较小,高转速时前侧叶片入水拍击区域的水流减少,如图 10所示,高航速前行则增强了水流的补充能力,增加了竖直方向作用强度;而作用频率随转速增加而增加.转矩整体上随航速增加而减小,随转速增加而增加,这是因为推力较托举力变化趋势明显且幅值大,转矩与推力变化趋势相近.
4 试验为了验证数值计算的正确性,搭建了推进器静水试验系统.试验系统由导轨、推进器、水平力传感器、滑块、传动系统和竖直力传感器组成,如图 18所示,结构参数同数值计算模型.

|
1—导轨;2—推进器;3—水平力传感器;4—滑块;5—传动系统;6—竖直力传感器 图 18 矢量推进器试验系统 Figure 18 Test system of vector propeller |
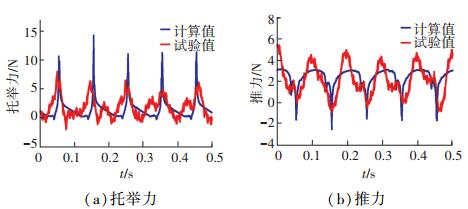
测得2.5 r/s转速下的托举力和推力曲线,与数值计算结果对比如图 19所示.由图 19可看出:计算曲线与试验曲线起伏变化趋势相同,作用周期均为10 Hz.且托举力计算与试验的均值分别为2.41、2.13 N,相差13.2%;推力计算与试验的均值分别为1.60、1.95 N,相差17.9%,误差在合理的范围内.力学特性曲线未完全对应是由叶片的柔性变化以及电机带动推进器导致转动角速度随阻力起伏引起的.
|
图 19 力学特性对比图 Figure 19 Contrast of force characteristic |
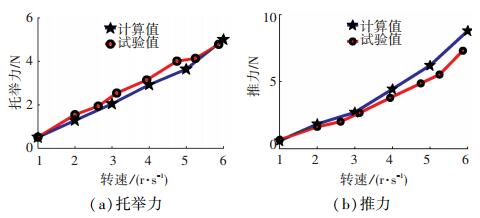
扩展测试不同转速下的托举力和推力性能如图 20所示,由图 20可看出:驱动力输出随转速增加而增加,数值计算值与试验值符合较好.
|
图 20 驱动力随转速变化的试验曲线 Figure 20 Test curves of driving properties changing with rotation velocity |
进一步得到转速变化对应的流场改变,如图 21所示.叶片与水流作用,后侧形成了负压气穴,由图 21可看出,随转速提高气穴空间增大,即相互作用强度增加,与图 10中数值计算结果相对应.

|
图 21 随转速变化的流场试验图 Figure 21 Test flow fluid changing with rotation velocity |
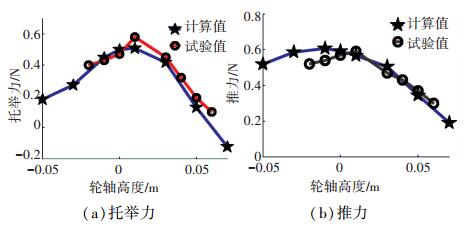
进行轮轴高度试验,受水池高度限制,同时大轮轴高度(小浸水深度)时阻力小电机转速高难以精确控制,测得部分高度的力学性能如图 22所示,可看出,托举力和推力均先增加后减小,试验曲线与数值计算曲线的变化规律一致,数值符合较好.
|
图 22 随高度变化力学性能的对比图 Figure 22 Test curves of driving properties changing with axle height |
同时获取了叶片流场,由图 23可看出,h=0.03 m时叶片近轴侧先入水;h=0.04 m时叶片平行于水面入水;h=0.05 m和h=0.06 m时叶片远轴侧先入水且倾斜角度随轮轴高度增加而增大,即随轮轴高度增加,叶片由近轴侧先入水过渡为远轴侧先入水,缓冲先减小后增大,入水缓冲的角度变化与图 13中数值计算结果相对应.

|
图 23 随高度变化的试验流场图 Figure 23 Test flow changing with axle height |
1) 结合矢量推进器的仿生机理分析,模拟蛇怪蜥蜴脚掌的身体位置,设计了水面平台和两栖平台,通过样机试验实现了推进器气穴式踏水和平台前倾式滑水航行,简化了结构并为平台减阻提速提供了新思路.进一步基于平台航行动力学分析获取了输出的可控参量,并建立平板旋转绕流模型,结合单叶片输出分析,研究了可控参量对驱动性能的影响并进行了试验验证.
2) 由单叶片三维驱动可推导推进器的周期性输出函数;叶片入水作用强度大且气穴中出水作用强度小,实现了对脚掌运动的仿生;60°轮辐与叶片夹角相对于0°和30°缓冲了作用强度,且三维驱动均衡输出.
3) 轮轴从水面开始升高,托举力和转矩振幅先增大后减小,推力振幅单调递减;从浸没水下开始提高,在h=0.01 m时,托举力取得最大值,在h=-0.01 m时,推力取得最大值,在浸没水中时,转矩最大.
4) 推力随航速增加而减小,随转速增加而增大;转矩整体变化趋势与推力相同;托举力随转速增加而增大,高转速且有来流条件下随航速增加而增大.
| [1] |
勒栓宝, 沈洋, 王东, 等. 基于数值试验及实船试航的喷水推进器改型设计[J]. 船舶力学, 2015, 19(11): 1312. JIN Shuanbao, SHEN Yang, WANG Dong, et al. Remodel design of waterjet with CFD and its sea trial[J]. Journal of Ship Mechanics, 2015, 19(11): 1312. DOI:10.3969/j.issn.1007-7294.2015.11.003 |
| [2] |
FAGONE E L. Rinspeed splash[J]. Car Design, 2004, 9: 76. |
| [3] |
宋桂霞.水陆两栖车辆减阻增速关键问题研究[D].南京: 南京航空航天大学, 2008 SONG Guixia. Main question research on reducing resistance and increasing speed foramphibious vehicle[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2008 http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D076117 |
| [4] |
王立权, 王海龙, 陈曦, 等. 八足仿蟹机器人行走稳定性分析[J]. 中南大学学报(自然科学版), 2014, 45(10): 3416. WANG Liquan, WANG Hailong, CHEN Xi, et al. Walking stability analysis of an octopod crab-like robot[J]. Journal of Central South University (Science and Technology), 2014, 45(10): 3416. |
| [5] |
王立权, 孙磊, 陈东良, 等. 仿生机器蟹样机研究[J]. 哈尔滨工程大学学报, 2005, 26(5): 591. WANG Liquan, SUN Lei, CHEN Dongliang, et al. A bionic crab-like robot prototype[J]. Journal of Harbin Engineering University, 2005, 26(5): 591. DOI:10.3969/j.issn.1006-7043.2005.05.007 |
| [6] |
郁树梅, 马书根, 李斌, 等. 蛇形机器人步态产生及步态分析[J]. 机器人, 2011, 33(3): 371. YU Shumei, MA Shugen, LI Bin, et al. Gait generation and analysis for snake-like robots[J]. Robot, 2011, 33(3): 371. DOI:10.3724/SP.J.1218.2011.00371 |
| [7] |
郁树梅, 王明辉, 马书根, 等. 水陆两栖蛇形机器人的研制及其陆地和水下步态[J]. 机械工程学报, 2012, 48(9): 18. YU Shumei, WANG Minghui, MA Shugen, et al. Development of an amphibious snake-like robot and its gaits on ground and in water[J]. Journal of Mechanical Engineering, 2012, 48(9): 18. DOI:10.3901/JME.2012.09.018 |
| [8] |
WHITE E, MILLER T. A serendipitous application of supercavitation theory to the water-running Basilisk Lizard[J]. Journal of Fluids Engineering, 2010, 132(5): 1. DOI:10.1115/1.4001487 |
| [9] |
FLOYD S, SITTI M. Design and development of the lifting and propulsion mechanism for a biologically inspired water runner robot[J]. Transactions on Robotics, 2008, 24(3): 698. DOI:10.1109/TRO.2008.924258 |
| [10] |
PARK H S, FLOYD S, SITTI M. Dynamic modeling and analysis of pitch motion of a basilisk lizard inspired quadruped robot running on water[C]//IEEE International Conference on Robotics and Automation. Kobe: IEEE, 2009, 2655. DOI: 10.1109/ROBOT.2009.5152556
|
| [11] |
魏鲜明, 徐林森, 曹凯, 等. 足式水上行走机器人智能控制方法设计[J]. 机器人, 2014, 36(1): 49. WEI Xianming, XUN Linsen, CAO Kai, et al. Intelligent control method design of foot robot walking on water[J]. Robot, 2014, 36(1): 49. DOI:10.3724/SP.J.1218.2014.00049 |
| [12] |
张仲志, 宋彬, 高飞, 等. 蛇怪蜥蜴踏水奔跑机理研究及仿生机构设计[J]. 机器人, 2016, 38(6): 760. ZHANG Zhongzhi, SONG Bin, GAO Fei, et al. Mechanism study and bionic design of water running of basilisk lizard[J]. Robot, 2016, 38(6): 760. DOI:10.13973/j.cnki.robot.2016.0760 |
| [13] |
GLASHEEN J W, MCMAHON T A. A hydrodynamic model of locomotion in the basilisk lizard[J]. Nature, 1996, 380(6572): 340. DOI:10.1038/380340a0 |
| [14] |
GHASSABZADEH M, GHASSEMI H. Automatic generation of the planning tunnel high speed craft hull form[J]. Journal of Marine Science and Application, 2012, 11(4): 453. DOI:10.1007/s11804-012-1155-9 |
| [15] |
董祖舜. 快艇动力学[M]. 武汉: 华中理工大学出版社, 1991: 30. DONG Zushun. Speedboat dynamics[M]. Wuhan: Journal of Huazhong University of Science and Technology Press, 1991: 30. |
| [16] |
杨楚泉. 水陆两栖车辆原理与设计[M]. 北京: 国防工业出版社, 2003: 84. YANG Chuquan. Theory and design of amphibious vehicle[M]. Beijing: National Defense Industry Press, 2003: 84. |
 2018, Vol. 50
2018, Vol. 50


