2. 沈阳华晨汽车工程研究院, 沈阳 110141
2. Brilliance Automotive Engineering Research Institute, Shenyang 110141, China
电梯门机系统驱动装置多为感应电机, 与之相比, 永磁同步电动机(permanent magnet synchronous motor, PMSM)具有体积小、效率高、转矩大、低速性能好等优点, 因此永磁同步电梯门机系统备受青睐.
在开关门过程中, 电梯门机存在带厅门和不带厅门两种运行状态, 由于厅门很重且电机与执行机构直接相连, 导致在这两种状态下, 折算到电机轴上转动惯量存在很大差异.此外, 为保障安全而设立的厅门自闭装置始终提供关门方向的力, 也造成在开门和关门时转动惯量的差别.目前采用最多的PI控制不能根据系统参数变化实时调节控制器参数, 因此导致电梯门碰撞、运行缓慢、震颤等问题[1].若根据门刀位置、厅门重量等具体因素实时调节控制器参数, 工作繁琐复杂, 并且对于不同型号的门机, 厅门重量和门刀带门位置不同, 传统控制器适用性差.为解决该问题, 有学者提出基于电机数学模型辨识PMSM转动惯量方法[2-3], 但模型精度会影响辨识结果同时存在辨识实时性、精确性和算法复杂性等问题.
本文提出永磁同步电梯门机系统自抗扰控制(active disturbance rejection control, ADRC)[4]策略解决上述问题. ADRC将转动惯量变化带来的影响视为扰动, 实时估计扰动并做出补偿.该方法控制效果不受门宽、门重、门刀带门位置等因素影响, 对电梯门机系统具有普遍适用性.
非线性自抗扰控制器(nonlinear active disturbance rejection control, NLADRC)在参数整定及控制性能分析等方面存在一定困难.一些学者对参数优化整定进行了探索, 文献[5-7]采用粒子群算法优化参数, 文献[8]采用神经网络的动态参数整定, 文献[9]提出参数自学习算法.这些方法处理过程繁琐, 不利于工程实现.与之相比, 线性自抗扰控制器(linear active disturbance rejection control, LADRC)参数整定简单, 易于工程实现, 且扰动跟踪性能几乎不随扰动幅度发生变化[4], 可取得较好的控制效果[10-11].为避免NLADRC参数整定的繁杂工作, 本文针对永磁同步电机设计LADRC, 在保留其参数易于整定优点的同时改善控制性能;对自抗扰控制器的核心部分线性扩张状态观测器(linear extended state observer, LESO)进行改进, 设计并联型LESO, 提高跟踪性能, 改善控制效果, 且控制过程易于实现.
1 PMSM电梯门机ADRC控制策略本文对永磁同步电机采用直轴电流id*=0双闭环矢量控制方式, 传统PI控制速度环控制器参数与转动惯量成正比, 当系统转动惯量大范围变化时必须实时调整控制器参数.并且, 电流环参数选取与电机的电阻和电感有关, 实际中电机是有饱和效应的, 永磁电机的交直轴电感在电机运行过程中会发生变化, 电阻参数也会随电机运行时的温度变化而改变, 此时已经标定参数的电流环PI控制器不能取得很好的控制效果.为此, 本文提出PMSM门机ADRC控制方案, 自抗扰控制器的设计不依赖被控对象的精确模型和参数, 能够使系统控制性能不受转动惯量变化及参数变化的影响, 且控制过程中无需调节控制器参数.
在转速外环, 本文对转速采用一阶自抗扰控制器, 二阶LESO的输出没有微分项, 因此跟踪微分器也不需要微分输出, 在实际设计中省略该环节.自抗扰控制器由1个二阶LESO和1个一阶线性状态误差反馈组成;电流环采用与上述结构相同的两个二阶LADRC用于d轴和q轴电流的解耦控制, 永磁同步门机自抗扰控制系统如图 1所示.

|
图 1 永磁同步电机自抗扰控制框图 Figure 1 Block diagram of PMSM's ADRC system |
永磁同步电机机械运动方程为
| $ J\frac{{{\rm{d}}{\omega _{\rm{r}}}}}{{{\rm{d}}t}} = {T_{\rm{e}}} - {T_{\rm{L}}} - B{\omega _{\rm{r}}}. $ | (1) |
式中:J为系统转动惯量, kg·m2;ωr为转子机械角速度, rad/s;Te、TL分别为电磁转矩和负载转矩, N·m;B为阻尼系数, N·m·s/rad.
为设计自抗扰控制器, 将转速方程表达为
| $ {{\dot \omega }_{\rm{r}}} = \frac{{{K_{\rm{C}}}}}{J}i_q^* + \frac{{{T_d}}}{J} = bu + a\left( x \right). $ | (2) |
式中:Td=KC(iq-iq*)-TL-Bωr, u=iq*为输入信号, b=KC/J为控制增益, a(x)=Td/J为模型未知部分.
为设计LESO, 将式(2)转化为标准形式:
| $ \left\{ \begin{array}{l} {{\dot \omega }_{\rm{r}}} = f + {b_0}u, \\ y = {\omega _{\rm{r}}}. \end{array} \right. $ | (3) |
式中f=a(x)+(b-b0)u为转速环总扰动.对于系统(3), 本文采用二阶LESO:
| $ \left\{ \begin{array}{l} e = {z_1} - y, \\ {{\dot z}_1} = {z_2} - {\beta _1}({z_1} - y) + {b_0}u, \\ {{\dot z}_2} = - {\beta _2}({z_1} - y). \end{array} \right. $ | (4) |
式中:y为系统输出;z1为输出y的观测值;z2为扰动f的观测值;e为观测误差;β1、β2为二阶LESO的参数, 合理选择观测器增益β1、β2, 二阶LESO能够实时估计状态和扰动, 即
| $ \left\{ \begin{array}{l} {z_1} \to {\omega _{\rm{r}}}, \\ {z_2} \to f. \end{array} \right. $ |
设定一个新的输入u0, 令
| $ u = \frac{{{u_0} - {z_2}}}{{{b_0}}}, $ | (5) |
则系统等效为线性系统:
| $ {{\dot \omega }_{\rm{r}}} = {u_0}. $ | (6) |
对于系统(6), 由于扰动已经通过LESO被抵消, 不需要积分控制, 故采用简单的比例控制即可达到良好的控制效果, 转速控制器最终形式为
| $ i_q^* = \frac{{{u_0} - {z_2}}}{{{b_0}}} = \frac{{{k_{\rm{p}}}(\omega _{\rm{r}}^* - {\omega _{\rm{r}}}) - {z_2}}}{{{b_0}}}. $ | (7) |
根据文献[12]中的LESO参数配置方法, 选取适当的观测器带宽ωo配置以下参数为
| $ \left\{ \begin{array}{l} {\beta _1} = 2{\omega _o}, \\ {\beta _2} = \omega _o^2. \end{array} \right. $ | (8) |
根据式(6), 可以得到系统的闭环传递函数为
| $ {G_{\rm{c}}}\left( s \right) = \frac{{{k_{\rm{p}}}}}{{s + {k_{\rm{p}}}}}, $ | (9) |
类似地, 可选取适当的控制器带宽ωc配置比例参数
| $ {k_{\rm{p}}} = {\omega _{\rm{c}}}, $ | (10) |
自抗扰控制器如图 2所示.
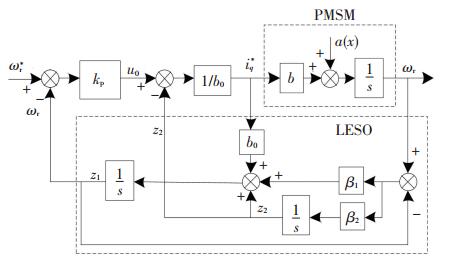
|
图 2 转速自抗扰控制器示意图 Figure 2 ADRC of speed loop |
虽然LESO简化了自抗扰控制器的参数配置过程, 但与NLESO相比观测效果仍然有待提高, 且在实际系统中其可实现带宽受限时, 会产生较大观测误差, 增加闭环控制器负担[13].在实际系统中, LESO的带宽往往不能设计成理想数值, 它受限于系统采样频率和传感器噪声等因素, 更高的带宽需求也意味着更高的硬件成本, 上述限制降低了LESO的观测性能, 本文提出并联型LESO结构解决上述问题, 在不提高系统成本不增加参数标定工作的前提下, 采用实际系统允许的观测带宽, 获得更优秀的扰动观测性能.并联LESO结构如图 3所示, 其中LESO1与LESO2均为二阶, 为不增加参数设计工作量, 本文中二者采用相同参数.
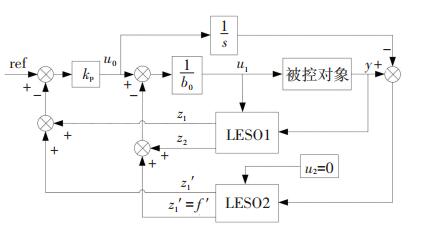
|
图 3 并联LESO结构示意图 Figure 3 Schematic diagram of parallel LESO structure |
当LESO1存在较大扰动观测误差时, 将总扰动f拆分成两部分, 即
| $ f = {z_2} + {f^\prime }, $ | (11) |
式中z2为LESO1对扰动f的观测值, f ′即为观测误差, 或称剩余扰动.当f ′较大时, 即便将z2在输入信号中补偿掉, 仍有剩余扰动对系统产生影响, 即此时扩张状态观测器存在较大误差, 观测效果及自抗扰控制器的控制性能并不理想.因此, 为了更加精确地补偿系统总扰动, 本文在LESO1的基础上并联另一个LESO2.对于系统(3)而言, 扰动补偿的目的是将原系统转化为一阶积分系统, 因此可以构造一个以u0为输入的一阶积分系统, 将此理想积分系统的输出量与实际系统输出做差, 所得即是剩余扰动对系统输出造成的影响, 根据LESO的设计原理, 可以构造如图 3所示的LESO2来观测f ′并将其抵消.
对LESO和并联LESO的观测能力进行仿真比较, 比较包括两部分:1)被控量对给定信号的跟踪效果对比;2)扩张状态观测器对系统总扰动的观测效果对比.仿真在按照图 4搭建的一阶系统上进行, 由于阶跃响应能够最直观地反映系统性能, 因此仿真时, 在系统扰动处和参考信号处分别施加幅值为1的方波信号和阶跃信号, 以便观察两种扩张状态观测器对扰动的跟踪效果及被控量对给定信号的跟踪效果, 设定观测器参数b0=5, 闭环增益系数kp=10, 传统型LESO和并联型LESO中的两个独立LESO均选取观测带宽ωo=10 Hz.
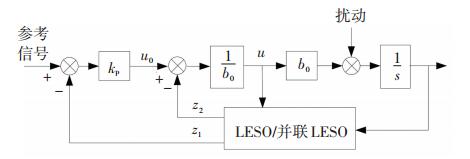
|
图 4 LESO与并联LESO观测效果仿真框图 Figure 4 Simulink block diagram of observation effect of LESO and parallel LESO |
被控量跟踪效果和扰动观测效果对比如图 5所示.可以看出, 在采用相同观测带宽时, 并联型LESO能够更加快速准确跟踪扰动, 提高观测能力, 系统受扰动的影响也更小.

|
图 5 LESO与并联LESO观测效果对比图 Figure 5 Comparison diagram of observation effect between LESO and parallel LESO |
仿真通过与PI控制对比的方法验证LADRC控制系统的调节性能及抗扰动性能, 采用实际永磁同步电机参数:额定功率为0.085 kW, 额定频率为50 Hz, 额定转矩为3 N·m, 额定转速为115 r/min, 额定电压为220 V, 额定电流为0.45 A, 定子电阻为50 Ω, d、q轴电感为0.032 H, 永磁体磁链为0.7 Wb, 极对数为5. PI控制系统电流环框图如图 6所示, 其中Rs为定子电阻, Ld为d轴电感.

|
图 6 q轴电流环框图 Figure 6 q-axis current loop diagram |
期望电流环响应时间为ts=5 ms, 时间常数T0=5/3 ms=1.67 ms, 计算得电流环PI参数为KCI=30 000, KCP=19.17.
取速度环的调节时间为tss=20ts=0.1 s, 计算得转速环PI参数为
并联型LESO中的两个LESO均与单LESO选用相同的带宽参数.取控制带宽ωc=50 Hz, 根据式(10), 得到kpr=50, 观测带宽通常为控制带宽的3~5倍, 本文取观测带宽ωo=3ωc=150 Hz, 根据式(8)的带宽法, 得到β1r=300, β2r=22 500, 取b0r=200, 比例控制器输出限幅设为±0.5.
电流环要求响应更快, 选取控制带宽ωc=100 Hz, ωo=3ωc=300 Hz, 同理可得到电流环ADRC参数为kpi=100, β1i=600, β2i=90 000, 取b0i=100.
2.1 阶跃响应效果验证电机转速给定幅值为100 r/min的阶跃信号, 在0.5 s时系统转动惯量由0.001 kg·m2阶跃至0.05 kg·m2, 系统突加负载1 N·m, 图 7是PI控制和本文设计的改进型LADRC控制的效果对比图.
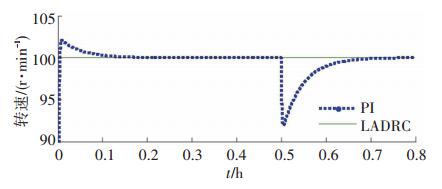
|
图 7 PI控制和LADRC控制的阶跃响应对比 Figure 7 Comparison of step response between PI control and LADRC control |
可以看出, 与PI控制相比, LADRC能消除转速在调节过程中的震荡, 实现快速无超调跟踪, 减小调节时间, 并且使之非常快速地进入稳态, 调节效果明显优于PI控制.当系统转动惯量变化和突加负载时, PI控制的转速发生波动, 而采用本文设计的控制器时转速未受到影响, 这说明了本控制器的抗扰性能.
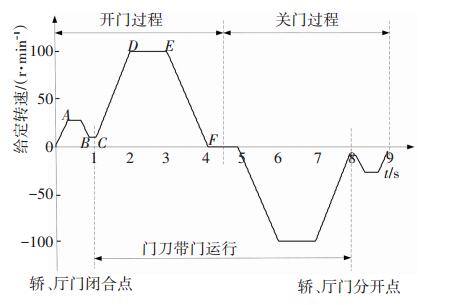
2.2 门机曲线响应效果验证电梯开关门给定转速曲线如图 8所示.开门过程中默认电机正转, AC为门刀单独动作阶段, 轿门和厅门静止不动, 门刀经过加速、匀速、减速和一小段低速运行后夹紧厅门滚轮, 带动厅门运行, 厅门和轿门同步打开;CD为厅门和轿门同步加速阶段, 达到一定速度后进入匀速运行阶段DE, EF为减速阶段, 直至开门到位.关门过程与开门过程基本相反, 不再详述.
|
图 8 永磁同步门机转速给定曲线 Figure 8 Given speed curve of PMSM |
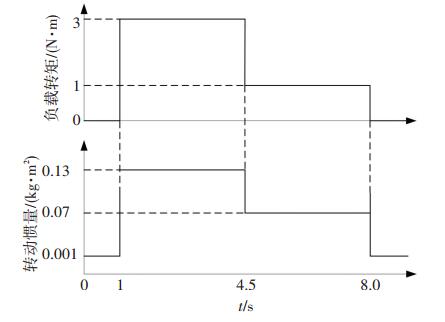
电梯门开时间和关门时间均为4.5 s, 假设厅门相当于2 N·m负载, 厅门自闭装置(重锤)相当于1 N·m负载, 开门运行至1 s时门刀带住厅门, 转动惯量增大, 至4.5 s时开门结束;之后门机开始反向转动执行关门动作, 关门运行至8 s时门刀与厅门脱离, 转动惯量减小, 直至关门结束.
由于厅门自闭装置提供关门方向的力, 因此关门过程与开门过程相比转动惯量较小, 带载也较小, 其变化如图 9所示.
|
图 9 转动惯量及负载变化曲线 Figure 9 Curve of movement of inertia and load |
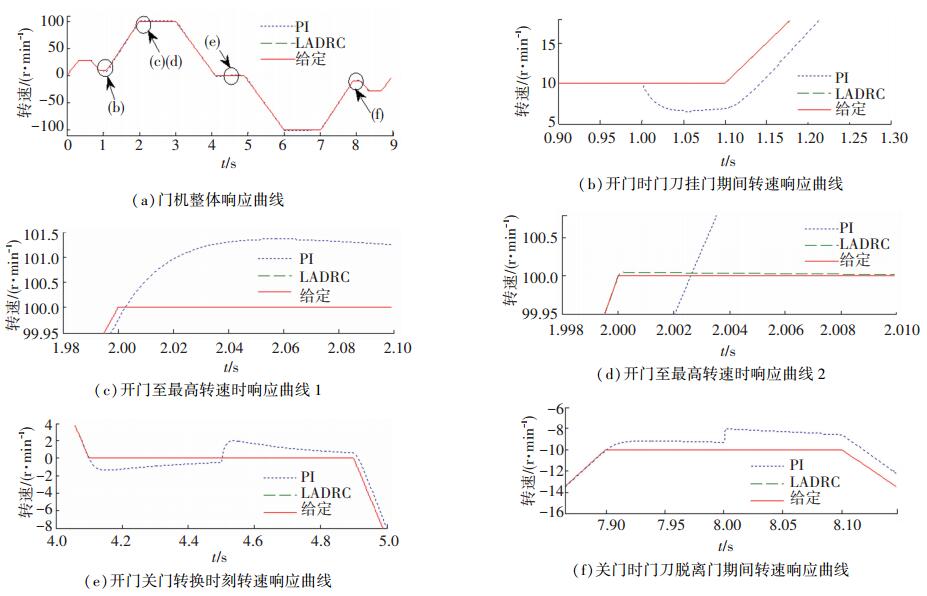
PI控制效果和本文提出的改进型LADRC控制效果对比如图 10所示. 图 10(a)是门机系统整体转速响应曲线, 图 10(b)~10(f)分别是对不同时刻响应效果的放大显示.从图 10(b)可以看出, 采用PI控制时, 系统在1 s处转动惯量增大导致转速大幅跌落, 速度跟踪产生延迟, 效果变差, 这也是实际中电梯出现开门动作缓慢的原因;在图 10(c)中2 s处电梯开门加速到最高速度时, 转速产生了超调, 这是因为转动惯量的大范围变化导致原来的PI参数已经不能快速跟踪给定信号, 图 10(d)是对该情况的细节放大图;从图 10(e)看到, 由于门厅自闭装置导致的开、关门时带载情况和转动惯量的差别, 在开门过程与关门过程的过渡点(4.5 s时), 转速产生了反向突变, 在关门过程的最初电机出现较小的正向转速, 导致电梯门仍然向开门方向运行, 解释了现实中电梯门在开、关门交替时的抖震现象;在图 10(f)中8 s时门刀脱离厅门, 转动惯量变小, 转速同样产生了突变.以上现象在采用LADRC控制时均未发生, 转速仍能准确地跟踪给定信号, 在图 10(b)、10(c)、10(e)、10(f)中, LADRC系统输出曲线与给定曲线重合, 在效果放大的图 10(d)中可以看到LADRC系统的输出量与给定量的微小差别.
|
图 10 PI控制和LADRC控制的门机曲线响应对比 Figure 10 Speed response comparison of PIand LADRC |
图 11展示了采用改进型LADRC控制与PI控制的电流环响应效果对比, 图 11(a)和图 11(b)分别为开门时和关门时q轴电流响应效果, 图 11(c)~11(e)为细节展示图.从图 11可以看出, 与PI控制相比, 采用LADRC时, q轴电流给定值能够更加快速且无超调地变化, 这是由于转速外环采用了自抗扰控制, 能够更迅速平稳地获得实现当前控制目的的控制量.此外, 从图 11(c)~11(e)可以看出, 采用LADRC控制的电流环能够比PI控制更加快速准确地跟踪电流给定值, q轴电流响应值与给定值几乎重合.以上结果证实了本文设计的控制器优良的调节性能和抗扰动能力.

|
图 11 PI控制和LADRC控制时q轴电流响应对比 Figure 11 q-axis current response comparison of PI control and LADRC control |
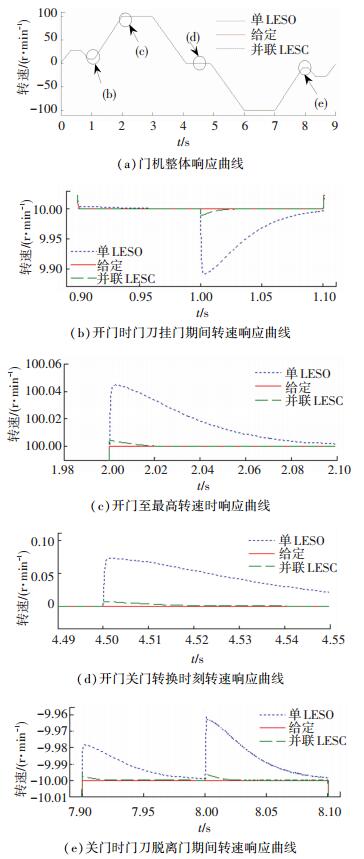
采用传统单LESO与并联型LESO的自抗扰控制效果对比如图 12所示. 图 13(a)是门机系统整体转速响应曲线, 图 12(b)~12(e)分别是对不同时刻响应效果的放大显示.从图 12(b)看出, 在1 s时电梯开门门刀挂门瞬间采用单LESO的自抗扰控制系统中转速跌落更严重;从图 12(c)中可以看出, 当电机达到最高转速时, 采用单LESO时转速出现更大超调, 经过更长时间准确跟踪到给定值;从图 12(d)中可以看出, 在4.5 s时系统由开门阶段切换为关门阶段, 在这个临界处采用单LESO时电机转速出现一个更大的波动;图 12(e)中可以看出, 在8 s时, 电梯关门门刀脱离门的瞬间, 采用单LESO的自抗扰控制系统中转速产生更大的突变.以上结果均证实, 在观测器带宽选取相同的数值时, 并联型LESO能够比传统的单LESO获得更好的观测效果, 实现LADRC更高的控制性能.
|
图 12 LADRC采用单LESO与并联LESO控制效果对比 Figure 12 Control effect comparison diagram of LADRC with single LESO and parallel LESO |
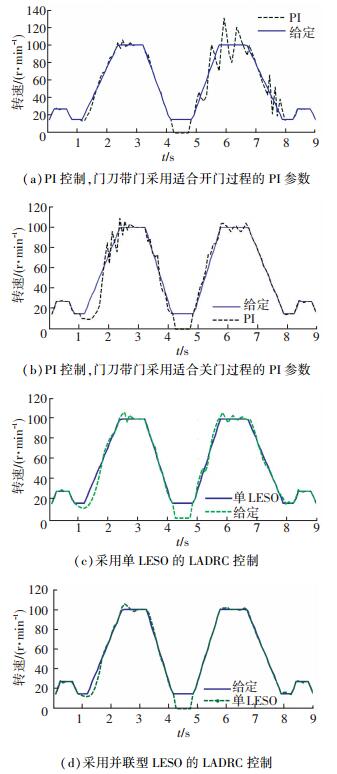
|
图 13 PI控制和LADRC控制的门机转速实验效果对比图 Figure 13 Comparison of experimental effect of PI control and LADRC control on door machine speed |
目前在实际电梯门机控制系统中采用的PI控制器需要人为地根据经验设定两组PI参数, 一组PI参数对应于门刀不带电梯门运行的情况, 此时系统转动惯量较小, 所需控制器参数较小, 下文简称该组参数为小PI参数, 另一组PI参数对应于门刀带动电梯门运行的情况, 此时所需PI参数较大, 简称为大PI参数.然而, 上述方法并未考虑实际门机系统中的厅门自闭装置, 从安全角度出发, 厅门自闭装置始终提供关门方向的力, 且其力度与电梯门重有关, 当门重较大时, 厅门自闭装置提供的关门力也较大, 这将导致开门和关门时门机系统的转动惯量和负载相差甚大, 因此不能兼顾开门和关门的控制效果.本文针对以下4种控制系统进行实验.
1) PI控制系统, 门刀不带门运行时采用小PI参数(kp=0.08, ki=1.2), 门刀带门运行时采用适合于开门过程的PI参数(kp=9.28, ki=139.2).
2) PI控制系统, 门刀不带门运行时采用小PI参数(kp=0.08, ki=1.2), 门刀带门运行时采用适合于关门过程的PI参数(kp=2.656, ki=39.84).
3) 采用单LESO的自抗扰控制系统(kpr=50, kpi=100, β1r=300, β2r=22 500, b0r=200, β1i=600, β2i=90 000, b0i=100).
4) 本文设计的并联型LESO自抗扰控制系统, 其中并联型LESO中的两个LESO均与单LESO选用相同的带宽参数(kpr=50, kpi=100, β1r=300, β2r=22 500, b0r=200, β1i=600, β2i=90 000, b0i=100).
实验中, 为方便观察控制效果在采集电机转速后均将其处理成正信号, 且在开、关门交替过程中给定一个不为0的较低转速值, 提供开门或关门力矩, 防止关门(开门)信号到来之前电梯门出现抖动或闭合(打开)的情况. 图14为4种情况的转速响应效果图, 图中实线为给定曲线, 虚线为跟踪曲线.
从图 13(a)可以看出, 当门刀带门运行时采用适合于开门过程的PI参数, 开门过程的转速跟踪效果可以接受, 但关门时, 厅门自闭装置提供的力导致电机轴上的转动惯量和所带负载都大幅度减小, 此时该组PI参数过大, 导致电机转速出现振荡, 实际的电梯门也产生抖震现象;从图 13(b)看出, 当采用适合关门过程的PI参数时, 此组控制参数对开门过程而言过小, 控制器不能及时输出所需控制量, 控制效果滞后, 导致转速与给定曲线相比出现跌落, 经过一段时间后跟上给定曲线, 但由于跟踪效果滞后, 转速又经过几次震荡后才较好地跟踪给定速度, 实际电梯门开门出现反应迟缓的现象, 关门过程控制效果可以接受;图 13(c)、13(d)分别反映了采用单LESO和并联型LESO的自抗扰控制效果, 可以看出采用自抗扰控制时, 不论门刀是否带动厅门一起运行, 无论开门或关门过程中, 转速都能比PI控制更好地跟踪给定曲线;LADRC采用传统的单LESO与采用并联型LESO相比, 门刀带门瞬间转速掉落较大, 关门过程中转速抖动也较大, 采用并联型LESO能更加快速准确地跟踪速度曲线.可见本文提出的方法达到了改进门机控制效果的目的, 大大减小了以往投入到控制器参数设计环节的工作量, 解决了LESO在实际应用中带宽受限的问题.
4 结论1) 提出了永磁同步门机线性自抗扰控制策略.实时检测转动惯量大范围变化引起的扰动并进行补偿, 实现转速快速准确跟踪给定值, 有效避免手动标定控制器参数的繁琐过程, 抗扰性能强且具有更优秀的调节性能.
2) 设计并联型LESO改进对扰动的观测效果.能够在实际带宽受限条件下获得比传统单LESO更加优良的观测性能, 进而降低控制系统应用成本, 更具有实际应用价值.
3) 该控制策略对不同型号电梯门具有普遍适用性, 有助于提高行业竞争力.
| [1] |
王莉娜, 朱鸿悦, 杨宗军. 永磁同步电动机调速系统PI控制器参数整定方法[J]. 电工技术学报, 2014, 29(5): 104. WANG Lina, ZHU Hongyue, YANG Zongjun. Tuning method for PI controllers of PMSM driving system[J]. Transactions of China Electrotechnical Society, 2014, 29(5): 104. DOI:10.3969/j.issn.1000-6753.2014.05.014 |
| [2] |
NIU L, XU D G, YANG M, et al. On-line inertia identification algorithm for PI parameters optimization in speed loop[J]. IEEE Transactions on Power Electronics, 2015, 30(2): 849. DOI:10.1109/TPEL.2014.2307061 |
| [3] |
徐东, 王田苗, 魏洪兴. 一种基于简化模型的永磁同步电机转动惯量辨识和误差补偿[J]. 电工技术学报, 2013, 28(2): 126. XU Dong, WANG Tianmiao, WEI Hongxing. A simplified model based inertia identification algorithm with error compensation of permanent magnet synchronous motors[J]. Transactions of China Electrotechnical Society, 2013, 28(2): 126. DOI:10.3969/j.issn.1000-6753.2013.02.017 |
| [4] |
高志强. 自抗扰控制思想探究[J]. 控制理论与应用, 2013, 30(12): 1498. GAO Zhiqiang. On the foundation of active disturbance rejection control[J]. Control Theory & Applications, 2013, 30(12): 1498. |
| [5] |
TANG Hui, LI Yangmin. Design, analysis, and test of a novel 2-DOF nanopositioning system driven by dual mode[J]. IEEE Transactions on Robotics, 2013, 29(3): 650. DOI:10.1109/TRO.2013.2248536 |
| [6] |
刘福才, 贾亚飞, 任丽娜. 基于混沌粒子群优化算法的异结构混沌反同步自抗扰控制[J]. 物理学报, 2013, 62(12): 120509. LIU Fucai, JIA Yafei, REN Lina. Anti-synchronizing different chaotic systems using active disturbance rejection controller based on the chaos particle swarm optimization algorithm[J]. Acta Physica Sinica, 2013, 62(12): 120509. DOI:10.7498/aps.62.120509 |
| [7] |
ZHANG Dongyang, YAO Xiaolan, WU Qinghe. Parameter tuning of modified active disturbance rejection control based on the particle swarm optimization algorithm for high-order system[C]//2016 IEEE International Conference on Aircraft Utility Systems (AUS). Beijing: IEEE, 2016: 290
|
| [8] |
武雷, 保宏, 杜敬利, 等. 一种自抗扰控制器参数的学习算法[J]. 自动化学报, 2014, 40(3): 556. WU Lei, BAO Hong, DU Jingli, et al. A learning algorithm for parameters of automatic disturbances rejection controller[J]. Acta Automatica Sinica, 2014, 40(3): 556. |
| [9] |
WANG Lu, SU Jianbo. Trajectory tracking of vertical take-off and landing unmanned aerial vehicles based on disturbance rejection control[J]. IEEE/CAA Journal of Automatica Sinica, 2015, 2(1): 65. DOI:10.1109/JAS.2015.7032907 |
| [10] |
TAN W, FU C. Linear active disturbance-rejection control: analysis and tuning via IMC[J]. IEEE Transactions on Industrial Electronics, 2016, 63(4): 2350. |
| [11] |
LI Jie, XIA Yuanqing, QI Xiaohui, et al. On the necessity, scheme and basis of the linear-nonlinear switching in active disturbance rejection control[J]. IEEE Trans on Industrial Electronics, 2016, 99: 1. |
| [12] |
GAO Z. Scaling and bandwidth-parameterization based controller tuning [C]//Proceedings of the American control conference.Denver: IEEE, 2003: 4989
|
| [13] |
李杰, 齐晓慧, 夏元清, 等. 线性/非线性自抗扰切换控制方法研究[J]. 自动化学报, 2016, 42(2): 202. LI Jie, QI Xiaohui, XIA Yuanqing, et al. On linear/nonlinear active disturbance rejection switching control[J]. Acta Automatica Sinica, 2016, 42(2): 202. |
 2018, Vol. 50
2018, Vol. 50


