航空发动机性能诊断技术是能够根据实测气路参数对发动机部件性能衰退进行在线评估的一项关键性发动机健康管理技术.国内外的航发性能诊断研究多集中于性能建模和噪声抑制两大问题, 性能建模方面的研究包含线性模型、非线性模型[1]和人工智能建模方法[2-5];采用卡尔曼滤波、人工免疫理论[6]、人工神经网络[7]以及传统可靠性分析方法[8], 研究消除数据噪声和粗大误差, 并在发动机数字仿真平台上取得了良好的实验效果.然而, 在民航发动机的商业运营过程中, 能在线获取的参数数量远不如数字仿真平台, 且发动机多变的工作环境会带来更为严重的数据噪声及粗大误差.因此, 实际应用场合中, 性能诊断技术需要算法具有更强的抗噪声能力, 还需要防止低可观测性问题所导致的诊断结果失真.
针对系统非线性问题, 本文采用机器学习的方法, 利用健康发动机的工作状态参数来建立标准发动机的稳态工作模型;在对商用发动机通用传感器布置方案和部件衰退特性进行分析的基础上, 定义具有代表性的发动机部件性能衰退因子;针对低可观性和数据噪声明显的问题, 利用所获得的发动机稳态模型和滑动窗口采样策略对无迹卡尔曼滤波器(unscented Kalman filter, UKF)进行定制化改造, 使之能够适用于发动机部件性能衰退的在线诊断.
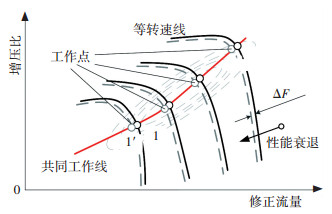
1 部件性能衰退特性分析典型的大涵道比双转子民航发动机可分解为推力风扇(FAN)、低压压气机(LPC)、高压压气机(HPC)、燃烧室(CC)、高压涡轮(HPT)和低压涡轮(LPT)6个部件, 各部件的性能特性可以用一组通用特性曲线来表征. 图 1给出了压气机部件通用特性曲线衰退指征示意图, 当压气机部件出现性能衰退时, 其相似流量、压缩比和效率特性曲线会出现等高线下降、曲线漂移等较为复杂的指征形式.为了量化部件的衰退程度, 需要对这些指征进行化简, 使之具有单一的数值形式.
|
图 1 压气机通用特性曲线衰退指征示意图 Figure 1 Compressor general characteristic curves indicating degradation status |
衰退因子法是一种被广泛采用的特性曲线漂移简化方法.其假设性能指标的衰减量相对于其初始数值在整个工作空间中具有等比例关系.一般情况下, 衰退因子ΔF表示方法如下:
| $ \Delta F = \left( {{F_{\text{d}}}-{F_{\text{s}}}} \right)/{F_{\text{s}}} \times 100\% . $ |
式中:Fs表示部件处于初始状态时的性能指标, Fd表示该部件衰退后的在同工况下的性能指标.
发动机所有部件的性能指标所对应的衰退因子总数为17个, 远超测量参数所能支持求解的上限.为了遴选具有代表性的衰退因子, 分析各部件衰退特征如下:发动机外涵道截面宽广, 多数型号的发动机不测量风扇后总压、总温, 仅有少数型号测量该处静压以指示风扇是否失速, 因此, 风扇的功率、流量衰退因子需要结合飞机飞行数据进行估计;LPC的流量主要取决于HPC的节流特性, 因而采用效率衰退因子更能有效表征其性能衰退程度;HPC的流量特性是整个内涵道的瓶颈, 其工作效率也对发动机的整体效能具有明显的影响, 因此需要对其流量和效率衰退因子进行同时评估;燃烧室的性能较为稳定, 且其压力恢复系数和燃烧完全系数受局部结构损伤影响较小, 其衰退因子评估可以省略;HPT的工作点仅在极窄的范围内变动, 因而效率衰退因子足够表征其衰退程度;LPT的流量由HPC和HPT的节流特性共同决定, 而落压比和效率则由其进口总压、喷口处大气静压与燃气流量三者共同决定, 因而选取其效率衰退因子作为衰退表征量更能反映其自身的衰退情况.综上得知, 需要进行评估的部件衰退因子(单位为%)为FAN流量衰退因子ΔwFAN、LPC效率衰退因子ΔηLPC、HPC流量衰退因子ΔwHPC、HPC效率衰退因子ΔηHPC、HPT效率衰退因子ΔηHPT、LPT效率衰退因子ΔηLPT.
2 航空发动机稳态建模发动机在稳态工作过程中, 其状态参数及工况参数之间具有很强的耦合性.部件性能衰退因子与测量参数之间不具有显式关联, 因而难以直接求解.为此需要建立发动机稳态工作模型来模拟系统观测过程.考虑到线性模型具有较大舍入误差[9], 而人工智能模型具有不可解释性, 本文首先对各个部件单独进行非线性建模, 而后将多个部件局部模型组装为整机稳态仿真模型, 并利用健康发动机的工况数据和气路状态参数数据实现各部件模型的批次训练.
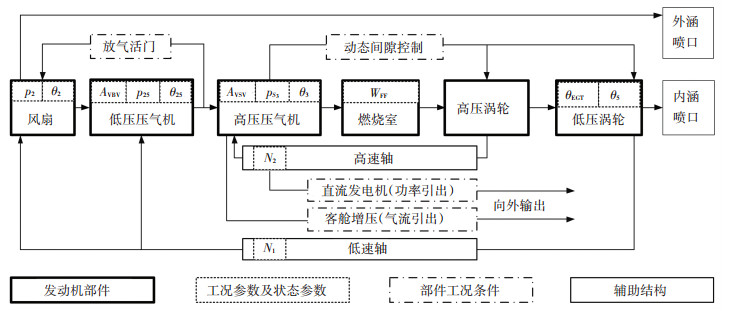
图 2给出了民航发动机的通用部件构成和状态参数测量位置的布置方案.图中参数分为工况参数和观测参数, 其中工况参数包含:进气道总温θ2、进气道总压p2、可调静子转叶开度AVSV、放气活门开度AVBV、风扇轴转速N1, 观测参数包括核心机进口总温θ25、核心机进口总压p25、燃烧室总温θ3、燃烧室静压ps3、燃油流量WFF、发动机排气温度θEGT、低压涡轮出口总温θ5、核心机转速N2.
|
图 2 民航发动机部件构成及状态参数测量位置框图 Figure 2 Scheme of commercial aero-engine components and measurement arrangements of their working conditions |
考虑到成本、安全和可维护性等因素, θ25、p25、θ5、ps3、θ3传感器在大多数机队发动机内并不实际安装.因此, 本文将借助少数发动机完备测量参数进行稳态建模, 仅依赖少量传感器数据(N2、WFF、θEGT)实现整个机队的性能诊断.
对未知部件的建模一般采用对已知部件通用特性曲线进行等比例放缩的方法[10].考虑到放缩法具有系统误差, 本文采用多元非线性函数来逼近目标部件的通用特性曲线[11]:
| $ \begin{gathered} \eta = {f_\eta }\left( {{N_{\text{c}}}, {p_{{\text{in}}}}, \gamma, \mu ;{\alpha _\eta }} \right), \hfill \\ w = {f_w}\left( {{N_{\text{c}}}, {p_{{\text{in}}}}, \gamma, \mu ;{\alpha _w}} \right), \hfill \\ \pi = {f_\pi }\left( {{N_{\text{c}}}, {p_{{\text{in}}}}, \gamma, \mu ;{\alpha _\pi }} \right). \hfill \\ \end{gathered} $ |
式中:f为多项式拟合函数, α为多项式系数, η为绝热效率, w为相似流量, π为压缩比, Nc为相似转速, pin为进口压力, 用以修正雷诺数效应的影响, γ为气体绝热系数, 用于修正变比热计算过程带来的误差, μ为部件外部控制量, 如AVSV、AVBV等.
将各部件模型组装为整机模型并采用机器学习方法进行参数训练, 损失函数为
| $ \begin{gathered} \hat g\left( {\varphi ;\alpha } \right) = \arg \mathop {\min }\limits_{\hat g\left( \alpha \right)} {L_{{\text{obj}}}} = \arg \mathop {\min }\limits_{\hat g\left( \alpha \right)} \frac{1}{N}\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^K {{w_j}\left\| {\Delta {b_j}\left( {{\varphi _i}} \right)} \right\|} } + \hfill \\ \;\;\;\;\;\;\;\;\;\frac{1}{N}\sum\limits_{i = 1}^N {\sum\limits_{n = 1}^C {{w_n}\left\| {{\zeta _n}\left( {{\varphi _i}} \right)} \right\|} } + \sum\limits_{j = 1}^K {R\left( {{\theta _j}} \right)}, {\varphi _i} \in \mathit{\boldsymbol{U}}, \hfill \\ \text{s.t.}\;\mathit{\boldsymbol{E}}\left( \mathit{\boldsymbol{U}} \right) = {\bf{0}}. \hfill \\ \end{gathered} $ |
式中:φi为第i条样本, U={φi}为所有样本的集合, N为样本数, Δb为仿真模型的预测误差, ζ为不同计算方法对效率、流量等不可测中间变量做出的预测结果之间的差值, w为各代数项的权重, R(·)为正则项, 用以防止模型过拟合, E为发动机各项稳态运行约束条件的集合.
3 气路部件衰退因子计算 3.1 基于UKF求解内涵道部件衰退因子获取发动机稳态模型后, 需要将其带入滤波过程以完成各部件衰退因子的评估.
发动机的实际工作状态不仅由其工作指令(N1)、大气压力(p2)、温度(θ2)所决定, 还受直流电机功率提取、客舱内增压分流、大气湿度、燃油热值、进气道结冰、传感器误差等因素带来的数据噪声的影响.线性卡尔曼滤波器和扩展卡尔曼滤波器由于依赖系统观测方程显式可导条件, 因此不能胜任降噪工作.而无迹卡尔曼滤波器(unscented Kalman filter, UKF)并不要求系统观测方程具有显式表达形式, 且对系统协方差和状态变量后验分布估计具有不低于三阶矩的精度, 因而被本文选作性能衰退因子的求解方法.
在滤波过程中, 发动机稳态模型的输出会同时受到各部件衰退因子和各项工况条件的影响.与此同时, 对比系统状态量和观测量的数目可以发现, 需要进行评估的部件衰退因子的数量(5个, ΔwFAN因风扇部件测量量过少而无法直接计算, 其相应估算方法将在3.2节给出)多于气路参数观测值(3个), 违背了系统可观测条件.如不针对这两项问题采取措施, 将造成滤波过程的发散.本文将针对这两类问题对UKF进行适当改造, 使之能够适用于发动机的性能诊断.
针对工况的影响问题, 本文将对UKF过程进行重新定义使之能够抵消工况影响.现定义发动机观测矢量φ、工况矢量β、观测矢量y和衰退状态矢量x分别为
| $ \begin{gathered} \mathit{\boldsymbol{\varphi }} = {\left[{{\mathit{\boldsymbol{\beta }}^{\text{T}}}, {\mathit{\boldsymbol{y}}^{\text{T}}}} \right]^{\text{T}}}, \mathit{\boldsymbol{\beta }} = {\left[{{P_2}, {N_1}, {\theta _2}, {A_{{\text{VSV}}}}, {A_{{\text{VBV}}}}} \right]^{\text{T}}}, \hfill \\ \mathit{\boldsymbol{y}} = {\left[{{\theta _{{\text{EGT}}}}, {N_2}, {W_{{\text{FF}}}}} \right]^{\text{T}}}, \hfill \\ \mathit{\boldsymbol{x}} = {\left[{\Delta {\eta _{{\text{LPC}}}}, \Delta {w_{{\text{HPC}}}}, \Delta {\eta _{{\text{HPC}}}}, \Delta {\eta _{{\text{HPT}}}}, \Delta {\eta _{{\text{LPT}}}}} \right]^{\text{T}}}. \hfill \\ \end{gathered} $ |
相应地, 发动机的衰退过程可以表示为
| $ \begin{gathered} {\mathit{\boldsymbol{x}}^{\left( t \right)}} = f\left( {{\mathit{\boldsymbol{x}}^{\left( {t-1} \right)}}} \right) + \mathit{\boldsymbol{v}}, \hfill \\ {\mathit{\boldsymbol{y}}^{\left( t \right)}} = g\left( {{\mathit{\boldsymbol{x}}^{\left( t \right)}}, {\mathit{\boldsymbol{\beta }}^{\left( t \right)}}} \right) + \mathit{\boldsymbol{\varepsilon }}. \hfill \\ \end{gathered} $ |
式中:x(t)、y(t)分别为t时刻的衰退状态矢量和观测矢量, g(·)为稳态模型, v和ε分别为系统状态误差和观测误差.与传统UKF不同的是, 系统观测方程同时受到β(t)和x(t)的双重影响.
针对系统的低可观性问题, 本文采用多点法[1]来加以解决:在一次滤波过程中引入多个最近的观测样本来实现观测矢量的扩充, 以此借助发动机自身的非线性使系统观测方程满秩;若假定x(t)与前τ-1个时刻近似相等(τ为一较小自然数), 若构建一个滑动采样窗口, 选取t~t-τ+1时刻的样本构造观测矢量, 则可使系统观测矢量维度增加到dim(y(t))×τ.不失一般性地, 令
| $ {\mathit{\boldsymbol{x}}^{\left( t \right)}} = f\left( {{\mathit{\boldsymbol{x}}^{\left( {t-1} \right)}}} \right) + \mathit{\boldsymbol{v}}, {\mathit{\boldsymbol{Y}}^{\left( t \right)}} = G\left( {\mathit{\boldsymbol{U}}, t, \tau } \right) + \mathit{\boldsymbol{\varepsilon }}. $ |
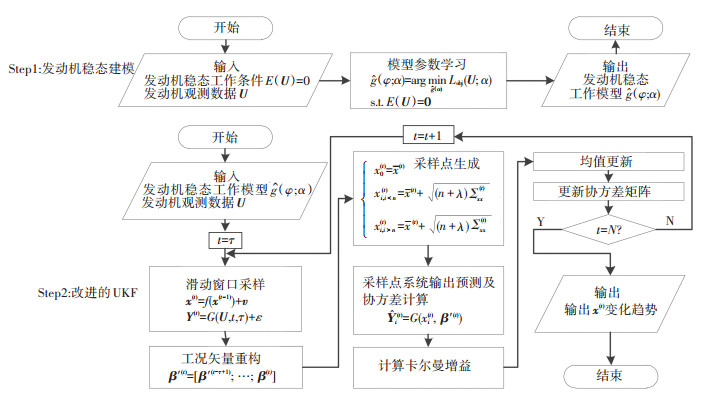
其中, Y(t)=[(g(x(t), β(t-τ+1))); …; (g(x(t), β(t)))]为3τ维的增广观测矢量, τ为采样窗口宽度.当τ较大时, 滤波对噪声的抵抗力更强;τ较小时, 滤波灵敏度更高.按系统可观测条件可以推得, 文中只要保证τ≥2即可保证滤波的收敛性和结果的唯一性.算法的总体流程如图 3所示.
|
图 3 发动机性能诊断方法总体流程 Figure 3 Overall flow chart of performance diagnosis of aero-engines |
如图 3所示, UKF通过Cholesky分解产生一组部件衰退因子的采样点集S(t)={xi(t)}, 以及对应的均值权值Wim和协方差权值Wic, 并令
| $ \begin{gathered} \mathit{\boldsymbol{x}}_0^{\left( t \right)} = {{\mathit{\boldsymbol{\bar x}}}^{\left( t \right)}}, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;W_i^{\text{m}} = \lambda /\left( {n + \lambda } \right), i = 0; \hfill \\ \mathit{\boldsymbol{x}}_i^{\left( t \right)} = {{\bar x}^{\left( t \right)}} + \sqrt {\left( {n + \lambda } \right)\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}{_{xx}^{\left( t \right)}} }, \;\;\;W_i^{\text{c}} = 1/2\left( {n + \lambda } \right), i = 1, \cdots, n; \hfill \\ \mathit{\boldsymbol{x}}_i^{\left( t \right)} = {{\bar x}^{\left( t \right)}}-\sqrt {\left( {n + \lambda } \right)\mathit{\boldsymbol{ \boldsymbol{\varSigma} }} {_{xx}^{\left( t \right)}} } ;\;\;\;W_i^{\text{c}} = 1/2\left( {n + \lambda } \right), i = n + 1, \cdots, 2n. \hfill \\ \end{gathered} $ |
式中:λ为采样点散布程度的控制量.在得到各采样点之后, 将其带入G(·)计算各自对应的输出Yi(t), 得到点集O(t)={Yi(t)}并估计系统观测量Y(t)和协方差矩阵ΣYY(t), 而后计算卡尔曼增益并对后验分布进行刷新.
为了防止滤波发散, 在计算时, 需要考虑到系统误差和观测误差造成的影响, 令
| $ \begin{gathered} {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{xx}}\left( {t + 1|t} \right) = \sum\nolimits_{i = 0}^{2n} {W_i^c\left( {\mathit{\boldsymbol{X}}_i^{\left( t \right)}- \mathit{\boldsymbol{\hat x}}\left( {t + 1|t} \right)} \right) \cdot } \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\left( {\mathit{\boldsymbol{X}}_i^{\left( t \right)}- \mathit{\boldsymbol{\hat x}}\left( {t + 1|t} \right)} \right)^{\text{T}}} + \mathit{\boldsymbol{ \boldsymbol{\varTheta} }}, \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{ \boldsymbol{\varTheta} }} = {\mathit{\boldsymbol{M}}_{{\text{diag}}}}\left( {\left[{\varepsilon _1^2, \cdots, \varepsilon _n^2} \right]} \right), \hfill \\ \end{gathered} $ |
| $ \begin{gathered} {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{YY}}\left( {t + 1|t} \right) = \sum\nolimits_{i = 0}^{2n} {W_i^{\text{c}}\left( {{\mathit{\boldsymbol{Y}}_i}\left( {t + 1|t} \right)- {{\mathit{\boldsymbol{\hat Y}}}_i}\left( {t + 1|t} \right)} \right) \cdot } \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\left( {{\mathit{\boldsymbol{Y}}_i}\left( {t + 1|t} \right)- {{\mathit{\boldsymbol{\hat Y}}}_i}\left( {t + 1|t} \right)} \right)^{\text{T}}} + \Delta, \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\Delta = {\mathit{\boldsymbol{M}}_{{\text{diag}}}}\left( {\left[{{\rho _1}, \cdots, {\rho _\tau }} \right]} \right). \hfill \\ \end{gathered} $ |
式中:Σxx(t+1|t)和ΣYY(t+1|t)分别为状态变量和观测变量的先验协方差矩阵, Θ、Δ分别为Σxx、ΣYY的修正值, Mdiag为对角矩阵, 考虑到发动机对各种随机因素的敏感度和传感器的测量精度, 建议取ε12=ε22…=εn2=1×10-4, ρ1=ρ2…=ρτ=[100, 0.04, 400]T.
3.2 风扇部件的性能诊断发动机风扇后测量量的不足使得其衰退因子难以准确评估.然而, 风扇外缘的性能衰退会对发动机的推力造成较为明显的影响, 因此可以借用飞机稳态巡航过程中的推力、阻力平衡条件评估其衰退因子.本文给出一种风扇的功率、流量衰退因子的粗略评估方法:当飞机稳定巡航时, 飞行阻力与巡航速度的平方成正比, 而在标准海平面状态下, 发动机的推进功率与风扇修正转速也具有一一对应的函数关系, 若忽略内涵道部件性能衰退所带来的推力下降, 可以认为发动机风扇外涵做功与飞机巡航阻力做功的比值恒定:
| $ {w_{{\text{FAN}}}}{V_{{\text{BP}}}}{\eta _{\Pr }} = {C_1}{F_{\text{R}}}{V_{{\text{aircraft}}}}. $ |
式中:VBP为外涵排气速度;ηPr为发动机推进效率, FR为飞行阻力;Vaircraft为飞机的指示空速;C1为常数, 由发动机涵道比、单架飞机安装发动机台数所决定.同时, 考虑到飞机的升力和自身重力相平衡, 而飞机升力也与巡航速度的平方成正比, 得
| $ {F_{\text{R}}}/{G_{\text{a}}} = {C_2}. $ |
式中C2为常数, 由飞机的升力系数和阻力系数共同决定.推导可以得
| $ \begin{gathered} {W_{{\text{FAN}}}} = f\left( {{N_{1, {\text{c}}}}} \right) = {C_3}\left( {{G_{\text{a}}}{M_n}{{\left( {\gamma R} \right)}^{- \frac{1}{2}}}/\left\{ {{p_{{s_0}}}\left[{1 + M_n^2\left( {\gamma-} \right.} \right.} \right.} \right. \hfill \\ \;\;\;\;\;\;\;\;\;\left. {\;\left. 1 \right){{\left. {/2} \right]}^{\gamma /\left( {\gamma -1} \right) + 1/2}}} \right\}. \hfill \\ \end{gathered} $ | (1) |
式中:N1, c为风扇相似转速, WFAN为风扇消耗的轴功率, ps0为飞行高度静压, R为气体常数, C3为由C1、C2和外涵道的设计特性所决定的常数.因此, 只需要将健康发动机的工况和气路参数代入式(1)计算N1, c-WFAN标准曲线, 而后对比待评估时间点的WFAN相对于标准曲线的下降比例ΔWFAN即可.同时, 若默认风扇的单位轮缘功不受其性能衰退的影响, 则可认为流量衰退因子ΔwFAN=ΔWFAN.
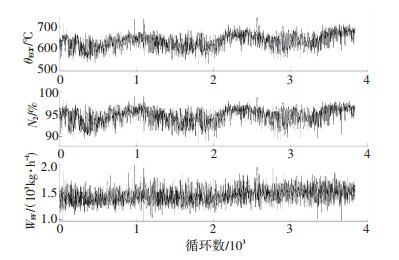
4 实验验证及结果分析 4.1 验证实验说明本文选用了机队中某台传感器安装完备发动机(第2节给出)的修后飞行记录, 构建发动机稳态仿真模型, 样本覆盖200个飞行循环, 部分数据见表 1.为了对另一台安装少量传感器的同型号发动机进行诊断, 选用了其两次大修之间的飞行记录数据来验证方法的有效性, 样本覆盖3 800个飞行循环, 对应的观测量θEGT、N2、WFF在图 4中给出. 表 1、图 4给出的数据都是通过“数据快照”的方式采样获得的, 即在每个航段的平稳飞行阶段, 数据采集装置对一小段时间内的传感器信号进行采样, 并将数据的平均值返回给地面数据基站.由图 4可知, 发动机的实际飞行数据具有非常明显的数据噪声.
| 表 1 测量条件完备发动机的部分传感器数据 Table 1 Partial sensor dataset of the fully tested aero-engine |
|
图 4 待诊断发动机观测值 Figure 4 Sensor readings of objective engine |
首先采用有限差分-BFGS方法完成发动机稳态系统的最小二乘优化.所获得的发动机稳态仿真模型对各工况下的气路参数具有较低的回归误差(如表 2[12]和图 5所示), 稳态模型精度足够支持性能诊断要求.
| 表 2 发动机稳态仿真模型气路参数回归误差 Table 2 Regression error of simulative engine model steady state |
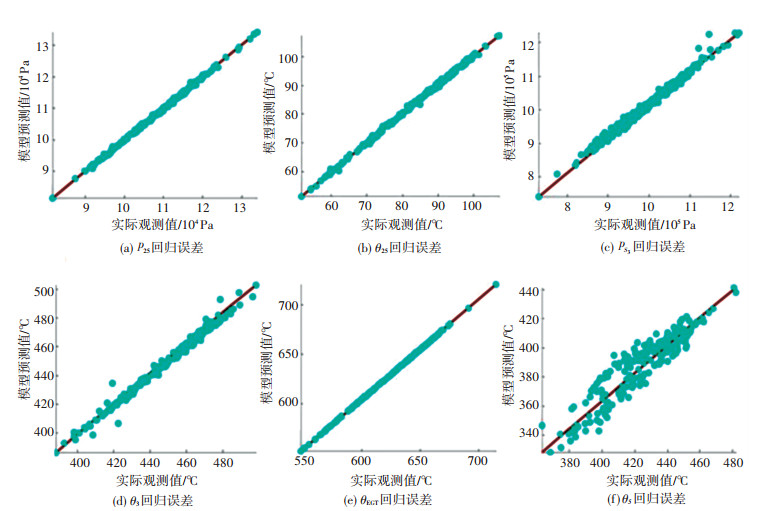
|
图 5 发动机稳态模型参数回归误差 Figure 5 Regression errors of engine steady state model |
文中利用改造后的UKF对观测量θEGT、N2、WFF进行滤波以评估部件衰退程度, 滤波窗口宽度τ=5.同时, 考虑到发动机部件的性能衰退实质上是其内部结构损伤在数据层面上的反应, 本文收集了发动机拆检时发现的部件损伤状态, 分析了各类损伤对部件性能的影响特点, 以验证诊断结果的可靠性.
改进后的UKF所给出的部件衰退因子变化趋势在图 6中给出, 部件损伤检查结果以及损伤影响分析在表 3中给出.观察各衰退因子变化趋势可以得知, 改造的UKF滤波算法能够快速收敛并对部件性能指标的变化进行稳定跟踪.同时, 结合图 4给出的发动机气路参数观测值和表 3给出的性能诊断结果可以看出, 部件内部的微小局部损伤对其自身性能影响较小, 而宏观结构的几何形状变化则会产生明显影响.同时, 由于大气湿度的季节性变化, 所得到的衰退因子都仍然具有一定的波动性特性, 但并不影响部件性能总体的性能变化趋势.
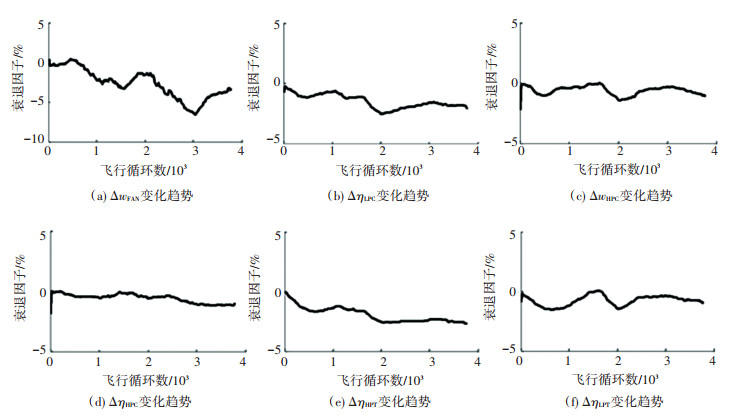
|
图 6 部件衰退因子变化趋势 Figure 6 Variation trends of engine component degradation factors |
| 表 3 拆检时发现的部件损伤、性能诊断结果及针对性分析结果 Table 3 Component damage found after engine removal and corresponding performance diagnosis and analysis |
1) 采用多元非线性函数进行部件通用特性的表达, 得到的稳态工作模型能够准确模拟发动机在各种工况下的工作过程, 并反映出部件性能衰退对整机健康状态参数的影响.
2) 通过引入发动机稳态工作模型和工况参数对经典UKF过程进行改造, 提升了性能诊断算法对数据噪声的抵抗能力.
3) 提出滑动窗口采样方法, 扩展了系统观测矢量, 解决了测量参数不足所导致的低可观测性问题.
本文提出的方法具有较高实用性, 能够满足航空公司的发动机性能监控和维修决策要求.
| [1] |
KRAFT J, SETHI V, SINGH R. Optimization of aero gas turbine maintenance using advanced simulation and diagnostic methods[J]. Journal of Engineering for Gas Turbines and Power, 2014, 136(11): 111601. DOI:10.1115/1.4027356 |
| [2] |
袁春飞, 姚华. 基于卡尔曼滤波和遗传算法的航空发动机性能诊断[J]. 航空发动机, 2007(Z1): 104. YUAN Chunfei, YAO Hua. Development of Kalman filter and genetic algorithm for aero-engine performance diagnostics[J]. Journal of Propulsion Technology, 2007(Z1): 104. DOI:10.3969/j.issn.1672-3147.2007.z1.032 |
| [3] |
周媛, 左洪福, 王丽娜. 基于簇特征加权的航空发动机状态监视方法[J]. 航空动力学报, 2015, 30(7): 1759. ZHOU Yuan, ZUO Hongfu, WANG Lina. Aero-engine condtion monitoring method based on cluster features weighting[J]. Journal of Aerospace Power, 2015, 30(7): 1759. DOI:10.13224/j.cnki.jasp.2015.07.030 |
| [4] |
孙见忠, 左洪福, 梁坤. 基于民航发动机状态数据的涡轮叶片剩余寿命评估[J]. 机械工程学报, 2015, 51(23): 53. SUN Jianzhong, ZUO Hongfu, LIANG Kun. Remaining useful life estimation method for the turbine blade of a civil aircraft engine based on the qar and field failure data[J]. Journal of Mechanical Engineering, 2015, 51(23): 53. |
| [5] |
KOBAYASHI T, SIMON D L. Hybrid neural-network genetic-algorithm technique for aircraft engine performance diagnostics[J]. Journal of Propulsion and Power, 2005, 21(4): 751. DOI:10.2514/1.9881 |
| [6] |
马安祥, 李艳军, 曹愈远, 等. 基于免疫理论的航空发动机磨损故障智能诊断[J]. 航空学报, 2015, 36(6): 1896. MA Anxiang, LI Yanjun, CAO Yuyuan, et al. Intelligent diagnosis for aircraft engine wear fault based on immune theory[J]. Acta Aeronautica Et Astronautica Sinica, 2015, 36(6): 1896. |
| [7] |
袁春飞, 姚华. 传感器测量偏差下的航空发动机智能性能诊断[J]. 航空动力学报, 2007, 22(1): 126. YUAN Chunfei, YAO Hua. Intelligent performance diagnosis of aeroengine with sensor measurement bias[J]. Journal of Propulsion and Power, 2007, 22(1): 126. DOI:10.3969/j.issn.1000-8055.2007.01.022 |
| [8] |
朱磊, 左洪福, 蔡景. 基于Wiener过程的民用航空发动机性能可靠性预测[J]. 航空动力学报, 2013, 28(5): 1006. ZHU Lei, ZUO Hongfu, CAI Jing. Performance reliability prediction for civil aviation aircraft engine based on Wiener process[J]. Journal of Propulsion and Power, 2013, 28(5): 1006. DOI:10.13224/j.cnki.jasp.2013.05.010 |
| [9] |
KAMBOUKOS P, MATHIOUDAKIS K. Comparison of linear and non-linear gas turbine performance diagnostics[C]// ASME Turbo Expo 2003, collocated with the 2003 International Joint Power Generation Conference. Atlanta: American Society of Mechanical Engineers, 2005: 451
|
| [10] |
KURZKE J. How to get component maps for aircraft gas turbine performance calculations[C]// ASME 1996 International Gas Turbine and Aeroengine Congress and Exhibition. Birmingham: American Society of Mechanical Engineers, 1996: V005T16A001-V005T16A001
|
| [11] |
KUMAR V, PANDA P, MONGIA H, et al. Innovative approaches for reducing CO2 emissions of aviation engines part 2: NPSS calibration with existing gas turbine engines[C]// AIAA 10th International Energy Conversion Engineering Conference. Atlanta: AIAA, 2012: 4228
|
| [12] |
TAN Zhixue, ZHONG Shisheng, LIN Lin. A model learning strategy adapted to health assessment of multi-component systems[C]//Prognostics and System Health Management Conference. Harbin: IEEE, 2017: 1. DOI: 10.1109/PHM.2017.8079223
|
 2019, Vol. 51
2019, Vol. 51


