情感计算是和谐人机交互中不可缺少的一个方面.机器人适当的情感表达可使人类更易于接受具有高度自主性的机器人以及一些类人的功能.机器人个性化的情感生成还可以迎合不同性格的人对机器人的个性化需求. Vikia机器人[1]的实验证明了情绪表达在人机交互中的有效性.
人工情感模型可分为基于规则和评价的情感模型、基于情绪维度理论的情感模型、基于统计学习的情感模型以及其他类型的情感模型.这些类别不是完全独立的,而是彼此之间有一定的交叉和联系.最早的基于规则和评价的情感模型是OCC情感模型,该模型研究了22种人类情感的推理产生过程并给出了相应的情感产生规则[2]. OCC情感模型为以后的许多情感模型提供了基础,Ojha等[3]在其基础上进行量化,形成情感计算模型.基于统计学习的模型包括基于隐性马尔可夫(HMM)的情感模型[4]、基于神经网络的人工情感建模[5]、扩展有限状态机情感模型[6]、基于强化学习的情感模型[7]等.由于情绪维度理论便于情感量化,目前,在仿人头像机器人上应用的人工情感模型多为在情绪维度理论基础上与规则评价理论相融合的情感计算模型,典型的有Kismet情感模型[8]等.此外,还有基于PAD(Pleasure、Arousal、Dominance)三维情感空间的情感模型,如基于PAD的个性化情感模型[9]等.还有一些其他类型的情感模型,如连续空间中机器人的情绪交互模型[10]、基于Gross认知重评的情感模型[11]、基于增量自适应的模糊情感推理[12]、分层次自治的情感模型[13]等.
另外,日本Pepper[14]和美国汉森公司Sophia[15]机器人的发布在人机交互领域引起了轰动,但对其情感生成的具体机制并不了解.这些模型大多都是针对特定的平台或规则进行设计的,缺乏可移植性和可扩展性,如文献[1]、[4]、[8]、[9]等.并且很多情感模型只停留在利用人工代理或者虚拟人仿真的阶段,如文献[5]、[7]、[9]等.
本文在PAD三维情感空间内,综合机器学习算法建立一种更具普遍性的人工情感计算模型,这种情感计算模型可对外界刺激进行一定的情感处理,拥有情绪决策和表达能力.并将其集成到仿人头像机器人上,进行人机情感交互实验.
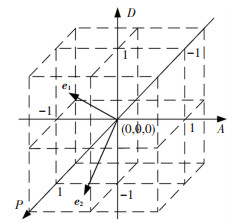
1 PAD三维情感空间情绪心理学中的PAD三维情感空间将情绪分为3个维度[16]:愉悦度(Pleasure-displeasure),即情绪状态的愉悦/不愉悦的程度,积极/消极的程度;激活度(Arousal-nonarousal),即情绪的生理激活水平和警觉性的高低;优势度(Dominance-submissiveness),即情绪对他人和外界环境的控制力和影响力.在PAD情绪空间中,情绪状态用坐标或者向量(e = [P, A, D])表示. (0, 0, 0)点表示情绪的平静状态,如图 1所示.
|
图 1 PAD三维情感空间 Figure 1 PAD 3D emotional space |
PAD三维情感理论带有一套简化版的PAD情绪量表.通过该量表,可以测出情绪的基准PAD坐标值.文献[17]介绍了中文简化版PAD情绪量表,并且在相关研究中将其应用在北京大学生中,测出了本土化的14种基本情绪的基准PAD值,表 1中为本文涉及到的8种情绪的基准PAD值(数据未经归一化,范围为[-4, 4]).
| 表 1 8种基本情绪在PAD空间中的映射 Table 1 Mapping of 8 basic emotions in PAD space |
人工情感模型共分为3个部分:1)外部事件检测及处理部分,主要负责外部情感刺激的检测及量化,生成外界刺激向量,输入到情感模型中. 2)PAD情绪响应向量生成及修正部分,采用情绪样本训练广义回归神经网络(GRNN),使其可对输入的外界刺激产生自主情绪响应,即生成PAD情绪响应向量.对性格和心情进行建模,并以此对PAD情绪响应向量进行修正. 3)情绪离散化部分,运用随机森林分类算法将修正后的PAD情绪响应向量与基本情绪的基准PAD情绪向量进行对比分类,得到具体的情绪种类并计算情绪强度.模型总体框架如图 2所示.

|
图 2 人工情感模型整体框架 Figure 2 Framework of artificial emotion model |
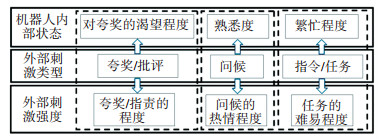
模型将外界刺激分类,根据不同的事件类型提取刺激强度和机器人内部特征.本文选取夸奖/批评、问候、指令/任务3类事件进行标注,其标注过程如图 3所示.外部刺激种类、外部刺激强度以及机器人内部特征这3个维度构成了一个三维的外界刺激向量:
|
图 3 外界刺激情感标注 Figure 3 Emotional annotation of external stimuli |
| $ {S_{{\text{outside}}}} = \left[{{C_{{\text{outside}}}}\;\;\;\;{F_{{\text{inside}}}}\;\;\;\;\;{I_{{\text{outside}}}}} \right]. $ |
式中:Coutside、Finside、Ioutside分别为外界刺激种类、机器人内部状态和外界刺激强度.
分别用1、0、-1来标注这3类事件的类别.采用模糊词来描述机器人内部特征和外界刺激强度,将其分为5级:一般、比较、很、非常、极其,分别对应相应的数值:0、0.25、0.50、0.75、1.00.
渴望夸奖程度的计算:假设机器人在之前的交互中得到的夸奖次数越多且程度越大,其对夸奖的渴望越趋于一般水平.第k次交互时, 机器人对夸奖的渴望程度drk(0.5≤drk≤1.0)如下:
| $ d_r^k = \left\{ \begin{gathered} 0.5, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;k = 1; \hfill \\ 0.5\frac{{\sum\limits_{j = 1}^{{k_r}-1} {\left( {1-{r_j}} \right)} }}{{2\left( {k-1} \right)}} + 0.5, \;\;\;\;k = 1. \hfill \\ \end{gathered} \right. $ |
式中:rj为机器人第j次所获得的夸奖/批评程度;rj∈[-1, 1],rj < 0为批评,rj>0为表扬;kr为自开始工作到受到新的表扬/批评之间已经受到的赞美/批评次数.
忙碌程度(疲劳程度)的计算:假设在之前的交互中,机器人执行任务的时间越长,任务的难度越大,则机器人的忙碌程度越高.第k次交互时,机器人的忙碌程度dbk(0≤dbk≤1)如下:
| $ d_{\text{b}}^k = \left\{ \begin{gathered} 1-\sum\limits_{j = 1}^{{k_{\text{b}}}-1} {\left( {1-{c_j}} \right){t_j}/\left( {2\Delta t} \right), } \;\;\;\;\;{c_j} < 0; \hfill \\ 1 - \sum\limits_{j = 1}^{{k_{\text{b}}} - 1} {{c_j}{t_j}/\left( {2\Delta t} \right)}, \;\;\;\;\;\;\;\;\;\;\;\;\;{c_j} > 0. \hfill \\ \end{gathered} \right. $ |
式中:cj为第j次任务的难易程度,cj∈[-1, 1];tj为完成第j项任务所花费的时间;Δt为自开始执行任务到接到新任务时的时间间隔;kb为自开始执行任务到接到新任务之间所执行的任务数量.
2.2 PAD情绪响应向量生成采用中文简化版PAD情绪量表作为情绪测量工具,获取情绪样本原始数据.每道问题保证有多人作答,并收回多份有效回答数据.采用多份回答数据的平均值为最终应用到模型中的样本数据.可以粗略地认为,经过处理得到的情绪样本不包括人的个性和心情对情绪的影响.原始数据经过处理后得到的PAD情绪向量e,和外界刺激标注向量soutside组成一组3输入3输出的样本,用于训练神经网络,实现PAD情绪响应向量的自主生成.
PAD情绪响应向量的生成本质上是一种非线性拟合问题.广义回归神经网络(generalized regression neural network,GRNN)具有很强的非线性映射能力,适用于小样本拟合,适合本文中的研究对象.训练好的GRNN网络,可对外界刺激生成相应的情绪响应向量
| $ \mathit{\boldsymbol{\hat e = }}\left[{\hat P\;\;\;\;\hat A\;\;\;\;\;\hat D} \right]. $ |
广为学者们接受的性格理论是心理学学者Goldberg提出的“大五”人格因素理论[18]. “大五”人格因素理论将人的性格分为5大类,见表 2.
| 表 2 “大五”人格因素表 Table 2 Big-Five personality factors table |
Mehrabiana运用统计学分析拟合,得出了PAD情绪维度与不同性格特质之间的相关关系[19]:
| $ \begin{gathered} P = 0.21{E_{\text{x}}} + 0.59{A_{\text{g}}} + 0.19{S_{\text{t}}}, \hfill \\ A = 0.30{A_{\text{g}}}-0.56{S_{\text{t}}} + 0.15{S_{\text{o}}}, \hfill \\ D = 0.60{E_{\text{x}}}-0.32{A_{\text{g}}} + 0.25{S_{\text{o}}} + 0.17{C_{\text{o}}}. \hfill \\ \end{gathered} $ |
将由“大五”人格量表得到的人群在各个维度上的平均分作为各维度的参考点,以参考点的位置为中性点,将超出中性点的部分作为影响PAD情绪的因子,经性格修正后的情绪响应向量计算式为
| $ {\mathit{\boldsymbol{\hat e}}_{\text{p}}} = \mathit{\boldsymbol{\hat e}} + \mathit{\boldsymbol{\hat e}}_{\text{p}}^*, $ |
| $ \Delta {E_{\text{x}}} = {E_{\text{x}}}-{\bar E_{\text{x}}}, \;\Delta {A_{\text{g}}} = {A_{\text{g}}}-{\bar A_{\text{g}}}, \Delta {S_{\text{t}}} = {S_{\text{t}}}-{\bar S_{\text{t}}}, $ |
| $ \Delta {S_{\text{o}}} = {S_{\text{o}}}-{\bar S_{\text{o}}}, \;\;\;\Delta {C_{\text{o}}} = {C_{\text{o}}}-{\bar C_{\text{o}}}, $ |
| $ \hat e_{\text{p}}^* = \left[{\begin{array}{*{20}{l}} {0.21}&{0.59}&{0.19}&0&0 \\ 0&{0.30}&{-0.56}&{0.15}&0 \\ {0.60}&{-0.32}&0&{0.25}&{0.17} \end{array}} \right] \cdot \left[\begin{gathered} \Delta {E_{\text{x}}} \hfill \\ \Delta {A_{\text{g}}} \hfill \\ \Delta {S_{\text{t}}} \hfill \\ \Delta {S_{\text{o}}} \hfill \\ \Delta {C_{\text{o}}} \hfill \\ \end{gathered} \right]. $ |
式中:
如果一个人此时的心情很愉快,那么在同样的外界刺激下,产生的负面情绪响应会变弱,而正向的情绪响应会加强.第k次交互中,心情对情绪的修正计算式如下:
| $ {\mathit{\boldsymbol{\hat e}}_{{\text{pm}}}} = \varphi {\mathit{\boldsymbol{m}}_k} + {\mathit{\boldsymbol{\hat e}}_{\text{p}}}. $ |
式中:
随着情绪的产生和积累,心情状态也会随之发生变化.心情状态修正情绪向量后,情绪状态也反过来影响心情,心情的更新过程如下:
| $ {m_{k + 1}} = \left\{ \begin{gathered} {m_0}, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;k = 0; \hfill \\ \frac{\gamma }{{{\mathit{\boldsymbol{e}}^{\left\| {{\mathit{\boldsymbol{m}}_0}} \right\|}}}}{{\mathit{\boldsymbol{\hat e}}}_{\text{p}}} + \left( {1-\frac{\gamma }{{{\mathit{\boldsymbol{e}}^{\left\| {{\mathit{\boldsymbol{m}}_0}} \right\|}}}}} \right){\mathit{\boldsymbol{m}}_k}, \;\;\;\;k > 0. \hfill \\ \end{gathered} \right. $ |
式中:γ为
在PAD三维情绪调查问卷中,被试者在根据情景提示填写情绪量表之前,还需将自己可能产生的情绪勾选出来.以2.2节中得到的PAD向量(e)作为输入样本,以这些被勾选出来的情绪作为输出样本,构成了一组用于情绪分类的原始样本,即每一个原始的PAD情绪向量对应一个或多个情绪类别.经拆分后,每组原始样本可拆分为9组,即9个同样的输入样本分别对应9个不同的输出类别.输出的9类类别标签取值分别为0、1~8(均为整数),其中1~8为情绪类别标签,分别对应温和、高兴、悲伤、惊讶、生气、厌恶、焦虑和失望8种情绪,其基准PAD值见表 1.如果某种情绪在该输入下出现,输出样本为其情绪类别标签对应的值;如果该种情绪没有出现,输出样本则为0,表达式为
| $ \begin{gathered} \mathit{\boldsymbol{s}}_{{\text{input}}}^{j \times i} = \left[{P_{\text{o}}^j\;\;\;\;A_{\text{o}}^j\;\;\;\;\;D_{\text{o}}^j\;\;\;\;l_{{\text{class}}}^i} \right], \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;s_{{\text{output}}}^{j \times i} = l_{{\text{out}}}^{j, i}. \hfill \\ \end{gathered} $ |
式中:sinputj×i为分类输入样本;Poj、Aoj、Doj为原始PAD情绪向量e在P、A、D三个维度上的值;j为原始样本集中样本的数目,j=1~132;lclassi为情绪类别标签,i=1~8;soutputj×i为分类输出样本;loutj, i为输出类别标签,loutj, i=0~8.
原始样本的特征集合只包括PAD情绪向量和其对应的情绪类别标签,与8种基本情绪的基准PAD值关联不大,因此需要对原始样本中所包含的信息进行挖掘.为充分利用原始样本中的信息,将特征集从原始的4维扩充到9维:
| $ \mathit{\boldsymbol{s}}_{{\text{input}}}^{j \times i} = \left[{\mathit{\boldsymbol{e}}_{\text{o}}^j\;\;\;\;l_{{\text{class}}}^i\;\;\;\;\left\| {\mathit{\boldsymbol{e}}_{\text{o}}^j-\mathit{\boldsymbol{e}}_{\text{s}}^i} \right\|\;\;\;\;\;\cos \left( {\mathit{\boldsymbol{e}}_{\text{o}}^j, \mathit{\boldsymbol{e}}_{\text{s}}^i} \right)\;\;\;\;\;\mathit{\boldsymbol{e}}_{\text{o}}^j-\mathit{\boldsymbol{e}}_{\text{s}}^i} \right]. $ |
式中:eoj为第j个原始三维PAD情绪向量;esi为第i种基本情绪对应的基准PAD情绪向量,其每个维度对应的值为Ps、As、Ds.
2.4.2 特征集选择特征集经扩充后,可能出现对分类来说冗余或无关的特征.因此应用信息增益率对扩充后的特征集进行特征选择,优化分类特征集.
在进行信息增益率计算之前,先采用二分法[20]对cos(eoj, esi)、‖eoj-esi‖、Po-Ps、Ao-As、Do-Ds这5个维度的特征进行离散化处理.经离散化处理后,计算特征集中每一维度的信息增益率.之后将其按降序排列,依次增加特征数目,构成新的特征子集.用这些特征子集对分类器进行训练,得到分类准确率与特征集中特征数的关系曲线.选取促使分类准确率曲线上升的特征组成新的特征子集.应用此特征子集构成的输入样本作为最终的分类样本对分类器进行训练.
2.4.3 情绪响应向量分类随机森林算法具有速度快、鲁棒性好、适合小样本训练等特点,因此选择其对PAD情绪向量进行分类.随机森林算法的输入为经特征选择后得到的优化后的输入样本,输出为对应的类别标签.该分类器经训练后用于PAD情绪响应向量的分类.
2.5 情绪表达1) 情绪强度计算.由于PAD情感空间并不是各向均匀的欧氏空间,不能直接使用欧氏距离衡量情绪的强度.因此,本文提出一种适用于PAD情感空间的情绪强度计算式:
| $ {\hat E_{{\text{pm}}}} = \left\{ \begin{gathered} \left\| {{{\mathit{\boldsymbol{\hat e}}}_{{\text{pm}}}}} \right\|\left| {\cos \theta } \right|/\left\| {{{\mathit{\boldsymbol{\hat e}}}_{\text{s}}}} \right\|, \;\;\;\;\;\;\;\;\;\;\hat E > 0; \hfill \\ 0, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\hat E \leqslant 0. \hfill \\ \end{gathered} \right. $ |
式中:
2) 机器人表情强度计算.若人工情感模型所产生的情绪响应中包括多种情绪,则增大情绪强度最大的情绪的比例,并对情绪强度归一化后按比例将所有产生的情绪合成,合成后的情绪强度作为表情强度:
| $ {I_{{{\hat E}_i}}} = \left\{ \begin{gathered} \left( {1 + \left( {1-{{\hat E}_{\max }}{{\left( {\sum\limits_{i = 1}^n {{{\hat E}_i}} } \right)}^{-1}}} \right)} \right)\frac{{\hat E_{\max }^2}}{{\sum\limits_{i = 1}^n {{{\hat E}_i}} }}, \;\;\;\;{{\hat E}_i} = {{\hat E}_{\max }}; \hfill \\ \left( {1-{I_{{{\hat E}_{\max }}}}} \right)\frac{{\hat E_i^2}}{{\sum\limits_{i = 1}^{n - 1} {{{\hat E}_i}} }}, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{{\hat E}_i} \ne {{\hat E}_{\max }}. \hfill \\ \end{gathered} \right. $ |
式中:
3) 语音问答实现.采用深圳电子时代公司出产的WEGASUN-M6语音识别模块对语音进行识别和合成.如要实现人机对话,需要先行编辑好包含问答语句的语音库存储到M6模块中.部分语音库见表 3.目前的语音库规模为45条,可扩展值至2 000条语句,每句75个字以内,可以满足一定的日常需要.语音库分为3个部分:问候部分、夸奖/批评部分以及指令/任务部分.并对问题语句按外界事件类型、所表达的情绪种类以及所表达的情绪强度进行标注,以上三者构成回答语句向量Aw:
| 表 3 部分语音库 Table 3 Segment of the speech library |
| $ {\mathit{\boldsymbol{A}}_{\text{w}}} = \left[{{c_{\text{c}}}\;\;\;{e_{\text{c}}}\;\;\;{{\hat E}_{\text{F}}}} \right]. $ |
式中:cc为所有产生的情绪中强度最大的情绪种类;ec为外界事件类型;
用高斯分布隶属函数和最大隶属度原则对人工情感模型生成的情绪强度进行模糊化.情感强度采用5个模糊集进行描述:很弱、较弱、一般、较强、很强,分别对应阿拉伯数字1~5,其对应的情绪强度分别为0.1、0.3、0.5、0.7、0.9(情绪强度的范围为[0, 1]).
3 人工情感模型仿真 3.1 仿真数据获取 3.1.1 GRNN网络训练按2.2节中的方法分3类(夸奖/批评、问候、任务)设计调查问卷问题,采用模糊化的语言,如非常、比较、些许等来描述事件的程度.每类事件在程度上共分成5级,每级中所描述的刺激强度在正向和负向上又分为9级,共136道问题.每道问题保证有5份有效回答数据,采用这5份回答数据的平均值为最终应用到模型中的样本数据.通过问卷的回答数据,计算出PAD情绪向量e,以问卷6为例,其计算后的数据见表 4.
| 表 4 调查问卷6处理后数据 Table 4 Processed data of questionnaire 6 |
对每道问题进行评分者信度检验,共有132道题目获得的样本符合要求,即共获取132组有效样本.
从样本中随机选取125组用于训练GRNN网络,7组用于检验网络拟合效果.仿真中所应用到的GRNN网络输入层和输出层各包含3个神经元,隐含层包括1个模式层和1个求和层,径向基函数的扩展速度取为0.2.经检验网络的拟合误差在PAD每个维度上的平均值可达到0.6(±0.3)以下.对比表 1中数据,0.6(±0.3)的误差基本不会改变PAD各维度的趋势.因此,虽然拟合误差对模型的准确度有一定影响,但影响不大,可以认为该网络已经达到模型要求,可实现对外界刺激的自主情绪响应.
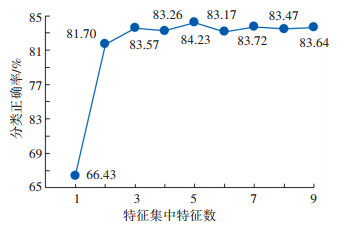
3.1.2 随机森林分类器训练按2.4.1中的方法和调查问卷中的得到的原始分类样本数据,可以得到132组原始分类样本,经拆分后得到共1 056组分类样本.按2.4.2中的方法计算输入样本集中每维特征的信息增益率如表 5所示.其分类准确率与特征集中特征数的关系曲线如图 4所示.选取促使分类准确率曲线上升的特征,即表 5中序号1、2、3、5、7对应的特征组成新的特征子集,此时的输入样本为:
| 表 5 各个特征信息增益率结果 Table 5 Information gain ratio result of each feature |
|
图 4 分类准确率与特征集中特征数的关系曲线 Figure 4 Relationship between classification accuracy and the number of features in feature set |
| $ \mathit{\boldsymbol{s}}_{{\text{input}}}^{j \times i} = \left[{P_{\text{o}}^j\;\;\;l_{{\text{class}}}^i\;\;\;\left\| {\mathit{\boldsymbol{e}}_{\text{o}}^j-\mathit{\boldsymbol{e}}_{\text{s}}^i} \right\|\;\;\;\;P_{\text{o}}^j-P_{\text{s}}^i\;\;\;\cos \left( {\mathit{\boldsymbol{e}}_{\text{o}}^j, \mathit{\boldsymbol{e}}_{\text{s}}^i} \right)} \right]. $ |
应用此输入样本再次对分类器进行训练,此时得到的分类准确率最高可达87.50%.
随机森林算法的输入为经特征选择后得到的5维输入样本,输出为对应的类别标签,确定随机树棵数为600棵.从1 056个样本中随机选出1 000个样本对随机森林进行训练,其余的样本作为测试样本,对随机森林分类器的分类性能进行测试,得到其分类准确率.经检验,随机森林分类器的分类准确率稳定在85.71%.
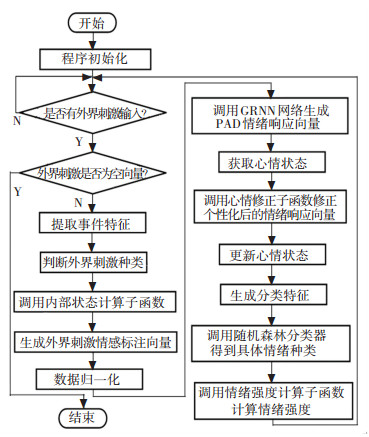
3.2 仿真结果及分析利用工具软件对本文所建立的人工情感计算模型进行编程仿真,图 5为仿真程序流程图.为模拟外界刺激,外界情感刺激的类型和强度通过手动直接输入到仿真程序中.
|
图 5 仿真程序流程 Figure 5 Simulation program flow chart |
设定机器人的性格为中性,初始心情状态为[0.1, 0, 0]T,即基本可以认为其心情状态为中性.选择有代表性的外界刺激事件进行9次连续交互,外界刺激标注向量及经情感模型计算得到的相关结果如表 6、表 7所示.
| 表 6 外界刺激标注向量及情绪响应向量 Table 6 External stimulus annotation vector and emotionresponse vector |
| 表 7 情绪种类及情绪强度 Table 7 Emotion class and emotion intensity |
可以看出,本文建立的人工情感计算模型很好地模拟了一些情况下人类的情绪变化.机器人不仅能够产生单一种类的情绪,还能根据自身状态产生多种情绪混合的相对复杂的情绪(如表 7中第1、7、8次交互).机器人有时甚至具有一定的“小情绪”. (如表 7中第7、8次交互).
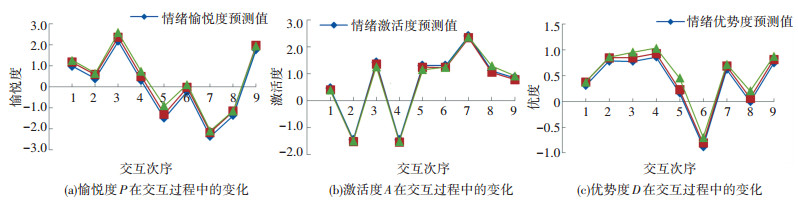
为考察个性等对机器人情绪响应的影响,设定机器人的性格因子分别为0.80、0.83、0.72、0.62、0.70,除神经质外均高于中性水平,即机器人应表现出乐观、积极的品质.初始心情仍设置为中性.个性以及心情对PAD情绪响应向量在3个维度上的影响如图 6所示.
|
图 6 PAD情绪响应向量各维度在交互过程中的变化 Figure 6 Changes of PAD emotional response vector in each dimension during interaction process |
可以看出在性格的影响下,愉悦度(P)和优势度(D)曲线较预测曲线明显上升,即机器人对正向情绪的体验增强,对负向情绪的体验减弱,符合机器人的性格定位.负向个性的仿真结果与此类似.
4 人机情感交互系统及实验 4.1 人机交互实验硬件及软件系统利用本实验室现有的H & F robot-Ⅲ型仿人头像机器人平台进行人机交互实验.该机器人由舵机驱动8个自由度实现面部表情控制点的运动[21].根据Ekman等[22]提出的面部行为编码系统(FACS)理论,机器人通过面部控制点的运动可以生成一些基本的表情:包括温和、高兴、惊讶、悲伤、失望、愤怒、生气和焦虑8种表情,如图 7所示.

|
图 7 仿人头像机器人8种基本面部表情 Figure 7 Eight basic facial expressions of humanoid head robot |
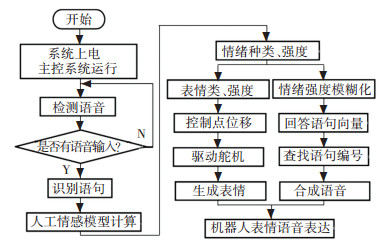
本实验中的外界刺激为语音信号,其硬件集成如图 8所示. 图 9为进行人机交互实验的软件流程.由搭载了人工情感模型的上位PC机作为主控机对外界语音信号进行处理,并生成相应的情绪和语音回答向量.上位机通过串行通信向舵机控制卡和语音识别模块发送控制信号,实现对机器人表情生成系统和语音合成模块的控制.

|
图 8 人-机交互硬件系统 Figure 8 Hardware of human-robot interaction system |
|
图 9 人机交互软件系统流程 Figure 9 Software of human-robot interaction system |
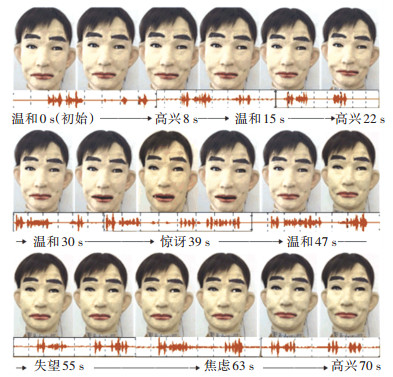
实验中设定机器人的性格及心情状态为中性,选择有代表性的外界刺激事件进行9次对话.以人类发出的交互语句作为外界刺激,其对应的外界刺激标注向量如表 8所示.机器人的表情合成强度和回答语句及其相关结果如表 9所示. 图 10为在进行人机交互时,机器人的正面表情变化截图及对应音频波形.交互时间一共持续了70 s.
| 表 8 外界刺激语句及其对应的外界刺激向量 Table 8 External stimulus words and their corresponding external stimulus vectors |
| 表 9 机器人表情强度和回答语句及其相关结果 Table 9 Strength of robot expressions and answer sentences and other related results |
|
图 10 机器人表情迁移截图及音频波形 Figure 10 Screenshots of robot expression migration and audio waveforms |
在初始时,机器人的表情为“温和”.对这9次交互的解释是:(1)一个陌生人向机器人十分热情的问候,机器人内部同时产生了温和、高兴、惊讶3种情绪,其表情转变为“高兴”;(2)机器人首次受到任务类型的刺激,其疲劳程度很低,其内部产生的情绪是温和,表情转变为“温和”;(3)机器人得到了表扬,其情绪为高兴,表情转变为“高兴”;(4)机器人被请求唱歌,其内部产生的情绪为温和,表情转变为“温和”;(5)机器人受到了较严重的批评,其内部产生的情绪为生气,表情也转变为“生气”;(6)由于此时机器人的忙碌程度不高,其内部产生的情绪是温和,表情转变为“温和”;(7)机器人受到了严厉的批评,其内部同时产生了惊讶、生气、讨厌、失望4种情绪,表情转变为“失望”;(8)机器人的疲劳程度已经很高,其内部产生的情绪是惊讶且焦虑,表情也转变为“焦虑”;(9)机器人得到了夸奖,它的情绪为高兴,表情也转变为“高兴”.
实验结果表明,搭载了人工情感计算模型的机器人可根据交互语句进行情绪响应,并且可根据所产生的情绪做出相应的表情变化和语音应答,实现语音和表情之间的协调,与人进行基本的交互,验证了模型的合理性和有效性.
5 结论1) 在PAD三维情感空间中建立了考虑性格和心情的人工情感模型框架,提出了有效的外部情感刺激标注方法,并基于情绪响应样本训练广义回归网络,其拟合误差达到0.6(±0.3),实现了对外界刺激输入的自主且个性化的情感响应.
2) 应用信息增益率对扩充后的原始情绪分类样本进行特征选择处理,去除情绪分类样本中的冗余无关特征后,训练随机森林分类器实现了情绪分类,分类准确率达85%以上.
3) 将引入了情绪与表情映射关系和语音问答规则的人工情感计算模型应用于自主研发的H & F robot-Ⅲ型仿人头像机器人系统,进行了人机交互实验.结果表明,机器人可以根据外界刺激产生相应的情绪,进行表情表达和对话,实现人机情感交互,验证了模型的有效性.
| [1] |
BRUCE A, NOURBAKHSH I, SIMMONS R. The role of expressiveness and attention in human-robot interaction[C]// IEEE International Conference on Robotics and Automation Proceedings 2002. Washington DC: IEEE Press, 2002: 4138
|
| [2] |
ORTONY A, CLORE G L, COLLINS A. The cognitive structure of emotions[J]. Contemporary Sociology, 1988, 18(6): 2147. DOI:10.2307/2074241 |
| [3] |
OJHA S, WILLIAMS M A. Emotional appraisal: a computational perspective[C]// 5th Conference on Advances in Cognitive Systems. Troy: [s.n.], 2017: 1
|
| [4] |
LIU Xin, XIE Lun, WANG Zhiliang, et al. Robot emotion and performance regulation based on HMM[J]. International Journal of Advanced Robotic Systems, 2013, 10(2): 1. DOI:10.5772/55607 |
| [5] |
KESTEREN A J V, AKKER R O D, POEL M, et al. Simulation of emotions of agents in virtual environments using neural networks[J]. University of Twente, 2000, 18(11): 137. |
| [6] |
MENG Qingmei, WU Weiguo. Artificial emotional model based on finite state machine[J]. Journal of Central South University of Technology, 2008, 15(5): 694. DOI:10.1007/s11771-008-0129-1 |
| [7] |
BROEKENS J, JACOBS E, JONKER C M. A reinforcement learning model of joy, distress, hope and fear[J]. Connection Science, 2015, 27(3): 215. DOI:10.1080/09540090 |
| [8] |
BREAZEAL C. Emotion and sociable humanoid robots[J]. International Journal of Human-Computer Studies, 2003, 59(1/2): 119. DOI:10.1016/S1071-5819(03)00018-1 |
| [9] |
杨勇, 张志瑜. 基于PAD的个性化情感模型[J]. 重庆邮电大学学报(自然科学版), 2012, 24(1): 96. YANG Yong, ZHANG Zhiyu. Personalized affective model based on PAD[J]. Journal of Chongqing University of Posts and Telecommunications, 2012, 24(1): 96. DOI:10.3979/j.issn.1673-825X.2012.01.019 |
| [10] |
解仑, 刘欣, 贺苗, 等. 连续空间中机器人的情绪交互模型[J]. 中南大学学报(自然科学版), 2016, 47(9): 3050. XIE Lun, LIU Xin, HE Miao, et al. Robot emotional interaction model in continuous space[J]. Journal of Central South University (Science and Technology), 2016, 47(9): 3050. DOI:10.11817/j.issn.1672-7207.2016.09.019 |
| [11] |
韩晶, 解仑, 刘欣, 等. 基于Gross认知重评的机器人认知情感交互模型[J]. 东南大学学报(自然科学版), 2015, 45(2): 270. HAN Jing, XIE Lun, LIU Xin, et al. Cognitive emotion interaction model of robot based on Gross cognitive reappraisal[J]. Journal of Southeast University(Natural Science Edition), 2015, 45(2): 270. DOI:10.3969/j.issn.1001-0505.2015.02.014 |
| [12] |
ZHANG Q, JEONG S, LEE M. Autonomous emotion development using incremental modified adaptive neuro-fuzzy inference system[J]. Neurocomputing, 2012, 86(4): 33. DOI:10.1016/j.neucom.2011.12.034 |
| [13] |
ESTEBAN P G, INSUA D R. An affective model for a non-expensive utility-based decision agent[J]. IEEE Transactions on Affective Computing, 2017, 11(8): 1. DOI:10.1109/TAFFC.2017.2737979 |
| [14] |
PANDEY A K, GELIN R. A mass-produced sociable humanoid robot: Pepper: the first machine of its kind[J]. IEEE Robotics & Automation Magazine, 2018, 25(3): 40. DOI:10.1109/MRA.2018.2833157 |
| [15] |
谢玮. 网红机器人索菲亚何许"人"也?[J]. 中国经济周刊, 2018(5): 84. XIE Wei. Who is web celebrity robot Sophia?[J]. China Economic Weekly, 2018(5): 84. |
| [16] |
MEHRABIAN A. Framework for a comprehensive description and measurement of emotional states[J]. Genet Soc Gen Psychol Monogr, 1995, 121(3): 339. |
| [17] |
李晓明, 傅小兰, 邓国峰. 中文简化版PAD情绪量表在京大学生中的初步试用[J]. 中国心理卫生杂志, 2008, 22(5): 327. LI Xiaoming, FU Xiaolan, DENG Guofeng. Preliminary application of the abbreviated PAD emotion scale to Chinese undergraduates[J]. Chinese Mental Health Journal, 2008, 22(5): 327. DOI:10.3321/j.issn:1000-6729.2008.05.003 |
| [18] |
GOLDBERG L R. An alternative "description of personality": the Big-Five factor structure[J]. Journal of Personality & Social Psychology, 1990, 59(6): 1216. |
| [19] |
MEHRABIANA. Analysis of the Big-Five personality factors in terms of the PAD temperament model[J]. Australian Journal of Psychology, 1996, 48(2): 86. DOI:10.1080/00049539608259510 |
| [20] |
蒋艳凰, 杨学军, 赵强利. 具有高可理解性的二分决策树生成算法研究[J]. 软件学报, 2003, 14(12): 1996. JIANG Yanhuang, YANG Xuejun, ZHAO Qiangli. Constructing binary classification trees with high intelligibility[J]. Journal of Software, 2003, 14(12): 1996. DOI:10.13328/j.cnki.jos.2003.12.003 |
| [21] |
鹿麟, 吴伟国, 孟庆梅. 具有视觉及面部表情的仿人头像机器人系统设计与研制[J]. 机械设计, 2007, 24(7): 20. LU Lin, WU Weiguo, MENG Qingmei. Design and development of a humanoid robot system with visual and facial expressions[J]. Journal of Machine Design, 2007, 24(7): 20. DOI:10.13841/j.cnki.jxsj.2007.07.020 |
| [22] |
EKMAN P, FRIESEN W V. Facial action coding system (facs): a technique for the measurement of facial actions[J]. Rivista Di Psichiatria, 1978, 47(2): 126. |
 2019, Vol. 51
2019, Vol. 51


