2. 河南西绕城公路发展有限公司,郑州 710000;
3. 济祁高速公路(砀山段)项目办公室,安徽 宿州 235300
2. Henan West by Pass Road Development, Zhengzhou 710000, China;
3. Jiqi Expressway (Dangshan Section) Project Office, Suzhou 235300, Anhui, China
随着高等级公路建设的迅速发展,对道路工程的使用寿命和基础承载能力的要求逐年提高,在影响道路质量和使用寿命的诸多因素中,压实度起着决定性的作用,而压路机在压实过程中的碾压轨迹及碾压遍数对道路的压实度有着重要的影响,将直接影响道路的压实质量.在常规公路施工过程中,主要是通过监理与现场施工人员的主观判断来控制压路机碾压作业,这种根据经验判断碾压轨迹、估算压实遍数的方法,通常存在管理上的疏忽,极易造成欠压、超压等现象,很难保证道路的施工质量.为了提高压路机的压实质量,国内外一些专家做了大量的相关研究.李江[1]通过建立压路机碾压遍数模型,开发关键仪器来解决碾压遍数控制难的问题;沈叶飞[2]等提出了建立压路机施工过程远程监控系统的方法,实现了对压路机运行状态、碾压轨迹等的监测;文献[3]根据沥青路面的施工技术特点,开发了一款名为Auto Pave的实时监控系统,能根据填料的类别自动优化碾压工艺.然而,目前国内已经应用的压路机碾压轨迹监控技术,因所采集的压实参数不能与施工地点的坐标相匹配,故无法准确判断出压实不达标的部位,而国外这些压实实时监控系统通常价格昂贵,并且只针对操作者的使用而设计开发,具有一定的弊端.本文利用GPS技术,在建立压路机施工平面坐标系的基础上,通过理论分析和试验验证得到了准确的压路机碾压轨迹定位算法,绘制出了压路机的碾压轨迹图并利用LabVIEW软件开发的监控平台实现了对压路机碾压轨迹的实时监控.
1 建立施工平面坐标系根据压路机在道路压实过程中的实际位置,将GPS接收机获取的数据进行处理和分析,建立压路机施工平面坐标系,该过程流程图如图 1所示.
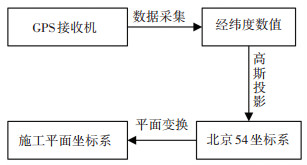
|
图 1 流程图 Figure 1 Flow chart |
GPS数据的采集是指从GPS接收机获取原始观测数据,通过接收机内部软件解算获得测站点的时间、纬度、经度等信息,提供导航服务.根据压路机在道路压实中的工况,对比GPS接收机的经济适用性,选取VK16U6G-MOUSEV1.0版GPS接收机,运用该接收机NMEA-0183通信协议解析中的RMC协议数据进行记录和解析.
1.2 建立北京54平面坐标系VK16U6 GPS接收机的参照坐标系是WGS-84世界大地坐标系,由于椭球上的大地计算在数值处理上比较繁琐且容易因为高程系统的不一致引起误差,故需将WGS-84坐标系中椭球面上的各个点的大地坐标投影到平面坐标系上.基于此,采用高斯-克吕格投影方法将大地坐标投影到北京54平面坐标系上[4].
高斯-克吕格投影是根据一定的经差值将地球椭球面进行划分,形成若干投影带.根据投影分度带划分准则,选取六度带分类方法.分度带投影图如图 2所示.
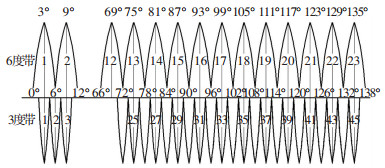
|
图 2 分度带投影图 Figure 2 Indexing projection map |
使用六分度带进行投影,则定位位置的中央子午线经度值L为
| $ L = 6 * \left( {N + 1} \right) - 3. $ |
式中:N为当前经度/6,取整数部分; N+1为6度带的带号.
因选取投影平面为北京54坐标系,参考克拉索夫斯基椭球[5],高斯-克吕格投影正算方程为
| $ \begin{array}{l} x = {X_0} + N\text{t}{\cos ^2}B\frac{{{l^2}}}{{{\rho ^2}}}\left[ {0.5 + \frac{1}{{24}}\left( {5 - {t^2} + 9{\eta ^2} + } \right.} \right.\\ \;\;\;\;\;\left. {\left. {4{\eta ^2}} \right){{\cos }^2}B\frac{{{l^2}}}{{{\rho ^2}}} + \frac{1}{{720}}\left( {61 - 58{t^2} + {t^4}} \right){{\cos }^4}B\frac{{{l^4}}}{{{\rho ^4}}}} \right], \end{array} $ | (1) |
| $ \begin{array}{l} y = N\cos B\frac{l}{\rho }\left[ {1 + \frac{1}{6}\left( {1 - {t^2} + {\eta ^2}} \right){{\cos }^2}B\frac{{{l^2}}}{{{\rho ^2}}} + } \right.\\ \;\;\;\;\;\left. {\frac{1}{{120}}\left( {5 - 18{{\rm{t}}^2} + {t^4} + 14{\eta ^2} - 58{\eta ^2}{t^2}} \right){{\cos }^4}B\frac{{{l^4}}}{{{\rho ^2}}}} \right], \end{array} $ | (2) |
| $ \begin{array}{l} {X_0} = 111\;134.861\;1B - \sin B\cos B\left( {32\;005,779\;9 + } \right.\\ \;\;\;\;\;\;\;133.923\;8{\sin ^2}B + 0.697\;3{\sin ^4}B + \\ \;\;\;\;\;\;\;\left. {0.003\;9{{\sin }^6}B} \right), \end{array} $ |
| $ N = a/\sqrt {1 - {e^2}{{\sin }^2}B} ,\;\;\;l = L - {L_0}, $ |
| $ {\eta ^2} = e'{\cos ^2}B,\;\;\;\;t = \tan B. $ |
式中:x,y分别为北京54平面坐标系的横、纵坐标,X0为赤道至该点的子午线弧长,B为以度为单位的纬度,N为西圈曲率半径,l为大地经度与投影带中央子午线经度差,ρ为极坐标系中的极径,L为点的经度,L0为点中央子午线的经度,a为参考椭球的长轴半径.
根据上述分析,在计算中央子午经线数值后,利用高斯-克吕格投影正算法将GPS接收机接收到的大地坐标转换成北京54平面坐标系上的平面坐标,便可以完成北京54平面坐标系的建立.
1.3 建立压路机施工平面坐标系在北京54平面坐标上,x、y坐标分别表示指向真北方向的纵坐标和与x轴相垂直的横坐标.为实现压路机施工过程的实时定位,需将北京54坐标系转换为施工平面坐标系[6],并将压路机向前行进的方向设为施工平面坐标系的纵向,将与压路机纵向相垂直的方向设为施工平面坐标系的横向.由于压路机施工坐标系与北京54坐标系方向不一致,所以需要进行平面坐标转换即参数转换.
采用平面四参数法进行转换.将坐标进行平移或者对控制点进行测量,获取施工路段中两个坐标系下两组以上的公共点值,代入平面四参数转换模型获得相应的转换参数[7-10],转换原理如图 3所示.
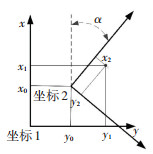
|
图 3 平面四参数转换法原理图 Figure 3 Schematic diagram of four-parameter plane conversion method |
图 3中:原坐标为(xi, yi)1,经过四参数转换后坐标为(xi, yi)2,需要求解的参数为(x0, y0, α, m),x0为x平移参数,y0为y平移参数,α为平面旋转参数,m为尺度因子,平面四参数转换公式如下:
| $ \begin{array}{*{20}{c}} {{{\left( {\begin{array}{*{20}{c}} {{x_i}}\\ {{y_i}} \end{array}} \right)}_2} = \left( {\begin{array}{*{20}{c}} {{x_0}}\\ {{y_0}} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {\cos \alpha }&{ - \sin \alpha }\\ {\sin \alpha }&{\cos \alpha } \end{array}} \right){{\left( {\begin{array}{*{20}{c}} {m{x_i}}\\ {m{y_i}} \end{array}} \right)}_1} = }\\ {{{\left( {\begin{array}{*{20}{c}} 1&0&{{x_i}}&{ - {y_i}}\\ 0&1&{{y_i}}&{{x_i}} \end{array}} \right)}_1}\left( {\begin{array}{*{20}{c}} {{x_0}}\\ {{y_0}}\\ {m\cos \alpha }\\ {m\sin \alpha } \end{array}} \right).} \end{array} $ | (3) |
压路机在施工平面坐标系下的坐标由北京54坐标系的坐标、转换参数和式(3)获得.
综上所述,为了实现压路机在压实过程中的实时定位,利用高斯-克吕格投影正算法求解得到压路机在北京54平面坐标系上的平面坐标,进而采用平面四参数转换法即可得到压路机在施工平面坐标系下的实时位置.
2 压路机碾压轨迹平面定位算法压路机碾压轨迹的平面定位是在实现压路机压实过程实时定位的基础上,直观、方便地反映压路机在施工平面坐标系的具体碾压路径、实时位置及压实遍数等重要信息.
2.1 压路机碾压轨迹纵向定位算法设定压路机开始施压时车身的左侧钢轮为基准点,用O表示,在施工平面坐标系中的横向坐标和纵向坐标分别用A、S表示,任意时刻压路机的施工坐标为(AK, SK),GPS接收机安装在压路机左侧钢轮振动轴上,施工坐标系示意简图如图 4所示.
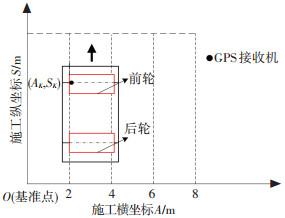
|
图 4 压路机施工平面坐标系示意简图 Figure 4 Schematic diagram of the roller's construction coordinate system |
分析压路机平面定位时,对相关参数进行定义如下:压路机的横向距离为M,车道数为N,默认起始时N=1.
压路机在压实过程中向前行进时,纵向位置随时间而改变,则纵向坐标可用时间函数表达如下:
| $ S = F\left( t \right). $ |
由式(1)和式(2)分别可得压路机在北京54平面坐标系下的纵坐标xi1和横坐标yi1,代入式(3)得到压路机的施工纵坐标yi2为
| $ {{\rm{y}}_{i2}} = {y_0} + m{x_{i1}}\sin \alpha + m{y_{i1}}\cos \alpha . $ |
式中:y0为y平移参数,α为平面旋转参数,m为尺度因子.
设压路机的采样频率为f,则采样周期T=1/f,在第k时刻,压路机的纵向位置的离散函数表示如下:
| $ S\left( k \right) = G\left( {kT} \right)\;\;\;\;k = 0,1,2, \cdots ,n. $ |
根据每一采样时刻下的纵向坐标可确定压路机的纵向位置,通过求取纵向坐标与基准点的纵坐标差值来进行轨迹的纵向定位.
为了验算压路机纵向定位的准确性,选取重庆地区某场地进行试验.该场地规格为105 m*68 m,以场地宽度与长度相交点作为坐标原点,以场地长为纵坐标,宽为横坐标,试验人员手持GPS接收机沿纵坐标行走,将GPS接收机获取的大地坐标转换成施工坐标后共得到108组数据,在此代表性地选取了部分数据,如表 1所示.
| 表 1 纵向定位试验数据 Table 1 Data sheet of vertical positioning experiment |
数据显示:GPS测量的总距离为99.72 m,误差为5.28 m,具体到相邻的位置信息值,最大误差为0.82 m,最小误差为0.58 m,平均误差为0.67 m.结合压路机在工程应用的实际情况,纵向两相邻位置误差值在可允许的2 m接收范围内,表明本文的GPS纵向定位方法对测量结果影响较小,可以采用.
2.2 压路机碾压轨迹横向定位算法根据式(1)和式(2)分别可得压路机在北京54平面坐标系下的纵坐标xi1和横坐标yi1,代入式(3)得到压路机的施工横坐标xi2为
| $ {x_{i2}} = {x_o} + m{x_{i1}}\cos \alpha - m{y_{i1}}\sin \alpha . $ |
式中:x0为x平移参数,α为平面旋转参数,m为尺度因子.
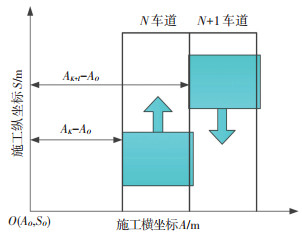
压路机在施工过程中,由于横向定位距离较短,对横向定位要求更加精准.特别是当压路机进行实际施工时, 在任一压实方式下都需要变道,故本文采用压路机所在的车道数进行横向定位.设定GPS接收机的误差值范围为(δ1,δ2),压路机每次变道变化的横向距离为L,基准点的横向坐标为AO,在K时刻的横向坐标为AK,在K+1时刻的横向坐标为AK+1,距离基准点的理论横向差值为Aeax,则压路机变道判别公式如下:
| $ \left\{ \begin{array}{l} {A_{{\rm{eax}}}} + {\delta _1} \le {A_K} - {A_O} \le {A_{{\rm{eax}}}} + {\delta _2},\\ {A_{{\rm{eax}}}} + {\delta _1} \le {A_{K + 1}} - {A_O} \le {A_{{\rm{eax}}}} + {\delta _2}. \end{array} \right. $ | (4) |
其中,Aeax=AO±kL,根据基准点的横坐标值进行相应车道数横坐标值范围设定,为防止GPS接收机数值的跳点或者突变,只有当压路机在K时刻和K+1时刻同时满足判别条件时,才认定压路机发生了变道[11-12],据此得到横向定位原理图如图 5所示.
|
图 5 横向定位原理图 Figure 5 Schematic diagram of horizontal positioning |
常见的压路机振动钢轮宽度集中在2.130 m,选取该值作为模拟实验的振动钢轮宽度,为保证两碾压道交接处碾压充分,压路机每次碾压的横向距离应为压路机钢轮宽度的90%,本文取横向碾压距离M为2.0 m.
同上文所述试验过程类似,设场地长为横坐标,宽为纵坐标,进行三组变道试验,每组都以2.0 m宽度进行变道.试验轨迹示意图如图 6所示.
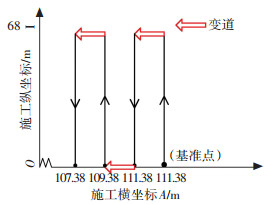
|
图 6 试验轨迹示意图 Figure 6 Schematic diagram of test trajectory |
实验中起始点的实际横坐标值为112.6 m,以起始点作为基准点,得到其在施工平面坐标系下的横坐标值为113.38 m,结合实验轨迹示意图可得:三次变道后在施工平面坐标系下的横坐标理论值应分别为111.38、109.38、107.38 m.由于三次变道得到的试验数据基数太大,本文仅代表性地列出第三次变道后的部分数据,如表 2所示.
| 表 2 第三组实验数据表 Table 2 The third set of experimental data sheet |
横向坐标实际值应与基准点横向坐标相差6 m, 由表 2可知,试验得到的距离基准点距离值与理论值非常接近.
综合第一、二次变道数据并分析,结果如表 3所示.
| 表 3 试验数据汇总分析表 Table 3 Analysis table of the experimental data |
由表 3可知,试验的最大误差值为0.77 m,最小值为0.20 m,第一、二、三次变道试验的平均误差分别为0.13、0.38、0.27 m.将试验数据的绝对误差值进行正态分布曲线拟合,拟合的正态分布曲线服从N(0.139 6,0.025 0),标准差δ为0.158 2,即μ=0.139 6,σ=0.158 2,且曲线关于0.139 6对称.
为确定GPS接收机的测量误差值,根据置信度要求:P(δ1≤A≤δ2)>0.95,换算成为标准正态分布,可得
| $ \begin{array}{l} p\left( {{\delta _1} \le A \le {\delta _2}} \right) = P\left( {\frac{{{\delta _1} - u}}{\delta } \le \frac{{A - u}}{\delta } \le \frac{{{\delta _2} - u}}{\delta }} \right) = \\ \;\;\;\mathit{\Phi }\left( {\frac{{{\delta _2} - u}}{\delta }} \right) - \mathit{\Phi }\left( {\frac{{{\delta _1} - u}}{\delta }} \right) > 0.95. \end{array} $ |
由于本样本绝对误差最小值为-0.77 m,则可设样本误差最低值为δ1=-0.70 m,根据式(4)可得
| $ \mathit{\Phi }\left( {\frac{{{\delta _1} - u}}{\sigma }} \right) = 0.000\;1. $ |
为使P(δ1≤X≤δ2)>0.95,则要求
| $ \mathit{\Phi }\left( {\frac{{{\delta _2} - u}}{\sigma }} \right) > 0.95 + 0.000\;1 = 0.950\;1, $ |
即Φ>0.950 1.查表可得
根据以上分析,可以获得GPS测量误差值,则压路机变道判别公式为
| $ {A_{{\rm{eax}}}} - 0.7 \le {A_K} - {A_O} \le {A_{{\rm{eax}}}} + 0.41, $ |
| $ {A_{{\rm{eax}}}} - 0.7 \le {A_{K + 1}} - {A_O} \le {A_{{\rm{eax}}}} + 0.41. $ |
按照规定,允许误差的范围必须在标准误差值的3倍以内.将标准误差记作δs,标准误差值的计算公式如下:
| $ {\delta _s} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {\left( {{x_k} - \bar x} \right)_i^2} } . $ | (5) |
式中:n为数据样本数,xk为压路机实际绝对误差值,x为压路机实际绝对误差平均值.
由式(5)得出标准误差值δs为0.43 m,则允许误差最大值是1.29 m,而样本设定的最大误差的绝对值0.70 m在允许误差范围内,满足要求.
根据工程实况、压路机判别公式和设定的车道数,横向定位数据表如表 4所示.
| 表 4 横向定位数据表 Table 4 Data sheet of horizontal positioning |
表 4中显示的车道与模拟的实际车道保持一致,说明本文采用的横向定位算法可有效解决压路机在施工过程中的横向定位问题.
3 压路机碾压轨迹用横坐标表示车道数,纵坐标表示距离基准点的纵向压实距离,分别用红橙黄绿青蓝紫灰八种颜色和不同的线条形状来对应1~8遍碾压遍数,以压路机完成第二遍压实,正在进行第三遍压实且位于第3车道为例,碾压轨迹示意图如图 7所示.
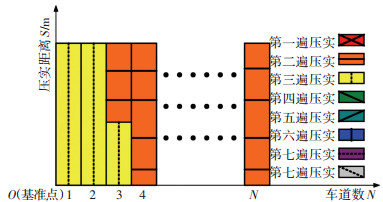
|
图 7 压路机碾压轨迹示意图 Figure 7 Schematic diagram of the roller track |
图 7不但能够实现压路机的平面定位,实时、直观地反映压路机在压实过程中的车道数、碾压遍数等信息,还有助于驾驶员宏观地查看道路压实的均匀性,便于施工过程中对道路压实的控制和调整.
4 压路机碾压轨迹的实时监控结合本文对压路机碾压轨迹平面定位算法的研究,利用LabVIEW软件开发的压路机压实过程实时监控系统在安徽省济祁高速公路上开展应用研究,试验路段全长520 km,其中砀山段为研究的主要测试路段,该段全长23.2 km,全线采用沥青混凝土路面,路面宽度为23.5 m,为双向6车道,试验选用戴纳派克CC624HF双钢轮振动压路机,压实遍数为8遍.由于试验数据较大,本文象征性地给出第三遍压实的某段数据,如表 5所示.
| 表 5 压路机实时监控系统相关数据 Table 5 Real-time monitoring system related data of the roller |
监控系统测试的第3遍碾压轨迹实时界面图如图 8所示[13-14].
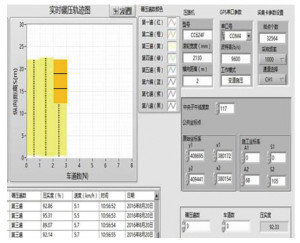
|
图 8 监控系统测试实时界面图 Figure 8 Real time interface of monitoring system |
该监控系统测试实时界面图中显示的压路机原始经纬度值、施工坐标系下的纵向距离和压路机所处车道位置、碾压遍数等信息与试验人员记录的一致,说明本文所做的研究准确合理,实现了对压路机碾压轨迹的实时监控并证明了该系统的快捷性、可靠性和实用性.
5 结论1) 运用高斯-克吕格投影和平面四参数转换法建立的压路机施工平面坐标系可准确地显示出压路的实际施工位置.
2) 将GPS接收机获取的大地坐标转换成压路机施工平面坐标系上的坐标可实现压路机碾压轨迹的平面定位.其中,纵向位置通过压路机与基准点的纵向距离来确定,横向位置通过压路机所在车道数来确定.
3) 通过对压路机碾压轨迹示意图的绘制,可清晰地观测到压路机的实时定位情况.结合该研究,在实际工程中利用压路机压实过程实时监控系统实现了压路机碾压轨迹的实时监控.
| [1] |
李江. 压路机碾压遍数控制研究及关键设备[J]. 公路交通科技, 2014(5): 1547. LI Jiang. Research on roller compacting control and key equipment for roller compacting[J]. Technology of Highway and Transport, 2014(5): 1547. |
| [2] |
沈叶飞, 陈一馨, 董华祥, 等. 压路机施工过程监控信息化管理系统研究[J]. 筑路机械与施工机械化, 2014(12): 103. SHEN Yefei, CHEN Yixin, DONG Huaxiang, et al. Roller construction process monitoring information management system of road roller[J]. Construction Machinery and Equipment, 2014(12): 103. DOI:10.3969/j.issn.1000-033X.2014.12.043 |
| [3] |
FURUYA H, KUSHIMA M. Real-time construction management by means of accelerometers installed in vibrating rollers[J]. Soil Mechanics & Foundation Engineering, 2002, 50(6): 19. |
| [4] |
杜文雅.智能压实中的GPS测距技术研究[D].太原: 太原科技大学, 2014. DU Wenya. Research on GPS range finder in intelligent compaction research[D]. Taiyuan: Taiyuan University of Science and Technology, 2014 http://cdmd.cnki.com.cn/Article/CDMD-10109-1014255409.htm |
| [5] |
陆彩红.椭球, 投影参数变化对高斯平面坐标的影响[D].上海: 同济大学, 2006 LU Caihong. Ellipsoid, the effect of projection parameter variation on gaussian plane coordinates[D]. Shanghai: Tongji University, 2006 http://cdmd.cnki.com.cn/Article/CDMD-10247-2006047757.htm |
| [6] |
常青, 柳重堪, 张其善. GPS定位与测速算法研究[J]. 北京航空航天大学学报, 2008, 24(5): 510. CHANG Qing, LIU Chongkan, ZHANG Qishan. Research on GPS positioning and velocity measurement[J]. Journal of Beijing University of Aeronautics and Astronautics, 2008, 24(5): 510. |
| [7] |
韦艳, 陈华根. GPS定位显示中的坐标转换[J]. 海洋测绘, 2010, 3(30): 16. WEI Yan, CHEN Huagen. GPS positioning display coordinate conversion[J]. Oceanographic Mapping, 2010, 3(30): 16. |
| [8] |
罗德安, 廖丽琼. 一种车载GPS系统坐标转换公式及应用[J]. 西南交通大学学报, 2001, 36(4): 365. LUO Dean, LIAO Liqiong. A coordinate conversion formula for vehicle GPS system and application[J]. Journal of Southwest Jiao Tong University, 2001, 36(4): 365. DOI:10.3969/j.issn.0258-2724.2001.04.007 |
| [9] |
李岳.坐标转换系统的设计与实现[D].北京: 中国地质大学, 2010 LI Yue. Design and implementation of coordinate conversion system[D]. Beijing: China University of Geosciences, 2010 |
| [10] |
MOSAVI, SHAFIEE. Narrowband interference suppression for GPS navigation using neural networks[J]. GPS Solutions, 2016, 20(3): 341. DOI:10.1007/s10291-015-0442-8 |
| [11] |
杜鹏, 傅梦印, 张鸿业, 等. GPS定位误差分析与建模[J]. 北京理工大学学报, 1998, 18(4): 456. DU Peng, FU Mengyin, ZHANG Hongye, et al. GPS positioning error analysis and modeling[J]. Journal of Beijing Institute of Technology, 1998, 18(4): 456. |
| [12] |
巩树涛.高等级公路路基压实质量实时监控系统的研制与应用[D].天津: 天津大学, 2014 GONG Shutao. Development and application of real-time monitoring system for high grade highway subgrade compaction quality[D]. Tianjin: Tianjin University, 2014 http://cdmd.cnki.com.cn/Article/CDMD-10056-1015018232.htm |
| [13] |
郑对元. 精通LabVIEW虚拟仪器程序设计[M]. 北京: 清华大学出版社, 2012: 23. ZHENG Duiyuan. Proficient in LabVIEW virtual instrument design[M]. Beijing: Tsinghua University Press, 2012: 23. |
| [14] |
韩琪.基于虚拟仪器的数据采集与分析系统研究与设计[D].北京: 北京交通大学, 2011: 123 HAN Qi. Research and design of data acquisition and analysis system based on virtual instrument[D]. Beijing: Beijing Jiao Tong University, 2011: 123 http://cdmd.cnki.com.cn/Article/CDMD-10004-1012319150.htm |
 2019, Vol. 51
2019, Vol. 51


