近年来,针对汽车行驶的安全性问题,全世界汽车制造商、研究学者都对其进行了深入的研究.汽车行驶安全技术主要分为被动安全技术和主动安全技术.主动安全技术通过先进的控制技术,如主动转向[1]、主动制动[2-3]、主动悬架[4]等提高汽车的横摆与侧翻稳定性.被动安全技术主要从车辆在生产研制过程中,设计合理的汽车结构参数从而提高其行驶稳定性.轮胎作为汽车行驶系的关键部件之一,其力学特性对汽车行驶安全性有重要影响.文献[5-7]对复杂工况下的轮胎力学特性与试验进行了深入研究.轮胎和整车横摆与侧翻稳定性是一个相互匹配的关系,文献[8-9]对影响汽车操稳性的充气轮胎力学特性进行了匹配研究.然而,装配普通充气轮胎的汽车在行驶过程中存在泄气、胎压不稳、爆胎等多个危险因素,据统计,由轮胎安全隐患引发的严重交通事故占比约50%,在高速公路的占比更高达60~70%[10],而且大多因扎钉、漏气而导致轮胎在运行中发生爆胎[11].
为克服充气轮胎存在的安全隐患,提高其行驶安全性,赵又群提出了一种新型结构形式的非充气机械弹性安全车轮(MEW),具有抗刺扎、防破损及承载能力强等优势,并对MEW的静力学特性[12]、接地特性[13]、纵向力学特性[14]、侧偏力学特性[15]、振动特性[16]以及通过性[17]等进行了大量的研究, 但还未对匹配MEW的汽车进行横摆与侧翻稳定性分析和评价.综合考虑MEW的自身结构特点,研究MEW的侧偏特性对汽车横摆与侧翻稳定性的具体影响规律,为车轮侧偏性能的改进及车轮结构优化提供相应的理论基础及试验依据.
1 机械弹性车轮力学模型机械弹性车轮是一种新型的非充气安全车轮,其结构如图 1所示, 主要由輮轮、铰链组和悬毂构成.将悬毂简化为刚性圆环,将弹性部件简化为连接在圆环上的弹性刷毛,刷毛与路面接触承受垂向、纵向和侧向力.不考虑胎宽影响,将所有变形集中到接触面的中分线上.基于刷子理论模型,分别建立了MEW的纵向和侧向力学模型.刷子模型建模机理简单且表达轮胎力学特性好,广泛应用于车辆动力学仿真分析中.

|
图 1 机械弹性车轮结构示意图 Figure 1 Structure of the ME-wheel |
当车轮与路面的接地印迹长度为2lp,以印迹中点为坐标原点建立车轮的纵向变形,如图 2所示.

|
图 2 车轮纵向变形示意 Figure 2 Tread deformation in longitudinal direction |
以刷毛单元A-A′为例,相对于车轮中心,刷毛单元A点以角速度ω向后转动,rw为等效半径,下端A′由于路面附着的作用,以速度vx向后运动.设刷毛单元在x方向的纵向变形为ξ,则有
| $ \xi = \left( {\omega {r_{\rm{w}}} - {v_x}} \right)\Delta t = \left( {\omega {r_{\rm{w}}} - {v_x}} \right)\frac{{\Delta t}}{{\Delta x}}\Delta x = \frac{{\omega {r_{\rm{w}}} - {v_x}}}{{\omega {r_{\rm{w}}}}}\Delta x. $ | (1) |
式中,Δx为刷毛单元A-A′从进入接触区到x点的纵向位移.定义纵向滑移δx=(ωrw-vx)/ωrw,而汽车行驶的纵向滑移率定义为sx=(rwωw-vx)/vx, 二者满足δx=sx/(1+sx), 式(1)化简为ξ=δxΔx=δx(lp-x),整个接触区域的纵向力为
| $ {F_x} = \int_{ - {l_{\rm{p}}}}^{{l_{\rm{p}}}} {{c_{{\rm{e}}x}}\xi {\rm{d}}x} = 2{c_{{\rm{e}}x}}l_{\rm{p}}^2{\delta _x}. $ |
式中,cex为刷毛单元纵向刚度.若地面附着系数为μ,则每一个刷毛单元的最大侧向力满足Fex≤ μFez,定义刷毛单元的垂向分布载荷Fez(x)=λc(lp2-x2),其中,λc为待定常数.整个印迹长度内的垂向力为
| $ {F_z} = \int_{ - {l_{\rm{p}}}}^{{l_{\rm{p}}}} {{F_{{\rm{e}}x}}\left( x \right){\rm{d}}x} = \int_{ - {l_{\rm{p}}}}^{{l_{\rm{p}}}} {{\lambda _{\rm{c}}}\left( {l_{\rm{p}}^2 - {x^2}} \right){\rm{d}}x} , $ | (2) |
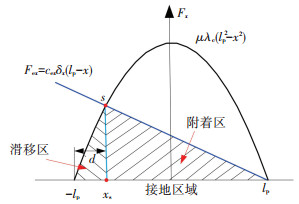
若Fz已知, 则由式(2)可得λc=3Fz/4lp3.轮胎在整个接地区域的纵向力分布Fex如图 3所示.
|
图 3 接地印迹纵向力分布示意 Figure 3 Sketch of the strains along the contact area of the tire |
当|xs| < lp时,临界点xs将整个接地区分为附着区和滑移区,前部分为附着区,后部分为滑移区,且cexδx(lp-xs)=μλc(lp2-xs2),化简得lp+xs=cexδx/μλc.令lp+xs=d,则d=cexδx/(μλc),当xs=lp时,d=2lp,此时的滑移率为2lpμλc/cex=δc, x,一般当滑移率在0.2左右时,纵向力达到最大值.故当δc, x设定时可求出cex.整个接地区域的纵向力为
| $ {F_x} = \mu \int_{ - {l_{\rm{p}}}}^{{x_{\rm{s}}}} {{\lambda _{\rm{c}}}\left( {l_{\rm{p}}^2 - {x^2}} \right){\rm{d}}x} + \int_{{x_{\rm{s}}}}^{{l_{\rm{p}}}} {{c_{{\rm{e}}x}}{\delta _x}\left( {{l_{\rm{p}}} - x} \right){\rm{d}}x} , $ | (3) |
式(3)可化简为
| $ {F_x} = \frac{1}{3}\mu {\lambda _{\rm{c}}}{d^2}\left( {3{l_{\rm{p}}} - d} \right) + \frac{1}{2}\mu {\lambda _{\rm{c}}}d{\left( {2{l_{\rm{p}}} - d} \right)^2}. $ |
以印迹中点为坐标原点建立车轮的垂向及侧向变形示意图如图 4所示.

|
图 4 车轮载荷分布及侧向变形示意 Figure 4 Tread deformation of the elements in lateral direction |
以刷毛单元A-A″为例,当车轮的侧偏角为α时,刷毛单元在Y方向的侧向变形为ζ=(lp-x)tan α.设cey为车轮的侧向分布刚度,在整个接触区域内,刷毛单元侧向形变的单元弹性力为Fey=ceyζ, 假设车轮在整个接地区域内无滑移,则侧向力为
| $ {F_y} = \int_{ - {l_{\rm{p}}}}^{{l_{\rm{p}}}} {{c_{{\rm{e}}y}}\zeta {\rm{d}}x} = 2{c_{{\rm{e}}y}}l_{\rm{p}}^2\tan \alpha , $ |
每一个刷毛单元的最大侧向力满足Fey≤μFez,则刷毛单元的最大侧向力为
| $ {F_{{\rm{e}}y,\max }} = \mu {\lambda _{\rm{c}}}\left( {l_{\rm{p}}^2 - x_{\rm{t}}^2} \right). $ |
考虑实际情况中整个接触区域内可能会有滑移的存在,因为随着轮胎侧偏角α的逐渐增大,车轮接地区域的后部会出现局部滑移. 图 4中,t是印迹区域内滑移区与附着区的临界点,xt为起滑点的纵坐标,其有效范围为-lp≤xt≤lp,当x=xt时,侧向分布力达到最大值.定义
| $ {\theta _y} = \left( {2{c_{{\rm{e}}y}}l_{\rm{p}}^2} \right)/3\mu {F_z}, $ |
则在整个接触区域内的侧向力为
| $ {F_y} = \int_{ - {l_{\rm{p}}}}^{{x_t}} {{F_{{\rm{e}}y,\max }}{\rm{d}}x} + \int_{{x_t}}^{{l_{\rm{p}}}} {{F_{{\rm{e}}y}}{\rm{d}}x} . $ |
当xt=lp时,车轮在接地区域内开始全部滑移,设此时的侧偏角为αc,则有tan αc=1/θy, 一般当侧偏角为8°~12°左右时,侧向力逐渐发生饱和.故而αc设定时,便可求出整个印迹区域内的侧向力Fy为
| $ {F_y} = \mu {F_z}{\theta _y}\left( {3\tan \alpha - 3{\theta _y}{{\tan }^2}\alpha + \theta _y^2{{\tan }^3}\alpha } \right). $ |
常用的室内轮胎试验台架可分为转鼓式、平板式和钢带式3种,其中平板式试验台的试验重复性较好,成本低,但是试验速度较低.钢带式试验台可实现高速轮胎特性试验,但成本高,难度大.利用自行研制的平板式轮胎力学特性试验台(见图 5),对MEW样机进行力学特性试验.

|
图 5 平板式轮胎力学特性试验台 Figure 5 Experimental set-up for tire mechanical characteristics |
试验状态参数主要包括纵向滑移率、侧偏角、垂向载荷、摩擦因数等.选取某型MEW的力学实验数据作为轮胎模型的参数,利用二次多项式拟合方法,得到车轮接地印迹半长和侧向分布刚度随着垂向载荷的变化关系,分别为
| $ {l_{\rm{p}}} = {a_1}F_z^2 + {a_2}{F_z} + {a_3},{c_{{\rm{e}}y}} = {b_1}F_z^2 + {b_2}{F_z} + {b_3}. $ |
其中参数a1~a3和b1~b3见表 1所示.
| 表 1 刷子模型拟合参数 Table 1 Fitted coefficient of brush model |
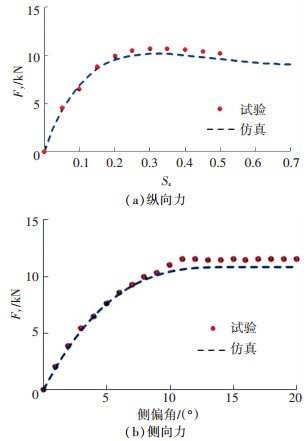
动力机构带动模拟路面以0.3 m/s的平移速度从试验台架一侧移至另一侧,利用建立的纵滑与侧偏力学模型对MEW力学特性进行仿真分析,其中垂向载荷为15 kN,摩擦因数为0.8,滑移率为0~0.7,侧偏角为0°~20°. MEW稳态纵滑与侧偏刷子模型的仿真结果和车轮物理样机的试验结果对比如图 6所示.
|
图 6 车轮力学关系曲线 Figure 6 Tire force response |
从图 6可知,理论模型的仿真与试验结果有较好的一致性.刷子模型在纵滑特性与侧偏特性整体趋势的表达上是准确的.为了对建立的车轮刷子理论模型的精度进行量化,采用精度偏差公式
| $ \delta ' = \sqrt {\sum\limits_{i = 1}^n {{{\left( {{x_{i\_{\rm{Ana}}}} - {x_{i\_{\rm{Mea}}}}} \right)}^2}} /\sum\limits_{i = 1}^n {x_{i\_{\rm{Mea}}}^2} } \times 100\% . $ | (4) |
式中:xi_Ana为理论模型的解析值, xi_Mea为车轮力学特性的试验值, n为所取数据点总数.
利用式(4)获得MEW侧偏刷子模型的预测精度.稳态纵滑工况下,该模型的纵向力预测平均相对误差为6%;稳态侧偏工况下,该模型的纵向力预测平均相对误差为7%,预测精度满足要求,从而验证了刷子理论模型的有效性.
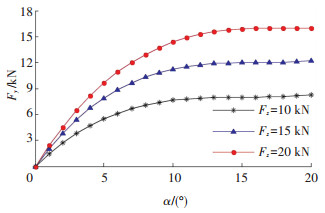
不同垂向载荷下MEW的稳态纵滑与侧偏特性结果分别如图 7、8所示.

|
图 7 不同载荷下MEW纵向力Fx与滑移率sx的关系曲线 Figure 7 Longitudinal tire force at different sx and different Fz |
|
图 8 不同载荷下MEW侧向力Fy与侧偏角α的关系曲线 Figure 8 Lateral tire force at different slip angles and different Fz |
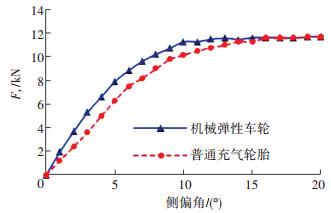
根据MEW的几何尺寸,选取与其外径及胎宽相近的37×12.5R16.5型子午线充气轮胎(300 kPa)作为MEW侧偏特性的对比参照轮胎,利用试验台分别对子午线胎和MEW样机进行稳态侧偏力学试验,并通过获取的侧偏试验数据对比分析两种轮胎在侧偏力学特性方面存在的差异.在15 kN垂向载荷工况下,两种轮胎的侧偏特性对比如图 9所示.
|
图 9 子午线胎与机械弹性车轮的侧偏特性对比 Figure 9 Cornering properties comparison: pneumatic tire vs. MEW |
从图 9可知,MEW与子午线充气轮胎侧偏特性曲线的变化趋势基本一致,侧向力峰值基本相同,但机械弹性车轮的侧偏刚度较大.
2 匹配MEW的Carsim仿真模型利用车辆动力学仿真标准软件Carsim,建立匹配MEW的某越野车仿真模型.忽略不同车速对车轮侧偏特性的影响,利用刷子模型获取轮胎力学数据,仿真用车辆主要参数与实验用车参数一致,车辆建模主要参数如表 2所示.
| 表 2 某越野车的主要车辆参数 Table 2 Parameters and values for off-road vehicle model |
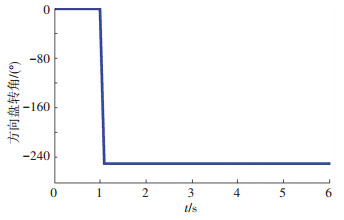
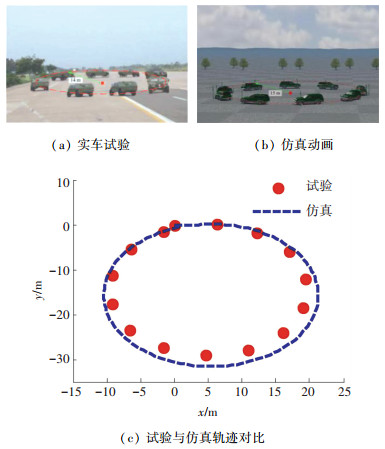
其他仿真参数取:质心到前轴距离lf=1.520 m,质心到后轴距离lr=1.830 m,质心到侧倾中心距离hs=0.570 m,横摆转动惯量Iz=5 757 kg·m2,侧倾转动惯量Ix=1 614 kg·m2,初始车速vx=60 km/h,路面附着系数μ=0.85,为了验证仿真模型的有效性,采用方向盘阶跃输入,如图 10所示,转向角值为-250°,实车试验与仿真的行驶轨迹对比如图 11所示.
|
图 10 方向盘阶跃输入(转向传动比为20) Figure 10 Steering wheel angle step input test |
|
图 11 稳态转向轨迹与转弯半径 Figure 11 The steady turning trajectory and radius |
从图 11中可以看出,建立的Carsim仿真模型能够比较准确地描述车辆的运动.匹配MEW与普通充气轮胎的汽车横摆与侧翻响应对比如图 12所示.侧向力对比如图 13所示.

|
图 12 匹配MEW与充气轮胎的汽车阶跃输入响应 Figure 12 Step input maneuver test by common tire and MEW |

|
FL、FR、RL和RR分别代表左前、右前、左后、右后轮 图 13 各车轮的侧向力对比 Figure 13 Lateral force comparisons of the four wheels |
从图 12中可以看出,与普通充气轮胎相比,在高速急转向时,匹配MEW的汽车侧翻稳定性较好,横摆稳定性较差,这主要与MEW侧偏刚度较大有关.
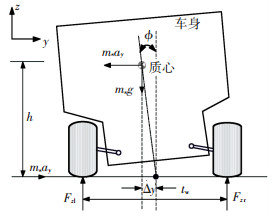
3 横摆与侧翻稳定性评价指标横摆稳定性以汽车的横摆角速度作为评价指标,基本能够描述汽车的横摆响应.为了能有效反映出汽车侧翻的动态情况,采用改进的载荷转移率(PLTR)作为侧翻稳定性的评价指标. 图 14为车辆侧倾时的简化示意图.
|
图 14 汽车侧翻简化模型力学分析 Figure 14 Force analysis of vehicle rollover model |
对图 14轮距中心点列稳态的力矩平衡式
| $ {m_{\rm{s}}}{a_y}h + {m_{\rm{s}}}g\Delta y = \left( {{F_{z{\rm{l}}}} - {F_{z{\rm{r}}}}} \right){t_{\rm{w}}}/2. $ | (5) |
其中Δy=h·sin φ.从力矩平衡方程(5)可以看出,影响汽车侧倾稳定性的因素有:质心处侧向加速度ay,质心到地面的高度h,两侧车轮的垂向载荷转移以及轮距中点相对于质心的横向偏差Δy.汽车在转向行驶时,用两侧车轮的垂向力的转移关系来预测汽车是否会发生侧翻,称为横向载荷转移率(nLTR),其表达式为
| $ {n_{{\rm{LTR}}}} = \frac{{{F_{z{\rm{r}}}} - {F_{z{\rm{l}}}}}}{{{F_{z{\rm{r}}}} + {F_{z{\rm{l}}}}}}. $ | (6) |
从式(6)可知,当左、右侧的车轮垂直载荷相等时,nLTR =0;当一侧车轮的垂直载荷为零时,nLTR为1或-1. nLTR的绝对值越大则表明汽车的侧翻风险越大.将式(5)代入式(6),并将汽车的簧载质量ms与总质量m近似处理,得到简化的nLTR的估计值表达式:
| $ {n_{{\rm{LTR}}}} = \frac{{2h}}{{{t_{\rm{w}}}}}\left[ {\frac{{{a_y}}}{g} + \sin \phi } \right]. $ | (7) |
考虑车轮的垂向载荷是随着车辆运动状态而不断变化的,nLTR的导数反映了其变化趋势,也从一定程度上反映未来时刻的nLTR,进而反映车辆的侧翻倾向.定义预测横向载荷转移率nPLTR为
| $ {n_{{\rm{PLT}}{{\rm{R}}_{{t_0}}}}}\left( {\Delta t} \right) = {n_{{\rm{LTR}}}}\left( {{t_0}} \right) + {{\dot n}_{{\rm{LTR}}}}\left( {{t_0}} \right) \cdot \Delta t. $ | (8) |
式中: Δt是预测时间,t0是当前时间.当侧倾角较小时, 假设sinϕ≈ϕ, 将式(7)代入式(8)得
| $ {n_{{\rm{PLT}}{{\rm{R}}_{{t_0}}}}}\left( {\Delta t} \right) = \frac{{2h}}{{{t_{\rm{w}}}}}\left[ {\frac{{{a_y}}}{g} + \phi } \right] + \frac{{2h}}{{{t_{\rm{w}}} \cdot g}}\left[ {{{\dot a}_y} + g \cdot \dot \phi } \right] \cdot \Delta t. $ |
选取侧偏刚度kα和侧向力峰值Fymax作为车轮侧偏特性的评价指标,利用汽车稳态转向特性分析MEW侧偏刚度对稳定性因素K的影响,从而得出车轮侧偏刚度对横摆稳定性的具体影响规律;利用定性分析方法得出侧向力峰值对汽车横摆与侧翻稳定性影响规律;最后利用相平面分析方法对上述理论分析进行了仿真验证.
4.1 车轮侧偏特性评价指标提取MEW的侧偏刚度kα、侧向力峰值Fymax作为车轮侧偏特性的评价指标,研究不同侧偏特性的MEW对汽车横摆与侧翻稳定性的具体影响规律.分析不同试验条件下的轮胎侧偏特性试验数据发现,车轮侧向力随侧偏角的变化趋势基本一致,当侧偏角<5°时,车轮的侧向力随侧偏角线性增大,当侧偏角继续增大时,车轮的侧向力非线性增加直到饱和.侧偏刚度是描述车轮侧偏特性的重要参数之一,其影响因素有车轮的结构参数和垂向载荷等.车轮在小侧偏角时,车轮的侧向力Fy与侧偏角α呈近似线性关系,车轮的侧向力主要与輮轮弹性变形的大小有关,此时
由线性二自由度动力学模型得汽车转向时的运动微分方程满足
| $ \left\{ \begin{array}{l} m\left( {{{\dot v}_y} + {v_x}\gamma } \right) = {k_{\rm{f}}}\delta - \left( {{k_{\rm{f}}} + {k_{\rm{r}}}} \right)\frac{{{v_y}}}{{{v_x}}} - \left( {{l_{\rm{f}}}{k_{\rm{f}}} - {l_{\rm{r}}}{k_{\rm{r}}}} \right)\frac{\gamma }{{{v_x}}},\\ {I_z}\dot \gamma = {l_{\rm{f}}}{k_{\rm{f}}}\delta - \left( {{l_{\rm{f}}}{k_{\rm{f}}} - {l_{\rm{r}}}{k_{\rm{r}}}} \right)\frac{{{v_y}}}{{{v_x}}} - \left( {l_{\rm{f}}^2{k_{\rm{f}}} + l_{\rm{r}}^2{k_{\rm{r}}}} \right)\frac{\gamma }{{{v_x}}}. \end{array} \right. $ |
式中:kf、kr分别为前、后轴车轮等效侧偏刚度,δ为前轮转角,γ为车辆的横摆角速度.
稳态转向时,有
| $ \gamma = \frac{{{v_x}/l}}{{1 + Kv_x^2}}\delta . $ |
式中:
| $ K = \frac{m}{{{l^2}}}\left( {\frac{{{l_{\rm{r}}}}}{{{k_{\rm{f}}}}} - \frac{{{l_{\rm{f}}}}}{{{k_{\rm{r}}}}}} \right),l = {l_{\rm{f}}} + {l_{\rm{r}}}, $ |
K为稳定性因素,K>0称为不足转向.为了保持车辆良好的操纵稳定性,汽车应该具有适度的不足转向.带入某越野车的试验参数和前后轴车轮等效侧偏刚度的拟合数据kf=2 198 N/(°)、kr=1 999 N/(°)得,K=0.022;将前后轴的拟合侧偏刚度同时增加和减少20%后得到的K分别为0.018和0.027.可知同时增大前后轴的侧偏刚度将减小汽车的不足转向,而同时减小汽车前后轴的侧偏刚度将增大汽车的不足转向.汽车的不足转向越小,汽车的灵敏性越高,汽车行驶安全性越差.
汽车失稳大多发生在轮胎进入非线性区域,侧向力达到饱和时,因此增大车轮的侧向力峰值可以提高汽车的横摆稳定性与侧翻稳定性.
4.3 汽车横摆与侧翻稳定性仿真分析以车轮的侧偏刚度kα和侧向力峰值Fymax作为变量,分析不同轮胎侧偏刚度值和侧向力峰值对车辆横摆与侧倾稳定性的影响.改变车轮的结构参数和材料特性,得到Fz=15 kN时的kα1~ kα3和Fy1max~ Fy3max的值,如表 3所示.
| 表 3 侧偏刚度和侧向力峰值取值 Table 3 Cornering stiffness and peak value of lateral force |
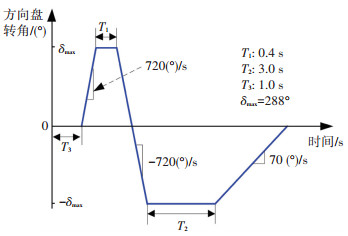
将车轮的侧偏刚度值在原来的基础上分别增加和减少20%,利用鱼钩试验仿真工况,最大转角为288°,如图 15所示,初始车速为60 km/h,得到输出的车辆横摆与侧倾响应的变化曲线图分别如图 16和17所示.
|
图 15 鱼钩转向试验 Figure 15 Steer angle input for Fishhook maneuver |

|
图 16 不同侧偏刚度的横摆响应对比 Figure 16 Yaw response comparison at different cornering stiffnesses |
|
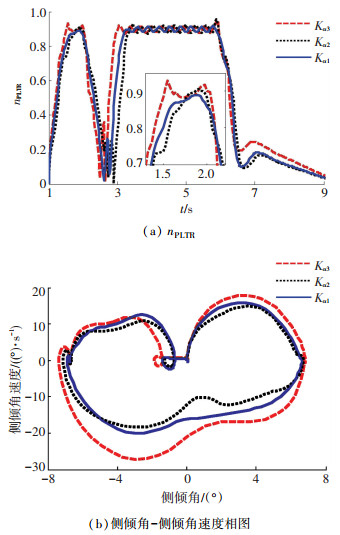
图 17 不同侧偏刚度的侧倾响应对比 Figure 17 Roll response comparison at different cornering stiffness |
从图 16(a)和图 17(a)可以看出,当侧偏刚度增大20%时,横摆稳定性评价指标增大了10%,侧倾稳定性评价指标nPLTR的最大值变化并不明显,但nPLTR的值均为0.85时, 对应的时刻比原来滞后0.1 s;当车轮的侧偏刚度减小20%时,横摆角速度减小了10%,nPLTR的最大值变化依然不明显,但nPLTR的值均为0.85时,对应的时刻比原来提前了0.1 s.
由图 16(b)和图 17(b)可知,当侧偏刚度增大20%时,质心侧偏角-横摆角速度相平面图曲线范围变大超过50%,侧倾角-侧倾角速度相平面图曲线范围变小在3%以内;当车轮的侧偏刚度减小20%时,质心侧偏角-横摆角速度相平面图曲线范围变小超过50%,侧倾角-侧倾角速度相平面图曲线范围变大在5%以内,图 18为不同侧偏刚度的三维仿真动画.
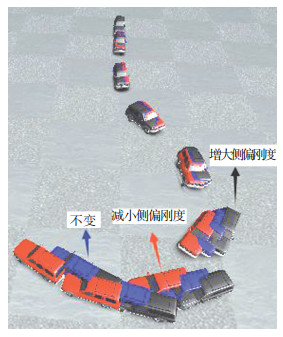
|
图 18 不同侧偏刚度的汽车鱼钩试验仿真动画 Figure 18 Vehicle trajectory comparison in Fishhook test at different ka |
由此可知,当车轮的侧向力峰值一定时,随着车轮侧偏刚度的增大,汽车的横摆稳定性变差,侧翻稳定性基本不变,汽车的灵敏性变高,仿真结果与理论分析保持一致.
4.3.2 车轮侧向力峰值对横摆与侧翻稳定性的影响将轮胎的侧向力峰值在原来的基础上增加和减少20%,保持侧偏刚度不变,其他条件不变,得到输出的车辆横摆与侧倾响应的变化曲线图如图 19、20所示.

|
图 19 不同侧向力峰值的横摆响应对比 Figure 19 Yaw response comparison at different Fymax |

|
图 20 不同侧向力峰值的侧倾响应对比 Figure 20 Roll response comparison at different Fymax |
从图 19(a)和图 20(a)可知,当车轮的侧向力峰值增大20%时,第一个波峰处的横摆角速度由最大值38(°)/s减小到30 (°)/s,nPLTR由最大值0.90减小到0.75;当车轮的侧向力峰值减小20%时,横摆角速度由原来的38(°)/s增加到45(°)/s,nPLTR由最大值0.9增加到1.1.由图 19(b)和图 20(b)可知,当车轮的侧向力峰值增大20%时,质心侧偏角-横摆角速度相平面图曲线范围变小超过30%,侧倾角-侧倾角速度相平面图曲线收敛范围变小超过10%;当车轮的侧向力峰值减小20%时,质心侧偏角-横摆角速度相平面图曲线范围变大3%以内,侧倾角-侧倾角速度相平面图曲线收敛范围变大超过50%. 图 21为不同侧向力峰值的三维仿真轨迹.
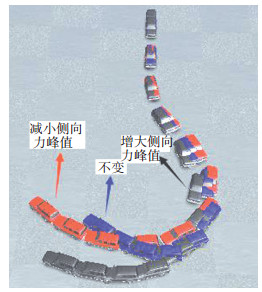
|
图 21 不同侧向力峰值的汽车鱼钩试验仿真动画 Figure 21 Vehicle trajectory comparison in Fishhook test at different peak values of lateral force |
由此可知,当侧偏刚度一定时,随着侧向力峰值的增大,汽车的横摆与侧翻稳定性均明显增强.
综上,通过改变车轮的结构参数与材料属性,在获得较大的侧向力峰值的同时适当减小车轮的侧偏刚度,可以提高匹配机械弹性车轮汽车的横摆与侧翻稳定性.
5 结论1) 机械弹性车轮与子午线充气轮胎侧偏特性曲线的变化趋势基本一致,侧向力峰值基本相同,但机械弹性车轮的侧偏刚度较大;与采用子午线胎的整车相比,匹配机械弹性车轮的整车侧翻稳定性较好,横摆稳定性较差.
2) 当侧向力峰值一定时,随着车轮侧偏刚度的增大,汽车的横摆稳定性变差,侧翻稳定性基本不变,汽车的灵敏性变高;当侧偏刚度一定时,随着车轮侧向力峰值的增大,汽车的横摆与侧翻稳定性均增强.
3) 在满足要求的情况下,通过改变车轮的结构参数与材料属性,在获得较大的侧向力峰值的同时适当减小车轮的侧偏刚度,可以提高匹配机械弹性车轮汽车的横摆与侧翻稳定性.
| [1] |
WU Jian, ZHAO Youqun, JI Xuewu, et al. Generalized internal model robust control for active front steering intervention[J]. Chinese Journal of Mechanical Engineering, 2015, 28(2): 285. DOI:10.3901/CJME.2015.0106.006 |
| [2] |
YANG Xiujian. Improvements in vehicle handling and stability by a novel wheel slip coordination control scheme[J]. International Journal of Vehicle Design, 2013, 62(2/3/4): 206. DOI:10.1504/IJVD.2013.052702 |
| [3] |
李占旗.基于差动制动的汽车横摆与侧翻稳定性集成控制研究[D].长春: 吉林大学, 2011 LI Zhanqi. Research on integrated control of vehicle yaw and rollover stability based on differential braking[D].Changchun: Jilin University, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10183-1011100237.htm |
| [4] |
LI Haiqing, ZHAO Youqun, LIN Fen, et al. Nonlinear dynamics modeling and rollover control of an off-road vehicle with mechanical elastic wheel[J]. Journal of the Brazilian Society of Mechanical Sciences & Engineering, 2018, 40(2): 1. DOI:10.1007/s40430-018-1009-8 |
| [5] |
GUO Konghui, LU Dang, CHEN S K, et al. The UniTire model: a nonlinear and non-steady-state tyre model for vehicle dynamics simulation[J]. Vehicle System Dynamic, 2005, 43(sup1): 341. DOI:10.1080/00423110500140690 |
| [6] |
杨一洋.胎面橡胶摩擦机理及复杂工况下轮胎侧偏特性研究[D].长春: 吉林大学, 2016 YANG Yiyang. Study of tread rubber friction mechanism and tire cornering properties under complex conditions[D].Changchun: Jilin University, 2016 http://cdmd.cnki.com.cn/Article/CDMD-10183-1017015830.htm |
| [7] |
WALLASCHEK J, WIES B. Tyre tread-block friction: modelling, simulation and experimental validation[J]. Vehicle System Dynamics, 2013, 51(7): 1017. DOI:10.1080/00423114.2013.803580 |
| [8] |
王国林, 梁辛欣. 基于操纵稳定性的轮胎特性匹配汽车操纵逆动力学研究[J]. 中国机械工程, 2013, 24(3): 422. WANG Guolin, LIANG Xinxin. Research on vehicle inverse dynamics based on compages of tire' characteristics for handing and stability[J]. China Mechanical Engineering, 2013, 24(3): 422. DOI:10.3969/j.issn.1004-132X.2013.03.028 |
| [9] |
胥永宫.轿车轮胎操纵稳定性匹配研究[D].长春: 吉林大学, 2011 XU Yonggong. Research on the match of vehicle and tire based on handling and stablility[D].Changchun: Jilin University, 2011 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=csjsllyj2015082487 |
| [10] |
郑宏宇, 宗长富, 刘海贞. 汽车爆胎特性建模与主动制动控制策略[J]. 中国公路学报, 2012, 25(4): 147. ZHENG Hongyu, ZONG Changfu, LIU Haizhen. Tire blow-out modeling and active braking control algorithm of vehicle[J]. China Journal of Highway and Transport, 2012, 25(4): 147. DOI:10.3969/j.issn.1001-7372.2012.04.024 |
| [11] |
JANG I G, SUNG Y H, YOO E J, et al. Pattern design of a non-pneumatic tyre for stiffness using topology optimization[J]. Engineering Optimization, 2011, 42(2): 119. DOI:10.1080/0305215X.2011.569546 |
| [12] |
ZHAO Youqun, ZANG Liguo, CHEN Yueqiao, et al. Non-pneumatic mechanical elastic wheel natural dynamic characteristics and influencing factors[J]. Journal of Central South University, 2015, 22(5): 1707. DOI:10.1007/s11771-015-2689-1 |
| [13] |
付宏勋, 赵又群, 林棻, 等. 胎圈结构参数对机械弹性车轮接地压力分布的影响[J]. 农业工程学报, 2015, 31(17): 57. FU Hongxun, ZHAO Youqun, LIN Fen. Influences of bead structure parameters on contact pressure distribution of mechanical elastic wheel[J]. Transactions of the Chinese Society of Agricultural Engineering, 2015, 31(17): 57. DOI:10.11975/j.issn.1002-6819.2015.17.008 |
| [14] |
LI Bo, ZHAO Youqun, ZANG Liguo, et al. Driving force model for non-pneumatic elastic wheel[J]. Transactions of Nanjing University of Aeronautics and Astronautics, 2016, 33(2): 231. DOI:10.16356/j.1005-1120.2016.02.231 |
| [15] |
DU Xianbin, ZHAO Youqun, LIN Fen, et al. Numerical and experimental investigation on the camber performance of a non-pneumatic mechanical elastic wheel[J]. Journal of the Brazilian Society of Mechanical Sciences & Engineering, 2017, 39(9): 3315. DOI:10.1007/s40430-016-0702-8 |
| [16] |
赵又群, 李小龙, 张明杰, 等. 机械弹性车轮随机振动理论与数值分析[J]. 哈尔滨工业大学学报, 2015, 47(7): 47. ZHAO Youqun, LI Xiaolong, ZHANG Mingjie, et al. Theoretical and numerical analysis on the random vibration of mechanical elastic wheel[J]. Journal of Harbin Institute of Technology, 2015, 47(7): 47. DOI:10.11918/j.issn.0367-6234.2015.07.007 |
| [17] |
汪伟, 赵又群, 黄超, 等. 新型机械弹性车轮的建模与通过性研究[J]. 中国机械工程, 2013, 24(6): 724. WANG Wei, ZHAO Youqun, HUANG Chao, et al. Modeling and trafficability analysis of new mechanical elastic wheel[J]. China Mechanical Engineering, 2013, 24(6): 724. DOI:10.3969/j.issn.1004-132X.2013.06.004 |
 2019, Vol. 51
2019, Vol. 51


