2. 上海机电工程研究所,上海 201109;
3. 上海飞机设计研究院,上海 201210
2. Shanghai Electro-Mechanical Engineering Institute, Shanghai 201109, China;
3. Shanghai Aircraft Design and Research Institute, Shanghai 201210, China
在大型客机的研制和适航取证工作中,对水上迫降性能有很高的要求.国内外对飞机水上迫降问题进行过大量研究,理论研究大多是在von Karman[1]和Wagner[2-3]的基础上展开.美国曾经进行过大量的飞机水上迫降实验研究,积累了很多经验.随着CFD技术的发展,数值模拟方法在水上迫降方面得到了广泛应用[4]. Guo等[5]数值研究了运输机迫降初始阶段俯仰角对迫降性能的影响,给出了最佳迫降俯仰角范围. Qu等[6]基于FLUENT软件,开发出整体运动网格方法,并采用该方法对NACA TN 2929飞机模型在平静水面迫降进行了数值模拟,详细研究了飞机模型各部件在水上迫降过程中的作用. Bensch等[7-8]采用理论分析结合经验参数的混合方法(hybrid method)对运输机有计划的平静水面迫降进行了数值模拟,可以快速估算出水上迫降的载荷,并给出机翼和机身的变形情况. Hua等[9]采用LS-DYNA软件中的ALE方法对一架三维全尺寸飞机低速平静水面迫降进行了数值模拟,并从安全迫降的角度对数值模拟结果进行了分析.
飞机水上迫降问题的研究大多是基于平静水面展开的,而一般情况下水面是存在波浪的.本研究首先数值模拟了三维平板斜向冲击入水、飞机模型平静水面迫降以及二维数值造波,验证了数值方法的有效性,在此基础上数值研究了飞机模型迎浪、顺浪以及平行于波浪迫降3种情况,分析了飞机在波浪中迫降的最优航向.
1 计算方法假设物体为刚体,忽略表面张力.采用VOF法捕捉自由液面,控制方程为非定常不可压缩的RANS方程,湍流模型为k-ω(SST-Menter).计算软件提供了刚性运动和加权变形两种动网格技术,刚性运动意味着网格完全跟随物体运动,加权变形则意味着求解器可以根据物体的具体运动位置和姿态对网格进行自适应变化,网格可以发生拉伸或扭曲变形,但网格总数不变[10].如果采用刚性动网格方法进行数值模拟,自由面附近的网格加密区会跟随飞机一起做刚性运动,无法保证自由面一直处于网格加密区内,从而导致自由面变模糊(见图 1(a)).对于飞机水上迫降的六自由度运动,在平移自由度上采用刚性运动方法,在旋转自由度上采用加权变形方法,以保证自由面一直处于网格加密区内.加权变形动网格技术的局限性在于网格只能在一定角度范围内扭转,当转动角度很大时,网格可能由于过度扭曲导致计算发散(见图 1(b)).

|
图 1 3种动网格方法效果对比 Figure 1 Comparison of three dynamic grid methods |
飞机在波浪水面迫降过程中转动角度很大,采用网格加权变形方法往往会出现计算发散现象,本文开发出的刚性动网格与滑移网格相结合的滑移动网格方法可有效处理此问题.将整个计算域划分为内外两部分:在物体附近划分球形内部计算域并进行网格加密,使其在六自由度方向都跟随物体做刚性运动;外面为外部计算域,为矩形,在自由面附近加密网格,外部计算域只跟随内部计算域在3个平移自由度上进行刚性运动,两个计算域交界面处采用滑移网格方法.该动网格方法在保证自由面处于网格加密区的同时可以模拟物体的任意姿态(图 1(c)). 3种动网格技术的效果对比见图 1.
由于滑移动网格在滑移交界面处会出现错位对接,尤其在入水初期流场变化比较剧烈,因此,需要对滑移面进行局部网格加密,同时增加内迭代次数以保证数据交互质量.
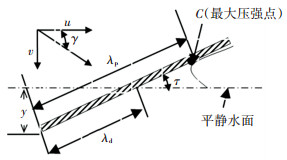
2 平静水面数值模拟分析 2.1 三维平板斜向冲击入水1951年,Smiley[11]对三维平板斜向冲击入水进行了一系列实验.平板以固定的倾角斜向冲击入水,给定初始水平速度和垂向速度,由于平板被一个质量很大的拖车拖行,惯性很大,在整个入水冲击过程中水平速度近似为匀速,而垂向速度受到水载荷作用逐渐减小.在斜向冲击入水过程中,平板受到一个垂直向上、大小等于重力的外力,见图 2.
|
图 2 平板斜向冲击入水示意 Figure 2 Diagram of plate oblique impact into water |
定义平板尾部到最大压强点的距离为湿润长度,平板尾部到平静水面的距离为水下长度,取平板的宽度b=0.305 m为特征长度, 得到量纲一的湿润长度λp和水下长度λd,水面抬升为λp-λd.
参考飞机水上迫降的姿态角范围,选择倾角τ=15°,初始水平和垂向速度分别为u=13.259 m/s, v=2.347 m/s, 平板质量为533.425 kg.由于平板在入水过程中姿态角保持不变,因此采用刚性动网格方法进行数值模拟.采用了粗、中、细三套网格进行网格收敛分析,在自由面附近设置了厚度为0.5 m的网格加密区,平板表面进行了网格细化和边界层加密,表 1为三套网格的参数.
| 表 1 网格参数 Table 1 Grid parameters |
图 3为三维平板斜向冲击入水过程中的垂向位移、垂向速度以及垂向冲击加速度曲线.可以看到,随着网格数增加,数值模拟的结果与实验值更加接近,总体吻合较好.

|
图 3 三维平板斜向冲击入水运动历程 Figure 3 Movement history of 3D plate oblique impact into water |
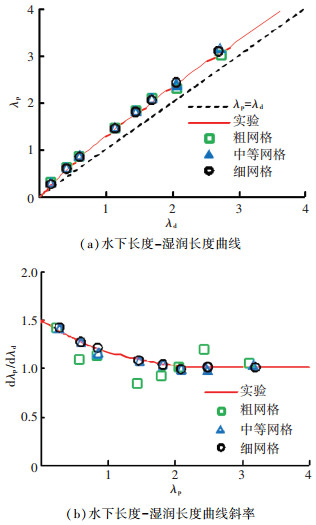
图 4给出数值模拟的水下长度和湿润长度曲线与Smiley的实验曲线对比.由图 4可知,中等网格和细网格与实验曲线吻合较好,粗网格差异较明显.在平板入水初期,存在明显的二维效应,水面抬升随λd增大而增加,dλp/dλd>1;随着入水深度的增加,三维效应增大,dλp/dλd逐渐减小到1并保持不变,大约在λp≥2时,水面抬升基本不再增加.
|
图 4 水下长度-湿润长度曲线及其斜率随湿润长度的变化 Figure 4 Relationship between the wetted length and the length below the undisturbed water surface |
图 5给出不同时刻平板底部中心线上的压强分布与实验的对比,在入水初期中等和细网格捕捉到的峰值压强与实验值更接近,粗网格的峰值压强比实验值低,压强峰值随入水深度增加逐渐减小.

|
图 5 不同时刻平板底部中心线压强分布 Figure 5 Pressure distribution at the center line of the bottom |
平板在斜向冲击入水过程中最大压强点C的速度为[11]
| $ \begin{array}{l} {v_C} = {u_{\rm{f}}}\left\{ {1 + 2\frac{{\sin \gamma }}{{\sin \left( {\gamma + \tau } \right)}}\left( {\frac{{{\rm{d}}{\lambda _{\rm{p}}}}}{{{\rm{d}}{\lambda _{\rm{d}}}}} - 1} \right)\cos \tau + } \right.\\ {\left. {{{\left[ {\frac{{\sin \gamma }}{{\sin \left( {\gamma + \tau } \right)}}\left( {\frac{{{\rm{d}}{\lambda _{\rm{p}}}}}{{{\rm{d}}{\lambda _{\rm{d}}}}} - 1} \right)} \right]}^2}} \right\}^{1/2}}. \end{array} $ |
式中:γ=arctan(v/u)为平板下滑角,uf=u+vcot τ为当量水平速度.
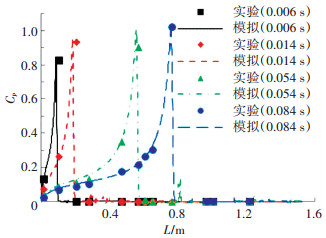
用vC对应的动压计算其压强系数,得到图 6所示中等网格数值模拟的不同时刻平板底部中心线压强系数分布情况.发现在入水初期,数值模拟以及实验都没有捕捉到最大压强,此时最大压强系数约为0.83,之后数值模拟的压强系数最大值均在1附近.随着入水深度的增加,垂向速度v、下滑角γ以及dλp/dλd均逐渐减小,故最大压强点速度vC减小,对应最大压强也逐渐减小.
|
图 6 不同时刻平板底部中心线压强系数分布 Figure 6 Cp distribution at the center line of the bottom |
分析结果表明,中等网格和细网格数值模拟的结果很接近,而粗网格数值模拟结果较差,因此后续的数值模拟采用中等密度网格设置.
2.2 飞机模型平静水面迫降数值模拟1953年,Mcbride等[12]实验研究了NACA TN 2929飞机不同后机身形状对水上迫降的影响,测量了迫降过程中速度、俯仰角和重心高度随时间的变化. Streckwall等[13]采用RANS求解器COMET和基于动量定理的DITCH求解器共同研究了A模型的水上迫降.
本文选用质量5.67 kg,初始俯仰角为10°,初始速度为9.144 m/s的模型A进行平静水面迫降的数值模拟,机身为旋成体,长1.219 m,长细比为6,翼展1.676 m,襟翼偏转60°.由于实验中模型尾部结构与机身连接较弱,受到水面冲击后平尾从机身脱落,因此采用无平尾模型进行数值模拟.
飞机在平静水面迫降时,忽略大攻角可能出现的空气非对称绕流,可认为流场具有对称性,因此采用半模进行计算,选用长方体计算域.设置对称面为对称边界条件,顶部和底部边界为指定压力条件,上游、下游以及侧边界为速度远场条件.
质心运动采用地面坐标系,初始质心位置为原点,x轴平行于水平面指向飞机初始水平速度方向,z轴竖直向下;机体坐标系原点始终处于质心并跟随飞机一同运动,OX轴平行于机身轴线,指向机头方向为正,OZ轴在飞机对称面内,垂直于OX轴并指向下方.
图 7给出滑移动网格方法数值模拟的运动历程与实验值、刚性动网格方法、加权变形动网格方法以及COMET和DITCH数值模拟结果的对比.

|
图 7 数值模拟的运动历程与实验及其他方法的对比 Figure 7 Movement history comparison of numerical simulation and experiments, other methods |
由图 7可知,滑移动网格数值模拟速度的变化趋势与实验结果相似,在迫降初期,速度衰减没有实验迅速,Streckwall等人认为实验中测出的速度迅速衰减有可能是错误的.
滑移动网格的俯仰角变化曲线与实验曲线的相位比较接近,但减小过程略早于实验,在0.25 s时刻达到最大值35°,小于实验的最大值38°,之后俯仰角逐渐减小,并在0.93 s时刻达到最小值-10°,实验的最小值为-8°;而刚性及加权变形动网格方法数值模拟的俯仰角最小值为-2°,相位与实验曲线相差也较大,但在最大值附近略好.
滑移动网格数值模拟重心高度的变化趋势也与实验相似,但平台期偏短,重心整体略高;刚性动网格方法数值模拟的迫降后期由于自由面模糊,重心高度偏高,与实验值相比误差较大;加权变形动网格方法的相位明显超前.由此可见,滑移动网格方法数值模拟的结果总体上比另外两种动网格方法以及COMET和DITCH更接近实验曲线.
3 飞机模型波浪中迫降数值研究 3.1 二维数值波浪验证根据全球有效波高和波向分布情况[14],发现大部分海域的有效波高在1.6~3.6 m,本文选择研究浪高为3.0 m的波浪.参考海况等级表,浪高3.0 m对应的为5级海况.根据军用飞机结构强度规范[15],波浪的波长与波高的比值(L/H)范围为20~ 40,本文选择L/H=30,则对应的波长L为90 m.
本文研究的NACA TN 2929飞机模型机身长1.2 m,而波音737客机的长度约为36 m,长度比例约为1/30.根据尺寸比例,数值模拟的波高H为0.1 m,波长L为3.0 m.假设波浪为深水波,可由Stokes二阶波近似解得到波浪的周期T和波面方程:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;T = \sqrt {2{\rm{\pi }}L/g} ,\\ \eta = H/2\cos \left( {kx - \omega t} \right) + {\rm{\pi }}H/4\left( {H/L} \right)\cos \left( {kx - \omega t} \right). \end{array} $ |
式中:k=2π/L为波数,ω=2π/T为波浪角频率.
选用13 m×16 m的长方形计算域进行二维波浪的数值模拟与验证.在x=0 m、4 m处设置波浪监测点,可以得到垂向位移随时间的变化. 图 8为模拟结果与近似理论解的对比,可以看出吻合较好.

|
图 8 不同监测点波形与理论值对比 Figure 8 Comparison of wave form and theoretical value of different monitoring points |
根据美国海岸警卫队1969年修改的飞机水上应急程序[16],飞机相对波浪的位置可以简化分为垂直于波浪和平行于波浪两种.数值模拟的波浪参数与3.1节相同,飞机模型和初始姿态与2.2节相同,都是无初始侧滑角的工况.由于无侧滑角, 垂直于波浪迫降的工况与平静水面迫降类似,可视为对称运动,故采用半模计算;而平行于波浪迫降的工况具有六自由度方向运动,故采用全模计算.
根据波浪的传播方向与飞机水平速度方向的相对关系,垂直于波浪迫降可分为迎浪迫降和顺浪迫降;平行于波浪迫降的工况为波浪从飞机前进方向的左侧向右侧传播.
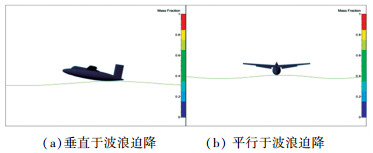
对于垂直于波浪迫降,应急程序认为应该避免降落在波浪的正面;对于平行于波浪迫降,应急程序认为应该尽可能降落在波峰处[16].为了便于分析比较,数值模拟的初始时刻均为飞机与波峰相撞时刻,如图 9所示.
|
图 9 迫降初始时刻飞机相对水面位置 Figure 9 Initial positions of ditching |
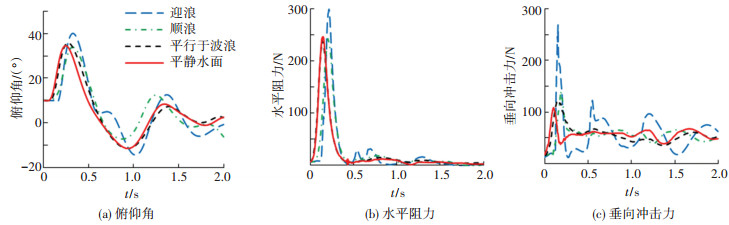
图 10为波浪中迫降的3种工况与平静水面迫降的俯仰角、水平力和垂向力随时间的变化曲线.所有工况的俯仰角变化趋势基本相似,迎浪迫降俯仰角峰值最大,约为40°,平行于波浪迫降的俯仰角峰值与平静水面迫降相同,约为35°,顺浪迫降俯仰角峰值略小于平静水面迫降,约为33°.迎浪迫降情况下产生较大的俯仰角峰值比较危险,而顺浪和平行于波浪迫降对俯仰角的变化影响较小.
|
图 10 波浪中迫降与平静水面迫降俯仰角及受力曲线 Figure 10 Pitch angle and force curves of ditching on wavy water and calm water |
迎浪迫降的水平阻力峰值最大,顺浪、平行于波浪迫降的水平阻力峰值与平静水面迫降相同.
波浪中迫降3种工况的垂向冲击力峰值均大于平静水面迫降,其中平行于波浪迫降的垂向冲击力峰值约为120 N,比平静水面迫降大12%;顺浪迫降的垂向冲击力峰值比平静水面迫降大29%;迎浪迫降的垂向冲击力峰值最大,约为270 N,比平静水面迫降大149%.由图 10(c)可以看到, 迎浪迫降在飞机入水产生第一个垂向冲击峰值后又产生了3次垂向冲击力峰值,这是由于迎浪迫降工况下飞机与波浪有更大的相对速度,飞机会遇到多次波浪冲击作用.
平行于波浪迫降的主要特点在于滚转和偏航运动,对于滚转和偏航运动的分析从地面坐标系转换到了机体坐标系,飞机前进方向的右侧偏航和顺时针滚转为正. 图 11给出了飞机模型平行于波浪迫降的过程(后视图,波浪从左到右传播).

|
图 11 平行于波浪迫降过程 Figure 11 Ditching process parallel to waves |
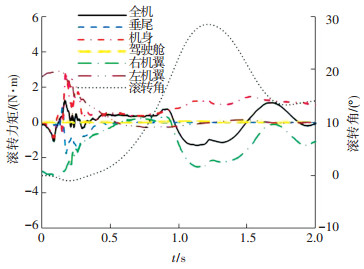
对滚转和偏航运动进行受力分析时,将飞机分解为机身、驾驶舱、左机翼、右机翼和垂尾5个部件分别进行研究. 图 12为飞机滚转角和各部件的滚转力矩随时间变化情况.在前1 s,滚转力矩主要由机身产生;在0.2~0.3 s,垂尾产生的滚转力矩抵消了部分机身产生的正滚转力矩,左右侧机翼提供的滚转力矩近似等值反向,飞机在正滚转力矩作用下逐渐开始正滚;在1.2 s时刻,滚转角达到最大值约28.5°,飞机的正滚运动直到右侧机翼触水产生了一个较大的负滚力矩才开始回落.虽然滚转角度变化较大,但是由于飞机的机身旋转半径较小(如波音737机身最大直径约为3.76 m),故不会对乘客造成较大危害.
|
图 12 飞机滚转角和各部件的滚转力矩随时间变化曲线 Figure 12 Variation of airplane roll angle and roll moment of different parts |
图 13为偏航角和各部件的偏航力矩随时间变化曲线.前0.5 s,虽然机身和垂尾偏航力矩明显,但总偏航力矩较小,偏航角约为0°;0.5 ~0.8 s,飞机在机身产生的负偏航力矩作用下逐渐向左偏航;随着右侧机翼与水面接触后受水的阻力作用产生正偏航力矩,飞机又逐渐向右偏航.虽然平行于波浪迫降后期出现了较大的偏航角,但是由于偏航角与飞机水平姿态关系不大,因此偏航角变化对飞机的迫降影响较小.

|
图 13 偏航角和各部件的偏航力矩随时间变化曲线 Figure 13 Variation of airplane yaw angle and yaw moment of different parts |
综上所述,当飞机在波浪水面迫降时,最优迫降航向是平行于波浪迫降,其垂向冲击力峰值比平静水面迫降只大12%,平行于波浪迫降的滚转和偏航运动造成的影响较小;最差的迫降航向是迎浪迫降,其垂向冲击力峰值比平静水面大149%,并且在迫降过程中会受到多次垂向冲击力峰值作用.
4 结论1) 对于带自由面的非定常运动问题,刚性动网格和加权变形动网格都有其局限性,本文结合滑移网格方法,在刚性动网格的基础上,开发出滑移动网格方法,在保证自由面模拟质量的同时,可以模拟物体的任意姿态运动.
2) 对三维平板斜向冲击入水进行数值模拟,分析了平板底部中心线上的压强分布、水面抬升与入水深度之间的关系以及二维和三维效应;采用滑移动网格方法数值模拟飞机平静水面迫降,将数值模拟的结果与其他数值方法和实验进行对比分析.模拟结果与实验吻合较好,验证了模拟方法的有效性.
3) 在数值造波的基础上,模拟了飞机在波浪水面中的迫降,分析了飞机的运动历程及受力情况,研究结果表明,本文研究的波浪水面迫降最优航向是平行于波浪迫降,其次是顺浪迫降,最危险的情况是迎浪迫降.
| [1] |
VON KARMAN T. The impact on seaplane floats during landing: NACA TN 321[R]. Washington: NACA, 1929
|
| [2] |
WAGNER H. Landing of seaplanes: NACA TM 622[R]. Washington: NACA, 1931
|
| [3] |
WAGNERH. Über stoβ-und gleitvorgänge an der oberfläche von flüssigkeiten[J]. Zeitschrift für Angewandte Mathematik und Mechanik, 1932, 12(4): 193. DOI:10.1002/-zamm.19320120402 |
| [4] |
郭保东.民用运输机水上迫降力学性能数值研究[D].北京: 北京航空航天大学, 2013 GUO Baodong. Numerical study on the hydrodynamic characteristics of civil transport in ditching[D]. Beijing: Beihang University, 2013 |
| [5] |
GUO Baodong, LIU Peiqing, QU Qiulin, et al. Effect of pitch angle on initial stage of a transport airplane ditching[J]. Chinese Journal of Aeronautics, 2013, 26(1): 17. DOI:10.1016/j.cja.2012.12.024 |
| [6] |
QU Qiulin, HU Mingxuan, GUO Hao, et al. Study of ditching characteristics of transport aircraft by global moving mesh method[J]. Journal of Aircraft, 2015, 52(5): 1. DOI:10.2514/1.C032993 |
| [7] |
BENSCH L, SHIGUNOV V, BEUCK G, et al. Planned ditching simulation of a transport airplane[C]//KRASH Users' Seminar. Phoenix: [s.n.], 2001
|
| [8] |
BENSCH L, SHIGUNOV V, SÖDING H. Computational method to simulate planned ditching of a transport airplane[C]//Second MIT Conference on Computational Fluid and Solid Mechanics. Boston: Computational Fluid & Solid Mechanics, 2003: 1251. DOI: 10.1016/B978-0080440460/-50307-9
|
| [9] |
HUA C, FANG C, CHENG J. Simulation of fluid-solid interaction on water ditching of an airplane by ALE method[J]. Journal of hydrodynamics, 2011, 23(5): 637. DOI:10.1016/S1001-6058(10)60159-X |
| [10] |
郭然. NUMECA系列教程[M]. 北京: 机械工业出版社, 2013. GUO Ran. NUMECA series of tutorials[M]. Beijing: Machinery Industry Press, 2013. |
| [11] |
SMILEY R F. An experimental study of water-pressure distributions during landings and planing of a heavily loaded rectangular flat-plate model: NACA TN 2453[R]. Washington: NACA, 1951
|
| [12] |
MCBRIDE E E, FISHER L J. Experimental investigation of the effect of rear-fuselage shape on ditching behavior: NACA TN 2929[R]. Washington: NACA, 1953
|
| [13] |
STRECKWALL H, LINDENAU O, BENSCH L. Aircraft ditching: a free surface/free motion problem[J]. Archives of Civil & Mechanical Engineering, 2007, 7(3): 177. DOI:10.1016/S1644-9665(12)60025-9 |
| [14] |
庄晓宵, 林一骅. 全球海洋海浪要素季节变化研究[J]. 大气科学, 2014, 38(2): 251. ZHUANG Xiaoxiao, LIN Yihua. Seasonal variation of global ocean wave[J]. Chinese Journal of Atmospheric Sciences, 2014, 38(2): 251. DOI:10.3878/j.issn.1006-9895.2013.13-109 |
| [15] |
中国人民解放军总装备部.军用飞机强度规范第5部分: 水上飞机的水载荷: GJB 67.5A—2008[S].北京: 国家军用标准, 2009 General Equipment Department of PLA. Military airplane strength specification Part 5: Water loads for seaplanes: GJB 67.5A—2008[S]. Beijing: Chinese Military Standard, 2009 |
| [16] |
United States Coast Guard. Aircraft emergency procedures over water[R]. Washington: Government Printing Office, 1969
|
 2019, Vol. 51
2019, Vol. 51


