跨声速涡轮内部流动是三维非定常黏性流动, 由于存在多排相对运动的叶片, 叶排间的相互干涉作用十分明显, 使得各排叶片表面压力呈现周期性脉动的特点.尤其是跨声速高压涡轮尾缘激波系的出现,会使得下游转子周期性的承受较大的作用力,造成涡轮性能下降的同时还带来了叶片振动问题,有可能导致高周疲劳[1-2].
倾斜和弯曲叶片是涡轮叶栅设计中常用的一种方式,该理论由王仲奇院士在20世纪60年代提出、形成并完善.王仲奇等[3]对20世纪弯曲/倾斜叶片的研究工作进行了全面的回顾,对其影响流动的物理机制和效果进行了归纳总结,从叶片与气流作用力、边界层径向迁移原理以及对横向二次流的影响3个方面解释了弯扭叶片降低能量损失的机理.随后大量实验与计算都表明,涡轮叶片采用倾斜和弯曲设计对性能有所改善[4-8].
随着叶轮机械流场研究的深入,倾斜弯曲叶片理论逐渐在非定常研究中应用.王松涛等[9]研究表明,叶片弯曲有助于涡轮效率提高和流量脉动降低; 毛明明等[10-11]研究表明弯、掠动叶降低了下游静叶气动负荷的非定常扰动,使静叶各气动负荷参数的波动幅值显著降低;段肖珑等[12]研究发现,弯曲有利于级间流动掺混,使流场更均匀.杨彤等[13]研究发现静叶弯曲可以使得转静干涉减弱,对于减小非定常流场中的压力脉动是有益的.但是在前人的研究中,大部分都只是对现象进行了分析,而对倾斜和弯曲影响非定常气动激励机理的讨论不够清晰和深入.
本文通过非定常数值模拟,研究倾斜/弯曲导叶构型对转子叶片表面不同展向位置气动扰动的影响规律,追踪跨声速涡轮内部非定常气动激励源头,以求获得倾斜/弯曲导叶影响转子叶片气动扰动的机理,为跨声速涡轮的非定常设计及优化提供理论依据.
1 数值方法及计算对象 1.1 研究对象本文以某小涵道比单级高压涡轮为研究对象, 对其级环境下的非定常流动进行了数值模拟,表 1给出了该高压涡轮的基本几何及流动参数.在直导叶构型时,导叶出口平均马赫数为1.27,进口雷诺数1.1×106.该跨声速涡轮原始导叶和转子的叶片数分别为27和84,为了使非定常计算所用各叶片排的通道数尽量少,把静子叶片数由27调整到28,这样根据区域缩放的原则,计算在1个静子通道和3个转子通道内进行.王远刚[14]通过对不同叶片约化方案(不同缩放比)数值模拟发现,在偏离原型不大的叶片约化方案计算结果中,流场参数的时均值及其各阶谐波幅值都与原几何模型方案计算结果吻合较好. Laumert[15-16]、jöcker[17]和Fruth[18]和杨彤[13]等也都采用了叶片约化的方法对涡轮内部非定常激励进行了研究.
| 表 1 跨声速高压涡轮基本参数 Table 1 Parameters of the transonic high-pressure turbine |
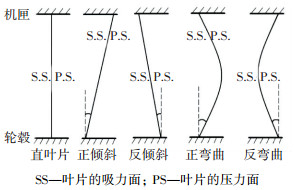
为了充分考虑倾斜/弯曲导叶构型对涡轮性能和流场的影响,按照文献[4, 7]中的指导,本文分别对该跨声速单级高压涡轮直导叶与较大倾斜/弯曲角度(倾斜±15°和弯曲±30°)导叶算例进行了非定常研究. 图 1中SS和PS分别代表叶片的吸力面和压力面,正弯/正倾斜叶片是指压力面与端壁成锐角的叶片,此时弯角/倾角为正值,反之称为反弯/反倾斜叶片.
|
图 1 倾斜/弯曲导叶定义 Figure 1 Definition of lean/bowed vanes |
本文计算采用ANSYS CFX 17.0求解非定常黏性Navier-Stokes(N-S)方程组.该求解器使用基于单元的有限体积法来离散控制方程,使其保持了单元几何剖分的灵活性以及有限体积法的守恒性.对于空间离散采用二阶精度格式,采用多重网格技术加速收敛,计算收敛最大残差均<10-4.基于剪切应力传输(SST)湍流模型的尺度自适应模拟方法(SAS-SST), 是一种LES/RANS混合方法,通过引入可根据当地流动拓扑自动调整的von Karman长度尺度,依靠流动状态动态的自适应湍流黏性,在稳定流动区域进行标准的URANS求解,而在流场中的非定常区域进行基于von Karman长度尺度的类似于LES的求解. SAS-SST方法可以在有限的计算资源下,准确有效地模拟上游非定常流动通过下游叶排时的输运过程和干涉作用.
给定计算域进口绝对总温、绝对总压、来流湍流度,给定出口边界平均静压强;叶型表面及机匣、叶顶、轮毂壁面采用无滑移、绝热、光滑固壁边界,并且与转子叶片联结的轮毂壁面与叶片(包括叶型表面和叶顶)转动,而其他部分以及机匣壁面设置为静止固壁.各叶片排周向方向两处边界条件定义为旋转周期性边界;转静交界面定义为瞬时转静交界面.
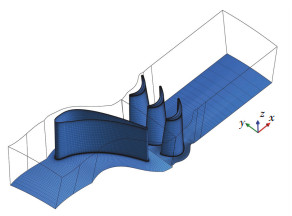
计算网格由TurboGrid软件生成.其中,网格采用H-O-H的拓扑结构:在进口区域、出口区域、叶栅通道内采用H型网格;而在环绕叶片表面采用O型网格.保证近叶片壁面、叶片顶端壁面、机匣壁面及轮毂壁面上的第一层网格的无量纲高度y+ < 1.计算域及网格设置如图 2所示.非定常计算时间步长为动叶扫过1个通道时间的1 /60,迭代若干个周期后计算效率与流量呈现明显的周期性,即计算达到收敛,然后对涡轮流场非定常信息进行统计.
|
图 2 计算域及网格设置 Figure 2 Computation domain and mesh |
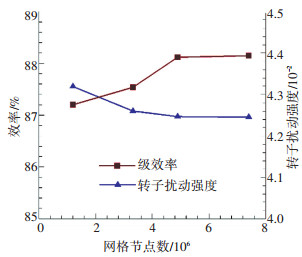
为验证不同网格设置对跨声速涡轮性能的影响,图 3给出一定网格节点数范围(120万~740万)内非定常计算得到的单级涡轮时均效率和转子叶中位置非定常扰动强度的对比.叶片表面某展向位置处压力扰动强度选择RMStotal参数进行衡量,该参数定义为
|
图 3 网格无关性验证结果 Figure 3 Validation of grid independence |
| ${\rm{RM}}{{\rm{S}}_{{\rm{total}}}} = \sqrt {\frac{{\int_{{\rm{arc}}} {\left( {\sum\limits_{i = 1}^n {p_i^{'2}} } \right){\rm{d}}s} }}{{n\int_{{\rm{arc}}} {{\rm{d}}\mathit{s}} }}} . $ |
式中pi′为叶片表面某弦长位置压力脉动值.
由图 3可见,在一定范围内随着网格数量的增大,涡轮级效率逐渐增加,而500万网格节点和740万网格节点计算得到的效率值基本保持不变,满足网格无关性的要求.转子叶中位置的叶片表面压力扰动强度则在网格数量超过330万以后变化不大(≤0.5%).考虑到非定常计算的计算资源问题,本文对直导叶构型涡轮级选择500万节点网格对涡轮非定常气动性能进行模拟计算,其他导叶构型网格设置与直导叶保持一致.
2 倾斜/弯曲导叶对涡轮气动性能的影响表 2列出了倾斜/弯曲导叶构型导叶出口总压损失系数、涡轮级时均效率及效率波动和流量的比较,发现正倾斜和正弯曲导叶都有效减小了导叶内的总压损失,有效改善涡轮导叶的气动性能;反弯曲和反倾斜导叶则明显恶化了涡轮导叶的气动性能.与导叶总压损失相对应,正倾斜和正弯曲导叶都提升了涡轮级效率,而反弯曲导叶具有一定的提升涡轮级性能的潜力,反倾斜导叶则明显恶化了涡轮级性能.非定常计算表明,与直导叶相比,+15°倾斜导叶可提高涡轮效率1.3%,而+30°弯曲导叶则将涡轮效率提高了1.1%.同时,正倾斜和正弯曲导叶均可以减小涡轮运行中的效率的波动水平,这也意味着采用该导叶构型后涡轮运行的更加平稳.此外,倾斜和弯曲导叶构型对涡轮质量流量的影响不超过1%,而且都在一定程度上增加了涡轮的流通能力.
| 表 2 倾斜/弯曲叶片对涡轮气动性能及流量的影响 Table 2 Effect of lean/bowed vanes on turbine performance and mass flow |
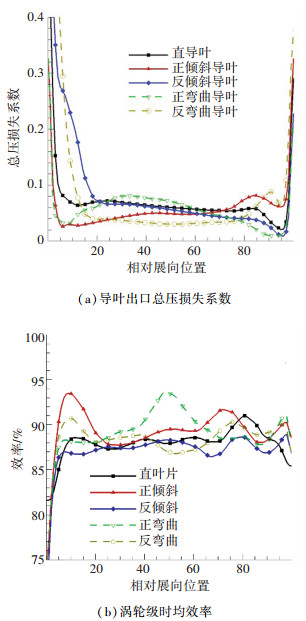
图 4中给出了不同涡轮导叶构型导叶通道出口总压损失系数以及涡轮级时均效率沿展向的分布,总压损失系数定义为
|
图 4 倾斜/弯曲叶片对涡轮性能参数沿展向分布的影响 Figure 4 Influence of lean/bowed vanes on spanwise distribution of turbine performance parameters of lean/bowed vanes |
| $\mathit{\xi = }\frac{{{p_{{\rm{t0}}}} - {p_{{\rm{t1}}}}}}{{\overline {{p_{{\rm{t0}}}}} }}, $ |
涡轮级时均效率定义为
| ${\mathit{\eta }_{{\rm{stg}}}} = \frac{{1 - \left( {{T_{{\rm{t2}}}}/{T_{{\rm{t0}}}}} \right)}}{{1 - {{\left( {{p_{{\rm{t2}}}}/{p_{{\rm{t0}}}}} \right)}^{\left( {\frac{{k - 1}}{k}} \right)}}}}. $ |
式中:pt0、pt1和pt2分别为导叶进口、导叶出口和转子出口相同展向高度周向平均的总压,Tt0和Tt2分别为导叶进口和转子出口相同展向高度周向平均的总温,$\overline {{p_{{\rm{t0}}}}} $为导叶进口平均总压.
由图 4(a)可以看到,和直导叶相比,正弯曲导叶显著降低了导叶上下端区的压力损失,叶中的损失系数略有增大,但总损失下降明显;正倾斜导叶大幅度降低了叶根到叶中大范围内的压力损失,叶尖损失增大,总损失下降明显.根据边界层径向迁移原理,决定叶片上的径向二次流的是其上的静压分布,由于正弯曲叶片可以获得压力面和吸力面沿叶高的压力呈“C”型分布,在端区获得负的径向压力梯度,在此作用下,端壁区内低能流体向叶中移动,在端区内形成一个低能流体较少的区域,从而低能流体在端区堆积引起的掺混损失减小,使该处总压损失系数较小;而反弯曲叶片则抑制端壁内形成的低能流体向叶中区域的移动,从而使端壁内低能流体积聚较多,造成端区较大的流动掺混损失.对于正倾斜叶片,在叶根位置获得负的径向压力梯度,抑制了叶根位置边界层的径向串流,端区二次流减弱,导致端区二次流损失降低,但是在叶尖位置由于较大的正径向压力梯度,损失有所增加;而反倾斜叶片影响效果相反.而对于小展弦比的高压涡轮而言,端区二次流损失在总损失中所占比例较大,因此正弯曲导叶和正倾斜导叶构型中,端区损失的降低均可以有效降低涡轮导叶通道内的总损失,从而对涡轮级效率的提升也是有益的.
由图 4(b)可以看到,和直导叶相比,正弯曲导叶构型主要通过提升叶中区域(30%~70%)的效率来提升涡轮级效率;正倾斜导叶构型则可以提高叶根到80%展向以及叶尖端区的效率值.对比图 4(a)中总压损失分布可以发现,正倾斜和正弯曲导叶构型对涡轮级展向效率分布的影响与导叶端区损失的重新分配并不是完全对应的,即导叶通道内局部区域总压损失的降低并不意味着对应展向位置处涡轮级时均效率的提高.造成该种现象的原因主要包括两个方面:1)导叶构型后涡轮级反力度沿叶高分布发生明显变化,可以提高涡轮级根部反动度,降低顶部反动度, 有利于改善级特性. 2)导叶构型改变了导叶出口气流角分布,改善了涡轮级间流动匹配,提高了涡轮级性能.由于论文重点在于分析转子叶片的气动激励,因此并未对该部分展开详细分析.但是结合表 2可以发现,总体影响上看来,不同的导叶构型情况下,导叶出口总压损失的降低和涡轮级效率的提升基本是伴随发生的.
3 倾斜/弯曲导叶对涡轮非定常性影响跨声速涡轮叶片工作环境恶劣,特别是转子叶片,不仅受到离心力的作用,还受到上游叶排尾迹、旋涡和位势的干扰,以及激波等周期性非定常气动激励的影响,这种影响是导致高周疲劳失效[2]等故障的重要原因.因此对倾斜/弯曲导叶构型对涡轮转子叶片和导叶的非定常性的影响进行分析,从而获得不同导叶构型影响涡轮叶片非定常性的规律及机理.
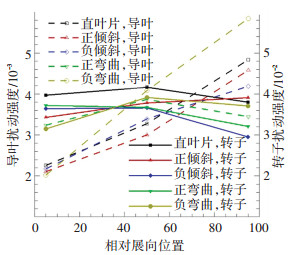
3.1 倾斜/弯曲导叶对非定常扰动强度影响图 5给出了不同导叶构型对跨声速涡轮导叶和转子叶片不同展向位置非定常压力扰动强度的影响,其中总扰动强度RMStotal定义与公式(1)相同.对比导叶和转子叶片表面压力扰动强度可以发现,导叶上的扰动强度比转子叶片低1个量级.
|
图 5 倾斜/弯曲叶片对跨声速涡气动激励的影响 Figure 5 Influence of stator and rotor blade of different vane models on transonic aerodynamic excitation |
导叶上的扰动基本呈现叶根(5%叶高)到叶尖(95%叶高)逐渐增大的趋势.与直导叶构型时导叶不同展向位置上的非定常扰动强度相比,正倾斜导叶构型可以在全叶高上降低导叶上的扰动强度;反倾斜导叶构型只能降低叶尖位置的扰动强度,对其他位置影响不明显;正弯曲导叶构型明显增大叶根和叶中位置的扰动强度,但是叶尖区域扰动强度明显降低;而反弯曲导叶会大幅度增加叶中和叶尖的扰动强度,但是叶尖位置的扰动强度大幅下降.
对比转子叶片上的扰动强度发现,与直导叶相比,除正倾斜导叶构型会略微增加叶尖处的扰动强度外,4种导叶构型方案均可以有效降低转子叶片上的扰动.
结合不同的导叶构型对涡轮级气动性能的影响可以发现,正倾斜导叶构型既可以提升涡轮级气动效率,又能降低导叶的气动扰动强度,而且转子叶片上的扰动水平在大部分的展向位置也可以有效降低;正弯曲导叶构型可以在提升涡轮级效率的基础上有效降低转子叶片上的气动扰动强度,避免疲劳失效.由此可见,合理的安排导叶构型,对于涡轮叶片的结构强度和气动性能都是有益的.在后面的讨论中主要选择直导叶、正倾斜以及正弯曲导叶构型进行分析讨论.
3.2 转子叶片气动激励分析由于转子叶片上气动激励水平更高,工作环境更加恶劣,所以降低转子叶片气动扰动强度对涡轮叶片结构强度非常重要.而要降低转子叶片扰动强度,必须理解转子叶片表面压力扰动与非定常流动畸变现象的对应关系.
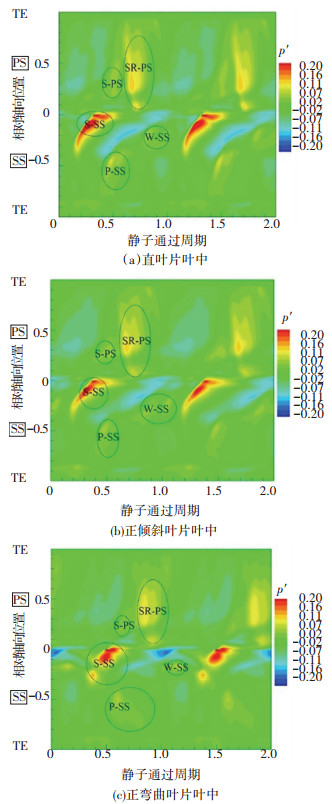
图 6给出了不同导叶构型转子叶中表面压力波动的时空图,其中横坐标为无量纲的静子通过周期;纵坐标为采用轴向弦长无量纲化的相对弦长位置(PS代表压力面,SS代表吸力面,LE代表叶片前缘,TE代表叶片尾缘),压力波动均采用涡轮级进口平均总压进行无量纲化.
|
图 6 不同导叶造型时转子叶中压力波动的时空图 Figure 6 Space-time figure of pressure perturbation at rotor mid-span for different vane models |
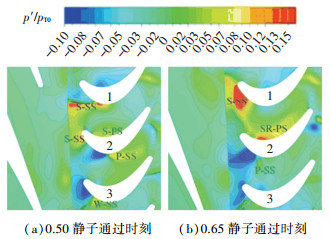
结合图 7给出的0.50和0.65静子通过时刻直导叶构型叶中通道内(2号叶片为图 6时空图对应转子叶片)瞬时压力波动云图,可以将时空图中的各压力波动峰值与通道内流动畸变现象进行关联,并且在图中进行标注.其中,S-SS为导叶尾缘激波外伸波在转子叶片吸力面上移动产生的压力扰动,SR-PS则是激波在吸力面表面反射到相邻叶片压力面产生的压力扰动,S-PS为尾缘激波外伸波在压力面上产生的弓形激波引起的压力扰动,P-SS为势场在吸力面上产生的压力扰动,W-SS则是尾迹在转子通道输运过程中在吸力面上产生的压力扰动.
|
图 7 直导叶叶中位置瞬时压力波动云图 Figure 7 Instantaneous pressure perturbation contour for straight vane at mid-span |
分析直导叶构型时转子叶中位置压力波动时空图可知,在吸力面前部主要扰动来源于导叶尾缘激波在转子叶片吸力面上的移动造成的大的压力梯度(S-SS),激波在吸力面上遇到固体壁面后反射到转子通道内到达相邻转子叶片的压力面产生新的压力扰动(SR-PS);随着导叶尾缘激波与吸力面干涉位置逐渐向前缘移动,当激波移动到转子前缘位置时,斜激波所能提供的最大折转角度无法满足气流所需的折转角度,形成弓形激波到达叶片压力面产生新的扰动(S-PS),此激波强度较弱因而引起的压力梯度较小. 图 6中可以明显看到尾迹扰动和位势干涉扰动峰值均明显低于激波扰动,这也和文献[14]所述在跨声速流动状态激波扰动成为涡轮转子叶片和静子叶片主导扰动来源的结论一致.
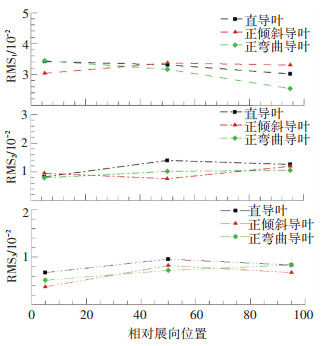
3.3 倾斜/弯曲影响转子叶片激励的机理分析图 8给出了不同导叶构型的导叶对转子叶片不同谐频下的压力扰动强度的展向分布.对于特定谐频压力扰动强度选择RMSn进行衡量,参数定义为
|
图 8 不同导叶构型对转子叶片不同谐频扰动强度的影响 Figure 8 Influence of different vane models on rotor blade excitation of different harmonics |
| ${\rm{RM}}{{\rm{S}}_n} = \sqrt {\frac{{\int_{{\rm{arc}}} {p_{n - {\rm{amp}}}^{'2}{\rm{d}}s} }}{{2\int_{{\rm{arc}}} {{\rm{d}}\mathit{s}} }}} . $ |
式中p′n-amp为叶片表面某弦长位置通过傅里叶变换得到的特定谐频下的压力扰动幅值,一阶谐频对应1倍导叶通过频率(1BPF).
对比直导叶构型发现,正倾斜导叶可以降低转子叶根处一阶谐频压力扰动强度,但会提升转子叶中及叶尖的一阶谐频扰动强度;正弯曲导叶可以降低转子叶中及叶尖一阶谐频压力扰动强度,但转子叶根位置的扰动水平会略有提升.正弯曲和正倾斜导叶可以明显降低转子叶中位置的二阶谐频扰动强度,但对叶根和叶尖区域的影响不明显.正倾斜和正弯曲导叶构型均可以有效抑制转子叶片上的气动激励带来三阶谐频扰动强度.
结合图 5可以发现,在转子叶尖区域不同导叶构型对总扰动强度和一阶谐频上扰动强度影响趋势一致,说明在叶尖区域一阶谐频的非定常扰动占据主导.对于转子叶根区域,正倾斜导叶主要通过降低一阶谐频上的扰动强度来降低叶根区域的扰动,而正弯曲导叶构型主要通过三阶谐频上的扰动幅值降低实现.在转子叶中区域,正倾斜导叶对一阶谐频上的扰动强度影响不大,而正弯曲导叶可以稍微降低一阶谐频扰动强度,但是两种构型二阶及更高阶次的谐频扰动幅值明显降低,说明正倾斜导叶构型主要通过抑制二阶及三阶谐频扰动来降低转子叶中的扰动强度,而正弯曲导叶构型则可以通用降低各阶谐频扰动来降低叶中区域扰动强度.对于高压涡轮的转子叶片而言,高阶谐频上扰动幅值的降低对避免高周疲劳大有裨益.
由此可见,不同的导叶构型对转子叶片不同叶高处的非定常扰动的控制机理是不同的.
为了分析不同导叶构型降低转子压力扰动强度对应的流动机理,图 9给出了不同导叶构型转子叶中各谐频上的压力扰动强度沿叶片表面的分布.
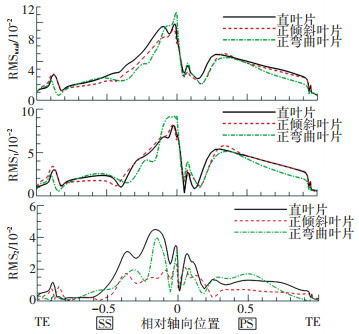
|
图 9 不同导叶构型转子叶中各谐频扰动强度分布 Figure 9 Distribution of rotor blade excitation of different harmonics for different vane models |
对比不同导叶构型转子叶中表面总扰动强度分布可知,正倾斜导叶可以有效降低吸力面大部分区域及压力面前部的压力扰动强度;正弯曲导叶会使得前缘区域压力扰动强度提升,但吸力面前部及整个压力面扰动水平大幅度下降.结合图 5可知,虽然倾斜和弯曲都能降低转子叶中的压力扰动强度,但是两者是通过影响不同的流动畸变现象来影响扰动强度的,机理不同.
对比一阶谐频压力扰动强度可知,正弯曲导叶会使转子叶中前缘区域的扰动增强,吸力面12%~37%轴向范围内扰动水平略有降低,压力面上扰动强度均有所降低,结合图 8可知,正弯曲导叶略微降低了一阶谐频扰动强度.结合图 6时空图中脉动压力的分布可知,虽然正弯曲导叶有效地减小了导叶尾缘激波对吸力面压力扰动的影响范围,但是扰动强度增大,导致一阶谐频的扰动幅值增大,对应图 9中转子前缘区域较大的扰动幅值;而压力面上主要扰动来源于吸力面激波反射到相邻转子压力面,激波和吸力面干涉范围减小必然会使得压力面上的扰动强度降低.由此可知,弯曲导叶主要通过减小导叶尾缘激波和转子叶片吸力面的干涉范围,进而减小吸力面激波反射到相邻转子叶片的压力面上的强度和范围来降低转子叶中位置的一阶谐频的扰动幅值.
正倾斜导叶对转子叶中一阶谐频扰动强度分布影响很小,对比时空图也可以发现正倾斜导叶转子叶中压力扰动的分布形式与直导叶基本一致.
对比时域内总的压力扰动强度及频域内一阶谐频扰动强度可以发现,虽然两种导叶构型中转子叶中总的压力脉动均有所降低,但是两者主要不是通过影响一阶谐频下的流动畸变获得的,因此必须要研究更高阶谐频的分布, 探究导叶构型影响转子叶片上压力扰动的机制.
对比二阶谐频的扰动强度发现,正倾斜导叶构型可以大幅度降低吸力面及压力面的二阶谐频扰动强度,而正弯曲叶片可以明显降低吸力面上的扰动强度.二阶谐频的扰动是由于转子叶片在一个静子通过周期内,连续经历了两个流动历程造成的.结合时空图中扰动峰值分布分析直导叶二阶扰动来源可知,吸力面16%轴向位置处峰值对应转子叶片在一个静子通过周期内连续经历激波扰动和尾迹扰动;吸力面36%轴向位置处峰值对应转子叶片连续通过势场扰动和尾迹扰动;压力面二阶谐频扰动峰值则对应于压力面激波扰动和相邻叶片吸力面激波反射激波带来的扰动.结合时空图可以发现,弯曲导叶会减小吸力面激波和转子叶片干涉区域,由此大幅度降低二阶谐频的扰动强度.倾斜导叶则是通过影响尾迹和位势干涉与叶片表面的干涉位置降低了吸力面上的二阶谐频扰动强度,通过减小压力面激波在压力面上的干涉范围减小了吸力面上的二阶谐频扰动,从而大幅度降低了转子叶中的二阶谐频扰动强度.
综上所述,正弯曲导叶构型转子叶中位置二阶谐频幅值降低主要是由于导叶尾缘激波和转子叶片吸力面的干涉范围减小;而正倾斜导叶构型转子叶中位置二阶谐频幅值降低则主要由于尾迹和上游势干涉在转子叶片上干涉位置的调整.
由此可见,不同导叶构型对转子不同位置的扰动强度降低机理是不同的,在高性能跨声速高压涡轮的气动设计中,可以根据控制机理充分利用导叶构型的潜力,降低转子叶片上的气动激励的强度.
4 结论1) 正倾斜和正弯曲导叶可以有效地提升涡轮级效率,并且减小了涡轮级效率波动水平,使得涡轮运行更加平稳.
2) 通过关联流动畸变与非定常气动激励,确定了跨声速涡轮内部气动扰动的来源,同时揭示了倾斜和弯曲对叶片总的扰动强度的影响来源.在超跨声速状态下,涡轮转子叶片上气动激励主要来源于导叶尾缘激波在下游转子叶片上移动及反射产生的压力扰动.正倾斜和正弯曲导叶可以有效地降低转子叶片上总的气动扰动强度,但是两者降低转子叶片气动激励的机理不同.
3) 正倾斜导叶主要通过影响一阶谐频的扰动强度来降低转子叶根总扰动强度和增加叶尖的总扰动强度,但是转子叶中扰动强度降低则通过降低二阶及更高阶谐频上的扰动实现.
4) 正弯曲导叶转子叶根位置的扰动强度降低主要通过三阶谐频的扰动强度降低实现,叶尖区域的扰动强度降低主要通过一阶谐频扰动降低来实现,而叶中区域的扰动强度则是通过各阶谐频上扰动强度共同降低实现的.
| [1] |
李伟, 史海秋. 航空发动机涡轮叶片疲劳-蠕变寿命试验技术研究[J]. 航空动力学报, 2001, 16(4): 323. LI Wei, SHI Haiqiu. Research on experimental technique for fatigue-creep life of the turbine blade in aeroengine[J]. Journal of Aerospace Power, 2001, 16(4): 323. DOI:10.13224/j.cnki.jasp.2001.04.005 |
| [2] |
方昌德. 飞机燃气涡轮发动机高周疲劳研究计划[J]. 国际航空, 2005(8): 63. FANG Changde. HCF Program for aero-turbine engine[J]. International Aviation, 2005(8): 63. |
| [3] |
王仲奇, 郑严. 叶轮机械弯扭叶片的研究现状及发展趋势[J]. 中国工程科学, 2000, 2(6): 40. WANG Zhongqi, ZHENG Yan. Research status and development of the bowed-twisted blade for turbomachines[J]. Engineering Science, 2000, 2(6): 40. DOI:10.3969/j.issn.1009-1742.2000.06.009 |
| [4] |
TAN C, YAMAMOTO A, CHEN H, et al. Flowfield and aerodynamic performance of a turbine stator cascade with bowed blades[J]. Aiaa Journal, 2004, 42(10): 2170. DOI:10.2514/1.1737 |
| [5] |
SEO S, CHOI S, KIM K. Design optimization of a low speed fan blade with sweep and lean[J]. Journal of Power and Energy, 2008, 222(1): 87. DOI:10.1243/09576509JPE410 |
| [6] |
BAGSHAW D A, INGRAM G L, GREGORY-SMITH, D G. An experimental study of reverse compound lean in a linear turbine cascade[J]. Journal of Power and Energy, 2005, 219(6): 443. DOI:10.1243/095765005X31199 |
| [7] |
ZHANG S, MACMANUS D G, LUO J. Parametric study of turbine NGV blade lean and vortex design[J]. Chinese Journal of Aeronautics, 2016, 29(1): 104. DOI:10.1016/j.cja.2015.12.005 |
| [8] |
WEINGOLD H D, NEUBERT R J, BEHLKE R F. Bowed stators:an example of CFD applied to improve multistage compressor efficiency[J]. Journal of Turbomachinery, 1997, 119(4): 161. DOI:10.1115/1.2841086 |
| [9] |
王松涛, 王仲奇, 冯国泰, 等. 非定常条件下叶片弯曲对流场参数的影响[J]. 航空动力学报, 2002, 17(3): 314. WANG Songtao, WANG Zhongqi, FENG Guotai, et al. The effect of blade bowing on aerodynamic parameters with rotor/stator interaction[J]. Journal of Aerospace Power, 2002, 17(3): 314. DOI:10.13224/j.cnki.jasp.2002.03.009 |
| [10] |
MAO Mingming, SONG Yanping, WANG Zhongqi. Numerical investigation of the unsteady flow in a transonic compressor with curved rotors[J]. Chinese Journal of Aeronautics, 2008, 21(2): 97. DOI:10.1016/S1000-9361(08)60013-8 |
| [11] |
毛明明, 宋彦萍, 王仲奇. 跨声速动叶弯和掠对非定常气动负荷的影响[J]. 工程热物理学报, 2010, 31(10): 1663. MAO Mingming, SONG Yanping, WANG Zhongqi. Effect of bowed and swept rotors on unsteady aerodynamic loading in a transonic compressor[J]. Journal of Engineering Thermophsics, 2010, 31(10): 1663. |
| [12] |
段肖珑, 欧阳华, 吴亚东, 等. 周向弯曲动叶级间非定常流动的数值研究[J]. 流体机械, 2010, 38(4): 8. DUAN Xiaolong, OUYANG Hua, WU Yadong, et al. Numerical study of inter-stage unsteady flow in axial fan with circumferential skewed rotor[J]. Fluid machinery, 2010, 38(4): 8. DOI:10.3969/j.issn.1005-0329.2010.04.003 |
| [13] |
杨彤, 王松涛, 姜斌. 弯曲叶片造型对涡轮叶栅作用力影响的非定常数值研究[J]. 推进技术, 2013, 34(6): 760. YANG Tong, WANG Songtao, JIANG Bin. Unsteady numerical study of effects on turbine blade forces for the bowed blade[J]. Journal of Propulsion Technology, 2013, 34(6): 760. |
| [14] |
王远刚.叶片数约化对叶轮机非定常流动影响的研究[D].西安: 西北工业大学, 2012 WANG Yuangang.Investigation into effects of blade sectors scaling on the turbomachinery unsteady flows[D].Xi'an: Northwestern Polytechnical University, 2012. |
| [15] |
LAUMERT B, MARTENSSON H, FRANSSON T H.Investigation of unsteady aerodynamic blade excitation mechanisms in a transonic turbine stage: part Ⅰ: phenomenological identification and classification[C]//Proceedings of the ASME Turbo Expo.New Orleans: ASME, 2001.DOI: 10.1115/2001-GT-0258
|
| [16] |
LAUMERT B, MARTENSSON H, FRANSSON T H.Investigation of unsteady aerodynamic blade excitation mechanisms in a transonic turbine stage: part Ⅱ: analytical description and quantification[C]//Proceedings of the ASME Turbo Expo.New Orleans: ASME, 2001.DOI: 10.1115/2001-GT-0259
|
| [17] |
JÖCKER M.Numerical investigation of the aerodynamic vibration excitation of high-pressureturbine rotors[D].Stockholm: Royal Institute of Technology (KTH), 2002
|
| [18] |
FRUTH F.Reduction of aerodynamic forcing in transonic turbomachinery[D].Stockholm: Royal Institute of Technology (KTH), 2013
|
 2019, Vol. 51
2019, Vol. 51


