2. 73151部队,福建 厦门 063100
2. Troop 73151, Xiamen 063100, Fujian, China
大部分行星齿轮箱在低速重载等恶劣的工作环境中运行,其太阳轮、行星轮和齿圈等关键结构易出现磨损和裂纹等损伤故障[1].行星齿轮箱特殊的传动结构特点,导致其振动信号耦合严重, 多模式混叠,故障特征微弱,给行星齿轮箱故障特征提取和故障诊断带来了较大的难度[2-3].行星齿轮箱的振动信号往往包含多个分量,采用传统的频率解调方法直接分析信号,具有一定的局限性.因此,近年来很多学者采用多分量分解的方法对原始振动信号进行信号分解.经验模态分解(EMD)方法是应用比较广泛的信号分解处理方法,它将非平稳信号分解为不同时间尺度的信号分量[4-5].但是, EMD方法存在模态混叠和端点效应,且当信号受到噪声污染时,分解误差较大.针对EMD方法存在的缺陷,Dragomiretskiy等[6]提出了一种新的信号分解方法——变分模态分解(VMD),该方法通过完全非递归的方式寻求变分模型的最优解,根据每个分解分量的中心频率和带宽,实现信号的频域分解与各分量的有效分离.和EMD方法相比,VMD具有分解效果好,鲁棒性强等优点[7-9].
对行星齿轮箱振动信号分解后,如何对各个分量提取故障特征是面临的另外一个问题.近年来, 基于非线性动力学参数的特征提取方法引起了广泛关注[10-11].其中,分形维数特征由于能够有效地描述非线性时间序列的自相似性和复杂度,因此在混沌序列和机械信号等信号分析中得到了广泛的应用[12-14].目前,常用的分形维数估计方法主要为盒计数法(BC)、去趋势波动分析(DFA)和形态学覆盖法(MC)等.但这些方法都存在一些不足,如BC方法在大尺度上存在过计数,在小尺度上存在欠计数的问题;DFA方法估计分形维数时,受残差序列趋势去除方法影响较大.
本文提出了一种利用VMD的双标度分形维数特征提取方法.首先,利用VMD方法将振动信号分解为多个本征模态函数(IMF)分量信号,利用互信息理论确定VMD方法中IMF分量的数目;然后,对得到的每个IMF分量信号进行正交化,根据分形维数理论,计算和绘制振动信号的时间尺度和多维超体体积的双对数曲线;对双对数曲线分段进行最小二乘线性拟合,得到振动信号的双标度分形维数特征.实验结果表明,提取的特征参数能够有效地区分行星齿轮箱不同的故障状态.
1 变分模态分解理论 1.1 变分模型的构造本质上,本征模态函数(IMF)应该是一个调幅-调频信号.因此,变分模态分解理论将IMF重新定义为如式(1)所示的信号.
| ${u_k}\left( t \right) = {A_\mathit{k}}\left( t \right)\cos \left( {{\mathit{\varphi }_\mathit{k}}\left( t \right)} \right). $ | (1) |
式中:Ak(t)、φk(t)分别为uk(t)的瞬时幅值和瞬时相位,且φk(t)是非减函数,ωk(t)=dφk(t)/dt≥0为瞬时角频率.
假设原信号x(t)为多分量信号,其由有限个具有不同中心频率、有限带宽的IMF分量uk(t)组成.VMD理论将信号分解问题转化为变分问题,在各IMF分量之和等于输入信号x(t)的约束下,寻求每个IMF分量的估计带宽之和最小,模型构建具体步骤如下:
1) 对每个IMF分量uk(t)作希尔伯特变换,构造解析信号.然后,对每个IMF分量的解析信号混合一预估中心频率e-jωkt,将每个IMF分量的频谱调制到相应的基频带上,即
| $\left[ {\left( {\mathit{\delta }\left( \mathit{t} \right) + {\rm{j/}}\left( {{\rm{ \mathit{ π} }}\mathit{t}} \right)} \right) * {u_k}\left( t \right)} \right]{{\rm{e}}^{ - {\rm{j}}{\mathit{\omega }_\mathit{k}}t}}. $ | (2) |
式中:δ(t)为冲击函数,“*”为卷积符号,{ωk}={ω1, ω2, …, ωK}为各IMF分量的中心频率,K为IMF分量的数目.
2) 计算式(2)所表示的解调信号梯度的L2范数,估计出各个IMF分量的带宽,引入约束条件,构造如下形式的变分模型:
| $\begin{array}{l} \mathop {\min }\limits_{\left\{ {{u_k}} \right\}, \left\{ {{\mathit{\omega }_\mathit{k}}} \right\}} \left\{ {\sum\limits_{k = 1}^K {\left\| {{\partial _t}\left[ {\left( {\mathit{\delta }\left( t \right) + \frac{{\rm{j}}}{{{\rm{ \mathit{ π} }}\mathit{t}}}} \right) * {u_k}\left( t \right)} \right]{{\rm{e}}^{ - {\rm{j}}{\mathit{\omega }_\mathit{k}}\mathit{t}}}} \right\|\begin{array}{*{20}{c}} 2\\ 2 \end{array}} } \right\}, \\ {\rm{s}}{\rm{.t}}{\rm{. }}\sum\limits_{k = 1}^K {{u_k}\left( t \right) = x\left( t \right).} \end{array} $ |
1) 引入二次惩罚因子α和拉格朗日乘法算子λ(t),构造扩展拉格朗日函数:
| $\begin{array}{l} L\left( {\left\{ {{u_k}} \right\}, \left\{ {{\mathit{\omega }_\mathit{k}}} \right\}, \mathit{\boldsymbol{\lambda }}} \right) = \mathit{\alpha }\sum\limits_{k = 1}^K {\left\| {{\partial _\mathit{t}}\left[ {\left( {\mathit{\delta }\left( t \right) + \frac{{\rm{j}}}{{{\rm{ \mathit{ π} }}\mathit{t}}}} \right) * {u_k}\left( t \right)} \right]{{\rm{e}}^{ - {\rm{j}}{\mathit{\omega }_\mathit{k}}\mathit{t}}}} \right\|} \begin{array}{*{20}{c}} 2\\ 2 \end{array} + \\ \left\| {x\left( \mathit{t} \right) - \sum\limits_{k = 1}^K {{u_\mathit{k}}\left( \mathit{t} \right)} } \right\|\begin{array}{*{20}{c}} 2\\ 2 \end{array} + \left\langle {\mathit{\boldsymbol{\lambda }} \left( \mathit{t} \right), \mathit{x}\left( \mathit{t} \right) - \sum\limits_{k = 1}^K {{u_k}\left( t \right)} } \right\rangle , \end{array} $ |
将约束性的变分问题转换为非约束性的变分问题.其中,二次惩罚因子α为较大的正数,保证在信号中含有高斯噪声的情况下有较好的重构精度,拉格朗日算子λ(t)使得约束条件保持严格性.
2) 利用乘法算子交替方向法(ADMM)求解上述变分模型,通过交替迭代更新ukn+1(t)、ωkn+1(t)和λn+1(t),求取扩展的拉格朗日函数的鞍点,此鞍点即为变分模型的最优解. VMD算法的流程如图 1所示.

|
图 1 VMD算法流程 Figure 1 Flowchart of VMD algorithm |
图 1中τ为更新因子,ε为判别精度. ukn+1(t)的更新求解方法为
| $\mathit{\hat u}_k^{n + 1}\left( \mathit{\omega } \right) = \frac{{\mathit{\hat x}\left( \mathit{\omega } \right) - \sum\limits_{i \ne k}^K {{{\hat u}_\mathit{i}}\left( \mathit{\omega } \right) + \mathit{\boldsymbol{\hat \lambda }}\left( \mathit{\omega } \right)/2} }}{{1 + 2\mathit{\alpha }{{\left( {\mathit{\omega + }{\mathit{\omega }_\mathit{k}}} \right)}^2}}}. $ | (3) |
对式(3)进行逆傅里叶变换,则可以得到时域的IMF分量.中心频率ωkn+1(t)更新求解方法为
| $\mathit{\omega }_k^{n + 1} = \left( {\int_0^\infty {\mathit{\omega }{{\left| {{{\mathit{\hat u}}_\mathit{k}}\left( \mathit{\omega } \right)} \right|}^2}{\rm{d}}\mathit{\omega }} } \right)/\left( {\int_0^\infty {{{\left| {{{\mathit{\hat u}}_\mathit{k}}\left( \mathit{\omega } \right)} \right|}^2}{\rm{d}}\mathit{\omega }} } \right). $ |
在使用VMD对信号进行分解时,需要预先设定分解分量的数目K,而不同的K值对分解结果会产生较大的影响.在信息论中,互信息定义为两个随机变量间不确定度的差值,用于测度两个随机变量的统计相关性.互信息的优势在于其既能描述两个变量间的线性相关性,又能描述两个变量间的非线性相关性.所以,本文采用互信息法确定VMD分解分量的数目.
在信息论中,互信息的计算公式如下式所示:
| $I\left( {\mathit{X|Y}} \right) = H\left( Y \right) - H\left( {Y|X} \right). $ | (4) |
式中:H(Y)为Y的信息熵,H(Y|X)为X对Y的条件信息熵. X与Y的相关性越强,互信息值则越大.本文中设Y为原始信号,X为分解得到的每个IMF分量,根据式(4)计算每个IMF分量和原信号的互信息值.对所有互信息值归一化,得
| ${\mathit{\delta }_\mathit{i}} = I\left( {{u_\mathit{i}, }x} \right)/\max \left( {I\left( {{u_\mathit{i}}, x} \right)} \right). $ |
设定一个阈值,当互信息值δi小于阈值时,则说明分解的该IMF分量和原信号的相关性较小,可认为原始信号已被合理地完全分解,从而得到合适的K值.
2 基于VMD的分形维数理论 2.1 分形维数基本原理众所周知,如果把正方体的边长L增大为原来的k倍,那么它的二维测度表面积S和三维测度体积V会分别增大到原来的k2倍和k3倍.上述关系推广到一般情况,即如果Y是一个具有D维测度的变量,则Y也应该满足上述关系,即
| $\mathit{L} \propto {\mathit{S}^{1/2}} \propto {V^{1/3}} \propto {Y^{1/\mathit{D}}}. $ | (5) |
根据式(5)所示的测度关系,即可定义和估计分形体的分形维数.
对于时间序列信号而言,分形的自相似性主要体现在信号的时域波形中. VMD分解产生的IMF分量本质上是一种多变量时间序列,每个机械振动信号通过VMD分解均可得到一个多变量时间序列.在多维测度空间中,某一时间段内多变量时间序列所占据的空间可以利用所谓的多维超体体积进行度量.根据式(5),若以时间尺度作为测量尺度,则时间尺度ε和多维超体的体积V应该存在如下幂律关系:
| $\mathit{\varepsilon } \propto {V^{1/D}}. $ |
根据多维超体的定义得知,若利用VMD分解得到的IMF分量计算体积,需要各IMF分量正交,而VMD分解的各IMF分量并非严格正交化,所以首先要将IMF分量正交化.本文采用正交坐标变换的方法对IMF分量正交化.
假设VMD将一维信号x(t)分解成K个IMF分量,即
| $\mathit{\boldsymbol{U = }}\left[ {{u_1}\left( \mathit{t} \right), {u_2}\left( \mathit{t} \right), \cdots , {\mathit{u}_\mathit{K}}\left( t \right)} \right]. $ |
式中:U∈RN×K,N为信号x(t)的数据长度.根据式(6)计算分量矩阵U的协方差矩阵
| $\varSigma {_U} = \frac{1}{n}{\mathit{\boldsymbol{U}}^{\rm{T}}}\mathit{\boldsymbol{U}}. $ | (6) |
对协方差矩阵ΣU进行正交对角化,获得K个特征值λ1≥λ2≥…≥λK及其对应的单位正交特征向量p1, p2, …, pK,定义正交的IMF分量
| $\left[ {{{\mathit{\tilde u}}_{\rm{1}}}\left( \mathit{t} \right), {{\mathit{\tilde u}}_{\rm{2}}}\left( \mathit{t} \right), \cdots , {{\mathit{\tilde u}}_\mathit{k}}\left( t \right)} \right] = \left[ {{\mathit{\boldsymbol{\lambda }}_{\rm{1}}}{\mathit{\boldsymbol{p}}_{\rm{1}}}, {\mathit{\boldsymbol{\lambda }}_{\rm{2}}}{\mathit{\boldsymbol{p}}_{\rm{2}}}. \cdots , {\mathit{\boldsymbol{\lambda }}_\mathit{K}}{\mathit{\boldsymbol{p}}_\mathit{K}}} \right]. $ |
设振动信号的长度为N,利用时间尺度ε将振动信号正交化的IMF分量
| ${L_\mathit{k}}\left( q \right) = \mathop {\max }\limits_{\left( {q - 1} \right)\mathit{\varepsilon } \le \mathit{t} \le \mathit{q\varepsilon }} \left\{ {{{\mathit{\tilde u}}_\mathit{k}}\left( t \right)} \right\} - \mathop {\min }\limits_{\left( {q - 1} \right)\mathit{\varepsilon } \le \mathit{t} \le \mathit{q\varepsilon }} \left\{ {{{\tilde u}_\mathit{k}}\left( t \right)} \right\}. $ |
式中:Lk(q)为多维超体在第q个区间的第k维空间中的边长,q=1, 2, …, p.
多维超体的体积计算方法为
| $V\left( \mathit{\varepsilon } \right) = \frac{1}{{{\mathit{\varepsilon }^\mathit{K}}}}\sum\limits_{q = 1}^\mathit{P} {\prod\limits_\mathit{k}^K {\left( {\mathop {\max }\limits_{\left( {q - 1} \right)\mathit{\varepsilon } \le \mathit{t} \le \mathit{q\varepsilon }} \left\{ {{u_\mathit{k}}\left( \mathit{t} \right)} \right\} - \mathop {\min }\limits_{\left( {q - 1} \right)\mathit{\varepsilon } \le \mathit{t} \le \mathit{q\varepsilon }} \left\{ {{u_\mathit{k}}\left( t \right)} \right\}} \right)} } . $ | (7) |
式中V(ε)表示时间尺度ε下多维超体的体积.通过改变时间尺度ε的大小,最终可得到一个多维超体体积序列.
2.4 分形维数估计根据式(7),振动信号的分形维数D可定义为
| $D = \mathop {\lim }\limits_{\mathit{\varepsilon } \to {\rm{0}}} \left( {\ln \mathit{V}\left( \mathit{\varepsilon } \right)/ln\mathit{\varepsilon }} \right). $ | (8) |
对于式(8)所示的极限问题,工程实际中很难求解.为此,引入最小二乘法(LSM)将上述极限问题转化为线性拟合问题进行处理,从而求取分形维数D的近似值.首先对ε和V(ε)进行对数变换,并绘制双对数曲线(ln ε,ln V(ε)),然后采用LSM对双对数曲线进行一阶线性拟合.拟合直线的斜率即为分形维数D的近似估计:
| $D = \frac{{n\sum\limits_{i = 1}^n {\ln {\mathit{\varepsilon }_\mathit{i}}\ln V\left( {{\mathit{\varepsilon }_\mathit{i}}} \right) - \sum\limits_{i = 1}^n {\ln {\mathit{\varepsilon }_\mathit{i}}\sum\limits_{i = 1}^n {\ln V\left( {{\mathit{\varepsilon }_\mathit{i}}} \right)} } } }}{{n\sum\limits_{i1}^n {{{\left( {\ln {\mathit{\varepsilon }_\mathit{i}}} \right)}^2} - \sum\limits_{i = 1}^n {{{\left[ {\ln V\left( {{\mathit{\varepsilon }_\mathit{i}}} \right)} \right]}^2}} } }}. $ |
式中[ε1, ε2, …,εn ]为时间尺度序列.
2.5 仿真信号分析为了评估所提分形维数估计方法的性能,选取分数布朗运动(FBM)信号作为标准分形信号进行研究.同时引入盒计数法、去趋势波动分析和EMD方法作为对比.
FBM信号本质上是一个具有平稳增量的自相似性和零均值高斯随机过程.如果两个FBM信号相互独立,则具有如下特性:
| $E\left( {{b_H}\left( t \right){b_H}\left( s \right)} \right) = {\mathit{\sigma }^{\rm{2}}}\left( {{{\left| t \right|}^{2H}} + {{\left| s \right|}^{2H}} - {{\left| {t - s} \right|}^{2H}}} \right). $ |
式中:E为数学期望,σ2为bH(t)和bH(s)的方差,H为Hurst指数,0 < H < 1. bH(t)的分形维数完全由Hurst指数决定,其理论分形维数D=2-H.
实验中利用Matlab分形工具箱生成FBM信号,信号的采样频率和采样时间分别为4 096 Hz和0.5 s. 图 2为5个具有不同分形维数的FBM信号.
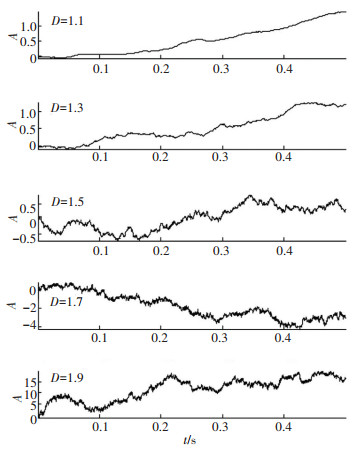
|
图 2 具有不同分形维数的FBM信号 Figure 2 FBM signals with different fractal dimensions |
随着分形维数的增加,FBM信号的波形变得越来越复杂.在VMD算法中,由于二次惩罚因子α取值在[100,4 000]范围内变化对结果基本没有影响,所以VMD分解过程中α取值设为2 000.利用互信息法确定分量数目K的阈值设定为0.01.
表 1给出了采用4种方法对FBM信号分形维数进行估计的结果,包括估计值和相对误差.其中,利用EMD估计分形维数的方法类似于使用VMD估计分形维数的方法,采用互信息法确定有用的IMF分量的数目,阈值设定为0.05.由于FBM信号的随机性,实验中每个给定的Hurst指数均生成了5个FBM信号,表 1中相应的数据为5个FBM信号的平均结果.
| 表 1 FBM信号分形维数估计结果 Table 1 Estimation results of fractal dimension for FBM signals |
由表 1可得,就平均相对误差而言,利用VMD方法估计的平均相对误差为4.71%,小于BC法的12.74%、DFA的8.78%和EMD的7.01%,同时利用VMD方法估计的最大相对误差仅为8.05%.由于BC法在大尺度上存在过计数和在小尺度上存在欠计数的问题,对于所有FBM信号,BC法估计的分形维数总是偏小,并且随着FBM信号波形复杂度的增加,分形维数的相对误差也增加,最大误差达到了25.68%. DFA估计的结果比BC法估计的结果稍好,但是由于DFA估计分形维数时受残差序列趋势去除方法影响较大,而目前没有成熟的理论合理选取残差序列趋势去除方法,其相对误差在1.58%~19.19%,平均相对误差8.78%,仍然很大.利用EMD估计分形维数的方法估计的结果相对于传统方法,估计结果得到了一定的改善,但是由于EMD方法本身固有的缺陷,导致估计结果比VMD方法较差.仿真实验结果表明,利用VMD的分形维数估计方法整体上优于BC法、DFA方法和EMD方法.
3 利用VMD的振动信号双标度分形维数特征 3.1 实验数据采集本文采集的振动信号来自一个行星齿轮箱实验系统,通过机械加工的手段在太阳轮、行星轮和齿圈的单个轮齿上设置了齿面磨损的局部故障,磨损形式如图 3所示.在太阳轮、行星轮和齿圈单个轮齿上分别设置了宽1.5 mm、深1 mm的磨损量.

|
图 3 齿轮预置故障 Figure 3 Introduced faults of gears |
采集的行星齿轮箱4种状态的原始振动信号如图 4所示.
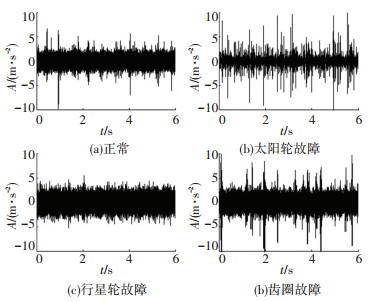
|
图 4 行星齿轮箱4种状态的原始振动信号 Figure 4 Original vibration signals of four states from planetary gearbox |
实验中,电动机转速控制在1 200 r/min,采样频率为20 kHz,分别采集正常状态、太阳轮故障、行星轮故障和齿圈故障4种运行状态数据各40组,共计160组.
3.2 振动信号的双标度分形特性利用VMD估计振动信号的分形维数时,每个振动信号都会得到一条时间尺度和多维超体体积的双对数曲线.在实验过程中,VMD的参数二次惩罚因子α取值设为2 000,利用互信息法设定分量数目K的阈值为0.01.
图 5为行星齿轮箱4种不同运行状态振动信号的双对数曲线及其拟合结果.
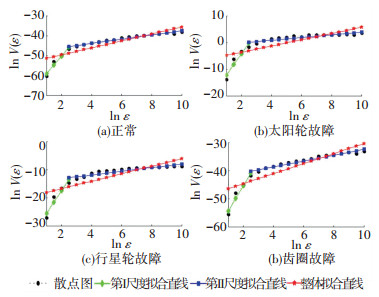
|
图 5 (ε, V(ε))双对数曲线及其线性拟合结果 Figure 5 Log-log curves and linear fitting results of V(ε) versus ε |
由图 5可知,坐标点(ε, V(ε))在二维空间并不呈现线性分布,在整个时间尺度上进行直线拟合的误差非常大,所估分形维数不能准确描述振动信号的分形特征.观察双对数曲线图发现,随着时间尺度逐渐增大,双对数曲线斜率会出现一个突变点,而突变点两边均表现出近似的线性关系.因此,为了更好地提取振动信号分形特征,在采用VMD计算振动信号的分形维数时,定义了双标度分形维数的概念.在图 5中,根据双对数曲线中的突变点将时间尺度划分为两部分,突变点左侧的时间尺度称为第Ⅰ尺度,突变点右侧的称为第Ⅱ尺度.第Ⅰ尺度表示的是时间尺度划分较为精细的部分,描述的是信号的细节信息,第Ⅱ尺度表示的是时间尺度划分较宽的部分,描述的是信号的趋势信息.从图中可以看出,与整体拟合直线相比,在第Ⅰ尺度和第Ⅱ尺度上的拟合结果要更好地贴合振动信号的双对数曲线,说明双标度分形维数能够更好地表征振动信号的分形特征.
3.3 双标度分界点的选取方法如何选择合适的分界点是提取振动信号双标度分形维数特征的关键,本文提出了如下的分界点自适应选取方法:
1) 对于时间尺度序列[ε1, ε2, …, εn],利用εi初步将时间尺度划分为第Ⅰ尺度和第Ⅱ尺度两部分,i=2, 3, …, n-1;
2) 采用最小二乘法分别对第Ⅰ尺度和第Ⅱ尺度对应的双对数曲线进行线性拟合,拟合直线分别记为l1和l2;
3) 计算整体拟合误差e(i)=e1(i)+e2(i),其中e1(i)和e2(i)分别为第Ⅰ尺度和第Ⅱ尺度的拟合误差;
4) 搜索e(i)的最小值emin,选择该最小值对应的时间尺度为最终分界点.
最终分界点对应的拟合直线l1和l2的斜率即为振动信号的双标度分形维数.
3.4 实验结果及分析将利用VMD的双标度分形维数特征提取方法应用于实测行星齿轮箱振动信号.作为对比实验,也使用BC法、DFA方法和EMD方法计算估计行星齿轮箱振动信号的分形维数.在VMD方法提取振动信号的分形维数特征时,同样也计算了利用整体拟合直线估计的分形维数,可称为VMD的单标度分形维数,实验结果如图 6所示.
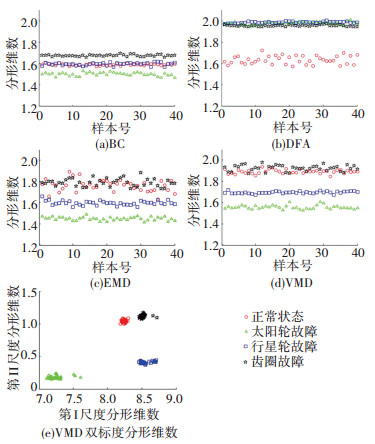
|
图 6 不同方法估计的分形维数结果 Figure 6 Fractal dimension estimation results of different methods |
从图 6可以看出,BC法估计的分形维数能够将行星齿轮箱的太阳轮故障和齿圈故障区分出来,但无法区分正常状态和行星轮故障. DFA方法估计的分形维数只能够有效地识别出正常状态,但对于行星齿轮箱其他3种故障状态基本无法区分. EMD方法能够区分太阳轮故障和行星轮故障,但对于正常信号和齿圈故障区分度不高. 图 6(d)为利用VMD采用整体拟合直线估计的单标度分形维数,该分形维数能够有效地识别出太阳轮故障和行星轮故障,对于正常状态和齿圈故障虽然能够有一定的区分度,但两种状态的差异并不明显. 图 6(e)为利用VMD的振动信号双标度分形维数特征,该特征准确地区分出了行星齿轮箱4种运行状态.可见,利用VMD方法估计的振动信号分形维数特征要明显好于BC法、DFA法和EMD方法.
为了进一步验证所提方法的有效性,将利用BC法、DFA方法、EMD方法估计的分形维数特征以及VMD的单标度和双标度分形维数特征输入分类器,比较分类准确率.分类器选择K-近邻分类器(K-NNC)、支持向量机(SVM)和极限学习机(ELM)3种分类器.实验中,将行星齿轮箱4种运行状态的160个样本随机分成两等份,其中一份为训练样本,另一份为测试样本.实验过程重复20次,每次实验样本重新随机划分,分类结果如表 2所示.
| 表 2 行星齿轮箱故障诊断准确率对比结果 Table 2 Comparison of accuracy for fault diagnosis of planetary gearbox |
从表 2可看出,利用VMD估计的分形维数分类准确率均优于BC法、DFA方法和EMD方法.对于双标度分形维数特征,不论哪种分类器,分类准确率都达到了100%,表明利用VMD的双标度分形维数特征能够准确地判别行星齿轮箱不同的运行状态.
4 结论本文提出了一种利用变分模态分解的双标度分形维数特征提取方法,通过仿真信号和实测行星齿轮箱振动信号得到以下结论:
1) 利用VMD方法将多分量振动信号分解为有限个IMF分量,在分解得到的IMF分量基础上定义了多维超体体积.根据分形理论,得到了信号时间尺度和多维超体体积的双对数曲线,并计算估计出信号的分形维数,仿真信号实验表明,基于VMD的分形维数优于BC法和DFA方法等传统的分形维数估计方法.
2) VMD方法通过完全非递归的方式寻求变分模型的最优解,根据每个分解分量的中心频率和带宽,实现信号的频域分解与各分量的有效分离.相比于EMD方法,利用VMD方法估计的分形维数误差小于EMD方法估计的分形维数.
3) 针对行星齿轮箱振动信号双对数曲线的特点,通过选择合理的分界点,在第Ⅰ尺度和第Ⅱ尺度两个尺度上对双对数曲线进行分段最小二乘拟合,得到振动信号的双标度分形维数特征.行星齿轮箱实验验证了利用VMD的双标度分形维数能够准确地描述行星齿轮箱振动信号的分形特性,有效地识别行星齿轮箱不同的运行状态,提高故障诊断的准确率.
| [1] |
雷亚国, 汤伟, 孔德同, 等. 基于传动机理分析的行星齿轮箱振动信号仿真及其故障诊断[J]. 机械工程学报, 2014, 50(17): 61. LEI Yaguo, TANG Wei, KONG Detong, et al. Vibration signal simulation and fault diagnosis of planetary gearboxes based on transmission mechanism analysis[J]. Journal of Mechanical Engineering, 2014, 50(17): 61. DOI:10.3901/JME.2014.17.061 |
| [2] |
熊一奇, 徐玉秀. 基于信号传播模型的行星齿轮缺齿故障识别[J]. 仪器仪表学报, 2016, 37(2): 249. XIONG Yiqi, XU Yuxiu. Identification of planetary geartooth missing fault based on signal propagation model[J]. Chinese Journal of Scientific Instrument, 2016, 37(2): 249. DOI:10.19650/j.cnki.cjsi.2016.02.002 |
| [3] |
雷亚国, 罗希, 刘宗尧, 等. 行星轮系动力学新模型及其故障响应特性研究[J]. 机械工程学报, 2016, 52(13): 111. LEI Yaguo, LUO Xi, LIU Zongyao, et al. A new dynamic model of planetary gear sets and research on fault response characteristics[J]. Journal of Mechanical Engineering, 2016, 52(13): 111. DOI:10.3901/JME.2016.13.111 |
| [4] |
冯志鹏, 褚福磊. 行星齿轮箱故障诊断的频率解调分析方法[J]. 中国电机工程学报, 2013, 33(11): 112. FENG Zhipeng, CHU Fulei. Frequency demodulation analysis method for fault diagnosis of planetary gearboxes[J]. Proceedings of the CSEE, 2013, 33(11): 112. DOI:10.13334/j.0258-8013.pcsee.2013.11.005 |
| [5] |
TENG Wei, WANG Feng, ZHANG Kaili, et al. Pitting fault detection of a wind turbine gearbox using empirical mode decomposition[J]. Journal of Mechanical Engineering, 2014, 60(1): 12. DOI:10.5545/sv-jme.2013.1295 |
| [6] |
DRAGOMIRETSKIY K, ZOSSO D. Variational mode decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 531. DOI:10.1109/TSP.2013.2288675 |
| [7] |
LAHMIRI S. Comparative study of ECG signal denoising by wavelet threshold in empirical and variational mode decomposition domains[J]. Healthcare Technology Letters, 2014, 1(3): 104. DOI:10.1049/htl.2014.0073 |
| [8] |
WANG Yanxue, MARKERT R, XIANG Jiawei, et al. Research on variational mode decomposition and its application in detecting rub-impact fault of the rotor system[J]. Mechanical Systems and Signal Processing, 2015, 60: 243. DOI:10.1016/j.ymssp.2015.02.020 |
| [9] |
马增强, 柳晓云, 张俊甲, 等. VMD和ICA联合降噪方法在轴承故障诊断中的应用[J]. 振动与冲击, 2017, 36(13): 201. MA Zengqiang, LIU Xiaoyun, ZHANG Junjia, et al. Application of VMD-ICA combined method in fault diagnosis of rolling bearings[J]. Journal of Vibration and Shock, 2017, 36(13): 201. |
| [10] |
李怀俊, 谢小鹏. 基于核特征模糊聚类及模糊关联熵的齿轮故障模式识别[J]. 仪器仪表学报, 2015, 36(4): 848. LI Huaijun, XIE Xiaopeng. Gearfault pattern recognition based on kernel feature fuzzy clustering and fuzzy association entropy[J]. Chinese Journal of Scientific Instrument, 2015, 36(4): 848. DOI:10.19650/j.cnki.cjsi.2015.04.016 |
| [11] |
李宝庆, 程军圣, 吴占涛, 等. 基于ASTFA和PMMFE的齿轮故障诊断方法[J]. 振动工程学报, 2016, 29(5): 928. LI Baoqing, CHENG Junsheng, WU Zhantao, et al. Gearfault diagnosis method based on the adaptive and sparsest time-frequency analysis method and partial mean multi-scale fuzzy entropy[J]. Journal of Vibration Engineering, 2016, 29(5): 928. DOI:10.16385/j.cnki.issn.1004-4523.2016.05.022 |
| [12] |
FERNÁNDEZ-MARTÍNEZ M, NOWAK M, SÁNCHEZ-GRANERO M A. Counterexamples in theory of fractal dimension for fractal structures[J]. Chaos, Solitons and Fractals, 2016, 89(1): 210. DOI:10.1016/j.chaos.2015.10.032 |
| [13] |
刘昱, 张俊红, 毕凤荣, 等. 基于Wigner分布和分形维数的柴油机故障诊断[J]. 振动、测试与诊断, 2016, 36(2): 240. LIU Yu, ZHANG Junhong, BI Fengrong, et al. Study on fault diagnosis of diesel valve trains based on wigner distribution and fractal dimension[J]. Journal of Vibration Measurement&Diagnosis, 2016, 36(2): 240. DOI:10.16450/j.cnki.issn.1004-6801.2016.02.005 |
| [14] |
张剑, 刘昌文, 毕凤荣, 等. 柴油机气门故障信号的双谱图形分形维数分析[J]. 内燃机学报, 2016, 34(2): 274. ZHANG Jian, LIU Changwen, BI Fengrong, et al. Analysis of bispectrum image fractal dimension for valve train fault signals in diesel engine[J]. Transactions of CSICE, 2016, 34(2): 274. |
 2019, Vol. 51
2019, Vol. 51


