Bennett机构是典型的空间过约束机构,可实现复杂运动规律,且承载能力强.许多空间过约束机构都是以Bennett机构为基础构建的,例如Goldberg 5R和6R机构、Myard机构等[1]. Bennett机构可以用来构建多种几何形式的可展机构,例如拱形[1-2]、抛物柱面[3]、圆柱形[4]等. Bennett单元阵列可展机构刚性好,可以应用到航空航天、应急救灾和医疗器械等领域,应用潜力巨大[2-4].
运动学和动力学的研究一直以来都是机构学的研究热点,大多数研究主要集中在单环空间机构和并联机构上[5-10]. Zhi等[5]研究了Bennett机构的运动学和动力学. Tsai、Zhao、贾晓辉、Kalani和Xin等[6-10]分别以不同的并联机构为对象研究了动力学问题.可展机构动力学主要集中在平面单元机构组成的可展机构[11-14],有关空间机构组成的可展机构动力学研究比较少.孙宏图等[11]研究了正方形可展机构的运动学和动力学. Sun等[12]研究了剪式单元机构组成的空间可展机构的运动学和动力学.李博等[13-14]研究了平面剪式阵列可展机构的动力学,并分析了运动副间隙耦合对其动力学的影响.动力学建模的方法主要包括牛顿-欧拉法、拉格朗日法、凯恩法和虚功原理法等,这些方法各有各的优势和适用范围[7-8, 15-16].虚功原理法把整个机构作为一个整体,无需计算各运动副的约束力. Bennett单元阵列可展机构具有多闭环和过约束的特性,因此它的动力学分析模型建立比较复杂,目前尚未见到有关Bennett单元阵列可展机构的动力学建模与分析方面的公开研究成果.
本文采用拆解法将可展机构中的各单元分解成多个串联开链机构.采用坐标变换法和螺旋理论分析了各串联开链机构的运动学,然后采用虚功原理将各串联开链机构组装在一起,建立了Bennett单元阵列可展机构的动力学分析模型.以4×4的Bennett单元阵列可展机构为例,分析了其运动学和动力学.该方法适用范围比较广,对多种空间机构组成的可展机构的运动学和动力学分析具有借鉴意义.
1 Bennett机构Bennett机构是由4个轴线不平行的运动副连接而成的空间四杆机构,相对的边长相等,结构简图见图 1(a).为了方便表示Bennett单元阵列可展机构,采用Chen[1]的方法把Bennett机构看作一个长方形来对其进行简化,具体见图 1(b).

|
图 1 Bennett机构 Figure 1 Bennett linkage |
杆AB作为机架,nA、nB、nC与nD分别为运动副A、B、C和D的轴线方向单位向量,分别垂直平面DAB、ABC、BCD和CDA.以A点为原点,杆AB所在的直线为x轴,运动副A的轴线为z轴,建立笛卡尔坐标系A-x1y1z1,简称坐标系1,本文以编号表示坐标系.以同样的方法建立图 1中的其他3个坐标系:B-x2y2z2、C-x3y3z3和D-x4y4z4. nA与nB、nC与nD的夹角都为α,nB与nC、nD与nA的夹角为β. Bennett机构满足下面两个几何条件[5]
| $ \begin{array}{*{20}{c}} {{l_1} = {l_3} = {l_a},}&{{l_2} = {l_3} = {l_b},} \end{array} $ |
| $ \frac{{\sin \alpha }}{{{l_a}}} = \pm \frac{{\sin \beta }}{{{l_b}}}. $ |
由上述几何条件可以得到△DAB≌△BCD和△ABC≌△BCD,进一步可得∠DAB=∠BCD=θ1和∠ABC=∠CDA=θ2,θ1和θ2被称为Bennett机构的内角.杆BC与x轴正向夹角为η1.为了便于表示,将θ1称为Bennett机构的输入角,θ2称为Bennett机构的内输出角,η1称为Bennett机构的外输出角,η1和θ2满足:η1=π-θ2.由文献[5]可得
| $ {\eta _1} = 2{\tan ^{ - 1}}\left( {\frac{{ - {f_2}\left( {{\theta _1}} \right) - \sqrt {f_2^2\left( {{\theta _1}} \right) - {f_1}\left( {{\theta _1}} \right){f_3}\left( {{\theta _1}} \right)} }}{{{f_1}\left( {{\theta _1}} \right)}}} \right). $ | (1) |
式中:
| $ {f_1}\left( {{\theta _1}} \right) = \left( {{l_a}/{l_b} - 1} \right)\left( {\cos {\theta _1} + 1} \right), $ |
| $ {f_2}\left( {{\theta _1}} \right) = \cos \alpha \sin {\theta _1}, $ |
| $ {f_3}\left( {{\theta _1}} \right) = \left( {{l_a}/{l_b} + 1} \right)\left( {\cos {\theta _1} - 1} \right). $ |
两个坐标系之间的变换包括两种:转动变换矩阵R和平移向量d.坐标系2到坐标系1的变换矩阵为
| $ {\mathit{\boldsymbol{T}}_{12}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{R}}_{12}}\left( \alpha \right)}&{{\mathit{\boldsymbol{d}}_{12}}}\\ {\bf{0}}&1 \end{array}} \right], $ |
式中
Bennett机构中其他相邻的坐标系之间的变换矩阵T23、T14以及T43都可以按照类似的方法得到.
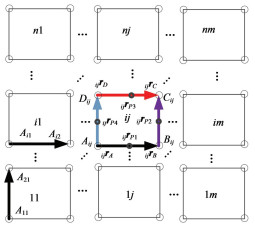
2 Bennett单元阵列可展机构的运动学和动力学 2.1 Bennett单元阵列可展机构相邻的Bennett机构单元可以通过共享连杆和运动副的方法连接在一起构成大型的可展机构,称之为Bennett单元阵列可展机构.此类可展机构中,最常见的是由n·m个相同的Bennett机构构成的n行m列可展机构,称为n×m阵列可展机构,其结构简图见图 2. 图 2中,Bennett单元阵列可展机构的最基本形式是由两个Bennett机构通过共享杆组成的,有两种组成方式:一种是行阵列形式,见图 3(a);一种是列阵列形式,见图 3(b).
|
图 2 n×m Bennett单元阵列可展机构 Figure 2 n×m Bennett unit array deployable mechanism |
|
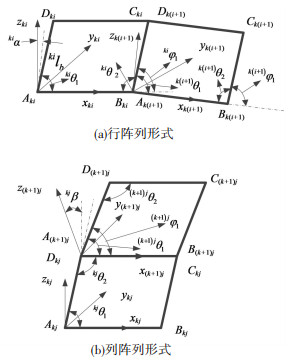
图 3 相邻Bennett机构单元之间的坐标系 Figure 3 Coordinate system of adjacent Bennett linkage units |
共享杆是组合机构中两个单元共同拥有的构件,图 3(a)中BkiCki就是行阵列机构中单元ki和单元k(i+1)的共享杆. Bennett单元阵列可展机构的相邻单元之间的坐标变换矩阵是其运动学和动力学分析的基础,建立图 3中的4个坐标系,可以得到Bennett单元阵列可展机构两种基本形式的坐标变换矩阵
| $ {}_R^k{\mathit{\boldsymbol{T}}_{i\left( {i + 1} \right)}} = \left[ {\begin{array}{*{20}{c}} {{}_R^k{\mathit{\boldsymbol{R}}_{i\left( {i + 1} \right)}}\left( {{}^{ki}\delta ,{}^{ki}\alpha } \right)}&{{\mathit{\boldsymbol{d}}_{i\left( {i + 1} \right)}}}\\ {\bf{0}}&1 \end{array}} \right], $ |
| $ {}_C^j{\mathit{\boldsymbol{T}}_{k\left( {k + 1} \right)}} = \left[ {\begin{array}{*{20}{c}} {{}_C^j{\mathit{\boldsymbol{R}}_{k\left( {k + 1} \right)}}\left( {{}^{kj}\theta ,{}^{kj}\beta ,{}^{kj}{\varphi _1}} \right)}&{{\mathit{\boldsymbol{d}}_{k\left( {k + 1} \right)}}}\\ {\bf{0}}&1 \end{array}} \right]. $ |
式中:kRRi(i+1)(kiδ, kiα)为坐标系k(i+1)到坐标系ki的转动变换矩阵,kiδ=k(i+1)θ1-kiφ1,di(i+1)为坐标系k(i+1)到坐标系ki的平移向量,jCRk(k+1)(kjθ,kjβ,kjφ1)为坐标系(k+1)j到坐标系kj的转动变换矩阵,dk(k+1)为坐标系(k+1)j到坐标系kj的平移向量.
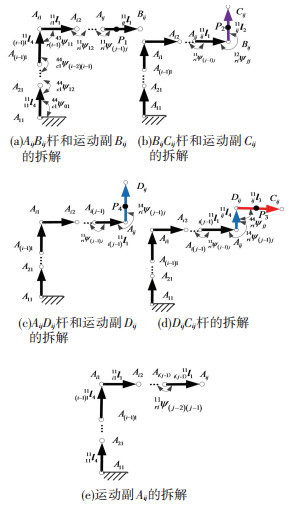
2.2 Bennett单元阵列可展机构的运动学分析将n×m的Bennett单元阵列可展机构第i行j列的单元机构编号为ij. ij中的杆件可以看作一个空间串联开链机构的末端.由图 2可以看出, 11ijrA有多种表达式,即可展机构中的一个杆可以有多种拆解路径,本文选择第1列各单元的杆AD和第i行各单元的AB进行拆解即按照图 2中黑色粗线和箭头所示的路线拆解.具体的拆解路径只会影响表达式,不会影响最终的分析结果.单元ij中各杆和各运动副的拆解路径如图 4所示.
|
图 4 单元ij各杆和各运动副的拆解路径 Figure 4 Disassembly path of all links and all kinematic pairs of the unit ij |
由图 4可以得到各运动副在全局坐标系11中的位置向量分别为
| $ {}_{ij}^{11}{\mathit{\boldsymbol{r}}_A} = {}_{11}^{11}{\mathit{\boldsymbol{l}}_4} + \cdots + {}_{\left( {i - 1} \right)1}^{11}{\mathit{\boldsymbol{l}}_4} + {}_{i1}^{11}{\mathit{\boldsymbol{l}}_1} + \cdots + {}_{i\left( {j - 1} \right)}^{11}{\mathit{\boldsymbol{l}}_1}, $ |
| $ {}_{ij}^{11}{\mathit{\boldsymbol{r}}_B} = {}_{ij}^{11}{\mathit{\boldsymbol{r}}_A} + {}_{ij}^{11}{\mathit{\boldsymbol{l}}_1}, $ |
| $ {}_{ij}^{11}{\mathit{\boldsymbol{r}}_C} = {}_{ij}^{11}{\mathit{\boldsymbol{r}}_A} + {}_{ij}^{11}{\mathit{\boldsymbol{l}}_1} + {}_{ij}^{11}{\mathit{\boldsymbol{l}}_2}, $ |
| $ {}_{ij}^{11}{\mathit{\boldsymbol{r}}_D} = {}_{ij}^{11}{\mathit{\boldsymbol{r}}_A} + {}_{ij}^{11}{\mathit{\boldsymbol{l}}_4}. $ |
hkpqle为第h行k列的单元机构中的杆e在坐标系pq中的位置向量.
由图 2和图 4可知,单元ij中各杆的质心P1、P2、P3和P4分别为杆AijBij、BijCij、DijCij和AijDij的中点,它们在全局坐标系11中的位置向量:
| $ {}_{ij}^{11}{\mathit{\boldsymbol{r}}_{P1}} = \left( {{}_{ij}^{11}{\mathit{\boldsymbol{r}}_A} + {}_{ij}^{11}{\mathit{\boldsymbol{r}}_B}} \right)/2,\;\;\;{}_{ij}^{11}{\mathit{\boldsymbol{r}}_{P2}} = \left( {{}_{ij}^{11}{\mathit{\boldsymbol{r}}_B} + {}_{ij}^{11}{\mathit{\boldsymbol{r}}_C}} \right)/2, $ |
| $ {}_{ij}^{11}{\mathit{\boldsymbol{r}}_{P3}} = \left( {{}_{ij}^{11}{\mathit{\boldsymbol{r}}_C} + {}_{ij}^{11}{\mathit{\boldsymbol{r}}_D}} \right)/2,\;\;\;{}_{ij}^{11}{\mathit{\boldsymbol{r}}_{P4}} = \left( {{}_{ij}^{11}{\mathit{\boldsymbol{r}}_A} + {}_{ij}^{11}{\mathit{\boldsymbol{r}}_D}} \right)/2. $ |
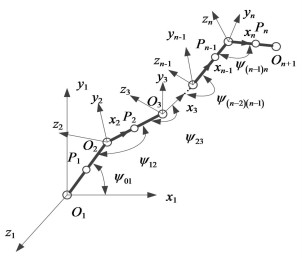
图 4中的各支链可以简化成一个由n个转动副串联而成的开链机构,分别以各运动副为原点,建立多个坐标系,如图 5所示.
|
图 5 n个转动副串联构成的开链机构 Figure 5 Open chain mechanism by n revolute pairs connected in series |
杆n质心Pn的位姿有射线坐标和轴线坐标两种表述形式.射线坐标形式
| $ {\mathit{\boldsymbol{x}}_{Pn}} = {\left( {{\mathit{\boldsymbol{\psi }}_n},{\mathit{\boldsymbol{r}}_{Pn}}} \right)^{\rm{T}}}, $ | (2) |
式中
| $ {\mathit{\boldsymbol{r}}_{Pn}} = {\mathit{\boldsymbol{l}}_1} + {\mathit{\boldsymbol{l}}_2} + \cdots + {\mathit{\boldsymbol{l}}_{n - 1}} + {\mathit{\boldsymbol{l}}_{Pn}}, $ |
式中:li=OiOi+1,lPn=OnPn.
杆n质心Pn位姿的轴线坐标形式为
| $ {}^a{\mathit{\boldsymbol{x}}_{Pn}} = \tilde \Delta {\mathit{\boldsymbol{x}}_{Pn}} = {\left( {{\mathit{\boldsymbol{r}}_{Pn}},{\mathit{\boldsymbol{\psi }}_n}} \right)^{\rm{T}}}. $ |
式中
Sei为运动副Oi的轴线在坐标系1的单位方向向量,Si为运动副Oi的轴线在坐标系i中的单位方向向量,则
| $ {\mathit{\boldsymbol{S}}_{ei}} = {\mathit{\boldsymbol{R}}_{1i}}{\mathit{\boldsymbol{S}}_i}. $ |
式中R1i为坐标系i到坐标系1的转动变换矩阵.
杆n的角速度可以表示为
| $ {\mathit{\boldsymbol{\omega }}_n} = {{\mathit{\boldsymbol{\dot \varphi }}}_n} = {{\dot \psi }_{01}}{\mathit{\boldsymbol{S}}_{e1}} + {{\dot \psi }_{12}}{\mathit{\boldsymbol{S}}_{e2}} + \cdots + {{\dot \psi }_{\left( {n - 1} \right)i}}{\mathit{\boldsymbol{S}}_{en}}. $ |
杆n质心Pn在全局坐标系中的速度
| $ {\mathit{\boldsymbol{v}}_{Pn}} = {{\mathit{\boldsymbol{\dot r}}}_{Pn}} = {{\mathit{\boldsymbol{\dot l}}}_1} + {{\mathit{\boldsymbol{\dot l}}}_2} + \cdots + {{\mathit{\boldsymbol{\dot l}}}_{n - 1}} + {{\mathit{\boldsymbol{\dot l}}}_{Pn}}. $ |
式中:
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\dot l}}}_k} = {\mathit{\boldsymbol{\omega }}_k} \times {\mathit{\boldsymbol{l}}_k},\left( {1 \le k \le n} \right),}&{{{\mathit{\boldsymbol{\dot l}}}_{Pn}} = } \end{array}{\mathit{\boldsymbol{\omega }}_n} \times {\mathit{\boldsymbol{l}}_{Pn}}. $ |
由此可得
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{v}}_{P\left( {n + 1} \right)}} = {{\dot \psi }_{01}}\left( {{\mathit{\boldsymbol{S}}_{e1}} \times {\mathit{\boldsymbol{l}}_{P1n}}} \right) + {{\dot \psi }_{12}}\left( {{\mathit{\boldsymbol{S}}_{e2}} \times {\mathit{\boldsymbol{l}}_{P2n}}} \right) + \cdots + }\\ {{{\dot \psi }_{\left( {n - 1} \right)n}}\left( {{\mathit{\boldsymbol{S}}_{en}} \times {\mathit{\boldsymbol{l}}_{Pnn}}} \right).} \end{array} $ |
式中:
| $ {\mathit{\boldsymbol{l}}_{Pjn}} = {\mathit{\boldsymbol{l}}_j} + \cdots + {\mathit{\boldsymbol{l}}_{n - 1}} + {\mathit{\boldsymbol{l}}_{Pn}} = {O_j}{P_n},\left( {1 \le j \le n} \right). $ |
对式(2)求时间的一阶和二阶导数,可得质心Pn的速度和加速度螺旋
| $ {{\mathit{\boldsymbol{\$}}}_{Pn}}={{\left( {{\mathit{\boldsymbol{\omega}}\text{ }}_{n}},{{\mathit{\boldsymbol{v}}}_{Pn}} \right)}^{\text{T}}}={{\mathit{\boldsymbol{J}}}_{Pn}}{{{\mathit{\boldsymbol{\dot{ }\!\!\psi\!\!\text{ }}}}}_{n}}, $ |
| $ {{\mathit{\boldsymbol{\varepsilon}}\text{ }}_{Pn}}={{\dot {\mathit{\boldsymbol{\$}}}}_{Pn}}={{\left( {{\mathit{\boldsymbol{\alpha}}\text{ }}_{n}},{{\mathit{\boldsymbol{\alpha}}\text{ }}_{Pn}} \right)}^{\text{T}}}={{\mathit{\boldsymbol{H}}}_{Pn}}{{{\mathit{\boldsymbol{\dot{\psi}\text{ }}}}}_{n}}+{{\mathit{\boldsymbol{J}}}_{Pn}}{{{\mathit{\boldsymbol{\ddot{\psi}\text{ }}}}}_{n}}. $ |
式中
| $ {\mathit{\boldsymbol{J}}_{Pn}} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{S}}_{e1}^{\rm{T}}}&{\mathit{\boldsymbol{S}}_{e2}^{\rm{T}}}& \cdots &{\mathit{\boldsymbol{S}}_{en}^{\rm{T}}}\\ {{{\left( {{\mathit{\boldsymbol{S}}_{e1}} \times {\mathit{\boldsymbol{l}}_{P1n}}} \right)}^{\rm{T}}}}&{{{\left( {{\mathit{\boldsymbol{S}}_{e2}} \times {\mathit{\boldsymbol{l}}_{P2n}}} \right)}^{\rm{T}}}}& \cdots &{{{\left( {{\mathit{\boldsymbol{S}}_{ei}} \times {\mathit{\boldsymbol{l}}_{Pnn}}} \right)}^{\rm{T}}}} \end{array}} \right] $ |
为杆n的质心Pn雅克比矩阵,
| $ {{\mathit{\boldsymbol{\dot \psi }}}_n} = {\left( {{{\dot \psi }_{01}},{{\dot \psi }_{12}}, \cdots ,{{\dot \psi }_{\left( {n - 1} \right)n}}} \right)^{\rm{T}}}, $ |
| $ {{\mathit{\boldsymbol{\ddot \psi }}}_n} = {\left( {{{\ddot \psi }_{01}},{{\ddot \psi }_{12}}, \cdots ,{{\ddot \psi }_{\left( {n - 1} \right)n}}} \right)^{\rm{T}}} $ |
分别为杆n的广义速度和加速度矢量,ψi(i+1)为杆i和杆i+1之间的夹角,
由该方法可以方便地得到可展机构中单元机构ij的各运动副的速度螺旋ij11$A、ij11$B、ij11$C和ij11$D,加速度螺旋ij11εA、ij11εB、ij11εC和ij11εD以及各杆质心的速度螺旋ij11$P1、ij11$P2、ij11$P3和ij11$P4,加速度螺旋ij11εP1、ij11εP2、ij11εP3和ij11εP4.
2.3 Bennett单元阵列可展机构的动力学分析Bennett单元阵列可展机构的自由度可以通过构型设计变成1.可展机构中,假定单元11为驱动单元,单元ij的内角和输出角位移都是单元11的驱动杆位移11θ1的函数.在可展机构运动的过程中,除了作用驱动单元机构杆4上的广义力矩,还有作用在各杆件上的惯性力螺旋,由虚功原理可得
| $ \begin{align} &{{w}_{\text{d}}}=\mathit{\boldsymbol{\tau}}\text{ }{{\delta }_{11}}{{\mathit{\boldsymbol{\psi }}\text{ }}_{P4}}+\sum\limits_{i=1}^{n}{\sum\limits_{j=1}^{m}{\left( {}_{ij}{{\mathit{\boldsymbol{\$}}}_{FP1}}\delta _{ij}^{a}{{\mathit{\boldsymbol{x}}}_{P1}}+{}_{ij}{{\mathit{\boldsymbol{\$}}}_{FP4}}\delta _{ij}^{a}{{\mathit{\boldsymbol{x}}}_{P4}} \right)}}+ \\ &\ \ \ \sum\limits_{i=1}^{n}{{}_{im}{{\mathit{\boldsymbol{\$}}}_{FP2}}\delta _{im}^{a}{{\mathit{\boldsymbol{x}}}_{P2}}}+\sum\limits_{j=1}^{n}{{}_{nj}{{\mathit{\boldsymbol{\$}}}_{FP3}}\delta _{nj}^{a}{{\mathit{\boldsymbol{x}}}_{P3}}}=\mathit{\boldsymbol{\tau}}\text{ }{{\delta }_{11}}{{\mathit{\boldsymbol{\psi}}\text{ }}_{P4}}+ \\ &\ \ \ \sum\limits_{i=1}^{n}{\sum\limits_{j=1}^{m}{\left( {}_{ij}{{\mathit{\boldsymbol{\$}}}_{FP1}}_{ij}^{a}{{\mathit{\boldsymbol{J}}}_{P1}}{{\delta }_{ij}}{{\mathit{\boldsymbol{\psi}}\text{ }}_{P1}}+{}_{ij}{{\mathit{\boldsymbol{\$}}}_{FP4}}_{ij}^{a}{{\mathit{\boldsymbol{J}}}_{P4}}{{\delta }_{ij}}{{\mathit{\boldsymbol{\psi}}\text{ }}_{P4}} \right)}}+ \\ &\ \ \ \sum\limits_{i=1}^{n}{{}_{im}{{\mathit{\boldsymbol{\$}}}_{FP2}}_{im}^{a}{{\mathit{\boldsymbol{J}}}_{P2}}\cdot {{\delta }_{im}}{{\mathit{\boldsymbol{\psi}}\text{ }}_{P2}}}+\sum\limits_{j=1}^{m}{{}_{nj}{{\mathit{\boldsymbol{\$}}}_{FP3}}_{nj}^{a}{{\mathit{\boldsymbol{J}}}_{P3}}{{\delta }_{nj}}{{\mathit{\boldsymbol{\psi}}\text{ }}_{P3}}}. \\ \end{align} $ |
式中:δ11ψP4=δ11θ1; τ为作用在驱动单元上的广义力矩; 由于ijψPe是广义变量11θ1的函数,可以得到δijψPe=ijfωPeδ11θ1,称之为单元ij中杆e广义速度矢量,ijfωPe为单元ij中杆e的广义速度矢量系数矩阵;ijaxPe是单元ij中杆e质心的射线坐标形式,ijaxPe=
将δ11P4ψ=δ11θ1和δijψPe=ijfωPeδ11θ1代入可得Bennett单元阵列可展机构的动力学分析模型:
| $ \begin{align} &\mathit{\boldsymbol{ }}\!\!\tau\!\!\text{ }+\sum\limits_{i=1}^{n}{\sum\limits_{j=1}^{m}{\left( {}_{ij}{{\mathit{\boldsymbol{\$}}}_{FP1}}_{ij}^{a}{{\mathit{\boldsymbol{J}}}_{P1ij}}{{\mathit{\boldsymbol{f}}}_{\omega P1}}+{}_{ij}{{\mathit{\boldsymbol{\$}}}_{FP4}}_{ij}^{a}{{\mathit{\boldsymbol{J}}}_{P4ij}}{{\mathit{\boldsymbol{f}}}_{\omega P4}} \right)}}+ \\ &\sum\limits_{i=1}^{n}{{}_{im}{{\mathit{\boldsymbol{\$}}}_{FP2}}_{im}^{a}{{\mathit{\boldsymbol{J}}}_{P2im}}{{\mathit{\boldsymbol{f}}}_{\omega P2}}}+\sum\limits_{j=1}^{m}{{}_{nj}{{\mathit{\boldsymbol{\$}}}_{FP3}}_{nj}^{a}{{\mathit{\boldsymbol{J}}}_{P3nj}}{{\mathit{\boldsymbol{f}}}_{\omega P3}}}=0. \\ \end{align} $ |
采用数值方法求解动力学方程,可以获得作用在驱动单元上的广义力矩.
3 算例以图 6中Bennett机构构成的4×4阵列可展机构为例,分析其运动学和动力学.

|
图 6 4×4 L型Bennett单元阵列可展机构 Figure 6 Schematic diagram of 4×4 L type Bennett unit array deployable mechanism |
在该可展机构中,所有的Bennett单元机构都是相同的,其参数见表 1,表 1中杆a和杆b对应图 1中的la和lb.假定单元11为驱动单元,杆A11B11为机架,电机作用在运动副A11上,为了保证机构展开的效率和稳定,驱动机构的运动规律分为3个阶段:加速阶段、匀速阶段和减速阶段.具体的运动规律如下:
| 表 1 Bennett单元机构的基本参数 Table 1 Basic parameters of Bennett unit linkage |
| $ \theta = \left\{ \begin{array}{l} \frac{1}{2}{\alpha _1}{t^2},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {0 \le t \le \frac{T}{6}} \right);\\ \frac{{{\alpha _1}Tt}}{6} - \frac{{{\alpha _1}{T^2}}}{{72}},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {\frac{T}{6} < t \le \frac{{2T}}{3}} \right);\\ \frac{1}{2}{\alpha _1}Tt - \frac{{{\alpha _1}{T^2}}}{8} - \frac{{{\alpha _1}{t^2}}}{4},\;\;\;\;\;\;\left( {\frac{{2T}}{3} < t \le T} \right). \end{array} \right. $ |
式中T为可展机构的运动周期.
Bennett机构在阵列后是否干涉与驱动角的运动范围有很大关系,如果阵列后所有单元的驱动角在展开过程中不超过其运动范围,则不会干涉. Bennett机构的运动范围与本身构件参数和形状的选择有关,为了考虑更大运动范围内的Bennett单元阵列可展机构的动力学问题,本文没有考虑Bennett单元构件的设计,假设Bennett单元机构的驱动角的运动范围为0~π.加速阶段驱动单元的加速度:α1=0.1 rad/s2,减速阶段驱动单元的加速度α2=-α1/2.展开过程中,第一行中所有单元的杆1和第一列中所有单元的杆4分别位于同一条直线上,如图 6中的粗线所示.可展机构的第一行及第一列的各Bennett单元机构的输入角和输出角可以通过式(1)得到
| $ \begin{array}{*{20}{c}} {{}_{1\left( {i + 1} \right)}{\theta _1} = {}_{1i}{\eta _1},}&{{}_{\left( {j + 1} \right)1}{\theta _1} = {}_{j1}{\eta _1}.} \end{array} $ |
式中:i= 1,2,3,j= 1,2,3.
第i+1行j+1列单元机构的输入角和输出角:
| $ {}_{\left( {i + 1} \right)\left( {j + 1} \right)}{\theta _1} = 2{\rm{ \mathsf{ π} }} - \left( {{}_{ij}{\theta _1} + {}_{\left( {i + 1} \right)j}{\theta _2} + {}_{i\left( {j + 1} \right)}{\theta _2}} \right). $ |
式中:i= 1, 2, 3; j=1, 2, 3.
该可展机构的输入角和输出角可以依次求解,然后按照此顺序求解出各个单元输入角和输出角的角速度及角加速度.为了验证所建模型的正确性,采用ADAMS对算例中的可展机构进行了动力学仿真.
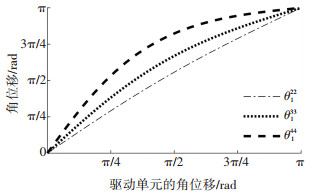
对于4×4阵列可展机构,对角线上的各单元的运动参数比较有代表性. 图 7~9给出了可展机构对角线上各单元机构的驱动角在运动范围内的角位移、角速度和角加速度.
|
图 7 对角线上各单元驱动角的角位移 Figure 7 Angular displacements of the driving angulars of all uints located on the digonal |
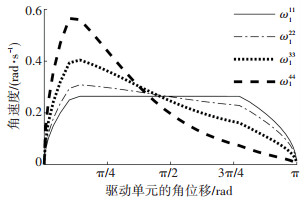
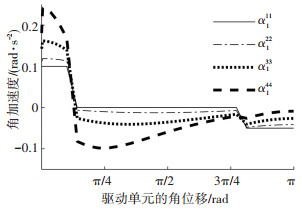
由图 7可看出,文中给定的参数使得可展机构各单元的驱动角在运动范围内变换比较平缓.可展机构中各单元的驱动角都在0~π,不会相互干涉.由图 8和图 9可看出,单元机构距离驱动单元愈远,驱动角的角速度和角加速度变化范围越大.
|
图 8 对角线上各单元驱动角的角速度 Figure 8 Angular velocities of the driving angulars of all uints located on the digonal |
|
图 9 对角线上各单元驱动角的角加速度 Figure 9 Angular accelerations of the driving angulars of all uints located on the digonal |
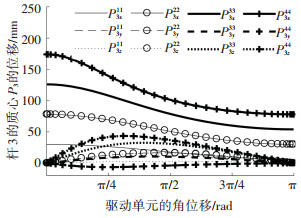
图 10~12给出了4×4 Bennett单元阵列可展机构对角线上各单元机构杆3的质心P3在x、y和z轴方向上的位移、速度和加速度.
|
图 10 对角线上各单元杆3的质心位移 Figure 10 Centroid displacements of the link 3 of all uints located on the digonal |

|
图 11 对角线上各单元杆3的质心速度 Figure 11 Centroid velocities of the link 3 of all uints located on the digonal |
|
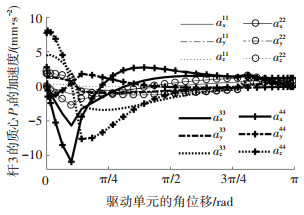
图 12 对角线上的各单元杆3质心加速度 Figure 12 Centroid accelerations of the link 3 of all uints located on the digonal |
由图 10和图 11可看出,各单元杆3的质心在x、y和z轴方向上的位移和速度在运动范围内变化比较平缓,运动比较平稳.由图 12可看出,在T/6以及3T/4附近,杆3质心处的加速度波动幅度比较大,离驱动单元越远,各单元杆3的质心在x轴和z轴方向上的加速度变化范围越大,加速度的稳定范围越小.
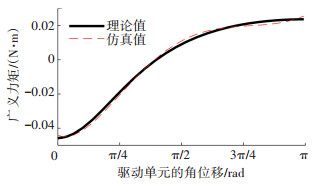
图 13是模型计算与仿真得到的作用在驱动杆上的广义力矩.可以看出,动力学模型计算结果和ADAMS仿真结果有一定的偏差,但是趋势上是吻合的,说明该运动学和动力学模型是可靠的.在整个运动范围内,广义力矩的变化比较平缓,不会出现载荷突然增加的情况,为该可展机构的控制提供了基础.
|
图 13 可展机构的广义力矩 Figure 13 Generalized moments of the deployable mechanism |
为了验证建立的运动学和动力学分析模型,搭建了Bennett单元阵列可展机构实验台,见图 14.实验台中可展机构驱动单元的驱动角与两个驱动杆之间的夹角相等,其运动规律由驱动杆长度、丝杠上滑块的运动距离确定,滑块的运动由电机的转动速度控制.该试验台可以测量可展机构中各运动副和各质心的加速度.给定丝杠上滑块的运动是梯形的,初始速度为0 mm·s-1,加速和减速阶段的加速度为6 mm·s-2,匀速阶段的速度为6 mm·s-1,初始位移为124 mm,运动距离为60 mm.算例中的杆件参数(见表 1)可以保证可展机构具有较大的运动范围,有利于工程应用,但是杆件的加工难度大,成本高.为了便于杆件加工和降低成本,实验台杆件的扭角取两个特殊的角度,具体参数见表 2.

|
图 14 Bennett单元阵列可展机构实验台 Figure 14 Experiment table of Bennett unit array deployable mechanism |
| 表 2 实验台的基本参数 Table 2 Basic parameters of the experiment platform |
表 2中杆a和杆b对应图 1中的la和lb,驱动杆ld是图 14中的驱动杆.虽然实验台中的可展机构运动范围小,但是在一定程度上可以用来验证本文建立的运动学和动力学分析模型和方法.
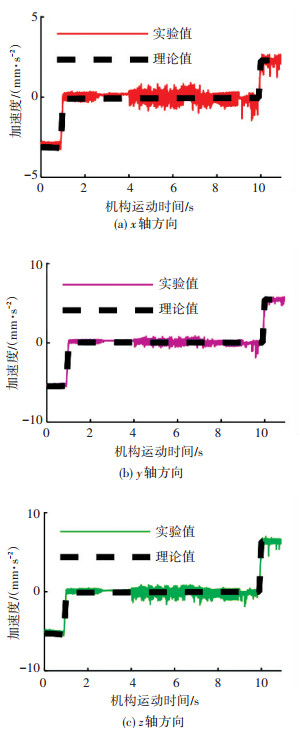
针对实验台中的可展机构,采用表 2中的杆件参数和滑块的运动条件进行了数值仿真计算.通过坐标变换可以将计算值和实验值放入同一坐标系中.对比了单元22中杆件3的质心P322的加速度在同一坐标系中的计算值和实验测量值,具体结果见图 15.可以看出实验结果和模型计算结果基本一致,误差是由丝杠偏心距、滑块和丝杠之间不够光滑等因素引起的.由模型计算和实验测量对比结果看,文中建立的运动学和动力学分析模型和方法是正确的,可以用来分析类似的Bennett单元阵列可展机构.
|
图 15 质心P322的加速度 Figure 15 Accelerations of the centroid P322 |
动力学分析结果可应用于此类可展机构的轨迹规划、控制器参数的整定以及动态设计等环节.
5 结论1) 根据Bennett单元阵列可展机构多闭环和重复的特性,将其拆解为多个空间串联开链机构,结合螺旋理论与坐标变换法,构建了Bennett单元阵列可展机构的运动学分析模型,采用虚功原理法建立了其动力学分析模型和动力学分析方法.该模型对任意个Bennett单元机构、不同组合方式构成的可展机构具有通用性;
2) 该运动学与动力学分析模型将虚功原理中相关的导数运算变换为向量之间的加乘运算,在一定程度上提高了可展机构的运动学和动力学分析运算效率;
3) 算例中的4×4 Bennett单元阵列可展机构在给定运动范围内运动平稳,广义力矩的变化比较平缓.
4) 采用ADAMS仿真和实验的方法对所建模型进行了验证,结果证明文中所建的动力学和运动学模型是正确的,可以用于此类可展机构的设计和分析.
| [1] |
CHEN Yan.Design of structural mechanisms[D].Oxford: University of Oxford, 2003
|
| [2] |
MELIN N O B.Application of Bennett mechanisms to long-span shelters[D].Oxford: University of Oxford, 2004
|
| [3] |
SONG Xiaoke, DENG Zongquan, GUO Hongwei, et al. Networking of Bennett linkages and its application on deployable parabolic cylindrical antenna[J]. Mechanism and Machine Theory, 2017, 109: 95. DOI:10.1016/j.mechmachtheory.2016.10.019 |
| [4] |
LU Shengna, ZLATANOV D, DING Xilun. Approximation of cylindrical surfaces with deployable Bennett networks[J]. Journal of Mechanisms and Robotics, 2017, 9(2): 1. DOI:10.1115/1.4035801 |
| [5] |
ZHI Changjian, WANG Sanmin, LI Jianfeng, et al. Kinematic and dynamic characteristics analysis of Bennett's Linkage[J]. Journal of Harbin Institute of Technology (New Series), 2015, 22(3): 95. DOI:10.11916/j.issn.1005-9113.2015.03.014 |
| [6] |
TSAI L W. Solving the inverse dynamics of a Stewart-Gough manipulator by the principle of virtual work[J]. Journal of Mechanical Design, 2000, 122(1): 3. DOI:10.1115/1.533540 |
| [7] |
ZHAO Yongjie, GAO Feng. Inverse dynamics of the 6-dof out-parallel manipulator by means of the principle of virtual work[J]. Robotica, 2009, 27(2): 259. DOI:10.1017/S0263574708004657 |
| [8] |
贾晓辉, 田延岭, 张大卫. 基于虚功原理的3-RRPR柔性精密定位工作台动力学分析[J]. 机械工程学报, 2011, 47(1): 68. JIA Xiaohui, TIAN Yanling, ZHANG Dawei. Inverse dynamics of 3-RRPR compliant precision positioning stage based on the principle of virtue work[J]. Journal of Mechanical Engineering, 2011, 47(1): 68. DOI:10.3901/JME.2011.01.068 |
| [9] |
KALANI H, REZAEI A, AKBATZADEH A. Improved general solution for the dynamic modeling of Gough-Stewart platform based on principle of virtual work[J]. Nonlinear Dynamics, 2016, 83(4): 2393. DOI:10.1007/s11071-015-2489-z |
| [10] |
XIN Guiyang, DENG Hua, ZHONG Guoliang. Closed-form dynamics of a 3-DOF spatial parallel manipulator by combining the Lagrangian formulation with the virtual work principle[J]. Nonlinear Dynamics, 2016, 86(2): 1329. DOI:10.1007/s11071-016-2967-y |
| [11] |
孙宏图, 袁茹, 王三民. 正方形可展机构的运动学与动力学特性研究[J]. 西北工业大学学报, 2013, 31(4): 620. SUN Hongtu, YUAN Ru, WANG Sanmin. Kinematics and dynamics characteristics of square developable structure[J]. Journal of Northwestern Polytechnical University, 2013, 31(4): 620. DOI:10.3969/j.issn.1000-2758.2013.04.027 |
| [12] |
SUN Yuantao, WANG Sanmin, MILLS J K, et al. Kinematics and dynamics of deployable structures with scissor-like-elements based on screw theory[J]. Chinese Journal of Mechanical Engineering, 2014, 27(4): 655. DOI:10.3901/CJME.2014.0519.098 |
| [13] |
李博, 王三民, 袁茹, 等. 基于剪式线性阵列可展结构对称性的动力学分析方法研究[J]. 西北工业大学学报, 2015, 33(4): 665. LI Bo, WANG Sanmin, Yuan Ru, et al. Dynamics analysis method study based on linear array deployable structure symmetry of scissor-like element[J]. Journal of Northwestern Polytechnical University, 2015, 33(4): 665. DOI:10.3969/j.issn.1000-2758.2015.04.024 |
| [14] |
李博, 王三民, 袁茹, 等. 运动副间隙耦合作用下平面剪式线性阵列可展结构的动力学分析[J]. 西北工业大学学报, 2017, 35(3): 455. LI Bo, WANG Sanmin, YUAN Ru, et al. Dynamics analysis of planar linear array deployable structures under the coupling action of clearance Joints[J]. Journal of Northwestern Polytechnical University, 2017, 35(3): 455. DOI:10.3969/j.issn.1000-2758.2017.03.015 |
| [15] |
智常建, 王三民, 孙远涛. 运动副间隙对多杆锁机构动力学特性的影响[J]. 哈尔滨工业大学学报, 2014, 46(8): 102. ZHI Changjian, WANG Sanmin, SUN Yuantao. Effect of kinematic pairs clearance on dynamic characteristics of multi-linkage lock mechanisms[J]. Journal of Harbin Institute of Technology, 2014, 46(8): 102. |
| [16] |
FILIPOVIC M, DJURIC A, KEVAC L. The significance of adopted Lagrange's principle of virtual work used for modeling aerial robots[J]. Applied Mathematical Modelling, 2015, 39(7): 1804. DOI:10.1016/j.apm.2014.09.019 |
 2019, Vol. 51
2019, Vol. 51


