2. 济祁高速公路(砀山段)项目办公室,安徽 宿州 235300;
3. 长安大学 公路工程学院,西安 710064
2. Jiqi Expressway(Dangshan section), Project Office, Suzhou 400074, Anhui, China;
3. Highway Engineering Institute, Chang'an University, Xi'an 710064, China
PVA纤维是一种直径仅为几个微米,且都以束状形态存在的材料,同时表面光滑还具有较强的亲水性,在水泥基复合材料中难以均匀分散,影响了PVA纤维水泥基复合材料的机能,限制了PVA纤维作为功能材料的普及运用[1-2].实验研究表明,在水泥基复合材料中掺入PVA纤维,可有效地改善水泥基复合材料的抗裂性能、抗冲击、抗渗、抗收缩性能以及弯曲韧性[3].因此,在PVA纤维掺入水泥基复合材料搅拌之前,需将PVA纤维束分散成单丝状并形成均匀的三维网状结构,使分散后的PVA纤维与水泥基复合材料材料更加容易拌和均匀,发挥出其对水泥基复合材料材料的改善作用.
一直以来,纤维分散的均匀性评价方法较多,国内外学者通过直观对比法、参数评价法和数值图像法等对PVA纤维进行分散均匀性评价[4-7].其中直观对比法只能进行分散效果比较明显,用肉眼能直接辨别的搅拌分散;参数评价法是用一些高精度测量仪器,测量搅拌后纤维溶液中的参数,用来定量评价纤维的分散效果,这种方法对操作要求高、测量仪器昂贵;数字图像法是利用数字图像处理技术,将搅拌分散后的纤维图像进行采集,分析图像特征信息,从而评价纤维分散效果.灰度共生矩阵法属于数字图像法的一种,通过提取图像纹理特征,获取图像的特征参数值来作为评价指标,这种方法具有操作简单、精度高、再现性好、获取信息多等优点.所以本文选用灰度共生矩阵法,依据纤维分散后的图像特征参数来评价纤维的分散效果,从分散剂、搅拌参数、搅拌设备部分开展纤维分散研究且评价分散均匀性.本文运用PVA纤维束搅拌设备样机,依据灰度共生矩阵理论,应用图像特征参数从分散剂种类、搅拌桨转速和搅拌桨类型三个方面来评价PVA纤维分散均匀性, 为PVA纤维束搅拌分散技术提供指导.
1 PVA纤维分散效果评价方法 1.1 灰度共生矩阵理论灰度共生矩阵表述的是图像中灰度在方向、相邻间隔和变化幅度方面的综合信息.灰度共生矩阵属于数字图像法的一种,通过提取纤维分散图像中的纹理特征,获取图像的特征参数值,依据纤维分散后的图像特征参数来评价纤维的分散效果.在整张图像中,统计每一组灰度对出现的频率为P(i, j, d, θ),称方阵[P(i, j, d, θ)]GxG为灰度共生矩阵.灰度共生矩阵实质上就为两像素点的联合直方图,若距离间隔值(Δx, Δy)取不同的数值组合,就能够获得图像沿一定方向θ、相距一定距离
| $ \begin{array}{l} P\left( {i,j,d,\theta } \right) = \\ \;\;\{ [\left( {x,y} \right),\left( {x + \Delta x,y + \Delta y} \right)|f\left( {x,y} \right) = \\ \;\;i;f\left( {x + \Delta x + \Delta y} \right) = i]\} . \end{array} $ |
为了便于实际中的计算,灰度共生矩阵元素往往用概率值来表示,即各元素P(i, j, d, θ)除以各元素之和S,获得各元素都小于1的归一化值
| $ \hat p\left( {i,j,d,\theta } \right) = p\left( {i,j,d,\theta } \right)/s. $ |
灰度共生矩阵具有大量的特征参数,Haralick等人定义了14个用于纹理分析的灰度共生矩阵参数[9].其中:熵值是表征纹理粗细和复杂度的参数,是图像所包含的信息量的表征; 角二阶矩是表征灰度分布均匀度的参数, 是图像灰度分布均匀性的表征.
1) 熵f1的表达式:
| $ {f_1} = - \sum\limits_{i = 0}^{G - 1} {\sum\limits_{j = 0}^{G - 1} {\hat P(i,j,d,\theta )} } lg\hat P(i,j,d,\theta ). $ | (1) |
若图像中无纹理,则灰度共生矩阵基本为零阵,其熵值f1接近为零.如果图像中布满着细纹理,则
2) 角二阶矩f2的表达式:
| $ {f_2} = \sum\limits_{i = 0}^{G - 1} {\sum\limits_{j = 0}^{G - 1} {{{\hat P}^2}(i,j,d,\theta )} } . $ | (2) |
从图像整体来看,纹理越粗,角二阶矩f1越大,也可以理解为粗纹理含有较多的能量.反之,纹理越细,则角二阶矩f1就越小,也就是它具有较少的能量.
1.3 Matlab实现本文的灰度共生矩阵法要借助于MATLAB编程算法来实现.在PVA纤维搅拌分散后,通过图像采集设备得到纤维的RGB真彩色图像,利用rgb2gray()程序将PVA纤维RGB图像转换为灰度图像.然后将灰度图像保存为bmp格式,导入灰度共生矩阵算法程序,得到灰度共生矩阵特征参数值.程序的算法步骤如下:
1) 将原始图像的256灰度级进行压缩,转化为16级灰度.
2) 取d=1,θ=0°、45°、90°和135°,分别计算4个灰度共生矩阵.
3) 对共生矩阵进行归一化处理.
4) 根据式(1)和式(2),计算灰度共生矩阵的角二阶矩和熵这两个特征参数值.
5) 分别对0°、45°、90°和135°这4个方向的特征值求平均值,得到最终的二维纹理特征.
2 试验及试验结果分析 2.1 试验设计本文研究的PVA纤维选用的是安徽皖维集团生产的混凝土用改性PVA纤维, 分散剂选用山东特耐斯化工有限公司生产的分散剂进行研究,搅拌设备为PVA纤维束搅拌样机,搅拌桨的结构类型为四直叶、三斜叶、四斜叶和组合桨, 如图 1~4所示.

|
图 1 四直叶 Figure 1 Four straight blades |

|
图 2 三斜叶 Figure 2 Triclinic blades |

|
图 3 四斜叶 Figure 3 Quadrature blades |

|
图 4 组合桨 Figure 4 Combined paddles |
为了保证试验数据的准确性与客观性,本文对分散剂种类、搅拌桨类型和搅拌桨转速每个变量都重复10组试验,通过图像采集和纹理特征提取之后,得到10组不同的角二阶矩和熵值.在数据处理中,将10组数据去除最大值和最小值后求平均值,将该平均值作为各组变量的数值.
在数字图像的采集、传送和转换过程中,由于噪声等原因会造成图像的模糊和失真,需要根据图像退化的逆向过程进行还原,因此在进行求解数字图像的特征参数之前,需要对真彩色图像进行压缩、灰度化、滤波去噪、直方图均衡化、集料小颗粒过滤、图形的膨胀与腐蚀、开运算以及闭运算以及中值滤波处理,提升对比度与灰度色调的变化,消除噪点,使得像素更加分明和逼真,为纹理特征的提取和计算提供更加可靠和准确的角二阶矩阵和熵值.
2.2 不同添加剂的分散效果评价PVA纤维缠敷性很强,机械搅拌时无法较好地将纤维束分散,添加分散剂可有效改善分散效果. PVA纤维表面具有极性羰基基团和羟基基团,使PVA纤维束具有较强的亲水性.选用的甲基纤维素(MC)、羟乙基纤维素(HEC)和羧甲基纤维素钠(CMC-Na)这3种分散剂都具有极性羟基基团[10].
在使用前,将分散剂均配为15%的水溶液.采用4种类型搅拌桨,转速设置为600 r/min,搅拌时间为3 min,分别进行无分散剂和添加MC、HEC和CMC-Na这3种分散剂的试验.试验中添加每种分散剂搅拌后,PVA纤维按照标签依次放置,如图 5所示.

|
图 5 试验搅拌后的PVA纤维 Figure 5 PVA fiber after agitation |
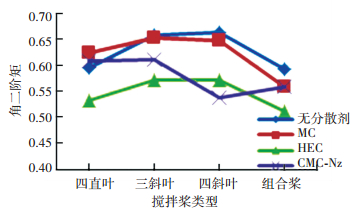
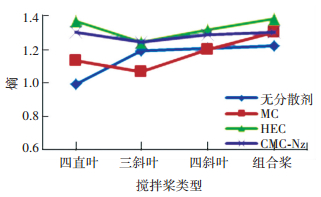
采集分散后PVA图像,进行灰度共生矩阵特征参数提取,试验得到的无分散剂和添加分散剂的角二阶矩和熵值曲线图如图 6、7所示.
|
图 6 不同分散剂种类的角二阶矩曲线图 Figure 6 Angular second moment curves of different dispersant types |
|
图 7 不同分散剂种类的熵值曲线图 Figure 7 Entropy curves of different dispersant types |
添加HEC和CMC-Na分散剂的角二阶矩曲线处于整个曲线图的下方,除四直叶工况CMC-Na角二阶矩大于无分散剂外,其他3种搅拌桨工况的2种分散剂角二阶矩均小于添加MC和无分散剂;处于曲线图上方的无分散剂和MC分散剂,除四直叶工况MC角二阶矩大于无分散剂外,其他2种搅拌桨工况的添加MC分散剂角二阶矩均小于无分散剂.在4种搅拌桨工况下,添加HEC分散剂的熵值均最大,在组合桨工况下达到最大值1.3825,其次是添加CMC-Na分散剂,其熵值略小于HEC分散剂;添加MC分散剂和无分散剂熵值曲线处于整个曲线图下方.
综上所述,根据角二阶矩越小,熵值越大,PVA纤维束分散效果越好的评价标准,得出以下试验结论:添加HEC分散剂对PVA纤维束的分散效果最好,而添加MC分散剂对纤维的分散效果最差.
2.3 不同转速的分散效果评价在试验过程中,观察到当高转速时,搅拌桨产生的离心力增大,虽然大于纤维的内摩擦力,但是纤维由于离心力的作用无法靠近搅拌叶片边缘,附着在搅拌槽壁面,无法充分分散;当低转速搅拌时,搅拌的离心力和剪切力小于纤维之间的内摩擦力,纤维依然呈缠敷状态,也无法充分分散.试验中高低转速时搅拌槽内的纤维状态图如图 8、9所示.

|
图 8 高转速时纤维状态图 Figure 8 Fiber state diagram at high speed |

|
图 9 低转速时纤维状态图 Figure 9 Fiber state diagram at low speed |
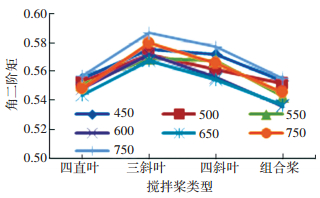
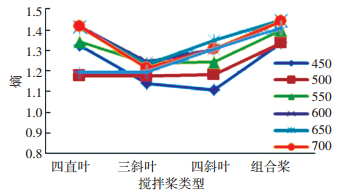
转速范围选取450~750 r/min区间,间隔为50 r/min.添加分散剂为HEC分散剂,搅拌桨选取四直叶、三斜叶、四斜叶及其组合桨.同样对每种转速进行10次试验,采集分散后的PVA纤维图像,进行灰度共生矩阵特征参数提取,得到不同转速下4种搅拌桨的角二阶矩和熵值曲线图, 如图 10、11所示.
|
图 10 整数转速的角二阶矩曲线图 Figure 10 Angular second moment curves of the integer rotational speed |
|
图 11 整数转速的熵曲线图 Figure 11 Entropy curves of integer speed |
根据搅拌桨转速的角二阶矩和熵值曲线图,对比分析可得:随着转速的增大,角二阶矩先增大后减小,转速750 r/min的角二阶矩在4种搅拌桨工况下大于其他转速,转速650 r/min的角二阶矩在4种搅拌桨工况下大于其他转速;随着转速的增大,角二阶矩先减小后增大,转速650 r/min的熵值在4种搅拌桨工况下大于其他转速,转速450、500 r/min的熵值在4种搅拌桨工况下最小.
综上所述,根据角二阶矩越小,熵值越大,PVA纤维束分散效果越好的评价标准,得出以下试验结论:在转速650 r/min时,角二阶矩最小,熵值最大, 因此650 r/min为分散PVA纤维的最佳搅拌转速.
2.4 不同搅拌桨的分散效果评价由于搅拌桨叶片的类型不同,其运动形态可以分为径向流、轴向流和切向流,因此不同形状的叶片类型对PVA纤维分散的效果有很大的影响.四直叶片属于径向流型叶片,其叶片末端的剪切作用力大,但是耗散的功率也较大.三斜叶、四斜叶属于轴流型叶片,混合效果较好.组合桨则属于混合型或者叠加型叶片,其剪切和混合效果有的只是简单的叠加,有的则是有显著的互补与促进分散的作用.
本文采用的4种类型搅拌桨可以有效地对流动形态进行试验研究,搅拌时间为3 min,添加分散剂为HEC分散剂,转速间隔为35 r/min,绘制出转速范围在450~750 r/min的4种不同类型搅拌桨的熵值曲线图, 如图 12、13所示.
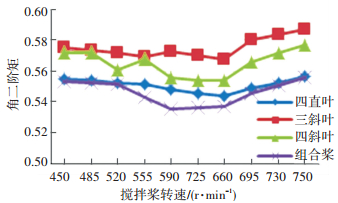
|
图 12 不同搅拌桨的角二阶矩折线图 Figure 12 The second order moments of different agitating paddles |
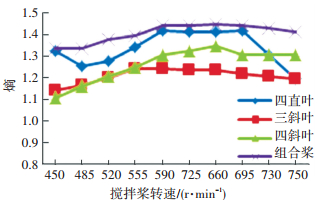
|
图 13 不同搅拌桨的熵值折线图 Figure 13 Entropy values of different agitating paddles |
在图 12中,4种搅拌桨都呈现先减小后增大的趋势,组合桨的角二阶矩均小于其余2种搅拌桨;在图 13中,4种搅拌桨都呈现先增大后减小的趋势,组合桨的熵均大于其余2种搅拌桨,在650r/min达到了最大值. 4种搅拌桨对PVA纤维的分散效果为:组合桨>四直叶>四斜叶>三斜叶.
综上所述,得到本文中PVA纤维束搅拌分散设备的最优搅拌作业参数为:添加HEC分散剂,转速650 r/min、组合桨.
3 结语1) 本文利用数字图像处理技术对拍摄的PVA纤维图像进行分析和预处理,在灰度共生矩阵理论的基础上,提出应用灰度共生矩阵特征参数熵值进行PVA纤维分散性判别的方法,运用MATLAB软件,依据试验后提取的PVA纤维图像特征参数的熵值,来评价PVA纤维的分散性,得到一种快速、准确的PVA纤维束分散效果评价方法.
2) 分析了在不同种类分散剂、不同搅拌转速、不同搅拌桨搅拌参数下PVA纤维的分散效果.结果表明:添加HEC分散剂使PVA纤维分散效果更好,可以有效促进PVA纤维束的分散;搅拌转速越大,PVA纤维分散效果越好,转速650 r/min是PVA纤维束搅拌设备的最佳搅拌转速;四直叶桨属于径流型搅拌设备,具有较好的剪切作用,四斜叶桨则为轴向型,能够产生良好的整体循环流动,组合桨在二者的交互作用下,总体对流循环与分散效果更好,能够产生更强的剪切与混合作用,可以更有效地促进PVA纤维束的搅拌分散.
| [1] |
张丽辉, 郭丽萍. 高延性水泥基复合材料的流变特性和纤维分散性[J]. 东南大学学报, 2014, 44(5): 1037. ZHANG Lihui, GUO Liping. Rheological properties and fiber dispersibility of high ductility cementitious composites[J]. Journal of Southeast University, 2014, 44(5): 1037. |
| [2] |
郭丽萍, 陈波, 杨亚男. PVA纤维对混凝土抗裂与增韧效应影响的研究进展[J]. 水利水电科技进展, 2015, 35(6): 113. GUO Liping, CHEN Bo, YANG Yanan. PVA fiber on concrete cracking and toughening effect of progress[J]. Water Resources and Hydropower Engineering Progress, 2015, 35(6): 113. |
| [3] |
Jr Sydney Fur lan, Joao Bento de Han nai. Shear behavior of fiber reinforced concrete beams[J]. Cement and Concrete Composites, 1997, 19(4): 359. DOI:10.1016/S0958-9465(97)00031-0 |
| [4] |
黄一磊, 胡健, 郑炽嵩. ξ电位对玻璃纤维分散的影响[J]. 造纸科学与技术, 2004, 23(1): 31. HUANG Yilei, HU Jian, ZHENG Zhisong. Effects of xi potential on the dispersion of glass fiber[J]. Science and Technology of Paper Making, 2004, 23(1): 31. |
| [5] |
KEREKES R J, SCHELL C J. Characterization of fiber flocculation regimes by a crowding factor[J]. Journal of Pulp and Paper Sicence, 1992, 18(1): 32. |
| [6] |
JEONG S H, KIM S H, HONG C J. The evaluation of evenness of nonwovens using image analysis method[J]. Fibers and Polymers, 2001, 2(3): 164. DOI:10.1007/BF02875331 |
| [7] |
关晓宇, 钱晓明, 杨棹航. 合成纤维在水中的分散手段与表征方法[J]. 产业用纺织品, 2015, 33(8): 35. GUAN Xiaoyu, QIAN Xiaoming, YANG Zhuohang. The dispersion methods and characterization methods of synthetic fibers in water[J]. Industrial Textiles, 2015, 33(8): 35. DOI:10.3969/j.issn.1004-7093.2015.08.008 |
| [8] |
侯群群, 王飞, 严丽. 基于灰度共生矩阵的彩色遥感图像纹理特征提取[J]. 国土资源遥感, 2013(4): 26. HOU Qunqun, WANG Fei, YAN Li. Texture feature extraction of color remote sensing images based on gray level co-occurrence matrix[J]. Remote Sensing of Land and Resources, 2013(4): 26. |
| [9] |
HARALICK R M. Statistical and structural approaches to texture[J]. Proceedings of the IEEE, 1979, 67(5): 786. DOI:10.1109/PROC.1979.11328 |
| [10] |
杨杰, 张文苑, 隋学叶, 等. 分散剂在陶瓷纤维分散过程中的应用[J]. 应用技术, 2014(4): 58. YANG Jie, ZHANG Wenyuan, SUI Xueye, et al. Application of dispersant in dispersion process of ceramic fiber[J]. Applied Technology, 2014(4): 58. |
 2019, Vol. 51
2019, Vol. 51


