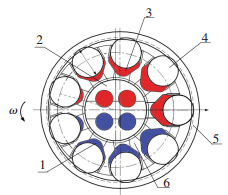
球塞泵是一种新型的径向液压泵,结构简图如图 1所示,依靠缸体与作用环的偏心作用来带动球状活塞在缸体孔中往复运动,从而实现吸油与压油过程.相比于传统的轴向柱塞泵,在相同的性能指标下,球塞泵的轴向尺寸大幅减小,占用空间小,功率密度高;构件少,结构简单紧凑,可靠性高;变量机构简单可靠,可以实现排量在一定范围内的无级变化.因此,球塞泵作为高性能车辆传动系统的重要组成元件,尤其在军用履带车辆的无级变速和转向中具有广泛的应用前景[1-3].
|
1—低压油腔; 2—配流轴; 3—高压油腔; 4—球活塞; 5—作用环; 6—缸体 图 1 球塞泵结构简图 Figure 1 Structure of the ball piston pump |
球塞泵工作过程中,配流轴需要通过一侧来排出高压油,另一侧来吸入低压油,这就造成两侧的受力不平衡,且在工作压力较大时,不平衡力非常大,靠动压支撑是无法满足的.在这种环境下,综合圆柱形配流副的结构设计经验,采用图 2所示的结构形式,锥形配流副主要由支承在轴承6上的锥形缸体4和完全处于浮动状态的锥形配流轴2组成,两者之间的配流面加工成平行锥面.由于受到排油孔8压紧力的作用,锥形配流轴沿轴向压紧锥形缸体,且配力不平衡;为了避免锥形缸体与锥形配流轴之间的金属接触,在锥形配流轴内设置节流阻尼用于沟通高压平衡油槽1和低压平衡油槽2,以使配流面间形成一定厚度的润滑油膜,产生一定的油膜力,以实现锥形配流副的轴向和径向受力平衡.同时,高压流道分布在上下两侧,低压流道分布在左右两侧,这样就消除了配流轴关于轴心的转矩,避免了偏转.

|
1—高压平衡油槽; 2—锥形配流轴; 3—低压平衡油槽; 4—缸体; 5—球活塞; 6—支撑轴承; 7—高压窗口; 8—高压油道; 9—低压窗口; 10—低压油道 图 2 球塞泵锥形配流副结构原理图 Figure 2 Schematic of the conical spindle distribution |
在国内,北京理工大学曾开展了球塞泵研究工作,对球塞泵进行了结构设计和性能参数的计算,同时对其关键摩擦副—球塞副的流场分布和泄漏量及其影响因素(球塞副的配合间隙、工作油液的压力和温度)进行了一定程度的理论研究[4-7].林硕[8]建立了球塞副偏心稳态运动的双边楔形缝隙流场数学模型,应用数值方法联合迭代求解雷诺方程和能量方程,得到了球塞副在不同入口压力、不同工作转速、不同滑转率下的泄漏特性,并对压差和剪切导致的泄漏进行了区别分析.
另外, 南昌大学游步东[9],黄丹[10],付蓓蓓[11]等进行了工作介质为水的低压球塞泵理论和试验研究,对球塞副的运动学和动力学特性进行了理论计算.国内对圆柱配流式球塞泵及其关键摩擦副进行了较为深入的研究,但针对球塞泵锥形配流副的研究工作较少.
锥形配流副在结构和工作原理上与径向—推力圆锥滑动轴承的模型具有相似之处,可以充分借鉴其研究结果来对配流副进行研究.圆锥滑动轴承的理论研究在已在近些年的发展中逐步完善. F.M.Stansfield是最早进行圆锥滑动轴承相关研究的学者,他用解析方法分析了单腔和多腔圆锥静压轴承的一维流动情况,借用了向心轴承和平面推力轴承在一维流情况下较完善的理论,计算得到了圆锥轴承在一维流动假设下的有效面积、承载能力、刚度、流量、阻力和功耗等性能指标的近似解析解[12].
P.J.Prabhu分别对毛细管和小孔节流的环形腔圆锥轴承的性能进行分析,在一维流状态用解析法导出了Constantinescu球面坐标下封油面上压力分布表达式,并得到了静态承载能力、静态刚度、流量、封油面上的摩擦功耗以及动态刚度、阻尼的解析解,并用差分法计算了环形腔圆锥轴承二维流时的静特性值及动刚度和阻尼系数[13-14]. A.EL.Kagar等对圆锥静压轴承的非牛顿流体工作状态进行了研究,这种静压轴承轴端设有静压腔,在整个圆锥面上油膜厚度连续,分析了锥角、转速、油腔大小端半径比及供油压力对轴承性能的影响,并用实验验证了其理论分析的正确性[15].
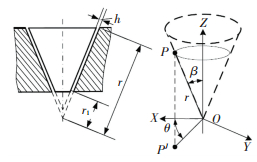
1 润滑模型 1.1 雷诺方程推导锥形配流轴与圆柱形配流轴的区别是存在一个锥角,使得其具有间隙自补偿的优点.锥形配流副的理想状态是始终处于全膜润滑状态,根据锥形配流副的结构形式,建立如图 3所示以圆锥顶点为原点,以圆周角、半锥角和极径为坐标轴的球坐标系.
|
图 3 锥形配流副坐标系 Figure 3 Coordinate system of the conical spindle distribution |
此状态下的锥形配流副流体连续性方程为
| $ \frac{{\partial \rho }}{{\partial t}} + \frac{1}{{{r^2}}}\frac{{\partial \left( {\rho {v_r}{r^2}} \right)}}{{\partial r}} + \frac{1}{{r\sin \beta }}\frac{{\partial \left( {\rho {v_\beta }\sin \beta } \right)}}{{\partial \beta }} + \frac{1}{{r\sin \beta }}\frac{{\partial \left( {\rho {v_\theta }} \right)}}{{\partial \theta }} = 0. $ |
根据薄膜润滑假设条件,得到球坐标系下的N-S方程为
| $ \frac{{\partial p}}{{\partial r}} = \frac{1}{{{r^2}}}\frac{\partial }{{\partial \beta }}\left( {\frac{{\mu \partial {v_r}}}{{\partial \beta }}} \right),\;\;\;\;\;\;\frac{{\partial p}}{{\partial \beta }} = 0, $ |
| $ \frac{{\partial p}}{{\partial \theta }} = \frac{{\sin \beta }}{r}\frac{\partial }{{\partial \beta }}\left( {\mu \sin \beta \frac{\partial }{{\partial \beta }}\left( {\frac{{{v_\theta }}}{{\sin \beta }}} \right)} \right) \cong \frac{{\sin \beta }}{r}\frac{\partial }{{\partial \beta }}\left( {\frac{{\mu \partial {v_\theta }}}{{\partial \beta }}} \right). $ |
带入无滑移的速度边界条件,整理得到等温条件下任意半锥角的锥形配流副雷诺方程为
| $ \frac{1}{r}\frac{\partial }{{\partial r}}\left( {r{h^3}\frac{{\partial p}}{{\partial r}}} \right) + \frac{1}{{{r^2}{{\sin }^2}\beta }}\frac{\partial }{{\partial \theta }}\left( {{h^3}\frac{{\partial p}}{{\partial \theta }}} \right) = 6\mu \mathit{\Omega }\frac{{\partial h}}{{\partial \theta }} + 12\mu \frac{{\partial h}}{{\partial t}}. $ |
不难发现,将β=0带入,则上式变为圆柱形轴配流的雷诺方程,将β=π/2带入,则上式变为端面配流的雷诺方程.可以说,锥形配流副是介于圆柱形轴配流和端面配流的一种配流方式.
由于配流轴具有径向和轴向两个方向的直线运动自由度,因此,配流轴位置的变化,会从轴向和径向两个方面影响油膜的膜厚变化.配流轴相对缸体的偏心引起径向方向上的膜厚变化,这与圆柱形滑动轴向的膜厚方程一致, 即
| $ h = e\cos \theta - {h_0} = {h_0}\left( {1 - \varepsilon \cos \theta } \right). $ |
其中,e为偏心量,h0为同心间隙,ε为偏心率.由此,可以得到垂直于锥面的膜厚方程为
| $ h = {h_0}\left( {1 - \varepsilon \cos \theta } \right)\cos \beta . $ |
径向运动使ε偏心率改变,轴向运动使同心间隙h0改变,二者共同影响锥形配流副的膜厚分布.
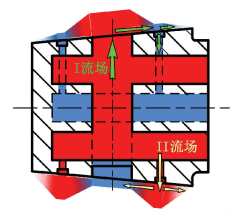
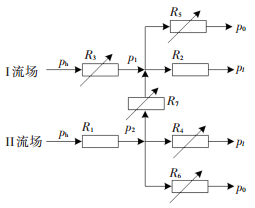
1.2 静压边界如图 4所示,以配流轴大端为例,高压油从排油口经间隙流入低压平衡槽,压力降至p1,一部分经过配流副间隙流出端面,压力降为环境压力,另一部分经阻尼孔泄漏到低压油口,将此流场定义为Ⅰ流场;此外,高压油还会通过与高压腔连通的阻尼孔流入高压平衡槽,压力降至p2,这部分流量一部分经间隙泄漏出端面,另一部分经间隙流入低压油口.除去轴向方向的流动,油液还有一部分在周向方向上从高压平衡槽泄漏到低压平衡槽,将此流场定义为Ⅱ流场.如图 5所示.
|
图 4 锥形配流副的流场边界 Figure 4 Flow field boundary of the conical spindle distribution |
|
图 5 锥形配流副的液阻网络 Figure 5 Hydraulic resistance networks of the conical spindle distribution |
为简便运算,在对模型精度影响不大的前提下,假设:配流间隙中油膜压力线性变化;端面处压力p0=0;油膜破裂处满足雷诺边界条件.则有
Ⅰ流场:
| $ \frac{{{p_{\rm{h}}} - {p_1}}}{{{R_3}}} + \frac{{{p_{\rm{2}}} - {p_1}}}{{{R_7}}} = \frac{{{p_1}}}{{{R_5}}} + \frac{{{p_1} - {p_l}}}{{{R_2}}}. $ |
Ⅱ流场:
| $ \frac{{{p_{\rm{h}}} - {p_2}}}{{{R_1}}} = \frac{{{p_{\rm{2}}} - {p_1}}}{{{R_7}}} + \frac{{{p_2}}}{{{R_6}}} + \frac{{{p_2} - {p_l}}}{{{R_4}}}. $ |
这样,就得到了润滑方程的边界条件.
2 动力学模型以缸体左端面的中点为左边原点,水平向右为轴向(z轴)的正方向,向下为径向(x轴)的正方向,如图 6所示.

|
图 6 锥形配流副受力分析 Figure 6 Force analysis of the conical spindle distribution |
当工作压力ph突然增大时,高压阻尼槽的压力p2和p2′也随之增大,但压力的传递存在一个过程,不是同步增大的,轴向和径向受力不平衡,引起配流轴的动态变化.压力随时间的变化过程为
| $ \frac{{{\rm{d}}p}}{{{\rm{d}}t}} = - \frac{1}{{CV}}\frac{{{\rm{d}}V}}{{{\rm{d}}t}}. $ | (1) |
式中: -dV/dt表示油液体积的减小速率,即流量减少量. C为体积压缩系数,特定的油液系数固定,可用经验公式计算得到:
| $ C = \left( {7.25 - \lg \mu } \right) \times {10^{ - 10}}. $ | (2) |
在锥形配流副的流场中,以大端高压平衡槽压力为例,当配流轴在轴向及径向位移时,平衡槽中的流量变化包括从阻尼管流入的流量及从密封带间隙中流出的流量.流入的流量为
| $ {Q_{{\rm{in}}}} = \frac{{{p_h} - {p_2}}}{{{R_0}}} $ | (3) |
密封带流出的流量包括两部分,一部分是由于压差的流出,一部分是由于挤压的流出,其计算公式分别为
| $ {Q_{{\rm{out1}}}} = \frac{{{p_2}}}{{{R_1}}} + \frac{{{p_2}}}{{{R_2}}}, $ | (4) |
| $ {Q_{{\rm{out2}}}} = \frac{{{\rm{d}}V}}{{{\rm{d}}t}}, $ | (5) |
其中,Vs为平衡槽体积及密封带处间隙的体积.
联立式(1)~(5),得到高压平衡槽压力的建压方程:
| $ \frac{{{\rm{d}}p}}{{{\rm{d}}t}} = \frac{1}{{C{V_s}}}\left( {{Q_{{\rm{in}}}} - {Q_{{\rm{out1}}}} - {Q_{{\rm{out2}}}}} \right). $ | (6) |
对于大端高压平衡槽:
| $ {V_s} = \frac{1}{{2\sin \beta }}\left( {{r_4}^2 - {r_7}^2} \right)\left( {\left( {{h_0} - z\tan \beta } \right)\alpha - 2x\sin \frac{\alpha }{2}} \right), $ | (7) |
| $ \frac{{{\rm{d}}{V_s}}}{{{\rm{d}}t}} = \frac{1}{{2\sin \beta }}\left( {{r_4}^2 - {r_7}^2} \right)\left( { - \dot z\tan \beta \alpha - 2\dot x\sin \frac{\alpha }{2}} \right). $ | (8) |
将式(7)与式(8)代入式(6)得
| $ \begin{array}{l} \frac{{{\rm{d}}{p_2}}}{{{\rm{d}}t}} = \frac{\quad {2\sin \beta }\quad }{{C\left( {{r_4}^2 - {r_7}^2} \right)\left( {\left( {{h_0} - z\tan \beta } \right)\alpha - 2x\sin \frac{\alpha }{2}} \right)}} \times \\ \;\;\;\;\;\;\;\;\;\left( {\frac{{{p_h} - {p_2}}}{{{R_1}}} - \frac{{{p_2}}}{{{R_4}}} - \frac{{{p_2}}}{{{R_6}}} - \frac{1}{{2\sin \beta }}\left( {{r_4}^2 - {r_7}^2} \right) \cdot } \right.\\ \;\;\;\;\;\;\;\;\;\left. {\left( { - \dot z\tan \beta \alpha - 2\dot x\sin \frac{\alpha }{2}} \right)} \right). \end{array} $ |
在锥形配流轴的动态变化过程中,随着工作压力与运动位置的变化,高压平衡槽压力也随之变化,使油膜承载性能也发生变化.
配流轴的轴向载荷大小为
| $ {F_p} = \frac{{\rm{ \mathsf{ π} }}}{2}{d_p}^2{p_h}. $ |
其中,dp为高压油孔直径.
根据推导得到的雷诺方程,并根据边界条件,可以通过数值求解的方式得到油膜的压力分布,这其中包含了油膜动压效应(pd(i, j))和挤压效应(pj(i, j))所产生的承载力.
在轴向方向的动压承载力和挤压承载力为
| $ {W_{dz}} = \sum\limits_{i = 1}^{i = m} {\sum\limits_{j = 1}^{j = n} {{p_d}\left( {i,j} \right)r{{\sin }^2}\beta {\rm{d}}r{\rm{d}}\theta } } , $ |
| $ {W_{jz}} = \sum\limits_{i = 1}^{i = m} {\sum\limits_{j = 1}^{j = n} {{p_j}\left( {i,j} \right)r{{\sin }^2}\beta {\rm{d}}r{\rm{d}}\theta } } . $ |
在径向方向的动压承载力和挤压承载力为
| $ {W_{dj1}} = \sum\limits_{i = 1}^{i = m} {\sum\limits_{j = 1}^{j = n} {{p_d}\left( {i,j} \right)r\cos {\theta _{i,j}}\sin \beta \cos \beta {\rm{d}}r{\rm{d}}\theta } } , $ |
| $ {W_{dj2}} = \sum\limits_{i = 1}^{i = m} {\sum\limits_{j = 1}^{j = n} {{p_d}\left( {i,j} \right)r\sin {\theta _{i,j}}\sin \beta \cos \beta {\rm{d}}r{\rm{d}}\theta } } , $ |
| $ {W_{dj}} = \sqrt {{W_{dj1}}^2 + {W_{dj2}}^2} , $ |
| $ {W_{jj1}} = \sum\limits_{i = 1}^{i = m} {\sum\limits_{j = 1}^{j = n} {{p_j}\left( {i,j} \right)r\cos {\theta _{i,j}}\sin \beta \cos \beta {\rm{d}}r{\rm{d}}\theta } } , $ |
| $ {W_{jj2}} = \sum\limits_{i = 1}^{i = m} {\sum\limits_{j = 1}^{j = n} {{p_j}\left( {i,j} \right)r\sin {\theta _{i,j}}\sin \beta \cos \beta {\rm{d}}r{\rm{d}}\theta } } , $ |
| $ {W_{jj}} = \sqrt {{W_{jj1}}^2 + {W_{jj2}}^2} . $ |
得到锥形配流轴轴向和径向的二自由度动力学方程为
| $ \left\{ \begin{array}{l} {W_{dz}} + {W_{jz}} - {F_p} = m\ddot z,\\ {W_{dj}} + {W_{jj}} = m\ddot x. \end{array} \right. $ | (9) |
使用雷诺边界条件和有限差分法对润滑模型进行数值求解,获得锥形配流副的动压和挤压承载力,用以进一步求解动力学方程式(9),动力学模型求解方法采用四阶Runge-Kutta方法.但由于每个步长下都需要迭代求解雷诺方程,因此计算耗时较长.配流副润滑特性仿真参数如表 1所示.
| 表 1 配流副仿真参数 Table 1 Simulation parameters of the conical spindle distribution |
实际工作中,载荷冲击通常是在一瞬间发生的,在对配流副动态分析过程中,用压力的阶跃增加来模拟载荷冲击.通过前文中所得到的动力学方程,得到突变压力为2 MPa时的高压平衡槽压力变化过程如图 7所示.
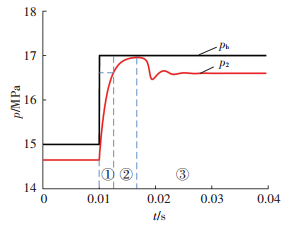
|
图 7 Δp =2 MPa高压平衡槽建压过程 Figure 7 Pressure building process of balanced high-pressure grooves(Δp=2 MPa) |
负载突变时,由于径向方向上的受力不平衡,配流轴做径向运动,增大偏心,径向运动过程中平衡槽及间隙中油液受到挤压,在挤压的过程中平衡槽压力快速升高,这个过程很快,大约0.002 s左右就上升到了最终的稳定值的大小.在这一阶段,配流轴做径向的加速运动,如图 7中①所示,可以称为快速上升阶段.在快速上升阶段结束时,随着平衡槽压力的上升,对不平衡力有了一定补偿,锥形配流轴径向受力接近平衡,继续偏心运动时,由于动压承载力增大,配流轴开始减速运动,直到速度减小为0,达到极限位置.此过程中,平衡槽压力也继续上升到最大值,如图 7中②阶段,可以称为超调上升阶段.当径向速度减为0时,偏心率达到最大,平衡槽压力也达到最大.随后配流轴在径向上做反方向运动,并经过一定振荡后,回到平衡位置.此时,高压平衡槽压力也恢复稳定,如图 7中③所示,这一阶段视为稳定调节阶段.
压力突变后,不仅在径向上配流轴发生剧烈运动,而且在轴向上,由于平衡槽压力的延迟增加,受力不平衡,发生剧烈运动.根据动力学方程可以求解得到任意时刻配流轴在轴向和径向的位置,因此,得到从压力突变开始到配流轴恢复稳定的这段时间内配流轴轴心的变化轨迹如图 8所示.黑色线条表示在刚受到冲击时,锥形配流轴在径向剧烈上下波动,但波动幅值在阻尼作用及高压平衡槽压力不断补偿下逐渐减小;在轴向方向上,由于轴向载荷是瞬间增大的,但平衡槽压力的滞后增加使得配流轴向z轴负向运动,但此过程很短,可以忽略.之后由于径向的偏心运动使动压承载力增大,使配流轴沿z轴正向运动,即配流轴与缸体出现脱开的趋势.综合轴径向的运动,便得到图 8中的黑色轨迹.在径向运动中,配流轴振荡幅值逐渐减小为0,且轴心逐渐恢复到与缸体同心的平衡位置上;与此同时,由于径向偏心率的减小,油膜承载力下降,配流轴在轴向上运动到极限位置后,也逐渐恢复到平衡位置,轨迹为图 8中红色线.从以上分析可以得知,当负载突变后,锥形配流副通过自身状态改变来实现油膜承载性能的变化,从而实现自身稳定性调节,这种不依靠外力来实现自身平衡的过程称为锥形配流副的自适应动态调节过程.
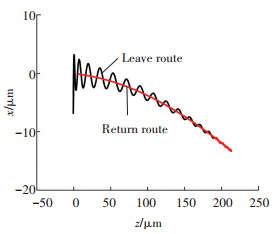
|
图 8 Δp =2 MPa时的轴心轨迹 Figure 8 Track of shaft axis (Δp =2 MPa) |
对于配流轴的动态变化过程,可以用偏心率ε和配流间隙h两个参数随时间的变化过程来表征.其中:偏心率体现出配流轴相对缸体的偏心程度,ε=0表示无偏心,ε=1表示二者发生接触,表达式为
| $ \varepsilon = \frac{{x\cos \beta }}{{{h_0} + z\sin \beta }}. $ |
配流间隙意为配流轴相对缸体无偏心时二者之间的间隙大小,配流副稳定工作的前提是有合适的配流间隙,h过大使得泄漏量增大,h过小又容易发生磨损.动态变化过程中,其表达式为
| $ h = {h_0} + z\sin \beta . $ |
其中,h0为初始配流间隙值.
下面在工作压力为15 MPa,转速n=1 500 r/min,分别施加2,5,10 MPa的阶跃压力,对配流轴的动态响应特性进行分析.
图 9为不同阶跃压力下配流间隙的动态变化过程,图 10为初始时刻的局部放大图.从图中可以看出,阶跃压力为5 MPa时与2 MPa时相对比,偏心率的变化范围明显增大,最大值已经接近0.8,说明配流轴在径向运动更加剧烈;而时与5 MPa相比偏心率变化范围差别并不大,这是因为5 MPa时的偏心率最大幅值已接近极限值,配流轴与缸体可能发生接触,因此,可以说,阶跃压力在5 MPa以上时,对锥形配流副的可靠工作具有不利的影响.
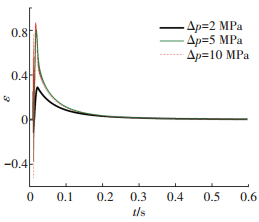
|
图 9 偏心率动态变化过程 Figure 9 Dynamic change of eccentricity |

|
图 10 偏心率动态变化过程局部放大 Figure 10 Partial amplification of dynamic change of eccentricity |
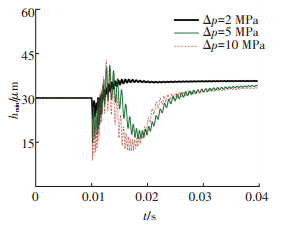
图 11为不同阶跃压力下配流间隙的动态变化过程,图 12为初始时刻的局部放大图.同偏心率的变化规律类似,配流间隙也是随工作压力突然增加而增大,在达到最大值时下降,并逐渐恢复到平衡状态.压力突变量越大,峰值配流间隙也越大,从图中可以看出,5 MPa和10 MPa时的配流间隙变化幅度显然比2 MPa时大.
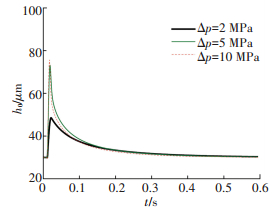
|
图 11 配流间隙的动态变化过程 Figure 11 Dynamic change of distribution gap |
|
图 12 配流间隙的动态变化局部放大图 Figure 12 Partial amplification of dynamic change of distribution gap |
在配流轴的动态变化过程中,配流轴与缸体的最小距离称为最小间隙值,用hmin表示,最小间隙值由配流间隙和偏心率共同决定,表达式为
| $ {h_{\min }} = h\left( {1 - \varepsilon } \right). $ |
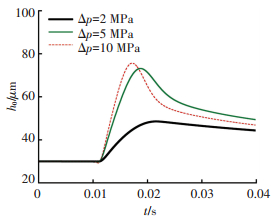
由图 13中可以看出,阶跃压力越大,最小间隙也越小,Δp=2,5及10 MPa时分别所能达到的最小间隙约为22,15和7 μm,根据对最小间隙的要求可以看出,Δp=10 MPa时的最小间隙已经接近极限值,可以说,如此大的载荷突变是非常危险的情况,实际工作过程中应该尽量避免.
|
图 13 最小间隙动态变化过程 Figure 13 Dynamic change of minimum gap |
球塞泵的工作转速虽然对静压边界影响较小,但是对动压承载力影响较大,在阶跃压力一定的情况下,转速不同,配流轴的动态变化特性也会有不同表现.接下来以ph=15 MPa,Δp=5 MPa的压力条件下对不同转速的下配流轴的动态变化过程分别进行分析.
图 14和15所示分别为n=500, 1 000及1 500 r/min时的配流间隙和偏心率动态变化过程.从图中可以看出,转速越高,配流间隙的峰值越大,而偏心率的变化幅值越小.这是因为动压承载力随转速线性变化,转速越高,动压承载力越大,在配流间隙增大的过程中所受的推力更大,位移随着增大;而在径向方向上,动压承载力增大,相当于油膜的刚度增加,使配流轴振动的幅值减小.因此,配流副在高速下具有更高的动态稳定性,但是也容易出现配流间隙过于增大发生泄压的现象,应该给予充分的重视.
|
图 14 配流间隙动态变化过程 Figure 14 Dynamic change of distribution gap |
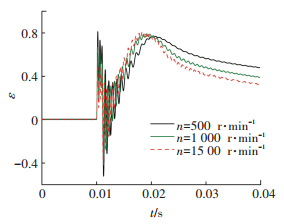
|
图 15 偏心率动态变化过程 Figure 15 Dynamic change of eccentricity |
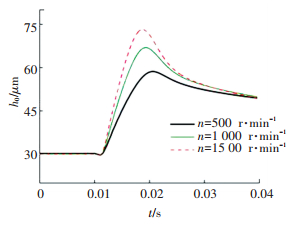
转速升高,配流间隙增大,而偏心率降低,使得最小间隙出现图 16中所示的趋势,总体来说转速越低,最小间隙值越小,如图所示,n=500,1 000,1 500 r/min时最小间隙分别约为8,12,16 μm,根据上节的可靠性工作条件可知,n=500 r/min条件下配流轴所受突变载荷时较为危险.同时,综合上节分析,球塞泵在实际工作时一定要避免低转速、大冲击的工况.

|
图 16 最小间隙动态变化过程 Figure 16 Dynamic change of minimum gap |
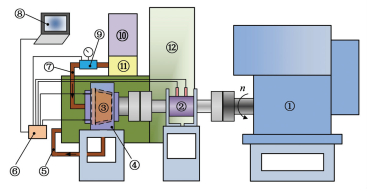
根据锥形配流副的工作原理,设计试验对锥形配流副的动态变化过程进行验证.根据试验目的和要求设计试验系统方案如图 17所示,系统主要包括三部分,分别是驱动电机(图 17中1所示)、锥形配流副被试件(图 17中4所示)以及高压泵站(图 17中12所示),并配备相应的传感器.在不影响锥形配流副的工作状态的前提下,为避免球塞副的干扰,被试件的设计采用图 18中方案.管接头1通过螺纹与端盖固定,其左端与配流轴内孔通过O型圈密封,因为端盖和配流轴之间存在轴向间隙、管接头和配流轴之间存在径向间隙.同时,在配流轴的左端,采用内外圈分离的滚子轴承支撑在缸体内,不限制配流轴的轴向移动,并且利用轴承的自身游隙使得配流轴在径向可以有微小位移,最终保证了锥形配流轴可以在一定范围内自由浮动.试验过程中,通过测量缸体的驱动力矩可以反映出配流副的润滑状态.
|
1—驱动电机; 2—转矩转速传感器; 3—锥形配流副组件; 4—被试件; 5—回油管; 6—信号采集系统; 7—进油管; 8—上位机; 9—流量压力传感器; 10—泵站驱动电机; 11—出口溢流阀; 12—高压泵站 图 17 锥形配流副试验系统原理图 Figure 17 Experimental schematic diagram of the conical spindle distribution |

|
1—管接头; 2—后端盖; 3—位移传感器; 4—壳体; 5—缸体; 6—锥形配流轴; 7—输入轴 图 18 锥形配流副模型试验示意图 Figure 18 Schematic diagram of test model of the conical spindle distribution |
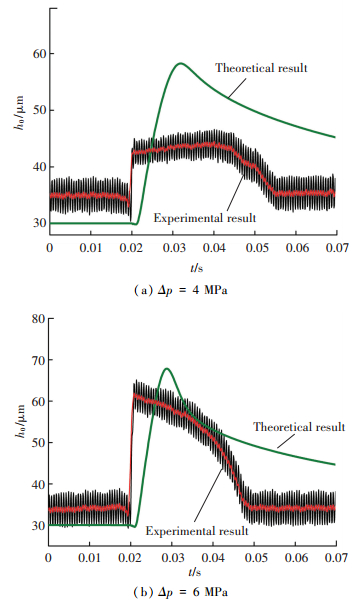
根据实验条件,在工作压力为4 MPa,转速为1 000 r/min的基础上,分别进行阶跃压力为2, 4, 6 MPa的冲击试验,得到配流间隙动态变化过程的理论与试验对比,如图 19所示.
|
图 19 配流间隙动态变化理论与试验对比 Figure 19 Theoretical and experimental comparison of dynamic change of the distribution gap |
传感器示数在一定范围内波动,取其平均值进行分析.可以看出,当压力阶跃上升时,配流间隙随之跳跃上升,并在非常短的时间内恢复到原来的稳定状态,且阶跃压力越大,配流间隙的变化幅值越大,这与理论计算的结果是非常相符的.另一方面,从图中的对比可知,配流间隙的实际变化幅值比理论值小,且阶跃压力越大,差值越小;试验过程中配流间隙从增大到稳定的变化时间比理论时间要短.出现这种误差的原因可能包括以下两点未被模型考虑的影响因素:
1) 被试件中锥形配流轴在径向上的位移受到管接头和后端盖支口的限位,实际偏心率与理论值相比较小,动态变化过程中相应的动压承载力小于理论值,导致轴向上受到的油液推力减小,行程较短.
2) 配流轴与管接头、后端盖间隙配合处靠O型圈密封,O型圈受挤压,在轴向上对配流轴有较大的摩擦力,在配流轴轴向受力较小的情况下摩擦力不仅限制了配流间隙变化的极值,也产生阻尼效应缩短动态变化时间.
综合理论与试验分析可以得知,锥形配流副在受到冲击载荷时存在能够在短时间内重新恢复到稳定状态工作的自适应调节特性,这使得球塞泵能够适应在恶劣极端工况下的工作,对于提高车辆转向性能具有重要意义.
5 结论1) 在受到冲击载荷时,高压平衡槽压力经历迅速上升、超调、稳定调节三个过程达到稳定,相比于工作压力的上升具有滞后性,从而导致了配流轴复杂的受力变化,在轴向与径向发生运动.
2) 锥形配流副在受到冲击载荷时,在径向方向上不断向下运动,并伴随着剧烈波动,轴向上向外运动,将配流轴推离缸体;在达到一定位置后,逐渐恢复到平衡位置,具有自适应的调节特性.
3) 冲击载荷越大,配流轴的动态变化越剧烈,配流间隙和偏心率峰值越大,最小间隙值越小,工作可靠性越低;工作转速越高,配流间隙峰值越大,偏心率峰值越小,最小间隙值越大,稳定性越高.因此,为保证可靠性,球塞泵在工作中应尽量避免大冲击、低转速的工况.
| [1] |
陈德民, 胡纪滨, 张心俊, 等. 具有广阔应用和发展前景的球塞泵[J]. 液压与气动, 2005(8): 68. CHEN Demin, HU Jibin, ZHANG Xinjun, et al. Ball plug pump with broad application and development prospects[J]. Hydraulics and Pneumatics, 2005(8): 68. DOI:10.3969/j.issn.1000-4858.2005.08.028 |
| [2] |
IVANTYSYN J, IVANTYSYNOVA M. Hydrostatic Pumps and Motors[M]. New Delhi: Academia Books International, 2001.
|
| [3] |
许路, 魏超, 荆崇波, 等. 车用球塞泵球塞副摩擦动力学模型的研究[J]. 汽车工程, 2016, 38(4): 506. XU Lu, WEI Chao, JING Chongbo, et al. Study on the pair friction dynamics model of ball plug pumps for vehicles[J]. Automotive Engineering, 2016, 38(4): 506-510. DOI:10.3969/j.issn.1000-680X.2016.04.019 |
| [4] |
胡纪滨, 张心俊, 苑士华. 球活塞式液压泵球塞副泄漏量的理论研究[J]. 机床与液压, 2005(8): 100. HU Jibin, ZHANG Xinjun, YUAN Shihua. Theoretical study on the loss of the ball plug piston of the ball piston hydraulic pump[J]. Machine Tool & Hydraulics, 2005(8): 100. DOI:10.3969/j.issn.1001-3881.2005.08.038 |
| [5] |
苑士华, 张心俊, 胡纪滨. 油液粘度变化对球塞泵球塞副泄漏量的影响[J]. 农业机械学报, 2007, 38(4): 135. YUAN Shihua, ZHANG Xinjun, HU Jibin. Effect of oil viscosity change on ball plug discharge of ball plug pump[J]. Transactions of the Chinese Society of Agricultural Machinery, 2007, 38(4): 135. DOI:10.3969/j.issn.1000-1298.2007.04.035 |
| [6] |
林硕, 荆崇波, 聂莹. 考虑黏度变化的球塞副稳态工况泄漏特性研究[J]. 北京理工大学学报, 2015, 35(3): 227. LIN Shuo, JING Chongbo, NIE Ying. Study on leakage characteristics of ball plugs in steady state conditions considering viscosity change[J]. Journal of Beijing Institute of Technology, 2015, 35(3): 227. |
| [7] |
XU L, WEI C, JING C B. The study on force and lubrication characteristics of ball piston in eccentric ball piston pump[J]. Journal of Tribology, 2017, 139(4): 041101. DOI:10.1115/1.4034955 |
| [8] |
林硕.球活塞式液压泵球塞副摩擦动力学模型与特性研究[D].北京: 北京理工大学, 2014 LIN Shuo. Research on the frictional dynamics model and characteristics of the ball piston hydraulic pump ball[D].Beijing: Beijing Institute of Technology, 2014 http://cdmd.cnki.com.cn/article/cdmd-10007-1014086762.htm |
| [9] |
游步东, 黄丹, 柯尊荣. 球塞泵定子轨道接触应力分析[J]. 南昌大学学报, 2011, 33(4): 378. YOU Budong, HUANG Dan, KE Zunrong. Analysis of contact stress of stator track of ball plug pump[J]. Journal of Nanchang University, 2011, 33(4): 378. DOI:10.3969/j.issn.1006-0456.2011.04.017 |
| [10] |
黄丹.球塞泵接触应力理论分析及试验研究[D].南昌: 南昌大学, 2012 HUANG Dan. Theoretical analysis and experimental study on contact stress of ball plunger pump[D].Nanchang: Nanchang University, 2012 |
| [11] |
付蓓蓓.基于运动学和动力学分析的海(淡)水球塞泵的优化设计与仿真研究[D].南昌: 南昌大学, 2010 FU Beibei. Optimization design and simulation of sea (light) water polo pump based on kinematics and dynamics analysis[D]. Nanchang: Nanchang University, 2010 http://cdmd.cnki.com.cn/article/cdmd-11902-2010247627.htm |
| [12] |
STANSFIELD F M. Application of hydrostatic bearing in machine tool[M]. Machinery Industry Press, 1978
|
| [13] |
PRABHU P J, GANESAN N. Characteristics of conical hydrostatic thrust bearings under rotation[J]. Wear, 1981, 73(1): 95. DOI:10.1016/0043-1648(81)90213-1 |
| [14] |
PRABHU P J, GANESAN N. Finite element application to the study of hydrostatic thrust bearings[J]. Wear, 1984, 97(2): 139. DOI:10.1016/0043-1648(84)90123-6 |
| [15] |
EL-KAYAR A, SALEM E A, KHALL M F, et al. Behavior of externally pressurized conical bearings lubricated with non-Newtonian fluids[J]. Wear, 1981, 61(2): 133. |
 2019, Vol. 51
2019, Vol. 51



