2. 重庆邮电大学 信息无障碍与服务机器人工程技术研究中心,重庆 400065
2. Engineering Research Center for Information Accessibility and Service Robots, Chongqing University of Posts and Telecommunications, Chongqing 400065, China
近年来,随着移动机器人智能化水平与计算机视觉处理技术的快速发展,移动机器人在家居生活、餐饮服务和自主导航等行业上的应用极为广泛.视觉同时定位与地图构建(Visual simultaneous localization and mapping, V-SLAM)是指移动机器人在行进过程中,通过自身携带的视觉传感器对周围环境进行重构并且估计出自身的位置[1-2].准确定位与高精度的V-SLAM算法是实现移动机器人自主导航的关键技术.
V-SLAM一般分为前端视觉部分和优化的后端部分[3].基于特征点法的前端视觉部分,一直以来都是视觉里程计(Visual Odometry,VO)的主流方法,它的任务是估算相邻图像之间的相机运动,给后端优化提供较好的初值,后端则处理地图模型的优化问题,依据前端视觉里程计测量的相机位姿,进行优化处理得到全局一致的轨迹和地图.视觉里程计的实现方法,应用最广泛的是通过ICP算法[4]对相机进行运动估计,传统ICP算法是建立在配准点集间完全包含的理论假设,然而实际点云配准中待配准点集间具有初始位姿偏差大,导致迭代精度不高,使得ICP算法陷入局部最优;匹配过程中随着待匹配点对数量的增多,导致误匹配累积增大,严重影响配准效果.针对ICP存在的问题,研究者们进行了多种算法的改进.文献[5]提出一种针对家庭室内环境常见物体的三维建模方法,该方法通过手持相机环绕进行采集帧数,可以进行三维模型的重构,但是无法估计相机的位姿.文献[6]提出了一种快速三维SLAM方法,在对应点对的筛选策略上仅使用RANSAC算法,对特征点进行随机配准,提高了算法的实时性和效率,但配准结果无法满足全局要求,易陷入局部最优使配准效果不好.文献[7]提出了一种移动机器人室内定位和地图构建系统,采用局部地图匹配虽然可以适用于大范围场景下快速建图,但是在机器人定位过程中效果较差,容易丢失.文献[8]提出了一种通过图像配准的3D室内环境重建方法,采用尺度不变特征变换和随机采样一致性算法确定相邻帧,将得到的变换矩阵作为精配准的初始点云数据.该方法可以进行环境地图重构,但是过度依赖图像的帧序列,难以满足真实环境下机器人的需求,而且无法估计机器人的位置和姿态.
针对以上研究现状,本文提出了一种三阶段点云配准的视觉SLAM方法.通过预处理、初配准、精配准三个阶段对点云的重构和位姿估计进行处理.在预处理阶段,选用RANSAC算法[9]通过设定欧氏距离阈值筛选可靠内点来进行初始位置估计;将预处理的结果作为初值,通过基于刚体变换一致性的双重距离阈值法完成初配准;在具有良好点云初始位置的条件下进行精配准,引入动态角度迭代因子,逐步减小误匹配.在后端优化的关键帧选取中采用滑动窗口法和随机采样法相结合的方法,实现三维地图的更新优化.
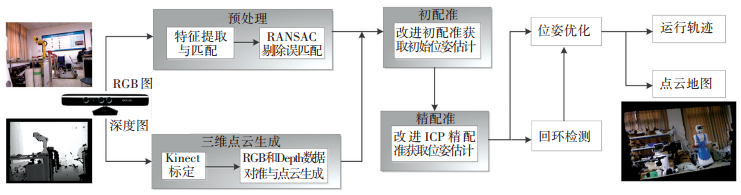
1 改进点云配准的V-SLAM系统框架本文提出的三阶段改进点云配准算法的视觉SLAM(V-SLAM)系统框架如图 1所示.通过标定的Kinect相机[10]采集环境的外部信息,对获取到的RGB图进行预处理,采用RANSAC进行外点剔除;再通过対生成的三维点云进行初配准获取初始位姿估计;最后通过改进的ICP算法完成精配准.在后端优化中选用滑动窗口和随机采样结合的方法选取关键帧,结合g2o图优化[11]实现点云地图和轨迹的更新与优化.
|
图 1 移动机器人的V-SLAM系统框架图 Figure 1 V-SLAM system framework of the mobile robot |
为了生成三维点云,需要获取Kinect的内参矩阵来进行RGB相机与深度相机之间的刚体变换,采取文献[12]的标定方法,该方法对RGB摄像机和深度相机进行标定,利用视差补偿模型对深度相机的畸变进行校正. RGB图像与Depth图像联合标定前如图 2(a)、标定后图 2(b)比较情况如图 2所示.

|
图 2 标定前、后对比图 Figure 2 Comparison before and after calibration |
在Kinect相机完成标定后,通过RGB图的像素坐标结合该点的Depth数据,就可以求得每个点的空间位置,从而可生成三维点云数据.空间点[x, y, z]和其在图像中的像素坐标[u, v, d] (d指Depth数据)具有如下对应关系:
| $ z = \frac{d}{s} $ |
| $ x = \frac{{\left( {u - {c_x}} \right) \cdot z}}{{{f_x}}}, $ |
| $ y = \frac{{\left( {u - {c_y}} \right) \cdot z}}{{{f_y}}}. $ |
式中:fx、fy分别代表相机在x、y轴线上的焦距;cx、cy代表相机的光圈中心,s是深度图的缩放比例因子(Depth数据与实际距离的比值),本文取值为1000.通常情况下fx、fy、cx、cy被定义为相机的内参矩阵C:
| $ \mathit{\boldsymbol{C}} = \left[ {\begin{array}{*{20}{c}} {{f_x}}&0&{{c_x}}\\ 0&{{f_y}}&{{c_y}}\\ 0&0&1 \end{array}} \right]. $ |
ORB特征是目前最具代表性的实时图像特征[13].它改善了快速检测子FAST[14]不定向的问题,并使用快速二进制描述子BRIEF[15],加快整个图像的特征提取.提取ORB特征分为如下两个步骤:
1) FAST角点提取:找出图像中的“角点”.
2) BRIEF描述子:对提取的特征点周围图像区域进行描述.
在提取了ORB图像特征之后进行点集元素的特征匹配. SLAM中的数据关联问题通过特征匹配来解决,即确定当前时刻看到的路标与之前看到的路标之间的对应关系,匹配帧间的图像描述子,可以为后续的姿态估计、优化等减轻工作量.为了符合在SLAM中的实时性需求,本文采用适合匹配点数量极多的FLANN(FAST Library for Approximate Nearest Neighbour,快速近似最近邻)算法[16]进行双向匹配.
本文采用RANSAC算法对误匹配进行剔除,对两组相邻的RGB图的特征点对进行预处理,设定一个阈值d,剔除大于阈值的匹配点对,得到符合的内点(真实对应),针对源点集A和目标点集B上的特征点集,d1和d2分别为A上一点在目标点集上的最近和次最近点的欧氏距离,依据工程上的经验方法在本文中设定d2 < αd1(其中α=0.5), 取内点数量最小阈值为N=13,若不满足则说明当前RGB图不满足本阶段要求,进行下组RGB图预处理.通过对内点进行最小二乘法的位姿估计,可对源点集A和目标源点集B进行一个微调,预处理后的两片点云分别记为P和Q.相机第i时刻的位姿pi和第j时刻相机的位姿pj的位姿变换关系为: pj= pi Tij,其中
| $ \mathit{\boldsymbol{T}}_i^j = \left[ {\begin{array}{*{20}{c}} {{R_{3 \times 3}}}&{{t_{3 \times 1}}}\\ 0&1 \end{array}} \right]. $ |
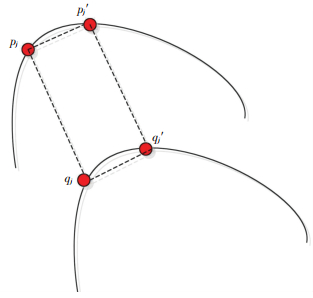
ICP算法用于精配准,需要满足配准点云之间初始位置相近的条件,否则由于其对初值的极大依赖使得迭代易陷入局部最优.仅仅依靠第一步的预处理,并不能保证待配准点云初始状态比较接近,所以不能直接使用ICP算法进行精配准,需要在预处理的基础上对点云进行一次初配准,初配准的结果作为精配准的初始值使其具有良好的初始状态.初配准的原理图如图 3所示.
|
图 3 初配准原理示意图 Figure 3 Initial registration principle |
同一片点云任一点与其邻点的拓扑结构保持不变,具有刚体变换一致性.因此对于点云P中任意一点pi与其近邻点p′i,在配对点云Q中也应是近邻点.在预处理的基础上获取良好的初始状态,若获取的匹配点对是正确的匹配点对,则对于任意两点对(pi,qj)和(p′i,q′j)应满足点对间的距离相等,如式(1)、(2)两个约束条件:
| $ \left| {\frac{{\left\| {{\mathit{\boldsymbol{p}}_i} - {{\mathit{\boldsymbol{p'}}}_i}} \right\| - \left\| {{\mathit{\boldsymbol{q}}_j} - {{\mathit{\boldsymbol{q'}}}_j}} \right\|}}{{\left\| {{\mathit{\boldsymbol{p}}_i} - {{\mathit{\boldsymbol{p'}}}_i}} \right\| + \left\| {{\mathit{\boldsymbol{q}}_j} - {{\mathit{\boldsymbol{q'}}}_j}} \right\|}}} \right| < {u_1}, $ | (1) |
| $ \left| {\frac{{\left\| {{\mathit{\boldsymbol{p}}_i} - {\mathit{\boldsymbol{q}}_j}} \right\| - \left\| {{{\mathit{\boldsymbol{p'}}}_i} - {{\mathit{\boldsymbol{q'}}}_j}} \right\|}}{{\left\| {{\mathit{\boldsymbol{p}}_i} - {\mathit{\boldsymbol{q}}_j}} \right\| + \left\| {{{\mathit{\boldsymbol{p'}}}_i} - {{\mathit{\boldsymbol{q'}}}_j}} \right\|}}} \right| < {u_2}. $ | (2) |
式中:pi与p′i分别表示点云P中的任意一点与其近邻点,qj与q′j分别表示pi与p′i在其配对点云Q中的对应匹配点. u1、u2为距离阈值,经过初配准可以剔除大部分噪声点,获得具有良好初始状态的配对点云S与L.
2.2.3 改进点云精配准ICP匹配算法基于两个点云完全重合的假设,采用全局搜索实现匹配点搜索.随着地图规模的扩大,全局搜索将带来计算量的增加.另一方面实际匹配过程中两片点云并不是全部点一一对应,存在大量的误匹配点对,因此会导致容易陷入局部最优,甚至收敛失败,所以比较好的点云初始位置,能更好地实现精配准.本文采用ICP算法的精配准目标是为了高效地配准具有良好初始状态的三维点云,从而得到一个旋转矩阵和平移向量.传统的ICP算法通过最小二乘优化思想求解式(3),使其中的R和T最小化.
| $ f\left( {\mathit{\boldsymbol{R}},\mathit{\boldsymbol{T}}} \right) = \sum\limits_{i = 1}^n {{{\left\| {{\mathit{\boldsymbol{L}}_i} - \left( {\mathit{\boldsymbol{R}}{\mathit{\boldsymbol{S}}_i} + \mathit{\boldsymbol{T}}} \right)} \right\|}^2}} . $ | (3) |
式中:n为匹配点对的数量,R为3×3的旋转矩阵,T为×1的平移矩阵,Si和Li分别为初始和目标点集.
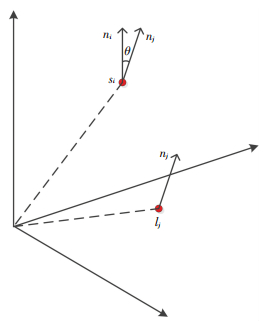
本文采用改进ICP算法完成精配准,其原理图如图 4所示,完成匹配点对的搜索后,通过最小二乘优化误差方程得到刚体变换矩阵,当ICP算法完成一次迭代之后,初始点云和目标点云的匹配可以更加准确.
|
图 4 精配准原理示意图 Figure 4 Accurate registration principle |
这意味着点云S与其匹配点云L之间的偏移角减小,因此下一次ICP匹配点搜索可以缩小搜索范围,不但减少了误匹配,而且减少了搜索计算量.经过初配准的处理,待匹配点云之间的初始位置良好,再结合动态角度迭代因子,ICP算法每实现一次迭代,点对之间的法向量夹角会更小,通过动态阈值减小错误迭代次数,避免局部最优和获得更好的位姿估计精度.本文将选择匹配点对之间的方向向量夹角的正弦值作为匹配点误差方程,匹配点的正弦值如式(4):
| $ \sin\theta = \sqrt {1 - {{\left( {\frac{{\overrightarrow {{\mathit{\boldsymbol{n}}_i}} \times \overrightarrow {{\mathit{\boldsymbol{n}}_j}} }}{{\left| {\overrightarrow {{\mathit{\boldsymbol{n}}_i}} } \right| \times \left| {\overrightarrow {{\mathit{\boldsymbol{n}}_j}} } \right|}}} \right)}^2}} . $ | (4) |
式中: ni和nj分别为点si与lj的近似法向量,θ为两匹配点对的法向量夹角.匹配点的权重由式(5)计算:
| $ Z_t^i\left( j \right) = \left\{ {\begin{array}{*{20}{c}} {1,}&{\sin \theta < E;}\\ {0,}&{其他.} \end{array}} \right. $ | (5) |
式中E为动态角度迭代阈值.匹配点的数量为
| $ {n_t} = \sum\limits_{j = 0}^N {\sum\limits_i {Z_t^i\left( j \right)} } , $ |
本文改进后的ICP精配准步骤如下:
Step 1 初配准获得初始对应点集Si0与Li0.
Step 2 由动态角度迭代阈值法进一步获得精配准点集Si1={s1, …, sn1}与Li1={l1, …, ln1}.
Step 3 采取SVD求解点集Si1与Li1之间的旋转矩阵R和平移向量t.
Step 4 根据式Si2=R1Si1+t1, 计算点集Si1经过一次迭代变换后的数据点集Si2.
Step 5 完成一次迭代后,E通过下式被缩小:
| $ E = E{D_{{\rm{dec}}}},{D_{{\rm{dec}}}} \in \left( {0,1} \right), $ |
然后重复Step 2~Step 5,直到满足
| $ \left\{ \begin{array}{l} {d_t} - {d_{t + 1}} < \varepsilon ;\\ {d_t} = \frac{1}{n}\sum\nolimits_{i = 1}^n {{{\left\| {{L_{it}} - {S_{it}}} \right\|}^2}} . \end{array} \right. $ |
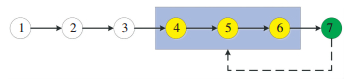
相机行进中会获取室内的环境信息,若将全部采集帧的图像位姿估计都作为状态变量传递给后端优化,将导致后端优化中重建模型的规模急剧变大,程序占用的内存也会越来越高.于是需要从采集帧中选取代表性的图像作为关键帧.而系统的精度与关键帧的选取有很大关系,当关键帧的选取十分稠密时,会增加回环检测与全局优化的计算量,并且会增加很多的冗余信息,无法满足实时性的要求;而当关键帧的选取比较稀疏时,则帧间配准容易失败的情况增加,甚至导致跟踪失败.为了满足帧间配准的成功率和系统实时性要求,对于当前帧,本文将采用图 5所示的滑动窗口法[17]与随机采样法[18]相结合的策略,选取相邻的m帧,以及随机采样的n帧作为关键帧.
|
图 5 滑动窗口法 Figure 5 Sliding window method |
本文在随机采样时,考虑机器人在较短时间内返回当前位置的可能性较小,因此过去时间较长的帧选取的可能性大,过去时间较短的帧选取的可能性小.若当前时刻有数量为N+m的帧,去除滑动窗口法选取的最近邻m帧,还剩N帧.那么第i帧被选中的概率为P(i)如下:
| $ P\left( i \right) = \frac{{\left( {N - i + 1} \right)}}{S},S = \frac{{N\left( {N + 1} \right)}}{2}. $ |
由上文得到机器人在不同时刻的帧间变换关系,各时刻相对于初始时刻的变换关系如下式:
| $ \mathit{\boldsymbol{T}}_0^k = \mathit{\boldsymbol{T}}_0^1 \times \mathit{\boldsymbol{T}}_1^2 \cdots \mathit{\boldsymbol{T}}_{k - 1}^k. $ |
然而,相邻帧间变换算法得到的矩阵Tk-1k是存在误差的,所以机器人位姿会产生累积误差.随着时间的推移,累积误差会越来越大,导致无法构建全局一致的地图.本文采用g2o优化对位姿变换过程中的累积误差进行优化,它将SLAM问题求解转化为基于最小二乘法的优化问题:
| $ F\left( \mathit{\boldsymbol{x}} \right) = \sum\limits_{\left\langle {i,j} \right\rangle \in C} {{e^{\rm{T}}}\left( {{\mathit{\boldsymbol{x}}_i},{\mathit{\boldsymbol{x}}_j},{\mathit{\boldsymbol{z}}_{ij}}} \right){\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_{ij}}e\left( {{\mathit{\boldsymbol{x}}_i},{\mathit{\boldsymbol{x}}_j},{\mathit{\boldsymbol{z}}_{ij}}} \right)} , $ |
| $ {\mathit{\boldsymbol{x}}^ * } = {\arg _x}\min F\left( \mathit{\boldsymbol{x}} \right). $ |
式中:xi代表机器人在g2o图中第i个节点的位姿; zij为节点xi和xj之间的边,也就是位姿xi和xj之间的约束即变换矩阵Tij; Ωij表示xi和xj之间的信息矩阵; e(xi, xj, zij)是g2o图中表示定点xi和xj满足约束zij的程度,若位姿xi和xj完全满足约束zij,那么e(xi, xj, zij)的值为0,即无需调整位姿xi和xj.
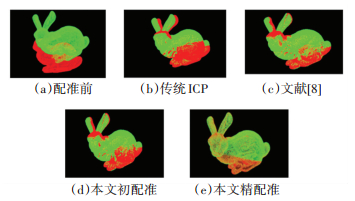
3 实验结果及分析 3.1 验证改进点云配准算法为了验证本文改进点云配准算法的有效性,采用基于三维点云标准模型的仿真实验进行验证.选用斯坦福大学的bunny数据的三维模型进行配准实验,对随机选取的两种视角模型分别进行了初配准和精配准,通过与传统ICP算法对比,同时也与文献[8]的算法进行了对比.基于Ubuntu14.04系统,采用PCL1.7.0版本点云库,在PC机上进行试验. 图 6为不同视角下bunny数据的点云配准效果图,其中图 6(a)为配准前数据,图 6(b)为传统ICP算法配准,图 6(c)为文献[8]算法配准,图 6(d)为本文算法初配准,图 6(e)为本文算法精配准.从图 6可以看出,文献[8]和本文算法相对传统ICP算法具有更高的精度,传统ICP算法达不到良好匹配精度,无法满足实际场景中机器人的需要.而且可以观察出本文算法的初配准效果基本已经达到文献[8]的效果,而且比传统ICP精度还高.
|
图 6 bunny模型配准效果 Figure 6 Bunny model registration effect |
可以看出本文算法对模型配准结果较好,能够达到点云配准的要求.在完成本文的精匹配之后,bunny的耳朵,脚趾等一些复杂度较高的部位具有更高的配准精度,即本文算法在配准精度上有很大的提高. 表 1为三种配准算法在迭代次数,均方匹配误差(MSE)上的对比结果.可以看出,本文算法在通过初配准后具有较好地初始位姿,能够有效地避免陷入局部最优,使得配准时间更短.在精配准阶段,本文采用动态迭代阈值因子减少误匹配,使得迭代次数更少且具有更高的配准精度.根据实验配准效果图和实验配准数据的对比,充分说明本文算法的有效性.
| 表 1 点云不同算法的配准结果对比 Table 1 Comparison of registration results by different algorithms |
为了验证本文算法在真实环境下的性能,搭建实验平台并进行实验.本文采用搭建的实验平台,平台包括:上下两个部分,上面是由一台Intel双核4.0 GHz主频的联想笔记本电脑,采用Ubuntu14.04的以Linux为内核的操作系统;下面部分安装有Kinect和Pioneer3-DX机器人,Kinect的图像分辨率为640×480,最高帧率为30帧/s,水平视场角为52°.实验场景是以一间80 m2的实验室作为室内真实环境,如图 7(a)所示,图 7(b)为实验设备.

|
图 7 试验场景及实验设备 Figure 7 Experimental site and experimental equipment |
实验过程中,搭载Kinect相机的Pioneer3-DX机器人,在实验室中以0.1 m/s的速度移动.其中Kinect相机的内参标定为:fx=518.0、fy=519.0、cx=325.5、cy=253.5、s=1 000.在标定的基础上,结合Kinect相机获取的室内彩色信息和深度信息,通过内外参数和校正深度值生成三维彩色点云数据,如图 8所示.

|
图 8 Kinect采集的帧数据和环境三维彩色点云 Figure 8 Frame data collected by Kinect and 3D color point cloud |
在帧间配准过程中,通过特征匹配算法得到的相邻帧间对应关系存在很多错误匹配. RANSAC算法进行预处理以消除点云误匹配,结果如图 9所示.从图 9中可以看出,经过RANSAC预处理,可以基本消除噪声对匹配结果的影响,获取比较好的初始位姿估计.

|
图 9 预处理实验结果 Figure 9 Pretreatment experiment results |
Pioneer3-DX机器人以0.1 m/s的线速度在室内环境下构建地图,真实实验过程中的最大迭代次数为50,初配准过程中的参数设定为u1=5 cm,u2=0.05,Ddec=0.5. 图 10(a)为采用传统ICP算法获取的三维重构的点云图,可以看出墙上的标板、柜子、椅子和显示屏的连接处存在大量的冗余点,物体的轮廓不清晰和存在重叠的情况. 图 10(b)为采用文献[8]构建的三维环境点云图,其中物体轮廓基本清晰,相比于图 10(a)在挂板和椅子上的重影减少,但是从柜子边缘和地图边缘的效果可得出,在构建的地图边缘处存在冗余点过多,细节精度不高的问题. 图 10(c)为本文三阶段改进点云配准算法的三维重构点云图,获取的点云图精度明显提高,柜子、挂板、椅子等轮廓均比较清晰,而且在地图的边缘冗余点较少,地图的精度有一定提高.

|
图 10 实验室环境下的三维重构结果 Figure 10 3D reconstruction results in laboratory |
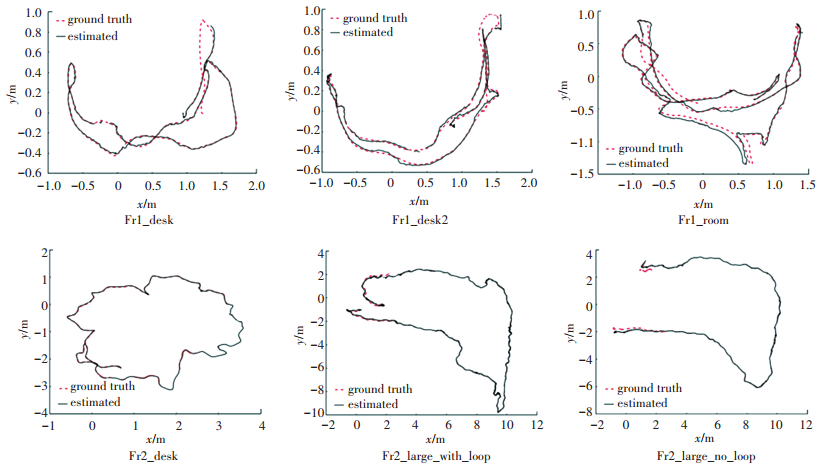
为检测本文SLAM算法在位姿估计精度方面的性能,从TUM数据集中,选用6组RGBD标准数据集进行试验.这些数据集都是通过深度相机获取的室内场景,并且数据集里都含有深度相机的真实轨迹.因此,机器人真实轨迹与估计位姿之间的误差情况可以通过均方根误差(RMSE)来评判位姿估计的精确度. 表 2是ORB-SLAM、RGBD-SLAM和本文算法在不同数据集下的真实轨迹与估计轨迹间的均方根误差(RMSE)结果.可以发现,相比RGBD-SLAM,本文算法轨迹估计准确率更高;而与采用同样特征子的ORB-SALM在没有闭环的小范围场景下相比,准确率相差不大;但在带有闭环的fre2_large_with_loop数据集下,由于本文构建更加精确的地图使得定位更加准确,从而可以更好地实现闭环检测,因此具有更加精确的轨迹. 图 11为6组TUM数据集在本文算法下的绝对轨迹误差图,可以直观地发现估计位姿与真实轨迹的误差值.其中,红色线表示真实轨迹,黑色线表示估计轨迹.通过以上实验验证,本文算法可以更精确地实现移动机器人的轨迹跟踪.
| 表 2 不同算法的位姿估计RMSE对比 Table 2 Comparison of RMSE by different algorithms |
|
图 11 真实轨迹与估计轨迹误差图 Figure 11 Error map of real and estimated trajectory |
1) 针对当前V-SLAM系统在帧间配准、位姿估计精度上存在不足的问题,本文提出一种基于改进点云配准算法的V-SLAM系统.为了满足精配准对匹配点云之间初始位置不能相差过大的要求,采用预处理和初配准两个阶段来保证点云具有良好的初始状态.
2) 不同于传统点云匹配方法,本文通过对RGB图的彩色信息进行处理来获取初始匹配内点进行微调;在不满足精匹配初始位姿的要求下,采用匹配点对的双重距离阈值法完成点云的初配准,从而获取良好初始位姿;引入动态迭代角度因子改进ICP来进行点云的精配准,通过误差的判定决定是否继续迭代下去,每实现一次迭代都会缩小搜索范围并且更加准确地剔除误匹配,从而满足V-SLAM系统对精度的需求,具有重要的现实意义.
3) 通过对标准点云模型的配准仿真实验,验证了算法在点云配准上具有更高的精度和效率,然后基于搭建的机器人实验平台,在真实环境下验证了本文算法的有效性,并且在TUM数据集实验中能够有效估计出机器人运行轨迹,证明了该算法在V-SLAM系统中的可行性.
| [1] |
ENDRES F, HESS J, STURM J, et al. 3-D mapping with an RGB-D camera[J]. IEEE Transactions on Robotics, 2014, 30(1): 177. DOI:10.1109/TRO.2013.2279412 |
| [2] |
CADENA C, CARLONE L, CARRILLO H, et al. Simultaneous localization and mapping: present, future, and the robust-perception age[J]. IEEE Transaction on Robotics, 2016, 32(6): 1309. DOI:10.1109/TRO.2016.2624754 |
| [3] |
FUENTES-PACHECO J, RUIZ-ASCENCIO J, RENDÓN-MANCHA J M. Visual simultaneous localization and mapping: a survey[J]. Artificial Intelligence Review, 2015, 43(1): 55. DOI:10.1007/s10462-012-9365-8 |
| [4] |
BESL P J, MCKAY N D. A method for registration of 3-d shapes[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1992, 14(2): 239. DOI:10.1109/34.121791 |
| [5] |
杨扬, 曹其新, 朱笑笑, 等. 面向机器人手眼协调抓取的3维建模方法[J]. 机器人, 2013, 35(2): 151. YANG Yang, CAO Qixin, ZHU Xiaoxiao, et al. A 3D modeling method for robot's hand-eye coordinated grasping[J]. Robot, 2013, 35(2): 151. DOI:10.3724/SP.J.1218.2013.00151 |
| [6] |
贾松敏, 王可, 郭兵, 等. 基于RGB-D相机的移动机器人三维SLAM[J]. 华中科技大学学报(自然科学版), 2014, 42(1): 103. JIA Songmin, WANG Ke, GUO Bing, et al. Mobile robot 3D SLAM based on RGB-D camera[J]. Journal of Huazhong University of Science and Technology(Nature Science), 2014, 42(1): 103. DOI:10.13245/j.hust.140122 |
| [7] |
侯荣波, 魏武, 黄婷, 等. 基于ORB-SLAM的室内机器人定位和三维稠密地图构建[J]. 计算机应用, 2017, 37(5): 1439. HOU Rongbo, WEI Wu, HUANG Ting, et al. Indoor robot localization and 3D dense mapping based on ORB-SLAM[J]. Journal of Computer Applications, 2017, 37(5): 1439. DOI:10.11772/j.issn.1001-9081.2017.05.1439 |
| [8] |
LI C, LU B, ZHANG Y, et al. 3D reconstruction of indoor scenes via image registration[J]. Neural Processing Letters, 2018(4): 1. DOI:10.1007/s11063-018-9781-0 |
| [9] |
FISCHLER M A, BOLLES R C. Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography[J]. Readings in Computer Vision, 1987, 24(6): 726. DOI:10.1145/358669.358692 |
| [10] |
ZHANG Z. Microsoft kinect sensor and its effect[J]. IEEE Multimedia, 2012, 19(2): 4. DOI:10.1109/MMUL.2012.24 |
| [11] |
王忠立, 赵杰, 蔡鹤皋. 大规模环境下基于图优化SLAM的后端优化方法[J]. 哈尔滨工业大学学报, 2015, 47(7): 75. WANG Zhongli, ZHAO Jie, CAI Hegao. A survey of front-end method for graph-based slam under large-scale environment[J]. Journal of Harbin Institute of Technology, 2015, 47(7): 75. DOI:10.11918/j.issn.0367-6234.2015.07.002 |
| [12] |
DANIEL H C, KANNALA J, HEIKKILA J. Joint depth and color camera calibration with distortion correction[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2012, 34(10): 2058. DOI:10.1109/TPAMI.2012.125 |
| [13] |
RUBLEE E, RABAUD V, KONOLIGE K, et al. ORB: an efficient alternative to SIFT or SURF[C]// International Conference on Computer Vision.Barcelona: IEEE Computer Society, 2011: 2564.DOI: 10.1109/ICCV.2011.6126544
|
| [14] |
ROSTEN E, DRUMMOND T. Machine learning for high-speed corner detection[C] //European Conference on Computer Vision. Heidelberg: Springer, 2006: 430. DOI: 10.1007/11744023_34
|
| [15] |
CALONDER M, LEPETIT V, STRECHA C, et al. BRIEF: binary robust independent elementary features[C] //European Conference on Computer Vision. Heidelberg: Springer, 2010: 778. DOI: 10.1007/978-3-642-15561-1_56
|
| [16] |
MUJA M, LOWE D G. Scalable nearest neighbor algorithms for high dimensional data[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2014, 36(11): 2227. DOI:10.1109/TPAMI.2014.2321376 |
| [17] |
STEFAN L, SIMON L, MICHAEL B, et al. Keyframe-based visual-inertial odometry using nonlinear optimization[J]. International Journal of Robotics Research, 2015, 34(3): 314. DOI:10.1177/0278364914554813 |
| [18] |
KARAMAN S, FRAZZOLI E. Sampling-based algorithms for optimal motion planning[J]. Sage Publications, Inc., 2010, 30(7): 5326. DOI:10.1177/0278364911406761 |
 2019, Vol. 51
2019, Vol. 51


