2. 汽车车身先进设计制造国家重点实验室(湖南大学), 长沙 410082
2. State Key Laboratory of Advanced Design and Manufacture for Vehicle Body (Hunan University), Changsha 410082, China
淬火工艺是挤压铝型材制备过程中重要的工序,是保证获得良好时效强化效果的前提条件[1].传统采用离线淬火炉来实现铝型材的淬火工艺,能耗高,生产周期长.而在线淬火技术,即型材挤压出模口后直接采用水冷或风冷,充分利用挤压产生的余热,具有能耗低、工艺流程短及生产效率高等优点,在挤压生产线上已广泛使用[2-3].目前,国内铝型材企业主要以生产建筑型材为主,工业型材所占的比重较少,通常只是在挤压机出模口处采用安装风机的方法对型材进行风冷淬火.对于大断面工业复杂铝型材,则需采用周向多路喷嘴淬火系统进行水淬或雾淬,然而由于型材的截面形状不规则及壁厚差异大,在线淬火过程中各部位冷却速率不同导致温度场不均匀和产生热应力,使型材发生翘曲或扭曲变形[4-6],且在后续的矫直工艺中很难进行消除[7].因此,研究大断面复杂铝型材挤压在线淬火工艺已成为提高型材产品质量的重要课题之一.
型材淬火冷却过程是介质流动、温度、应力等相互影响的复杂非线性过程,传统方法难以精确跟踪淬火过程中型材的温度场和应力场演变规律,对于预测淬火残余变形的分布有一定局限性.数值仿真技术具有计算精度和效率高,信息量大等优点,而且还能兼顾各因素的耦合影响,为解决这一问题提供了新思路和方法[8-9].近几年来,国内外已有大量学者对型材挤压淬火过程进行有限元分析和预测. Yang等[10]基于Fluent软件模拟了A357铝合金大型复杂构件所用淬火槽内介质流场分布, 分别采用未置搅拌系统和配置搅拌系统对槽内介质流速均匀性进行模拟计算.徐戎等[11]建立某地铁挤压铝型材在线风淬火的有限元模型,采用反求的界面换热系数作为界面换热参数,实现了型材挤压在线风淬过程的模拟.李杰等[12]建立了铝合金H形截面板筋件淬火过程的热力耦合分析模型,研究在转移和淬火过程中其温度场和应力场的变化以及淬火结束后残余应力的分布规律. Wang等[13]通过淬火实验获得6061铝合金的冷却曲线和界面换热系数,并运用Abaqus软件动态模拟了带筋圆管的在线淬火过程. Yang等[14]采用有限元模拟计算的方法分析了用3种淬火介质对A357铝合金大型复杂薄壁构件淬火过程的残余应力及变形的分布和大小进行预测.
已有淬火过程温度场和残余应力应变的仿真研究大多不考虑淬火介质的流动,在有限元模拟中假设介质与型材各表面的换热系数为恒定值.对复杂截面挤压铝型材在线淬火过程淬火介质流动对型材各表面的换热行为影响以及淬火装置周向各路喷嘴流速的优化设计研究则相对缺乏.为此,本文以π字形大断面铝型材为研究对象,基于Fluent和Workbench软件平台建立了在线淬火过程的有限元模型,对淬火介质和型材的换热过程进行耦合分析.为了确定仿真中的热边界条件,采用末端淬火实验和反热传导相结合的方法,获得了不同喷水流量下的界面换热系数.系统分析了3种不同喷嘴流速方案下铝型材实际挤压在线淬火冷却过程中的温度场、应力场和残余变形.研究方法和结果为大断面复杂铝型材挤压在线淬火系统喷嘴流速的制定提供理论指导.
1 铝合金喷水淬火界面换热系数求解 1.1 末端淬火实验型材在线淬火过程的数值模拟中,介质与型材表面的换热系数是建立热边界条件的最重要参数,直接影响到型材温度场、应力场和残余变形的求解精度.目前界面换热系数主要通过查表或经验获取,不能反映实际的界面换热状态,导致仿真精度较低.本文通过利用末端淬火实验和反分析相结合的方法,研究喷水流量对铝型材喷水界面换热系数的影响.实验材料为国内某企业生产的6082挤压态棒材,直径为32 mm.实验所采用的末端喷水淬火装置如图 1所示,装置的下端为水池,水泵通过水管将水抽出,在水管中间装有流量计,可通过流量计调节冷却水的流量.对试样末端进行喷水的喷嘴呈圆形,直径为10 mm,距离试样端面约80 mm.试验过程中的室温水作为冷却介质可循环使用.
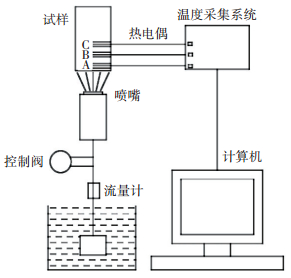
|
图 1 末端淬火实验装置 Figure 1 Set-up diagram of spray quenching |
末端淬火试样直径为30 mm,长度为125 mm,在距离试样端面分别为3,10和20 mm的位置钻取深度为15 mm,直径为3 mm的的盲孔(图 2),用于安装K型热电偶.为能更快地将试样从电阻炉中取出并迅速固定在末端淬火试验台的支架上,在试样顶部打一个直径6 mm,深度为15 mm的螺纹孔并装上螺钉.为等效模拟挤压型材与淬火介质的表面换热行为,试样端面的粗糙度通过精加工以与挤出型材实际的表面粗糙度保持一致.为使界面接触传热可近似成一维传热,需减少喷水时圆柱侧面的热量传递,采用保温棉和锡箔纸包裹圆柱侧面.在喷水淬火实验时,将安装好热电偶的试样放在电阻炉中加热至520 ℃并保温3 h,取出试样后快速安放在喷嘴上方的支架上,然后立即用室温水(约20 ℃)对准试样底面进行喷水冷却.温度采集仪通过热电偶将3个特征点的温度变化曲线在计算机中记录下来,利用反热传导程序便可求出型材与介质的界面换热系数.
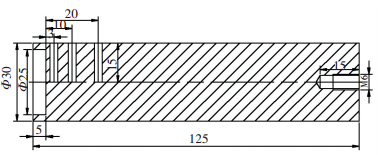
|
图 2 末端淬火试样尺寸(单位: mm) Figure 2 Schematic diagram of quenching sample |
采用反传热算法求解界面换热系数时,首先通过工件内部已知的温度场来计算界面的热流,再求解界面换热系数.采用反传热方法对介质与工件间界面换热系数求解需要采用迭代的方法,为了使程序能够持续执行并且达到所要求的求解精度,必须要建立收敛判据,也就是要建立优化模型,根据冷却过程换热系数反向求解的特点,以实验测量温度与每一次迭代计算所得温度的差的范数为收敛判据,所建立的收敛判据为[15]
| $ \begin{array}{l} S\left( h \right) = \sum\limits_{t = 1}^{{N_t}} {\sum\limits_{j = 1}^{{N_m}} {\frac{1}{{\sigma _T^2}}{{\left[ {T_{ij}^m - T_{ij}^c\left( h \right)} \right]}^2}} } + \\ \;\;\;\;\;\;\;\;\;\;\;\sum\limits_{k = 1}^{{N_h}} {\frac{1}{{\sigma _k^2}}{{\left[ {{h_k} - h_k^0} \right]}^2}} . \end{array} $ | (1) |
式中:Tijm为测量点xj(j=1, …, Nm)随时间ti(i=1, …, Nt)变化的测量温度,℃;Tijc(h)为对应计算温度,℃;h={h1, h2, …, hNh}为未知的界面换热系数,W/m2·℃;Nh为要求解的换热系数个数;δT为测量温度的误差,℃;δk为每一次迭代过程中h被允许的最大变化量,W/m2·℃;hk0是假设的初始换热系数,W/m2·℃.
为求解界面换热系数h,需使函数S(h)最小,即[16]
| $ \begin{array}{*{20}{c}} {\frac{{\partial S}}{{\partial {h_l}}} = \sum\limits_{t = 1}^{{N_t}} {\sum\limits_{j = 1}^{{N_m}} {\frac{{\left( { - 2} \right)}}{{\sigma _T^2}} \cdot \left[ {T_{ij}^m - T_{ij}^c\left( h \right)} \right] \cdot } } }\\ {{X_{i\;\;jl}} + \frac{2}{{\sigma _l^2}}\left[ {{h_l} - h_l^0} \right] = 0.} \end{array} $ | (2) |
式中, Xijl为敏感系数,用泰勒公式在换热系数hl处线性展开:
| $ \begin{array}{l} {X_{ijl}} = \frac{{\partial T_{ij}^c\left( h \right)}}{{\partial {h_l}}} \cong \\ \frac{{T_{ij}^t\left( {{h_1}, \cdots ,{h_l} + \delta {h_l}, \cdots ,{h_{{N_h}}}} \right) - T_{ij}^c\left( {{h_1}, \cdots ,{h_l}, \cdots ,{h_{{N_h}}}} \right)}}{{\delta {h_l}}}. \end{array} $ | (3) |
式中:δhl为前一次迭代hl的变化量,W/m2·℃,用来计算敏感系数,在温度场计算过程中下一次迭代的温度Tijc(hv+1)也被线性化,即
| $ T_{ij}^c\left( {{h^{v + 1}}} \right) \cong T_{ij}^c\left( {{h^v}} \right) + \sum\limits_{k = 1}^{{N_h}} {X_{ijk}^v \cdot \Delta {h_k}} , $ | (4) |
式中换热系数的变化量Δhk通过下面方程式求得:
| $ \sum\limits_{k = 1}^{{N_h}} {{A_{lk}} \cdot \Delta {h_k}} = {f_l}, $ | (5) |
| $ {A_{lk}} = \sum\limits_{t = 1}^{{N_t}} {\sum\limits_{j = 1}^{{N_m}} {\frac{{{X_{ijk}} \cdot {X_{ijl}}}}{{\sigma _T^2}} + \frac{{{\delta _{lk}}}}{{\sigma _l^2}}} } , $ | (6) |
| $ {f_l} = \sum\limits_{t = 1}^{{N_t}} {\sum\limits_{j = 1}^{{N_m}} {\frac{1}{{\sigma _T^2}}\left[ {T_{ij}^m - T_{ij}^c\left( {{h^v}} \right)} \right] \cdot {X_{ijl}} - \frac{1}{{\sigma _l^2}}} } \left( {h_l^v - h_l^0} \right). $ | (7) |
用反传热方法求解淬火过程中工件与介质之间的界面换热系数,详细的求解过程如下:
1) 通过末端淬火实验获得试样上3个特征点温度随时间变化的数据;
2) 假设初始界面换热系数h0={h10, h20, …, h0Nh},并设置最大迭代次数M;
3) 通过数值模拟计算得到试样的温度场Tijc(h);
4) 通过方程式(3),计算敏感系数Xijl;
5) 通过方程式(5)~(7),求解得到换热系数的变化量Δhk,如果|Δhk/hk| < ε,计算停止,输出换热系数h,否则,换热系数hkv+1=hkv+Δhk,到第3)步.
在上述的求解过程中,为反向求解界面换热系数,正向求解温度场需要运算(Nh+1)×M次,这必然会消耗大量的计算时间,因此本文采用一维末端喷水淬火试验可以缩短正向求解的运算时间,提高反运算效率.
图 3为不同喷水流量距离试样端面10 mm处的冷却曲线.由图 3可知,不同喷水流量下的特征点温度都经历了快速下降和缓慢下降两个阶段.高温淬火的10 s短时间内,巨大的界面温差使得试样温度急剧下降,4种流量下的冷却曲线基本重合.当淬火进行到10 s以后,随着喷水流量的增大,单位时间内到达试样端面的水量增加,界面的换热量增大导致淬火冷却速率越快.当淬火进行到20 s左右以后,喷水流量为0.3 m3/h和0.4 m3/h对应的冷却速率很小,温度基本保持不变,而喷水流量为0.55 m3/h以上的冷却速率明显要大,温度继续下降直到120 s左右趋于平稳. 图 4为反求得到的不同喷水流量的界面换热系数曲线.由图 4可知,界面换热系数与淬火表面温度之间呈非线性关系,各喷水流量下的换热系数在淬火初期较小,随着淬火过程的持续进行逐渐增大,并在100~200 ℃范围内达到最大值.达到峰值以后开始下降,在100 ℃左右降到一个极小值后又略有上升,当试样表面温度降到接近室温(50 ℃以下)时,界面换热系数又减小.这是由于温度在200 ℃以上为过渡沸腾,换热系数逐渐增大,温度在100~200 ℃为核沸腾,气膜破裂带走一部分热量,换热系数略有减小;温度低于100 ℃时进入对流换热阶段.由于水的比热大,单位时间内水和工件表面之间的换热量较大,导致对流换热阶段换热系数值又有所增大.但当工件降到50 ℃以下接近室温,水和工件之间的温差较小,传热速度又会减小.喷水流量为0.3 m3/h,峰值界面换热系数为15 707.4 W/m2· ℃.随着喷水流量的增大,界面换热系数增加,且到达峰值的时刻越晚.当喷水流量增加到1 m3/h时,界面换热系数增加到34 975 W/m2· ℃,相比0.3 m3/h增大122.7%,峰值到达时刻晚82 s.由此可知,喷水流量对型材淬火的冷却速率具有重要影响,在实际挤压生产在线淬火过程中,可根据需要调整喷水流量的大小.不同喷水流量下的界面换热系数反分析求解为挤压型材在线淬火过程的数值仿真热边界条件的确定提供理论依据.
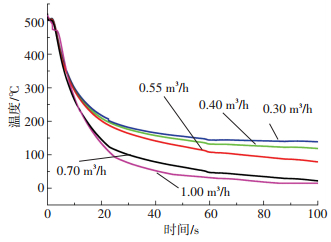
|
图 3 不同喷水流量下距离端面10 mm处的冷却曲线 Figure 3 Cooling curves at location of 10 mm from interface under different spray water fluxes |
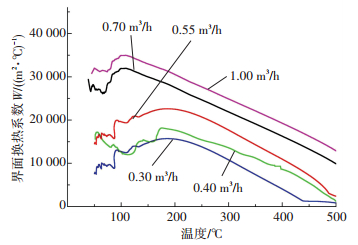
|
图 4 反求得到的不同喷水流量的界面换热系数 Figure 4 Calculated heat transfer coefficients under different spray water fluxes |
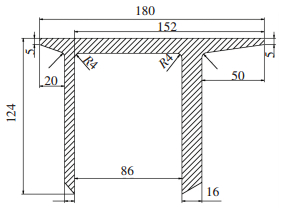
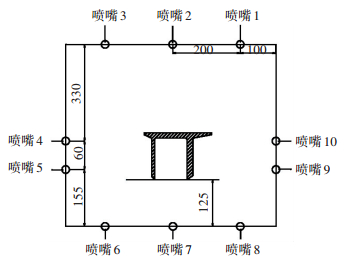
本文的研究对象为轨道交通用6082高强铝合金型材,形状为π字形(图 5),断面尺寸大,最大宽度和高等分别为180和124 mm,且壁厚不均匀,最大和最小厚度分别为16和5 mm.挤压在线淬火试验在某挤压厂家的4000T卧式挤压机上完成.由于该型材淬火敏感性高,断面尺寸和壁厚差异大,所采用的淬火方式需要能提供足够的冷却强度,使型材具有所需的微观组织与力学性能,同时又不发生变形.如果采用简单的风冷式淬火,往往造成淬火不充分及出现淬火后变形等问题,因此该型材的淬火方式需采用水淬.喷水冷却系统垂直于型材横截面方向周向布置了多路喷水的管道和喷嘴(图 6).喷嘴方向、间距、流速以及喷嘴的开闭等,均可由计算机根据型材的材料、形状和尺寸规格等进行自动控制,以保证型材经淬火后既能获得所需的性能,又不产生过大的扭曲变形.淬火系统实际所用喷嘴为普通扇形喷嘴,喷射出来的水流形状如图 7所示,喷射角度约为60°.
|
图 5 大断面铝型材截面尺寸(mm) Figure 5 Section size of large section aluminum profile(mm) |
|
图 6 喷嘴分布图(mm) Figure 6 Distribution of nozzles(mm) |

|
图 7 喷嘴射流形状 Figure 7 Shape of nozzle jet |
在线淬火工艺中,淬火系统或装置中影响型材各部位冷却均匀效果的因素众多,包括各路喷嘴的方向、喷嘴间距、喷嘴流速和喷嘴的开闭等.本文的研究对象π字形型材的翘曲变形主要是由于两悬臂和中间截面的冷却速度不均匀而导致的.在实际生产中,挤压厂家主要通过调节各路喷嘴的流速来使型材各部位的冷却速度达到均匀.因此,本文主要研究冷却系统中各路喷嘴的流速大小对型材淬火后温度场、应力场和残余变形的影响,为铝型材实际挤压生产中在线淬火冷却系统中各喷嘴流速方案的设定提供理论指导.
挤压生产厂家原采用的初始方案一,冷却系统各路喷嘴的流速为:1,3号为10 m/s,4,5号为15 m/s,7,8号为40 m/s,9,10号为20 m/s,2,6号喷嘴关闭.由水流流动特点可知,水流速度越快的地方,单位时间内与型材表面接触的水量越大,换热量也越大,型材冷却速度较快,同时距离喷嘴较近的型材端面,需要较小的喷水速度.基于以上原则,对不同喷嘴位置的喷水流速进行调整,获得不同的喷水冷却方案(表 1).
| 表 1 不同喷水冷却方案中的各路喷嘴流速 Table 1 Water spray velocities of circumferential nozzles in different quenching scheme |
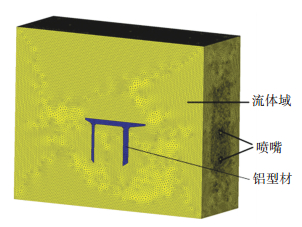
为减少仿真模型大小,求解的计算域型材长度约300 mm.利用Unigraphics NX软件建立型材、流体和喷嘴入口的三维几何模型,型材的放置位置以及喷嘴的分布与实际挤压在线淬火过程保持一致,然后导入到Workbench软件中进行前处理,所建立的挤压型材在线淬火有限元模型如图 8所示.模型中间区域为型材,开口朝下,周围为流体区域,四周小孔表示喷嘴,模拟中不计喷嘴内部结构,直接将喷嘴出口作为流场的入口.为提高求解精度和计算效率,挤压型材和空间域采用五面体网格.型材横截面最薄处至少有4个自由节点,网格尺寸为1.6 mm,约为型材最小壁厚的1/5;空间域网格尺寸为5.5 mm,仿真模型总的网格数量为261 000.网格划分完成后,网格单元质量需满足如下基本条件:1)最小尺寸>0.1;2)长宽比<12;3)最小角度>15°,最大角度<165°;4)雅克比>0.7.经检查网格质量满足上述要求.
|
图 8 挤压型材在线淬火有限元网格模型 Figure 8 Finite element model of quenching process for extruded profile |
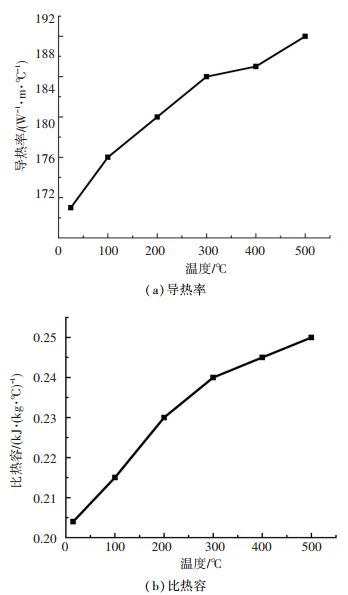
在线淬火冷却过程中,铝型材的导热率、比热容等热物性参数在不同温度下存在很大差异,为提高仿真精度需对其进行精确设定. 图 9为6082铝合金在不同温度下的导热率和比热容[17].随着温度的增加,导热率和比热容逐渐增加.温度为500 ℃时的导热率和比热容分别比常温时增加9.71%和22.55%.型材表面与淬火介质之间的换热系数也是淬火过程数值模拟的重要参数.由于沿型材挤压方向的传热很小,假设型材两端为绝热,只将换热系数加载在型材表面.界面换热系数采用反热传导法求解的不同喷水流量的换热系数曲线. 表 1中各喷嘴流速换算为流量大小范围为0.18~0.883 m3/h,可见反求出的不同喷水流量的界面换热系数可以直接用于淬火有限元模型中,10和12.5 m/s的换热系数可通过外插值得到.
|
图 9 6082铝合金的导热率和比热容 Figure 9 Thermal conductivity and specific heat capacity of 6082 aluminum alloy |
本研究建立的淬火数值模拟中,采用mixture两相流模型及标准k-ε湍流模型;流场入口为速度边界条件,喷嘴最大流速约50 m/s,出口为压力边界条件,其值为标准大气压;固体和流体的交界面假设为采用Convection热类型无滑移的wall边界条件;型材挤压出口为均匀温度场,值约为500 ℃,初始应力为0;流体温度为27 ℃,密度为1 000 kg/m3.
2.4 流场控制方程本研究中流体区域为两相流,包括水和空气.流体流动过程中要受物理守恒定律的支配,主要包括质量守恒定律、动量守恒定律及能量守恒定律[18],计算过程中忽略辐射传热和蒸发传热的影响.由于型材在整个淬火冷却过程中温度场都是变化的,故冷却过程是个瞬态的过程,分析时可假设水是不可压缩的,水的密度为常数,雷诺数Re>12 000,属于湍流流动状态.因此,喷水过程认为是非定常不可压缩黏性流体的湍流流动,应满足以下控制方程.
连续性方程为
| $ \frac{{\partial u}}{{\partial x}} + \frac{{\partial u}}{{\partial y}} + \frac{{\partial u}}{{\partial z}} = 0. $ |
能量守恒方程为
| $ \begin{array}{*{20}{c}} {\rho \left[ {\frac{{\partial T}}{{\partial t}} + \frac{{\partial \left( {uT} \right)}}{{\partial x}} + \frac{{\partial \left( {vT} \right)}}{{\partial y}} + \frac{{\partial \left( {wT} \right)}}{{\partial z}}} \right] = }\\ {{S_T} + \frac{\partial }{{\partial x}}\left[ {\frac{{k \cdot \partial T}}{{{c_p} \cdot \partial x}}} \right] + \frac{\partial }{{\partial x}}\left[ {\frac{{k \cdot \partial T}}{{{c_p} \cdot \partial y}}} \right] + \frac{\partial }{{\partial x}}\left[ {\frac{{k \cdot \partial T}}{{{c_p} \cdot \partial z}}} \right].} \end{array} $ |
运动方程为
| $ \begin{array}{l} \rho \left[ {\frac{{\partial u}}{{\partial t}} + u\frac{{\partial u}}{{\partial x}} + v\frac{{\partial u}}{{\partial y}} + w\frac{{\partial u}}{{\partial z}}} \right] = \\ \;\;\;\;\; - \frac{{\partial p}}{{\partial x}} + u\left[ {\frac{{{\partial ^2}u}}{{\partial {x^2}}} + \frac{{{\partial ^2}u}}{{\partial {y^2}}} + \frac{{{\partial ^2}u}}{{\partial {z^2}}}} \right] + {F_x}, \end{array} $ |
| $ \begin{array}{l} \rho \left[ {\frac{{\partial v}}{{\partial t}} + u\frac{{\partial v}}{{\partial x}} + v\frac{{\partial v}}{{\partial y}} + w\frac{{\partial v}}{{\partial z}}} \right] = \\ \;\;\;\;\; - \frac{{\partial p}}{{\partial y}} + u\left[ {\frac{{{\partial ^2}v}}{{\partial {x^2}}} + \frac{{{\partial ^2}v}}{{\partial {y^2}}} + \frac{{{\partial ^2}v}}{{\partial {z^2}}}} \right] + {F_y}, \end{array} $ |
| $ \begin{array}{l} \rho \left[ {\frac{{\partial w}}{{\partial t}} + u\frac{{\partial w}}{{\partial x}} + v\frac{{\partial w}}{{\partial y}} + w\frac{{\partial w}}{{\partial z}}} \right] = \\ \;\;\;\;\; - \frac{{\partial p}}{{\partial z}} + u\left[ {\frac{{{\partial ^2}w}}{{\partial {x^2}}} + \frac{{{\partial ^2}w}}{{\partial {y^2}}} + \frac{{{\partial ^2}w}}{{\partial {z^2}}}} \right] + {F_z}. \end{array} $ |
式中:u、v和w表示速度矢量u在x、y和z方向的分量,m/s;p为流体微元体上的压力,Pa;ρ为流体密度,kg/m3;t为时间,s;μ为流体的动力黏度,Pa·s;ν为流体的运动黏度,m2/s;T是温度,℃;cp为比热容,J/(kg· ℃);ST为流体的内热源及由于黏性作用流体机械能转换为热能的部分,J;k为湍动能,m2/s2;Fx、Fy和Fz为微元体上的体力,N,若体力只有重力且y轴竖直向上,则Fx= 0,Fy = -ρg,Fz = 0.
基于Fluent 14.0软件平台运用有限体积法对控制方程组进行离散,离散格式为二阶迎风.采用SIMPLEC方法进行速度压力耦合求解,代数方程则采用超松弛法进行迭代求解,压力修正项为0.3,动量修正项为0.7.在计算的过程中,根据收敛情况,确定是否要对松弛因子进行调整,收敛残差标准均设为10-5.
3 模拟结果与分析 3.1 流体速度场分析喷嘴出口速度的大小直接影响铝型材淬火各端面冷却快慢和均匀性.经模拟计算后得到的3种不同喷水方案下模型中间截面的喷水速度矢量分布如图 10所示,颜色越深代表流速越大.由图 10可知,上下左右各路喷嘴出口处的射流速度大小均比较准确符合表 1中不同冷却方案中喷嘴所设置的值,射流散射成60°左右,当射流往两边散射以后速度矢量有所减小,这说明模拟结果能较好地符合实际要求,为获得准确的型材淬火温度场和应力场提供了条件.

|
图 10 不同方案的喷水速度矢量分布 Figure 10 Velocity vector distribution of water spraying in different quenching schemes |
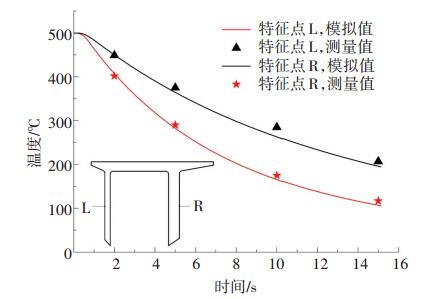
采用有限元模拟可以获得型材喷水冷却过程中的温度场、应力场和残余变形,但模型的可靠性必须进行试验验证.淬火冷却过程的温度场是求解热应力和残余变形的基础,直接影响仿真模拟精度,且能实现现场测量.挤压出口速度为6 m/min,通过合理设计导流模,型材挤压出模口的温度控制在500 ℃左右,然后直接进入在线淬火冷却系统,并在进入淬火系统的0.2、0.5、1和1.5 m处分别采用热电偶测温仪测量π字形型材两侧表面中心位置的温度,经换算成时间2、5、10和15 s与仿真模拟的对应时间点的温度进行对比分析.由图 11可知,特征点R和L仿真与试验测量的温度变化趋势一致,其中特征点L 4个测量点的相对误差范围为0.1%~7.8%;特征点R 4个测量点的相对误差范围为-1.1%~4.3%.仿真和试验结果验证了本文所建立的有限元模型是准确的,可以用来研究型材的在线喷水淬火冷却过程.
|
图 11 型材两侧特征点R和L仿真与试验的温度对比 Figure 11 Comparison of simulated and measured temperatures at feature point R and L |
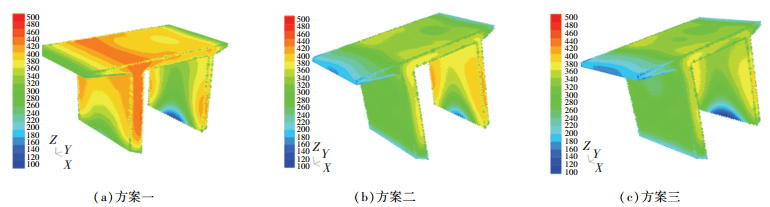
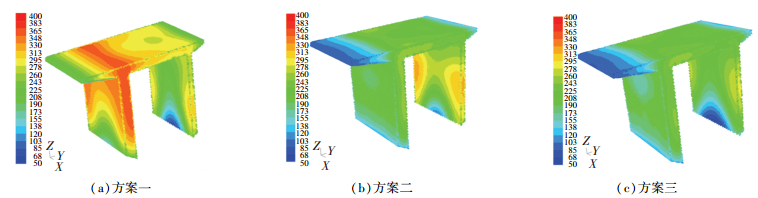
淬火冷却过程中型材温度的变化直接反映了型材表面与冷却介质间的换热情况,也是计算残余应力和变形的依据.在相同的合金材料、冷却系统中喷嘴大小和喷嘴角度下,型材各表面冷却均匀性取决于喷嘴的流速以及型材的壁厚形状等几何特征.距离喷嘴较近的端面,水流从喷嘴出口喷射到达型材表面的过程中散射量不大,水流速度变化不大,因而只需较小的喷水速度.壁厚大的端面,单位时间内冷却所需的喷射水量和换热量要大,需要更高的喷嘴流速.此外,各喷嘴喷射出的水最终都流经型材两侧,故两端下侧也比较容易冷却,所需的冷却水流速度较小.为了直观全面地分析不同喷水冷却方案中型材表面温度场的分布规律,选取5和10 s时型材的温度场进行对比.由图 12可知,在5 s左右,方案一型材薄的悬臂端温度较低,约300 ℃左右,厚的悬臂端和上端温度较高,约为380~440 ℃;与方案一相比,方案二的型材温度分布更为均匀,但薄的悬臂端温度偏高,约为380 ℃,厚的悬臂端和上端温度较低,约320 ℃; 方案三的型材左右两端和上端温度分布都比较均匀,均在300~340 ℃左右.由图 13可知,型材淬火冷却到10 s时,方案一型材厚的悬臂端和上端温度显著大于薄的悬臂端,温差大小约为130 ℃;方案二的型材温度分布较方案一稍微均匀,但薄的悬臂端偏高,厚的悬臂端和上端较低,温差大小约为90 ℃;方案三的型材各端面温度分布比较均匀,均在200 ℃左右.
|
图 12 不同喷水方案型材表面淬火5 s时的温度分布 Figure 12 Temperature distribution of profile surface during different quenching schemes at 5 s |
|
图 13 不同喷水方案型材表面淬火10 s时的温度分布 Figure 13 Temperature distribution of profile surface in different quenching schemes at 10 s |
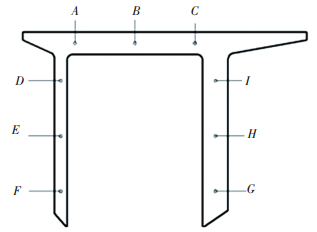
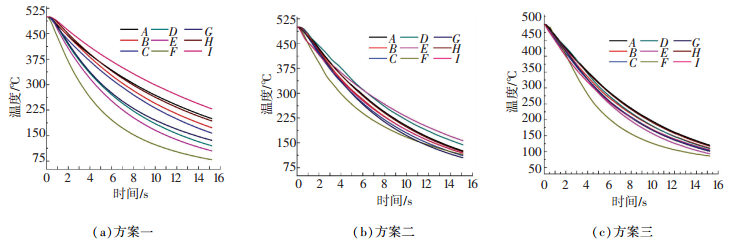
为对比研究3种不同喷水冷却方案型材内部温度场的变化,在型材左右和上端中间截面不同位置取9个特征点(图 14).由图 15可知,方案一9个特征点的冷却速度相差较大,特别是薄的悬臂端D,E,F三点冷却最快.方案二条件下,冷却速度差距有所减小,但差别依然比较明显.方案三条件下,除F点冷却较快之外,其余8个特征点的冷却速度基本一致,最大温差大小在15 ℃以内.
|
图 14 型材中间截面位置选取的特征点 Figure 14 Feature points distribution on the middle section of the profile |
|
图 15 不同喷水方案型材中间截面9个特征点的温度变化 Figure 15 Cooling curves of feature points during quenching |
通过对型材表面和中间截面温度场分析可知,在型材较薄的悬臂端和靠近边缘位置,换热面积与体积比较大,温度下降更快,需要小的喷嘴流速;相反,在型材较厚的悬臂端和靠近中间位置,单位换热面积对应的体积更大,蓄热量更大,使得相同换热条件下此处的温度下降更缓慢,需要更大的喷嘴流速.型材中间截面位置温度变化趋势与前面得到的表面温度场变化趋势吻合较好,表明喷水冷却方案三能得到更为均匀的温度场.
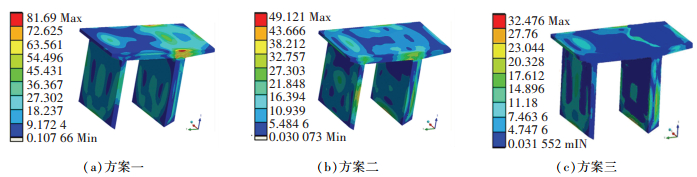
3.4 残余应力场分析在线淬火在提高型材组织力学性能的同时,也会在型材内部产生一定的残余应力.残余应力会影响型材的疲劳强度和抗应力腐蚀能力,降低型材的机械性能.因此,有必要对其进行有限元分析,为减少型材淬火变形提供参考.在淬火过程中,型材内部可能产生组织应力和热应力,前者是型材内微观组织转变不均匀引起的;而后者是型材不同部位冷却收缩不一致引起的.由于铝型材淬火过程中几乎不发生相变,本文只考虑冷却过程温度不均匀而产生的热应力.将3种淬火方案计算的温度场结果导入到Workbench软件平台中,得到淬火完成后的铝型材残余应力分布(图 16).由图 16可知,方案一型材淬火后厚悬臂端接头处存在较大的残余应力,最大值为81.69 MPa,且左右悬臂端都存在30 MPa左右的残余应力.这主要是由于型材表面温度冷却速率快并发生收缩,接头心部受到材料内部导热限制仍处于高温状态,在表面收缩应力的作用下,型材内部发生弹塑性变形.随后型材冷却到室温,中心部位温度降低幅度大于表面,收缩量大以弹性变形的形式保留在材料中,结果导致型材表面出现大的压应力和心部出现大的拉应力.相比方案一,方案二的型材残余应力大幅度减少,型材上端面与厚悬臂端接头处的最大残余应力减少到49.12 MPa,其余部分区域的残余应力只有20 MPa左右;方案三的型材上端面与厚悬臂端接头处残余应力基本为0,最大残余应力位于厚悬臂端的下缘,最大值为32.47 MPa,其余各部分的残余应力较小,基本在10 MPa以下.
|
图 16 不同喷水方案淬火后的型材残余应力分布 Figure 16 Residual stress distributions of aluminum profile in different quenching schemes |
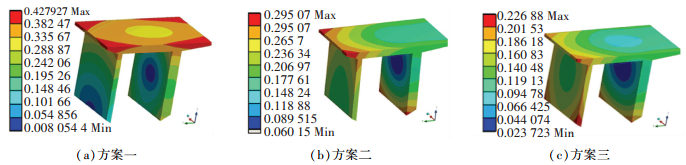
复杂截面铝型材各部位厚度差别较大,由于各部分的热传导状况不同,整体冷却不均匀产生较大的热应力.当热应力超过材料的屈服强度时,产生弹塑性变形.当弹塑形变形积累到一定程度时,型材将产生扭曲.同时不同冷却温度下材料的力学属性和热物性参数也不相同,导致型材各部位所产生的残余变形也有差异.淬火15 s后的型材残余变形如图 17所示.由图 17可知,由于方案一型材淬火后的温度场很不均匀,上端面发生内凹翘曲,变形量为0.3~0.5 mm左右,同时左右两端存在0.1~0.2 mm的变形;方案二型材的残余变形量有所减小,最大值位于型材上端面的边缘及薄悬臂端的下缘位置,最大值为0.3243 mm.方案三的残余变形量最小,型材大部分区域只有0.1 mm左右的变形量.
|
图 17 不同喷水方案淬火后的型材残余变形 Figure 17 Residual deformation of aluminum profile in different quenching schemes |
综上所述,喷嘴流速大小直接影响淬火介质与型材的换热大小和行为,进而影响淬火后的温度场、残余应力和弹塑性变形.因此,针对大断面复杂铝型材,需合理调节淬火系统周向各路喷嘴的流速大小,使型材断面外部和中心部位得到更为均匀的温度场,以减小淬火冷却过程收缩产生大的残余应力以及弹塑性变形.结合前面得到的温度场可知,相比方案一和方案二,方案三设定的周向各路喷嘴流速大小能得到较为理想的冷却效果.
4 结论1) 当喷水流量为0.3 m3/h时,峰值界面换热系数为15 707.4 W/m2· ℃;随着喷水流量的增大,界面换热系数增加且到达峰值的时刻越晚.当喷水流量增加到1.0 m3/h,界面换热系数相比0.3 m3/h增大122.7%,到达峰值的时刻晚82 s.
2) 型材挤压在线淬火有限元模拟的特征点温度与试验测量的温度变化趋势一致,相对误差范围为-1.1%~7.8%,验证了所建立的淬火有限元模型是准确的.
3) 初始淬火方案一,铝型材上端和左右端壁厚差异大,在线淬火过程中各部位冷却不均匀在接头处产生较大的热应力,使上端面发生内凹. 3种不同喷水冷却方案中,方案三中型材表面和中间截面位置淬火冷却过程能得到更为均匀的温度场,残余应力和变形最小.研究方法和结果可为大断面复杂铝型材挤压在线淬火系统喷嘴流速的制定和优化提供理论指导.
| [1] |
ZHANG J, DENG Y, YANG W, et al. Design of the multi-stage quenching process for 7050 aluminum alloy[J]. Materials & Design, 2014, 56(4): 334. DOI:10.1016/j.matdes.2013.09.029 |
| [2] |
张君, 杨合, 谢东钢, 等. 大型挤压铝型材淬火技术与装置[J]. 机械工程学报, 2007, 43(7): 133. ZHANG Jun, YANG He, XIE Donggang, et al. Fast-cooling technique and equipments of large-size aluminium profile[J]. Journal of Mechanical Engineering, 2007, 43(7): 133. DOI:10.3321/j.issn:0577-6686.2007.07.024 |
| [3] |
ZHANG Y, YI Y, HUANG S, et al. Influence of temperature-dependent properties of aluminum alloy on evolution of plastic strain and residual stress during quenching process[J]. Metal, 2017, 7(6): 228. DOI:10.3390/met7060228 |
| [4] |
NOWAK M, GOLOVKO O, NVRNBERGER F, et al. Water-air spray cooling of extruded profiles: process integrated heat treatment of the alloy EN AW-6082[J]. Journal of Materials Engineering & Performance, 2013, 22(9): 2580. DOI:10.1007/s11665-013-0563-6 |
| [5] |
FENG X, ZHANG L, LI Z, et al. FEM simulation and experimental study on the quenching residual stress of aluminum alloy 2024[J]. Proceedings of the Institution of Mechanical Engineers Part B: Journal of Engineering Manufacture, 2013, 227(7): 954. DOI:10.1177/0954405412465232 |
| [6] |
BIKASS S, ANDERSSON B, PILIPENKO A, et al. Simulation of the distortion mechanisms due to non-uniform cooling in the aluminum extrusion process[J]. International Journal of Thermal Sciences, 2012, 52(2): 50. DOI:10.1016/j.ijthermalsci.2011.06.002 |
| [7] |
CAO H L, LI X W, LI Y N, et al. Numerical simulation of quenching and pre-stretching residual stress in 7085 aluminum alloy plate[J]. Materials Science Forum, 2016, 852: 211. DOI:10.4028/www.scientific.net/MSF.852.211 |
| [8] |
WANG H, YANG H B. 6063 Aluminum alloy online quenching surface heat transfer coefficient and the temperature field simulation[J]. Applied Mechanics & Materials, 2014, 446-447: 146. DOI:10.4028/www.scientific.net/AMM.446-447.146 |
| [9] |
李落星, 胡理中, 刘志文, 等. 铝合金挤压型材淬火模拟研究及工艺参数的改进[J]. 湖南大学学报(自科版), 2013, 40(2): 71. LI Luoxing, HU Lizhong, LIU Zhiwen, et al. Simulation study of the quenching process and parameter improvement of aluminum extrusion[J]. Journal of Hunan University(Natural Sciences), 2013, 40(2): 71. DOI:10.3969/j.issn.1674-2974.2013.02.012 |
| [10] |
YANG X W, ZHU J C, LI W Y. CFD-supported optimization of flow distribution in quench tank for heat treatment of A357 alloy large complicated components[J]. Transactions of Nonferrous Metals Society of China, 2015, 25(10): 3399. DOI:10.1016/S1003-6326(15)63975-9 |
| [11] |
徐戎, 李落星, 姚再起. 交通用铝型材挤压在线淬火过程的数值模拟和实验验证[J]. 中南大学学报(自然科学版), 2017, 48(12): 3263. XU Rong, LI Luoxing, YAO Zaiqi. Numerical simulation and experimental verification of extrusion online quenching process of aluminum profile used for traffic[J]. Journal of Central South University(Science and Technology), 2017, 48(12): 3263. DOI:10.11817/j.issn.1672-7207.2017.12.017 |
| [12] |
李杰, 周杰, 郑斯佳, 等. 铝合金H形截面板筋件淬火过程热力耦合数值模拟[J]. 兵器材料科学与工程, 2017, 40(5): 82. LI Jie, ZHOU Jie, ZHENG Sijia, et al. Coupled thermal-mechanical simulation on quenching of aluminum alloy H-shaped section plate reinforced part[J]. Ordnance Material Science and Engineering, 2017, 40(5): 82. DOI:10.14024/j.cnki.1004-244x.20170907.006 |
| [13] |
WANG M J, YANG G, HUANG C Q, et al. Simulation of temperature and stress in 6061 aluminum alloy during online quenching process[J]. Transactions of Nonferrous Metals Society of China, 2014, 24(7): 2168. DOI:10.1016/S1003-6326(14)63328-8 |
| [14] |
YANG X W, ZHU J C, LAI Z H, et al. Finite element analysis of quenching temperature field, residual stress and distortion in A357 aluminum alloy large complicated thin-wall workpieces[J]. Transactions of Nonferrous Metals Society of China, 2013, 23(6): 1751. DOI:10.1016/S1003-6326(13)62657-6 |
| [15] |
FORESTIER R, MASSONI E, CHASTEL Y. Estimation of constitutive parameters using an inverse method coupled to 3D finite element software[J]. Journal of Materials Processing Technology, 2002, 125-126: 594. DOI:10.1016/S0924-0136(02)00406-5 |
| [16] |
STORCH R B, PIMENTEL L C G, ORLANDE H R B. Identification of atmospheric boundary layer parameters by inverse problem[J]. Atmospheric Environment, 2007, 41(7): 1417. DOI:10.1016/j.atmosenv.2006.10.014 |
| [17] |
袁俭, 张伟民, 刘占仓, 等. 不同冷却方式下换热系数的测量与计算[J]. 材料热处理学报, 2005, 26(4): 115. YUAN Jian, ZHANG Weimin, LIU Zhancang, et al. The measurement and calculation of heat transfer coefficient under different cooling conditions[J]. Transactions of Materials & Heat Treatment, 2005, 26(4): 115. DOI:10.3969/j.issn.1009-6264.2005.04.029 |
| [18] |
LI H, ZHAO G, HE L. Finite element method based simulation of stress-strain field in the quenching process[J]. Materials Science & Engineering A, 2008, 478(1-2): 276. DOI:10.1016/j.msea.2007.05.101 |
 2019, Vol. 51
2019, Vol. 51


