超空泡因其在水下高速航行体减阻和降噪领域的潜在应用受到了各国家的广泛关注[1],其通常有自然超空泡和通气超空泡两类.通气超空泡技术通过主动通气的方式形成稳定且易于控制的超空泡,为水下武器的减阻提供了新方法,基于这种技术设计的水下武器的速度可得到大幅度提升,令敌方舰艇无法在短时间内做出反应措施,增加了水下武器的突防能力.
因实验条件和相关技术的制约,国内外针对超空泡武器的研究主要针对定深航行,忽略了超空泡武器在纵平面的机动性,使其作战能力受到一定限制.因此随着研究的不断深入,超空泡武器的机动能力也亟待解决.德国自20世纪80年代开始了超空泡武器机动性试验研究,发展了小型、快速且机动能力良好的超空泡反鱼雷武器,即Anti Torpedo Torpedo(ATT)项目[2].从当今超空泡武器的发展来看,超空泡武器的机动问题仍旧备受关注.中国对超空泡机动技术的数值研究偏重于以水平运动的情形.张广等[3-4]利用非惯性圆柱坐标系数值模拟研究了单独空化器水平转弯运动时通气超空泡轴线上的压力分布情况以及空泡周围的流线特征并且分析了重力效应对通气空泡的影响.李振旺[5]研究了空化器转弯运动的空泡形态,比较了内外侧的气体速度差异.王威等[6]研究了航行体水平转弯运动的空泡形态及流体动力变化规律,分析了沾湿区域的压力分布特性.在纵平面机动研究中,黄小腾[7]利用动网格技术数值模拟研究超空泡航行体空化器周期性摆动时的流体动力分布规律.李其弢[8]通过水洞实验研究了航行体纵平面摆动运动的空泡稳定性.潘展程[9]运用动网格技术,结合水洞实验结果数值模拟研究了航行体纵平面摆动运动时的空泡内部压力分布特性,弥补了水洞实验的一些不足.从上述研究成果来看,在超空泡武器的机动性能研究中并未考虑水深h的变化对空泡形态的影响,忽略了超空泡武器作战效能对高度机动性的要求.纵平面回转运动需同时考虑航行体航行方向及高度的变化,能对超空泡武器机动性能开展更为全面的研究.而这方面的研究并不多见,尤其是低弗劳德数下,空泡回转运动时空泡两侧的压力分布规律还未见文献报道.
本文利用数值模拟软件Fluent的动网格技术建立了单独空化器纵平面内的机动回转运动的数值计算模型,研究了通气空化器在水下纵平面机动回转运动的非定常多相流动问题,着重分析了水深及回转半径的变化对空泡形态以及流场压力分布特性的影响,以期为超空泡武器的机动性分析与结构设计提供基础.
1 数值计算模型 1.1 基本控制方程在纵平面回转运动的数值模拟中,为避免航行体沾湿区对压力场的影响,着重分析纵平面转弯运动中水深h与回转半径R对空泡形态和流场压力分布的影响,航行体模型为通气圆盘空化器.由于空化器运动过程中的速度较低,自然空化现象较弱,仅考虑空气和水两相的相互作用[10],采用VOF多相流模型[11],控制方程如下.
1) 连续性方程:
| $ \frac{\partial \rho_{m}}{\partial t}+\frac{\partial\left(\rho_{m} u_{i}\right)}{\partial x_{i}}=0. $ |
式中:混合介质的密度
2) 动量方程:
| $ \frac{\partial\left(\rho_{m} u_{i}\right)}{\partial t}+\frac{\partial\left(\rho_{m} u_{i} u_{j}\right)}{\partial x_{j}}=\rho_{m} g_{i}-\frac{\partial p}{\partial x_{i}}+\frac{\partial \tau_{i j}}{\partial x_{j}}. $ |
式中:黏性应力
3) 湍流方程.根据陈鑫[12]对通气空泡流的研究,本文选择RNG k-ε湍流模型对通气空泡流进行研究,该模型由文献[13]提出,该模型适合的流动类型广泛,对研究边界层流动和分离流动等有效,可以很好地处理高应变率及弯曲程度较大的流动.关于k和ε的输运方程如下:
| $ \begin{array} [c]{c} \frac{\partial\left(\rho_{m} k\right)}{\partial t}+\frac{\partial\left(\rho_{m} k u_{i}\right)}{\partial x_{i}}=\frac{\partial}{\partial x_{j}}\left(\alpha_{k} \mu_{t} \frac{\partial k}{\partial x_{j}}\right)+\\ G_{k}+G_{b}-\rho_{m} \varepsilon-Y_{M}+S_{k}, \\ \frac{\partial\left(\rho_{m} \varepsilon\right)}{\partial t}+\frac{\partial\left(\rho_{m} \varepsilon u_{i}\right)}{\partial x_{i}}=\frac{\partial}{\partial x_{j}}\left(\alpha_{\varepsilon} \mu_{t} \frac{\partial \varepsilon}{\partial x_{j}}\right)+\\ C_{1 \varepsilon} \frac{\varepsilon}{k}\left(G_{k}+C_{3 \varepsilon} G_{b}\right)-C_{2 \varepsilon} \rho_{m} \frac{\varepsilon^{2}}{k}-R_{\varepsilon}+S_{\varepsilon} . \end{array} $ |
式中:k为湍动能; ε为湍动能耗散率; μt为湍动黏度; Gk由平均速度梯度引起的湍动能产生; Gb由浮力影响引起的湍动能产生; YM为可压缩湍流脉动膨胀对总的耗散率的影响;αk、αε分别为k和ε的负向效应对应的普朗特数,αk=αε≈1.393;C1ε、C2ε、C3ε为常数; Sk、Sε为自定义源项.
1.2 量纲一的定义本文的计算域中气体流速较低,暂不考虑气体的压缩性[14],文中涉及量纲一的转弯运动时间τ、通气率Cq、空化数σ、弗劳德数Fr、阻力系数CD,空泡量纲一的最大直径D、压力系数Cp分别定义为:
| $ \tau=\frac{t-0.1}{2 {\rm{ \mathsf{ π} }} / \omega}, C_{q}=\frac{Q}{V_{\infty} D_{n}^{2}}, \sigma=\frac{p_{\infty}-p_{\mathrm{c}}}{\frac{1}{2} \rho V^{2}}, F r=\frac{V}{\sqrt{g D_{n}}}, $ |
| $ C_{D}=\frac{F}{\frac{1}{2} \rho V^{2} A}, \bar{D}=\frac{D_{\mathrm{c}}}{D_{n}}, C_{p}=\frac{p}{\frac{1}{2} \rho V^{2}}. $ |
式中:t为空化器运动时间;Q为气体体积流量;Dn为空化器直径;g为重力加速度;ω为空化器转弯过程的角速度;Q为气体体积流量;p∞为流域远场压力;pc为空泡内压力;ρ为流体密度;V为空化器运动速度;F为空化器在运动过程中所受到的阻力;A为空化器的面积;Dc为空泡最大直径.
1.3 动网格技术动网格模型可用于模拟流体域边界随时间改变的问题[15].本文利用动态网格技术,令整个计算网格区域在xoy平面上作刚体运动,区域节点之间没有相对位移,航行体的运动方式如图 1所示(以向上回转运动为例),空化器先进行直线运动,待空化器的空泡形态相对稳定后,令航行体以半径R在纵平面进行回转运动.

|
图 1 空化器运动方式 Fig. 1 Movement of cavitator |
水洞实验是研究超空泡形态的一种有效的方法.Cao等[16]利用水洞实验对空化器的空泡形态进行研究,得到了稳定的空泡形态及与之对应的空化数σ.为验证本文数值方法的可靠性,根据实验条件对Fr=18和Cq=0.15工况下,空化器直径Dn=20 mm的模型进行数值计算,并与实验结果进行比较,如图 2所示.

|
图 2 实验和数值模拟结果比较 Fig. 2 Comparison of experimental and numerical results |
比较两种方法下空泡的最大空泡直径Dcmax和半长Lhalf,其中半长定义为空泡开始和最大直径位置之间的距离,从图 2可以看出数值模拟结果与实验结果吻合良好.从实验结果和模拟结果均可看出空泡随着向下游延伸,空泡尾部闭合位置逐渐开始向上偏移,这是由于在当前流动条件下受到重力效应的影响[17-18].
为进一步验证数值模拟结果,将空泡内同一位置处(P1)的压力对应的空化数σ进行比较.实验中σ为0.20,数值模拟的σ为0.19,数值模拟与实验结果的一致性良好.
为验证本文数值方法在机动性计算方面的可行性,选取文献[19]中的俯仰角1°,角速度10π的航行体周期性俯仰运动工况,根据实验条件对相同尺度模型进行数值计算,得到监测点两个周期内的压力系数Cp变化历程与实验结果对比如图 3所示,两者具有基本相同的变化规律,且两者平均误差在10%以内,满足要求.综上所述,通过数值模拟与实验在空泡尺度与压力系数等方面的对比,验证了本文数值模拟方法的有效性.

|
图 3 压力系数对比 Fig. 3 Pressure coefficient comparison |
本文圆盘空化器模型直径Dn=5 mm,空化器和整体计算域网格的几何尺寸如图 4所示,整个计算域采用六面体结构化网格离散,最小网格尺寸0.2 mm,节点数量约25万,网格质量大于0.5,满足计算要求.计算域的边界条件设置如图 5所示.

|
图 4 计算模型及网格 Fig. 4 Computation model and grids |

|
图 5 计算域及边界条件 Fig. 5 Computational region and boundary conditions |
本文采用动网格模型实现空化器模型的回转运动.计算域的进口、出口以及壁面均设置为压力出口,通气孔则设置为质量流率入口条件,空化器其余部分为壁面条件.计算过程中采用有限体积法对控制方程进行离散,采用“QUICK”格式离散对流项;收敛精度设置为10-6.运动过程中空化器速度v=5 m/s,通气系数Cq=0.4.
计算流域尺度,尤其流域径向尺度对通气空泡的数值研究有很大影响.文献[20]指出当流域的径向尺度足够大时,阻塞效应以及黏性效应可以被忽略.提取上述计算模型下的p∞等值线分布如图 6所示,可以看出压力等值线没有与流域的上、下边界线相交,且前后段分别与水平线相交于流域内部的M点和N点后趋于重合,满足文献[21]中通气多相流计算对流域径向和轴向尺度的无关性要求,使得流域远场压力p∞的取值不受计算域尺度的影响.

|
图 6 数值模拟p∞等值线分布 Fig. 6 The p∞ contour distribution of numerical simulation |
回转过程中空泡形态的变化极易使航行体的沾湿区位置和大小发生改变,进而影响航行体回转过程中的运动稳定性,造成航行体失稳甚至更严重的后果,因此有必要对回转过程中空泡形态进行分析.
空化器直线运动过程中,由于重力作用形成了尾部上漂的水平超空泡,待空泡尺度稳定后利用动网格的方法,实现空化器在纵平面内的回转运动.空化器在不同偏转角α时的空泡形态的侧视图见表 1、2.
| 表 1 空泡形态随向下回转角的变化(R=0.5 m) Tab. 1 Cavity shape changes with the downward turning angle (R=0.5 m) |
| 表 2 空泡形态随向上回转角的变化(R=0.5 m) Tab. 2 Cavity shape changes with the upward turning angle (R=0.5 m) |
由表 1、2可以看出,空化器在纵平面做回转运动时,空泡轴线产生弯曲变形,空泡尾部相对稳定的双涡管泄气现象逐渐消失,逐步演变为单涡管泄气[4].并且随着偏转角度的增大,空泡轴线的弯曲程度逐渐增大,空泡轴线的弯曲变形同空化器的回转轨迹同向.完整航行体在纵平面回转运动过程中,应调整航行体的姿态以避免沾湿区的大幅度变化[6],避免回转运动过程中严重失稳现象的发生.
从表 1、2不难发现转弯运动造成了空泡长细比的改变,文中空泡的长细比定义为
| $ λ=L_{c}/D_{c}, $ |
式中Dc、Lc分别为空泡的最大直径和最大长度.
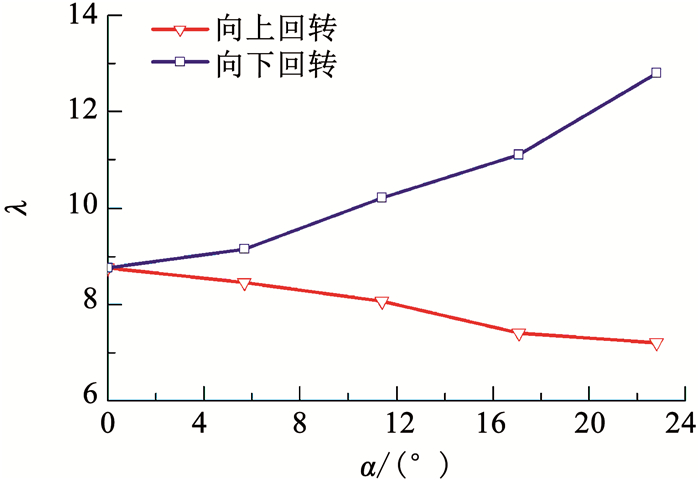
图 7分别给出了偏转角度α变化时空化器向上和向下回转运动时空泡长细比的变化特性.可以看出随偏转角度α的增大,向下回转运动时空泡长细比显著增大,向上回转过程中空泡长细比逐渐减小,且变化趋势相对向下运动平缓,这是因为空化器向上运动时空泡受环境的逆压梯度影响,限制了空泡在长度方向的发展.
|
图 7 不同偏转角度下的空泡长细比 Fig. 7 Slenderness ratio at different deflection angles |
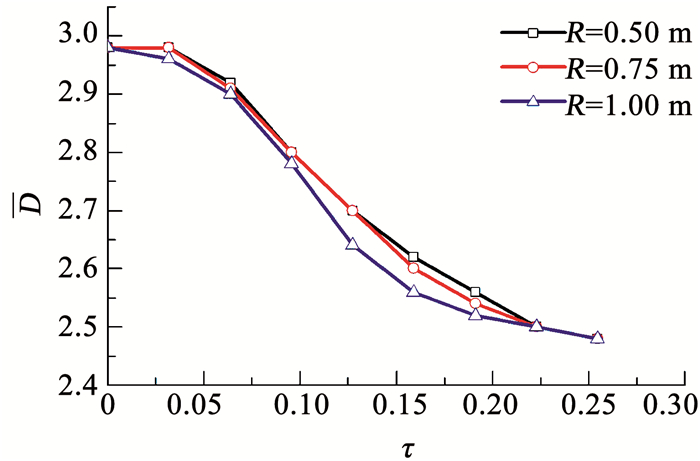
从表 1、2中空泡形态的变化可知空泡最大直径Dc发生了变化,进一步对不同回转半径下空化器纵平面回转运动下空泡的量纲一的最大直径D进行研究.张宇文等[22]利用Logvinovich空泡截面独立膨胀原理研究了考虑水深变化下空化器纵平面回转运动时的空泡最大直径变化规律.本文进一步考虑了空泡轴线沿水深变化的流场压力梯度影响,数值模拟研究了空化器在回转半径R分别为0.50,0.75,1.00 m时的空泡直径,如图 8、9所示.
|
图 8 不同向下回转半径的空泡直径变化 Fig. 8 Cavity diameter changes of different downward turning radii |

|
图 9 不同向上回转半径的空泡直径变化 Fig. 9 Cavity diameter changes of different upwards turning radii |
由图 8、9可知,空化器向下回转过程中,由于重力的作用,空泡的最大直径不断减小,不同回转半径间的最大直径差异较小;空化器向上回转过程中,空泡最大直径不断增大,且向上回转运动时回转半径的变化对空泡最大直径的影响更大.
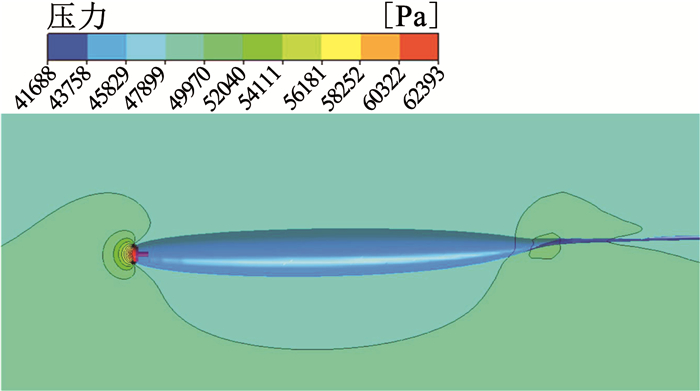
4.2 机动运动过程中的压力场分析通气空泡在水平运动条件下的空泡形态(α1=0.5)以及压力场分布情况如图 10所示.
|
图 10 水平运动下空泡形态及周围压力分布 Fig. 10 Cavity shape and surrounding pressure distribution under horizontal motion |
由图 10可知空化器头部和空泡尾部闭合区域都形成局部高压区.直线运动时空泡上下表面的压力分布如图 11所示,可见在稳定的水平运动条件下,空泡的上、下表面的压力大致相等,空泡尾部由于重力梯度有相对较大的压力差,这也解释了水平直线运动下空泡尾部的上漂现象.

|
图 11 沿空泡轴线位置压力分布情况 Fig. 11 Pressure distribution along the axis of the cavity |
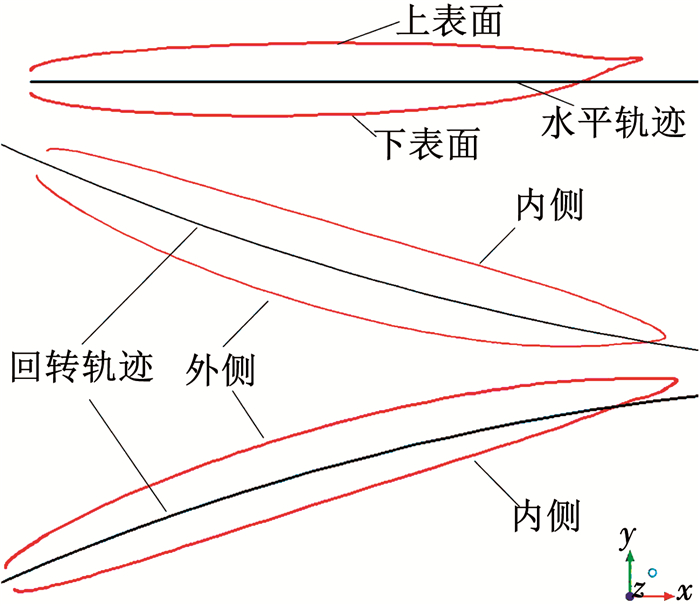
在重力和回转运动的影响下,空化器在纵平面运动中的空泡形态的变化主要受空泡上下表面(水平直线运动)或内外侧(纵平面回转运动)的压力差的影响.为方便分析空泡周围压力和空泡形态之间的关系,图 12给出了纵截面内空泡上、下表面和内、外侧的示意图.
|
图 12 上、下表面及内、外侧的定义 Fig. 12 Schematic of upper and lower surfaces and inner and outer sides |
分析当空化器开始做回转运动后空泡内外侧压力分布情况的关系.由回转运动过程中的空泡形态比较不同转弯角度下空泡形态的比较可知由于空化器在纵平面的回转运动,空泡形态在垂直方向发生了相应的弯曲变形.因此在分析回转过程中空泡内外的压力差时,不再研究压力随水平位置坐标变化的分布情况,而是以空化器在某一回转角度下空泡某一位置相对于垂直方向偏转角度θ为变量,研究空化器在不同偏转角度θ(11.4°、22.8°、34.2°)时的空泡内外两侧压力分布情况,如图 13所示,曲线由左向右分别对应空化器的偏转角度为11.4°、22.8°、34.2°.

|
图 13 沿向下偏转角度的压力分布情况 Fig. 13 Pressure distribution along the downward deflection angle |
图 13给出了空化器在不同回转半径R条件时的向下运动过程中空泡内外两侧压力随偏转角度变化的分布情况,可以看出空泡内侧的压力是高于外侧的,并且这在转弯半径较小的情况下空泡内外侧的压力差值更为明显.分析造成这一现象的原因可以从产生压力差的两个主要方面入手.一是重力梯度的作用使得处于水深较低处的内侧具有更高的压力;由图 13可知,随着空化器回转半径增大,空泡内外两侧的压力差变小,图 8可知空化器向下回转的半径R变化时,空泡最大直径无明显差异,因此回转半径变化时由重力梯度引起的压力差变化较小.二是空泡内外两侧的流速差异大小对压差的影响,根据势流理论,超空泡边界的流体速度v为[8]
| $ v=v_{ ∞} \sqrt {1+σ} , $ |
式中v∞为来流水速.
回转运动过程中,空化器周边的速度是不同的,因此空泡周边的速度大小也不同,内侧表面的速度相对外侧表面的速度要小一些,根据伯努利方程可以得出内侧表面的压力要大于外侧表面的压力.按照势流理论假设流体无粘,可认为空泡内外两侧的角速度相同,大小等于空化器的角速度.3种不同半径下空化器的线速度大小不变,当转弯半径增大时相应的角速度减小,进而产生速度差异.如下式所示,可以看出Δv的变化主要受到D/R的影响.
| $ ω=v/R, ΔR=D, Δv=ωΔR=v \frac{{D}}{{R}} . $ |
式中:ω为空化器的回转角速度;v为空化器的回转线速度;ΔR为同一偏转角度下空泡内外侧的径向距离;D为空泡任一位置处对应的空泡直径大小;Δv为同一偏转角度下空泡内外侧的速度差.
由图 13结果可知,随着空化器回转半径的增大,空泡内外两侧的压力差变小.由图 8可知空化器向下回转的半径R变化时,空泡最大直径无明显差异,因此回转半径变化时由重力梯度引起的压力差变化较小.可以认为压力差变化主要受内外两侧速度差异的影响,从上式分析可知,D/R随回转半径的增大应呈减小的趋势.
为证明上述分析的正确性,图 14给出了空泡最大直径与回转半径相对大小Dc/R在不同回转半径随时间的变化情况,可以看出Dc/R随半径的增大而减小.

|
图 14 不同回转半径和时间下的Dc/R Fig. 14 Dc/R at different rotating radius and time |
从上述分析可知空泡两侧的重力梯度和速度差异使空泡内外侧产生压力差,空泡内外侧的压力差形成沿回转半径方向的合力,即运动过程中的离心力.离心力的存在使空泡的形态发生变化,引起空泡的变形及空泡的尾部外漂,尾部位于回转轨迹的外侧.
图 15给出了向上回转运动过程中空化器在不同偏转角度θ(11.4°、22.8°、34.2°)时的空泡内外两侧的压力分布情况,曲线由左向右分别对应空化器的偏转角度为11.4°、22.8°、34.2°.

|
图 15 沿向上偏转角度的压力分布情况 Fig. 15 Pressure distribution along the upward deflection angle |
从图 15可以发现,相比于图 13中空化器向下回转运动过程中空泡内外侧所形成的较大压力差,空化器向上的回转运动中,空泡内外侧的压力差几乎为零,这与上文所述的形成内外侧的压力差的两个原因所形成的压力差方向相反有关,两个方向的压力差起到了中和的作用.因此在所列举的角度范围内空化器向上回转运动产生的离心力也相对很小.可以看出空泡尾部也没有如空化器向下回转运动过程明显的外漂现象,而是在回转开始的阶段由于空泡的迟滞性影响,空泡尾部在回转轨迹的内侧,随着回转角度的增大,空泡轴线逐渐与回转轨迹重合.
向下回转运动回转轨迹两侧空泡较大的压力差也解释了空泡向下回转过程中长细比逐渐增大且变化较为明显的现象.而向上回转过程中内外两侧的压力差接近为零且受逆压梯度的限制,也就有了相应较为平缓减小的长细比.较大的压力差往往意味着空泡较大的形态变化,这意味着在航行体向下回转过程比向上回转过程更需要及时通过调整航行体的姿态或通气系数等方式来控制沾湿区的变化,进而保证航行体回转运动的稳定性.
5 结论1) 空化器做纵平面回转运动后,原本稳定的空泡形态发生变形,空泡轴线与回转轨迹大致吻合.向下回转时空泡的最大直径逐渐减小,向上回转时最大直径逐渐增大.需要及时采取一定的措施,如调整运动航行体的姿态、航行速度和通气系数等,来避免航行体沾湿区大幅度变化产生的运动失稳.
2) 纵平面回转运动使得空泡由于速度差异和重力梯度的原因在回转轨迹内外两侧产生压力差,形成垂直于回转轨迹方向的离心力造成了纵平面回转运动时空泡尾部闭合位置的偏转,向下回转时空泡尾部的外漂和向上小角度回转时空泡尾部的内漂.
3) 空化器向下回转运动时回转轨迹空泡两侧较大的压力差使空泡回转过程中长细比显著增大;而向上回转过程中内外两侧的压力差接近为零,并受逆压梯度的限制,空泡长细比平缓减小,随着回转角度的增大,空泡轴线逐渐与回转轨迹重合.
| [1] |
NESTERUK I. Supercavitation[M]. Berlin, Heidelberg: Springer-Verlag, 2012. DOI:10.1007/978-3-642-23656-3
|
| [2] |
李凝, 杨飚. 德国轻型超空泡鱼雷研发现状及展望[J]. 鱼雷技术, 2008, 16(2): 1. LI Ning, YANG Biao. R & Dstatus quo and perspective of lightweight supercavitating torpedo in Germany[J]. Torpedo Technology, 2008, 16(2): 1. DOI:10.3969/j.issn.1673-1948.2008.02.001 |
| [3] |
张广, 于开平, 周景军. 转弯运动通气超空泡形态及流场结构数值研究[J]. 船舶力学, 2011, 15(12): 1335. ZHANG Guang, YU Kaiping, ZHOU Jingjun. Numerical research on ventilated supercavity shape and flow structure in the turning motion[J]. Journal of Ship Mechanics, 2011, 15(12): 1335. DOI:10.3969/j.issn.1007-7294.2011.12.001 |
| [4] |
张广, 于开平, 周景军. 通气空泡重力效应三维数值仿真研究[J]. 工程力学, 2012, 29(8): 366. ZHANG Guang, YU Kaiping, ZHOU Jingjun. Three dimensional numerical simulation on the gravity effect of ventilated cavity[J]. Engineering Mechanics, 2012, 29(8): 366. DOI:10.6052/j.issn.1000-4750.2010.11.0844 |
| [5] |
李振旺.水下高速航行体机动运动非定常超空泡数值模拟[D].哈尔滨: 哈尔滨工业大学, 2013 LI Zhenwang. Transient numerical study on maneuverable motion of high speed supercavitating vehicles[D]. Harbin: Harbin Institute of Technology, 2013 http://cdmd.cnki.com.cn/Article/CDMD-10213-1014003705.htm |
| [6] |
王威, 王聪, 魏英杰. 超空泡航行体转弯运动多相流场特性[J]. 哈尔滨工业大学学报, 2018, 50(10): 124. WANG Wei, WANG Cong, WEI Yingjie. Multiphase flow characteristics of supercavitating vehicle in the tuning motion[J]. Journal of Harbin Institute of Technology, 2018, 50(10): 124. DOI:10.11918/j.issn.0367-6234.201609075 |
| [7] |
黄小腾.锥形空化器航行体非定常流体动力特性研究[D].哈尔滨: 哈尔滨工业大学, 2012 HUANG Xiaoteng. Research on unsteady hydrodynamics of supercaviting vehicle with conical cavitator[D]. Harbin: Harbin Institute of Technology, 2012 http://cdmd.cnki.com.cn/Article/CDMD-10213-1013037272.htm |
| [8] |
李其弢.通气超空泡航行体水下摆动运动试验与模拟[D].上海交通大学, 2009 LI Qitao. Experimental investigations and simulations to the ventilated supercavitating flows on dynamic model manipulated with pitching motion[D]. Shanghai: Shanghai Jiaotong University, 2009 http://d.old.wanfangdata.com.cn/Thesis/Y1836242 |
| [9] |
潘展程.通气超空泡流动结构与稳定性研究[D].上海交通大学, 2013 PAN Zhancheng. Study on the stability and flow structure of ventilated supercavitating flow[D]. Shanghai: Shanghai Jiaotong University, 2013 http://cdmd.cnki.com.cn/Article/CDMD-10248-1015807755.htm |
| [10] |
周景军.通气超空泡流动及航行体流体动力数值模拟研究[D].哈尔滨: 哈尔滨工业大学, 2011 ZHOU Jingjun. Numerical simulation study on the ventilated supercavitating flow and hydrodynamics of vehicle[D]. Harbin: Harbin Institute of Technology, 2011 http://cdmd.cnki.com.cn/Article/CDMD-10213-1012000458.htm |
| [11] |
HIRT C W, NICHOLS B D. Volume of fluid (VOF) method for the dynamics of free boundaries[J]. Journal of Computational Physics, 1981, 39(1): 201. DOI:10.1016/0021-9991(81)90145-5 |
| [12] |
陈鑫.通气空泡流研究[D].上海: 上海交通大学, 2006 CHEN Xin. An investigation of the ventilated cavitatingflow[D]. Shanghai: Shanghai Jiaotong University, 2006 http://cdmd.cnki.com.cn/Article/CDMD-10248-2006194531.htm |
| [13] |
LAUNDER B E, SPALDING D B. Lectures in mathematical models of turbulence[M]. New York: Academic Press, 1972.
|
| [14] |
贾力平.空化器诱导超空泡特性的数值仿真与实验研究[D].哈尔滨: 哈尔滨工业大学, 2007 JIA Liping. Numerical simulation and experimental study on supercavity characteristic induced by cavitators[D]. Harbin: Harbin Institute of Technology, 2007 http://cdmd.cnki.com.cn/Article/CDMD-10213-2008193149.htm |
| [15] |
马庆鹏, 魏英杰, 王聪, 等. 不同头型运动体高速入水空泡数值模拟[J]. 哈尔滨工业大学学报, 2014, 46(11): 24. MA Qingpeng, WEI Yingjie, WANG Cong, et al. Numerical simulation of high speed water entry cavity of cylinders[J]. Journal of Harbin Institute of Technology, 2014, 46(11): 24. DOI:10.11918/j.issn.0367-6234.2014.11.004 |
| [16] |
CAO Lei, KARN A, ARNDT R E A, et al. Numerical investigations of pressure distribution inside a ventilated supercavity[J]. Journal of Fluids Engineering, 2017, 139(2): 1. DOI:10.1115/1.4035027 |
| [17] |
陈伟政, 张宇文, 袁绪龙, 等. 重力场对轴对称体稳定空泡形态影响的实验研究[J]. 西北工业大学学报, 2004, 22(3): 274. CHEN Weizheng, ZHANG Yuwen, YUAN Xulong, et al. Experimental study of the influence of gravity field on the shapes of axially symmetric steady cavity[J]. Journal of Northwestern Polytechnical University, 2004, 22(3): 274. DOI:10.3969/j.issn.1000-2758.2004.03.003 |
| [18] |
袁绪龙, 张宇文, 王育才, 等. 水下航行体通气超空泡非对称性研究[J]. 力学学报, 2004, 36(2): 146. YUAN Xulong, ZHANG Yuwen, WANG Yucai, et al. On asymmetry of ventilated supercavity of underwater vehicle[J]. Chinese Journal of Theoretical and Applied Mechanics, 2004, 36(2): 146. DOI:10.3321/j.issn:0459-1879.2004.02.003 |
| [19] |
PAN Zhancheng, LU Chuanjing, CHEN Ying, et al. Numerical study of periodically forced-pitching of a supercavitating vehicle[J]. Journal of Hydrodynamics, 2010, 22(5): 899. |
| [20] |
ZHOU Jingjun, YU Kaiping, MIN Jingxin, et al. The comparative study of ventilated super cavity shape in water tunnel and infinite flow field[J]. Journal of Hydrodynamics, 2010, 22(5): 689. DOI:10.1016/s1001-6058(09)60104-9 |
| [21] |
WANG Wei, WANG Cong, WEI Yingjie, et al. A study on the wake structure of the double vortex tubes in a ventilated supercavity[J]. Journal of Mechanical Science and Technology, 2018, 32(4): 1601. DOI:10.1007/s12206-018-0315-5 |
| [22] |
张宇文, 袁绪龙, 邓飞. 超空泡航行体流体动力学[M]. 北京: 国防工业出版社, 2014. ZHANG Yuwen, YUAN Xulong, DENG Fei. Fluid dynamics of supercavitating vehicle[M]. Beijing: National Defense Industry Press, 2014. |
 2019, Vol. 51
2019, Vol. 51












