2. 哈尔滨工业大学 航天学院, 哈尔滨 150001;
3. 中国运载火箭技术研究院 研究发展中心, 北京 100076
2. School of Astronautics, Harbin Institute of Technology, Harbin 150001, China;
3. R & D Center, China Academy of Launch Vehicle Technology, Beijing 100076, China
天梯系统作为一种能够持续使用兼顾高效、低成本的空间运输系统,主要由绳索、天顶锚、攀爬器组成.天梯系统可以视为空间绳系卫星的一种特殊版本,其绳索需要承受巨大的张力, 是天梯系统的关键组成部分[1],而碳纳米管是目前最有希望的材料[2].天梯绳索构型的计算基本采用均匀应力设计原则,这使其截面具有锥度变化的特点[3-5].自Edwards[6]、汪小卫等[7-8]较为全面系统地分析和总结了天梯的概念、组成、特点以及关键技术和可行性后.针对天梯系统的研究在国内外逐渐火热起来.在研究过程中,为体现绳索柔性和黏弹性的特点,基于集中质量法建立的弹簧质点模型[9-11]是广泛采用的柔性绳索模型.此类高维系统模型可以很好地计算出绳索的振形、模态,更接近真实绳索[12],但是其动力学与控制问题的研究比较困难.为此,很多学者为了研究天梯系统动力学的基础特性,忽略了绳索柔性与黏弹性,将绳索简化为理想的刚性绳索模型[3, 13-15],在系统的动力学响应以及振动抑制等方面获得了很多具有指导意义的成果.其中具有代表性的如:Cohen等[3, 14]建立一个较完善刚性绳索的系统模型,研究了攀爬器的运动对绳索造成的纵向振荡和横向振荡,以及对海面浮动锚固平台的扰动影响;Williams等[15]采用高斯伪普法对攀爬器的爬升过程速度优化,来抑制绳索的振荡.
从目前的研究现状来看,攀爬器的运动对系统动力学响应以及绳索振动抑制问题一直是研究的重点.但诸如系统稳定性一直没有详尽的论证,尽管Beletskii等[13]研究了天梯系统赤道面内零点附近的稳定性问题,但其模型过于简单,仅论证了面内摆动稳定性.其次,虽然通过对攀爬器的速度优化控制可以实现抑制系统残余振荡, 但Cohen等[14]在分析时假设攀爬器的加速段和减速段时间相等的原因,没有对攀爬器具体在加速、匀速还是减速阶段对系统残余振荡抑制效果最佳做出详细说明.
为论证赤道天梯系统在赤道面内外的稳定性特征以及攀爬器的运动对系统残余振荡的抑制规律,本文采用拉格朗日方法,建立了一个比较完善两自由度的刚性绳索模型,基于小角度摆动假设,对其拓扑等价的线性化系统的平衡点进行稳定性分析,最后引入加速时间比和减速时间比两个参数详细分析攀爬器各个阶段对系统的残余振荡抑制效果.
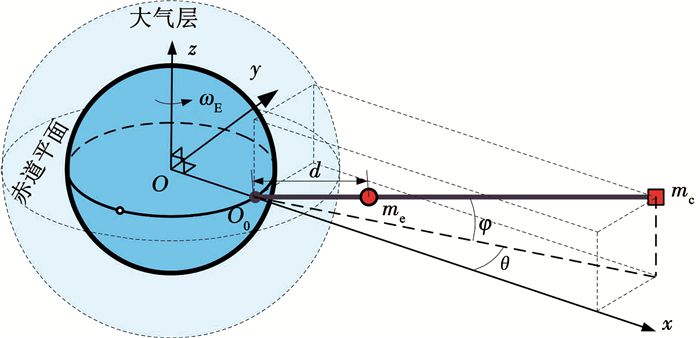
1 天梯系统动力学建模由于攀爬器以及天顶锚的体积相对整个绳索来说可以忽略不计,将攀爬器和天顶锚视为质点,系统的模型如图 1所示.天顶锚的质量为mc,位于绳索的末端,绳索的长度为l,质量为me的攀爬器以
|
图 1 赤道天梯系统刚性绳索模型 Fig. 1 Rigid tether model of equatorial space elevator system |
建立地表旋转坐标系O0-xyz:定义绳索的锚固点O0为旋转坐标系的原点,x轴沿当地铅垂线指向外太空;y、x轴构成地球赤道平面,方向与锚固点的线速度方向相同;z轴垂直于赤道平面,与x、y轴构成右手系.绳索与垂直位置的夹角为θ(面内摆动角),绳索与垂直位置在垂直于赤道面的夹角为φ(面外摆动角).
为建立系统的动力学方程,令攀爬器、天顶锚以及绳索微元在地心旋转坐标系中的位移分别为re、rc和r(s),其中s为任意位置处绳索微元至锚固点的距离.攀爬器的位移的表达式为
| $ \begin{array}{l} {\mathit{\boldsymbol{r}}_{\rm{e}}} = \left( {{R_{\rm{E}}} + d\cos \theta \cos \varphi } \right)\mathit{\boldsymbol{i}} + \\ \;\;\;\;\;\;(d\sin \theta \cos \varphi )\mathit{\boldsymbol{j}} + (d\sin \varphi )\mathit{\boldsymbol{k}}, \end{array} $ | (1) |
式中i、j、k分别为沿x、y、z轴的单位向量.通过对式(1)求导,得攀爬器在绳索上的运动速度为
| $ \begin{array}{l} {{\mathit{\boldsymbol{\dot r}}}_{\rm{e}}} = [\dot d\cos \theta \cos \varphi - (\dot \theta + \omega )d\sin \theta \cos \varphi - \dot \varphi d\cos \theta \sin \varphi ]\mathit{\boldsymbol{i}} + \\ \;\;\;\;\;\;\left[ {\dot d\sin \theta \cos \varphi + \dot \theta d\cos \theta \cos \varphi + \omega \left( {{R_{\rm{E}}} + d\cos \theta \cos \varphi } \right) - } \right.\\ \;\;\;\;\;\;\dot \varphi d\sin \theta \sin \varphi ]\dot j + (\dot d\sin \varphi + \dot \varphi d\cos \varphi )\mathit{\boldsymbol{k}}. \end{array} $ | (2) |
天顶锚和绳索微元的速度表达式与式(2)具有相同的形式,只需令l、s分别代替式中参数d.注:式中
| $ \begin{array}{l} K = \frac{1}{2}{m_{\rm{e}}} \cdot {{\mathit{\boldsymbol{\dot r}}}_{\rm{e}}} \cdot {{\mathit{\boldsymbol{\dot r}}}_{\rm{e}}} + \frac{1}{2}{m_{\rm{c}}} \cdot {{\mathit{\boldsymbol{\dot r}}}_{\rm{c}}} \cdot {{\mathit{\boldsymbol{\dot r}}}_{\rm{c}}} + \\ \;\;\;\;\;\;\frac{1}{2}\int_0^l \rho (s){{\mathit{\boldsymbol{\dot r}}}_{\rm{s}}} \cdot {{\mathit{\boldsymbol{\dot r}}}_{\rm{s}}}{\rm{d}}s. \end{array} $ | (3) |
式中:ρ(s)=γA(s)为绳索的线性密度;γ为绳索材料的密度,绳索的截面积A(s)采用Pearson[1]给出的计算公式为
| $ A(s) = {A_{\rm{m}}}\exp \left\{ {\frac{{\gamma \mu }}{{{\sigma _0}{R_{\rm{G}}}}}\left[ {\frac{3}{2} - \frac{{{R_{\rm{G}}}}}{{{R_{\rm{E}}} + s}} - \frac{{{{\left( {{R_{\rm{E}}} + s} \right)}^2}}}{{2R_{\rm{G}}^2}}} \right]} \right\}. $ |
其中:Am为GEO轨道处绳索截面积; RG为GEO轨道半径; σ0为绳索设计应力.系统受到的势能为
| $ \begin{array}{l} V = - \frac{{\mu {m_{\rm{e}}}}}{{\sqrt {R_{\rm{E}}^2 + 2{R_{\rm{E}}}d\cos \theta \cos \varphi + {d^2}} }} - \\ \;\;\;\;\;\frac{{\mu {m_{\rm{c}}}}}{{\sqrt {R_{\rm{E}}^2 + 2{R_{\rm{E}}}l\cos \theta \cos \varphi + {l^2}} }} - \\ \;\;\;\;\;\int_0^l {\frac{{\mu \rho (s)}}{{R_{\rm{E}}^2 + 2{R_{\rm{E}}}s\cos \theta \cos \varphi + {s^2}}}{\rm{d}}s} , \end{array} $ | (4) |
式中μ为地球引力常数.
将式(3)、(4)代表的系统动能及势能表达式,代入拉格朗日方程,可以求得系统的动力学方程.其中,选取θ、φ为广义坐标.对于系统所受到的非保守力仅考虑绳索在摆动过程中受到的大气阻力.由于绳索的摆动是一个低速运动的过程,绳索微元受到的空气阻力dF与阻力系数k、迎风面积dS以及微元的速度v成正比,即dF=kvdS,其中,阻力系数k与大气密度有关,微元速度v=
| $ \mathit{\boldsymbol{F}} = \left[ {\begin{array}{*{20}{c}} {\dot \theta \int {{k_1}} {S_1}s{\rm{d}}s}\\ {\dot \varphi \int {{k_2}} {S_2}s{\rm{d}}s} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{c_1}\dot \theta }\\ {{c_2}\dot \varphi } \end{array}} \right], $ |
式中c1、c2分别为绳索面内、外摆动阻力系数.
通过拉格朗日方程求解,可得刚性绳索天梯系统动力学方程:
| $ \begin{array}{l} \ddot \theta = - \frac{{2{m_{\rm{e}}}d\dot d(\dot \theta + \omega )}}{{{M_1}}} - \frac{{{c_1}}}{{{M_1}{{\cos }^2}\varphi }}\dot \theta + \\ \;\;\;\;\;\;2\dot \varphi (\dot \theta + \omega )\tan \varphi - \frac{{{M_2}{R_{\rm{E}}}{\omega ^2}\sin \theta }}{{{M_1}\cos \varphi }} + \\ \;\;\;\;\;\;\begin{array}{*{20}{l}} {\frac{{\mu {R_{\rm{E}}}\sin \theta }}{{{M_1}\cos \varphi }}\left[ {\frac{{{m_{\rm{c}}}l}}{{{{\left( {R_{\rm{E}}^2 + 2{R_{\rm{E}}}l\cos \theta \cos \varphi + {l^2}} \right)}^{\frac{3}{2}}}}} + } \right.}\\ {\frac{{{m_{\rm{e}}}d}}{{{{\left( {R_{\rm{E}}^2 + 2{R_{\rm{E}}}d\cos \theta \cos \varphi + {d^2}} \right)}^{\frac{3}{2}}}}} + } \end{array}\\ \left. {\;\;\;\;\;\;\int_0^l {\frac{{\rho (s)s}}{{{{\left( {R_{\rm{E}}^2 + 2{R_{\rm{E}}}s\cos \theta \cos \varphi + {s^2}} \right)}^{\frac{3}{2}}}}}{\rm{d}}s} } \right]. \end{array} $ | (5) |
| $ \begin{array}{l} \ddot \varphi = - 2\frac{{{m_{\rm{e}}}d\dot d}}{{{M_1}}}\varphi - \frac{{{c_2}}}{{{M_1}}}\dot \varphi - {(\dot \theta + \omega )^2}\cos \varphi \sin \varphi - \\ \;\;\;\;\;\;\frac{{{M_2}}}{{{M_1}}}{\omega ^2}{R_{\rm{E}}}\cos \theta \sin \varphi + \\ \;\;\;\;\;\;\frac{{\mu {R_{\rm{E}}}\cos \theta \sin \varphi }}{{{M_1}}}\left[ {\frac{{{m_{\rm{c}}}l}}{{{{\left( {R_{\rm{E}}^2 + 2{R_{\rm{E}}}l\cos \theta \cos \varphi + {l^2}} \right)}^{\frac{3}{2}}}}} + } \right.\\ \;\;\;\;\;\;\frac{{{m_{\rm{e}}}d}}{{{{\left( {R_{\rm{E}}^2 + 2{R_{\rm{E}}}d\cos \theta \cos \varphi + {d^2}} \right)}^{\frac{3}{2}}}}} + \\ \left. {\;\;\;\;\;\;\int_0^l {\frac{{\rho (s)s}}{{{{\left( {R_{\rm{E}}^2 + 2{R_{\rm{E}}}s\cos \theta \cos \varphi + {s^2}} \right)}^{\frac{3}{2}}}}}{\rm{d}}s} } \right]. \end{array} $ | (6) |
其中:
| $ {M_1} = {m_{\rm{e}}}{d^2} + {m_{\rm{c}}}{l^2} + \int_0^l \rho (s){s^2}{\rm{d}}s, $ |
| $ {M_2} = {m_{\rm{e}}}d + {m_{\rm{c}}}l + \int_0^l \rho (s)s{\rm{d}}s. $ |
由式(5)、(6)可以看出,随着攀爬器的运动,天梯系统可以看成是一个变阻尼、变刚度的强迫振动系统.
2 系统稳定性分析该复杂动力学系统具有的强非线性特征,使其不具有解析精确解.因此在对系统进行近似定量分析前有必要对其进行充分的定性分析.本文首先将系统动力学方程转化为相对应的一阶微分方程组形式;其次通过对其线性化系统的双曲特征进行判断,确认近似系统与原系统在平衡点附近的拓扑等价性;最后基于两系统的拓扑等价性,通过对双曲型线性系统进行稳定性分析进而间接得到原系统的稳定性特征.
假设天梯系统是在一个小角度范围内做摆动运动,则可以认为cos θ≈1和cos φ≈1.令x1=θ,x2=
| $ \left\{ {\begin{array}{*{20}{l}} {{{\dot x}_1} = {x_2},}\\ {{{\dot x}_2} = - \frac{{{c_1}}}{{{M_1}}}{x_2} - {J_1}\sin {x_1} + 2{x_4}\left( {{x_2} + \omega } \right)\sin {x_3},}\\ {{{\dot x}_3} = {x_4},}\\ {{{\dot x}_4} = - \frac{{{c_2}}}{{{M_1}}}{x_4} - {J_2}\sin {x_3} - {x_2}\left( {{x_2} + 2\omega } \right)\sin {x_3},} \end{array}} \right. $ | (7) |
其中:
| $ {M_3} = \frac{{{m_{\rm{e}}}l}}{{{{\left( {{R_{\rm{E}}} + l} \right)}^3}}} + \frac{{{m_{\rm{e}}}d}}{{{{\left( {{R_{\rm{E}}} + d} \right)}^3}}} + \int_0^l {\frac{{\rho \left( s \right)s}}{{{{\left( {{R_{\rm{E}}} + s} \right)}^3}}}{\rm{d}}s} , $ |
| $ {J_1} = \frac{{{M_2}{\omega ^2} - {M_3}\mu }}{{{M_1}}}{R_{\rm{E}}},{J_2} = {J_1} + {\omega ^2}. $ |
上述动力学方程是一个互相耦合的4个一阶非线性动力学方程,原点是方程组的奇点.在奇点x0附近对式(7)线性化.线性化系统与原系统具有相同稳定性特征的充分条件即为,两系统在平衡点附近拓扑等价,而拓扑等价判定的充要条件则为该线性近似系统为双曲系统.则线性化后系统的荣斯基阵为
| $ \underline {\mathit{\boldsymbol{{A}}}} = {\left. {\frac{{\partial \underline f }}{{\partial \underline x }}} \right|_{\underline x = {{\underline x }_0}}} = \left[ {\begin{array}{*{20}{c}} \lambda &1&0&0\\ {{J_1}}&{\lambda + {c_1}/{M_1}}&0&0\\ 0&0&\lambda &1\\ 0&0&{{J_2}}&{\lambda + {c_2}/{M_1}} \end{array}} \right]. $ |
由系统的荣斯基阵可以获得四阶特征方程式为
| $ \begin{array}{*{20}{c}} {{\lambda ^4} + \frac{{{c_1} + {c_2}}}{{{M_1}}}{\lambda ^3} - \left( {{J_1} + {J_2} - \frac{{{c_1}{c_2}}}{{M_1^2}}} \right){\lambda ^2} - }\\ {\left( {{J_2}\frac{{{c_1}}}{{{M_1}}} + {J_1}\frac{{{c_2}}}{{{M_1}}}} \right)\lambda + {J_1}{J_2} = 0.} \end{array} $ | (8) |
对特征方程式(8)求解,得到线性化后系统的4个特征根为:
| $ {\lambda _{1,2}} = - \frac{1}{2}\left( {\frac{{{c_1}}}{{{M_1}}}} \right) \pm \frac{1}{2}\sqrt {{{\left( {\frac{{{c_1}}}{{{M_1}}}} \right)}^2} - 4{J_1}} , $ |
| $ {\lambda _{3,4}} = - \frac{1}{2}\left( {\frac{{{c_2}}}{{{M_1}}}} \right) \pm \frac{1}{2}\sqrt {{{\left( {\frac{{{c_2}}}{{{M_1}}}} \right)}^2} - 4{J_2}} . $ |
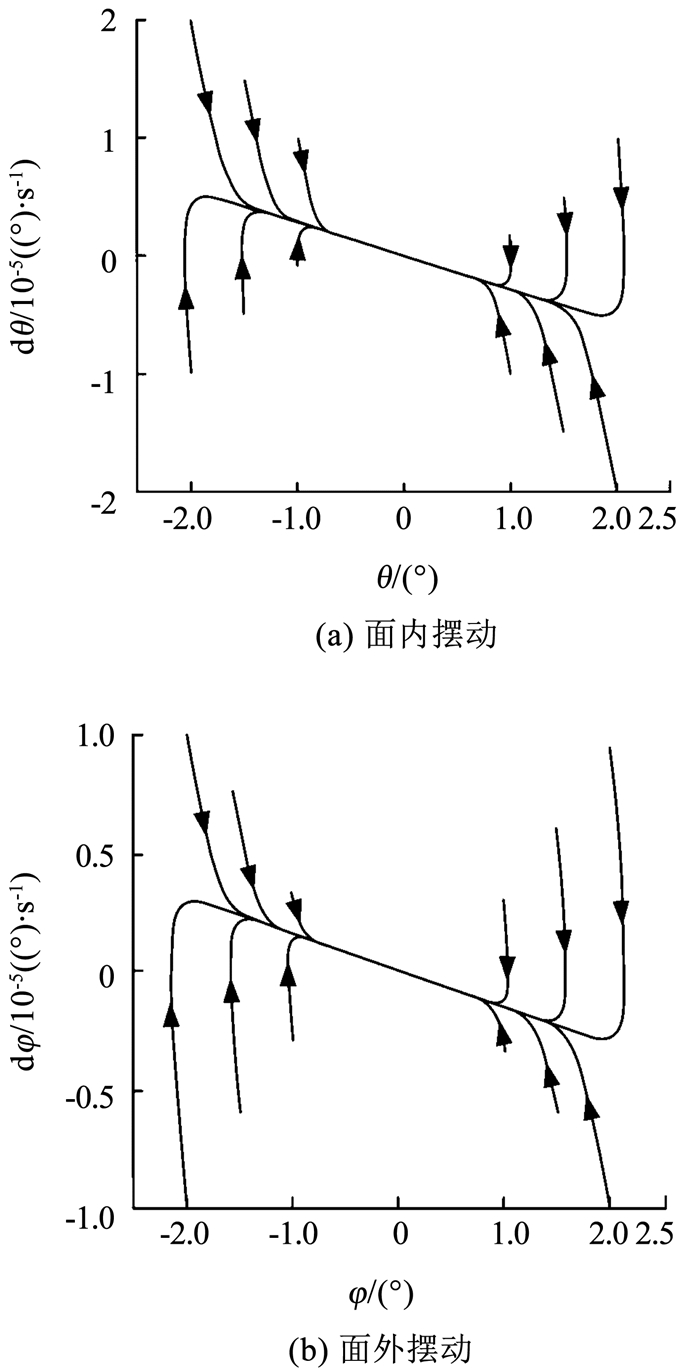
图 2~4给出了大气阻尼取不同数值时,系统面内、外摆动在奇点附近的相图.绳索材料参数见表 1.
|
图 2
系统相图(c1/M1=5 |

|
图 3
系统相图(c1/M1=2 |
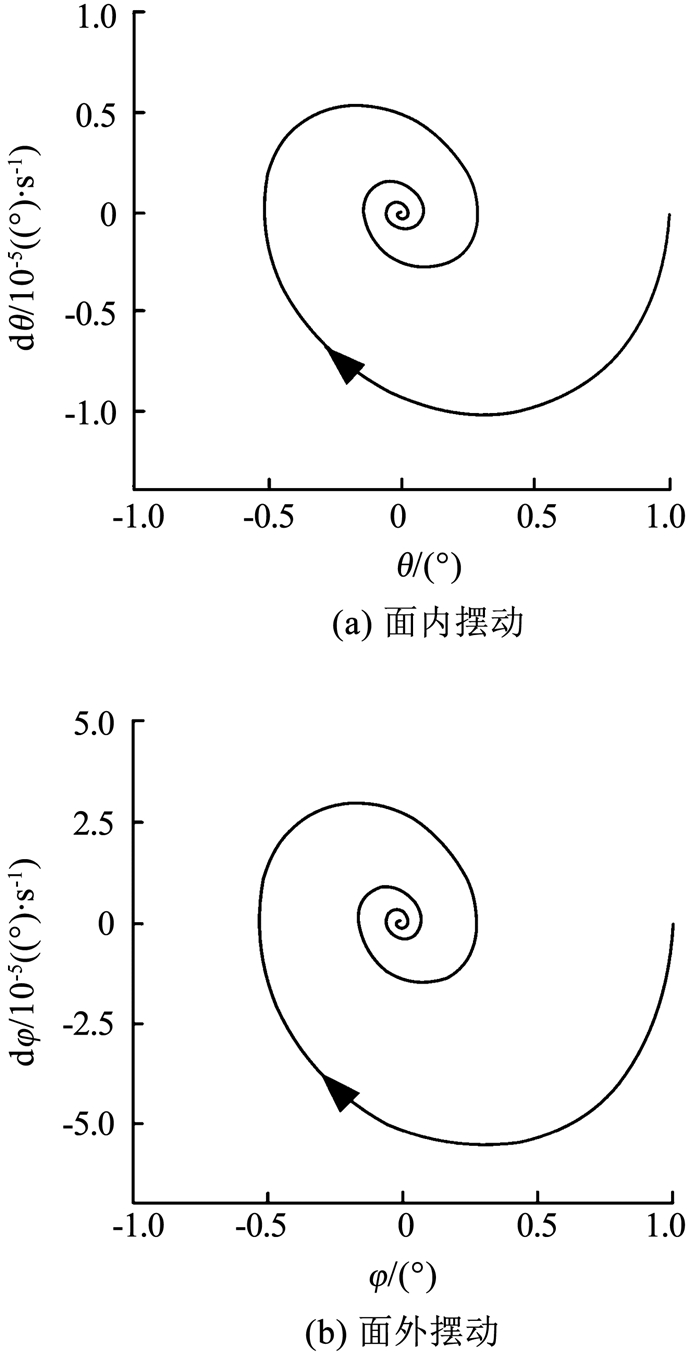
|
图 4
系统相图(c1/M1=2/5 |
| 表 1 绳索材料参数 Tab. 1 Parameters of tether material |
结合线性系统的相图 2~4,分析此系统特征值,可以归纳为如下4种情况:
1) 若(c1/M1)2-4J1>0,(c2/M1)2-4J2>0,则特征方程的根为4个相异的负实根,奇点为稳定结点,故而非线性方程组(7)的零解是渐进稳定的;
2) 若(c1/M1)2-4J1=0,(c2/M1)2-4J2=0,则特征方程的根为两两相等的负实根,奇点为稳定的退化结点,非线性方程组(7)的零解是渐进稳定的;
3) 若(c1/M1)2-4J1 < 0,(c2/M1)2-4J2 < 0,则特征方程的根为两对带负实部的共轭复根,奇点为稳定焦点,非线性方程组的零解为渐进稳定的;
4) 若c1=c2=0,则特征方程的根为两对实部为零的共轭复根λ1, 2=±i
可以发现,当阻力不为零时系统不存在零实部特征根,线性化系统与原系统拓扑等价,即当考虑阻力的情况下线性化系统与原系统在平衡点附近稳定性特征相同.即原非线性系统具有渐进稳定性特征.
3 系统动力学响应分析一般来说,增大攀爬器的质量以及巡航速度会增大系统的残余振荡,但是这与经济性、效率以及其他任务需求相违背.在本文中,探讨了一种攀爬器运输方案,提出一种近似时间比的被动控制方法,使得攀爬器的运动对系统产生的残余振动的影响最小化.
3.1 攀爬器运动规律预测为检验攀爬器的运动对系统造成的扰动影响,其运动规律

|
图 5 攀爬器的速度加载规律 Fig. 5 Velocity profile of climber |
攀爬器运动的表达式可以通过参数Ta、Tc、Td和vc来定义,其表达式为
| $ \dot d(t) = \left\{ {\begin{array}{*{20}{l}} {\frac{{{v_{\rm{c}}}}}{2}\left[ {1 - \cos \left( {\frac{{{\rm{ \mathsf{ π} }}t}}{{{T_{\rm{a}}}}}} \right)} \right],0 \le t \le {T_{\rm{a}}};}\\ {{v_{\rm{c}}},{T_{\rm{a}}} \le t \le {T_{{\rm{ac}}}};}\\ {\frac{{{v_{\rm{c}}}}}{2}\left\{ {1 - \cos \left[ {\frac{{{\rm{ \mathsf{ π} }}\left( {t - {T_{{\rm{ac}}}} + {T_{\rm{d}}}} \right)}}{{{T_{\rm{d}}}}}} \right]} \right\},{T_{{\rm{ac}}}} \le t \le {T_{{\rm{ad}}}}.} \end{array}} \right. $ | (9) |
攀爬器的加速度可以对式(9)微分获得.为了便于进行参数分析,引进加速时间比kac=Ta/Tc和减速时间比kdc=Td/Tc,作为研究系统响应的重要参数.攀爬器到达预定轨道的运动规律可以通过参数Tad、kac、kdc、vc和HT计算获得:
| $ {v_{\rm{c}}}{T_{{\rm{ad}}}} = \frac{{2{H_{\rm{T}}}\left( {1 + {k_{{\rm{ac}}}} + {k_{{\rm{dc}}}}} \right)}}{{2 + {k_{{\rm{ac}}}} + {k_{{\rm{dc}}}}}}. $ | (10) |
式(9)、(10)用来设计攀爬器的运动规律.如果攀爬器处于爬升状态,则vc>0;相反,返回时vc < 0.
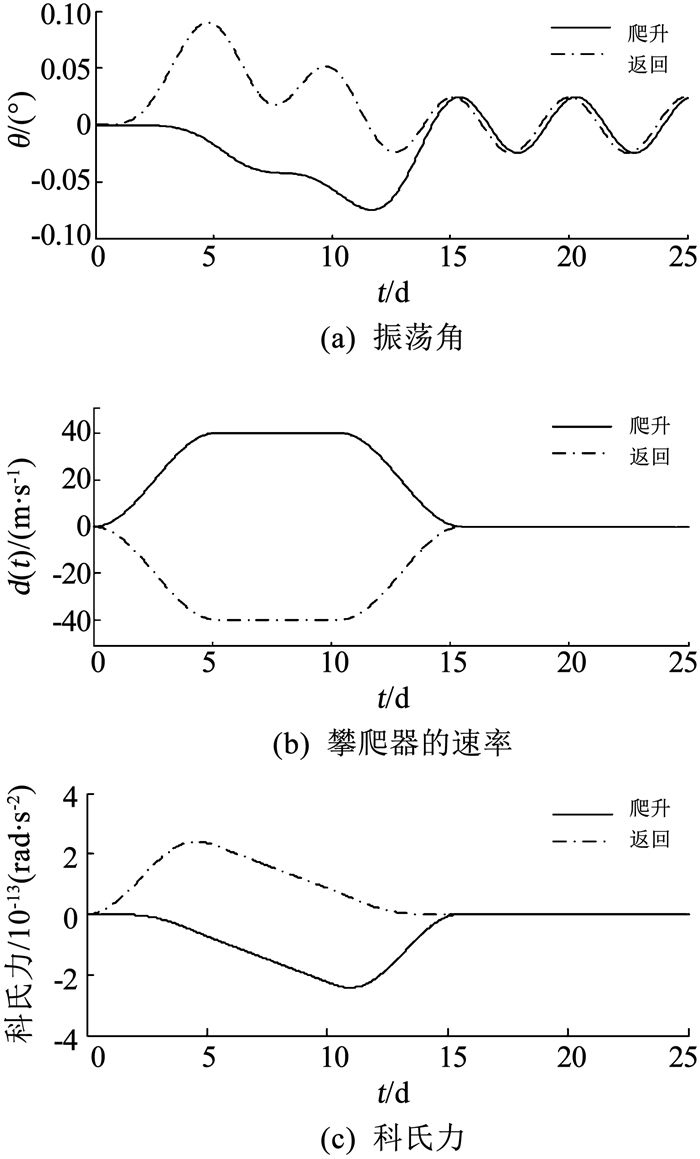
图 6分别给出了攀爬器从地球表面沿绳索爬升至GEO轨道以及从GEO轨道返回地表过程中,系统的振荡响应.仿真采用ODE45积分方法求解系统的动力学方程(6),绳索参数见表 1,攀爬器的质量采用极限质量为16 t,巡航速度vc=40 m/s (即vc=144 km/h),时间比kac=kdc=1.
|
图 6 攀爬器爬升至目标轨道对系统的影响 Fig. 6 Effect of a climber ascending from the bottom of the ribbon to the top on the space elevator |
图 6中所示,初始时刻天梯系统静止在零初始位置,一旦攀爬器开始运动,科氏力效应将引起系统向一侧摆动.在攀爬器爬升的Tac阶段,科氏力逐渐增大导致系统的偏摆角阶梯性增大(与地球自转方向相反),此时科氏力做正功.在攀爬器爬升的Td阶段,科氏力逐渐增加至最大值后开始缓慢减小,攀爬器向系统内引入的振动能量开始减小,进而有向平衡位置恢复的趋势,此时科氏力做负功抵消系统回摆的动能.当攀爬器停止爬升时,系统动能不为零将进入自由振动阶段.攀爬器从GEO轨道返回地面过程与爬升过程类似,但是系统的偏摆角与地球自转方向相同.爬升和返回所用的总时间T均为15.5 d,系统的残余振荡角幅值均为0.024 6°.在图 6(a)中,系统的残余振荡也可以看出系统在赤道面内的摆动周期约为5 d,并且在无阻尼情况下振荡角幅值以及摆动周期没有衰减.
残余振动角幅值与攀爬器的质量、巡航速度以及目标轨道高度有关,所有参数均有上限值.如果所有的参数接近最大值,诱发的系统振荡角将在10-1度量级,这验证了系统稳定性分析假设条件.但需要注意的是,即使微小的振荡角传递到绳索几百千米甚至更高的位置,也将产生几十甚至上百千米的振幅.考虑到运输经济性、效率以及减小振荡等问题,需要合理设置攀爬器的质量、巡航速度等参数,以避免产生较大的残余振荡影响.
3.2 最小化残余振荡分析为减小系统残余振荡带来的不利影响,本文采用调整攀爬器加、减速时间比的方法来实现系统残余振荡角的被动控制.攀爬器加速时间比kac的数值从0.1增大至1.0,减速时间比kdc从0.1增大至2.0,攀爬器以vc= 40 m/s的巡航速度爬升至GEO轨道.仿真结果如图 7、8所示.

|
图 7 系统响应与攀爬器加、减速时间比的关系(vc=40 m/s) Fig. 7 Relationship between the response of the system and the time ratio of acceleration and deceleration |

|
图 8 不同攀爬器巡航速度条件下系统响应(kac= 0.1) Fig. 8 System response under different cruise velocity |
图 7给出了系统残余振荡角幅值以及攀爬器总的运输时间随攀爬器的加、减速时间比之间的变化关系.图 7(a)中可以看出,增大攀爬器减速时间比kdc能够有效抑制系统残余振荡角;确保系统残余振荡角幅值获得最小值,同时攀爬器的加速时间比则决定了系统最优减速时间比的取值.这是因为攀爬器逐渐平缓的减速,延长了科氏力消耗系统能量的时间,使得系统从减速开始时的位置缓慢的向平衡位置运动.但是过长的减速时间反而导致攀爬器处在较长时间的低速运行阶段,产生的科氏力太小对系统回摆过程的抑制效果减弱,因此系统残余振荡角幅值会有一个较小的回弹.增大攀爬器的加速度时间比kac,需要更大的减速时间比kdc来消耗系统的能量,才能取得相同的抑制效果.图 7(b)中可以看出,攀爬器运行至目标轨道所需的总时间与加、减速时间比存在单调递增的关系,即增大加、减速时间比都会导致攀爬器的运行周期增大,降低了经济性和效率.以kac=0.1为例,取得最佳抑制效果时的减速时间比kdc=1.1,天梯系统的残余振荡角幅值为0.003 956°,是kdc=0.1时的5%,但攀爬器的爬升时间增长约2.8 d的时间;当加速时间比kac从0.1增大至1.0,且系统振荡角幅值取得最小值时,攀爬器运行至目标轨道所需要的时间增加约2 d.因此,从经济性和效率的角度出发,攀爬器的加速时间段越短越好.
图 8给出了不同攀爬器巡航速度工况下系统残余振荡角幅值的抑制效果.为减小加速时间比对系统的影响,kac取值为0.1.通常来说,攀爬器的巡航速度越大,其诱发的系统残余振荡也越大.但通过调整减速时间比也可以产生10-3度量级的最佳残余振荡抑制效果,如图 8(a)所示.攀爬器巡航速度越大,为了取得最佳抑制效果所需要的攀爬器减速时间越长;在较高的攀爬器巡航速度条件下,系统残余振荡角幅值随着kdc增加的逐渐平缓.图 8(b)中可以看出在获得最佳残余振荡抑制时,增大攀爬器巡航速度可以缩短攀爬器的运行时间.
4 结论1) 基于小角度振荡假设构造与天梯系统拓扑等价的线性化系统,该系统平衡点在大气阻尼作用下在赤道平面内、外均具有渐进稳定特征.
2) 令攀爬器按照经典3段速度曲线运行,引入加、减速时间比(kac和kdc)并通过优化,可将系统残余振荡可控制在10-3~10-1度的量级范围内,同时论证了小角度假设的合理性.
3) 对攀爬器减速时间比(kdc)的选取可确保系统残余振荡取得极小值,同时加速时间比则决定了系统最优减速时间比的取值.
4) 在攀爬器处于最优减速时间比时,同时增大巡航速度并减小攀爬器的加速时间可以提高系统运行效率和经济性.
| [1] |
PEARSON J. The orbital tower:A spacecraft launcher using the Earth's rotational energy[J]. Acta Astronautica, 1975, 2(9/10): 785. DOI:10.1016/0094-5765(75)90021-1 |
| [2] |
ⅡJIMAS. Helical microtubules of graphitic carbon[J]. Nature, 1991, 354(6348): 56. DOI:10.1038/354056a0 |
| [3] |
COHEN S S, MISRA A K. Elastic oscillations of the space elevator ribbon[J]. Journal of Guidance, Control and Dyanmics, 2007, 30(6): 1711. DOI:10.2514/1.29010 |
| [4] |
GASSEND B. Non-equatorial uniform-stress space elevators[C]//Proceeding of the 3rd Space Elevator Conference. Washington, DC: [s.n.], 2004
|
| [5] |
WANG Zhenkun, FAN Yonghua, CUI Naigang, et al. Non-equatorial space elevator design approach[EB/OL]. (2018-08-30)[2018-09-11]. http://journals.sagepub.com/doi/10.1177/0954410018797879. DOI: 10.1177/0123456789123456
|
| [6] |
EDWARDS B C. Design and deployment of a space elevator[J]. Acta Astronautica, 2000, 47(10): 735. DOI:10.1016/S0094-5765(00)00111-9 |
| [7] |
汪小卫, 鲁宇, 刘丙利, 等. 天梯技术研究进展[J]. 导弹与航天运载技术, 2015, 338(2): 41. WANG Xiaowei, LU Yu, LIU Bingli, et al. Progress of study on the space elevator technology[J]. Missiles and Space Vehicles, 2015, 338(2): 41. DOI:10.7654/j.issn.1004-7182.20150210 |
| [8] |
张普卓, 汪小卫, 刘丙利, 等. 天梯系统指标初步研究[J]. 导弹与航天运载技术, 2016, 345(3): 5. ZHANG Puzhuo, WANG Xiaowei, LIU Bingli, et al. Preliminary study on system indicators of the space elevator[J]. Missiles and Space Vehicles, 2016, 345(3): 5. DOI:10.7654/j.issn.1004-7182.20160302 |
| [9] |
朱仁璋, 雷达, 林华宝. 绳系卫星系统复杂模型研究[J]. 宇航学报, 1997, 20(3): 7. ZHU Renzhang, LEI Da, LIN Huabao. A sophisticated dynamical model of tethered satellite systems[J]. Journal of Astronautics, 1997, 20(3): 7. DOI:10.3321/j.issn:1000-1328.1999.03.002 |
| [10] |
WILLIAMS P, BLANKSBY C, YEO S. Heating and modeling effects in tethered aerocapture missions[J]. Journal of Guidance, Control, and Dynamics, 2003, 26(4): 643. DOI:10.2514/2.5093 |
| [11] |
WILLIAMS P, TRIVAILO P. Performance optimization for a towed-cable system with attached wind sock[J]. Journal of Guidance, Control, and Dynamics, 2006, 29(6): 1415. DOI:10.2514/1.23875 |
| [12] |
WILLIAMS P. Dynamic multibody modeling for tethered space elevators[J]. Acta Astronautica, 2009, 65(3/4): 399. DOI:10.1016/j.actaastro.2008.11.016 |
| [13] |
BELETSKⅡ V V, IVANOV M B, OTSTAVNOV E I, et al. Model problem of a space elevator[J]. Cosmic Research, 2005, 43(2): 152. DOI:10.1007/s10604-005-0029-1 |
| [14] |
COHEN S S, MISRA A K. The effect of climber transit on the space elevator dynamics[J]. Acta Astronautica, 2009, 64(5/6): 538. DOI:10.1016/j.actaastro.2008.10.003 |
| [15] |
WILLIAMS P, OCKELS W. Climber motion optimization for the tethered space elevator[J]. Acta Astronautica, 2009, 66(9/10): 1458. DOI:10.1016/j.actaastro.2009.11.003 |
 2019, Vol. 51
2019, Vol. 51


