无人机技术在军用、民用领域都展示出了巨大的优势.在实际应用中,无人机所面临的环境往往充满随机因素,因此具备在线自主规划能力相当重要,而这也对航迹规划算法的实时性和路径搜索能力提出了很高的要求[1].
目前常用的无人机航迹规划算法有人工势场算法(APF)、快速扩展随机树(RRT)方法以及一些群体智能算法如粒子群算法(PSO)、遗传算法(GA)、人工蜂群算法(ABC)等.尹高扬等[1]将无人机动力学约束加入RRT方法的搜索过程,使得规划出的航迹尽可能接近最优,但搜索耗时几乎成倍增加. Xue等[2]改进了APF的势能场函数,并引入滚动规划算法,改善了路径震荡和局部最小问题,但规划航迹存在无法保证最优的问题.近年来群体智能优化算法[3]凭借通用性强、鲁棒性强、操作简单等优势,逐渐被广泛采用,但也普遍存在局部最优的问题.方群等[4]利用改进粒子群算法提高了无人机在线航迹重规划的精度,但整个规划过程所需时间较长.Cui等[5]引入双向搜索机制提高了蚁群算法的收敛性能与全局优化性能,但规划航迹平滑性有待提升.Bagherian等[6]利用遗传算法实现了无人机三维航迹规划,但搜索速度慢、实时性差.Lai等[7]引入混沌理论、对位学习以及加权因子改进人工蜂群算法,实现了无人机的航迹规划,但存在收敛速度慢的问题.Alihodzic[8]利用烟花算法实现了无人机航迹规划,但方法的可用性低,时有出现无法规划出可行航迹的情况.Zhang等[9]结合差分进化算法与改进的水平比较法,实现了多约束条件下的无人机三维航迹规划,但算法中后期收敛性能较差.Chen等[10]引入遗传算法中的交叉、变异算子来改进狼群搜索算法,但改进后的算法计算量大,航迹规划实时性差.
乌贼算法作为一种新型的群体智能优化算法,由Eesa等[11-12]提出,通过模拟乌贼的变色行为解决全局优化问题.乌贼算法同时兼顾良好的全局搜索与局部搜索,搜索速度较快,与蜂群算法、粒子群算法等相比全局优化精度更高.目前,乌贼算法已被成功运用到多个领域[13-16].
在将乌贼算法应用到无人机航迹规划的过程中,通过大量仿真分析发现,乌贼算法细致搜索的能力较差,在最优解附近搜索时,容易错过最优解.且当航迹规划后期接近全局最优时,种群多样性降低,容易陷入局部最优,从而导致搜索精度变差.鉴于此,本文提出一种联合修正的自适应乌贼算法(简称自适应乌贼算法),保证搜索效率的同时,提高搜索精度.同时分别提出两种基于混沌扰动和变异学习的增强搜索机制,并利用迭代进程加权,将其结合成一种联合的增强搜索方式,有效加强算法的搜索深度,防止错过最优解,提高搜索精度.另一方面,采用一种动态自适应权重方法,根据个体适应度自适应地缩小搜索范围,保证算法的搜索效率;特别地,通过适应度自动筛选机制,对部分适应度较高的个体适度扩大搜索空间以保证种群多样性,改善陷入局部最优的问题.通过6个基准函数测试验证了所提算法的先进性,同时在不同的场景下进行离线/在线航迹规划仿真,与粒子群算法、传统乌贼算法对比,仿真结果验证了所提算法的有效性,尤其是随着场景复杂度的提高,所提算法提高搜索精度的效果越显著.
1 基于乌贼算法的无人机航迹规划 1.1 乌贼算法的仿生原理乌贼算法将乌贼的变色行为归纳为细胞的反射(reflection)和可见性(visibility)两个过程,反射代表细胞反射入射光线的机制,可见性代表乌贼与周围环境匹配的可见度.乌贼算法利用反射和可见性两个过程作为一种搜索策略来寻找新的解Snew,即
| $ {\mathit{\boldsymbol{S}}^{{\rm{new}}}} = {\rm{reflection}} + {\rm{visibility}}, $ |
同时,对应乌贼变色的6种反射光线情况,乌贼算法将细胞种群分为G(1)、G(2)、G(3)、G(4)4组协同搜索,每组对应不同的反射和可见性过程.
1.2 航迹代价函数利用航迹代价函数J可将航迹规划转化为一个最优化问题, 在满足各项约束的条件下,求得最佳控制点位置,构成最佳航迹,使得代价函数J此时取得最小值.
为了兼顾算法的计算效率和方便数学处理,本文将各项约束以“违背量”的形式包含到航迹代价函数中,所得的航迹代价越小,则表明相关约束的违背量越小.代价函数J定义为[17]
| $ J = {w_1}{L_{\rm{s}}} + {w_2}{T_{{\rm{th}}}} + {w_3}{L_{\rm{i}}}. $ | (1) |
式中:J为当前航迹的代价值; w1、w2、w3分别为惯性权重系数;Ls为规划航迹的长度;Tth为航迹威胁指数;Li为航迹控制点间的最大距离, 通过约束Li来确保控制点间间隔适当,以便生成满足无人机机动性能的平滑航迹.
1.3 面向无人机航迹规划的乌贼算法实现乌贼算法利用细胞的反射和可见性两个过程搜索新解Snew,以调整航迹中各控制点的位置.基于乌贼算法的无人机航迹规划具体实现步骤如下.
Step1 初始化.在整个搜索范围内随机生成N个细胞的解.本文同时构建了一条直接连接起点与终点的线段作为初始航迹引导搜索,其余航迹则在其周围随机分布.
Step2 利用式(1)计算每个细胞的代价函数J,保存细胞种群中代价函数最小的解,记为全局最优解Sbest.
Step3 将细胞分为G(1)、G(2)、G(3)、G(4)4组搜索新解Snew,若Snew的代价值低于细胞当前解,则用Snew替换当前解;若Snew的代价值低于Sbest,则用Snew替换Sbest.
1) 对于G(1)组中的细胞,其反射和可见性两个过程表示如下:
| $ {\rm{reflectio}}{{\rm{n}}_j} = R * \mathit{\boldsymbol{G}}_{i,j}^{(1)}, $ | (2) |
| $ {\rm{visibilit}}{{\rm{y}}_j} = V * \left( {\mathit{\boldsymbol{S}}_j^{{\rm{best}}} - \mathit{\boldsymbol{G}}_{i,j}^{(1)}} \right), $ | (3) |
| $ R = {\rm random}\left( \; \right) * \left( {{r_1} - {r_2}} \right) + {r_2}, $ | (4) |
| $ V = {\rm random}\left( \; \right) * \left( {{v_1} - {v_2}} \right) + {v_2}. $ | (5) |
式中:j={1, 2},分别表示x、y坐标; R为反射程度; V为可见性程度;Gi, j(1)为G(1)组中第i个细胞第j维上的解; random( )生成(0,1)之间的随机数;r1、r2分别为限制色素细胞伸展间隔的常数;v1、v2分别为限制可见性程度的常数.在G(1)中V设为1.
2) 对于G(2)组中的细胞,其反射和可见性两个过程表示如下:
| $ {\rm{reflectio}}{{\rm{n}}_j} = R * S_j^{{\rm{best}}}, $ | (6) |
| $ {\rm{visibilit}}{{\rm{y}}_j} = V * \left( {\mathit{\boldsymbol{S}}_j^{{\rm{best}}} - \mathit{\boldsymbol{G}}_{i,j}^{(2)}} \right), $ | (7) |
式中, Gi, j(2)为G(2)组中第i个细胞的第j维上的解.在G(2)中R设为1,V由式(5)计算.
3) 对于G(3)组中的细胞,其反射过程用式(7)表示,可见性过程表示如下
| $ {\rm{visibilit}}{{\rm{y}}_j} = V * \left( {\mathit{\boldsymbol{S}}_j^{{\rm{best}}} - \mathit{\boldsymbol{S}}_j^{{\rm{avg}}}} \right), $ | (8) |
式中:Sjavg为Sjbest的平均值.在G(3)中R设为1,V由式(5)计算.
4) 对于G(4)组中的细胞,在搜索范围内随机寻找新解,即
| $ \mathit{\boldsymbol{G}}_j^{\left( 4 \right)\_{\rm{new}}} = {\rm{random}}\left( \; \right) * \left( {\mathit{\boldsymbol{L}}_j^{{\rm{upper}}} - \mathit{\boldsymbol{L}}_j^{{\rm{lower}}}} \right) + \mathit{\boldsymbol{L}}_j^{{\rm{lower}}}. $ | (9) |
式中:Gj(4)_new为G(4)组中细胞随机搜索找到的第j维上的新解; Ljupper、Ljlower分别为第j维上搜索范围的上、下边界.在应用到航迹规划中时, 为避免G(4)搜索的杂乱无序,利用G(4)搜索到的控制点还需按照其位置坐标进行排序重组,即
| $ \mathit{\boldsymbol{S}}_j^{{\rm{new}}} = {\rm{sort}}\left( {\mathit{\boldsymbol{G}}_j^{\left( 4 \right)\_{\rm{new}}}} \right), $ | (10) |
式中, sort为进行排序的函数.
Step4 判断是否达到最大迭代次数,若是,则循环结束输出全局最优解Sbest,否则返回Step3中的1)开始新一轮迭代.
2 联合修正的自适应乌贼算法 2.1 利用混沌扰动的增强搜索混沌是确定系统中的一种随机状态,它由非线性系统通过确定性规则演化而来[18].混沌具有随机性、遍历性和规律性等特性,表现出良好的深度搜索能力,可以有效改善陷入局部最优的问题[3].基于混沌扰动的增强搜索分为以下3个步骤.
1) 利用下式生成混沌变量XT[19]:
| $ {X_{\rm{T}}} = \left\{ {\begin{array}{*{20}{l}} {2{x_{\rm{T}}},0 \le {x_{\rm{T}}} \le 0.5;}\\ {2\left( {1 - {x_{\rm{T}}}} \right),0.5 < {x_{\rm{T}}} \le 1.0.} \end{array}} \right. $ |
式中:xT为在[0, 1]区间符合均匀分布的随机变量.
2) 利用下式生成混沌扰动量Xnew[19]:
| $ \mathit{\boldsymbol{X}}_j^{{\rm{new}}} = \mathit{\boldsymbol{X}}_j^{{\rm{min}}} + \left( {\mathit{\boldsymbol{X}}_j^{{\rm{max}}} - \mathit{\boldsymbol{X}}_j^{{\rm{min}}}} \right){X_{\rm{T}}}. $ |
式中:Xjmin、Xjmax分别为Xjnew的最小、最大值.
3) 利用下式进行混沌扰动:
| $ \mathit{\boldsymbol{X}}_j^{{\rm{c\_new}}} = \gamma \mathit{\boldsymbol{X}}_j^{\rm{c}} + \left( {1 - \gamma } \right)\mathit{\boldsymbol{X}}_j^{{\rm{new}}}. $ | (11) |
式中:Xjc_new为混沌扰动搜索到的第j维新解;γ为[0, 1]区间均匀分布的随机数;Xjc为当前进行混沌扰动搜索的个体Xc的第j维.
2.2 利用变异学习的增强搜索本文同时提出一种基于变异学习的增强搜索.在该搜索机制中,进行变异学习的个体,通过向全局最优个体以及某个表现优异的个体学习,具备了高效的进化能力,又可有效避免单方向学习可能导致的搜索单一性.同时,利用符合高斯分布的变异因子控制变异学习的程度,在当前个体附近加强局部搜索.另一方面,在该搜索机制中同时加入与当前个体代价值相关的扰动项,在一定程度上始终保证种群个体间差异,在加强探索能力的同时避免陷入局部最优.利用变异学习的增强搜索具体表示如下:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{X}}_j^{{\rm{d\_new}}} = \mathit{\boldsymbol{X}}_j^{\rm{d}} + {\xi _1}\left( {\mathit{\boldsymbol{S}}_j^{{\rm{best}}} - \mathit{\boldsymbol{X}}_j^{\rm{d}}} \right) + {\xi _2}\left( {\mathit{\boldsymbol{X}}_j^{\rm{k}} - \mathit{\boldsymbol{X}}_j^{\rm{d}}} \right) + }\\ {{\xi _3}\left[ {3 + \exp \left( {\frac{{J - {{J'}_{{\rm{avg}}}}}}{{{J_{{\rm{GB}}}} - {{J'}_{{\rm{avg}}}} + a}}} \right)} \right].} \end{array} $ | (12) |
式中:Xjd_new为变异学习搜索到的第j维新解;Xjd为当前进行变异学习搜索的个体Xd的第j维;ξ1、ξ2分别为变异因子;ξ3用来控制扰动程度,三者皆为符合期望为μ,标准差为σ的正态分布随机数;Xk为代价值小于种群平均代价的某个体;J为Xd的代价函数值;JGB为Sbest的代价值;Javg为种群的平均代价值,J′avg为代价值小于Javg的个体的平均代价值;a为一常数.
2.3 迭代进程加权的增强搜索利用混沌扰动的增强搜索能始终保持较强的深度搜索能力,但同时也会影响算法收敛的稳定性[20];利用变异学习的增强搜索具有较快的收敛速度,但搜索前期种群就可能快速聚集.基于上述分析,本文利用算法迭代进程将两种增强搜索机制加权结合,在搜索初期,混沌扰动起主要作用,在个体周围不断进行深入探索;而在搜索后期,变异学习起主要作用,兼顾收敛速度的同时继续保持深入而精细的探索.通过加权结合方式,在保证算法搜索效率的同时有效加强深度探索能力, 防止错过最优解.加权的联合搜索表示为
| $ {\mathit{\boldsymbol{S}}^{{\rm{new}}}} = \left( {1 - \frac{\mathit{\boldsymbol{t}}}{{{\mathit{\boldsymbol{t}}_{{\rm{max}}}}}}} \right){\mathit{\boldsymbol{X}}^{{\rm{c\_new}}}} + \left( {\frac{\mathit{\boldsymbol{t}}}{{{\mathit{\boldsymbol{t}}_{{\rm{max}}}}}}} \right){\mathit{\boldsymbol{X}}^{{\rm{d\_new}}}}. $ | (13) |
式中:t为当前迭代次数; tmax为最大迭代次数; Xc_new、Xd_new分别由式(11)、(12)求得.
2.4 自适应权重的增强搜索为保证算法的搜索效率,保持种群个体的多样性,本文采用一种动态自适应权重的方法,根据个体适应度自适应地缩减搜索空间.对适应度高的个体设置较小的权重,以加强其局部搜索能力.同时引入适应度自动筛选机制,筛选G(1)、G(2)组中部分适应度较高的个体,设置相对较大的权重,适当扩大其搜索范围,防止种群过度集中,改善局部最优.
对于G(1)组中,代价值大于Javg的个体,需加强其全局搜索能力使其尽快改变当前状态;对于代价值处于Javg与J′avg之间的个体,采用余弦的规律调整权重,使其在算法前期保持较大的全局搜索能力,后期则进行相对更精细的搜索[21];对于代价值小于J′avg的个体,主要加强其细致搜索的能力,特别地,为改善局部最优的问题,这部分个体中越接近全局最优解的个体,设置权重反而相对越大,其全局搜索能力相对越强.权重g1的具体设置如下:
| $ {g_1} = \left\{ {\begin{array}{*{20}{l}} {1,}&{J > {J_{{\rm{arg}}}},}\\ {{g_{{\rm{bl}}}} + \left( {{g_{{\rm{al}}}} - {g_{{\rm{b1}}}}} \right)\frac{{1 + \cos \left( {\frac{{t - 1}}{{{t_{{\rm{max}}}} - 1}}{\rm{ \mathsf{ π} }}} \right)}}{2},}&{{{J'}_{{\rm{avg}}}} \le J \le {J_{{\rm{ag}}}},}\\ {{g_{{\rm{cl}}}} + \left( {{g_{{\rm{bl}}}} - {g_{{\rm{cl}}}}} \right)\frac{{J - {{J'}_{{\rm{avg}}}}}}{{{J_{{\rm{CG}}}} - {{J'}_{{\rm{avg}}}}}},}&{J < {{J'}_{{\rm{avg}}}}.} \end{array}} \right. $ |
式中:J为当前个体的代价值; ga1、gb1、gc1分别为对权重取值范围进行限制的常数,且ga1>gb1>gc1.
在自适应乌贼算法中,G(1)组的反射和可见性两个过程表示如下:
| $ {\rm{reflectio}}{{\rm{n}}_j} = {g_1} * R * \mathit{\boldsymbol{G}}_{i,j}^{\left( 1 \right)}, $ | (14) |
| $ {\rm{visibilit}}{{\rm{y}}_j} = V * \left( {\mathit{\boldsymbol{S}}_j^{{\rm{best }}} - {g_1} * \mathit{\boldsymbol{G}}_{i,j}^{(1)}} \right), $ | (15) |
式中:V=1, R由式(4)计算得到.
对于G(2)组,对适应度相对较差的个体(J>J′avg),其代价函数值越高,设置权重相对越大,以期尽快改变当前状态;而对于适应度相对较好的个体(J<J′avg),为增强种群多样性,这部分个体中越接近全局最优解的个体,设置权重相对越大.权重g2的具体设置如下:
| $ {g_2} = \frac{1}{{1 + b\exp \left( { - \left| {\frac{{J - {{J'}_{{\rm{avg}}}}}}{{{J_{{\rm{GB}}}} - {{J'}_{{\rm{avg}}}} + c}}} \right|} \right)}}. $ |
式中:b、c为常数,且b>0.
自适应乌贼算法中G(2)组的反射过程用式(6)表示,反射程度R=1.可见性过程表示如下:
| $ {\rm{visibilit}}{{\rm{y}}_j} = {g_2} * V * \left( {\mathit{\boldsymbol{S}}_j^{{\rm{best}}} - \mathit{\boldsymbol{G}}_{i,j}^{\left( 2 \right)}} \right), $ | (16) |
式中V由式(5)计算得到.
对于G(3)组,采用余弦的规律调整权重,搜索范围随迭代次数的提高而减小,以此提高算法的搜索效率.权重g3的具体设置如下:
| $ {g_3} = {g_{{\rm{a3}}}} + \frac{1}{2}\left( {1 - {g_{{\rm{a3}}}}} \right)\left[ {1 + \cos \left( {\frac{{t - 1}}{{{t_{\max }} - 1}}{\rm{ \mathsf{ π} }}} \right)} \right], $ |
式中ga3 < 1.
自适应乌贼算法中G(3)组的反射过程用式(6)表示,反射程度R=1.可见性过程表示如下:
| $ {\rm{visibilit}}{{\rm{y}}_j} = {g_3} * V * \left( {\mathit{\boldsymbol{S}}_j^{{\rm{best}}} - \mathit{\boldsymbol{S}}_j^{{\rm{avg}}}} \right), $ | (17) |
式中V由式(5)计算得到.
自适应乌贼算法中G(4)依旧用式(9)、(10)表示.
3 面向航迹规划的联合修正自适应乌贼算法实现利用联合修正的自适应乌贼算法实现无人机航迹规划的具体步骤如下.
Step1 初始化.
Step2 利用式(1)计算每个细胞的代价函数J,保存细胞种群中代价函数最小的解Sbest.
Step3 计算Javg、J′avg.
Step4 将细胞种群分为G(1)、G(2)、G(3)、G(4)4组搜索新解Snew,若Snew的代价值低于细胞当前解,则用Snew替换当前解,并更新Javg与J′avg;若Snew的代价值低于Sbest,则用Snew替换Sbest.
1) 对于G(1)组,利用式(14)、(15)搜索Snew.
2) 对于G(2)组,利用式(6)、(16)搜索Snew.
3) 对于G(3)组,利用式(6)、(17)搜索Snew.
4) 对于G(4)组,利用式(9)、(10)搜索Snew.
5) 在整个细胞种群完成一次动态自适应搜索后,对于G(1)组中的细胞,按式(13)利用加权联合的增强搜索再次寻找新解Snew.
Step5 判断是否达到最大迭代次数,若是,则循环结束输出全局最优解,否则返回Step4中的1)开始新一轮迭代.
4 典型基准函数的寻优测试分别在3个单峰基准函数Sphere、Quadric、Rosenbrock以及3个多峰基准函数Rastrigin、Griewank、Schwefe上对所提自适应乌贼算法进行寻优测试[22-23],同时选取传统乌贼算法与粒子群算法作为对比,验证本文所提的自适应乌贼算法的有效性与优越性.
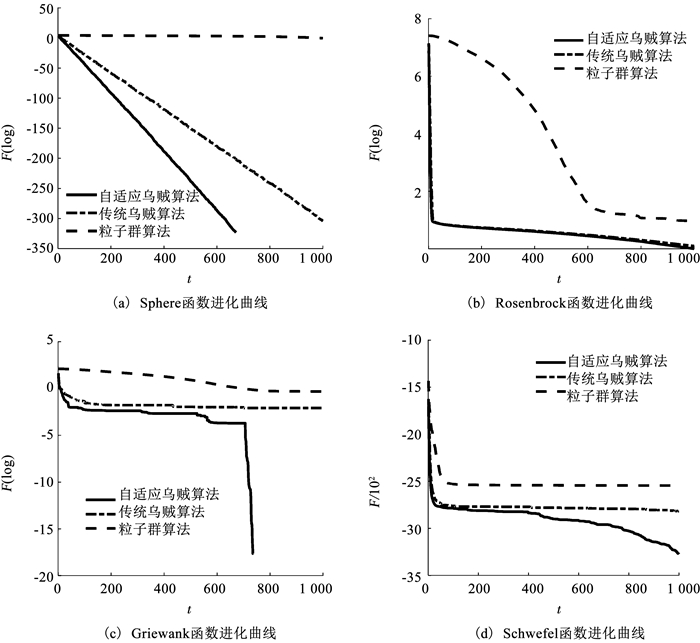
为保证计算结果具有统计意义,针对每个基准函数,所有算法需进行50次Monte Carlo仿真,通过对比各函数50次Monte Carlo计算的平均值、方差等统计指标来评估3种算法的寻优性能.实际计算结果见表 1,其中:Aavg为实际最优解的均值; Mmin为最小值; Mmax为最大值; Sstd为标准差.各基准测试函数进化曲线如图 1所示,图中:t为当前迭代次数; F为迭代过程中函数最优解的平均值.受篇幅所限,本文仅给出部分基准函数的进化曲线.
| 表 1 基准函数测试结果比较 Tab. 1 Test results comparison of different benchmark functions |
|
图 1 各基准测试函数进化曲线 Fig. 1 Progress curves of different benchmark functions |
从表 1和图 1可以看出,无论是单峰函数还是多峰函数,自适应乌贼算法的收敛性能与寻优精度均优于传统乌贼算法与粒子群算法,全局优化能力强,鲁棒性强,从而证明了所提自适应乌贼算法能有效改善陷入局部最优的问题,在高效搜索的同时其全局优化精度高.
5 离线航迹规划仿真为验证本文所提的自适应乌贼算法的离线航迹规划性能,将其与粒子群算法、传统乌贼算法对比,在3个不同的场景下进行二维离线航迹规划的仿真.具体场景设置如图 2(a)、图 3(a)、图 4(a)所示.场景中黑色矩形部分为障碍物,圆形部分为威胁区. 3个场景复杂度依次递增.需要注意的是,场景中障碍物与威胁区的模型相比其实际尺寸增大了2 units,以便无人机沿规划航迹飞行时仍有余地.

|
图 2 场景1下3种算法规划结果的比较 Fig. 2 Results comparison of three algorithms in simulation scene 1 |

|
图 3 场景2下3种算法规划结果的比较 Fig. 3 Results comparison of three algorithms in simulation scene 2 |

|
图 4 场景3下3种算法规划结果的比较 Fig. 4 Results comparison of three algorithms in simulation scene 3 |
每种算法各进行100次的Monte Carlo仿真,若出现航迹与障碍物或威胁区发生碰撞的现象,则该次数据被剔除,航迹规划效果主要根据规划的航迹长度进行判断.统计结果见表 2,其中:Nnb为碰撞次数;Mmax为最长航程;Mmin为最短航程;Aavg为航程均值;Sstd为航程标准差.3个场景下3种算法规划航迹结果分别如图 2~4所示,图中x、y为横、纵坐标轴,t为当前迭代次数,JGB为全局最优代价值.
| 表 2 3种算法性能比较 Tab. 2 Performance comparison of three algorithms |
从结果来看,所提自适应乌贼算法始终能保持100%的规划成功率,除了场景1、场景3下的最短航程指标略高于传统乌贼算法(差距甚至可忽略不计),其余各指标均优于其他两种算法,其规避障碍物与威胁区的能力最强、鲁棒性高、收敛速度快、规划航迹性能最佳,从而证明所提自适应乌贼算法能有效改善陷入局部最优的问题,在保证搜索效率的同时其全局优化精度高.另一方面,对比3个场景下的统计结果,可以发现所提自适应乌贼算法在越复杂环境下,提高搜索精度的效果越显著.
6 在线航迹规划仿真与离线航迹规划不同,本文在线航迹规划需要利用机载传感器不断探测周围环境情况,在探测半径为100 units的区域内规划出一条最优航迹分段.当无人机沿航迹飞行至距离分段节点约40 units时,机载传感器再次扫描周围环境,确定下一分段节点,并以当前分段节点为新的起始点规划下一段航迹.如此重复以上步骤,直到无人机到达飞行目标终点.
6.1 修正的航迹代价函数为解决航迹段间的衔接处的非平滑造成的航迹转弯角度过大问题,本文利用角度限制项w4α来修正航迹代价函数J,即
| $ J = {w_1}{L_{\rm{s}}} + {w_2}{T_{{\rm{th}}}} + {w_3}{L_{\rm{i}}} + {w_4}\alpha . $ | (18) |
式中:α为航迹最大转弯角度; w4为惯性权重系数; 其余参数与式(1)相同.
6.2 航迹分段节点的选取在线航迹规划分段节点需要在实时探测的过程中选取.本文假设障碍物分布信息已知,机载传感器探测范围内威胁信息完全可知[24].若飞行目标终点处于当前探测区域内,则目标终点即为分段节点,否则从探测区域的右半部分半圆边界上选取若干个点构成分段节点备选序列Z′.依次规划起点到备选点的航迹分段,根据启发式方法[25-26],定义启发式代价Js:
| $ {J_{\rm{s}}} = J + {w_5}{L_{\rm{T}}}. $ |
式中:LT为当前备选点到飞行目标终点的距离; w5为惯性权重系数; J为规划的航迹分段代价,可由式(18)求得.选择Z′中令启发式代价Js最小的点作为分段节点Zsub,即
| $ {Z^{{\rm{sub}}}} = \arg \mathop {\min }\limits_{Z'} {J_{\rm{s}}}. $ |
本文设计了3个不同场景进行无人机在线航迹规划仿真验证,3个场景的复杂度依次递增.选取传统乌贼算法作为比较对象,验证所提自适应乌贼算法在线规划的实时性与在线搜索精度.
两种算法各进行100次的Monte Carlo仿真,统计结果见表 3,表中:Nnb为碰撞次数;Mmax为最长航程;Mmin为最短航程;Aavg为航程均值;Sstd为航程标准差.3个场景下规划航迹分别如图 5~7所示.
| 表 3 两种算法在线规划性能比较 Tab. 3 Performance comparison between the two algorithms for online path planning |

|
图 5 场景1下在线航迹规划结果的比较 Fig. 5 Results comparison of online path planning in simulation scene 1 |
|
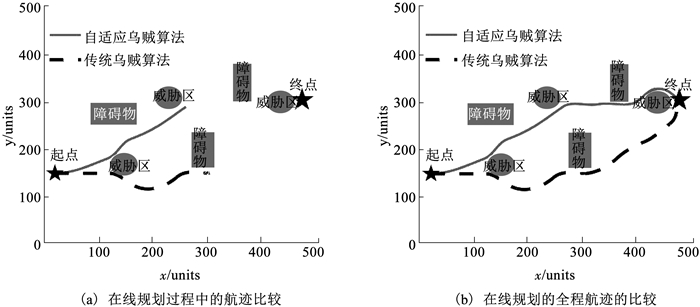
图 6 场景2下在线航迹规划结果的比较 Fig. 6 Results comparison of online path planning in simulation scene 2 |
|
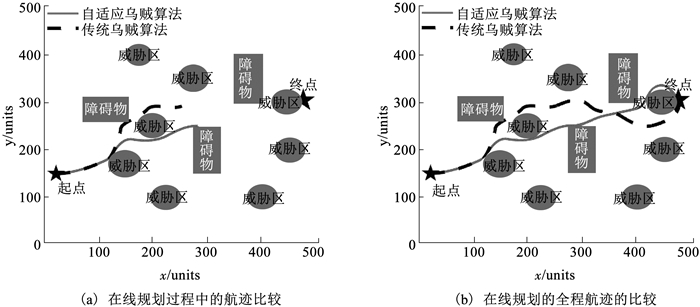
图 7 场景3下在线航迹规划结果比较 Fig. 7 Results comparison of online path planning in simulation scene 3 |
进行在线航迹规划时,无人机以5 units/s的速度匀速飞行,仿真过程中所提自适应乌贼算法的航迹分段, 最长规划时间为6.3 s,传统乌贼算法最长为5.4 s,两种算法均能满足实时性要求.
从仿真结果来看,总体来说,所提的自适应乌贼算法在线航迹规划性能仍优于传统乌贼算法,始终保持了100%的在线规划成功率.除了场景1下由于设置简单,无法完全显示出所提自适应乌贼算法的优势,导致其规划航程均值虽然较低,但100次仿真结果在均值附近的波动性相比传统乌贼算法稍大.多数情况下所提自适应乌贼算法的鲁棒性更强,在搜索精度上的提高也较为显著.特别地,从航程均值指标看,相比传统乌贼算法,所提自适应乌贼算法对复杂度高的场景的适应性更好.
7 结论1) 针对无人机在线/离线航迹规划应用,本文提出一种联合修正的自适应乌贼航迹规划算法.分别提出两种基于混沌扰动与变异学习的增强搜索,并基于算法的迭代进程,将其加权结合成一种联合的增强搜索方式,实现高效的深度搜索;引入自适应权重以约减搜索空间,引入适应度自动筛选机制来解决乌贼种群过度聚集,最终获得高搜索效率、高搜索精度的用于无人机航迹规划的联合修正自适应乌贼算法.
2) 通过6个基准函数测试验证了所提算法的有效性与先进性,然后对所提的自适应乌贼算法进行离线航迹规划仿真分析,结果显示所提算法始终能实现100%的规划成功率,具有较好的鲁棒性和全局搜索精度,特别是在复杂环境下效果显著.
3) 应用所提自适应乌贼算法进行在线航迹规划,为此引入了转弯角度约束条件,来改善航迹段衔接突变问题,同时利用启发式方法对航迹分段的节点进行优化选取.仿真结果显示所提算法能够在较短时间内规划出可行的平滑航迹,满足实时性要求;在线规划成功率高达100%,规划航迹精度高,且越复杂的环境下效果越显著.
4) 大量仿真表明,相比简单场景,在线航迹规划在复杂场景下,航迹段衔接处的平滑性有所降低.
| [1] |
尹高扬, 周绍磊, 吴青坡. 基于改进RRT算法的无人机航迹规划[J]. 电子学报, 2017, 45(7): 1764. YIN Gaoyang, ZHOU Shaolei, WU Qingpo. An improved RRT algorithm for UAV path planning[J]. Acta Electronica Sinica, 2017, 45(7): 1764. DOI:10.3969/j.issn.0372-2112.2017.07.029 |
| [2] |
XUE Qian, CHENG Peng, CHENG Nong, et al. Dynamic obstacle avoidance path planning of UAVs[C]//Proceedings of the 34th Chinese Control Conference, CCC 2015. Hangzhou: IEEE, 2015: 8860. DOI: 10.1109/ChiCC.2015.7261039
|
| [3] |
江铭炎, 袁东风. 人工蜂群算法及其应用[M]. 北京: 科学出版社, 2014: 10. JIANG Mingyan, YUAN Dongfeng. Artificial bee colony algorithm and its application[M]. Beijing: Science Press, 2014: 10. |
| [4] |
方群, 徐青. 基于改进粒子群算法的无人机三维航迹规划[J]. 西北工业大学学报, 2017, 35(1): 66. FANG Qun, XU Qing. 3D route planning for UAV based on improved PSO algorithm[J]. Journal of Northwestern Polytechnical University, 2017, 35(1): 66. DOI:10.3969/j.issn.1000-2758.2017.01.011 |
| [5] |
CUI Can, WANG Nan, CHEN Jing. Improved ant colony optimization algorithm for UAV path planning[C]// Proceedings of the IEEE 5th International Conference on Software Engineering and Service Sciences. Beijing: IEEE, 2014: 291. DOI: 10.1109/ICSESS.2014.6933566
|
| [6] |
BAGHERIAN M, ALOS A. 3D UAV trajectory planning using evolutionary algorithms: A comparison study[J]. Aeronautical Journal, 2015, 119(1220): 1271. DOI:10.1017/S0001924000011246 |
| [7] |
LAI Lei, QU Shiru. Path planning for Unmanned Air Vehicles using an improved artificial bee colony algorithm[C]//Proceedings of the 31st Chinese Control Conference. Hefei: IEEE, 2012: 2486 https://ieeexplore.ieee.org/document/6390343/
|
| [8] |
ALIHODZIC A. Fireworks algorithm with new feasibility-rules in solving UAV path planning[C]//Proceedings of the 3rd International Conference on Soft Computing and Machine Intelligence. Dubai, United Arab Emirates: IEEE, 2017: 53. DOI: 10.1109/ISCMI.2016.33
|
| [9] |
ZHANG Xiangyin, DUAN Haibin. An improved constrained differential evolution algorithm for unmanned aerial vehicle global route planning[J]. Applied Soft Computing Journal, 2015, 26: 270. DOI:10.1016/j.asoc.2014.09.046 |
| [10] |
CHEN Yongbo, MEI Yuesong, YU Jianqiao, et al. Three-dimensional unmanned aerial vehicle path planning using modified wolf pack search algorithm[J]. Neurocomputing, 2017, 266: 445. DOI:10.1016/j.neucom.2017.05.059 |
| [11] |
EESA A S, BRIFCANI A M A, OMMAN Z. Cuttlefish algorithm—a novel bio-inspired optimization algorithm[J]. International Journal of Scientific & Engineering Research, 2013, 4(9): 1978. |
| [12] |
EESA A S, BRIFCANI A M A, OMMAN Z. A new tool for global optimization problems-cuttlefish algorithm[J]. International Journal of Mathematical, Computational, Physical, Electrical and Computer Engineering, 2014, 8(9): 1235. |
| [13] |
RIFFI M E, BOUZIDI M. Discrete cuttlefish optimization algorithm to solve the travelling salesman problem[C]// Proceedings of the 3rd World Conference on Complex Systems. Marrakech, Morocco: IEEE, 2016: 1. DOI: 10.1109/ICoCS.2015.7483231
|
| [14] |
EESA A S, ORMAN Z, BRIFCANI A M A. A novel feature-selection approach based on the cuttlefish optimization algorithm for intrusion detection systems[J]. Expert Systems with Applications, 2015, 42(5): 2670. DOI:10.1016/j.eswa.2014.11.009 |
| [15] |
LENIN K, REDDY B R, KALAVATHI M S. Voltage profile amplification and attenuation of real power loss by using new cuttlefish algorithm[J]. Control Theory and Informatics, 2014, 4(9): 50. |
| [16] |
GIERNACKI W, FRAIRE T E, KOZIERSKI P. Cuttlefish optimization algorithm in autotuning of altitude controller of unmanned aerial vehicle (UAV)[C]//Ollero A, Sanfeliu A, Montano L, et al. ROBOT 2017: Third Iberian Robotics Conference. Advances in Intelligent Systems and Computing. Cham: Springer, 2017: 841. DOI: 10.1007/978-3-319-70833-1_68
|
| [17] |
舒纬伟, 敬忠良, 董鹏. 基于乌贼算法的无人机航迹规划[J]. 科学技术与工程, 2017, 17(2): 122. SHU Weiwei, JING Zhongliang, DONG Peng. UAV trajectory planning based on cuttlefish algorithm[J]. Science Technology and Engineering, 2017, 17(2): 122. DOI:10.3969/j.issn.1671-1815.2017.02.021 |
| [18] |
LIU Xueying, FU Meiling. Cuckoo search algorithm based on frog leaping local search and chaos theory[J]. Applied Mathematics and Computation, 2015, 266: 1083. DOI:10.1016/j.amc.2015.06.041 |
| [19] |
CHENG Xiaoya, JIANG Mingyan. An improved artificial bee colony algorithm based on gaussian mutation and chaos disturbance[J]. Lecture Notes in Computer Science, 2012, 7331(1): 326. DOI:10.1007/978-3-642-30976-2_39 |
| [20] |
胥小波, 郑康锋, 李丹, 等. 新的混沌粒子群优化算法[J]. 通信学报, 2012, 33(1): 24. XU Xiaobo, ZHENG Kangfeng, LI Dan, et al. New chaos-particle swarm optimization algorithm[J]. Journal on Communications, 2012, 33(1): 24. DOI:10.3969/j.issn.1000-436X.2012.01.004 |
| [21] |
陈国初, 俞金寿. 增强型微粒群优化算法及其在软测量中的应用[J]. 控制与决策, 2005, 20(4): 377. CHEN Guochu, YU Jinshou. Enhanced particle swarm optimization and its application in soft sensor[J]. Control and Decision, 2005, 20(4): 377. DOI:10.3321/j.issn:1001-0920.2005.04.004 |
| [22] |
董文永, 康岚兰, 刘宇航, 等. 带自适应精英扰动及惯性权重的反向粒子群优化算法[J]. 通信学报, 2016, 37(12): 1. DONG Wenyong, KANG Lanlan, LIU Yuhang, et al. Opposition-based particle swarm optimization with adaptive elite mutation and nonlinear inertia weight[J]. Journal on Communications, 2016, 37(12): 1. DOI:10.11959/j.issn.1000-436x.2016224 |
| [23] |
张振兴, 杨任农, 房育寰, 等. 自适应Tent混沌搜索的蚁狮优化算法[J]. 哈尔滨工业大学学报, 2018, 50(5): 152. ZHANG Zhenxing, YANG Rennong, FANG Yuhuan, et al. Ant lion optimization algorithm based on self-adaptive Tent chaos search[J]. Journal of Harbin Institute of Technology, 2018, 50(5): 152. DOI:10.11918/j.issn.0367-6234.201706044 |
| [24] |
温乃峰.低空复杂环境下小型无人机的在线航迹规划算法研究[D].哈尔滨: 哈尔滨工业大学, 2016 WEN Naifeng. Research on the small UAV online path planning algorithms in complex and low-altitude environments[D]. Harbin: Harbin Institute of Technology, 2016 http://cdmd.cnki.com.cn/Article/CDMD-10213-1016739340.htm |
| [25] |
WEN Naifeng, SU Xiaohong, MA Peijun, et al. Online UAV path planning in uncertain and hostile environments[J]. International Journal of Machine Learning & Cybernetics, 2017, 8(2): 469. DOI:10.1007/s13042-015-0339-4 |
| [26] |
WEN Naifeng, ZHAO Lingling, SU Xiaohong, et al. UAV online path planning algorithm in a low altitude dangerous environment[J]. IEEE/CAA Journal of Automatica Sinica, 2015, 2(2): 173. DOI:10.1109/JAS.2015.7081657 |
 2019, Vol. 51
2019, Vol. 51



