随着科技的进步和技术的发展,越来越多的人开始把目光投到尚未被完全探索的海洋.水下航行器可以代替人类深入海洋中去探索和开发海洋资源,是目前开发和利用海洋的重要工具之一.因此,研发新型水下航行器也成为当前的趋势之一.但由于水动力复杂难测,特别是对于新型航行器,其精确建模难以实现,因此开展对水下航行器建模研究具有重要的意义[1].
水下航行器建模主要包括机理建模和黑箱建模.机理建模是根据物理规律确定水下航行器的数学模型.目前,水下航行器模型一般选用美国海军舰船研究与发展中心(DTNSRDC)提出的描述潜艇操作运动的六自由度度标准运动方程[2].该方程在统一水下航行器坐标系和符号上起了重要作用[3],但随着新型水下航行器的涌现,其水动力方面内容难以与实际相吻合,此方程也难以精准描述新型水下航行器的数学模型.目前已有许多研究者用系统辨识方法对水下航行器建模进行了相关研究.Sabet等[4]利用非线性卡尔曼滤波器对水动力系数进行辨识,从而建立了水下航行器模型. Shafiei等[5]利用神经网络和遗传算法对水下航行器进行了有效的建模研究.朱胜庭等[6]利用最小二乘法对水下航行器水动力参数进行辨识,建立了较为准确的数学模型.目前,现有文献和方法主要对水下航行器模型的水动力参数进行辨识,从而建立水下航行器模型,而且大部分航行器原型是鱼雷式水下航行器.面对不断涌现的具有不同外形和推进方式的新型水下航行器,有必要开展相关的黑箱建模研究.
水下航行器数学模型是一个高度复杂耦合的非线性系统.寻求其模型各状态之间的非线性映射关系,是实现水下航行器黑箱建模的主要难点.支持向量机是一种以统计学习理论为基础的基于结构风险最小化原理的机器学习方法,善于处理小样本问题,在分类和回归方面具有优良的性能[7].该方法已被广泛应用到众多领域.Isa等[8]利用支持向量机方法较好实现了文本识别.邴其春等[9]利用支持向量机实现了较高准确率的短时交通流局域预测.徐锋等[10]应用最小二乘支持向量机实现了船舶操纵运动的黑箱建模.利用支持向量机可以在小样本情况下获得水下航行器各状态之间的非线性映射关系,从而建立其较为准确的黑箱模型.
支持向量机参数的选择将会直接影响其分类和回归性能,因此在水下航行器黑箱建模过程,如何选择适当的参数是一个重要问题.粒子群算法[11]是一种较好的智能优化技术,其具有较快的计算速度和较好的全局搜索能力[12].Kim等[13]提出利用粒子群算法寻找PID参数,有效改善了PID控制器效果.Gaing[14]设计了针对AVR系统的基于粒子群参数寻优的PID控制器,实验结果证明其具有更强的鲁棒性.为了寻求更为准确的水下航行器黑箱模型,可以利用粒子群智能算法寻求合适的支持向量机参数,来完成整个黑箱建模.
本文根据水下航行器通用模型推导出黑箱模型的输入和输出,并利用支持向量机在仅已知运动状态信息和推进器力情况下实现黑箱建模,获得水下航行器黑箱模型.为了获得较好的黑箱模型,利用粒子群智能优化算法来寻得适当的支持向量机参数.基于此,本文提出了一种针对水下航行器基于粒子群参数寻优的支持向量机黑箱建模方法,并用新型四旋翼水下航行器的两种空间运动验证了该方法的有效性.
1 水下航行器黑箱建模| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot x}} = \mathit{\boldsymbol{J}}\left( \mathit{\boldsymbol{x}} \right)\mathit{\boldsymbol{q}},}\\ {\mathit{\boldsymbol{M\dot q}} + \mathit{\boldsymbol{C}}\left( \mathit{\boldsymbol{q}} \right)\mathit{\boldsymbol{q}} + \mathit{\boldsymbol{D}}\left( \mathit{\boldsymbol{q}} \right)\mathit{\boldsymbol{q}} + \mathit{\boldsymbol{G}}\left( \mathit{\boldsymbol{x}} \right) = \mathit{\boldsymbol{\tau }},}\\ {\mathit{\boldsymbol{\tau }} = \mathit{\boldsymbol{Bu}}.} \end{array} $ | (1) |
式中:x=[x, y, z, φ, θ, φ]为水下航行器在惯性坐标系下的3个位置和3个姿态角;q=[u, v, w, p, q, r]为水下航行器在载体坐标系下的线性速度和角速度;J(x)为惯性坐标系和载体坐标系之间的速度转换矩阵;M为水下航行器动力学中的惯性力矩阵;C(q)为水下航行器科氏和离心力矩阵;D(q)为水下航行器阻尼力矩阵;G(x)为由水下航行器重力和浮力引起的恢复力和力矩构成的向量;τ为由推进器产生的六自由度力和力矩向量;u为推进器力;B为推进器力与六自由度力之间的关系矩阵.
采用前向差分法对式(1)中的加速度项进行离散化,即:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot x}}\left( k \right) = \left( {\mathit{\boldsymbol{x}}\left( {k + 1} \right) - \mathit{\boldsymbol{x}}\left( k \right)} \right)/h,}\\ {\mathit{\boldsymbol{\dot q}}\left( k \right) = \left( {\mathit{\boldsymbol{q}}\left( {k + 1} \right) - \mathit{\boldsymbol{q}}\left( k \right)} \right)/h.} \end{array} $ | (2) |
式中:h为采样间隔;k、k+1分别为相邻的采用时刻.
改写并整理式(1)可得:
| $ \begin{array}{l} \mathit{\boldsymbol{\dot x}} = \mathit{\boldsymbol{J}}\left( \mathit{\boldsymbol{x}} \right)\mathit{\boldsymbol{q}},\\ \mathit{\boldsymbol{\dot q}} = - {\mathit{\boldsymbol{M}}^{ - 1}}\left( {\mathit{\boldsymbol{C}}\left( \mathit{\boldsymbol{q}} \right)\mathit{\boldsymbol{q}} + \mathit{\boldsymbol{D}}\left( \mathit{\boldsymbol{q}} \right)\mathit{\boldsymbol{q}} + \mathit{\boldsymbol{G}}\left( \mathit{\boldsymbol{x}} \right) - \mathit{\boldsymbol{\tau }}} \right), \end{array} $ | (3) |
式(3)等式右边都是与x、q和τ有关的向量.
把式(2)代入式(3),可得如下模型:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{x}}\left( {k + 1} \right) = \mathit{\boldsymbol{J}}\left( {\mathit{\boldsymbol{x}}\left( k \right)} \right)\mathit{\boldsymbol{q}}\left( k \right)h + \mathit{\boldsymbol{x}}\left( k \right),}\\ {\mathit{\boldsymbol{q}}\left( {k + 1} \right) = - {\mathit{\boldsymbol{M}}^{ - 1}}\left\{ {\mathit{\boldsymbol{C}}\left( {\mathit{\boldsymbol{q}}\left( k \right)} \right){\mathit{\boldsymbol{q}}}\left( k \right) + \mathit{\boldsymbol{D}}\left( {\mathit{\boldsymbol{q}}\left( k \right)} \right)\mathit{\boldsymbol{q}}\left( k \right) + } \right.}\\ {\left. {\mathit{\boldsymbol{G}}\left( {\mathit{\boldsymbol{x}}\left( k \right)} \right) - \mathit{\boldsymbol{\tau }}\left( k \right)} \right\}h + \mathit{\boldsymbol{q}}\left( k \right),} \end{array} $ | (4) |
上式建立了水下航行器与推进器力之间的非线性映射关系.由此可以得到,水下航行器的黑箱建模就是寻求{x(k), q(k), τ(k)}与{x(k+1), q(k+1)}之间的映射关系.因此,水下航行器黑箱模型输入{x(k), q(k), τ(k)},输出为{x(k+1), q(k+1)},其中τ(k)=Bu(k).
2 支持向量机及粒子群寻优原理 2.1 支持向量机支持向量机(support vector machines, SVM)是在统计学习理论的基础上发展起来的一种机器学习理论.它可以在有限样本情况下,获得较好的学习泛化性能.支持向量机起初主要针对模式识别问题,后随着ε-不敏感损失函数的引入,其已大量成功应用于非线性回归估计[17].本文也即采用ε-支持向量机对式(4)进行非线性回归估计,完成水下航行器操纵运动的黑箱建模.
对于给定的多输入单输出系统,训练样本集为{(Xi, yi), i=1, 2, …, n},所求的回归估计函数模型为f(X)=wΦ(X)+b,其中:Xi∈Rl为输入,l为它的维度;y∈R为输出;n为样本数量;w为权重向量;Φ(X)为训练样本的高维非线性映射;b为偏置.
支持向量机核心思想是分类超平面最大化间隔,即
| $ \mathop {\max }\limits_w \frac{2}{{\left\| \mathit{\boldsymbol{w}} \right\|}}, $ |
其等价为
| $ \mathop {\min }\limits_w \frac{1}{2}{\mathit{\boldsymbol{w}}^{\rm{T}}}\mathit{\boldsymbol{w}}. $ |
对于回归问题,可把训练集各样本输出分别增加ε和减少ε,形成对应的两类新样本数据,则原所求回归估计函数为该两类新样本数据的分类超平面,原回归问题转为分类问题.考虑到不可分等因素,需通过引入松弛因子ξi,ξi*软化约束条件,即新的约束条件为
| $ \left\{ \begin{array}{l} {y_i} - \left[ {{\mathit{\boldsymbol{w}}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {{\mathit{\boldsymbol{X}}_i}} \right) + b} \right] \le \varepsilon + {\xi _i},\\ {\mathit{\boldsymbol{w}}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {{\mathit{\boldsymbol{X}}_i}} \right) + b - {y_i} \le \varepsilon + \xi _i^ * ,\\ {\xi _i},\xi _i^ * \ge 0, \end{array} \right. $ | (5) |
式中ε又称为不敏感因子,其为设定参数.
为避免松弛因子取太大值,目标函数中需对它加以惩罚,故所求的目标函数为
| $ \mathop {\min }\limits_{w,b,\xi } \left\{ {\frac{1}{2}{\mathit{\boldsymbol{w}}^{\rm{T}}}\mathit{\boldsymbol{w}} + C\sum\limits_{i = 1}^l {\left( {{\xi _i} + \xi _i^*} \right)} } \right\}, $ | (6) |
式中C>0为惩罚因子,其为事先设定的参数.
综上所述,式(5)、(6)构成原所求的回归估计问题.根据凸优化理论[18],可知其对偶问题为
| $ \begin{array}{*{20}{c}} {\mathop {\min }\limits_{\mathit{\boldsymbol{\alpha }},{\mathit{\boldsymbol{\alpha }}^*} \in {R^1}} \left\{ {\frac{1}{2}\sum\limits_{i,j = 1}^l {\left( {\alpha _i^* - {\alpha _i}} \right)} \left( {\alpha _j^* - {\alpha _j}} \right)K\left( {{\mathit{\boldsymbol{X}}_i},{\mathit{\boldsymbol{X}}_j}} \right) + } \right.}\\ {\left. {\varepsilon \sum\limits_{i = 1}^l {\left( {{\alpha _i} + \alpha _i^*} \right)} - \sum\limits_{i = 1}^l {{y_i}} \left( {\alpha _i^* - {\alpha _i}} \right)} \right\}.} \end{array} $ |
式中:α、α*分别为l维的拉格朗日系数向量;K(Xi, Xj)为核函数,K(Xi, Xj)=Φ(Xi)·Φ(Xj),即Φ(Xi)和Φ(Xj)的内积.相应的约束条件式(5)可变为
| $ \sum\limits_{i = 1}^l {\left( {{\alpha _i} - \alpha _i^*} \right)} = 0,0 \le {\alpha _i},\alpha _i^* \le C $ |
对应回归估计函数模型为
| $ f\left( \mathit{\boldsymbol{X}} \right) = \sum\limits_{i = 1}^l {\left( {\alpha _i^* - {\alpha _i}} \right)K\left( {{\mathit{\boldsymbol{X}}_i},\mathit{\boldsymbol{X}}} \right) + b} . $ |
根据支持向量机KKT条件,可得[17]:
| $ \begin{array}{*{20}{l}} {\varepsilon + {y_j} - \left( {\sum\limits_{i = 1}^l {\left( {\alpha _i^* - {\alpha _i}} \right)} K\left( {{\mathit{\boldsymbol{X}}_i},{\mathit{\boldsymbol{X}}_j}} \right) + b} \right) = 0,}\\ {\forall \alpha _j^* = 0,0 < {\alpha _j} < C;} \end{array} $ | (7) |
| $ \begin{array}{*{20}{l}} {\varepsilon - {y_k} + \sum\limits_{i = 1}^t {\left( {\alpha _i^* - {\alpha _i}} \right)} K\left( {{\mathit{\boldsymbol{X}}_i},{\mathit{\boldsymbol{X}}_k}} \right) + b = 0,}\\ {\forall {\alpha _k} = 0,0 < \alpha _k^* < C,} \end{array} $ | (8) |
由式(7)、(8),可得b的计算公式为
| $ \begin{array}{*{20}{c}} {b = {y_j} - \sum\limits_{i = 1}^l {\left( {\alpha _i^* - {\alpha _i}} \right)K\left( {{\mathit{\boldsymbol{X}}_i},{\mathit{\boldsymbol{X}}_j}} \right)} + \varepsilon ,}\\ {\forall \alpha _j^* = 0,0 < {\alpha _j} < C;} \end{array} $ | (9) |
或
| $ \begin{array}{*{20}{c}} {b = {y_k} - \sum\limits_{i = 1}^t {\left( {\alpha _i^* - {\alpha _i}} \right)K\left( {{\mathit{\boldsymbol{X}}_i},{\mathit{\boldsymbol{X}}_k}} \right)} - \varepsilon ,}\\ {\forall {\alpha _k} = 0,0 < \alpha _k^* < C,} \end{array} $ | (10) |
由式(9)、(10)可知,b由α, α*决定.此外,实际计算中b最终值取所有上述值的平均值.
α, α*可通过SMO算法求解,从而可得出最终的回归估计函数模型.虽然上述回归问题是针对多输入单输出系统,但只要分别对不同输出利用上述方法求解,便可求出多输入多输出系统的回归模型.由水下航行器模型可知,其输出维数是12,记其分别对应的回归估计函数模型为
| $ {f_i}\left( \mathit{\boldsymbol{X}} \right) = {\mathit{\boldsymbol{w}}_i}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( \mathit{\boldsymbol{X}} \right) + {b_i}, $ |
式中i=1, 2, …, 12.则基于支持向量机所建立的水下航行器模型为以下形式:
| $ \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{x}}(k + 1)}\\ {\mathit{\boldsymbol{q}}(k + 1)} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{f_1}(\mathit{\boldsymbol{X}})}\\ {{f_2}(\mathit{\boldsymbol{X}})}\\ \vdots \\ {{f_{12}}(\mathit{\boldsymbol{X}})} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{w}}_1}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}(\mathit{\boldsymbol{X}}) + {b_1}}\\ {{\mathit{\boldsymbol{w}}_2}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}(\mathit{\boldsymbol{X}}) + {b_2}}\\ \vdots \\ {{\mathit{\boldsymbol{w}}_{12}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}(\mathit{\boldsymbol{X}}) + {b_{12}}} \end{array}} \right]. $ |
式中:X为模型输入,即{x(k), q(k), τ(k)};wi、bi分别由前述的支持向量机求解方法求出.需指出的是,本文核函数选为径向基函数:
| $ K\left( {{\mathit{\boldsymbol{X}}_i},{\mathit{\boldsymbol{X}}_j}} \right) = \exp \left( { - {{\left\| {{\mathit{\boldsymbol{X}}_i} - {\mathit{\boldsymbol{X}}_j}} \right\|}^2}/{\sigma ^2}} \right), $ |
式中σ为设定的参数.
2.2 粒子群寻优粒子群算法(particle swarm optimization,PSO)具有较快的计算速度和较强的全局搜索能力,已广泛应用于工程优化问题.
在利用支持向量机求解回归估计模型时,有3个参数需事先设定,即惩罚因子C、不敏感因子ε、核函数参数σ.为获得较准确的模型,本文使用粒子群算法来寻找这3个参数的最优值.
为了判断所求回归估计模型的优劣,本文采用了k-折交叉确认方法[19]:把l个训练点随机分成k个互不相交数量相同的子集,然后进行k次训练和测试;每次训练和测试时,选取第k个集合作为测试集,其他都为训练集,记录每次测试错误点个数;k次训练和测试完成后,所有错误点个数之和与所有训练点个数的比值作为每次求得的回归估计模型的优劣评价标准.本文选取k=10.
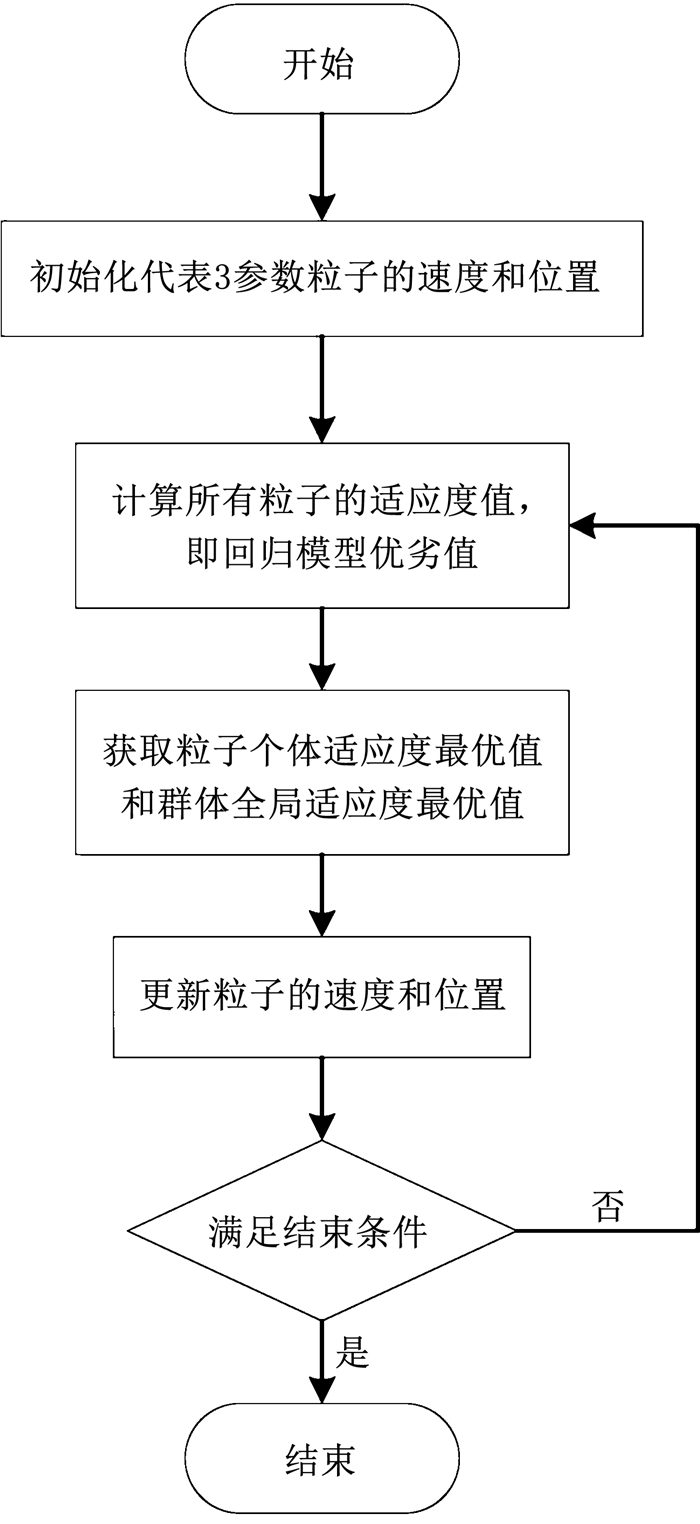
粒子群算法寻找3个参数最优值的具体流程如图 1所示.
|
图 1 粒子群算法参数寻优流程 Fig. 1 Flow chart of selecting optimal parameters with PSO algorithm |
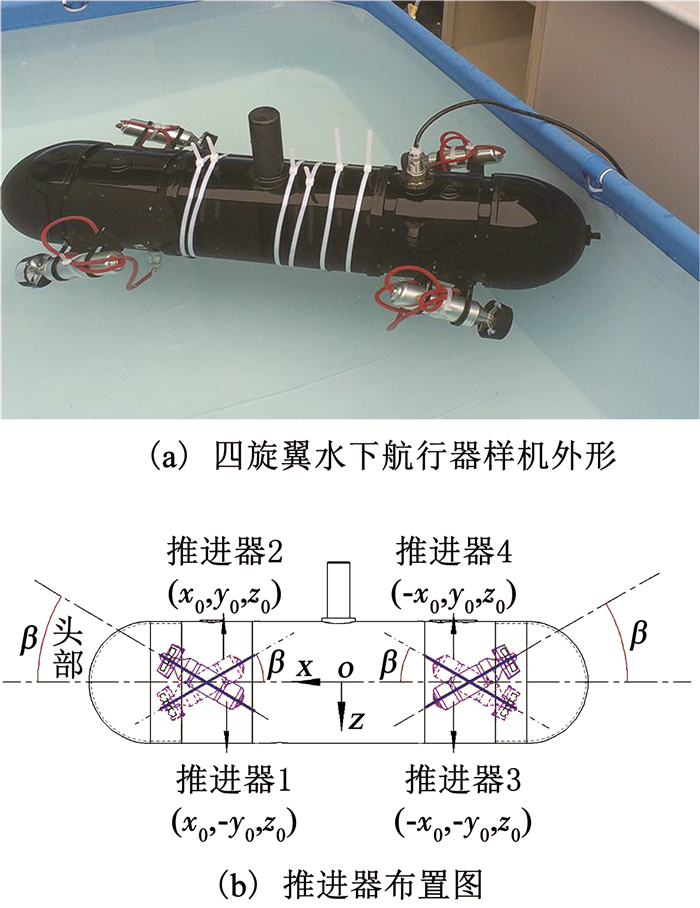
为有效检验上述方法对水下航行器黑箱建模的有效性,选取了本实验室研制的新型四旋翼水下航行器[20]作为研究对象.整体航行器外形结构如图 2(a)所示.图 2(b)给出了推进器的布置方式:4个推进器两两分布在航行器两侧,并与水平面成一定角度β(0° < β < 90°);两侧推进器恰形成两“X”型.
|
图 2 四旋翼水下航行器样机 Fig. 2 Sample of the quadrotor-like unmanned underwater vehicle prototype |
本文以某次空间运动的前半段作为黑箱建模所需训练数据,后半段作为预报和检验数据,并根据推进器力u的是否时变性选取了两种空间运动来进行实验验证.
当u为常数时,即u={15,-20, 20,-15},其训练与预报结果如图 3所示,分别显示了线性速度(u, v, w)、角速度(p, q, r)、位置(x, y, z)和姿态角(φ, θ, φ)的训练和预报结果.后半段运动预报的效果用均方根误差来评价,其结果见表 1.从图 3、表 1中可以看出,训练结果和预报结果都与原始实际数据基本吻合,说明当推进器力u为常数时,支持向量机所建立的黑箱模型与实际模型基本吻合.

|
图 3 u为常数时的训练和预报结果 Fig. 3 Results of training and prediction when u is constant |
| 表 1 u为常数时的预报精度 Tab. 1 Precision of prediction results when u is constant |
当u为时变函数时,即
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{u}} = [0.2t, - 0.3t,0.3t, - 0.2t],0 \le t \le 75,}\\ {\mathit{\boldsymbol{u}} = [ - 0.2t,0.3t, - 0.3t,0.2t],75 < t \le 150,} \end{array}} \right. $ |
式中:t为时间,训练与预报结果如图 4所示,分别显示了线性速度(u, v, w)、角速度(p, q, r)、位置(x, y, z)和姿态角(ϕ, θ, φ)的训练和预报结果.后半段运动预报的效果用均方根误差来评价,其结果见表 2.从图 4、表 2中可以看出,训练和预报结果都与实际值基本吻合,说明当推进器力u时变时,支持向量机所建立的黑箱模型与实际模型也基本吻合.

|
图 4 u为时变的训练和预报结果 Fig. 4 Results of training and prediction when u varies with time |
| 表 2 u为时变的预报精度 Tab. 2 Precision of prediction results when u varies with time |
从上述两种运动的训练与预报结果可以看出,通过粒子群参数寻优的支持向量机所建立的水下航行器黑箱模型与实际模型基本吻合,预报结果均方根误差较小,能比较准确预测水下航行器的各项运动信息,为以后新型水下航行的运动控制等进一步研究奠定基础.
4 结论1) 本文提出了应用粒子群参数寻优和支持向量机的水下航行器黑箱建模方法.该方法利用支持向量机获得水下航行器模型输入和输出之间的非线性映射关系,并利用粒子群优化算法获得支持向量机3组参数的最佳值,进而获得水下航行器黑箱模型.
2) 本文以新型四旋翼水下航行器为例,通过两种空间运动前期数据训练获得了其黑箱模型,并以该模型预报了后期水下航行器的运动.实验结果表明,上述方法在仅已知运动状态信息和推进器力情况下,所获得黑箱模型对空间运动预报的均方根误差较小,空间运动预报结果与实际运动一致,黑箱模型与实际模型基本吻合.
3) 应用粒子群参数寻优和支持向量机可较好地构建水下航行器黑箱模型,所建模型能有效预报新型水下航行器运动,从而有利于新型水下航行器进一步应用研究.
| [1] |
ANTONELLI G. Underwater robots: Motion and force control of vehicle-manipulator systems[M]. Heidelberg, Berlin: Springer, 2010.
|
| [2] |
FELDMAN J. DTNSRDC revised standarrd submarine equations of motion: DTNSRDC/SPD-0393-09[S]. Washington, DC: David Taylor Naval Ship Research and Development Center, 1979
|
| [3] |
陈强. 水下无人航行器[M]. 北京: 国防工业出版社, 2014. CHEN Qiang. Unmanned underwater vehicle[M]. Beijing: National Defense Industry Press, 2014. |
| [4] |
SABET M T, SARHADI P, ZARINI M. Extended and Unscented Kalman filters for parameter estimation of an autonomous underwater vehicle[J]. Ocean Engineering, 2014, 91: 329. DOI:10.1016/j.oceaneng.2014.09.013 |
| [5] |
SHAFIEI M H, BINAZADEH T. Application of neural network and genetic algorithm in identification of a model of a variable mass underwater vehicle[J]. Ocean Engineering, 2015, 96: 173. DOI:10.1016/j.oceaneng.2014.12.021 |
| [6] |
朱胜庭, 朱大奇, 邓志刚. 多新息最小二乘法辨识水下机器人动力学模型[J]. 系统仿真学报, 2013, 25(6): 1399. ZHU Shengting, ZHU Daqi, DENG Zhigang. Identification of underwater vehicle dynamic model using multi-innovation least squares algorithm[J]. Journal of System Simulation, 2013, 25(6): 1399. DOI:10.16182/j.cnki.joss.2013.06.050 |
| [7] |
CORTES C, VAPNIK V. Support-vector networks[J]. Machine Learning, 1995, 20(3): 273. DOI:10.1007/BF00994018 |
| [8] |
ISA D, LEE L H, KALLIMANI V P, et al. Text document preprocessing with the Bayes formula for classification using the support vector machine[J]. IEEE Transactions on Knowledge and Data Engineering, 2008, 20(9): 1264. DOI:10.1109/TKDE.2008.76 |
| [9] |
邴其春, 龚勃文, 杨兆升, 等. 一种组合核相关向量机的短时交通流局域预测方法[J]. 哈尔滨工业大学学报, 2017, 49(3): 144. BING Qichun, GONG Bowen, YANG Zhaosheng, et al. A short-term traffic flow local prediction method of combined kernel function relevance vector machine[J]. Journal of Harbin Institute of Technology, 2017, 49(3): 144. DOI:10.11918/j.issn.0367-6234.2017.03.023 |
| [10] |
徐锋, 邹早建, 徐小卡, 等. 基于支持向量机的船舶操纵运动黑箱建模[J]. 北京航空航天大学学报, 2013, 39(11): 1553. XU Feng, ZOU Zaojian, XU Xiaoka, et al. Black-box modeling of ship manoeuvring motion based on support vector machines[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(11): 1553. DOI:10.13700/j.bh.1001-5965.2013.11.026 |
| [11] |
KENNEDY J, EBERHART R. Particle swarm optimization[C]//Proceedings of the International Conference on Neural Networks. Perth, WA: IEEE, 1995: 488968. DOI: 10.1109/ICNN.1995.488968
|
| [12] |
杨维, 李歧强. 粒子群优化算法综述[J]. 中国工程科学, 2004, 6(5): 87. YANG Wei, LI Qiqiang. Survey on particle swarm optimization algorithm[J]. Engineering Science, 2004, 6(5): 87. DOI:10.3969/j.issn.1009-1742.2004.05.018 |
| [13] |
KIM T H, MARUTA I, SUGIE T. Robust PID controller tuning based on the constrained particle swarm optimization[M]. Tarrytown, NY: Pergamon Press, Inc, 2008. DOI:10.1016/j.automatica.2007.08.017
|
| [14] |
GAING Z L. A particle swarm optimization approach for optimum design of PID controller in AVR system[J]. IEEE Transactions on Energy Conversion, 2004, 19(2): 384. DOI:10.1109/TEC.2003.821821 |
| [15] |
FOSSEN T I. Handbook of marine craft hydrodynamics and motion control[M]. New York: Wiley, 2011.
|
| [16] |
DO K D, PAN Jie. Control of ships and underwater vehicles[J]. London: Springer, 2009. DOI:10.1007/978-1-84882-730-1 |
| [17] |
SMOLA A J, SCHOLKOPF B. A tutorial on support vector regression[J]. Statistics and Computing, 2004, 14(3): 199. DOI:10.1023/B:STCO.0000035301.49549.88 |
| [18] |
BOYD S, VANDENBERGHE L. Convex optimization[M]. Cambridge: Cambridge University Press, 2004.
|
| [19] |
BRERETON R G, LLOYD G R. Support vector machines for classification and regression[J]. Analyst, 2010, 135(2): 230. DOI:10.1039/b918972f |
| [20] |
BIAN Jingwei, XIANG Ji. QUUV: A quadrotor-like unmanned underwater vehicle with thrusts configured as X shape[J]. Applied Ocean Research, 2018, 78: 201. DOI:10.1016/j.apor.2018.06.017 |
 2019, Vol. 51
2019, Vol. 51


