可控释放体系可以根据需要调控活性物质的释放，进而在不同时间维持目标的活性物质质量浓度^[1].近年来，基于其安全有效的特性，在药物、食品等众多领域得到了广泛的关注与应用^[2-3]，尤其是在药物领域，可控释放体系已成为热点研究方向.药物释放行为通常呈现出先“突释”然后按一级动力学扩散的现象.所谓的“突释”，是指释放初期的释放速率很高，之后快速降低的这种现象.“突释”效应会导致药剂使用过量并对人体产生毒副作用^[4]，因此，人们在药物的使用过程中要尽量避免“突释”的发生.为了能够减少“突释”所带来的危害，并实现药物的可控释放，多层平板体系以及其他各种几何形状的控释体系模型被广泛研究.其中，多层平板药物控释体系结构简单，便于控制，并且已有研究证明在多层平板体系中，对初始药物质量浓度分布进行适当的调节可以有效控制“突释”^[5].

相比于可控释放体系模型的研究工作，优化体系中药物释放行为的研究相对较少.Lu等^[6]针对不同的目标释放，利用优化控制理论和变分法优化了多层平板体系中药物初始质量浓度分布；Nauman等^[7]利用随机搜索方法，对多层平板控释体系的初始质量浓度分布进行了优化以改善带“突释”的恒速释放等药物释放行为；黄建敏等^[1]利用混合Newton-Tikhonov正则化方法优化了球形扩散控制体系中的药物初始质量浓度分布及扩散系数.

反问题是数学中一个重要的研究方向，许多实际问题都可以归结为反问题的求解，控释体系中药物释放行为的优化也不例外.本文基于数学物理反问题的思路，将多层平板控释体系中的药物初始质量浓度分布的优化问题归结为一个扩散方程反问题，然后进行求解.而在反问题的求解中，被普遍采用并行之有效的方法是由数学家Tikhonov^[8]提出的Tikhonov正则化方法.自Tikhonov正则化方法提出后，众多学者对其进行了研究和改进.李功胜等^[9]基于传统的正则化方法，提出了一种新的正则化算法，在求解第一类Fredholm积分方程上取得了很好的效果；Lin等^[10]基于加权半范数提出了一种新的正则化方法，结合一维、二维积分方程算例, 验证了该方法的有效性；Maass^[11]基于Bregman映射提出了一种求解非线性不适定问题的迭代正则化方法；Shi^[12]等采用卷积正则化方法研究了一类严重不适定的线性抛物型方程反问题，提出了一种新的广义偏差原理.

本文基于紧算子的奇异值系统理论，构造了一种新的正则化滤子函数，进而提出了一种新的吉洪诺夫正则化算法，并用于研究药物在多层平板控释体系中的初始质量浓度分布问题，从而使药物释放行为能够接近或达到所需的目标释放.

1 多层平板体系扩散模型建立及反问题提出

多层平板药物控释体系由于其结构简单，便于调控，能够有效控制药物释放的特点，被广泛的应用于药品开发、药物制备等领域，是目前最常用的药物控释体系之一.多层平板药物控释装置的核心基质处包含有药物或者其他的活性物质，外面则包裹有多层可以调节药物释放速率的隔离层.也就是不同平板层均包含有药物，但各层的药物质量浓度不同.现有的实验及理论说明，非均匀的药物初始质量浓度分布能够调节药物的释放，从而有效的控制突释效应以及产生符合人们预期的药物释放要求.为了能够更好的理解和模拟这些复杂的药物控释体系的药物释放机理，通过建立相应的数学模型来进行研究是非常有必要的.

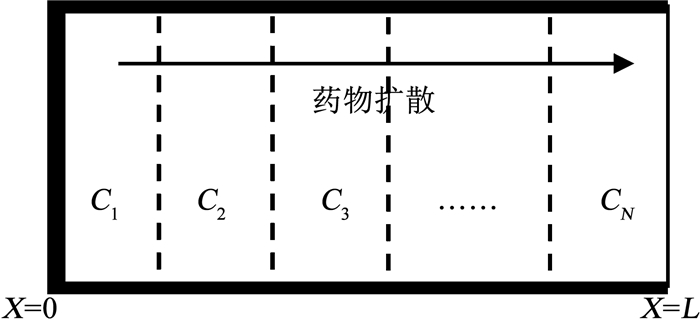
1.1 多层平板药物控释体系的数学模型

N层平板药物释放体系如图 1所示.设C₁, C₂, …, C_N为体系中每层的药物质量浓度分布，L为厚度，V(X)为体系在初始时刻的药物质量浓度曲线.若假设体系所释放出的药物能够被最外侧的液体迅速地转移或吸收，那么就可以用一维扩散来模拟药物在多层平板体系中由里层到外层的释放.由于低药物浓度对药物的扩散性不会产生影响，因此只考虑低药物浓度的情况，同时不考虑体系中基质的溶解和溶胀，并假设药物扩散是速率可控的.

在数学上，该扩散过程可以用菲克第二定律描述为如下偏微分方程：

$ \frac{{\partial C}}{{\partial \tau }} = \frac{\partial }{{\partial X}}\left( {D\frac{{\partial C}}{{\partial X}}} \right). $

(1)

式中：C为药物质量浓度分布；τ为释放时间；X为一维扩散过程的位置；D为药物扩散系数.

假设最里层内侧界面的扩散通量为零，最外层与外界环境接触面的药物质量浓度设为零.这样，边界条件可以表示如下：

$ {\left. {\frac{{\partial C}}{{\partial X}}} \right|_{X = 0}} = 0,\tau > 0; $

(2)

$ C(\tau ,L) = 0,\tau > 0. $

(3)

方程(1)的初始条件为：

$ C(0,X) = V(X),\tau = 0,0 < X < L. $

(4)

体系最外层与环境接触面的单位时间单位面积的药物扩散量称为扩散通量，用J表示，它是药物的释放速率.由菲克第一定律，J可表示为

$ J(\tau ,L) = - {D_{\left( {X = L} \right)}}\frac{{\partial C}}{{\partial X}}\left| {,\tau > 0} \right.. $

(5)

1.2初值反问题模型

对于数学模型(1)~(5)，若初始条件和边界条件已知，计算质量浓度分布函数C(τ, X)为正问题.对应地，在边界条件和附加条件已知的情形下，求解初始条件(药物初始浓度分布V(X))即为一个典型的初值反问题，而反问题通常是不适定的.

假设扩散系数取常数，并进行归一化处理可得：

$ c = C/{C_0},v = V(X)/{C_0},x = X/L, $

$ t = {D_0}\tau /{L^2},j = JL/{D_0}{C_0},d = D/{D_0} = 1. $

式中：C₀、D₀分别为参考质量浓度和参考扩散系数.

则数学模型变为

$ \frac{{\partial c}}{{\partial t}} = \frac{{{\partial ^2}c}}{{\partial {x^2}}}, $

(6)

边界条件为

$ {\left. {\frac{{\partial c}}{{\partial x}}} \right|_{x = 0}} = 0,t > 0; $

(7)

$ c(t,1) = 0,t > 0, $

(8)

初始条件为

$ c(0,x) = v(x),t = 0,0 < x < 1. $

(9)

附加条件设为释放体系与周遭环境接触面上的扩散通量(药物释放速率).

$ j(t,1) = - {\left. {\frac{{\partial c}}{{\partial x}}} \right|_{x = 1}} = j(t),t > 0. $

(10)

结合边界条件以及附加条件j(t)来确定药物初始质量浓度分布v(x)，就是一个扩散方程反问题.该扩散方程反问题实际上是一个如何求解第一类Fredholm积分方程的问题.第1步先求解正问题(6)~(9)，采用分离变量法求得

$ \begin{array}{l} c(t,x) = \sum\limits_{k = 0}^\infty {2{{\rm{e}}^{ - {{\left[ {\left( {k + \frac{1}{2}} \right){\rm{ \mathsf{ π} }}} \right]}^{{2_t}}}}}} \cos \left( {k + \frac{1}{2}} \right){\rm{ \mathsf{ π} }}x\int_0^1 v (x) + \\ \;\;\;\;\;\;\;\;\;\;\;\cos \left( {k + \frac{1}{2}} \right){\rm{ \mathsf{ π} }}x{\rm{d}}x. \end{array} $

(11)

式(11)为所求正问题的解析解，基于式(11)即能够计算出式(10)中扩散通量j(t)的具体表达式.将式(11)代入式(10)中可得：

$ \begin{array}{l} j(t) = - {\left. {\frac{{\partial c}}{{\partial x}}} \right|_{x = 1}} = \\ \;\;\;\;\;\;\;\;\;\sum\limits_{k = 0}^\infty 2 {{\rm{e}}^{ - {{\left[ {\left( {k + \frac{1}{2}} \right){\rm{ \mathsf{ π} }}} \right]}^{{2_t}}}}}\left( {k + \frac{1}{2}} \right){\rm{ \mathsf{ π} }}\sin \left( {k + } \right.\\ \;\;\;\;\;\;\;\;\;\begin{array}{*{20}{l}} {\left. {\frac{1}{2}} \right){\rm{ \mathsf{ π} }}\int_0^1 v (x)\cos \left( {k + \frac{1}{2}} \right){\rm{ \mathsf{ π} }}x{\rm{d}}x = }\\ {\sum\limits_{k = 0}^\infty 2 \cdot {{( - 1)}^k}\left( {k + \frac{1}{2}} \right){\rm{ \mathsf{ π} }} \cdot } \end{array}\\ \;\;\;\;\;\;\;\;\;{{\rm{e}}^{ - {{\left[ {\left( {k + \frac{1}{2}} \right){\rm{ \mathsf{ π} }}} \right]}^{{2_t}}}}}\int_0^1 v (x)\cos \left( {k + \frac{1}{2}} \right){\rm{ \mathsf{ π} }}x{\rm{d}}x = \\ \;\;\;\;\;\;\;\;\;2\int_0^1 {\left[ {\sum\limits_{k = 0}^\infty {{{( - 1)}^k}} \left( {k + \frac{1}{2}} \right){\rm{ \mathsf{ π} }}{{\rm{e}}^{ - {{\left[ {\left( {k + \frac{1}{2}} \right)p} \right]}^{{2_t}}}}}\cos \left( {k + } \right.} \right.} \\ \;\;\;\;\;\;\;\;\;\left. {\left. {\frac{1}{2}} \right){\rm{ \mathsf{ π} }}x} \right]v(x){\rm{d}}x. \end{array} $

(12)

基于式(12)，数学反问题模型即可归纳为第一类Fredholm积分方程：

$ \int_a^b k (s,t)x(s){\rm{d}}s = y(t), $

由扩散通量j(t)求初始质量浓度分布v(x)的问题，即求解积分方程：

$ 2\int_0^1 {\left[ {\sum\limits_{k = 0}^\infty {{{( - 1)}^k}} \left( {k + \frac{1}{2}} \right){\rm{ \mathsf{ π} }}{{\rm{e}}^{{{\left[ {\left( {k + \frac{1}{2}} \right){\rm{ \mathsf{ π} }}} \right]}^{{2_t}}}}}\cos \left( {k + \frac{1}{2}} \right){\rm{ \mathsf{ π} }}x} \right]} \cdot v(x){\rm{d}}x = j(t). $

(13)

2 改进Tikhonov正则化方法

基于正则化滤子函数^[13]的概念，Tikhonov正则化方法的滤子函数为：q(α, μ)=$\frac{{{\mu _2}}}{{\alpha + {\mu _2}}}$.2006年，张瑞等^[14]设计了一种新的正则化滤子函数：q(α, μ)=$\frac{{{\mu ^\sigma }}}{{{{\left( {\alpha + {\mu ^{\sigma r}}} \right)}^{\frac{1}{r}}}}}$，r＞0, σ≥1，证明了正则化参数的适当选择能够有助于求得的正则解具有最优的渐进收敛率.在本文中基于截断奇异值正则化方法和上述改进正则化方法，给出了一种改进的Tikhonov正则化方法，对解的收敛性及其渐进最优阶估计进行了证明，并通过具体算例验证了方法的有效性.

下面给出关于正则化滤子函数的相关引理.

引理1^[13]  设X，Y均为Hilbert空间，K:X→Y是紧算子，K的奇异系统为(μ_i, x_i, y_i)，函数q:(0, +∞)×(0, ‖K‖]→R，具有以下性质：

1)|q(α, μ)|≤1, ∀α∈(0, +∞), ∀μ∈(0, ‖K‖];

2) 对∀α∈(0, +∞)，存在常数c(a)＞0，使得, |q(α, μ)|≤c(α)μ, ∀μ∈(0, ‖K‖];

3) $\mathop {\lim }\limits_{a \to 0} q\left( {\alpha , \mu } \right) = 1$, ∀μ∈(0, ‖K‖].

则由下式定义的算子R_α:Y→X, 即

$ {R_\alpha }y = \sum\limits_{i = 1}^\infty {\frac{{q\left( {\alpha ,{\mu _i}} \right)}}{{{\mu _i}}}} \left( {y,{y_i}} \right){x_i}, $

可以确定一个正则化方法，且‖R_a‖≤c(α).本文称具有以上3条性质的二元函数q(α, μ)为算子K的正则化滤子函数.

Tikhonov正则解即是Tikhonov泛函的极小值，也可以基于奇异系统概念表示为

$ x_\alpha ^\delta = {R_\alpha }{y_\delta } = \sum\limits_{i = 1}^\infty {\frac{{q\left( {\alpha ,{\mu _i}} \right)}}{{{\mu _i}}}} \left( {{y_\delta },{y_i}} \right){x_i}, $

式中$q\left( {\alpha , \mu } \right) = \frac{{{\mu ^2}}}{{\alpha + {\mu ^2}}}$, α＞0, 0＜μ≤‖K‖即为传统Tikhonov正则化方法的滤子函数.

下面，本文将基于一类新的正则化滤子函数来构造一种改进的Tikhonov正则化方法.

2.1 新正则化滤子函数

文献[14]中所提出的新滤子函数为

$ q(\alpha ,\mu ) = \frac{{{\mu ^\sigma }}}{{{{\left( {\alpha + {\mu ^{\sigma r}}} \right)}^{\frac{1}{r}}}}},r > 0,\sigma \ge 1. $

截断奇异值(TSVD)正则化方法的滤子函数为

$ q(\alpha ,\mu ) = \left\{ {\begin{array}{*{20}{l}} {1,\mu \ge \alpha ;}\\ {0,\mu < \alpha .} \end{array}} \right. $

本文基于上述两种滤子函数，提出了一种新的正则化滤子函数

$ q(\alpha ,\mu ) = \left\{ \begin{array}{l} 1,{\mu ^{\sigma r}} \ge \alpha ;\\ \frac{{{\mu ^\sigma }}}{{{{\left( {\alpha + {\mu ^{\sigma r}}} \right)}^{\frac{1}{r}}}}},{\mu ^{\sigma r}} < \alpha , \end{array} \right. $

(14)

式中:α>0, 0 < μ≤‖K‖, r>0, σ≥1.

基于此种滤子函数的正则化方法在保证大的奇异值不被修正的同时，也能够过滤小的奇异值，解的精确性也不会受到影响.关于这种新滤子函数，本文可以证明如下定理.

定理1  式(14)定义的函数q(α, μ)是一类正则化滤子函数.

证明  1)当μ^σr≥α时，q(α, μ)=1≤1；

当μ^σr < α时，因为μ^σ=(μ^σr)^1/r < (α+μ^σr)^1/r，所以$q\left( {\alpha , \mu } \right) = \frac{{{\mu ^\sigma }}}{{{{\left( {\alpha + {\mu ^{\sigma r}}} \right)}^{1/r}}}} < 1$.

2) 当μ^σr≥α时，$\frac{{{\mu ^{\sigma r}}}}{\alpha } \ge 1 \Rightarrow \frac{\mu }{{{\alpha ^{1/\sigma r}}}} \ge 1$，所以|q(α, μ)|=1≤$\frac{1}{{{\alpha ^{1/\sigma r}}}}$·μ；

当μ^σr < α时，q(α, μ)=$\frac{{{\mu ^\sigma }}}{{{{\left( {\alpha + {\mu ^{\sigma r}}} \right)}^{1/r}}}}$.

当$q = \frac{\sigma }{{\sigma - 1}}$时有，

$ q(\alpha ,\mu ) = \frac{\mu }{{{{\left( {\alpha + {\mu ^r}} \right)}^{1/r}}}} \le \frac{\mu }{{{\alpha ^{1/r}}}}. $

当σ>1时，由Yong不等式α+μ^σr≥α^1/p·μ^σr/q，取p=σ，$q = \frac{\sigma }{{\sigma - 1}}$，则α+μ^σr≥α^1/σ·μ^r(σ-1).于是(α+μ^σr)^1/r≥α^1/rσ·μ^σ-1, 所以

$ \frac{{{\mu ^\sigma }}}{{{{\left( {\alpha + {\mu ^{\sigma r}}} \right)}^{1/r}}}} \le \frac{{{\mu ^\sigma }}}{{{\alpha ^{1/\sigma r}} \cdot {\mu ^{\sigma - 1}}}} = \frac{\mu }{{{\alpha ^{1/\sigma r}}}}, $

因此，对∀σ≥1，都有q(α, μ)≤$\frac{\mu }{{{\alpha ^{1/\sigma r}}}}$.

所以，对∀α>0，|q(α, μ)|≤$\frac{1}{{{\alpha ^{1/\sigma r}}}}$·μ=c(α)μ.

3) 当α→0时，q(α, μ)=1.

由引理1可知$q\left( {\alpha , \mu } \right) = \left\{ \begin{array}{l} 1, {\mu ^{\sigma r}} \ge \alpha ;\\ \frac{{{\mu ^\sigma }}}{{{{\left( {\alpha + {\mu ^{\sigma r}}} \right)}^{\frac{1}{r}}}}}, {\mu ^{\sigma r}} < \alpha , \end{array} \right.$, 是一类正则化滤子函数，其对应的正则化算子R_α:Y→X为

$ {R_\alpha }y = \sum\limits_{i = 1}^\infty {\frac{{q\left( {\alpha ,{\mu _i}} \right)}}{{{\mu _i}}}} \left( {y,{y_i}} \right){x_i}. $

(15)

2.2 正则解的误差估计

定理2  假设Kx=y的解为x⁺=(K^*K)^vz∈R(K^*K)^v，z∈X，且‖z‖≤E，对式(15)确定的正则化算子R_α:Y→X，若选取正则参数α(δ)=$c{\left( {\frac{\delta }{E}} \right)^{\frac{{\sigma r}}{{2v + 1}}}}$(c>0为常数)，则有误差估计为

$ \left\| {x_{\alpha (\delta )}^\delta - {x^ + }} \right\| = {\rm{O}}\left( {{\delta ^{\frac{{2v}}{{2v + 1}}}}} \right). $

证明  方程Kx=y的“真解”x⁺与正则解x_α^δ之间的误差为

$ \left\| {x_\alpha ^\delta - {x^ + }} \right\| \le \left\| {{R_\alpha }} \right\| \cdot \delta + \left\| {{R_\alpha }y - {x^ + }} \right\|. $

由定理1可知，‖R_α‖≤c(α)=$\frac{1}{{{\alpha ^{1/\sigma r}}}}$.利用算子K的奇异系统，又有

$ \begin{array}{l} {\left\| {{R_\alpha }y - {x^ + }} \right\|^2} = \sum\limits_{i = 1}^\infty {{{\left| {q\left( {\alpha ,{\mu _i}} \right) - 1} \right|}^2}} \cdot {\left| {\left( {{x^ + },{x_i}} \right)} \right|^2} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{i = 1}^\infty {{{\left| {q\left( {{\alpha ,{\mu _i}}} \right) - 1} \right|}^2}} \cdot {\left| {\left( {{{\left( {{K^*}K} \right)}^v}z,{x_i}} \right)} \right|^2} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{i = 1}^\infty {{{\left| {q\left( {\alpha ,{\mu _i}} \right) - 1} \right|}^2}} \cdot \left| {\left( {{{\left. {\sum\limits_{j = 1}^\infty {\mu _i^{2v}} \left( {z,{x_j}} \right){x_j},{x_i}} \right|}^2} = } \right.} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{i = 1}^\infty {{{\left| {q\left( {\alpha ,{\mu _i}} \right) - 1} \right|}^{2v}}} \cdot {\left| {\mu _i^2\left( {z,{x_i}} \right)} \right|^2} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{i = 1}^\infty {{{\left| {q\left( {\alpha ,{\mu _i}} \right) - 1} \right|}^2}} \cdot \mu _i^4 \cdot {\left| {\left( {{z_i}{x_i}} \right)} \right|^2}. \end{array} $

当μ^σr < α时，因为0 < q(α, μ) < 1，所以q(α, μ_i)-1 < 1，即

$ \left| {q\left( {\alpha ,{\mu _i}} \right) - 1} \right| \cdot \mu _i^{2v} < \mu _i^{2v} = {\left( {\mu _i^{\sigma r}} \right)^{2v/\sigma r}} < {\alpha ^{2v/\sigma r}}. $

当μ^σr≥α时，q(α, μ)=1，所以

$ \left| {q\left( {\alpha ,{\mu _i}} \right) - 1} \right| \cdot \mu _i^{2v} = 0 \cdot \mu _i^{2v} = 0 < {\alpha ^{2v/\sigma r}}, $

因此q(α, μ_i)-1·μ_i^2v < α^2v/σr，故有

$ \begin{array}{*{20}{c}} {{{\left\| {{R_\alpha }y - {x^ + }} \right\|}^2} < {\alpha ^{4v/\sigma r}}\sum\limits_{i = 1}^\infty {{{\left| {\left( {z,{x_i}} \right)} \right|}^2}} = }\\ {{\alpha ^{4v/\sigma r}} \cdot {{\left\| z \right\|}^2} \le {\alpha ^{4v/\sigma r}} \cdot {E^2},} \end{array} $

即‖R_αy-x⁺‖ < α^2v/σr·E.从而有

$ \left\| {x_\alpha ^\delta - {x^ + }} \right\| \le \frac{1}{{{\alpha ^{1/\sigma r}}}} \cdot \delta + {\alpha ^{\frac{{2v}}{{\sigma \tau }}}} \cdot E. $

若选取α(δ)=$c{\left( {\frac{\delta }{E}} \right)^{\frac{{\sigma r}}{{2v + 1}}}}$，则

$ \begin{array}{*{20}{l}} {\left\| {x_{\alpha (\delta )}^\delta - {x^ + }} \right\| \le \delta \cdot {{\left[ {c{{\left( {\frac{\delta }{E}} \right)}^{\frac{{\sigma r}}{{2v + 1}}}}} \right]}^{ - \frac{1}{{\sigma r}}}} + {{\left[ {c{{\left( {\frac{\delta }{E}} \right)}^{\frac{{\sigma r}}{{2v + 1}}}}} \right]}^{\frac{{2v}}{{\sigma r}}}} \cdot E = }\\ {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\delta \cdot \left[ {{c^{ - \frac{1}{{\sigma r}}}} \cdot {{\left( {\frac{\delta }{E}} \right)}^{\frac{1}{{2v + 1}}}}} \right] + {c^{\frac{{2\nu }}{{\sigma r}}}} \cdot {{\left( {\frac{\delta }{E}} \right)}^{\frac{{2v}}{{2v + 1}}}} \cdot E = }\\ {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\begin{array}{*{20}{l}} {{c^{ - \frac{1}{{\sigma r}}}} \cdot {E^{\frac{1}{{2v + 1}}}} \cdot {\delta ^{1 - \frac{1}{{2v + 1}}}} + {c^{\frac{{2v}}{{\sigma r}}}} \cdot {\delta ^{\frac{{2v}}{{2v + 1}}}} \cdot {E^{1 - \frac{{2v}}{{2v + 1}}}} = }\\ {\left( {{c^{ - \frac{1}{{\sigma e}}}} + {c^{\frac{{2v}}{{\sigma r}}}}} \right) \cdot {E^{\frac{1}{{2v + 1}}}} \cdot {\delta ^{\frac{{2v}}{{2v + 1}}}},} \end{array}} \end{array} $

因此，式(15)给出的正则解的误差满足:

$ \left\| {x_{\alpha (\delta )}^\delta - {x^ + }} \right\| = {\rm{O}}\left( {{\delta ^{\frac{{2v}}{{2v + 1}}}}} \right). $

由此可知，本文提出的新正则化方法可以使正则解的误差达到渐进最优阶.

3 控释体系中药物释放的优化 3.1 优化药物初始浓度

对于多层平板控释体系数学模型，影响药物释放的一个重要参数是初始质量浓度的分布.当且仅当确定了合适的初始质量浓度分布时，药物释放到环境中的释放速率才能达到预期，从而实现最优的药物释放.基于反问题的求解框架，可以依据已知的目标药物释放去反推初始质量浓度分布，从而将药物释放优化问题转变成典型的数学反问题.对转换而来的数学反问题，就可以采用传统的Tikhonov(吉洪诺夫)正则化方法及改进Tikhonov(吉洪诺夫)正则化方法来求解，实现药物释放行为的优化.

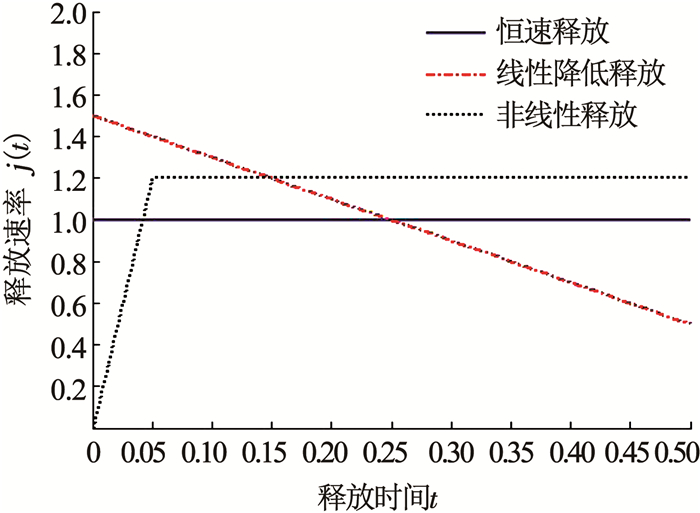
本文主要考察3种目标释放，分别为恒速、线性下降和先线性增加后恒速的非线性释放. 图 2给出了对应的目标释放曲线.针对这3种目标释放曲线，分别采用两种正则化方法求解第1类Fredholm积分方程(13)，优化多层平板体系中的药物初始质量浓度的分布，从而完成药物释放反问题的求解.计算时间从t=0到t=0.5.

3.1.1 恒速目标释放

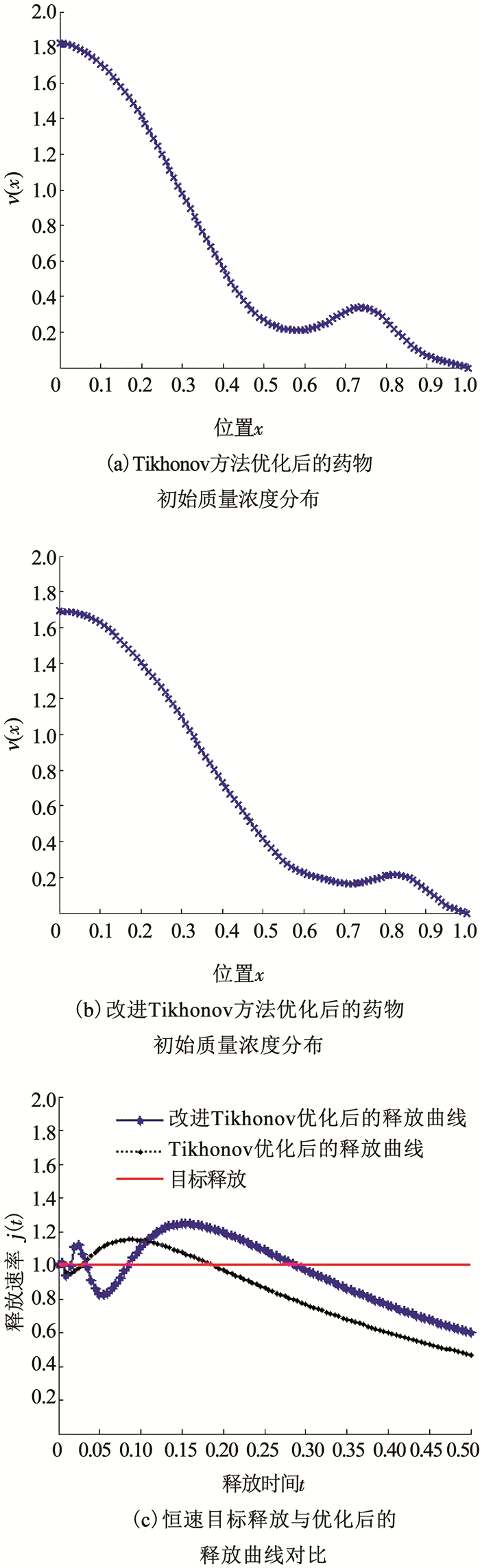
首先考虑的情况为：体系最外层与环境接触面的单位面积药物释放速率j(t)=1, 0≤t≤0.5, 这对应一种最理想的释放行为(释放速率为常数).对于式(13)，取j(t)=1，然后采用吉洪诺夫正则化和改进吉洪诺夫正则化方法求解. 图 3(a)、(b)给出了反演得到的最优药物初始质量浓度分布曲线.依据所得到的药物初始质量浓度分布曲线，由正问题计算得到对应的药物释放速率. 图 3(c)显示了数值计算得到的结果与预期释放曲线的对比，由图 3(c)可以看到：基于Tikhonov正则化方法优化所得到的释放曲线在释放前期比较平缓，与预期释放吻合较好，但随后而来的就是一个快速下降过程，从而导致与预期释放曲线的偏离越来越大.而基于改进Tikhonov正则化方法的释放曲线在释放初期虽说也有一定的波动，但与前者相比，其偏离较小，下降较为缓慢.纵观整个计算区间，其释放速率曲线与预期释放速率曲线误差较小.基于传统Tikhonov正则化方法得到的误差为Err₁=0.217 4，显著大于改进之后的算法误差Err₂=0.169 2.(注：误差可用一个量代表)

3.1.2 线性下降目标释放

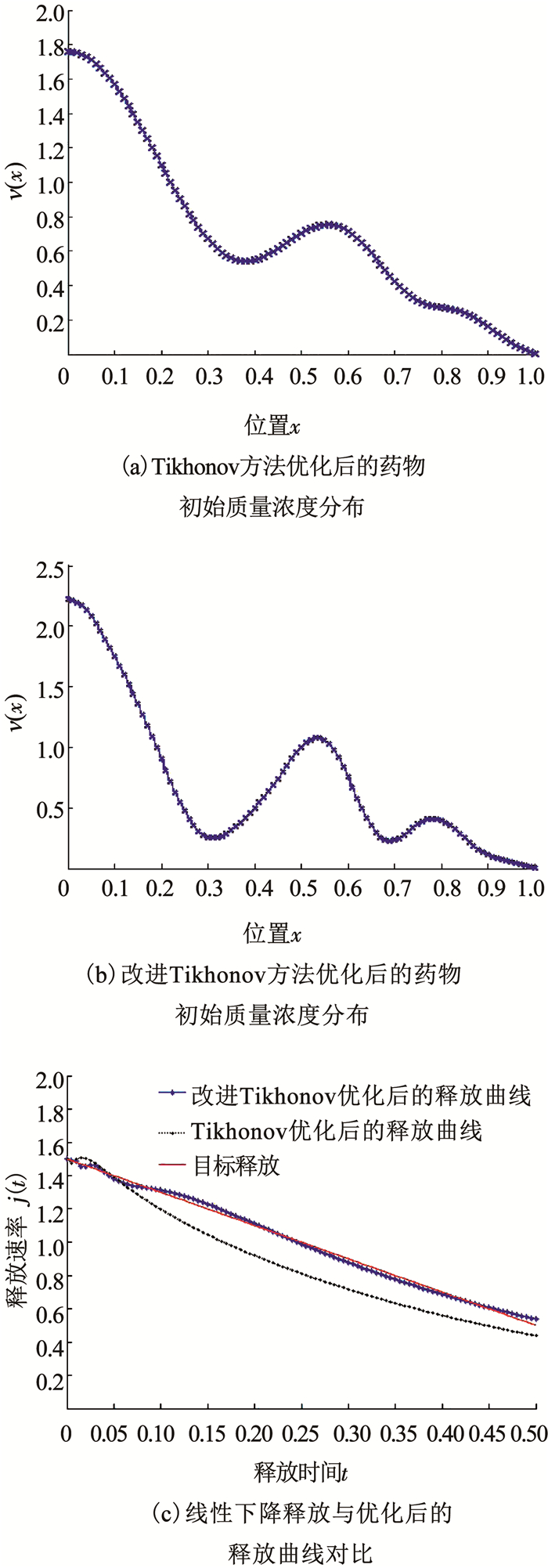
相对而言，呈线性下降的药物释放曲线会更加平缓.基于此，本文考察一种线性下降的药物释放曲线情况，其释放速率函数选择为j(t)=1.5-2t，0≤t≤0.5.采用两种正则化方法优化得到的结果如图 4所示.从图 4可以看到Tikhonov正则化方法所得到的药物释放与预期的线性下降释放速率偏离严重，而改进Tikhonov正则化方法得到的释放曲线则与目标释放曲线基本重合，体现了新算法的优越性.此时，Tikhonov正则化方法得到的误差为Err₁=0.128 5，改进算法的误差为Err₂=0.016 4.

3.1.3 非线性目标释放

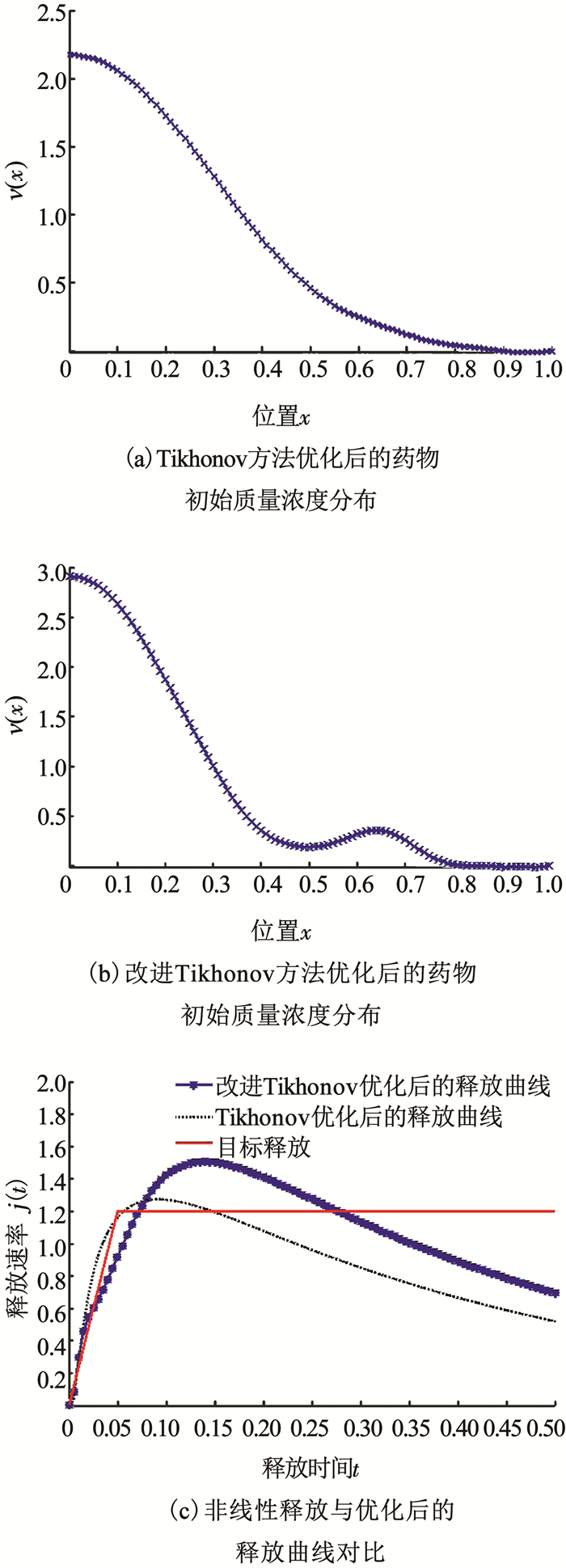
目前，在使用抗癌药物时，希望达到的效果为初期释放量小，后期以恒速释放，避免“突释”效应的影响.鉴于此，本文考察一种前期线性增加后期恒速的非线性释放行为.释放初期，药物释放速率呈线性增长至恒速目标j(t)=1.2，然后保持恒速释放，释放速率的具体函数式为$j\left( t \right) = \left\{ \begin{array}{l} 24t, 0 \le t \le 0.05;\\ 1.2, 0 \le t \le 0.50. \end{array} \right.$采用两种正则化方法优化得到的结果如图 5所示.

从图 5中可以看出，基于Tikhonov正则化方法的药物释放速率曲线释放初期增长快速，直至达到恒速目标速率，然后走出一个快速下降的趋势，从而与恒速释放曲线的偏差逐渐增大.相应的，基于改进Tikhonov正则化方法的释放速率曲线开始为线性增加表现并存在微小波动，到达释放后期后，与恒速目标释放曲线偏离较小，下降趋势较为缓慢.Tikhonov正则化方法得到的误差为Err₁=0.301 9，显著小于改进算法的误差Err₂=0.216 4.

通过以上3种不同情况的对比研究，不难看出，改进Tikhonov正则化方法的优化效果整体上要好于Tikhonov正则化方法, 得出的结果更加令人满意.尤其值得一提的是，对于线性降低目标释放这种情况，基于改进Tikhonov正则化方法得出的结果与目标释放曲线只存在很小的偏差，两条曲线基本吻合.这有力的显示了本文提出的改进Tikhonov正则化方法在求解此类反问题上的有效性.从得出的结果还可以看出，改进方法的数值求解精度要明显高于原有方法，因此能够较好的指导呈现线性降低目标释放趋势的药物控释体系的优化设计工作.

3.2 药物初始浓度分布的加噪反演

在上述研究过程中，本文基于数学物理反问题的框架，采用不同的正则化方法由已知目标释放函数反演求解了多层平板控释体系内的初始质量浓度分布，效果良好.具体实施时，本文假定积分方程(13)的右端项取准确值.但在实际中，人们能够得到的药物释放速率j(t)通常是由实验测量得到的，不可避免的会存在着误差.接下来，本文考虑基于存在误差的药物释放数据来反演多层平板药物控释体系中的初始质量浓度分布.在数学模型中，体现为积分方程(13)的右端项用带有误差δ的扰动数据j_δ来替换.对于存在扰动误差的情况，本文基于改进Tikhonov正则化方法进行加噪反演，从而进一步考察所提算法的稳定性.

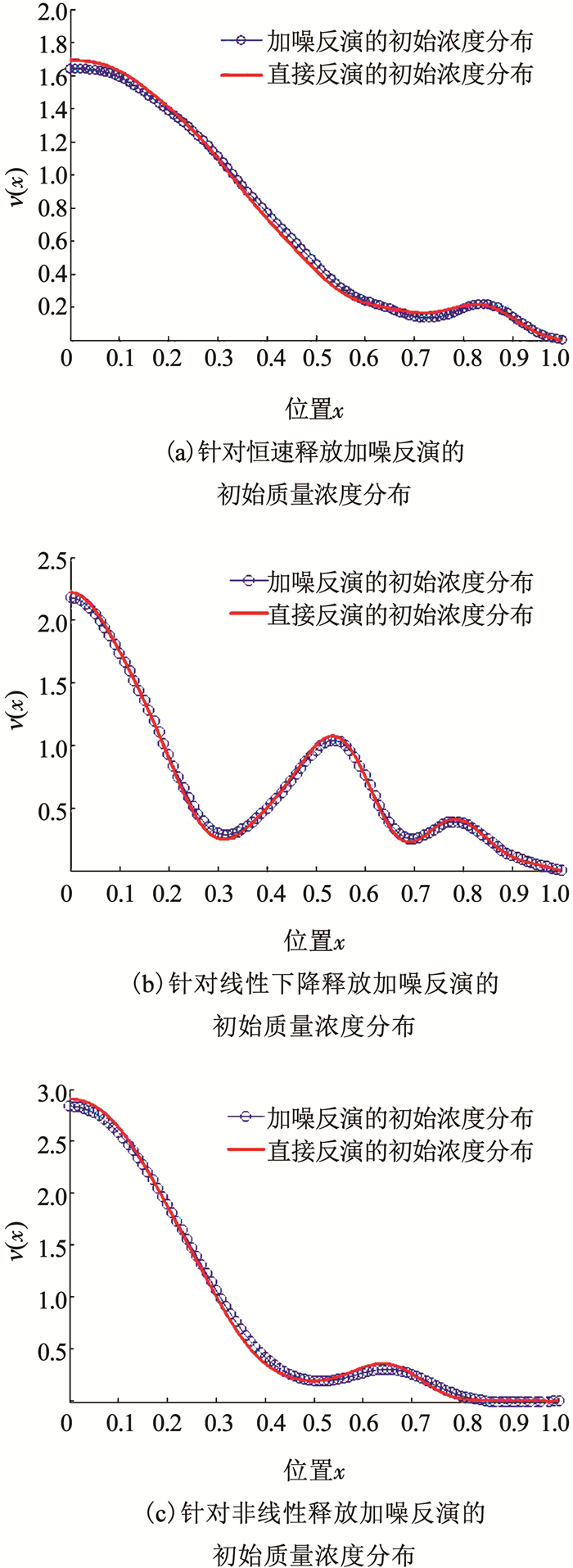
本文仍旧考察恒速释放(j(t)=1)，线性下降释放(j(t)=1.5-2t)和非线性释放($j\left( t \right) = \left\{ \begin{array}{l} 24t, 0 \le t \le 0.05;\\ 1.2, 0 \le t \le 0.50. \end{array} \right.$)这3种不同的情况.假设测量得到的扰动数据为j_δ，|j^δ-j|≤δ，取δ=0.1.改进方法得到结果与未加噪的结果对比图 6所示.由图 6中可以看出，对于3种目标释放速率曲线，改进Tikhonov正则化方法加噪反演的初始质量浓度分布曲线与直接反演的结果几乎重合.这说明本文提出的改进Tikhonov正则化方法在具有良好的抗噪性，数据合理的扰动并不会影响反演结果的精确度.

4 结论

1) 基于多层平板药物控释体系数学模型，将药物释放优化问题转化为扩散方程初值反问题的求解.

2) 针对此类反问题，基于紧算子奇异值系统理论，构造了一种新的正则化滤子函数，从而提出了一种改进的Tikhonov正则化方法，并从理论上给出了改进方法所得正则解的渐进最优阶估计.

3) 采用改进Tikhonov正则化方法对多层平板体系药物释放行为进行了优化，效果整体上好于经典Tikhonov正则化方法.基于改进算法得到的初始质量浓度分布，数值模拟的药物释放曲线与目标释放曲线偏离较小，多层平板体系的药物释放基本实现了拟恒速、拟线性下降及拟非线性的药物释放行为.

4) 对目标释放函数添加10%的噪声后，反演的初始质量浓度分布曲线与未加噪的反演结果几乎重合，验证了改进Tikhonov正则化方法良好的抗噪性.