2. 大连理工大学 计算机科学与技术学院, 辽宁 大连 116024
2. School of Computer Science and Technology, Dalian University of Technology, Dalian 116024, Liaoning, China
随着现代军事逐渐无人化的发展,无人机已经成为了航空科技领域中最活跃和最重要的发展方向之一[1].预计到21世纪初,全球军用无人机的数量将达到23 000多架,这些无人机将主要被应用在侦察,电子对抗,以及攻击战斗等领域.如何使无人机在敌方的雷达、武器等威胁环境中成功完成任务,是一个备受关注的问题.目前世界上已经掀起了一场关于无人机的研究热潮,无人机的航路规划也将会来到一个新的阶段.
粒子群算法在航路规划中得到了非常广泛的应用.文献[2-4]分别对基本粒子群算法在航路规划中的使用做了相应的改进.文献[5-6]对PSO,(RandomWalkPSO, RWPSO)以及一些其他改进的PSO算法包括(QuantumPSO, QPSO)等进行了比较与分析,结果表明RWPSO算法在运行时间,跳出局部最优的能力等方面较大部分改进PSO算法有一定的优势.本文首先验证了RWPSO优化算法在航路规划领域的可行性与优越性,并进一步的将RWPSO与马尔科夫链生存模型相结合,可以实时的评估无人机的状态概率.非常直观的了解无人机在有敌方威胁的环境中执行任务时其状态转移变化与生存率情况.
1 无人机航路规划问题建模 1.1 基于PSO的航路规划模型粒子群算法是一种模拟鸟群寻食的算法,每一只鸟的个体被抽象成没有质量与体积的粒子.在d维的搜索空间中,每个粒子都有自己的位置向量Xi=(xi1,xi2,…, xid),速度向量Vi=(vi1,vi2,…, vid), 以及一个最为关键的适应度值J(n).适应度值由适应度函数确定,在每一次的迭代中,粒子自身的个体最优解为Pbest=(pi1,pi2,…, pid),整个群体找到的全局最优解为Gbest=(gi1,gi2,…, gid),然后根据下面的迭代公式来更新第i个粒子的位置和速度.
| $ \begin{array}{*{20}{c}} {{V_i}(t + 1) = w*{v_{ij}}(t) + {c_1}*\left( {{p_{ij}} - {x_{ij}}(t)} \right) + }\\ {{c_2}*\left( {{g_{ij}} - {x_{ij}}(t)} \right), }\\ \end{array} $ | (1) |
| $ {X_i}(t + 1) = {V_i}(t + 1) + {X_i}(t). $ | (2) |
式中:w为惯性权重,c1、c2为加速因子.c1是粒子的认知部分的权重,表明粒子吸取自身经验的能力,c2是粒子社会部分的权重,表明粒子间的交互能力.相对来说:认知能力越强的粒子收敛的越快,但易于陷入局部最优,社会能力越强的粒子,越能找到最优解,但是算法效率越低.
本文适应度函数的基本结构如下:
| $ \begin{array}{*{20}{c}} {J(n) = {w_{\rm{S}}}*{C_{\rm{S}}}(n) + {w_{\rm{P}}}*{C_{\rm{P}}}(n) + {w_{\rm{R}}}*}\\ {{C_{\rm{R}}}(n) + {w_{\rm{O}}}*{C_{\rm{O}}}(n) + {w_{\rm{H}}}*{C_{\rm{H}}}(n).} \end{array} $ | (3) |
其综合考虑了无人机的生存代价、任务的完成代价、参考路径代价,无人机油耗代价,飞行高度代价.
1) 生存代价:wS*CS(n)
CS(n)=Sn-Sn-1;Sn为第n次搜索后的生存代价,Sn-1为已执行路径的生存代价和.其差值将作为本次搜索所持有的生存代价,wS为生存代价的权重值.
2) 任务完成的代价:wP*CP(n)
CP(n)=|Ptarget-Pn|;Ptarget为下一个任务点的位置,Pn为第n步搜索后的位置,取空间中这两点的模即为任务完成的代价,wP为任务重要性的权重值.如果任务点都执行完毕,则下一个任务点为终点.
3) 参考路径代价:wR*CR(n)
CR(n)=Dn(Pn, Lreference);Lreference为参考路径如图 1所示.Dn为点Pn到直线段Lreference距离的函数,返回值即为参考路径对飞行航线的代价.如果wR越大,无人机的飞行轨迹越靠近参考路线.
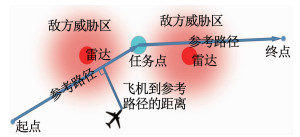
|
图 1 参考路径和约束表示 Fig. 1 Reference path and constraint representation |
4) 油耗与飞行高度代价:wO*CO(n)+wH*CH(n)
| $ {C_{\rm{O}}}(n) = \left\{ {\begin{array}{*{20}{l}} {0, \;\sum\limits_{n = 1}^n {{\rm{ oil}}} *{\rm{Di}}{{\rm{s}}_{\rm{n}}} < {\rm{oi}}{{\rm{l}}_{{\rm{All}}}};}\\ {{C_{{\rm{destory}}}}, \;\sum\limits_{n = 1}^n {{\rm{oil}}} *{\rm{Di}}{{\rm{s}}_{\rm{n}}} \ge {\rm{oi}}{{\rm{l}}_{{\rm{All}}{\rm{.}}}}} \end{array}} \right. $ | (4) |
式中:oil为耗油率, Disn为第n次搜索的步长,oilAll为总的油量.当总油量不能够支称第n步搜索所需的油耗量时,则引入惩罚Cdestory.
| $ {C_{\rm{H}}}(n) = \left\{ {\begin{array}{*{20}{l}} {0, {H_{\min }} < {H_{\rm{n}}} < {H_{\max }};}\\ {{C_{{\rm{destory }}}}, {\rm{ otherwise}}{\rm{.}}} \end{array}} \right. $ | (5) |
同上,当无人机下一次搜索的高度在约束的空间Hmin,Hmax外,同样引入惩罚Cdestory.wO,wH分别为两者的权重.
1.2 RWPSO优化算法在对PSO算法的优化问题中,通过调整参数来提高性能是最为常见的一种方法[7-8].
通过对适应度函数的介绍,可以发现权重对其代价或约束起到一个非常重要的权衡作用,直接影响到飞行的规划航迹.标准的PSO算法中,主要是靠粒子间的相互影响来寻优的,如果固定权重系数,粒子很难兼顾全局寻优与局部寻优的能力.但是采取随机游走策略来更新权重,算法的寻优速度会得到大大提升,这使无人机在航路规划时遇到敌方雷达或武器后会有更快的反应速度,尽早脱离危险区域,提高生存率.图 2为RWPSO算法的流程图:
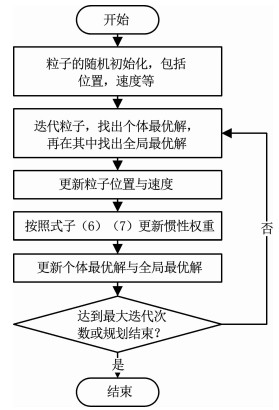
|
图 2 RWPSO算法流程图 Fig. 2 Flow diagram of RWPSO |
RWPSO算法的权重随机游走策略是通过将代价的权重系数设置为服从某种随机分布的数.如果粒子在初始化时就已经在最优点附近,那么RWPSO算法会找出相对小的权重值来增加收敛速度.如果不在最优解附近,甚至陷入局部最优时,由于RWPSO算法中的粒子受到不等权重的影响,会不断尝试跳出局部最优.具体权重值设置如下:
| $ w = \mu + \sigma *N(0, 1). $ | (6) |
式中:w为RWPSO算法的权重系数,μ为权重的均值,σ为方差,Ν(0, 1)是服从标准正态分布的随机数.
| $ \mu = {\mu _{\min }} + \left( {{\mu _{\max }} - {\mu _{\min }}} \right)*{\mathop{\rm rand}\nolimits} (0, 1). $ | (7) |
式中:μmax,μmin分别为随机权重的最大值与最小值,rand(0, 1)为取一个(0, 1)之间随机数的函数.这约束了在路径规划中无人机生存代价和任务代价过低或过高的情况发生.
2 基于马尔科夫链的无人机生存概率模型本文使用时间连续状态离散的马尔科夫链构建一个包含五种生存状态[9]的概率模型,用来描述无人机在穿过敌方雷达武器等威胁区域后的生存概率.文献[10]提出了一种状态之间的转移强度和代价函数.通过将RWPSO算法与状态转移强度相结合,规划出一条包含生存概率的航线.
2.1 五状态生存概率模型五状态即为飞机的5种状态:未被发现(undetected);被侦测(detected);被追踪(tracked);交战(engage);被击落(hit).生存状态之间是可以相互转换的,但只能是相邻的两个状态转换.假设无人机从安全区飞入敌方雷达区,无人机可能就会被敌方雷达发现而进入被侦测状态,甚至再由被侦测转移到被追踪状态,此时如果无人机飞离敌方雷达区域,将又会由被追踪转移到被侦测状态,而不能直接由被追踪转移到未被发现状态.无人机一旦从交战状态转移到了被击落状态,则为吸收态,将永远处于被击落状态.状态概率计算公式:
| $ \begin{array}{*{20}{c}} {P\left( {{X_{{\rm{t}} + \Delta }} = j|{X_{\rm{t}}} = i} \right) = {\lambda _{ij}}\Delta , }\\ {P\left( {{X_{{\rm{t}} + \Delta }} = i|{X_{\rm{t}}} = i} \right) = 1 - \sum\limits_{k \ne i} {{\lambda _{ik}}} \Delta .} \end{array} $ |
式中:i与j,k分别为无人机的两相邻生存状态,λij为两状态间的转移强度,Δ为无限小的时间长,P为状态间的转移概率.因为RWPSO算法收敛速度快,所以当无人机发现危险时,特别当任务点在敌方威胁区域内时,能够在完成任务后把在威胁区域内总的Δ缩小,迅速飞离危险区,以提高生存率.
2.2 转移强度与代价函数 2.2.1 转移强度的设定转移强度描述了从一个状态到另一个状态的转移概率[9],为λij.
图 3中的U,D,T,E,H分别为五种生存状态,右边部分为无人机所处的区域,包括安全区与威胁区,威胁区又分为雷达区和武器区.转移强度默认值的设置将参考文献[10],但是在威胁区域中所有点采用其固定的默认值,会导致生存代价相同.因此本文使用下面的公式来更新威胁区域内不同点的转移强度:

|
图 3 状态转移强度的设定 Fig. 3 Setting of transfer strength |
| $ {\lambda _{ij}} = \left\{ {\begin{array}{*{20}{l}} {{\lambda _{{\rm{ou}}{{\rm{t}}_ - }{\rm{ij}}}}, {\rm{ position }} \in S;}\\ {\lambda _{{\rm{i}}{{\rm{n}}_ - }{\rm{ij}}}^*(r - d)/r, {\rm{ position }} \notin S.} \end{array}} \right. $ | (8) |
position为无人机的位置,S为安全区域,λout_ij,λin_ij为无人机在威胁区域外和内的默认转移强度.r为威胁半径,d为点position距离威胁中心的欧式距离.
2.2.2 重叠区域的转移强度设定如果无人机飞入了雷达和武器都辐射到的范围,那么式(8)中的d将无法表示.关于重叠区域转移强度的计算公式如下:
| $ \lambda _{ij}^{\rm{c}} = \left\{ \begin{array}{l} \lambda _{ij}^1 + \lambda _{ij}^2, (i, j) = (U, D){\rm{\& }}(D, T), \\ \max \left( {\lambda _{ij}^1, \lambda _{ij}^2} \right), (i, j) = (T, E){\rm{\& }}(E, H), \\ \frac{{\lambda _{ij}^1\lambda _{ij}^2\left( {\lambda _{ij}^1 + \lambda _{ij}^2} \right)}}{{\lambda _{ij}^1\lambda _{ij}^2 + {{\left( {\lambda _{ij}^1} \right)}^2} + {{\left( {\lambda _{ij}^2} \right)}^2}}}, (i, j) = (D, U){\rm{\& }}(T, D), \\ 都是搜索雷达\\ \min \left( {\lambda _{ij}^1, \lambda _{ij}^2} \right), (i, j) = (D, U){\rm{\& }}(T, D), \\ 不都是搜索雷达\\ \min \left( {\lambda _{ij}^1, \lambda _{ij}^2} \right), (i, j) = (E, T). \end{array} \right. $ | (9) |
式中:λijc为重叠区域无人机的转移强度,λij1为针对第一个威胁点区域的转移强度,λij2为针对第二个威胁点区域的转移强度.
2.2.3 代价函数代价为无人机在执行第n次搜索前后的生存概率变化.生存概率是通过该点的转移强度值来计算得到的[9].具体计算公式为
| $ \left( {\begin{array}{*{20}{l}} {{{\dot p}_{\rm{U}}}({\rm{n}})}\\ {{{\dot p}_{\rm{D}}}({\rm{n}})}\\ {{{\dot p}_{\rm{T}}}({\rm{n}})}\\ {{{\dot p}_{\rm{E}}}({\rm{n}})}\\ {{{\dot p}_{\rm{H}}}({\rm{n}})}\\ {\underbrace {\dot \xi ({\rm{n}})}_{{\rm{\dot X}}\left( {{{\rm{t}}_{\rm{n}}}} \right)}} \end{array}} \right) = \left( {\underbrace {\begin{array}{*{20}{c}} { - {v_{\rm{U}}}({\rm{n}})}&{{\lambda _{{\rm{DU}}}}({\rm{n}})}&{{\lambda _{{\rm{TU}}}}({\rm{n}})}&{{\lambda _{{\rm{EU}}}}({\rm{n}})}&{{\lambda _{{\rm{HU}}}}({\rm{n}})}&0\\ {{\lambda _{{\rm{UD}}}}({\rm{n}})}&{ - {v_{\rm{D}}}({\rm{n}})}&{{\lambda _{{\rm{TD}}}}({\rm{n}})}&{{\lambda _{{\rm{ED}}}}({\rm{n}})}&{{\lambda _{{\rm{HD}}}}({\rm{n}})}&0\\ {{\lambda _{{\rm{UT}}}}({\rm{n}})}&{{\lambda _{{\rm{DT}}}}({\rm{n}})}&{ - {v_{\rm{T}}}({\rm{n}})}&{{\lambda _{{\rm{ET}}}}({\rm{n}})}&{{\lambda _{{\rm{HT}}}}({\rm{n}})}&0\\ {{\lambda _{{\rm{UE}}}}({\rm{n}})}&{{\lambda _{{\rm{DE}}}}({\rm{n}})}&{{\lambda _{{\rm{TE}}}}({\rm{n}})}&{ - {v_{\rm{E}}}({\rm{n}})}&{{\lambda _{{\rm{HE}}}}({\rm{n}})}&0\\ {{\lambda _{{\rm{UH}}}}({\rm{n}})}&{{\lambda _{{\rm{DH}}}}({\rm{n}})}&{{\lambda _{{\rm{TH}}}}({\rm{n}})}&{{\lambda _{{\rm{EH}}}}({\rm{n}})}&{ - {v_{\rm{H}}}({\rm{n}})}&0\\ {{\xi _{\rm{U}}}({\rm{n}})}&{{\xi _{\rm{U}}}({\rm{n}})}&{{\xi _{\rm{U}}}({\rm{n}})}&{{\xi _{\rm{U}}}({\rm{n}})}&{{\xi _{\rm{U}}}({\rm{n}})}&0 \end{array}}_{{\rm{A}}({\rm{n}})}} \right)\left( {\begin{array}{*{20}{l}} {{p_{\rm{U}}}({\rm{n}})}\\ {{p_{\rm{D}}}({\rm{n}})}\\ {{p_{\rm{T}}}({\rm{n}})}\\ {{p_{\rm{E}}}({\rm{n}})}\\ \begin{array}{l} {p_{\rm{H}}}({\rm{n}})\\ \;\underbrace {\xi ({\rm{n}})}_{{\rm{X}}\left( {{{\rm{t}}_{\rm{n}}}} \right)} \end{array} \end{array}} \right) $ | (10) |
式中:pI(n)为第n+1次搜索时处于I状态的概率,I为U, D, T, E, H中的某一状态.
| $ \begin{array}{*{20}{c}} {{v_I}(n) = \sum\limits_{i \ne j} {{\lambda _{ij}}} (n), }\\ {{\xi _{\rm{M}}}(n) = {b_i} + \sum\limits_{i \ne j} {{\lambda _{ij}}} (n){C_{ij}}.} \end{array} $ |
其中,ξM(n)为截至前n次搜索飞机累计生存代价.bi为处于i状态时,其每个单位时间的生存代价.由于i有5种状态,故bi用b=(0, bD, bT, bE, 0)表示.
| $ {C_{ij}} = \left\{ {\begin{array}{*{20}{l}} {{C_{{\rm{destory }}}}, i = E, j = H;}\\ {0, {\rm{ otherwise}}{\rm{.}}} \end{array}} \right. $ | (11) |
式中:Cij为从状态i转移到状态j的转移代价,最后可以算出生存代价的矩阵向量X(tn+1).
| $ X\left( {{t_{{\rm{n}} + 1}}} \right) = {{\rm{e}}^{{\rm{A}}(n)*\Delta t}}X\left( {{t_{\rm{n}}}} \right). $ |
在Intel Core i5- 4460@3.2 GHz, 8 G内存的硬件,Matlab2017a版软件环境下进行的仿真实验.场景参数由表 1给出,其中搜索雷达的搜索半径为150 km,火控雷达的打击半径为90 km,任务点的半径为15 km.转移强度具体参数如表 2,状态代价如表 3.
| 表 1 场景参数 Tab. 1 Parameters of the scene |
| 表 2 转移强度参数 Tab. 2 Parameters of transfer strength |
| 表 3 状态代价参数 Tab. 3 Parameters of state cost |
一方面为了证明随机游走策略的优越性,在下面分别对任务权重,生存权重采用控制变量法,并将仿真结果与标准的PSO优化算法进行比较,在最后将改进的QPSO与任务生存权重均随机游走的RWPSO进行对比.另一方面根据粒子群算法与马尔科夫链的结合模型,分别给出每次航路的无人机生存状态概率分布图.
3.2.1 基于随机游走的任务代价权重首先设定初始的代价权重值,其设置如表 4所示:
| 表 4 初始权重值设置 Tab. 4 Setting of initial weight value |
在此权重值下,PSO优化算法的搜索路径如图 4中的黑色虚线所示,任务权重随机游走的RWPSO算法将按照式(6)对其任务权重进行更新,并且设置μmax=6,μmin=4,最后RWPSO搜索路径如图 4中的红色实线所示,其中横纵坐标表示位置.
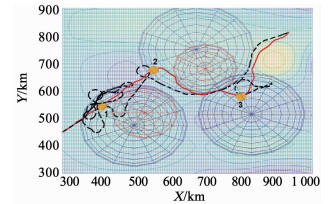
|
图 4 基于RWPSO(红实)与PSO(黑虚)航路搜索俯视 Fig. 4 Top view of route search based on RWPSO (red solid line) and PSO (black dotted line) |
观察图 4发现,在任务点1,2,3中,PSO优化算法都出现局部最优的情况,特别是任务点1与3.但是RWPSO优化算法很好的避免了这个问题,跳出局部最优的能力显然强于PSO算法.
图 5为这两条搜索航线的状态概率图,横坐标为执行的步数,每次搜索执行4步,纵坐标为每步搜索对应的状态概率,且5状态概率相加始终等于1.在图 5中可以发现PSO算法陷入了局部最优,导致其生存状态概率不断跳变.同样,生存状态概率图提供了一个有力的参考证据,用来评估在这种威胁环境中是否适合使用无人机去完成本次任务.
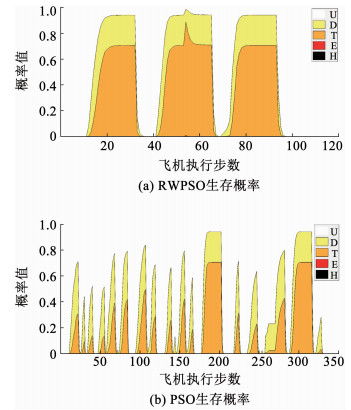
|
图 5 基于RWPSO与PSO的生存状态概率 Fig. 5 Survival state probability diagram based on RWPSO and PSO |
生存代价的初始权重设置的是0.6,属于使无人机具有较高的生存能力,当然这是现代战争所必然的.现在将wS设置为0.3,其他权重值不变,这样做的好处是方便对RWPSO优化算法与PSO优化算法在收敛速度与寻优能力方面进行比较.
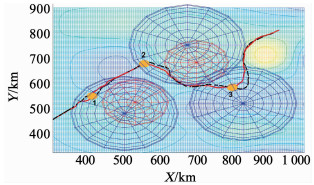
与设置任务权重一样.生存权重随机游走的RWPSO算法是把生存权重按照式(6)进行更新,μmax,μmin分别设置为0.4与0.2,其他权重值按照表 4给出.仿真效果如图 6:
|
图 6 基于RWPSO(红实)与PSO(黑虚)的航路搜索俯视 Fig. 6 Top view of route search based on RWPSO (red solid line) and PSO (black dotted line) |
在图 6中的2号任务点,执行完任务后,PSO优化算法由于收敛较慢,使得无人机飞入敌方武器威胁区域.RWPSO优化算法由于生存代价是不固定的,故种群肯定会往高生存率方向移动,即可迅速飞离危险区,也就避免出现图 7中被hit的状态.
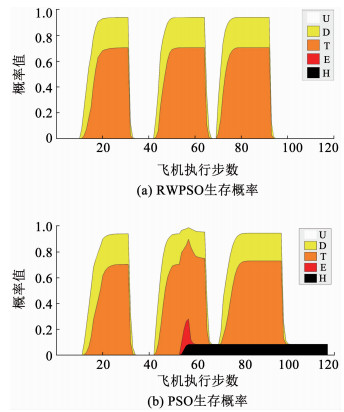
|
图 7 基于RWPSO与PSO的生存状态概率 Fig. 7 Survival state probability diagram based on RWPSO and PSO |
同样在3号任务点附近的轨迹也验证了这一结论的正确性,RWPSO优化算法在完成3号任务后可以迅速转移到高生存率的地方,减少在威胁区域内的飞行时间.
3.2.3 基于随机游走的任务与生存代价权重在表 4的权重参数中,实验一组生存代价与任务代价权重都是基于随机游走的数据,并将此实验结果与QPSO进行对比.一般的PSO优化算法都需要迭代100次左右[11-12],但本文实验只初始化了30个种群,迭代30次,缩小了约3倍的时间.
仿真效果如图 8所示:RWPSO的搜索路径用红实线标出,QPSO的搜索路径用黑虚线标出.与图 4相比,生存权重与任务权重均随机游走的RWPSO在2号任务点与3号任务点之间不会出现一直贴着敌方武器雷达飞行的情况出现,避免了图 5中RWPSO在第55步附近出现被追踪概率骤增的情况发生.QPSO在执行完2号任务点后依旧飞入了敌方的武器雷达区域,导致了图 9中约30%的被击毁概率.3号任务点时QPSO飞出任务区域后的收敛速度依旧不及RWPSO,过多时间处于敌方搜索雷达范围内.
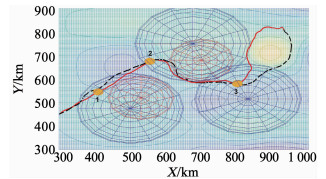
|
图 8 基于RWPSO(红实)与QPSO(黑虚)的航路搜索俯视图 Fig. 8 Top view of route search based on RWPSO (red solid line) and PSO (black dotted line) |
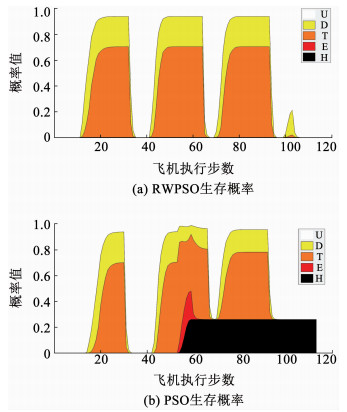
|
图 9 基于RWPSO与QPSO的生存状态概率 Fig. 9 Survival state probability diagram based on RWPSO and QPSO |
图 10对上面的6条航路的生存代价进行了对比,由于高生存权重的PSO优化算法陷入了局部最优故没有在图中标出.在低生存权重时:基于任务权重随机游走的RWPSO算法航路代价低于PSO算法.高生存权重时:两条RWPSO算法航路代价也只是略高于低生存权重PSO算法的航路代价值,QPSO由于飞入敌方武器威胁区域过多导致航路代价超过7 000.
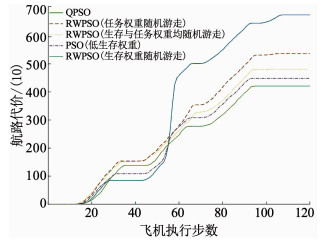
|
图 10 生存代价对比 Fig. 10 Cost of survival contrast diagram |
通过对比RWPSO优化算法与PSO、QPSO优化算法在无人机航路规划应用中的仿真效果与实验数据,证明了RWPSO优化算法跳出局部最优能力强,收敛速度快等特点.再结合马尔科夫链生存模型,实时的对飞行路径中的每一个点进行生存代价的评估,得到生存概率图,为无人机在复杂场景中的航路规划与生存状态动态评估提供了一种可行方法.
| [1] |
NONAMI K. Prospect and recent research & development for civil use autonomous unmanned aircraft as UAV and MAV[J]. Journal of System Design & Dynamics, 2007, 1(2): 120. DOI:10.1299/jsdd.1.120 |
| [2] |
WANG Qiang, ZHANG An, QI Linghui. Three-dimensional path planning for UAV based on improved PSO algorithm[C]//The 26th Chinese Control and Decision Conference (2014 CCDC). IEEE, 2014: 3981. DOI: 10.1109/CCDC.2014.6852877
|
| [3] |
GENG Qingbo, ZHAO Zheng. A kind of route planning method for UAV based on improved PSO algorithm[C]//2013 25th Chinese Control and Decision Conference (CCDC). IEEE, 2013: 2328. DOI: 10.1109/CCDC.2013.6561326
|
| [4] |
MARINI F, WALCZAK B. Particle swarm optimization (PSO). A tutorial[J]. Chemometrics & Intelligent Laboratory Systems, 2015, 149: 153. DOI:10.1016/j.chemolab.2015.08.020 |
| [5] |
CHEN Chenyu, CHANG Kuochou, HO S H. Improved framework for particle swarm optimization: Swarm intelligence with diversity-guided random walking[J]. Expert Systems with Applications, 2011, 38(10): 12214. DOI:10.1016/j.eswa.2011.03.086 |
| [6] |
FU Yangguang, DING Mingyue, ZHOU Chengping. Phase angle-encoded and quantum-behaved particle swarm optimization applied to three-dimensional route planning for UAV[J]. IEEE Transactions on Systems, Man, and Cybernetics-Part A: Systems and Humans, 2011, 42(2): 511. DOI:10.1109/tsmca.2011.2159586 |
| [7] |
CHEN H C, FENG H M, LIN T H, et al. Adapt DB-PSO patterns clustering algorithms and its applications in image segmentation[J]. Multimedia Tools and Applications, 2016, 75(23): 15327. DOI:10.1007/s11042-015-2518-4 |
| [8] |
SHI Y, EBERHART R C. Empirical study of particle swarm optimization[C]//Proceedings of the 1999 Congress on Evolutionary Computation-CEC99 (Cat. No. 99TH8406). IEEE, 1999, 3: 1945. DOI: 10.1109/CEC.1999.785511
|
| [9] |
ERLANDSSON T, NIKLASSON L. A five states survivability model for missions with ground-to-air threats[C]//Modeling and Simulation for Defense Systems and Applications Ⅷ. International Society for Optics and Photonics, 2013, 8752: 875207. DOI: 10.1117/12.2015022
|
| [10] |
ERLANDSSON T. Route planning for air missions in hostile environments[J]. The Journal of Defense Modeling and Simulation: Applications, Methodology, Technology, 2015, 12(3): 289. |
| [11] |
NEX F, REMONDINO F. UAV for 3D mapping applications: a review[J]. Applied Geomatics, 2014, 6(1): 1. DOI:10.1007/s12518-013-0120-x |
| [12] |
高芳, 崔刚, 吴智博, 等. 求解背包问题的病毒协同进化粒子群算法[J]. 哈尔滨工业大学学报, 2009, 41(6): 103-107. GAO Fang, CUI Gang, WU Zhibo, et al. Virus-evolutionary particle swarm optimization algorithm for knapsack problem[J]. Journal of Harbin Institute of Technology, 2009, 41(6): 103-107. DOI:10.3321/J.issn:0367-6234 |
| [13] |
MUELLER M, SMITH N, GHANEM B. A Benchmark and Simulator for UAV Tracking[J]. Far East Journal of Mathematical Sciences, 2016, 2(2): 445. |
| [14] |
MARINAKIS Y, MARINAKI M. A hybrid multi-swarm particle swarm optimization algorithm for the probabilistic traveling salesman problem[J]. Computers & Operations Research, 2010, 37(3): 432. DOI:10.1016/j.cor.2009.03.004 |
| [15] |
WANG Gaige, GUO Lihong, DUAN Hong, et al. A bat algorithm with mutation for UCAV path planning[J]. The Scientific World Journal, 2012, 2012: 1. DOI:10.1100/2012/418946 |
| [16] |
GUPTA L, JAIN R, VASZKUN G. Survey of important issues in UAV communication networks[J]. IEEE Communications Surveys & Tutorials, 2016, 18(2): 1123. DOI:10.1109/COMST.2015.2495297 |
| [17] |
HUANG Yu, GUO Feng, LI Yongling, et al. Parameter estimation of fractional-order chaotic systems by using quantum parallel particle swarm optimization algorithm[J]. Plos One, 2015, 10(1): e0114910. DOI:10.1371/journal.pone.0114910 |
 2019, Vol. 51
2019, Vol. 51


