2. 东北电力大学 电气工程学院, 吉林 吉林 132012
2. School of Electrical Engineering, Northeast Electric Power University, Jilin 132012, Jilin China
有效的功率控制是无线传感器网络及其节点能够进行持久工作的前提条件.文献[1-2]提出一种加权协作传输模式,将功率分配描述成凸问题,利用拉格朗日乘数法求解,可提升网络的生存周期,但该方式只适用于协作节点较少的情况,具有一定的局限性.文献[3]分析链路容量影响因子和干扰模型的不足,设计一种信道联合优化算法,其忽略了信息有效传输速率的问题.文献[4]引用效用函数实现功率控制,将链路可靠性和逻辑邻居有界作为约束条件,建立发射功率与网络效用的对应模型,淡化了节点的能耗问题.文献[5]讨论一种干扰影响度模型,在节点生命周期模型中引入期望传输次数,在保证网络连通的基础上得出最优功率,算法后期复杂度会增加.文献[6]提出一种信道冲突避免机制来降低整个网络能耗,虽然可以减少信息的堵塞,但没有考虑节点的有效传输和能量利用率等问题.文献[7]提出一种基于信息编码的解析方案来实现侦听机制,在不引入新负荷的情况下提高传播速率与效率,以获取数据包中的信息,却增加了网络的额外负担.文献[8]建立一种链路可靠性和网络能耗相对应的功率控制模型,通过自适应调整控制器参数得出最优发射功率,但该算法仅考虑单参数对系统的影响.文献[9]设计目的是为保证传感器动态加入或退出网络时所有节点依然能够进行数据传输,通过发射功率的优化达到较大信干噪比值,节点剩余能量衰减较快.文献[10]将网络组建阶段和拓扑维护阶段交替运行,设计一种最小功耗下的功率控制,对冗余节点的能量损耗考虑较少.文献[11-12]利用几何理论计算节点间的干扰、能耗和速率之间的关系,保证链路可靠性的同时减小功率,但是受限于节点计算能力有限,因此实时性不高.
以上算法在研究中未能将节点干扰、发射功率和能耗问题进行综合考虑.为解决由发射功率不当引起的生存周期短、网络效用低的问题,本文通过搭建有效干扰模型,获取信道间有效干扰,利用效用函数最优化博弈框架,使每个节点得到对应的最佳发射功率以降低节点能耗,延长网络生存周期,达到系统最优性能.
1 系统模型博弈论通常用来处理相互合作或竞争过程的策略选择问题,通过调整参与者的行为,以最小化代价获得最大化收益.为简化建模过程,对所研究对象及相应环境做如下设定[13]:
1) 网络节点随机分布后静止不动,汇聚节点位于整个区域中心且能量不受限制;
2) 节点能感知通信半径范围内的各节点位置和发射功率等信息;
3) 所有节点初始信息相同,包括初始能量、初始发射功率、感知半径等,并且节点发射功率可控.
1.1 干扰模型假设监控区域内随机分布的传感器节点个数为N.在传统网络运行模式中,为获得更高的网络收益,每个节都点会以较大的发射功率进行数据传送,链路会受到严重的干扰.假设仅在节点i感知半径R内的节点j会对其产生干扰,建立如下有效干扰模型为
| $ {I_i} = \sum\limits_N {{p_j}} {g_{ij}}{\alpha _{ij}} + {\eta ^2}. $ | (1) |
式中:pj为节点j的发射功率,gij为节点i和节点j的链路增益,
| $ \left\{ {\begin{array}{*{20}{l}} {{\alpha _{ij}} = \exp \left( { - \frac{D}{R}} \right), }\\ {D = \sqrt {{{\left( {{x_i} - {x_j}} \right)}^2} + {{\left( {{y_i} - {y_j}} \right)}^2}} .} \end{array}} \right. $ | (2) |
式中:D为节点i、j之间的欧氏距离,可以看出,当节点距离增大时,节点j对链路的影响权重和干扰值逐渐减小.根据以上分析,结合文献[14]对信干噪比的定义,给出改进后的信干噪比模型
| $ {S_{{\rm{INR}}}} = \frac{W}{{{R_i}\left( {{p_i}, {I_i}} \right)}}\frac{{{p_i}{g_i}}}{{\sum\limits_N {{p_j}} {g_{ij}}{\alpha _{ij}} + {\eta ^2}}}. $ | (3) |
式中:W为传播带宽,gi为节点i到下一跳节点的链路增益,Ri(pi, Ii)为最优功率下得到的信息传输速率.
1.2 速率模型信息的传输速率可以用功率—干扰模型来计算.速率的优化问题可转化为式(4)的最优化,即:
| $ \left\{ {\begin{array}{*{20}{l}} {\max \;{R_i}\left( {{p_i}, {I_i}} \right), }\\ {{\rm{s}}{\rm{.t}}{\rm{.}}\;\;{\rm{ }}{p_i} \ge 0.} \end{array}} \right. $ | (4) |
式(4)表明传感器节点能支持的最大传输速率与此时节点受到的干扰相关,即节点i的速率Ri为发射功率pi和受到干扰Ii的函数,而节点i受到的有效干扰Ii为pj的函数,则有以下速率模型
| $ {R_i}\left( {{p_i}, {I_i}} \right) = \ln \left( {1 + \frac{{{p_i}{g_i}}}{{\sum\limits_N {{p_j}} {g_{ij}}{\alpha _{ij}} + {\eta ^2}}}} \right). $ | (5) |
网络在进行大量的数据传输时,给其他链路带来的负面因素致使其信干噪比降低,因此节点会提高发射功率来弥补期望的SINR,这就导致相互干扰愈加严重,可以看出,节点在每次迭代时需要根据周围节点的特性来决定自身的发射功率,因此需要感知邻居节点的状态信息,这并不是局部优化问题[15].传输速率为发射功率和有效干扰的函数,这三者之间相互作用又相互独立,据此,可以搭建由相关因素构成的合作博弈模型[16].在合作博弈中,强调最终均衡结果趋于整体最优值,每个节点采取的策略是当前提条件下最优响应.
本文选用的策略博弈数学模型是Г= < P, f > , 各个元素分别为
1) 策略空间:P={pi, p-i}(i=1, …, n)为一个策略组合,pi为节点i的策略选择,p-i为其余节点的策略选择.
2) 效用函数:f={f(Ri(pi, Ii), Ei)}为节点i在算法迭代后,以发射功率pi进行数据通信时的网络收益,Ei为节点初始能量与剩余能量之比,其公式为
| $ \begin{array}{l} f\left( {{R_i}\left( {{p_i}, {I_i}} \right), {E_i}} \right) = {c_1}{R_i}\left( {{p_i}, {I_i}} \right) - {c_2}{p_i}{g_i}{E_i}\\ \;\;\;\;\;\;\;\;\;\; = {c_1}{R_i}\left( {{p_i}, {I_i}} \right) - {c_2}{p_i}{g_i}\frac{{{e_0}(i)}}{{{e_d}(i)}}\\ = {c_1}\ln \left( {1 + \frac{{{p_i}{g_i}}}{{\sum\limits_N {{p_j}} {g_{ij}}{\alpha _{ij}} + {\eta ^2}}}} \right) - {c_2}{p_i}{g_i}\frac{{{e_0}(i)}}{{{e_d}(i)}}. \end{array} $ | (6) |
式中:第一项中c1、c2为效用权重因子,e0(i)为节点i的初始能量,ed(i)为节点i的剩余能量.从第二项可以看出,当节点剩余能量ed(i)逐渐减小时,网络效用呈现下降趋势,故应适当减小发射功率,以延缓剩余能量的下降速度.
定义1 节点i综合考虑周围节点状态动态调整自身策略,产生最大效益时的最优功率策略集为p={p1, …, pn},其元素为
| $ p = \mathit{arg}\;\max f\left( {{R_i}\left( {{p_i}, {I_i}} \right), {E_i}} \right). $ | (7) |
重复博弈是指同一博弈形式不断出现,所有参与者根据当前收益和未来可能收益决定采取的策略.策略式重复博弈规定每个阶段都是标准的策略博弈,实际判定中,策略式重复博弈需满足:1)参与者i的策略集合属于一个非空、闭的、有界的凸集;2)效用函数f={f(Ri(pi, Ii), Ei)}是pi的连续函数,在pi∈[pimin, pimax]上是拟凹的,即满足
| $ \frac{{{\partial ^2}f\left( {{R_i}\left( {{p_i}, {I_i}} \right), {E_i}} \right)}}{{\partial p_i^2}} < 0. $ | (8) |
在整个博弈过程中,每个节点均动态选择适合的功率,根据重复博弈的定义,若所有参与者的最优响应满足上述两个条件,则必然存在纳什均衡点[17].
定义2 在此合作博弈模型中,该效用函数存在纳什均衡点.
证明 对于博弈模型Г= < P, f > ,存在:Г < {p1, p-1}, {p2, p-2}, …, {pn.p-n}; {f(R1, E1), f(R2, E2), …, f(Rn, En)}>,且pmin≤pi≤pmax与0≤Ii≤Imax,符合重复博弈中的约束条件.对效用函数f求关于发射功率pi的一阶偏导为
| $ \frac{{\partial f}}{{\partial {p_i}}} = {c_1}\frac{{{g_i}}}{{\sum\limits_N {{p_j}} {g_{ij}}{\alpha _{ij}} + {\eta ^2} + {p_i}{g_i}}} - {c_2}{g_i}\frac{{{e_0}(i)}}{{{e_d}(i)}}. $ | (9) |
效用函数的二阶偏导数为
| $ \frac{{{\partial ^2}f}}{{\partial p_i^2}} = - {c_1}\frac{{g_i^2}}{{{{\left( {\sum\limits_N {{p_j}} {g_{ij}}{\alpha _{ij}} + {\eta ^2} + {p_i}{g_i}} \right)}^2}}}. $ | (10) |
由式(10)可看出,
根据最优化理论[18],对于可微函数,令可得
| $ {p_i} = \frac{1}{{{g_i}}}\left( {\frac{{{c_1}{e_d}(i)}}{{{c_2}{e_0}(i)}} - \sum\limits_{j \ne i} {{p_j}} {g_{ij}}{\alpha _{ij}} - {\eta ^2}} \right). $ | (11) |
本文算法伪代码
输入:初始能量E0,链路增益gi,数据包长度L,背景噪声η2,效用权重因子c1、c2,最大迭代次数Rmax
算法描述
1:for r=1:Rmax
2:for i=1:n
3:for j=1:n
4:计算第i个节点与其他节点的距离D
5:if距离在阈值内
6:找出这样的节点j,根据式(2)得出距离权重因子αij
7:利用式(1)计算i的干扰总和
8:else
9:αij=0
10:end
11:end
12:产生一个随机数β
13:if β < 0.5
14:节点完成一次数据传输,消耗相应能量
15:else
16:节点能量不变
17:end
18:计算剩余能量与初始能量比值
19:根据公式(4)、(6)、(9),得出最优功率集、传输速率、网络效用值
20:更新节点i参数,进行下一轮计算
21:end
22:end
本文提出的合作博弈下实现无线传感器网络功率控制的具体步骤是:
Step1:设置初始参数,节点间发送自身位置信息列表、能量和当前发射功率;
Step2:根据式(1)、(2),计算节点i的有效总干扰值Ii;
Step3:通过式(4)、(6),得出此时的传输速率与网络效用;
Step4:设置节点i以一定的概率进行数据包传输,并计算Ei;
Step5:由式(11)计算单节点最优发射功率pi;
Step6:将单节点的pi结果返回到Step1中逐步迭代;
Step7:计算在以上更新后参数作用下的网络收益.
4 实验数据及仿真分析本文仿真实验中待测区域为100×100 m2,节点个数为50,实验初始参数设置如表 2所示[19-20].
| 表 2 仿真参数 Tab. 2 Simulation parameters |
确定效用函数中的权重因子c1和c2的取值,仿真实验结果如图 1所示.
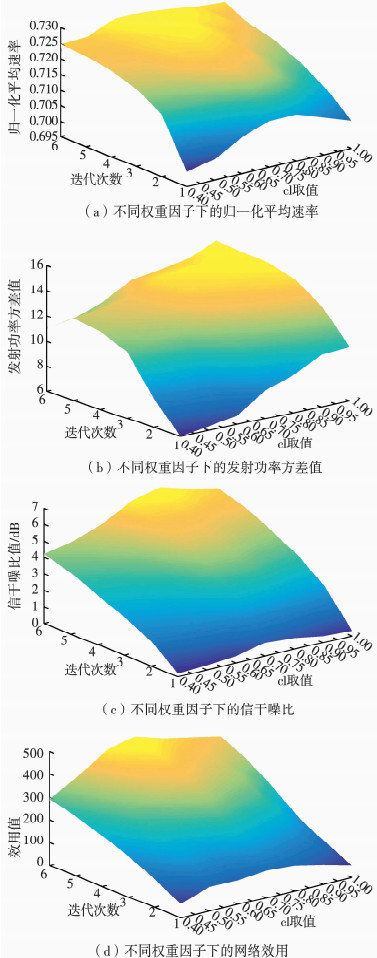
|
图 1 权重因子对系统各项性能的影响 Fig. 1 Influence of weight factors on system performance |
本文设置权重参数c1、c2之和为1,并且由于效用函数为两项相减的形式,c1取值过小将有可能导致效用函数为负,因此仿真中只研究c1≥0.4的情况.图 1(a)表示在c1=0.77、c2=0.23时本文算法得到信息传输速率达到最优;图 1(b)表示通过本文算法得出的最优发射功率的方差值,可以看出,在算法运行初期方差值出现小高峰,随着迭代次数增加,不同参数下的最优功率的波动程度均越来越小,系统达到稳定状态,可证明本文算法的可收敛性,选取适中的方差值c1=0.65、c2=0.35;图 1(c)在c1=0.84、c2=0.16时信干噪比达到最高;图 1(d)表示在选取不同大小权重因子时本文算法得到的网络效用,可以看出c1=0.72、c2=0.28时,效用实现最大化.因此,综合图 1实验结果,选取c1=0.73、c2=0.27为权重因子的仿真系数.
4.2 性能分析为验证本文算法的有效性,选取PCOA算法[3]、DRMD算法[21]、PLPC算法[22]、OSPC算法[23]、传统分布式功率控制算法[24]进行实验对比.
图 2为6种不同算法在收敛后得到的最优发射功率,传统分布式功率控制算法的发射功率最大,收敛速度也较缓慢,OSPC算法、PCOA算法、DRMD算法和PLPC算法的收敛轮数大概为12次、13次、15次和17次,本文算法在第10次迭代时达到收敛水平,并且提供了较低等级的发射功率,能有效地减少节点能量消耗,提高网络生命周期.
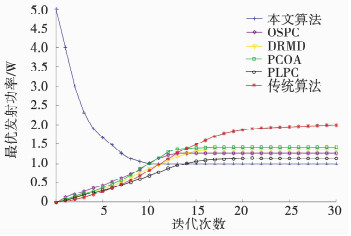
|
图 2 不同算法最优功率比较 Fig. 2 Comparison of optimal power of different algorithms |
图 3数据为不同算法的发射功率方差值统计,由于传统分布式功率控制算法复杂度高,不易收敛,因此该算法的发射功率方差值最大;PLPC算法采用自适应模糊神经网络以反馈、循环方式调整发射功率,方差值较为平缓,发射功率取值波动小;OSPC算法利用延迟列生成技术简化复杂问题,算法收敛速度快,方差波动小;DRMD算法将混合整数规划问题转化成单变量优化问题,算法复杂度小,易收敛,方差较小;PCOA算法与本文算法方差值趋势相似,算法后期方差迅速下降,达到收敛状态.
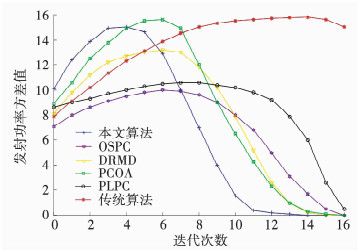
|
图 3 不同算法发射功率方差比较 Fig. 3 Comparison of transmit power variance of different algorithms |
为讨论不同算法下节点的生存周期(如图 4),节点死亡数为50%时传统分布式功率控制算法、PLPC、OSPC、PCOA、DRMD、本文算法的轮数分别为:300、510、600、690、720、800.传统分布式功率控制算法由当前的信干噪比值和发射功率确定最佳发射功率,其最早实现节点50%死亡;PLPC算法采用自适应模糊控制器通过学习训练集对功率进行优化控制,OSPC算法整合路由调度、能源效率和功率控制因素对网络进行优化,PCOA算法主要考虑节点能耗和信道容量对发射功率的影响,DRMD算法将队列调度和能量消耗联合优化,均使节点死亡50%的时间得以延后;本文算法在效用函数中引入剩余节点能量比值,明显推迟了半数节点死亡时间,提高网络健壮性.
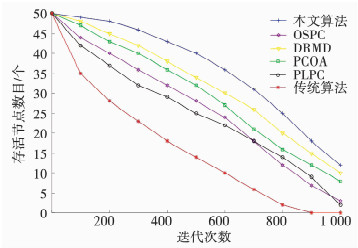
|
图 4 不同算法节点存活时间比对 Fig. 4 Comparison of survival time of nodes with different algorithms |
图 5是不同算法在相同迭代次数时的信干噪比性能的对比,由于传统分布式功率控制算法和PLPC算法预先设定信干噪比值,通过不断提高发射功率达到期望值,在完成目标后不再改变发射功率,PCOA算法仅根据节点干扰调节信干噪比值,OSPC算法根据信道条件联合优化调度和功率控制问题,DRMD算法整合资源分配、功率控制影响因素,提高信干噪比值,故4种算法对信干噪比的改善各有不同.本文算法利用不断变化的信息传输速率与节点干扰得到信干噪比以调整节点发射功率,噪声性能优于其他4种算法.
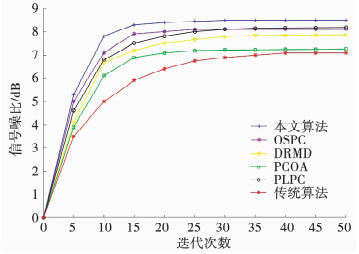
|
图 5 不同算法信干噪比随迭代次数变化关系 Fig. 5 The relationship between signal-to-interference-noise ratio and iterative times of different algorithms |
图 6可以看出不同算法随着迭代次数的增加,产生的网络收益均逐渐收敛,而本文算法收敛速度更快.当5种算法都达到收敛时,本文效用分别比OSPC算法、DRMD算法、PCOA算法、PLPC算法、传统分布式功率控制算法提高约2.06%、2.96%、9.83%、15.24%、20.6%.
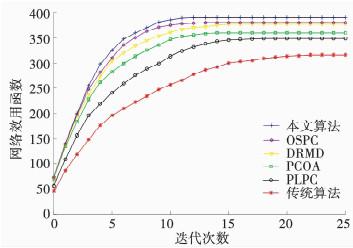
|
图 6 不同迭代次数时网络效用对比 Fig. 6 Comparison of network utility with different iterations |
针对无线传感器网络工作过程中由发射功率选择不当给网络性能带来的消极影响,本文引入博弈论相关理论,借助合作博弈理念研究无线传感器网络功率控制策略,将节点受到的总干扰、信息传输速率和能量因素引入效用函数,利用不断更新的网络信息寻找每个节点的最佳功率.仿真实验表明,本算法通过调整节点的最佳功率,提高了网络效用值,网络生存周期较长,可得到较高的信干噪比值,系统性能具有优越性,能适应不断变化的网络.由于本文采用重复博弈方式,在一定程度上增加算法复杂度,造成不必要的能量消耗,因此下一阶段将在本文研究基础上优化算法以降低其复杂度,减少节点在算法迭代过程中的功率消耗,延长网络生命周期.
| [1] |
汪志勇, 张沪寅, 徐宁. 认知无线电网络中基于随机学习博弈的信道分配与功率控制[J]. 电子学报, 2018, 46(12): 2870. WANG Zhiyong, ZHANG Huyin, XU Ning. Channel allocation and power control based on stochastic learning game in Cognitive Radio Networks[J]. Acta Electronica Sinica, 2018, 46(12): 2870. DOI:10.3969/j.issn.0372-2112.2018.12.008 |
| [2] |
张继, 张大方, 谢鲲, 等. 一种基于演化博弈的分簇协作路由算法[J]. 电子学报, 2016, 44(9): 2158. ZHANG Ji, ZHANG Dafang, XIE Kun, et al. A clustering cooperative routing algorithm based on evolutionary game[J]. Acta Electronica Sinica, 2016, 44(9): 2158. DOI:10.3969/j.issn.0372-2112.2016.09.020 |
| [3] |
郝晓辰, 刘金硕, 姚宁, 等. 无线传感器网络基于容量和传输能耗的功率与信道联合博弈算法[J]. 电子与信息学报, 2018, 40(7): 1715. HAO Xiaochen, LIU Jinshuo, YAO Ning, et al. Power and channel joint game algorithm based on capacity and transmission energy consumption in Wireless Sensor Networks[J]. Journal of Electronics and Information, 2018, 40(7): 1715. DOI:10.11999/JEIT170927 |
| [4] |
刘韬. 无线传感器网络中基于效用模型的分布式功率控制机制[J]. 电子学报, 2016, 44(2): 301. LIU Tao. Distributed power control mechanism based on utility model in Wireless Sensor Networks[J]. Acta Electronica Sinica, 2016, 44(2): 301. DOI:10.3969/j.issn.0372-212.2016.02.009 |
| [5] |
郝晓辰, 姚宁, 解力霞. 联合功率与信道的WSN生命期优化博弈算法[J]. 通信学报, 2019, 40(4): 62. HAO Xiaochen, YAO Ning, XIE Lixia. WSN lifetime optimization game algorithm combining power and channel[J]. Journal of Communications, 2019, 40(4): 62. DOI:10.11959/j.issn.1000436x.2019.097 |
| [6] |
LIU Daibo, CAO Zhichao, ZHANG Yi, et al. Achieving accurate and real time link estimation in low power wireless sensor networks[J]. IEEE/ACM Transactions on Networking, vol.25, no.4, pp. 2096. DOI: 10.1109/TNET.2017.2682276
|
| [7] |
AMIR S, CHOI Y J. Interference coordination scheme between WiFi and Zigbee networks[C]//Sensor, Mesh & Ad Hoc Communications & Networks. IEEE, 2012. DOI: 10.1109/SECON.2012.6276357
|
| [8] |
刘伟, 刘军. 时延敏感传感器网络中分布式动态资源管理研究[J]. 通信学报, 2017, 38(7): 70. LIU Wei, LIU Jun. Research on distributed dynamic resource management in delay Sensitive Sensor Networks[J]. Journal of Communications, 2017, 38(7): 70. DOI:10.11959/J.ISSN.1000-436x.2017.144 |
| [9] |
邵奇可, 冯淑娜. 面向WSN的自适应模糊功率控制算法研究[J]. 传感技术学报, 2015, 26(4): 563. SHAO Qike, FENG Shuna. Research on adaptive fuzzy power control algorithm for WSN[J]. Journal of Sensing Technology, 2015, 26(4): 563. DOI:10.3969/j.issn.1004-1699.2015.04.019 |
| [10] |
陈宏滨, 冯久超. 一种动态传感器网络中的功率控制方法[J]. 西南师范大学学报(自然科学版), 2010, 35(6): 127. CHEN Hongbin, FENG Jiuchao. A power control method in Dynamic Sensor Networks[J]. Journal of Southwest Normal University (Natural Science Edition), 2010, 35(6): 127. DOI:10.13718/j.cnki.xsxb.2010.06.048 |
| [11] |
MOHAMED Y, IZZET F. Topology management techniques for tolerating node failures in wireless sensor networks: A survey[J]. Computer Networks, 2013, 12(24): 254. DOI:10.1007/978-3-642-40009-4 |
| [12] |
SHANMUHI M, RAMANAIAH O B V. Cluster based comb needle model for energy efficient data aggregation in wireless sensor networks[C]//Applications & Innovations in Mobile Computing. IEEE, 2015. DOI: 10.1109/AIMOC.2015.7083828
|
| [13] |
薛亮, 陈晰, 赵继军. 无线传感器网络中基于Voronoi覆盖及Delaunay三角剖分图的最小刚性拓扑控制算法[J]. 自动化学报, 2016, 42(10): 1570. XUE Liang, CHEN Xi, ZHAO Jijun. Minimum rigid topology control algorithm based on Voronoi Covering and Delaunay Triangulation in Wireless Sensor Networks[J]. Acta Automatic Sinica, 2016, 42(10): 1570. DOI:10.16383/j.aas.2016.c150702 |
| [14] |
滕志军, 吕金玲, 张力, 等. WSN中基于博弈论的节点功率控制算法[J]. 控制理论与应用, 2018, 35(5): 717. TENG Zhijun, LV Jinling, ZHANG Li, et al. Node power control algorithm based on game theory in WSN[J]. Control Theory and Application, 2018, 35(5): 717. DOI:10.7641/CTA.2018.70921 |
| [15] |
胡松华, 张建军. 基于博弈论功率控制的串行干扰消除算法[J]. 通信学报, 2015, 36(9): 215. HU Songhua, ZHANG Jianjun. Serial interference cancellation algorithm based on game theory power control[J]. Journal of Communications, 2015, 36(9): 215. DOI:10.11959/j.issn.1000-436X.2015176 |
| [16] |
徐宁, 胡晓辉. 一种能耗均衡的WSN分布式拓扑博弈算法[J]. 信息与控制, 2019, 48(2): 156. XU Ning, HU Xiaohui. A WSN distributed topology game algorithm with balanced energy consumption[J]. Information and Control, 2019, 48(2): 156. DOI:10.13976/j.nki.xk.2019.8178 |
| [17] |
TAREK A, MANEL G Z. Game theory for energy efficiency in Wireless Sensor Networks: Latest trends[J]. Journal of Network and Computer Applications, 2015, 54(16): 67. DOI:10.1016/j.jnca.2015.03.011 |
| [18] |
刘芳. 基于马尔可夫博弈的WSN功率控制研究[J]. 计算机技术与发展, 2017, 27(4): 188. LIU Fang. Research on WSN power control based on markov game[J]. Computer Technology and Development, 2017, 27(4): 188. DOI:10.3969/j.issn.1673-629X.2017.04.042 |
| [19] |
叶波. 基于负载均衡度的云计算任务调度算法[J]. 东北电力大学学报, 2019, 39(1): 88. YE Bo. Cloud computing task scheduling algorithm based on load balance[J]. Journal of Northeast Electric Power University, 2019, 39(1): 88. DOI:10.19718/j.issn.1005-2992.2019-01-0088-08 |
| [20] |
孙增友. 基于整体公平的D2D无线资源分配算法[J]. 东北电力大学学报, 2019, 39(1): 81. SUN Zengyou. D2D radio resource allocation algorithm based on overall fairness[J]. Journal of Northeast Electric Power University, 2019, 39(1): 81. DOI:10.19718/j.issn.1005-2992.2019-01-0081-07 |
| [21] |
ETANCELIN J, FABBRI A, GUINAND F. DACYCLEM: A decentralized algorithm for maximizing coverage and lifetime in a mobile wireless sensor network[J]. Ad Hoc Networks, 2019, 87(7): 174. DOI:10.1016/j.adhoc.2018.12.008 |
| [22] |
胡黄水, 赵航. 基于路径损耗自学习的WSN功率控制方法[J]. 长春工业大学学报, 2018, 39(2): 113. HU Huangshui, ZHAO Hang. WSN power control method based on path loss self learning[J]. Journal of Changchun University of Technology, 2018, 39(2): 113. DOI:10.15923/j.cnki.cn.22-1382/T.2018.2.02 |
| [23] |
LIU L, CHENG Y, CAO Xianghui. Joint optimization of scheduling and power control in Wireless Networks: Multi-dimensional modeling and decomposition[J]. IEEE Transactions on Mobile Computing, 2018, 1. DOI:10.1109/TMC.2018.2861859 |
| [24] |
陈立建, 周雪. 一种基于功率控制的WSN自适应能量高效传输模式研究[J]. 传感器技术学报, 2014, 27(6): 835. CHEN Lijian, ZHOU Xue. Research on a WSN adaptive energy efficient transmission mode based on power control[J]. Journal of Sensor Technology, 2014, 27(6): 835. DOI:10.3969/j.isssn.1004-1699.2014.06.023 |
 2019, Vol. 51
2019, Vol. 51


