求解多峰优化问题的改进布谷鸟算法

引用本文

张艺瀛, 金志刚. 求解多峰优化问题的改进布谷鸟算法[J]. 哈尔滨工业大学学报, 2019, 51(11): 89-99. DOI: 10.11918/j.issn.0367-6234.201902003.

ZHANG Yiying, JIN Zhigang. An improved cuckoo search for multimodal optimization problems[J]. Journal of Harbin Institute of Technology, 2019, 51(11): 89-99. DOI: 10.11918/j.issn.0367-6234.201902003.

基金项目

国家自然科学基金(71502125)

作者简介

张艺瀛(1993—), 男, 博士生;
金志刚(1972—), 男, 教授, 博士生导师

通信作者

金志刚, zgjin@tju.edu.cn

文章历史

收稿日期: 2019-02-01

Abstract Full text Figures/Tables PDF

求解多峰优化问题的改进布谷鸟算法

张艺瀛, 金志刚

天津大学电气自动化与信息工程学院, 天津 300072

收稿日期: 2019-02-01

基金项目: 国家自然科学基金(71502125)

作者简介: 张艺瀛(1993—), 男, 博士生;
金志刚(1972—), 男, 教授, 博士生导师

通信作者: 金志刚, zgjin@tju.edu.cn

摘要: 布谷鸟算法是一种简便而高效的元启发式算法.然而, 布谷鸟算法在求解复杂的多峰优化问题时通常存在易陷入局部最优解的缺点.针对布谷鸟算法的这种缺点, 结合神经网络算法和布谷鸟算法的特性, 提出一种基于神经网络的布谷鸟算法.该算法的核心思想是借助改进神经网络算法的强大全局搜索能力和动态种群策略来平衡布谷鸟算法的全局搜索能力和局部搜索能力, 从而减少布谷鸟算法陷入局部最优的可能性.该算法首先将种群中的个体依照适应度值的优劣进行排序, 然后对种群中最好的一半个体通过布谷鸟算法进行优化, 对种群中最差的一半个体通过改进的神经网络算法进行优化, 最后将所有个体组成一个新的种群, 并从中筛选出最优解.采用24个复杂基准测试函数检验所提出算法求解多峰优化问题的性能, 并将优化结果与神经网络算法, 布谷鸟算法以及一些改进的布谷鸟算法所获取的优化结果相比较.实验结果表明：所提出的算法充分地展现了神经网络算法和布谷鸟算法的优势, 其在求解质量, 求解效率以及求解稳定性上均显著优于其它算法.

关键词: 人工神经网络生物神经系统布谷鸟搜索多峰优化

An improved cuckoo search for multimodal optimization problems

ZHANG Yiying, JIN Zhigang

School of Electrical and Information Engineering, Tianjin University, Tianjin 300072, China

Abstract: Cuckoo search algorithm is a simple and efficient meta-heuristic algorithm, while it can be easily trapped into local optimum when solving complex multimodal optimization problems. To tackle this problem, an improved cuckoo search algorithm based on neural networks was proposed by combining the characteristics of neural network algorithm and cuckoo search algorithm. The core idea of this algorithm is to balance global search ability and local search ability of cuckoo search algorithm with powerful global search ability of the improved neural network algorithm and dynamic population strategy, thereby reducing the possibility of the cuckoo algorithm falling into local optimum. The algorithm firstly sorts the individuals in the population according to the fitness values. Then the best half individuals of the population are performed by the cuckoo search algorithm, whereas the worst half individuals are optimized by the improved neural network algorithm. Finally all individuals are grouped into a new population, from which the optimal solution can be selected. In this experiment, 24 complex multimodal optimization problems were employed to study the optimization performance and compare between the proposed algorithm and neural network algorithm, cuckoo search algorithm, and other improved cuckoo algorithms. Results show that the proposed algorithm fully demonstrated the advantages of the modified neural network algorithm and the cuckoo search algorithm, which was significantly better than other algorithms in resolution quality, convergence speed, and stability.

Keywords: artificial neural networks biological nervous cuckoo search multimodal optimization

在实际优化问题中，如复杂系统参数及结构优化等，常存在着多个局部最优解和一个全局最优解，它们都可统称为多峰函数优化问题^[1].与传统优化算法相比，元启发式算法更适用于求解这类复杂优化问题^[2-3].作为一种现代优化技术，元启发式算法是随机算法与局部搜索算法相结合的产物^[4].

布谷鸟算法(cuckoo search algorithm，CS)是元启发式算法的一个典型代表，它通过莱维飞行和随机游走的方法来模拟自然界中某些种属布谷鸟的寄生育雏^[5].布谷鸟具有以下特点^[6]1)模型简单，控制参数少；2)能从理论上证明满足全局收敛；3)在搜索过程中兼顾局部搜索与全局搜索; 4)采用莱维飞行机制.鉴于这些特点，布谷鸟自提出以来，就不断被国内外学者应用到各种优化领域，比如资源分配^[7]，旅行商问题^[8]，阵列天线优化^[9]，电力系统稳定器设计^[10]和数据聚类^[11]等.然而，布谷鸟算法在解决复杂的多峰优化问题时，呈现出易落入局部最优解的缺陷.为了克服这种缺陷，许多学者提出了一些改进的布谷鸟算法，如基于搜索趋化策略的布谷鸟算法^[12]，强化全局和局部搜索的布谷鸟算法^[13]，混沌型布谷鸟算法^[14]，自适应步长的布谷鸟算法^[15]，一阶布谷鸟算法^[16]，自适应步长和发现概率的布谷鸟算法^[17]等.

针对布谷鸟算法求解多峰优化问题存在的缺陷，本文提出一种基于神经网络的布谷鸟算法(cuckoo search based on neural networks，NNCS).神经网络算法(neural network algorithm, NNA)是最新提出元启发式算法之一.得益于神经网络的独特结构，NNA具有良好的全局搜索能力^[18].为了在NNCS中充分利用NNA的全局搜索能力，本文提出了一种改进的神经网络算法(modified neural network algorithm, MNNA).NNCS的核心思想是借助MNNA算法的强大全局优化能力以及动态种群策略来减少CS算法陷入局部最优解的概率，其基本思路可以简述如下：首先将布谷鸟的巢穴依据适应度值排序; 然后对较优的一半巢穴执行标准的CS算法，对较劣的一半巢穴执行MNNA算法; 最后，完成一次迭代之后，将两部分巢穴组成在一起，挑选出最优的巢穴作为当前最优解，重新划分巢穴执行下一次迭代.为了检验所提出算法的优化性能，本文采用NNCS算法求解24个经典的基准测试问题，并将其与CS，NNA，MNNA以及2个最近提出的CS改进算法相比较.实验结果表明：与这些算法相比，NNCS算法在解决多峰优化问题时，其在求解质量、求解效率以及稳定性方面均展现出明显优势.

1 布谷鸟算法

CS算法是模拟某些种属布谷鸟的寻窝产卵行为.在自然界中，这种行为实际上是非常复杂的.为了构建简便的数学模型，CS算法的作者通过以下3条理想化的规则对这种行为进行了简化^{[5, 6]}：1)每个布谷鸟每次只产一个蛋，并将其放入随机选择的巢穴中孵化；2)在随机选择的一组巢穴中，最好的巢穴将被保留到下一代；3)可用的寄主巢穴是固定的，且寄主能以概率p_a(p_a∈(0, 1))发现外来的蛋.此时，寄主可以消灭该布谷鸟蛋.数学上，这3条规则可以表述如下：

$ X_i^{t + 1} = x_i^t + \alpha \times \left( {x_i^t - x_{{\rm{best}}}^t} \right) \otimes {\rm{Lévy}}(\lambda ). $

(1)

$ X_i^{t + 1} = x_i^t + r \otimes H\left( {{p_{\rm{a}}} - \varepsilon } \right) \otimes \left( {x_j^t - x_k^t} \right), j \ne k. $

(2)

式中：t是当前迭代次数，α是步长，r和ε是2个来自于均匀分布(0, 1)的随机数，p_a是发现概率，H(u)是海维赛德函数，Lévy(λ)是服从Lévy分布的随机数，x_i^t为第i个巢穴在第t次迭代时的位置，x_j^t为第j个巢穴在第t次迭代时的位置，x_k^t为第k个巢穴在第t次迭代时的位置.在布谷鸟算法中，式(1)用于执行全局搜索，式(2)用于执行局部搜索.关于该算法的具体实现以及相关参数对算法的影响可参见文献[4-5].

2 神经网络算法

NNA算法是受人工神经网络(artificial neural networks，ANNs)的结构以及生物神经元系统激励而提出的一种元启发式算法.ANNs是受生物神经网络结构和功能方面的启发而建立的计算模型. ANNs通过密集互连的人工神经元模拟生物的神经网络.根据ANNs的连接结构，ANNS可以分为以下两大类：1)前馈神经网络.前馈网络通常是“静态”的，因为这些网络结构没有回路，只产生一组输出值，而不是来自给定输入数据集的值序列；2)递归网络.递归网络通常“动态”的，因为这些网络中由于反馈连接而发生循环.

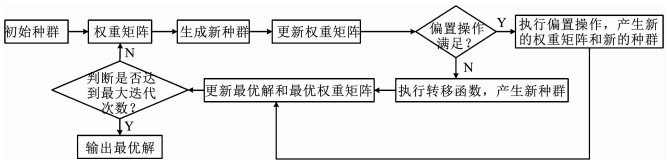
NNA通过结合ANNs的结构以及一些既定的迭代规则来解决优化问题.ANNs主要用于预测目的，其试图将输入数据映射到目标数据，并通过不断的调整权值来减少预测解和目标解间的误差.然而，优化问题的目的是为了在所有可行方案中找到一个未知的最优解.受ANNs启发，NNA在每次迭代中获得的最优方案被假定为目标解. 图 1给出了NNA算法的流程图.

图 1 NNA算法流程图 Fig. 1 Flowchart of NNA

从图 1中可看到，NNA的关键步骤有以下4个：

1) 种群生成.图 2给出了NNA中的种群生成方法.在NNA中，该操作由式(3)完成：

图 2 NNA算法基于神经网络的种群生成示意 Fig. 2 Population regeneration of NNA based on ANNs

$ S_i^{t + 1} = s_i^t + \sum\limits_{i = 1}^N {w_{i, j}^t} \times s_i^t, j = 1, 2, \cdots , N. $

(3)

式中N是种群大小，s_i^t是第i个个体在第t次迭代时的位置，w_{i, j}^t是权重矩阵在第t次迭代时的第i行，第j列的值.此外，权重矩阵满足式(4)，即

$ \sum\limits_{j = 1}^N {w_{i, j}^t} = 1, i = 1, 2, \cdots , N, w_{i, j}^t \in (0, 1). $

(4)

2) 权重矩阵更新.在NNA中，权重矩阵的更新满足式(5)，即：

$ w_i^{t + 1} = \left| {w_i^t + 2 \times r \times \left( {w_{{\rm{opt}}}^t - w_i^t} \right)} \right|, i = 1, 2, \cdots , N. $

(5)

式中r是一个满足(0, 1)均匀分布的随机数，w_opt^t是最优权重.最优权重w_opt^t是和最优解s_opt^t同时变动的，设在第t次迭代时, s_opt^t=s_m^t(m∈[1, N])，则w_opt^t=w_m^t.

3) 偏置操作.偏置操作中的一个关键变量称为修正因子β，它是用来决定偏置比例的.β的值越大，表明NNA有更大概率执行偏置操作而有较小概率执行转移函数操作.β的初始化为1，迭代过程中的更新依据式(6)^[18]，即

$ {\beta ^{t + 1}} = 0.99 \times {\beta ^t}. $

(6)

在NNA中的偏置操作包括2个部分，种群个体偏置和权重矩阵偏置.种群个体偏置，首先选取一个随机数P^t(对随机数β^t×D进行向上取整，D是个体的维度)，然后从需要偏置的个体x_i^t中随机选取P^t个元素进行更换，如第j个元素被选中，则

$ {x_{i, j}} = {l_j} + \left( {{u_j} - {l_j}} \right) \times b. $

(7)

式中b是一个满足(0, 1)均匀分布的随机数，l_j和u_j分别是第j个元素的上限和下限.至于权重矩阵偏置，首先选取一个随机数Q^t(对随机数β^t×N进行向上取整)，然后从需要偏置的权重w_i^t中随机选Q^t个元素进行更换，如第j个元素被选中，则

$ {w_{i, j}} = c. $

(8)

式中c是一个满足(0, 1)均匀分布的随机数.

4) 转移函数.在NNA中，执行转移函数是为了获取更好质量的解，其满足式(9)，即

$ S_i^{t + 1} = S_i^{t + 1} + 2 \times q \otimes \left( {s_{{\rm{opt }}}^t - s_i^t} \right), i = 1, 2, \cdots , N. $

(9)

式中q是一个元素数量为D且满足(0, 1)均匀分布的随机向量.

3 改进的布谷鸟算法

如何平衡算法的全局搜索和局部搜索是每一个元启发式算法都要着重考虑的问题，它与算法的寻优结果密切关联.在CS算法中，作者采用莱维飞行执行全局搜索，如式(1)所示；采用局部随机路径执行局部搜索，如式(2)所示.此外，发现概率p_a用来调整局部搜索和全局搜索在算法执行过程中的比例.CS算法的这种兼顾局部与全局搜索的机制在算法执行的前期是非常奏效的.但是随着迭代次数的增加，个体之间的差异将会逐渐缩小(如式(1)中x_i^t和x_best^t的差异，式(2)中x_j^t和x_k^t的差异)，CS算法将会逐渐偏重局部搜索、弱化全局搜索，从而一旦陷入局部最优将很难挣脱.可以说，CS算法以个体差异为基础的操作算子是其陷入局部最优的根本原因.

为了解决CS算法后期全局搜索与局部搜索严重失衡的问题，我们提出了NNCS算法.NNCS算法通过借助NNA算法的强大全局优化能力以及动态种群策略来平衡CS算法的全局搜索与局部搜索能力，从而减少CS算法陷入局部最优的可能性. NNA算法不依赖个体差异执行全局搜索，因而可以避免CS算法面临的困境.此外，为了在NNCS算法中更加充分地利用NNA算法的全局优化能力，本文提出了MNNA算法，然后结合MNNA和标准的CS算法提出了NNCS算法.

3.1 改进的神经网络算法

NNA是在人工神经网络结构的基础上，结合一些迭代准则而构建的元启发式算法.NNA中的偏置操作用来模拟人工神经网络中的偏置项来改善它的全局优化能力.NNA通过修正因子β来控制偏置比例.β的值越大，表明NNA有更大概率执行偏置操作而有较小概率执行转移函数的操作，同时随机数P^t和Q^t的值也会越大.此时，NNA具有较强的全局优化能力.β的值越小，表明NNA有更小概率执行偏置操作而有较大概率执行转移函数的操作，同时随机数P^t和Q^t的值也会越小.此时，NNA具有较弱的全局优化能力.考虑到算法的收敛性，NNA中的β值是逐渐变小的.也就是说，NNA的全局搜索能力是逐渐弱化的.为了充分利用NNA算法的全局优化能力，我们提出了MNNA算法. 图 3给出了MNNA算法的实现流程图.

图 3 MNNA算法流程图 Fig. 3 Flowchart of MNNA

与标准的NNA算法相比，MNNA主要做出了两点改进：1)MNNA中的修正因子设置为1，即丢弃了转移操作机制而保留了偏置操作机制，这样能够使得MNNA仅进行全局搜索；2)MNNA通过随机因子u来控制随机数P^t和Q^t的值.随机数P^t和Q^t的值可以表述为

$ {{\theta ^t} = u, } $

(10)

$ {{P^t} = \left\lceil {{\theta ^t} \times D} \right\rceil , } $

(11)

$ {{Q^t} = \left\lceil {{\theta ^t} \times N} \right\rceil .} $

(12)

式中:u是随机因子，其服从(0, 1)均匀分布的随机数，θ^t为在第t次迭代时的随机因子.在MNNA中，通过随机因子u来替代修正因子β，可以使得MNNA的全局搜索能力一直处于非常活跃的状态.这样可以有效地避免由于β值下降引起的算法全局搜索能力的减弱.

3.2 基于神经网络的布谷鸟算法

图 4给出了NNCS算法的流程图，NNCS算法的具体实现步骤如下：

图 4 NNCS算法流程图 Fig. 4 Flowchart of NNCS algorithm

步骤1 初始化种群大小N，解空间的维度D、解空间上限u和下限l，目标函数f(·)，发现率p_a，步长α，当前迭代次数t(t=0)，当前函数评价次数T_current(T_current=0)和最大函数评价次数T_max.此外，依据求解空间的上下限和维度随机初始化种群X^t=[x₁^t, x₂^t, …, x_N^t]^T，依据式(4)随机产生一个初始化权重矩阵W^t=[w₁^t, w₂^t, …, w_E^t]^T(E等于$\frac{N}{2}$，因为仅用MNNA优化种群中的一半个体).

步骤2 对种群中进行评价，并挑选出最优个体G_best^t作为当前最优解.依据式(13)更新评价次数：

$ {T_{{\rm{current }}}} = {T_{{\rm{current }}}} + N. $

(13)

假如T_current≥T_max，算法结束，否则继续执行步骤3.

步骤3 依据获得的适应度值将种群分为2个子种群，即最优子种群X_best^t(最优的一半个体)和最差子种群X_worst^t(最劣的一半个体).

步骤4 对最差子种群X_worst^t执行MNNA算法.首先，从该种群中选择出最优解及其对应的最优权重向量.然后，由式(3)和(5)分别更新种群及权重矩阵.接着，由式(7)、(8)、(10)~(12)执行偏置操作.最后，新的子种群X_worst^t+1产生.

步骤5 对最优子种群X_best^t执行CS算法.首先，从该种群中选择出最优巢穴，由式(1)获取新的布谷鸟巢穴.然后，对巢穴进行优化筛选，即若新生成的巢穴优于原巢穴，则新生成的巢穴替代原位置，

否则原位置保持不变.接着，由式(2)执行寄主发现布谷鸟操作，并产生新的巢穴.最后，再次执行巢穴的优化的筛选，新的子种群X_best^t+1产生.

步骤6 种群重组.将种群X_best^t+1和种群X_worst^t+1合并为新的种群X_best^t+1，从种群X_best^t+1中选出最优解G_best^t+1.

步骤7 更新当前函数评价次数依据式(14) T_current=T_current+1.5×N.

假如T_current≥T_max，算法结束，否则跳转到步骤3.

4 实验结果及分析 4.1 基准测试函数

实验中用到的测试函数摘自于经典的基准测试函数集(http://www.sfu.ca/~ssurjano/).这些函数的基本属性如表 1所示.

表 1 基准测试函数(“U”和“M”分别代表单峰和多峰) Tab. 1 Benchmark test functions("U" and "M" stand for unimodal and multi-model respectively)

编号	函数名	函数表达式	维度	取值区间	函数类型
F₁	Sphere	$ f(x) = \sum\limits_{i = 1}^D {x_i^2} $	30	[-100, 100]	U
F₂	Sum Squares	$ f(x) = \sum\limits_{i = 1:}^D i \times x_i^2$	30	[-10, 10]	U
F₃	Schewefel 2.22	$ f(x) = \sum\limits_{i = 1:}^D {\left\| {{x_i}} \right\|} + \prod\limits_{i = 1}^D {\left\| {{x_i}} \right\|} $	30	[-10, 10]	U
F₄	Schewefel 1.2	$ f(x) = \sum\limits_{i = 1}^D {{{\left( {\sum\limits_{j = 1}^i {{x_j}} } \right)}^2}} $	30	[-100, 100]	M
F₅	Rosenbrock	$ f(x) = \sum\limits_{i = 1}^{D - 1} 1 00{\left( {{x_{i + 1}} - x_i^2} \right)^2} + {\left( {{x_i} - 1} \right)^2}$	30	[-30, 30]	M
F₆	Griewank	$ f(x) = \frac{1}{{4\;000}}\sum\limits_{i = 1}^D {x_i^2} - \prod\limits_{i = 1}^D {\cos } \frac{{{x_i}}}{{\sqrt i }} + 1$	30	[-600, 600]	M
F₇	Alpine	$ f(x) = \sum\limits_{i = 1}^D {\left\| {{x_i}\sin \left( {{x_i}} \right) + 0.1{x_i}} \right\|} $	30	[-10, 10]	M
F₈	Ackley	$ f(x) = - 20\exp ( - 0.2\sqrt {\frac{1}{D}\sum\limits_{i = 1}^D {x_i^2} } ) - \exp \left( {\frac{1}{D}\sum\limits_{i = 1}^D {\cos } 2{\rm{ \mathsf{ π} }}{x_i}} \right) + 20 + e30$	30	[-32, 32]	M
F₉	Schaffer	$ f(x) = 0.5 + \frac{{{{\sin }^2}(\sqrt {\sum\limits_{i = 1}^D {x_i^2} } ) - 0.5}}{{{{\left( {1 + 0.001\left( {\sum\limits_{i = 1}^D {x_i^2} } \right)} \right)}^2}}}$	30	[-100, 100]	M
F₁₀	Rastrigin	$ f(x)=\sum_{i=1}^{D} x_{i}^{2}-10 \cos \left(2 {\rm{ \mathsf{ π} }} x_{i}\right)+10$	30	[-5.12, 5.12]	M

表 1 基准测试函数(“U”和“M”分别代表单峰和多峰) Tab. 1 Benchmark test functions("U" and "M" stand for unimodal and multi-model respectively)

表 1中的函数包括3个单峰函数和7个多峰函数.此外，为了进一步检验所提出算法解决复杂多峰优化问题的能力，在表 1所示函数的基础上，给出了14个组合的多峰函数，如表 2所示.这些组合函数的表达式表述为

表 2 组合测试函数(“M”代表多峰函数) Tab. 2 Composition test functions ("M" stands for multi-model function)

$ F = {F_{{\rm{first }}}} + \eta \times {F_{{\rm{second }}}}. $

(15)

式中:F是组合函数，F_first为第1个函数，F_second为第2个函数，η是权重因子.总体上来说，相比于表 1中的函数，表 2中的测试函数更加复杂.

4.2 实验参数设置

本文所提出的NNCS算法是基于CS和MNNA，它也是一种改进的CS算法.因而，所设计的实验着重比较NNCS与CS、NNA、MNNA以及一些最近提出的CS改进算法.为了尽可能保证比较的公平，所有算法均具有相同的种群数量和最大函数评价次数，其余参数来自于算法的原文献.此外，所有算法对于每个优化问题均独立重复执行30次.这些算法的具体参数设置如下：

NNCS算法：发现概率p_a=0.25，步长a=0.01，种群大小N=20，最大函数评价次数T_max=100 000.

CS算法^[5]：发现概率p_a=0.25，步长a=0.01，种群大小N=20，最大函数评价次数T_max=100 000.

自适应CS算法(ACSA)^[15]：发现概率p_a=0.25，步长a=0.01，种群大小N=20，最大函数评价次数T_max=100 000.

改进的CS算法(ICS)^[17]：发现概率的最大值p_max=0.5，发现概率的最小值p_max=0.005，步长的最大值a_max=0.5，步长的最小值a_min=0.01，种群大小N=20，最大函数评价次数T_max=100 000.

NNA算法^[18]：修正因子β=1，种群大小N=20，最大函数评价次数T_max=100 000.

MNNA算法：种群大小N=20，最大函数评价次数T_max=100 000.

4.3 算法评价指标

在本文中，3个评价指标被用于比较不同算法之间的优化性能差异.

平均绝对误差(Mean Absolute Error，ME)和标准方差(Standard Deviation, SD)：ME是所有观测值与真实值偏差的绝对值的平均，常用来衡量算法的寻优能力的强弱；SD是方差的算术平方根，常用来反映一个数据集的离散程度. ME的值越小，表明算法的寻优能力越强；SD的值越小，表明算法的稳定性越强.

Tied rank^[19]：Tied rank(TR)是一个定量排序的有效方法，它将所有算法按照指定的指标从最好到最坏进行排序.如果多个算法具有相同的指标，那么它们具有相同排列序号.在我们的实验中，选取的排序指标是多次独立重复实验的平均绝对误差，即对于某个问题，如果某个算法的平均绝对误差是最小的，那么就标记为所有算法中的第1名；如果是最大的，则标记为所有算法中的倒数第1名.

威尔逊秩和检验^[20]：威尔逊秩和检验是一种常用的无参数检验法.相比于T检验，威尔逊秩和检验具有以下优势：其一，不要求测试样本严格服从正态分布；其二，受异常值的影响更小.这些优势使得威尔逊秩和检验法比T检验法更有效的展现算法间的性能差异.

4.4 实验结果分析

表 3给出了6种算法在24个测试函数上的平均绝对误差和标准方差.可以清晰的看到，除了F₁₅之外，本文提出的NNCS算法能够在其余23个测试函数上均具有最优的平均绝对误差及标准方差，并且这种优势是非常明显的.此外，在F₁₅上，NNCS能获取与NNA、CS、ACS和ICS相同的平均绝对误差；在F₁₀，F₁₉和F₂₀上，NNCS能够取得实际最优解.仔细观察会发现，对于所有的测试函数而言MNNA是所有算法中寻优能力最差的.这是因为，为了充分利用NNA的全局优化能力，我们在提出的MNNA中仅保留了偏置操作而丢弃了转移函数的操作，这会导致MNNA的探索能力和勘探能力的严重失衡，最终呈现出糟糕的寻优结果.然而，需要看到的是，正是借助于MNNA的强大的全局优化能力，NNCS的收敛性能才会大幅优于标准的NNA和CS算法.

表 3 6种算法对于基准测试函数的优化结果(最好的结果用粗体标注) Tab. 3 Experimental results of 6 optimizers for benchmark functions (best results highlighted in boldface)

编号	指标	NNA	MNNA	CS	ICS	ACS	NNCS
F₁	ME	9.03×10^-18	2.13×10⁴	5.89×10^-13	2.52×10^-23	7.21×10^-13	2.22×10^-61
	SD	1.06×10^-17	4.17×10³	5.86×10^-13	3.07×10^-23	7.73×10^-13	1.22×10^-60
F₂	ME	1.49×10^-6	4.09×10²	4.91×10^-2	4.16×10⁰	4.87×10^-2	3.13×10^-27
	SD	1.04×10^-6	4.82×10¹	2.13×10^-2	1.45×10⁰	2.29×10^-2	1.71×10^-26
F₃	ME	1.09×10^-10	6.61×10¹	3.62×10^-7	6.70×10^-13	3.25×10^-6	9.87×10^-39
	SD	1.24×10^-10	2.43×10¹	2.31×10^-7	9.48×10^-13	2.46×10^-6	5.21×10^-38
F₄	ME	1.42×10^-4	3.99×10⁴	3.95×10⁰	3.98×10²	1.70×10⁰	6.32×10^-24
	SD	9.35×10^-5	5.59×10³	2.78×10⁰	8.62×10¹	8.88×10^-1	3.46×10^-23
F₅	ME	2.24×10¹	4.61×10⁵	2.42×10¹	2.14×10¹	2.13×10¹	1.53×10^-9
	SD	1.19×10⁰	1.57×10⁵	1.41×10¹	1.26×10⁰	1.27×10⁰	7.04×10^-9
F₆	ME	6.43×10^-14	1.94×10²	7.50×10^-4	1.48×10^-13	1.15×10^-4	0.00×10⁰
	SD	2.43×10^-13	4.43×10¹	2.97×10^-3	5.74×10^-13	6.27×10^-4	0.00×10⁰
F₇	ME	6.91×10^-1	3.54×10¹	2.86×10⁰	1.14×10⁰	5.12×10⁰	3.84×10^-18
	SD	1.28×10⁰	2.84×10⁰	1.33×10⁰	1.31×10⁰	2.42×10⁰	2.10×10^-17
F₈	ME	5.92×10^-10	1.85×10¹	7.30×10^-1	7.37×10^-6	6.21×10^-2	8.88×10^-16
	SD	5.41×10^-10	4.02×10^-1	6.41×10^-1	4.03×10^-5	2.36×10^-1	0.00×10⁰
F₉	ME	3.40×10^-2	5.00×10^-1	2.06×10^-1	7.00×10^-2	1.31×10^-1	4.21×10^-3
	SD	1.33×10^-2	1.09×10^-4	5.66×10^-2	1.67×10^-2	3.20×10^-2	4.90×10^-3
F₁₀	ME	6.21×10⁰	2.79×10²	3.88×10¹	4.77×10¹	6.86×10¹	0.00×10⁰
	SD	4.40×10⁰	2.79×10¹	1.04×10¹	1.09×10¹	1.73×10¹	0.00×10⁰
F₁₁	ME	2.27×10^-12	5.00×10⁴	9.04×10^-7	5.39×10^-8	1.09×10^-7	8.95×10^-33
	SD	4.58×10^-12	5.61×10³	1.04×10^-6	3.85×10^-8	9.17×10^-8	4.39×10^-32
F₁₂	ME	2.18×10^-17	2.06×10⁴	1.00×10^-12	1.81×10^-23	6.04×10^-13	1.50×10^-79
	SD	4.40×10^-17	4.45×10³	1.23×10^-12	2.42×10^-23	6.64×10^-13	5.80×10^-79
F₁₃	ME	2.44×10^-11	4.18×10²	1.19×10^-2	2.93×10⁰	1.46×10^-2	1.39×10^-28
	SD	2.68×10^-11	4.90×10¹	8.76×10^-3	1.37×10⁰	7.10×10^-3	7.60×10^-28
F₁₄	ME	4.54×10^-10	4.10×10²	5.09×10^-3	4.77×10⁰	5.61×10^-3	4.44×10^-16
	SD	3.74×10^-10	6.01×10¹	5.50×10^-3	1.37×10⁰	5.86×10^-3	0.00×10⁰
F₁₅	ME	1.45×10¹	3.19×10⁵	1.45×10¹	1.45×10¹	1.45×10¹	1.45×10¹
	SD	9.67×10^-15	1.34×10⁵	2.39×10^-1	4.15×10^-5	9.21×10^-4	3.61×10^-9
F₁₆	ME	1.05×10^-10	7.43×10¹	3.64×10^-7	5.48×10^-13	3.38×10^-6	9.47×10^-40
	SD	1.41×10^-10	2.09×10¹	3.06×10^-7	6.52×10^-13	2.42×10^-6	3.55×10^-39
F₁₇	ME	2.53×10¹	4.70×10⁵	2.99×10¹	2.48×10¹	2.51×10¹	1.41×10¹
	SD	1.09×10^-1	1.52×10⁵	1.52×10¹	6.06×10^-1	4.06×10^-1	1.50×10^-3
F₁₈	ME	1.43×10^-9	1.87×10¹	1.41×10⁰	1.19×10^-4	1.76×10^-1	8.88×10^-16
	SD	2.09×10^-9	4.71×10^-1	9.52×10^-1	6.01×10^-4	5.36×10^-1	0.00×10⁰
F₁₉	ME	8.12×10⁰	2.77×10²	3.97×10¹	5.66×10¹	7.59×10¹	0.00×10⁰
	SD	2.69×10⁰	2.95×10¹	1.04×10¹	1.20×10¹	1.15×10¹	0.00×10⁰
F₂₀	ME	5.40×10⁰	2.72×10²	4.59×10¹	5.47×10¹	7.18×10¹	0.00×10⁰
	SD	3.93×10⁰	2.94×10¹	8.79×10⁰	1.37×10¹	1.32×10¹	0.00×10⁰
F₂₁	ME	6.01×10^-3	5.12×10⁰	7.89×10^-1	2.45×10^-1	4.31×10^-1	1.30×10^-17
	SD	2.57×10^-2	8.05×10^-1	2.24×10^-1	8.95×10^-2	1.54×10^-1	6.13×10^-17
F₂₂	ME	5.73×10⁰	4.41×10¹	8.28×10⁰	5.53×10^-5	7.37×10⁰	6.66×10^-16
	SD	4.20×10⁰	3.83×10⁰	2.84×10⁰	2.92×10^-4	4.41×10⁰	0.00×10⁰
F₂₃	ME	6.23×10^-1	3.56×10¹	3.08×10⁰	1.20×10⁰	5.19×10⁰	8.81×10^-38
	SD	5.66×10^-1	3.67×10⁰	1.09×10⁰	1.34×10⁰	2.43×10⁰	4.58×10^-37
F₂₄	ME	2.52×10¹	4.59×10⁵	2.47×10¹	2.19×10¹	2.22×10¹	6.70×10^-1
	SD	1.09×10¹	1.62×10⁵	1.41×10¹	7.27×10^-1	1.27×10⁰	1.51×10^-6

表 3 6种算法对于基准测试函数的优化结果(最好的结果用粗体标注) Tab. 3 Experimental results of 6 optimizers for benchmark functions (best results highlighted in boldface)

表 4给出了依据平均绝对误差的Tied rank的排序结果. 表 4给出了依据平均绝对误差的排序结果.从表 4可以看到，NNCS能够在23个测试函数上获取第1名，在1个测试函数上并列第1名，这表明所提出算法具有强大的全局搜索能力.依据表 4中的所有测试函数的平均排序值，这些算法由最优到最劣的顺序如下：NNCS、NNA、ICS、ACS、CS和MNNA.

表 4 基于平均绝对误差的排序结果(“AVG”表示排序的平均值) Tab. 4 Ranking results of algorithms on the basis of mean absolute errors("AVG" stands for the average value)

Algorithm	F₁	F₂	F₃	F₄	F₅	F₆	F₇	F₈	F₉	F₁₀	F₁₁	F₁₂	F₁₃	F₁₄	F₁₅	F₁₆	F₁₇	F₁₈	F₁₉	F₂₀	F₂₁	F₂₂	F₂₃	F₂₄	AVG
NNA	3	2	3	2	4	2	2	2	2	2	2	3	2	2	3	3	4	2	2	2	2	3	2	5	2.54
MNNA	6	6	6	6	6	6	6	6	6	6	6	6	6	6	6	6	6	6	6	6	6	6	6	6	6.00
CS	4	4	4	4	5	5	4	5	5	3	5	5	3	3	3	4	5	5	3	3	5	5	4	4	4.17
ICS	2	5	2	5	3	3	3	3	3	4	3	2	5	5	3	2	2	3	4	4	3	2	3	2	3.17
ACS	5	3	5	3	2	4	5	4	4	5	4	4	4	4	3	5	3	4	5	5	4	4	5	3	4.04
NNCS	1	1	1	1	1	1	1	1	1	1	1	1	1	1	3	1	1	1	1	1	1	1	1	1	1.08

表 4 基于平均绝对误差的排序结果(“AVG”表示排序的平均值) Tab. 4 Ranking results of algorithms on the basis of mean absolute errors("AVG" stands for the average value)

表 5展示了威尔逊秩和检验结果(显著性水平α=0.05).在表 5中，“R(+)”，“R(-)”，“p-value”和“S”分别表示正秩和、负秩和、检验P值和检验符号.依据检验准则，若正秩和大于负秩和且检验P值小于显著性水平值，则检验符号标记为“+”，即第1个算法优于第2个算法；若正秩和小于负秩和且检验P值小于显著性水平值，则检验符号为“-”，即第1个算法劣于第2个算法.从表 5可以看到，NNCS在所有测试函数上均优于MNNA、CS、ICS和ACS.在F₁₅上，NNA优于NNCS，但是其劣于NNCS在其余23个测试函数上.总的来说，相比于其它5种算法，NNCS算法在解决多峰优化问题时展现出更好的优化性能.

表 5 算法的威尔逊秩和检验结果(显著性水平设定为α=0.05) Tab. 5 Pairwise comparison of several algorithms by Wilcoxon signedrank test (α=0.05)

No.	NNCS vs. NNA				NNCS vs. MNNA				NNCS vs. CS				NNCS vs. ICS				NNCS vs. ACS
No.	R(+)	R(-)	p-value	S	R(+)	R(-)	p-value	S	R(+)	R(-)	p-value	S	R(+)	R(-)	p-value	S	R(+)	R(-)	p-value	S
F₁	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+
F₂	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+
F₃	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+
F₄	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+
F₅	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+
F₆	243	222	3.13×10^-2	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	292.5	172.5	6.10×10^-5	+	465	0	1.73×10^-6	+
F₇	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+
F₈	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+
F₉	462	3	2.35×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+
F₁₀	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+
F₁₁	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+
F₁₂	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+
F₁₃	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+
F₁₄	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+
F₁₅	133.5	331.5	1.42×10^-2	-	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	443	22	1.49×10^-5	+	465	0	1.73×10^-6	+
F₁₆	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+
F₁₇	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+
F₁₈	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+
F₁₉	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+
F₂₀	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+
F₂₁	435.5	29.5	3.69×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+
F₂₂	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+
F₂₃	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+
F₂₄	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+	465	0	1.73×10^-6	+
+/-/=	23/1/0				24/0/0				24/0/0				24/0/0				24/0/0

表 5 算法的威尔逊秩和检验结果(显著性水平设定为α=0.05) Tab. 5 Pairwise comparison of several algorithms by Wilcoxon signedrank test (α=0.05)

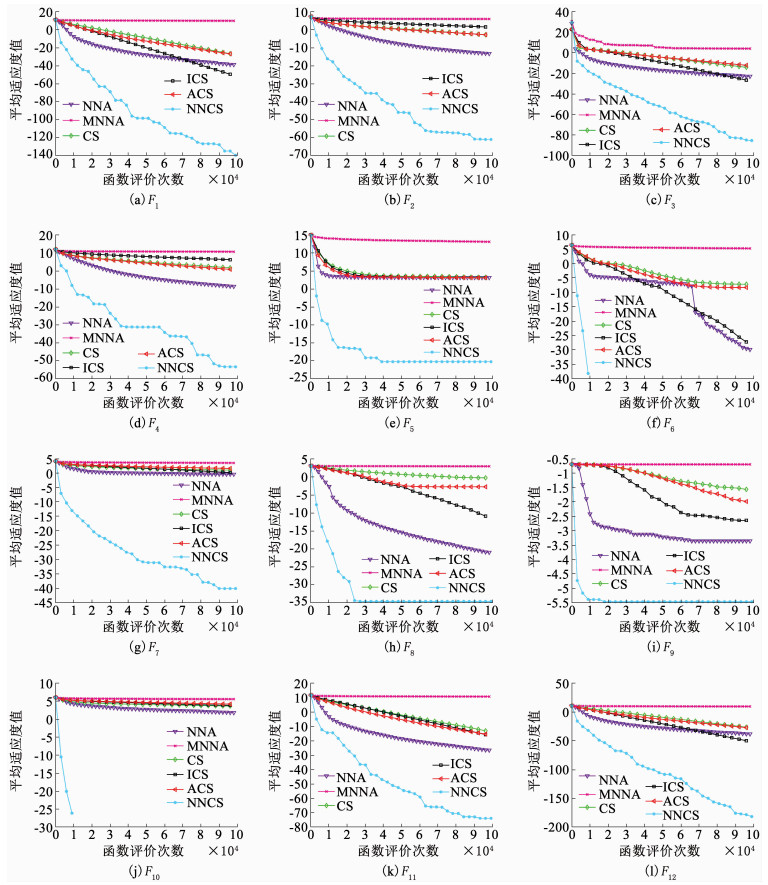
为了更加直观的观察不同算法在不同测试函数上的收敛性能，图 5给出了6种算法在24个测试函数上的平均适应度值的对数值在不同函数评价次数下的表现情况.下面将测试函数分为基准测试函数(F₁~F₁₀)和组合测试函数(F₁₁~F₂₄)两类进行比较分析.对于基准测试函数，与其它5种算法相比，NNCS在所有函数上均有非常明显的收敛优势.这种收敛优势不但体现在收敛速度上，而且展现在收敛到的全局最优解.其中，在F₆和F₁₀上，NNCS的这种优势得到了显著的体现，即其能快速地收敛到实际最优解0.对于组合测试函数，与其它5种算法相比，NNCS具有以下特点：1)NNCS在F₁₅和F₁₇上的收敛优势并不明显，尤其在F₁₅上；2)NNCS在除F₁₅和F₁₇以外的函数上具有明显的收敛优势；3)NNCS在F₁₉和F₂₀上的收敛优势最为明显，其能在这2个函数上，快速收敛到全局最优解0.总的来说，相较于其余5种算法，本文提出的NNCS在所有测试函数上均能展现出更好的收敛优势.这种优势不但体现在寻优精度上，而且体现在计算效率上.

图 5 6种优化算法在测试函数上的收敛曲线 Fig. 5 Convergence curves of 6 optimizers on test functions

通过对上述3个评价指标的分析，本文提出的NNCS在求解复杂多峰优化问题时，其在寻优精度，收敛速度及鲁棒性等方面均具有较好的表现.与原始的布谷鸟算法相比较，本文提出的NNCS在上述3个指标上的优势则更为明显，这充分表明了所提出改进策略的有效性.

5 结论

针对布谷鸟算法求解多峰优化问题存在易陷入局部最优解的缺陷，本文提出了一种基于神经网络的布谷鸟算法(NNCS)，其主要从以下方面对布谷鸟算法进行了优化：1)动态种群机制.采用动态种群机制能够在一定程度上丰富种群的多样性，抑制种群的早熟收敛；2)改进的神经网络算法(MNNA).为了在所提出的NNCS算法中充分利用神经网络算法的全局搜索能力，本文提出了MNNA. NNCS通过MNNA算法和动态种群机制增强CS算法的全局优化能力，提升CS算法在解决复杂优化问题时挣脱局部最优解的能力.

对24个复杂的基准函数进行测试表明：与神经网络算法、布谷鸟算法以及一些改进的布谷鸟算法相比，提出的NNCS算法在求解复杂多峰优化问题时，其在寻优精度，收敛速度及鲁棒性上均显著优于其它算法.实验结果充分表明了所提出改进策略的有效性.

参考文献

[1]	DAS S, MAITY S, QU Boyang, et al. Real-parameter evolutionary multimodal optimization—A survey of the state-of-the-art[J]. Swarm and Evolutionary Computation, 2011, 1(2): 71. DOI:10.1016/j.swevo.2011.05.005
[2]	ZHANG Jinhao, MI Xiao, GAO Liang, et al. Queuing search algorithm: a novel meta-heuristic algorithm for solving engineering optimization problems[J]. Applied Mathematical Modelling, 2018, 63: 464. DOI:10.1016/j.apm.2018.06.036
[3]	RAO R V, SAVSANI V J, VAKHARIA D P. Teaching learning-based optimization: an optimization method for continuous non-linear large scale problems[J]. Information Sciences, 2012, 183(1): 1. DOI:10.1016/j.ins.2011.08.006
[4]	ESKANDAR H, SADOLLAH A, BAHREININEJAD A, et al. Water cycle algorithm-A novel metaheuristic optimization method for solving constrained engineering optimization problems[J]. Computers & Structures, 2012, 110(10): 151. DOI:10.1016/j.compstruc.2012.07.010
[5]	YANG X S, DEB S. Cuckoo Search via Lévy flights[C]//2009 World Congress on Nature & Biologically Inspired Computing (NaBIC). IEEE, 2009: 210. DOI: 10.1109/NABIC10.1109/NABIC.2009.5393690
[6]	YANG X S, DEB S. Cuckoo search: recent advances and applications[J]. Neural Computing and Applications, 2014, 24(1): 169. DOI:10.1007/s00521-013-1367-1
[7]	李东生, 高杨, 雍爱霞. 基于改进离散布谷鸟算法的干扰资源分配研究[J]. 电子与信息学报, 2016, 38(4): 899. LI Dongsheng, GAO Yang, YONG Aixia. Jamming resource allocation via improved discrete cuckoo search algorithm[J]. Journal of Electronics & Information Technology, 2016, 38(4): 899. DOI:10.11999/JEIT150726
[8]	张子成, 韩伟, 毛波. 基于模拟退火的自适应离散型布谷鸟算法求解旅行商问题[J]. 电子学报, 2018, 46(8): 1849. ZHANG Zicheng, HAN Wei, MAO Bo. Adaptive Discrete Cuckoo Algorithm Based on Simulated Annealing for Solving TSP[J]. Acta Electronica Sinica, 2018, 46(8): 1849. DOI:10.3969/j.issn.0372-2112.2018.08.008
[9]	梁爽, 孙庚, 刘衍珩. 改进布谷鸟算法用于阵列天线方向图优化[J]. 西安电子科技大学学报, 2019, 46(1): 174. LIANG Shuang, SUN Geng, LIU Yanheng. Improved cuckoo search algorithm for optimizing the beam patterns of linear antenna arrays[J]. Journal of Xidian University, 2019, 46(1): 174. DOI:10.19665/j.issn1001-2400.2019.01.027
[10]	CHITARA D, NIAZI K R, SWARNKAR A, et al. Cuckoo search optimization algorithm for designing of multimachine power system stabilizer[J]. IEEE Transactions on Industry Applications, 2018, 54(4): 3056. DOI:10.1109/TIA.2018.2811725
[11]	BOUSHAKI S I, KAMEL N, BENDJEGHABA O. A new quantum chaotic cuckoo search algorithm for data clustering[J]. Expert Systems with Applications, 2018, 96: 358. DOI:10.1016/j.eswa.2017.12.001
[12]	马卫, 孙正兴. 采用搜索趋化策略的布谷鸟全局优化算法[J]. 电子学报, 2015, 43(12): 2429. MA Xing, SUN Zhengxing. A global cuckoo optimization algorithm using coarse-to-fine search[J]. Acta Electronica Sinaca, 2015, 43(12): 2429. DOI:10.3969/j.issn.0372-2112.2015.12.013
[13]	SALGOTRA R, SINGH U, SAHA S. New cuckoo search algorithms with enhanced exploration and exploitation properties[J]. Expert Systems with Applications, 2018, 95: 384. DOI:10.1016/j.eswa.2017.11.044
[14]	HUANG Li, DING Shuai, YU Shouhao, et al. Chaos-enhanced Cuckoo search optimization algorithms for global optimization[J]. Applied Mathematical Modelling, 2016, 40(5-6): 3860. DOI:10.1016/j.apm.2015.10.062
[15]	SARANGI S K, PANDA R, DAS P K, et al. Design of optimal high pass and band stop FIR filters using adaptive Cuckoo search algorithm[J]. Engineering Applications of Artificial Intelligence, 2018, 70: 67. DOI:10.1016/j.engappai.2018.01.005
[16]	TAWFIK A S, BADR A A, ABDEL-RAHMAN I F. One rank cuckoo search algorithm with application to algorithmic trading systems optimization[J]. International Journal of Computer Applications, 2013, 64(6): 30. DOI:10.5120/10641-5394
[17]	VALIAN E, TAVAKOLI S, MOHANNA S, et al. Improved cuckoo search for reliability optimization problems[J]. Computers & Industrial Engineering, 2013, 64(1): 459. DOI:10.1016/j.cie.2012.07.011
[18]	SADOLLAH A, SAYYAADI H, YADAV A. A dynamic metaheuristic optimization model inspired by biological nervous systems: Neural network algorithm[J]. Applied Soft Computing, 2018, 71: 747. DOI:10.1016/j.asoc.2018.07.039
[19]	RAKHSHANI H, RAHATI A. Snap-drift cuckoo search: A novel cuckoo search optimization algorithm[J]. Applied Soft Computing, 2017, 52: 771. DOI:10.1016/j.asoc.2016.09.048
[20]	DERRAC J, GARCíA S, MOLINA D, et al. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms[J]. Swarm & Evolutionary Computation, 2011, 1(1): 3. DOI:10.1016/j.swevo.2011.02.002