2. 西北工业大学 航天学院,西安 710072
2. School of Astronautics, Northwestern Polytechnical University, Xi′an 710072, China
由于复合材料具有很高的比强度和比刚度,近年来,先进复合材料层合板在高性能航空航天结构及民用产品等领域获得了越来越广泛的应用.复合材料多钉连接是工程中经常采用的一种连接形式.由于复合材料的各向异性及脆性等影响,在多钉连接中载荷再分配能力较差,造成各载荷分配产生严重不均匀性,极大地影响多钉连接的效率.
国内外学者对钉载分配的计算及优化进行了广泛的研究.在众多计算钉载分配的理论和数值方法的研究中,复势函数法[1-2]、弹簧质量法[3-7]、三维有限元法[8]以及基于结构单元的二维有限元法[9-10]等得到了广泛的应用.1946年,Tate和Rosenfeld[3]等针对各向同性材料多钉双剪接头,根据变形一致性条件,建立了关于螺栓载荷的递推公式,奠定了弹簧质量模型的基础.Nelson[4]等在Rosenfeld工作基础上,将双剪连接的钉载分配模型进一步推广到单剪接头上.McCarthy[5-6]等将弹簧质量模型分别推广到考虑钉孔间隙和摩擦因素的情况,并通过有限元模型和试验结果进行了验证.谢宗蕻[7]等对弹簧质量模型进行了改进,改进后的模型可用于规则排列复合材料螺接修理钉载比例的分析.
在有限元方面,为提高计算效率,Gray[8]和Ekh[9]等通过梁元和壳元分别模拟螺栓和连接板,并采用基于结构单元的二维有限元模型分析多钉连接的钉载分配,能够将计算时间节省97%以上.Bortman[10]等通过Fastener单元和Link单元分别模拟钉孔之间的挤压作用和螺栓端头之间的剪切作用对钉载分配进行研究.目前,基于结构单元的二维有限元方法已经成为分析钉载分配的一种非常高效的方法.
在钉载分配的优化方面,Yun[11]等以单钉双剪接头的极限载荷作为外载荷,分别作用到多钉连接的各个螺栓上,从而得到各个螺栓的相对位移情况,并以此为基础设计钉孔配合的间隙量.采用该方法设计的多钉连接结构,接头的承载能力提高了13.1%~21.8%.邵祝涛[12]等针对复合材料层合板多排多列机械连接的优化,提出了连接效率的判别指标.并利用枚举法对排列布局进行了优化.Gamdani等[13]通过对多钉连接接头、开孔板拉伸、填充孔拉伸、销钉拉伸以及单钉单剪等试验件的测试,提出了多钉连接接头强度上限的理论.随着螺栓数目的增加,多钉连接接头的强度逼近开孔板的拉伸强度,即多钉连接接头强度的上限为开孔板的拉伸强度,且试验件越窄,接头强度达到该上限所需的螺栓数目越少.该结论对复合材料多钉连接的优化具有重要的指导意义.Kabeel等[14]采用粘聚力模型对多钉连接接头进行了优化.研究发现,对于给定螺栓数目进行优化后的接头,通过继续增加螺栓数目,对接头强度的影响微弱,但是在增加螺栓数目后若重新进行优化,则往往能够较明显地提高接头的承载能力.Oinonen等[15]对受偏心载荷的多钉连接接头的螺栓布局进行了优化,优化后接头上的冯米塞斯应变减少20%以上.Peng等[16]采用自动化建模技术建立多钉连接的有限元模型并结合遗传算法对连接板厚度和铺层顺序进行了优化,优化后钉载分布的不均匀性得到了有效的降低.谢宗蕻等[17]基于弹簧质量模型建立了考虑钉孔间隙的复合材料钉载分配均匀化方法,但由于是解析模型,仅能得到各钉的钉载情况,无法对孔边应力进行分析.Ekh[9]等基于结构单元技术结合Solnp优化算法对多钉连接的钉载分配进行了优化,优化结果显示,接头最大挤压应力由220 MPa减小到120 MPa,净截面拉伸应力也得到减小.目前,采用基于结构单元的二维有限元技术并结合遗传算法和神经网络算法等的优化技术已经成为钉载分配优化的一种通用技术,但由于该方法计算量大,优化过程复杂等,在一定程度上限制了该方法在多钉连接设计上的应用.
在众多影响钉载分配的因素中,钉孔间隙的影响最为显著[18-19].文献[9]的研究表明,在外载荷不变的情况下,螺栓载荷与钉孔间隙之间近似满足线性的关系.本文在有限元分析的基础上,通过将钉载关于钉孔间隙进行一阶泰勒展开,进而建立钉载和钉孔间隙之间的线性方程组.然后在指定外载荷条件下,以钉载均匀分配时的螺栓载荷为已知量,以钉孔间隙为未知量,求解该线性方程组,计算各钉近似均匀分配时的钉孔间隙.
1 钉载分配均匀化的泰勒展开方法典型的复合材料多钉连接接头如图 1所示.连接板长度为L,宽度为w,厚度分别为tP、tS(上下连接板用符号“S”表示,中间的连接板用符号“P”表示),接头主要承受面内拉伸载荷的作用,外载荷记为F.螺栓的数目为n,编号由左侧开始,分别记为1, 2, …, n,另外,记钉孔之间的间隙为c =(c1, c2, …, cn)T.一般情况下,对该类多钉连接接头,首钉的钉载较大.为改善该类多钉连接接头钉载分配的不均匀性,本文优化模型采用以下目标函数:
| $ \min g=\sum\limits_{i=1}^{n}\left(f_{i}(\boldsymbol{c})-\bar{f}\right)^{2}. $ | (1) |
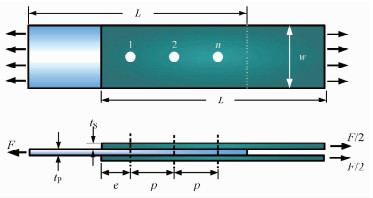
|
图 1 复合材料多钉连接接头构型 Fig. 1 Multi-bolt composite joint configuration |
式中:fi(c)为多钉连接接头中第ith个螺栓上的载荷.对于存在钉孔间隙的多钉连接接头,螺栓载荷为钉孔间隙的函数.f为钉载均匀分配时各钉的载荷,本文中记该载荷为目标载荷
| $ \bar{f}=\frac{F}{n}. $ |
目标函数g反映了钉载不均匀性的程度,g值越大,钉载不均匀程度越明显.
定义钉载比例为各钉载荷与外载荷之比,即
| $ r_{i}=\frac{f_{i}}{F} \times 100 \%. $ |
因此,钉载均匀分配时,各钉载比例满足
| $ r_{i}=\frac{1}{n}, i=1, 2, \cdots, n. $ |
由数学知识可知,式(1)取极小值的条件为等式右端的每一项都为0,因此问题转化为寻找钉孔间隙c,使其满足
| $ f_{i}(\boldsymbol{c})=\bar{f}, i=1, 2, \cdots, n. $ | (2) |
任意钉孔间隙情况下的钉载可通过泰勒展开写成以下形式
| $ f_{i}(\boldsymbol{c})=f_{i}\left(\boldsymbol{c}^{(0)}\right)+\sum\limits_{j=1}^{n}\left(\frac{\partial f_{i}}{\partial c_{j}} \delta c_{j}+O\left(\delta c_{j}^{2}\right)\right) i=1, 2, \cdots, n $ |
式中:δcj=cj-cj(0), j=1, 2, …, n.由于钉载随钉孔间隙几乎线性变化[9],因此只保留钉孔间隙的一次项,上式可近似写成
| $ f_{i}(\boldsymbol{c}) \approx f_{i}\left(\boldsymbol{c}^{(0)}\right)+\sum\limits_{j=1}^{n} \frac{\partial f_{i}}{\partial c_{j}} \delta c_{j}, i=1, 2, \cdots, n. $ | (3) |
式(3)中
| $ \left[ {\begin{array}{*{20}{c}} {\frac{{\partial {f_1}}}{{\partial {c_1}}}}&{\frac{{\partial {f_1}}}{{\partial {c_2}}}}& \cdots &{\frac{{\partial {f_1}}}{{\partial {c_n}}}}\\ {\frac{{\partial {f_2}}}{{\partial {c_1}}}}&{\frac{{\partial {f_2}}}{{\partial {c_2}}}}& \cdots &{\frac{{\partial {f_2}}}{{\partial {c_n}}}}\\ \vdots & \vdots & \ddots & \vdots \\ {\frac{{\partial {f_n}}}{{\partial {c_1}}}}&{\frac{{\partial {f_n}}}{{\partial {c_2}}}}& \cdots &{\frac{{\partial {f_n}}}{{\partial {c_n}}}} \end{array}} \right]\left( {\begin{array}{*{20}{c}} {\delta {c_1}}\\ {\delta {c_2}}\\ \vdots \\ {\delta {c_n}} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {{f_1}\left( {{{\boldsymbol{c}}^{(0)}}} \right)}\\ {{f_2}\left( {{{\boldsymbol{c}}^{(0)}}} \right)}\\ \vdots \\ {{f_n}\left( {{{\boldsymbol{c}}^{(0)}}} \right)} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{f_1}({\boldsymbol{c}})}\\ {{f_2}({\boldsymbol{c}})}\\ \vdots \\ {{f_n}({\boldsymbol{c}})} \end{array}} \right). $ | (4) |
式(4)中第1项的系数矩阵为H,该系数矩阵可根据钉载分配的有限元分析结果并采用小扰动的方法得到.令c(0)=(0, 0, …, 0)T,计算各钉的钉载fi(c(0)), i=1, 2, …, n.然后,给定扰动量Δc1,同时令Δc2=…=Δcn=0,计算钉孔间隙为c =(Δc1, 0, …, 0)T时各钉的钉载比例fi(c), i=1, 2, …, n.由于,c(0)=(0, 0, …, 0)T, 因此δci=ci,则根据式(4)有
| $ \frac{\partial f_{i}}{\partial c_{1}} \Delta c_{1}+f_{i}\left(\boldsymbol{c}^{(0)}\right)=f_{i}(\boldsymbol{c}), i=1, 2, \cdots, n. $ |
即
| $ \frac{\partial f_{i}}{\partial c_{1}}=\frac{f_{i}(\boldsymbol{c})-f_{i}\left(\boldsymbol{c}^{(0)}\right)}{\Delta c_{1}}, i=1, 2, \cdots, n. $ | (5) |
因此,可以得到系数矩阵的第1列.同理,当另外n-1个螺栓钉孔间隙扰动量非零时,可得到剩余的系数矩阵元素.
结合式(2)和式(4)可得钉载均匀分配时,钉孔间隙满足
| $ \left( {\begin{array}{*{20}{c}} {\delta {c_1}}\\ {\delta {c_2}}\\ \vdots \\ {\delta {c_n}} \end{array}} \right) = \left[ {\begin{array}{*{20}{c}} {\frac{{\partial {f_1}}}{{\partial {c_1}}}}&{\frac{{\partial {f_1}}}{{\partial {c_2}}}}& \cdots &{\frac{{\partial {f_1}}}{{\partial {c_n}}}}\\ {\frac{{\partial {f_2}}}{{\partial {c_1}}}}&{\frac{{\partial {f_2}}}{{\partial {c_2}}}}& \cdots &{\frac{{\partial {f_2}}}{{\partial {c_n}}}}\\ \vdots & \vdots & \ddots & \vdots \\ {\frac{{\partial {f_n}}}{{\partial {c_1}}}}&{\frac{{\partial {f_n}}}{{\partial {c_2}}}}& \cdots &{\frac{{\partial {f_n}}}{{\partial {c_n}}}} \end{array}} \right]\left( {\left( {\begin{array}{*{20}{c}} {\bar f}\\ {\bar f}\\ \vdots \\ {\bar f} \end{array}} \right) - \left( {\begin{array}{*{20}{c}} {{f_1}\left( {{\mathit{\boldsymbol{c}}^{(0)}}} \right)}\\ {{f_2}\left( {{\mathit{\boldsymbol{c}}^{(0)}}} \right)}\\ \vdots \\ {{f_n}\left( {{\mathit{\boldsymbol{c}}^{(0)}}} \right)} \end{array}} \right)} \right). $ | (6) |
| $ c_{j}=c_{j}^{(0)}+\delta c_{j}, j=1, 2, \cdots, n. $ | (7) |
特别对于cj(0)=0, j=1, 2, …, n的情况,有
| $ c_{j}=\delta c_{j}, j=1, 2, \cdots, n $ |
式(6)中右端的系数矩阵H是与载荷无关的量,另外,目标载荷向量以及钉孔间隙为0时各钉的载荷与外载荷成正比,因此钉载均匀分配时的钉孔间隙与外载荷之间满足c ∝F.
另外,由式(6)~(7)可以看到,为得到钉载均匀分配时各钉孔的间隙,只需已知系数矩阵H、均匀分配时各钉的载荷f以及钉孔间隙c(0)=(0, 0, …, 0)T情况下各钉的钉载.系数矩阵可通过n个独立的、钉孔间隙有扰动量Δcj≠0, j=1, 2, …, n时的钉载分配分析结果结合c(0)=(0, 0, …, 0)T情况下的钉载得到,共需进行(n+1)次有限元分析.假设单个钉载分配模型的计算时间为T,对于本文提出的优化模型,总的计算时间为(n+1)×T,模型的计算量与螺栓数目之间满足线性的关系.
2 钉载分配有限元模型本文采用p型有限元的方法分析钉载分配.p型有限元分析钉载分配时可以采用二维紧固件单元模型和三维多体接触模型两种方法.二维模型可模拟紧固件和板之间的接触,钉孔配合,紧固件剪切刚度等因素对钉载分配的影响,无法考虑拧紧力矩、板之间的摩擦以及板的二次弯曲对钉载分配的影响.但考虑到拧紧力矩以及板之间的摩擦对钉载分配影响不大,且连接结构多为薄板,另外,工程中,考虑螺栓的松弛效应,分析螺栓连接结构时,往往采用偏保守的设计方案[20].因此,本文分析中不考虑摩擦效应以及预紧力等的影响,采用二维有限元模型对钉载分配进行分析.
典型的多钉连接钉载分配二维有限元分析模型如图 2所示,连接板采用8节点等参数平面应力单元模拟,螺栓和钉孔之间的挤压作用采用Fastener单元模拟,Fastener单元之间采用Link单元连接,模拟螺栓的剪切和弯曲变形.模型左端固支,右端施加均匀分布载荷.
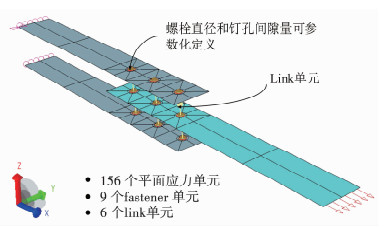
|
图 2 多钉连接有限元模型 Fig. 2 Finite element model of multi-bolt joint |
钉载分配的有限元模型采用文献[5]中的数据进行了验证,本文多钉连接的钉载分配采用该验证的有限元模型计算.
2.1 Fastener单元Fastener单元(见图 3)是p型有限元中一种特殊的紧固件单元,用于模拟钉孔之间的挤压作用.Fastener单元可考虑钉与孔之间的过盈配合以及间隙配合.该单元有一个刚性核,该刚性核与周围的平面单元连接在一起,有两个刚体位移自由度(ux, uy),刚性核与平面单元之间的接触用刚度为Kr的分布式弹簧描述.分布式弹簧的刚度可通过求解圆盘在径向压缩下的平面应变问题计算得到,本模型中弹簧刚度根据下式计算
| $ K_{\mathrm{r}}=\frac{2 E}{D(1+\nu)(1-2 \nu)}. $ |
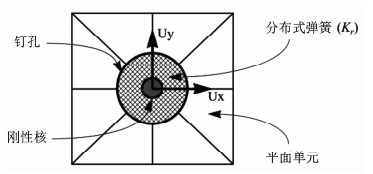
|
图 3 紧固件单元 Fig. 3 Fastener element |
式中:E与ν分别为Fastener单元的弹性模量和泊松比,D是孔径.
螺栓杆与孔之间的相互作用通过下式确定:
| $ T_{\mathrm{r}}=\left\{\begin{array}{cl}{0, } & {\text { if } \delta_{\mathrm{r}} \leqslant 0}; \\ {-K_{\mathrm{r}} \delta_{\mathrm{r}}, } & {\text { if } \delta_{\mathrm{r}}>0}.\end{array}\right. $ |
式中Tr为作用在孔边的法向力,δr由下式确定
| $ \delta_{\mathrm{r}}=u_{\mathrm{r}}+u_{\mathrm{x}} \cos \theta+u_{\mathrm{y}} \sin \theta+\Delta_{\mathrm{r}}. $ |
式中:ur为孔边的法向变形;θ为极坐标的极角,坐标原点为钉孔中心,极轴沿x轴方向;Δr为钉孔之间配合的过盈量/间隙量,Δr为正表示过盈配合,为负表示间隙配合.
2.2 Link单元刚性核可与其它的Fastener单元通过Link单元连接起来.通过Link单元可限制Fastener单元的一个或两个方向的自由度,也可以在Fastener单元上直接施加载荷或者位移.Link单元和Fastener单元的组合使模型能够同时考虑紧固件的剪切刚度和径向刚度.
将两个Fastener单元通过一个Link单元连接时(如图 4所示),可以模拟单个螺栓连接形式,其中螺栓剪切载荷与钉孔位移的关系满足以下条件:
| $ \left( {\begin{array}{*{20}{l}} {{F_{x1}}}\\ {{F_{x2}}}\\ {{F_{y1}}}\\ {{F_{y2}}} \end{array}} \right) = {K_{\rm{s}}}\left[ {\begin{array}{*{20}{c}} 1&{ - 1}&0&0\\ { - 1}&1&0&0\\ 0&0&1&{ - 1}\\ 0&0&{ - 1}&1 \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{u_{x1}}}\\ {{u_{x2}}}\\ {{u_{y1}}}\\ {{u_{y2}}} \end{array}} \right]. $ |
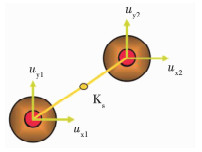
|
图 4 螺栓模型 Fig. 4 Bolt model |
式中Ks为Link单元的剪切刚度,表示的是钉两端发生单位相对位移所对应的剪切载荷.
2.3 螺栓刚度关于螺栓的刚度,国内外有不同的计算方法.较常用的为Tate和Rosenfeld[3]和Nelson[4]等给出的方法.
对于双面贴补修理
| $ \begin{array}{l} \frac{1}{{{K_{\rm{s}}}}} = \frac{{2{t_{\rm{s}}} + {t_{\rm{p}}}}}{{3{G_{\rm{B}}}{A_{\rm{B}}}}} + \frac{{8t_{\rm{S}}^3 + 16t_{\rm{s}}^2{t_{\rm{p}}} + 8{t_{\rm{s}}}t_{\rm{P}}^2 + t_{\rm{P}}^3}}{{192{E_{\rm{B}}}{I_{\rm{B}}}}} + \\ \;\;\;\;\;\;\;\frac{{2{t_{\rm{S}}} + {t_{\rm{P}}}}}{{{t_{\rm{S}}}{t_{\rm{P}}}{E_{\rm{B}}}}} + \frac{1}{{{t_{\rm{S}}}{E_{\rm{S}}}}} + \frac{2}{{{t_{\rm{P}}}{E_{\rm{P}}}}}. \end{array} $ | (8) |
式中:GB为螺栓的剪切模量;EB为螺栓的弹性模量;AB为螺栓的横截面积;IB为螺栓的惯性矩.式(8)中第1项描述的是螺栓的剪切变形,第2项描述的是螺栓的弯曲变形,第3项描述的是螺栓的挤压变形,第4项和第5项分别描述的是搭接板和蒙皮的挤压变形.
文献[4]将式(8)推广到单搭接接头的情况:
| $ \frac{1}{K_{\mathrm{s}}}=\frac{2\left(t_{\mathrm{s}}+t_{\mathrm{P}}\right)}{3 G_{\mathrm{B}} A_{\mathrm{B}}}+\left(\frac{2\left(t_{\mathrm{S}}+t_{\mathrm{P}}\right)}{t_{\mathrm{S}} t_{\mathrm{P}} E_{\mathrm{B}}}+\frac{1}{t_{\mathrm{S}} E_{\mathrm{S}}}+\frac{1}{t_{\mathrm{P}} E_{\mathrm{P}}}\right)(1+3 \beta). $ | (9) |
相比式(8)、(9)缺少第2项,并在后3项乘了一个因子(1+3β).因子β描述了层压板与螺栓之间的接触力沿厚度方向的不均匀性所引起的弯曲效应占总弯矩的比例.弯矩的另外一部分由螺栓头部和螺母承担,即螺栓头部和螺母的作用效果用(1-β)表示.对于无侧边支撑的接头,如销钉连接,弯矩完全由孔边沿厚度方向的接触力承担,此时β=1,对于沉头螺栓可近似取0.5,对于带有螺栓头部和螺母的情况取值较小,当有较大的垫片且孔径/厚度比较大时,取值会更小.文献[4]中的垫片相对较小,孔径/厚度比D/t为2.0,结果显示,当采用β=0.15进行分析时,得到的载荷/位移曲线和试验结果吻合较好.
3 算例图 5为复合材料-金属多钉连接接头几何尺寸[11],连接形式为双剪连接.中间连接板的材料为SK碳纤维/环氧树脂基复合材料,材料属性见表 1,铺层顺序为[0/45/0 /-45/90/0/-45/0/45/0/90/0]s.根据经典层合板理论计算得到层压板的等效弹性模量为Ex=77.05 GPa,Ey=37.80 GPa,Gxy=14.27 GPa,νxy=0.305.螺栓和上下连接板为不锈钢,为各向同性材料,弹性模量E为206 GPa,泊松比ν为0.3,螺栓直径为7.92 mm.
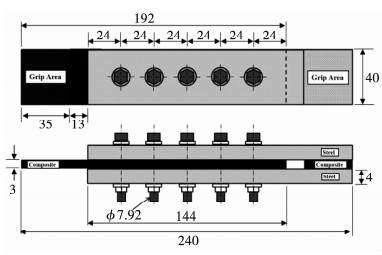
|
图 5 复合材料-金属多钉连接接头几何尺寸(mm) Fig. 5 Geometry of composite-steel multi-bolt joints(mm) |
含钉孔间隙的多钉连接接头,钉载比例与外载荷有关,因此均匀化前必须指定外载荷(设计载荷)大小.取文献[11]中试验得到的失效载荷作为本算例的设计载荷,即F=64.98 kN,则各钉均匀分配时各钉的载荷为f =12.996 kN,载荷比例为20%.
首先计算钉孔间隙为0时各钉的钉载,为(29.33, 14.27, 8.38, 6.18, 6.82)T(kN),各钉钉载比例分别为(45.1, 22.0, 12.9, 9.5, 10.5)T(%).然后分别取扰动量Δci=-0.001 mm, i=1, 2, …, 5(为负表示该处钉孔配合方式为间隙配合,间隙的大小为0.001 mm),同时令其他的钉孔间隙Δcj=0, j≠i,计算扰动情况下各钉钉载.将钉载分配结果代入式(5),计算系数矩阵各元素,从而可以得到以下矩阵:
| $ \begin{array}{l} \mathit{\boldsymbol{H}} = \left[ {\begin{array}{*{20}{c}} {9.02}&{ - 4.87}&{ - 2.10}&{ - 1.19}&{ - 0.87}\\ { - 4.90}&{11.73}&{ - 3.92}&{ - 1.70}&{ - 1.21}\\ { - 2.08}&{ - 4.02}&{12.12}&{ - 3.91}&{ - 2.12}\\ { - 1.19}&{ - 1.71}&{ - 3.99}&{11.85}&{ - 4.95}\\ { - 0.88}&{ - 1.25}&{ - 2.17}&{ - 5.03}&{9.33} \end{array}} \right] \times \\ {10^4}{\rm{N}}/{\rm{mm}} \end{array} $ |
由以上系数矩阵可以看到,矩阵的主对角元素均为正,其余元素均为负.表明,在其他螺栓钉孔间隙不变的情况下,对给定螺栓,增加钉孔间隙,螺栓的载荷减小,其余螺栓的载荷增加.该现象主要是由于钉孔间隙会延迟螺栓的承载,而这部分载荷将由其他螺栓分担.另外,观察矩阵各列的元素可以发现,离对角线越近,元素的值越大,离对角线越远,元素的值越小.说明,钉孔间隙变化时,对距离较近的螺栓载荷影响较大,而对距离较远的螺栓载荷影响较小,距离越远,影响越小.
根据系数矩阵、均匀分配时的目标载荷以及钉孔间隙为0时各钉的钉载,结合式(6)可得到钉载均匀分配时各钉孔的间隙.计算结果见表 2,表中同时给出了文献[17]的优化结果,可以看到,本文优化模型的计算结果和文献数据一致.图 6为复合材料-金属多钉连接接头优化前后各钉的钉载比例.优化前,首钉的钉载比例为45.1%,约为承载最小的第4排钉的钉载比例的5倍.优化后,通过在承载较大的钉孔位置引入钉孔间隙,各钉钉载比例的不均匀性得到明显改善,各钉钉载比例均在18.8%~23.0%之间.首钉钉载比例为23.0%,较优化前钉载比例下降约22.1%.
| 表 2 钉孔配合间隙优化结果 Tab. 2 Optimization results of bolt-hole clearance |
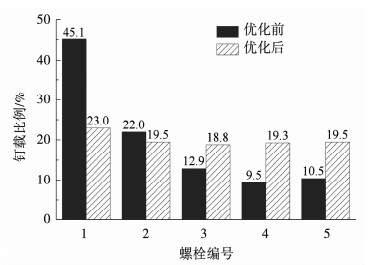
|
图 6 接头优化前后各钉钉载比例情况 Fig. 6 Bolt load distribution of pristine and optimized joint |
图 7给出了复合材料连接板优化前后孔边的应力分布情况.可以看到,优化后,无论是拉伸应力还是压缩应力都有了明显的降低,优化后,孔边拉伸应力降低26%,压缩应力降低39%,应力集中程度减缓明显.
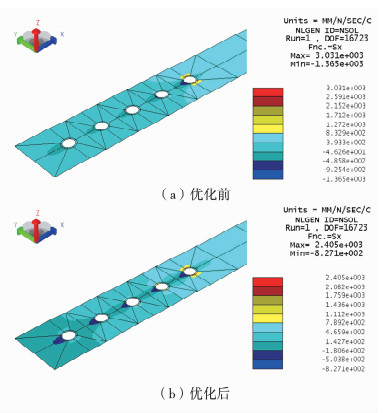
|
图 7 优化前后孔边应力分布情况 Fig. 7 Stress distribution around bolted hole before and after optimization |
图 8给出不同设计载荷情况下钉孔间隙的优化结果,优化后,各钉的钉载比例在18.8%~23.3%之间.优化得到的钉载均匀分配时的钉孔间隙与设计载荷有关,两者之间近似满足线性关系.实际中,可基于某一设计载荷情况下的优化结果,外推获得其他载荷情况下的钉孔间隙.
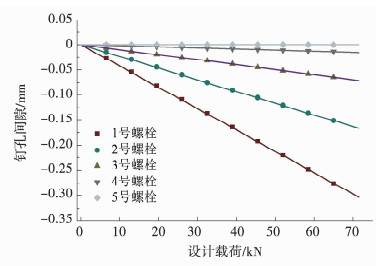
|
图 8 设计载荷对配合间隙优化结果的影响 Fig. 8 Effect of design load on optimized clearance values |
螺栓数目是多钉连接接头中的一个重要的设计参数,为验证模型在不同螺栓数目多钉连接问题中的有效性性,本文分别选择2~4个螺栓的多钉连接进行了计算,其优化前后各钉的载荷比例见表 3.可以看到,优化前各钉的钉载比例相差较大,优化各钉的钉载比例均接近于各钉载荷平均分配的情况.
| 表 3 不同螺栓数目多钉连接优化前后钉载分配结果 Tab. 3 Optimization results of bolt load ratio in bolted joints with different numbers of bolts |
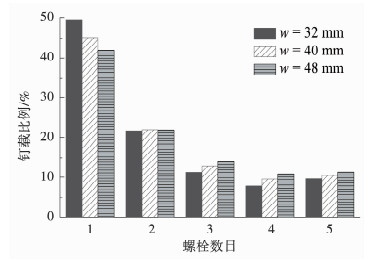
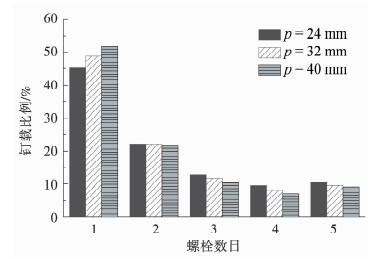
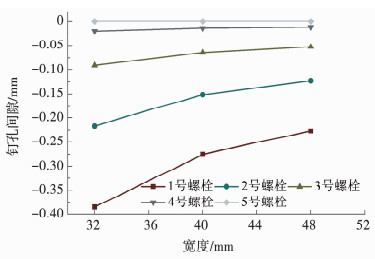
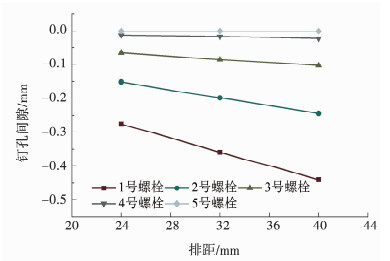
在连接板厚度和孔径给定的情况下,连接设计中宽度和排距等几何参数的选择对钉载分配也会产生影响.相应地,当宽度和排距等变化时,优化的钉孔间隙也会随之变化.在保持其他参数不变的情况下,图 9、10分别给出了宽度和排距对多钉连接钉载分配的影响.结果显示,随着宽度增加,钉载分配的不均匀性降低,而排距增加会进一步加剧钉载分配的不均匀性.事实上,钉载分配的不均匀性的程度取决于连接板与螺栓的刚度之比,刚度比越大,钉载分配不均匀性越大,而宽度增加、排距减小相当于增加连接板刚度,因此钉载分配的不均匀性会增加.图 11、12则给出了不同宽度和排距情况下配合间隙的优化结果,可以看到,配合间隙随接头宽度增加而减小,随排距增加而增加.结合优化前钉载分配的结果可以发现,钉载分配越不均匀,优化的配合间隙值越大.
|
图 9 宽度对钉载分配的影响 Fig. 9 Effect of width on bolt load distribution |
|
图 10 排距对钉载分配的影响 Fig. 10 Effect of pitch distance on load distribution |
|
图 11 宽度对配合间隙优化结果的影响 Fig. 11 Effect of width on optimized clearance values |
|
图 12 排距对配合间隙优化结果的影响 Fig. 12 Effect of pitch distance on optimized clearance values |
为进一步研究本文提出的优化模型的计算效率,在保持孔径、厚度、宽度、排距等参数不变的情况下,图 13分别给出了螺栓数目分别为2~5 4种情况时模型的计算时长.可以看到,随着螺栓数目增加,计算时长近似线性增加.

|
图 13 计算时长与螺栓数目的关系 Fig. 13 CPU time vs. number of bolts |
采用本文提出的优化模型对多钉连接结构进行钉载分配均匀化时,要求在给定设计载荷范围内,系数矩阵H为常量,另外需要已知目标载荷f,因此应用该优化模型时需满足以下条件:1)在外载荷不变的情况下,螺栓载荷与钉孔间隙之间近似满足线性的关系;2)均匀分配时各钉的钉载即目标载荷可定量给出.对满足以上条件的多钉连接接头,模型能够根据不同的设计载荷进行钉载分配的均匀化设计.另外,模型可考虑接头宽度、排距等几何参数的影响.由于模型主要用于改善钉载分配的不均匀性,而钉载分配的大小主要对挤压破坏有决定性的作用,因此,优化算法主要针对挤压型破坏进行设计.模型计算简便,分析效率较高,模型分析复杂度随螺栓数目增加缓慢增长.优化模型是关于钉孔间隙的一组线性方程组,求解不存在迭代等数值问题,可用于复合材料多钉连接的快速设计.
4 结论本文针对复合材料多钉连接钉载分配不均的问题,提出了一种钉载分配均匀化的泰勒展开方法,以钉孔间隙为设计变量对多钉连接进行了优化,研究发现:
1) 优化后,通过在承担载荷较大的钉孔位置引入间隙配合,其钉载比例有了明显的降低,钉载比例仅23.0%,较优化前降低约22.1%,各钉孔均匀承载.另外,优化后,孔边应力水平明显降低,孔边拉伸应力降低26%,压缩应力降低39%.
2) 钉载均匀分配时的钉孔间隙与设计载荷有关,两者之间近似满足线性的关系.
3) 对排距、宽度等参数的分析发现,钉孔间隙的大小与优化前钉载分配的不均匀程度有关,钉载分配越不均匀,优化的配合间隙值越大.
4) 模型计算效率较高,随着螺栓数目增加,计算量近似呈线性增长.
| [1] |
杨旭, 章怡宁, 许希武. 复合材料层板多钉机械连接强度计算方法[J]. 航空学报, 1998, 19(1): 24. YANG Xu, ZHANG Yining, XU Xiwu. Strength analysis method of composite plate with multiple bolted joints[J]. Acta Aeronautica et Astonautica Sinica, 1998, 19(1): 24. DOI:10.3321/j.issn:1000-6893.1998.01.005 |
| [2] |
蒋持平, 张行. 多钉连接件钉传载荷计算的一个解析方法[J]. 航空学报, 1994, 15(3): 310. JIANG Chiping, ZHANG Xing. An analytical method of pin load computations for joints with multi-fasteners[J]. Acta Aeronautica et Astronautica Sinica, 1994, 15(3): 310. DOI:10.3321/j.issn:1000-6893.1994.03.009 |
| [3] |
TATE M B, ROSENFELD S J. Preliminary investigation of the loads carried by individual bolts in bolted joints[R]. Virginia: NACA, 1946
|
| [4] |
NELSON W D, BUNIN B L, HART-SMITH L J. Critical joints in large composite aircraft structures[R]. Washington: NASA, 1983
|
| [5] |
MCCARTHY M A, MCCARTHY C T, Padhi G S. A simple method for determining the effect of bolt-hole clearance on load distribution in single-column multi-bolt composite joints[J]. Composite Structures, 2006, 73(1): 78. DOI:10.1016/j.compstruct.2005.01.028 |
| [6] |
MCCARTHY C T, GRAY P J. An analytical model for the prediction of load distribution in highly torqued multi-bolt composite joints[J]. Composite Structures, 2011, 93(2): 287. DOI:10.1016/j.compstruct.2010.09.017 |
| [7] |
谢宗蕻, 李想, 杨淋雅, 等. 基于弹簧质量模型的复合材料螺接修理载荷传递计算方法[J]. 航空学报, 2016, 37(12): 3742. XIE Zonghong, LI Xiang, YANG Linya, et al. A calculation method for load transfer in bolted repair of composite laminates based on spring-mass model[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(12): 3742. DOI:10.7527/S1000-6893.2016.0211 |
| [8] |
GRAY P J, MCCARTHY C T. A global bolted joint model for finite element analysis of load distributions in multi-bolt composite joints[J]. Composites Part B: Engineering, 2010, 41(4): 317. DOI:10.1016/J.COMPOSITESB.2010.03.001 |
| [9] |
EKH J, SCHN J. Finite element modeling and optimization of load transfer in multi-fastener joints using structural elements[J]. Composite Structures, 2008, 82(2): 245. DOI:10.1016/j.compstruct.2007.01.005 |
| [10] |
BORTMAN J, SZABO B A. Nonlinear models for fastened structural connections[J]. Computer & Structures, 1992, 43(5): 909. DOI:10.1016/0045-7949(92)90305-J |
| [11] |
YUN J H, CHOI J H, KWEON J H. A study on the strength improvement of the multi-bolted joint[J]. Composite Structures, 2014, 108(1): 409. DOI:10.1016/j.compstruct.2013.09.047 |
| [12] |
邵祝涛.层合板机械连接强度分析与优化及软件开发[D].大连: 大连理工大学, 2012 SHAO Zhuao. Trength analysis and optimization of mechanical joints in composite laminates and development of software[D]. Dalian: Dalian University of Technology, 2012 http://cdmd.cnki.com.cn/Article/CDMD-10141-1012393582.htm |
| [13] |
GAMDANI F, BOUKHILI R, VADEAN A. Tensile strength of open-hole, pin-loaded and multi-bolted single-lap joints in woven composite plates[J]. Materials and Design, 2015, 88: 702. DOI:10.1016/j.matdes.2015.09.008 |
| [14] |
KABEEL A M, MAIMí P, GONZáLEZ E V, et al. Net-tension strength of double-lap joints under bearing-bypass loading conditions using the cohesive zone model[J]. Composite Structures, 2015, 119: 443. DOI:10.1016/j.compstruct.2014.08.036 |
| [15] |
OINONEN A, TANSKANEN P, BJÖRK T, et al. Pattern optimization of eccentrically loaded multi-fastener joints[J]. Struct Multidisc Optim, 2010, 40: 597. DOI:10.1007/s00158-009-0392-2 |
| [16] |
PENG Xiaobo, CHI Hou, WAN Xiaopeng. Research on the auto-modeling technology and load distribution optimization for multi-bolt composite joints[J]. Advanced Materials Research, 2013, 721: 556. DOI:10.4028/www.scientific.net/AMR.721.556 |
| [17] |
谢宗蕻, 李想, 郭家平, 等. 考虑间隙配合的复合材料钉载分配均匀化方法[J]. 复合材料学报, 2016, 33(4): 806. XIE Zonghong, LI Xiang, GUO Jiaping, et al. Load distribution homogenization method of multi-bolt composite joint with consideration of bolt-hole clearance[J]. Acta Materiae Compositae Sinica, 2016, 33(4): 806. DOI:10.13801/j.cnki.fhclxb.20151013.003 |
| [18] |
MCCARTHY M A, MCCARTHY C T. Finite element analysis of the effects of clearance on single-shear, composite bolted joints[J]. Journal of Plastics, Rubber and Composites, 2002, 32(2): 1. DOI:10.1179/146580103225001390 |
| [19] |
EKH J, SCHN J. Load transfer in multi row, single shear, composite-to-aluminium lap joints[J]. Composite Science and Technology, 2006, 66(7-8): 875. DOI:10.1016/j.compscitech.2005.08.015 |
| [20] |
MCCARTHY M A, LAWLOR V P, O'DONNELL P C, et al. Measurement of bolt pre-load Torqued Composite Joints[J]. Strain, 2005, 41: 109. DOI:10.1111/J.1475-1305.2005.00201.X |
 2019, Vol. 51
2019, Vol. 51


