随着我国基础结构建设项目的不断增加,特厚钢板的市场需求量越来越大[1-3],热处理是高强韧、大断面特厚钢板核心生产工艺,通过控制不同的冷却制度可以改变钢板内部的组织结构,提高产品性能[4, 5].热处理是高强韧、大断面特厚钢板核心生产工艺.目前,150~300 mm厚钢板普遍采用浸入式淬火,冷却效率低、均匀性差,已成为制约特厚钢板高质量热处理的瓶颈[6].基于辊式淬火技术的射流冲击水冷有别于其他换热方式,能在壁面过热度较高时实现较大的对流热通量,且随着壁面温度的微小变化,热流密度变化明显[7],这一特点为特厚钢板高强度、高均匀性淬火提供了新的途径.
然而,射流冲击水淬过程包含了内部三维导热、滞止区射流换热、核态及过渡沸腾换热、膜态沸腾换热、辐射换热等多种形式,单相强制对流与沸腾换热相互耦合,热交换过程十分复杂[8].此外,钢板表面换热与射流速度、射流直径、喷射角度、过冷度、壁面过热度等诸多因素有关,进一步增加了钢板内部温度场和温度梯度的调控难度[9].Lee等[10]研究了双圆孔射流冷却过程钢板表面换热规律,采用热电偶测量近壁面瞬态温度变化.Karwa等[11]建立了Leidenfrost条件下过热壁面射流冷却过程气膜厚度、壁面热通量和壁面过热度理论模型,并研究了冷却水聚集对射流冲击冷却过程传热的影响.Waldeck等[12]采用数值模拟方法建立了高温金属表面射流冷却过程传热数值模型,预测了局部表面温度、热流密度和表面温度梯度.
上述研究局限于瞬态或稳态条件,研究较薄规格(≤25 mm)钢板淬火温降规律,这与大断面特厚钢板淬火测试条件相差较大,测试结果存在偏差.本文利用开发的特厚钢板专用辊式淬火装置和多通道钢板温度记录仪进行160~300 mm厚、2.3 m宽、8 m长特厚钢板连续辊式淬火试验,得出钢板表面及纵断面厚向典型位置温降曲线,研究多排阵列射流条件下钢板厚向温度场、温度梯度、热流密度变化规律,对比分析不同表面换热条件对钢板厚向冷速的影响.相关研究将为特厚钢板厚向淬火冷速和冷却均匀性研究提供理论算法和实验数据,为进一步调控特厚钢板断面组织提供有效方法.
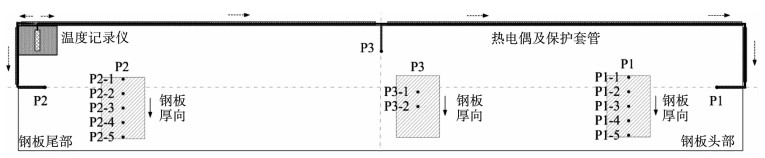
1 实验材料及方法实验材料为热轧后合金钢板,化学成分(质量分数%):0.14C,0.08Si,0.52Mn,0.006P,0.000 6S,2.4Cr,1.07Mo,0.07Ni,0.04Cu,Ceq=0.932.钢板厚度分别为160 mm、220 mm、300 mm,宽度均为2 300 mm,长度均为8 000 mm.钢板侧面打孔,孔深350 mm,孔径5.1 mm.孔内插入WRNK-191型铠装热电偶,材质为NiCrSi-NiSiMg.在测试钢板尾端开槽,放置钢板温度记录仪.温度记录仪与热电偶连接,测量并记录各测温点实时温度.钢板测温点位置如图 1所示.
|
图 1 钢板测温点位置 Fig. 1 Plate temperature measurement positions |
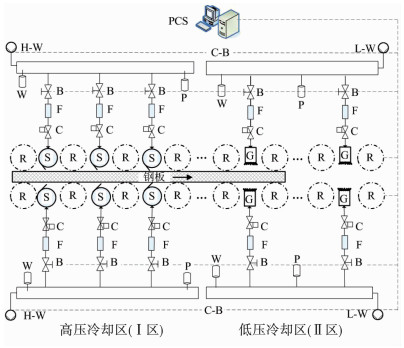
特厚钢板辊式淬火实验装置总长20 m,如图 2所示.装置入口侧为高压冷却区(Ⅰ区),长度4 m,喷水压力0.8 MPa,最大喷水量4 400 m3·h-1;装置出口侧为低压冷却区(Ⅱ区),长度16 m,喷水压力0.4 MPa,最大喷水量5 500 m3·h-1.钢板由上下对称布置的辊道实现速度、加速度及流量分区控制.装置入口和出口配置跟踪定位仪表,实现钢板位置精确跟踪.钢板淬火温降测试时,水温由水温仪测量,喷水压力由电动调节阀配合压力传感器闭环控制,喷水量由电磁流量计配合变频供水泵频率闭环控制,喷嘴开闭由气动开闭阀控制.
|
C调节阀;B开闭阀;W水温仪;F流量计;P压力传感器;S缝隙射流喷嘴;G多排圆孔射流喷嘴;R辊道;PCS控制中心;C-B控制及反馈电缆;H-W高压供水系统;L-W低压供水系统 图 2 淬火实验装置布置 Fig. 2 Arrangement of quenching experimental device |
钢板加热后,由外部机械化臂放置到输送辊道上,按一定速度依次通过淬火装置Ⅰ区和Ⅱ区,并在Ⅱ区摆动直至钢板温度降至Mf点以下,之后由辊道运出.钢板加热温度Th、加热时间th、移动速度v、淬火冷却时间tq,以及实验装置Ⅰ区水量WH、Ⅱ区水量WL参数设定值如表 1所示,测试过程共采集温度值3.24×106个.Ⅰ区和Ⅱ区射流喷嘴的出流速度vN、射流冲击换热区水流密度ρw、射流冲击流动Re数、钢板表面射流冲击速度vJ如表 2所示.
| 表 1 实验工艺参数设定值 Tab. 1 Set values of test technical parameters |
| 表 2 钢板表面射流参数 Tab. 2 Plate surface jet parameters |
基于实测温降曲线,利用导热微分方程,采用反传热法计算特厚钢板淬火温度场.本文建立三维非稳态导热方程,考虑热物性参数随温度的变化,如式(1)所示.式中将相变潜热划归钢板的平均比热内,建立无内热源的导热方程
| $ \begin{array}{c}{\frac{\partial T}{\partial \tau}=\frac{\lambda(T)}{c(T) \rho(T)}\left(\frac{\partial^{2} T}{\partial x^{2}}+\frac{\partial^{2} T}{\partial y^{2}}+\frac{\partial^{2} T}{\partial z^{2}}\right) 0<x<H}, \\ {0 <y<B, 0<z<L, \tau>0}.\end{array} $ | (1) |
式中:为钢板三维温度场,λ(T)为钢板导热系数,ρ(T)为钢板密度,c(T)为钢板比热,τ为冷却时间,H为钢板厚度,B为钢板宽度,L为钢板长度.
导热方程采用第三类边界条件,假设钢板侧向热流密度为0,且钢板下半厚度与上半厚度区间无热量交换,则初始条件和边界条件可表示为
| $ \begin{array}{l} T(x, y, z) = \mathit{\Phi }, (\tau = 0, 0 \le x \le H, 0 \le y \le B, 0 \le z \le L)\\ \dot q(y, z, \tau ) = h(y, z, \tau )\left( {{T_{\rm{s}}} - {T_{\rm{w}}}} \right), (x = 0, \mathit{or}, x = H)\\ \dot q(x, z, \tau ) = - \lambda (T)\frac{{\partial T}}{{\partial y}} = 0, (y = 0, \mathit{or}, y = B)\\ \dot q(x, y, \tau ) = - \lambda (T)\frac{{\partial T}}{{\partial z}} = 0, (z = 0, \;\mathit{or}{\rm{, }}z = L). \end{array} $ | (2) |
式中:Φ为钢板初始温度场,q为钢板热流密度,h为钢板表面换热系数,Ts为钢板壁面温度,Tw为水温,其余同式(1).
钢板表面热流密度可通过求解目标函数f(pi)极小值获得,该目标函数定义了表面温度测量值与计算值的差值,有
| $ f\left(p_{i}\right)=\frac{1}{N_{\mathrm{t}} N_{\mathrm{p}}} \sum\limits_{m=1}^{N_{\mathrm{t}}} \sum\limits_{n=1}^{N_{\mathrm{p}}}\left(\frac{T e_{\mathrm{n}}^{\mathrm{m}}-T_{\mathrm{n}}^{\mathrm{m}}}{T e_{\mathrm{n}}^{\mathrm{m}}}\right)^{2}. $ | (3) |
式中:Tenm、Tnm分别为测温点m在τn时刻的实测和计算温度,采用有限元法求解式(1)获得.
目标函数f(pi)极小值可通过拟牛顿法求解.采用BFGS算法,得到近似海森矩阵的对称正定矩阵[13].由于BFGS算法需要计算式(3)目标函数值及其导数值,将式(3)转化为
| $ \frac{\partial f\left(p_{i}\right)}{\partial p_{j}}=\frac{-2}{N_{\mathrm{t}} N_{\mathrm{p}}} \sum\limits_{m=1}^{N_{\mathrm{t}}} \sum\limits_{n=1}^{N_{\mathrm{p}}}\left(\frac{T e_{\mathrm{n}}^{\mathrm{m}}-T_{\mathrm{n}}^{\mathrm{m}}}{T e_{\mathrm{n}}^{\mathrm{m}}}\right) \frac{\partial T_{\mathrm{n}}^{\mathrm{m}}}{\partial p_{j}}. $ | (4) |
式中:pi为最小化参,NP为单一测温点记录温度数,Nt为测温点数.
采用巧凑边点族立方单元形函数,基于反传热法和实测钢板近表面温度计算钢板表面换热系数h
| $ h(y, z, \tau)=\sum\limits_{i=1}^{12} F_{i} P_{i}(\tau). $ | (5) |
式中:Fi为立方单元体形函数,函数Pi(τ)描述某一时间段内每个单元节点换热系数的变化
| $ P_{i}(\tau)=\sum\limits_{j=1}^{3} W_{j}(\eta) p_{i j}. $ | (6) |
式中:Wj为二次样条函数,pij为最小化参数,可由节点换热系数表示.
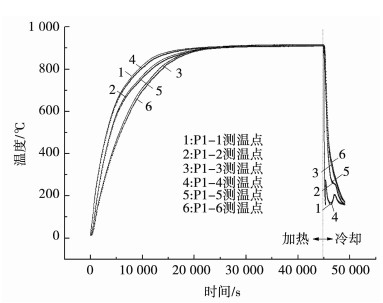
2.2 计算结果图 3为300 mm厚钢板在测温点P1-1~P1-6处计算温降曲线与实测值比较图,两者吻合较好,偏差小于4 %.温降曲线计算过程中,采用的表面换热系数基于实测钢板表面温度曲线反算出.由于表面测温点个数有限,越靠近实际测温点,钢板表面换热系数越接近实测值,温度场计算结果越精确.由于本文研究范围为测温点附近钢板纵断面厚向区域,现有计算精度能够满足进一步分析需要.
|
图 3 300 mm厚钢板温降曲线计算值与实测值比较 Fig. 3 Comparison between calculated values and measured values of temperature drop curve of 300mm thick steel plate |
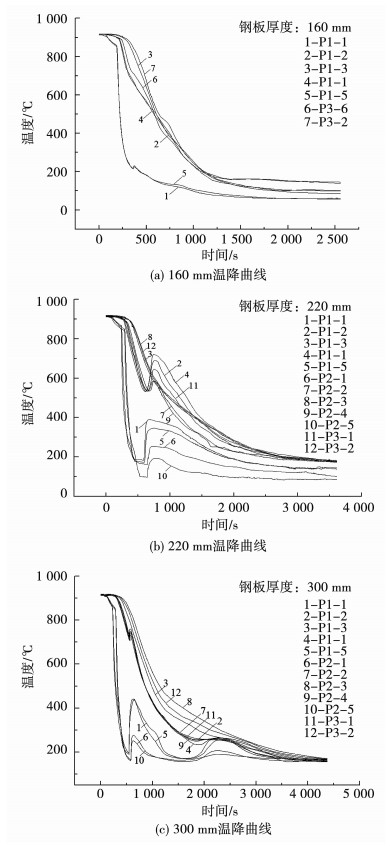
图 4为不同厚度特厚钢板温降曲线.160 mm、220 mm、300 mm厚钢板心部冷至200 ℃所需淬火时间分别为13.9 min、29.6 min、49.3 min.160 mm厚钢板1/4H温降与心部相比先快后慢,两处在降至500 ℃以下时温降曲线基本一致,而表面温降曲线与1/4H和心部相差较大;随着厚度增加至220 mm和300 mm,除表面温降曲线差异明显外,1/4H和心部温降曲线差异增大.Ding等[14]指出钢板厚度变化导致心部-表面温度梯度变化,心部-表面各处温降曲线差异增大,其中心部-1/4H区间温度梯度对钢板心部温降影响更大,这与本文实测温降曲线吻合.为实现钢板上下表面对称温降,可通过改变钢板上下表面水流密度,进而改变上下表面平均热流密度,弥补上下表面换热形式不同引起的温降差异.测试中,Ⅰ区上下表面水流密度比为1: 1.25,Ⅱ区为1: 1.4.对比图 4中钢板头部上下表面(P1-1/P1-5、P2-1/P2-5)温降曲线发现,曲线基本重合,温度平均偏差<12 ℃,表面钢板上下表面温降对称性较好.
|
图 4 钢板淬火温降曲线 Fig. 4 Temperature drop curves of plate quenching |
对比图 4发现,钢板由高压冷却区(Ⅰ区)进入低压冷却区(Ⅱ区)时,220 mm厚、300 mm厚钢板淬火温降曲线出现“返温”现象,160 mm厚钢板“返温”现象不明显.其中,220 mm厚钢板表面返温102 ℃~196 ℃、1/4H返温55 ℃~104 ℃、心部无返温,300 mm厚钢板表面返温150 ℃~250 ℃,1/4H返温约52 ℃、心部无返温.图 5为钢板由Ⅰ区进入Ⅱ区期间头部半厚度范围内温度梯度分布.160 mm厚钢板在Ⅰ区内冷却时,1/4H至表面区间温度梯度(grad T1/4→s)先迅速增大至约12 ℃·mm-1,并维持该值,心部至1/4H区间温度梯度(grad Tc→1/4)也较迅速增大至约4 ℃·mm-1,表明Ⅰ区内因较高的冷却强度,钢板厚向迅速形成较大温度梯度,1/4H、心部温降明显;钢板进入Ⅱ区后,grad T1/4→s和grad Tc→1/4均维持较高值,并缓慢减小,此时钢板表面温度持续降低,心部向1/4H以及1/4H向表面传导热量并未受表面换热形式变化而改变,因此“返温”现象不明显.220 mm厚钢板在Ⅰ区内冷却时,grad T1/4→s先增加后持续降低,grad Tc→1/4逐渐增加并维持在约4 ℃·mm-1,表明该过程中钢板厚向最大热流密度(MHF)点逐渐由1/4H~表面区间移至心部~1/4H区间,1/4H温度较低(约530 ℃);当钢板进入Ⅱ区时,grad T1/4→s进一步显著降低,grad Tc→1/4仍维持在4 ℃·mm-1左右50 s后再显著降低,因此1/4H~表面区间内热量迅速传导至表面,出现“返温”现象,而心部~1/4H区间内热量也迅速向1/4H传导,1/4H也出现明显的“返温”现象.由于grad Tc→1/4在进入Ⅱ区后维持约50 s后减小,结合图 4可知,1/4H(P1-2、P1-4、P2-2、P2-4、P3-1)“返温”滞后于表面(P1-1、P1-5、P2-1、P2-5).随着钢板厚度增加至300 mm厚,Ⅰ区内钢板grad T1/4→s持续增加并维持在7 ℃·mm-1左右,而grad Tc→1/4缓慢增加,表明此时钢板厚向MHF点在1/4H~表面区间内,心部~1/4H区间温降缓慢,1/4H处温度较高(约700 ℃);当钢板进入Ⅱ区,grad T1/4→s显著持续减小,grad Tc→1/4也相应减小,表明此时1/4H~表面区间热流密度显著增加,钢板表面“返温”明显,而心部~1/4H区间内热流密度有所增加,钢板1/4H也有相应的“返温”.依据能量守恒定律,不同厚度钢板心部持续向表面传递热量,未观察到“返温”现象.可见,“返温”现象一方面与不同厚度钢板表面热流密度改变有关,另一方面与钢板厚向因温度梯度变化引起的MHF点位置改变有关.

|
图 5 不同厚度钢板半厚度区间温度梯度(头部测温点) Fig. 5 Half thickness temperature gradient of different-thickness steel plates (plate head) |
分析发现,220 mm厚钢板表面测温点由Ⅰ区进入Ⅱ区过程中,温降曲线先出现“平台”、后快速上升(如图 4 220 mm厚钢板P1-1、P1-5、P2-1、P2-5温降曲线),而300 mm厚钢板表面温降曲线没有“平台”出现.Nobari等[15]指出,壁面过热度影响钢板射流冷却表面换热形式,进而影响换热效率.结合式(1)、(2)和图 5可知,220 mm厚钢板经过Ⅰ区时,表面换热系数h高达25 000 W·(m2℃)-1,持续高强冷却使壁面过热度迅速下降至150 ℃以下,表面凝结气泡的能力减弱,对流换热强度降低;同时,grad T1/4→s持续减小、grad Tc→1/4持续增大,导致钢板厚向1/4H~表面导热能力减弱,由此维持了钢板表面换热与内部导热的平衡状态,产生了表面温降曲线“平台”.相比之下,300 mm厚钢板经过Ⅰ区时,grad T1/4→s减小缓慢,导致钢板内部热量持续传递至表面,壁面过热度持续下降,表面温降曲线未出现“平台”.可见持续的高强度冷却(Ⅰ区)使钢板厚向形成较大温度梯度,但随着壁面过热度降低,表面对流换热能力减弱,随后适当减小冷却强度(Ⅱ区),可提高壁面过热度并维持厚向较大温度梯度,对特厚钢板心部~1/4H厚度区间温降有利.
图 6为3种厚度钢板冷却过程热流密度分布,由钢板上半厚度、下半厚度曲线基本一致可以看出,钢板上下表面冷却对称性较好,进一步验证了式(2)边界条件的正确性,表明改变上下表面水流密度可以有效均匀化上下表面热流密度,弥补由冷却水重力作用产生的上下表面冷却差异.钢板上下表面射流换热区分布不同,下表面以射流冲击换热区为主.为实现对称冷却,下表面水流密度增加,对流换热系数相应增加,强化了单相强制对流换热能力,导致下表面MHF值高于上表面约20%.图 4中温降曲线“返温”现象也可由热流密度曲线解释.依据Newton冷却定律,钢板表面热流密度与壁面过热度有关:高温钢板接触射流冷却水,大壁面过热度导致热流密度快速达到MHF值;随后壁面过热度降低并维持在<150 ℃,表面热流密度达到极小值点(MHF’),此时grad T1/4→s已达到或超过极大值点;当钢板进入Ⅱ区时,水流密度的变化打破了壁面换热与内部导热的平衡,壁面过热度增大,表面出现“返温”现象,表面热流密度增加导致grad T1/4→s显著减小,进而钢板1/4厚度温度降低明显;依据Fourier定律,钢板厚向内部热流密度与温度梯度有关,1/4厚度温降明显导致grad Tc→1/4增加,钢板1/4厚度也出现“返温”现象.

|
图 6 不同厚度钢板淬火热流密度曲线 Fig. 6 Heat flux curves during plate quenching of different-thickness steel plates |
1) 特厚钢板辊式淬火过程中,钢板厚度变化导致心部-表面温度梯度变化,心部-表面各处温降曲线差异增大,为实现上下表面对称冷却,高压冷却区上下表面水流密度比为1: 1.25,低压冷却区上下表面水流密度比为1: 1.4.
2) 220 mm、300 mm后钢板由高压冷却区进入低压冷却区时,上下表面及上下1/4H位置出现“返温”现象,一方面与钢板表面热流密度改变有关,另一方面与钢板厚向因温度梯度变化引起的MHF点位置改变有关.
| [1] |
刘清梅, 魏丽艳. 特厚板品种生产现状及新技术研究[J]. 上海金属, 2011, 33(6): 57. LIU Qingmei, WEI Liyan. Manufacturing status of special heavy-thickness plate grades and the study of new technique[J]. Shanghai Metals, 2011, 33(6): 57. DOI:10.3969/j.issn.1001-7208.2011.06.014 |
| [2] |
沈继刚, 李宏图, 王勇. 浅论我国大单重特厚钢板的轧制生产技术[J]. 宽厚板, 2011, 17(2): 23. SHEN Jigang, LI Hongtu, WANG Yong. Discussion on rolling and processing of extra heavy steel plate with large single piece weight in China[J]. Wide and Heavy Plate, 2011, 17(2): 23. DOI:10.3969/j.issn.1009-7864.2011.02.006 |
| [3] |
耿明山, 刘艳, 黄衍林. 大型特厚板坯料制造技术现状和发展趋势[J]. 中国冶金, 2014, 24(8): 10. GENG Mingshan, LIU Yan, HUANG Yanlin. Present situation and development tendency of manufacturing technologies of the large slab for heavy gauge plate[J]. China Metallurgy, 2014, 24(8): 10. DOI:10.13228/j.boyuan.issn1006-9356.20130137 |
| [4] |
CAO Zhiqiang, BAO Yanping, XIA Zhenghai, et al. Toughening mechanisms of a high-strength acicular ferrite steel heavy plate[J]. International Journal of Minerals, Metallurgy and Materials, 2010, 17(5): 567. DOI:10.1007/s12613-010-0358-9 |
| [5] |
王国栋. 中国中厚板轧制技术与装备[M]. 北京: 冶金工业出版社, 2009. WANG Guodong. Plate rolling technology and equipment in China[M]. Beijing: Metallurgical Industry Press, 2009. |
| [6] |
YU Wei, LI Gaosheng, CAI Qingwu. Effect of a novel gradient temperature rolling process on deformation, microstructure and mechanical properties of ultra-heavy plate[J]. Journal of Materials Processing Technology, 2015, 217: 317. DOI:10.1016/j.jmatprotec.2014.11.011 |
| [7] |
WANG Hemu, YU Wei, CAI Qingwu. Experimental study of heat transfer coefficient on hot steel plate during water jet impingement cooling[J]. Journal of Materials Processing Technology, 2012, 212(9): 1825. DOI:10.1016/j.jmatprotec.2012.04.008 |
| [8] |
Karwa N, Gambaryan-Roisman T, Stephan P, et al. Experimental investigation of circular free-surface jet impingement quenching: Transient hydrodynamics and heat transfer[J]. Experimental Thermal and Fluid Science, 2011, 35(7): 1435. DOI:10.1016/j.expthermflusci.2011.05.011 |
| [9] |
Karwa N, Stephan P. Experimental investigation of free-surface jet impingement quenching process[J]. International Journal of Heat and Mass Transfer, 2013, 64(5): 1118. DOI:10.1016/j.ijheatmasstransfer.2013.05.014 |
| [10] |
Gun L S, Massoud K, Jungho L. Quench subcooled-jet impingement boiling: Two interacting-jet enhancement[J]. International Journal of Heat and Mass Transfer, 2018, 126: 1302. DOI:10.1016/j.ijheatmasstransfer.2018.05.113 |
| [11] |
Karwa N, Gambaryan-Roisman T, Stephan P, et al. A hydrodynamic model for subcooled liquid jet impingement at the Leidenfrost condition[J]. International Journal of Thermal Sciences, 2011, 50(6): 993. DOI:10.1016/j.ijthermalsci.2011.01.021 |
| [12] |
Waldeck S, Woche H, Specht E, et al. Evaluation of heat transfer in quenching processes with impinging liquid jets[J]. International Journal of Thermal Sciences, 2018, 134: 160. DOI:10.1016/j.ijthermalsci.2018.08.001 |
| [13] |
Andrei N. Accelerated scaled memoryless BFGS preconditioned conjugate gradient algorithm for unconstrained optimization[J]. European Journal of Operational Research, 2010, 204(3): 410. DOI:10.1016/j.ejor.2009.11.030 |
| [14] |
DING Jingguo, ZHAO Zhong, JIAO Zhijie, et al. Central infiltrated performance of deformation in ultra-heavy plate rolling with large deformation resistance gradient[J]. Applied Thermal Engineering, 2016, 98: 29. DOI:10.1016/j.applthermaleng.2015.12.021 |
| [15] |
Nobari A H, Prodanovic V, Militzer M. Heat transfer of a stationary steel plate during water jet impingement cooling[J]. International Journal of Heat and Mass Transfer, 2016, 101: 1138. DOI:10.1016/j.ijheatmasstransfer.2016.05.108 |
 2019, Vol. 51
2019, Vol. 51


