分辨率是图像清晰度的一个重要评价指标,高分辨率图像清晰度好,拥有高像素密度,提供更多细节,使得人们可以迅速、准确地获取到更多信息,在医学、军事、遥感、视频监控等领域都有广泛应用.图像超分辨率重建技术能够将一幅低分辨率(Low Resolution, LR)图像或图像序列恢复出高分辨率(High Resolution, HR)图像,是近年来图像领域一个重要研究方向,一般可分为单帧图像重建和多帧图像重建,经历了插值重建、序列图像重建和基于学习的图像超分辨率重建三个重要发展阶段[1].
传统的基于学习的超分辨率重建模型如Steerable filters[2]、Image Analogies[3]等需要从若干成对出现的低、高分辨率图像中学习先验信息,对训练样本库依赖性强,训练模型形式单一且受人为干扰较大,近年来,基于深度学习的方法[4]取得了突破性进展,主要思路是充分利用图像本身的先验信息,将深度神经网络作为学习模型,直接学习从低分辨率图像到高分辨率图像的端到端的映射关系.
2014年Dong等[5]提出的基于卷积神经网络的图像超分辨率重建模型(SRCNN)在3个卷积层上进行非线性映射得到高分辨率图像,然而由于输入是由双三次插值[6]得到的较高分辨率图像,卷积计算复杂,重建效率低下.针对该问题,Shi等[7]提出的ESPCN模型采用在低分辨率图像上直接计算卷积进行特征提取后使用子像素卷积层进行图像大小变换的方式,有效提高了图像重建效率,然而一旦模型设置较大的放大倍数时,会导致得到的结果过于平滑,细节缺乏真实感,不能很好提高重建图像的视觉效果.
另外,Kim等[8]根据低分辨率图像和高分辨率图像拥有相似的低频信息这一理论,提出VDSR模型,利用残差学习来加快模型收敛速度,但仍然存在收敛和梯度传输困难的问题.于是在残差网络和VDSR模型的启发下,Tai等[9]提出DRRN模型,将深度增加至52层,并递归使用权重共享的网络模块,得到的训练结果相对于VDSR模型有提高但并不明显.
针对上述模型层次过多以及梯度传输困难导致训练时间长、重建图像视觉效果不理想的问题,在单帧低分辨率图像重建上本文提出一种改进残差块和对抗损失的GAN[10]图像超分辨率重建模型,旨在实现高效、高质量的图像重建,主要贡献如下:
1) 设计剔除多余批规范化操作的残差块.生成模型由剔除块中冗余批规范化操作的残差块组合而成,同时使用深度卷积网络作为判别模型来指导整个模型的训练,减少模型计算量,加快训练速度,提高图像重建效率.
2) 引入Earth-Mover(EM)距离设计对抗损失函数.通过计算高、低分辨率图像之间的EM距离来反映真实数据集和生成数据集的分布距离远近以提供非零梯度来确保训练继续,有效缓解模型梯度消失问题.
3) 引入L1损失函数计算图片间的L1距离.使用L1损失函数替换普遍使用的MSE损失函数,将重建图像与对应高分辨率图像间的L1距离作为两张图片相似程度的度量,指导模型权重更新,从而提高重建图像的峰值信噪比,加强重建图像视觉效果.
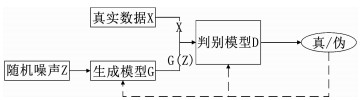
1 改进残差块和对抗损失的GAN图像超分辨率重建模型 1.1 模型整体设计为在单帧低分辨率图像重建中取得良好的重建效果,在模型结构设计中,借鉴Goodfellow提出的一种生成式模型—生成对抗网络GAN.该网络的核心思想来源于博弈论的纳什均衡[11-12],结构如图 1所示.网络设定参与游戏的双方分别为一个生成模型和一个判别模型,生成模型的目标是尽量去学习真实的数据分布,而判别模型的目标是尽量正确判断输入数据是真实数据还是来自生成模型;为取得游戏胜利,这两个游戏参与者需要不断优化来各自提高自己的生成能力和判别能力,这个学习优化过程就是寻找二者之间的一个纳什均衡.
|
图 1 GAN结构 Fig. 1 Structure of the GAN |
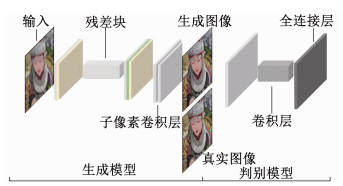
本文通过建立一个基于生成对抗网络的模型进行图像超分辨率重建,模型由生成模型和判别模型两部分组成,分别学习生成与高分辨率图像相似的超分辨率图像和更准确地区分出超分辨率图像与真实高分辨率图像,模型整体设计如图 2所示,其中,生成模型由剔除多余批规范化操作的残差块与子像素卷积层构成,判别模型由深度卷积网络与全连接层构成.
|
图 2 模型整体设计 Fig. 2 Overall structure of the model |
模型训练过程中,低分辨率图像经过生成模型生成对应的超分辨率图像,再将生成的超分辨率图像和真实高分辨率图像一起输入判别模型进行判定,判别模型的输出代表对每张输入图像的真假判定,求取判定结果的误差后对模型参数进行调整,使模型在迭代学习中自动更新内部参数,模型目标函数定义为
| $ \begin{array}{*{20}{c}} {\mathop {\min }\limits_{\rm{G}} \mathop {\max }\limits_{\rm{D}} {\rm{V}}({\rm{D}}, {\rm{G}}) = {{\rm{E}}_{x \sim {{\rm{p}}_{{\rm{data }}(x)}}}}[\log {\rm{D}}(x)] + }\\ {\quad {{\rm{E}}_{z \sim {{\rm{P}}_{z(z)}}}}[\log (1 - {\rm{D}}({\rm{G}}(z)))].} \end{array} $ | (1) |
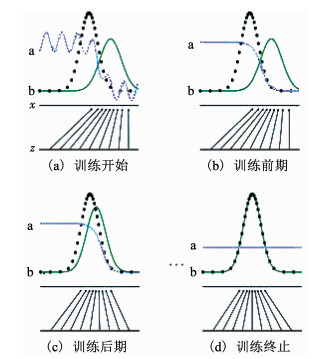
式中:x为真实样本,D(x)为x通过判别模型被判断为真实样本的概率;z为输入生成样本的噪声,G(z)为生成网络由噪声z生成的样本,而D(G(z))为生成样本通过判别模型后,被判断为真实样本的概率.生成模型的目标是要让生成样本越接近真实样本越好,即D(G(z))越接近1越好,这时V(D, G)会变小;判别模型的目标是要让D(x)接近1,而让D(G(z))接近0,这时V(D, G)会增大.当D(x)收敛于1/2时,即判别模型无法区分生成样本和真实样本,训练终止.整个训练过程中样本的分布如图 3所示,其中,虚线为真实样本分布,实线a为判别模型的样本分布,实线b为生成模型的样本分布.在训练过程中,生成模型的样本分布(实线b)逐渐与真实样本分布(虚线)重合,判别模型的样本分布(实线a)逐渐变为一条直线即无法正确区分真实样本与生成模型的样本从而完成模型的训练.
|
图 3 生成模型、判别模型样本示意 Fig. 3 Schematic diagram of generative model and discriminant model |
神经网络使用梯度下降法来计算网络损失,通过反向传播法对网络中所有权重计算损失函数的梯度,将其反馈给梯度下降法来更新神经网络中每个神经元的权值以最小化损失函数.深度越深的神经网络能够表达越丰富的特征,拥有越出色的性能,然而梯度本身是一个很小的值,随着深度的增加经过多次连乘变得越来越小.也就是说,网络深度越深,梯度越小,最后就会出现梯度消失的现象,导致深层神经网络无法训练.何恺明等[13]提出的深度残差网络,通过残差学习有效简化模型训练、缓解梯度弥散现象.同时,Kim等[8]又提出低分辨率图像和高分辨率图像共享低频部分的信息,因此,只需要学习高分辨率图像和低分辨率图像之间的高频部分的残差就可以实现超分辨率重建.
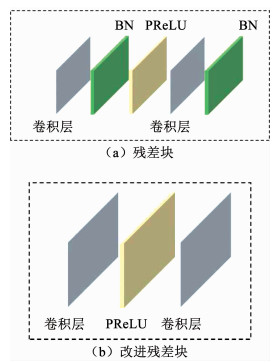
为能够充分学习低分辨率图像到高分辨率图像端到端的映射关系,本文生成模型引入深度残差网络.深度残差网络的残差块由卷积层、批规范化层[14](Batch-normalization,BN)、PReLU激活函数[15]组成,如图 4(a)所示.本文设计并使用仅由2个卷积层和PReLU激活函数构成的残差块,如图 4(b)所示.在深度学习中,批规范化操作在一定程度上解决深度神经网络在训练中由于梯度随机下降而带来的梯度弥散现象,提高了模型的训练速度和准确度.但在图像超分辨率重建问题上,图像经过批规范化操作会导致色彩分布被归一化、原始图像的空间表征被破坏,进而在重建中需要模型的部分层或者额外参数来恢复这种表征.因此,本文将Lim等[16]剔除残差网络中批规范化的思想引入到本文设计的基于生成对抗网络的图像超分辨率重建中,在生成模型中剔除批规范化操作来减少模型计算量、防止提取到的图像特征被归一化,从而提高模型精度和重建效果.
|
图 4 改进前后的残差块 Fig. 4 Residual blocks and modified residual blocks |
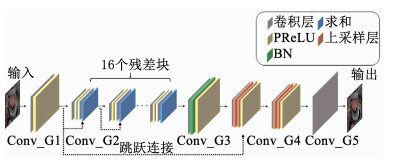
本文生成模型的整体结构如图 5所示,前一部分为深度残差网络,用于提取原始图像特征,后面连接2个子像素卷积层[7],用于放大特征图像.其中,深度残差网络由16个剔除批规范化操作的残差块组合而成,图 5中“16个残差块”表示16个残差块依次连接,残差块使用图 4(b)所示结构,块内剔除了批规范化操作即图 4(a)中的绿色块,使用步幅为1、卷积核大小为3×3的卷积层来提取足够数量的特征图,块与块之间使用跳跃连接以促进梯度反向传播、加快模型训练速度;子像素卷积层输入通道为1、大小为W×H×1的特征图,获得具有c2个通道、大小为W×H×c2的特征图,再将特征图每个像素的c2个通道重排成一个c×c的区域,对应于高分辨率图像中一个c×c的子区域,从而获得一个大小为cW×cH×1的高分辨率图像.其中,c是一个常数,表示一幅特征图经过一个子像素卷积层之后放大c倍.在本文中,令c=2,即图像经过两个子像素卷积层后放大4倍.生成模型剩余参数设置如表 1所示,Conv_G1~Conv_G5为生成模型内卷积层,其中,Conv_G2为残差块中的卷积层.
|
图 5 生成模型结构 Fig. 5 Structure of the generative model |
| 表 1 生成模型卷积层参数设置 Tab. 1 Parameter setting of convolution neural network in the generative model |
为使生成模型生成的超分辨率图像更加接近于真实的高分辨率图像,本文训练了一个与之对应的判别模型.
本文的判别模型使用深度卷积网络,在搭建中参考Radford等[17]提出的判别模型结构.模型内部共包括11个卷积层,所有卷积层均使用Leaky ReLU[18]作为激活函数(α=0.2),从而避免在整个网络结构中使用Max Pooling操作,以简化计算过程.除第一个卷积层,在每个卷积层之后使用批规范化操作以避免训练时梯度消失,加快模型的收敛速度,增加模型稳定性.最后添加全连接层,将卷积层提取到的图像特征进行分类组合后输出.由于原始生成对抗网络的判别模型用于判断输入是真实数据还是生成数据,输出结果映射在0、1之间,解决的是二分类问题,而本文模型引入EM距离,去掉模型最后的sigmoid层,连续的输出结果使判别模型转变为解决回归问题.判别模型整体结构如图 6所示,参数设置如表 2所示,Conv_D1~Conv_D11为判别模型内卷积层.

|
图 6 判别模型结构 Fig. 6 Structure of the discriminant model |
| 表 2 判别模型卷积层参数设置 Tab. 2 Parameter setting of convolution neural network in the discriminant model |
定义高分辨率图像为IH,其对应的低分辨率图像为IL,通过模型重建得到的高分辨率图像被称为超分辨率图像IS.定义低分辨率图像的宽度为W,高度为H,图像的颜色通道数目为C,定义缩放倍数为r,则IL的大小为W×H×C,IH和IS的大小为rW×rH×C.
本文模型的最终目标是训练一个生成函数G,输入低分辨率图像IL,输出预测的超分辨率图像IS,即G(IL)=IS.为实现这个目标,需要训练一个卷积神经网络GθG,并优化损失函数lS得到θG= W1:L; b1:L,其中W1:L为网络第L层的权重、b1:L为偏差,进而可以通过给定高分辨率图像训练集IHn(n=1, …, N)和对应的低分辨率图像ILn优化式(2)得到θG:
| $ {\hat \theta _{\rm{G}}} = \arg \mathop {\min }\limits_{{{\rm{ \mathsf{ θ} }}_{\rm{G}}}} \frac{1}{N}\sum\limits_{{\rm{n}} = 1}^{\rm{N}} {{l_{\rm{S}}}} \left( {{{\rm{G}}_{{\rm{ \mathsf{ θ} C}}}}\left( {{I_{{{\rm{L}}_{\rm{n}}}}}} \right), {I_{{{\rm{H}}_{\rm{n}}}}}} \right). $ | (2) |
本文设计的损失函数根据感知相关特征来评估解决方案,由内容损失(lX)和对抗损失(lGen)两部分组成:
| $ l_{\mathrm{G}}=l_{\mathrm{X}}+10^{-3} l_{\mathrm{Cen}}. $ |
在确定模型的对抗损失时,首先引入Goodfellow等[10]提出的生成模型损失函数:
| $ \mathrm{E}_{x \sim \mathrm{P}_{\text {data }}}[\log (1-\mathrm{D}(x))]. $ | (3) |
由最原始生成对抗网络的判别模型损失函数可以推出最优判别模型:
| $ \mathrm{D}^{*}(x)=\frac{P_{\text {data }}(x)}{P_{\text {data }}(x)+P_{z}(x)}. $ | (4) |
式中:Pdata(x)为真实数据域的样本,Pz(x)为噪声z生成的样本.式(3)加上一个不依赖于生成模型的项得到新的损失函数Ex~Pdata[logD(x)]+Ex~Pz[log(1-D(x))],最小化这个损失函数等价于最小化式(3),将其带入式(4),化简得到JS散度表示的损失函数为
| $ 2 \mathrm{J}_{\mathrm{JS}}\left(P_{\mathrm{data}} \| P_{z}\right)-2 \log 2. $ |
然而,在训练判别模型的过程中,随着判别模型越来越接近最优效果时,由式(1)可知,最小化生成模型损失也会越来越接近于最小化真实数据域和生成数据域间的JS散度,但这建立在两个数据域有重叠的基础上,一旦没有重叠,JS散度就会固定为常数log2,梯度下降法中梯度变为0,造成生成梯度消失.与此同时,在最小化生成模型损失的过程中,模型在最小化生成分布与真实分布的KL散度的同时最大化两者的JS散度,这是一个矛盾的任务,并且KL散度是一个不对称的衡量,对生成样本多样性和准确性的衡量标准不一致会导致模式坍塌.因此,本文引入EM距离来替代JS散度和KL散度.相比于JS散度和KL散度,EM距离在两个分布没有重叠或重叠部分可忽略时,仍能反映它们的远近,提供非零梯度,并且距离是平滑的、不会突变.
EM距离的定义为
| $ {\rm{W}}\left(P_{\text {data }}, P_{z}\right)=\inf\limits _{\gamma \sim \Pi\left(P_{ \text {data }\left., P_{z}\right)}\right.} {\rm{E}}_{(x, y) \sim \gamma}[\|x-y\|]. $ | (5) |
式中:Π(Pdata, Pz)为Pdata和Pz组合起来所有可能的联合分布集合.由于定义中
| $ \begin{array}{l} {\rm{W}}\left( {{P_{{\rm{data }}}}, {P_z}} \right) = \frac{1}{K}{\sup _{{{\left\| f \right\|}_{{\rm{L}} \le {\rm{K}}}}}}{{\rm{E}}_{x - {{\rm{P}}_{{\rm{data }}}}}}[f(x)] - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{{\rm{E}}_{x \sim {{\rm{P}}_z}}}[f(x)]. \end{array} $ | (6) |
式中:K为函数f的Lipschitz常数,使得定义域内任意两个元素x1和x2都满足|f(x1)-f(x2)| ≤K|x1-x2|.特别地,可以用一组参数ω来定义一系列可能的函数fω(x),此时求解式(6)可近似变为求解式(7):
| $ \begin{array}{*{20}{c}} {K \cdot {\rm{W}}\left( {{P_{{\rm{data }}}}, {P_z}} \right) \approx \mathop {\max }\limits_{\omega :{{\left| {{f_\omega }} \right|}_{\rm{L}}} \le {\rm{K}}} {{\rm{E}}_{x \sim {{\rm{P}}_{{\rm{data }}}}}}\left[ {{f_\omega }(x)} \right] - }\\ {{{\rm{E}}_{x \sim {{\rm{P}}_z}}}\left[ {{f_\omega }(x)} \right].} \end{array} $ | (7) |
因此,构造一个含参数ω且最后一层不是非线性激活层的判别模型D(x),使得L=Ex~Pdata[D(x)]- Ex~Pz[D(x)]尽可能最大,此时L就会近似于真实分布与生成分布之间的EM距离.最小化L得到对抗损失函数如式(8)所示和判别模型的损失函数如式(9)所示:
| $ l_{\mathrm{Gen}}=-\mathrm{E}_{x \sim \mathrm{P}_{z}}[\mathrm{D}(x)], $ | (8) |
| $ l_{\mathrm{D}}=\mathrm{E}_{x-\mathrm{P}_{z}}[\mathrm{D}(x)]-\mathrm{E}_{x \sim \mathrm{P}_{\text {data }}}[\mathrm{D}(x)]. $ | (9) |
在基于深度神经网络的超分辨率重建模型中,通常使用像素级MSE损失函数如式(10)所示,直接优化高、低分辨率图像像素间的平方差,使得生成的图像有较高的峰值信噪比.
| $ {l_{{\rm{MSE}}}} = \frac{1}{{{r^2}WH}}\sum\limits_{{\rm{x}} = 1}^{{\rm{rW}}} {\sum\limits_{{\rm{y}} = 1}^{{\rm{rH}}} {{{\left( {{{\left( {{I_{\rm{H}}}} \right)}_{x, y}} - {{\left( {{{\rm{G}}_{{{\rm{ \mathsf{ θ} }}_{\rm{G}}}}}\left( {{I_{\rm{L}}}} \right)} \right)}_{x, y}}} \right)}^2}} } . $ | (10) |
MSE损失函数的目标形式包含平方项,梯度容易计算,同时具有很好的收敛特性.然而对于图像超分辨率重建而言,MSE损失函数具有对异常点进行大量加权的缺点,并由于对每一项都进行了平方,导致对大误差的惩罚多于小误差.同时,MSE损失函数基于原始误差度量的方式,没有考虑人眼的视觉特性,并不能提高人眼视觉感受的质量.而L1损失函数属于原始误差度量方式,并不会过度惩罚大误差项,且每个像素的误差对L1损失的影响与误差的绝对值成正比.
本文将像素级L1损失函数计算得到的高分辨率图像(IH)x, y和重建图像(GθG(IL))x, y之间的L1距离作为2张图片相似程度的惩罚项,设计内容损失函数为
| $ {l_{\rm{X}}} = {l_{{\rm{L}}1}} = \frac{1}{{{r^2}WH}}\sum\limits_{{\rm{x}} = 1}^{{\rm{rW}}} {\sum\limits_{{\rm{y}} = 1}^{{\rm{rH}}} {\left| {{{\left( {{I_{\rm{H}}}} \right)}_{x, y}} - {{\left( {{{\rm{G}}_{{{\rm{ \mathsf{ θ} }}_{\rm{G}}}}}\left( {{I_L}} \right)} \right)}_{x, y}}} \right|} } . $ |
实验结果证明,相比于MSE损失函数,使用L1损失函数可以达到更好的实验效果.同时,L1损失函数是随着误差的增大线性增长,可以有效防止梯度爆炸的产生,并指导模型权重更新以使重建得到的超分辨率图像拥有更高的峰值信噪比.
3 实验结果及分析 3.1 实验环境及数据集本文实验环境采用谷歌云计算平台,内存为18G,显卡为NVIDIA Tesla K80,显存为12GB,平台搭载的操作系统为Ubuntu16.04 LTS,使用Tensorflow-gpu 1.4,TensorLayer 1.8.0,Python 3.6.
实验使用DIV2K数据集,该数据集是一种新发布的用于图像复原任务的高质量图像数据集,包含800张训练图像,100张验证图像和100张测试图像.由于测试数据集资料尚未发布,因此在验证数据集上比较模型性能.另外,增加Set5,Set14两个标准基准数据集(分别包含5张和14张图像)来进一步比较模型性能.
生成模型和判别模型的权重使用均值为0、方差为0.02的高斯分布进行随机初始化.误差反向传播采用随机梯度下降算法Adam,beta1为0.9,初始学习率为0.000 1,初始衰减率为0.1,最小批尺寸为16,训练过程中交替更新生成模型和判别模型.
3.2 评价指标本文使用峰值信噪比(peak signal to noise ratio, PSNR)、结构相似性(structural similarity index, SSIM)、主观质量评分(mean opinion score, MOS)作为图像质量评估指标.
3.2.1 峰值信噪比峰值信噪比(PSNR),单位dB,是最普遍、最广泛使用的评估压缩图像质量指标,一般通过均方误差(Mean-square Error,MSE)进行定义.两幅W×H单色图像X和Y的均方误差定义为
| $ M_{\mathrm{MSE}}=\frac{1}{W H} \sum\limits_{i=0}^{W-1} \sum\limits_{j=0}^{H-1}[X(i, j)-Y(i, j)]^{2}. $ |
对于RGB彩色图像,每个像素点有RGB 3个值,其均方误差的定义为所有值的方差总和除以图像大小再除以3,如式(11)所示:
| $ M_{\mathrm{MSE}}=\frac{1}{3 W H} \sum\limits_{i=0}^{W-1} \sum\limits_{j=0}^{H-1}\left[X(i, j)_{\mathrm{R}, \mathrm{G}, \mathrm{B}}-Y(i, j)_{\mathrm{R}, \mathrm{C}, \mathrm{B}}\right]^{2}. $ | (11) |
因此,峰值信噪比定义为
| $ P_{\mathrm{PSNR}}=10 \log \left(\frac{X_{\mathrm{MX}}^{2}}{M_{\mathrm{MSE}}}\right)=20 \log \left(\frac{X_{\mathrm{MA}}}{\sqrt{M_{\mathrm{MSE}}}}\right). $ |
式中:XMAX为图像中可能的最大的像素值.如果每个采样点都有B位线性脉冲编码调制表示,那么XMAX就是2B-1,即如果每个采样点有8位表示时,XMAX=255.
目前,峰值信噪比是超分辨率重建质量评估最常用的指标,峰值信噪比越高,代表图像重建质量越好.然而峰值信噪比越高,并不代表图像的视觉效果越好.如图 7所示,图 7(a)图的PSNR值高于图 7(b)图,但图 7(a)图更加模糊,视觉效果差于图 7(b)图,这表明峰值信噪比在评价超分辨率重建视觉效果上存在一定的局限性.

|
图 7 PSNR与图像视觉效果 Fig. 7 elationship between PSNR and image visual effect |
结构相似性(SSIM)是测量两幅数字图像之间相似度的指标,能反映人眼的主观感受.给定两幅图像x和y,通过亮度L(x, y)、对比度C(x, y)和结构S(x, y)定义结构相似性:
| $ \mathrm{L}(x, y)=\frac{2 \mu_{x} \mu_{y}+C_{1}}{\mu_{x}^{2}+\mu_{y}^{2}+C_{1}}, $ | (12) |
| $ {\rm{C}}(x, y) = \frac{{2{\sigma _x}{\sigma _y} + {C_2}}}{{\sigma _x^2 + \sigma _y^2 + {C_2}}}, $ | (13) |
| $ \mathrm{S}(x, y)=\frac{\sigma_{x y}+C_{3}}{\sigma_{x} \sigma_{y}+C_{3}}, $ | (14) |
| $ \mathrm{S}_{\mathrm{SSIM}}(x, y)=[\mathrm{L}(x, y)]^{\alpha}[\mathrm{C}(x, y)]^{\beta}[\mathrm{S}(x, y)]^{\gamma}. $ | (15) |
式中:式(12)中μx与μy分别为x和y的平均值,式(13)、(14)中σx和σy分别为x和y的标准差,σxy为x和y的共变异数字,C1、C2、C3皆为常数.式(15)中α>0,β>0,γ>0.在实际应用中,通常α=β=γ=1及C3=C2/2.
与峰值信噪比相比,结构相似性更符合对图像视觉效果的评估,但仍在反映图像的视觉效果上同样存在局限性.
3.2.3 主观质量评分主观质量评分(MOS)是图像质量最具代表性的主观评价方法,可以直接反映人眼对图像质量的评价.其中,主观质量评分使用绝对分类评分标准,将差评和好评分映射到1至5之间的数字,如表 3所示.
| 表 3 绝对分类评分标准 Tab. 3 Absolute classification criteria |
在主观质量评估测试中,最终评分被计算为N位受试者针对给定图像进行的单一评分的算术平均值为
| $ M_{\mathrm{MOS}}=\frac{\sum\limits_{i=1}^{\mathrm{N}} R_{i}}{N}. $ |
式中:Ri为单人评分.本文的主观质量评分是基于随机抽取的50名学生对给定图像的评分计算得到.
3.3 残差块质量评价本文在深度残差网络的基础上,剔除了网络残差块中多余的批规范化操作,为证明改进残差块的有效性,相同实验环境下,在Set5,Set14两个标准基准数据集上,对原始残差网络作为生成模型的模型、改进残差网络作为生成模型的模型分别进行迭代训练,且两个模型均使用本文设计的损失函数.原始模型耗时约28小时,改进后的模型耗时约24小时.
固定模型迭代次数500、600、800,比较PSNR、SSIM、MOS和单次迭代耗时,如表 4所示.在不同迭代次数下,本文模型相比于改进前模型,PSNR在Set5数据集上平均约提高1.15 dB,在Set14数据集上平均约提高0.16 dB;SSIM在Set5数据集上平均约提高0.030,在Set14数据集上平均约提高0.017;MOS在Set5数据集上平均约提高0.19,在Set14数据集上平均约提高0.18.改进后的残差块,剔除块中冗余批规范化操作,减少网络计算量,使得迭代耗时由原来的200秒变为175秒,减少25秒,证明改进残差块对加快模型训练速度、提高重建效率的有效性.
| 表 4 残差块实验对比 Tab. 4 Results of residual blocks experiment |
表 4数据显示,当迭代次数达到500次以上时,本文模型的评价指标值趋于收敛,增长并不迅速且有降低趋势,因此,本文以下实验均采用模型500次迭代时的结果来验证模型有效性.
3.4 损失函数性能对比本文引入L1损失函数替换普遍使用的MSE损失函数,并在此基础上引入EM距离,为证明改进损失函数的有效性和保证实验的公平性,模型均使用本文改进的残差块来进行实验.
首先,在Set5,Set14两个标准基准数据集上,将使用MSE损失的和使用L1损失及EM距离的本文模型在相同实验环境下分别进行500次迭代训练,两者均耗时约24小时,实验部分结果如图 8所示.其中图 8(a)列是高分辨率图像;图 8(b)列是改进前模型的重建图像;图 8(c)列是本文模型的重建图像.观察图 8可以发现本文模型重建得到的图片清晰度较高,视觉效果较好,细节较丰富,改进前模型重建得到的图片清晰度较低,图像过于平滑,细节较为粗糙.

|
图 8 重建效果 Fig. 8 The reconstructed images |
其次,为进一步证明L1损失和EM距离的有效性,在Set5和Set14数据集上比较本文模型和改进前模型的PSNR、SSIM和MOS,如表 5所示.本文模型相比于改进前的模型,PSNR在Set5数据集上提高约0.19 dB,在Set14数据集上提高约0.24 dB;SSIM在Set5数据集上提高约0.012,在Set14数据集上提高约0.017;MOS在Set5数据集上提高约0.26,在Set14数据集上提高约0.35,实验数据证明引入L1损失和EM距离对提高重建效果的有效性.
| 表 5 损失函数实验对比 Tab. 5 Results of loss experiment |
选择典型的双三次插值(Bicubic)模型、SRCNN模型、VDSR模型以及DSRN模型[19]与本文模型在PSNR、SSIM和MOS 3个图像质量评价指标上进行对比实验.双三次插值直接根据图像中距离每个像素点最近的16个像素点计算得到目标超分辨率图像,而SRCNN模型、VDSR模型和DSRN模型是3个典型的基于深度学习的重建模型,通过学习低分辨率图像到高分辨率图像的端到端的映射关系来得到目标超分辨图像.
本次实验通过Python中的OpenCV库对图像进行双三次插值;SRCNN模型和DSRN模型使用作者提供的源代码进行重建;VDSR模型使用Tensorflow框架下的代码进行重建.实验结果如图 9所示,分别展示每个模型在Set5数据集上重建的超分辨率图像的效果.其中图 9(a)列是原始高分辨率图像;图 9(b)列是Bicubic模型的重建图像;图 9(c)列是SRCNN模型的重建图像;图 9(d)列是VDSR模型的重建图像;图 9(e)列是DSRN模型的重建图像;图 9(f)列是本文模型的重建图像.

|
图 9 Set5数据集的重建图像 Fig. 9 Reconstructed images based on Set5 dataset |
其中,第1、4、5行分别是在baby、head、woman人物图像上的重建结果,采用双3次插值法重建的图像人物面部特征都比较模糊,SRCNN、VDSR、DSRN和本文模型重建的图像都比较清晰,其中本文模型重建的图像细节更丰富、与原图更接近;第2行是在bird图像上的重建结果,5种模型重建的图像背景整体效果类似,而采用双3次插值法的鸟的头部比较模糊,SRCNN、VDSR和DSRN模型的结果则比较清晰,但都比本文模型重建的结果要模糊;第3行是在butterfly图像上的重建结果,采用双3次插值法重建的图像锯齿较多,SRCNN和VDSR模型重建的图像虽然锯齿较少但比较模糊,DSRN和本文模型重建的图像则比较平滑,都与原图比较接近.
为对比本文模型与其他模型的重建效果,在Set5数据集上分别计算每个模型重建得到每张图像的PSNR、SSIM和MOS,如表 6所示.
| 表 6 在Set5上的实验结果对比 Tab. 6 Test results based on Set5 dataset |
为进一步验证本文模型的有效性,在Set14数据集上进行实验.Set14数据集中14幅图像的实验结果如表 7所示.从表 6和表 7中各项数据可知,本文模型重建得到的图像虽然在个别图像上PSNR和SSIM得分并不是最高,但在MOS评分整体上是最优的,再次证明其在提高视觉效果方面的有效性.
| 表 7 在Set14上的实验结果对比 Tab. 7 Test results based on Set14 dataset |
本文针对基于深度学习的图像重建模型层次过多导致训练时间长、重建效率低的问题,设计剔除多余批规范化操作的残差块组合成生成模型,同时将深度卷积网络作为判别模型以指导模型训练.针对重建模型中梯度传输困难导致训练难以继续的问题,引入EM距离设计对抗损失函数,同时使用L1损失函数来指导模型权重更新,加强重建图像视觉效果.在不同数据集上的实验结果表明,本文模型针对单帧图像的重建效率与重建视觉效果相对于优秀的同类方法有一定的提升,但适用于特定的使用双三次插值的降质模型,对于通过不同降质过程获得的低分辨率图像,重建效果并不理想.最后,本文对未来的工作归纳如下:
1) 超分辨率重建模型使用的L1损失函数忽略了图像的部分高频特征,导致重建图像的细节与实际不太相符.如何改进损失函数,从而使重建得到的图像细节更为丰富且与实际更为接近,将有助于提高重建图像的准确率.
2) 基于生成对抗网络的超分辨率重建模型的计算量仍然太大,导致模型运行效率低下,无法达到实际应用水平.如何简化生成模型结构或者使用更高效的计算方式来降低计算量,将有助于提高模型的重建效率.
| [1] |
杨帅锋.基于学习的超分辨率重建算法研究[D].北京: 北京交通大学, 2015 YANG Shuaifeng. Super-resolution reconstruction algorithms based on learning method[D]. Beijing: Beijing Jiaotong University, 2015 |
| [2] |
FREEMAN W T, ADELSON E H. The design and use of steerable filters[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1991, 13(9): 891. DOI:10.1109/34.93808 |
| [3] |
HERTZMANN A, JACOBS C E, OLIVER N, et al. Image analogies[C]// Conference on Computer Graphics & Interactive Techniques. ACM, 2001. DOI: 10.1145/383259.383295
|
| [4] |
孙旭, 李晓光, 李嘉锋, 等. 基于深度学习的图像超分辨率复原研究进展[J]. 自动化学报, 2017(5): 697. SUN Xu, LI Xiaoguang, LI Jiafeng, et al. Review on deep learning based image super-resolution restoration algorithms[J]. Acta Automatica Sinica, 2017(5): 697. DOI:10.16383/j.aas.2017.c160629 |
| [5] |
DONG C, LOY C C, HE K, et al. Image super-resolution using deep convolutional networks[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2014, 38(2): 295. DOI:10.1109/TPAMI.2015.2439281 |
| [6] |
KEYS R G. Cubic convolution interpolation for digital image processing[J]. IEEE Transactions on Acoustics Speech & Signal Processing, 2003, 29(6): 1153. DOI:10.1109/TASSP.1981.1163711 |
| [7] |
SHI W, CABALLERO J, HUSZAR F, et al. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network[C]//2016 IEEE Conference on Computer Vision & Pattern Recognition. IEEE Computer Society, 2016: 1874. DOI: 10.1109/CVPR.2016.207
|
| [8] |
KIM J, LEE J K, LEE K M. Accurate image super-resolution using very deep convolutional networks[C]// 2016 IEEE Conference on Computer Vision & Pattern Recognition. IEEE Computer Society, 2016: 1646. DOI: 10.1109/CVPR.2016.182
|
| [9] |
TAI Ying, YANG Jian, LIU Xiaoming. Image super-resolution via deep recursive residual network[C]//2017 IEEE Conference on Computer Vision and Pattern Recognition. IEEE Computer Society, 2017: 2790. DOI: 10.1109/CVPR.2017.298
|
| [10] |
GOODFELLOW I J, POUGET-ABADIE J, MIRZA M, et al. Generative adversarial networks[J]. Advances in Neural Information Processing Systems, 2014, 3: 2672. |
| [11] |
NASH J F. Non-Cooperative games[J]. Annals of Mathematics, 1951, 54(2): 286. DOI:10.2307/1969529 |
| [12] |
NASH J F. Equilibrium points in N-person games[J]. National Academy of Sciences, 1950, 36(1): 48. DOI:10.1073/pnas.36.1.48 |
| [13] |
HE Kaiming, ZHANG Xiongyu, REN Shaoqing, et al. Deep residual learning for image recognition[C]//2016 IEEE Conference on Computer Vision and Pattern Recognition. IEEE Computer Society, 2016: 770. DOI: 10.1109/CVPR.2016.90
|
| [14] |
LOFFE S, SZEGEDY C. Batch normalization: Accelerating deep network training by reducing internal covariate shift[J]. arXiv preprint arXiv: 1502.03167, 2015
|
| [15] |
HE Kaiming, ZHANG Xiongyu, REN Shaoqing, et al. Delving deep into rectifiers: Surpassing human-level performance on ImageNet classification[C]//2015 IEEE International Conference on Computer Vision. IEEE Computer Society, 2015: 1026. DOI: 10.1109/ICCV.2015.123
|
| [16] |
LIM B, SON S, KIM H, et al. Enhanced deep residual networks for single image super-resolution[C]//2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops. IEEE Computer Society, 2017: 1132. DOI: 10.1109/CVPRW.2017.151
|
| [17] |
RADFORD A, METZ L, CHINTALA S. Unsupervised representation learning with deep convolutional generative adversarial networks[J]. Computer Science, 2015. |
| [18] |
MAAS A L, HANNUN A Y, Ng A. Y. Rectifier nonlinearities improve neural network acoustic models[C]// Proc. icml. 2013, 30(1): 3
|
| [19] |
HAN Wei, CHANG Shiyu, LIU Ding, et al. Image super-resolution via dual-state recurrent networks[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2018: 1654. DOI: 10.1109/CVPR.2018.00178
|
 2019, Vol. 51
2019, Vol. 51


