2. 海军航空大学, 山东 烟台 264001
2. Naval Aeronautical University, Yantai 264001, Shandong, China
战机自主作战机动决策对无人战机的发展和有人战机辅助决策的研究都具有重要意义.自主作战机动决策主要是通过数学优化、人工智能等方法构建由作战态势到机动指令的映射.根据求解映射的思路不同,主要有:矩阵对策[1-2]、影响图对策[3-5]、遗传算法[6]、遗传模糊树[7-8]和神经网络[9]等方法.针对不同想定利用这些方法解决战机自主决策的问题,取得了很多成果[10-12].然而,这些方法仍面临着“维数灾难”、“人类主观性影响”、“规则漏洞”等问题的困扰.当战机面临难以预知的复杂状况时,决策的不确定性随之提升.
智能围棋程序AlphaGo[13]基于深度强化学习(Deep Reinforcement Learning,DRL)通过自我对弈提升棋力,击败了人类顶级围棋选手,并在对弈的过程中使用了许多人类意料之外的创新招式.这为研究战机自主决策提供了新的思路.利用DRL研究战机自主决策,通过其与环境的交互对算法进行训练,无人类主观影响;不需要经典样本案例;通过深度神经网络拟合机动策略,避免维数灾难;使战机通过自我对战提升自主决策能力成为可能.所以DRL在战机自主机动决策中具有很好的应用前景.
利用DRL依据态势信息对动作选择做出决策,实现向攻击区域的自主机动,是研究不同想定中利用DRL支撑战机自主机动决策的基础.然而,由于战机活动空域巨大、各向探索能力不均匀,直接引入DRL则训练交互空间巨大、攻击区域样本分布设置困难,训练过程难以收敛.
针对该问题,提出双网络智能决策方法,在设置锥形空间的基础上,从战机与攻击区域的距离和速度矢量与攻击区域视线夹角两个维度出发,分别基于强化学习算法,利用深度神经网络实现战机对攻击区域距离捕获和角度捕获两种机动策略的拟合.这极大压缩了训练时的探索空间,避免了攻击区域样本的分布设计,有效解决了战机依据态势信息向攻击区域自主机动决策的问题.
1 战机自主作战机动背景 1.1 战机作战机动想定在对战机进行自主机动决策的研究中有多种想定,如双机空战[14]、对地攻击[15]、多机协同[16]等.在这些复杂想定下利用DRL研究战机自主决策,必须以战机能够基于态势信息自主选择动作,向既定区域机动为支撑.例如,在敌我双机空战的想定中,双方均在不断摆脱对方威胁区域,而向己方攻击区域机动.
研究中设置的想定是,单架战机在规定空域内巡航,当通过自身传感器或外部信息支援获得某一攻击区域坐标时,由战机基于态势信息,依据DRL得到的策略进行动作选择决策,实现向攻击区域的自主机动.该想定中,战机为固定翼飞机;不考虑来自空域内其他不确定因素的威胁,及不同情报源的影响;攻击区域坐标按照均匀分布概率在设定的战机活动空域内随机出现.
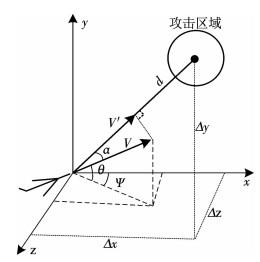
1.2 战机作战态势描述战机作战态势描述是研究战机机动决策的模型基础.参照马耀飞等[17]提出的空中态势评估参数,选取战机与攻击区域中心的相对坐标、距离、相对速度等参量对态势信息进行描述.战机在机动中向攻击区域进行机动的态势定义为S =(Δx, Δy, Δz, d, V, V′, α),其中(Δx, Δy, Δz)为战机与攻击区域中心的坐标差,d为飞机与攻击区域中心的距离,V为飞机飞行速度,V′为飞机速度沿攻击区域方向的速度分量,α为飞机速度矢量与攻击区域中心视线夹角.各参量的位置如图 1所示.
|
图 1 各参量几何示意 Fig. 1 Diagram of geometric parameters |
设飞机的坐标为(xr, yr, zr),攻击区域中心的坐标为(xt, yt, zt),则上述各参数利用式(1)求解:
| $ \left\{ {\begin{array}{*{20}{l}} {(\Delta x, \Delta y, \Delta z) = \left( {{x_{\rm{r}}} - {x_{\rm{t}}}, {y_{\rm{r}}} - {y_{\rm{t}}}, {z_{\rm{r}}} - {z_{\rm{t}}}} \right);}\\ {d = \sqrt {\Delta {x^2} + \Delta {y^2} + \Delta {z^2}} ;}\\ {\alpha = \arccos [\Delta z\sin \psi \cos \theta - \Delta x\cos \psi \cos \theta - \Delta y\sin \theta ];}\\ {{V^\prime } = V\cos \alpha .} \end{array}} \right. $ | (1) |
式中:θ和ψ为航迹倾斜角和航迹偏转角.
1.3 动作集设计由于研究重点是战机向攻击区域的机动决策,所以战机飞行动力学模型的建立主要考虑对战机飞行轨迹、基本性能的仿真.假设飞机在运动过程中无侧滑运动,航迹倾斜角与俯仰角一致,发动机推力方向与速度方向一致,不考虑风速、重力变化以及地球自转、曲率的影响.在航迹坐标系下飞机的3自由度质心动力学方程[18]为
| $ \left\{\begin{array}{l}{\frac{\mathrm{d} V}{\mathrm{d} t}=g\left(n_{\mathrm{x}}-\sin \theta\right)}; \\ {\frac{\mathrm{d} \theta}{\mathrm{d} t}=\frac{g}{V}\left(n_{\mathrm{y}} \cos \gamma-\cos \theta\right)}; \\ {\frac{\mathrm{d} \psi}{\mathrm{d} t}=-\frac{g}{V \cos \theta} n_{\mathrm{y}} \sin \gamma}.\end{array}\right. $ | (2) |
式中:nx为切向加速度,ny为法向加速度,γ滚转角,g为重力加速度.
由式(1)和、(2)可得,已知nx,ny,γ,给定飞机V,θ,ψ初值的情况下,就可以由飞机的初始空间位置(x0, y0, z0),计算出飞机当前空间位置(x, y, z)为
| $ \left\{\begin{array}{l}{x=x_{0}+\int_{t_{0}}^{t_{1}} V \cos \theta \cos \psi \mathrm{d} t} ;\\ {y=y_{0}+\int_{t_{0}}^{t_{1}} V \sin \theta \mathrm{d} t} ;\\ {z=z_{0}-\int_{t_{0}}^{t_{1}} V \cos \theta \sin \psi \mathrm{d} t}.\end{array}\right. $ | (3) |
式中控制量nx,ny,γ表达式为
| $ \left\{ {\begin{array}{*{20}{l}} {{n_{\rm{x}}} = \frac{{\Delta V}}{g} + \sin \theta ;}\\ {{n_{\rm{y}}} = \frac{1}{{\cos \gamma }}\left( {\frac{{\Delta V\Delta \theta }}{g} + \cos \theta } \right);}\\ {\gamma = - \frac{{\Delta \psi V\cos \theta }}{{g{n_{\rm{y}}}.}}} \end{array}} \right. $ | (4) |
战机的机动动作在控制量作用下产生,机动轨迹由方程(3)计算的位置坐标组成.本文采用美国国家航天局(NASA)学者提出的7种基本操纵动作[19],即最大过载俯冲、最大过载爬升、最大过载右转、最大过载左转、最大减速、最大加速和平稳直飞.
2 背景理论 2.1 强化学习强化学习是指针对序列决策问题,智能体通过与环境交互,采用“试错”的方式,在回报函数的引导下,获得最优策略[20-21].
强化学习可以用马尔科夫决策过程(MDPs)描述.标准的MDPs定义为(S, A, R, T, γ),其中S为状态集合即战机面临的态势集合,A为动作集合即战机动作集,R为回报函数,T为态转移函数,γ为折扣因子.战机在状态s∈S时,采取动作a∈A,到达新的状态s′∈S,获取回报为r=R(s, a).对于无模型的MDPs,转移函数T未知[20].
状态动作值函数为
| $ {q_{\rm{ \mathsf{ π} }}}(s, a) = {E_{\rm{ \mathsf{ π} }}}\left[ {\sum\limits_{{\rm{k}} = 0}^\infty {{\gamma ^k}} {r_{{\rm{t + k + 1}}}}|{s_{\rm{t}}} = s} \right]. $ | (5) |
式中:π、st为策略和t时刻状态.状态动作值函数表示依据策略π,在状态s下采取动作a时对未来总回报的估计.最大状态动作值函数为
| $ q_{*}(s, a)=\max q_{\pi}(s, a). $ | (6) |
在不同策略中,最优策略π*是指在状态s时选取最大q*(s, a)所对应的行为
| $ {\pi ^*} = {\max _{{\rm{a}} \in {\rm{A}}}}{q_*}(s, a). $ | (7) |
获取最优策略主要有策略迭代、Q学习等方法.由于战机面临的态势空间为连续空间,所以这些强化学习方法并不适用.
2.2 深度强化学习DRL将利用强化学习解决决策问题的范围扩展到高维甚至连续状态和动作空间[22], 可利用其对战机自主机动决策问题进行研究.在DRL领域内,具有突破性的工作是Mnih等提出的深度Q网络[23](Deep Q-Network,DQN),将深度神经网络和强化学习中的Q算法相结合,实现了“端到端”的策略学习[24],从高维图像输入直接得到控制策略,在一系列雅达利游戏中超过了人类水平.
DQN利用深度神经网络实现在连续状态空间内对策略的拟合,基于智能体与环境交互产生的数据,对网络参数进行更新,实现策略演化.网络参数的更新过程,是采用梯度下降方法,最小化损失函数为
| $ \text { Loss }=E\left[\left(r+\gamma Q\left(a^{\prime}\right)-Q(a)\right)^{2}\right], $ | (8) |
其中
| $ Q(a)=q_{\pi}(s, a), $ | (9) |
| $ Q\left(a^{\prime}\right)=\max _{a \in A}\left[q_{\pi}\left(s^{\prime}, a\right)\right]. $ | (10) |
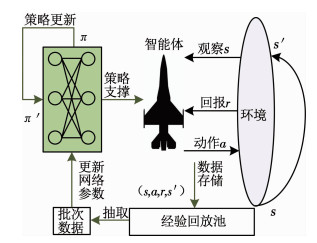
具体过程如图 2所示.
|
图 2 基于经验回放机制的DQN原理 Fig. 2 Diagram of DQN based on experience replay |
从战机与攻击区域的距离d和速度矢量与攻击区域视线夹角α两个维度出发,在划定锥形空间的基础上,分别基于DQN算法构建拟合调整偏离角策略的角度捕获网络与拟合距离趋近策略的距离捕获网络.两者协作,实现战机向攻击区域自主机动决策.
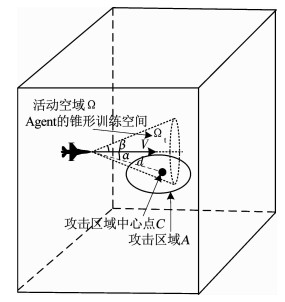
锥形空间的设置,如图 3所示.设战机的活动空域为Ω;以战机速度V为轴线,在其正前方设置锥形训练空间Ωt,顶角为2β;战机速度V与攻击区域中心C的视线夹角为偏离角α,战机到攻击区域之间的距离为d,攻击区域半径为d′.当偏离角α < β时,完成角度捕获;当距离d < d′时,完成距离捕获战机进入攻击区域A
|
图 3 锥形空域位置示意 Fig. 3 Diagram of conical airspace location |
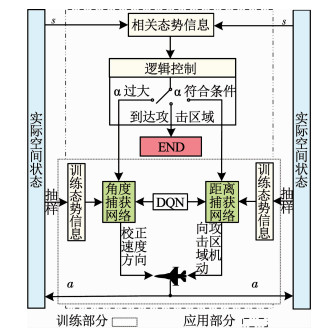
双网络智能决策方法如图 4所示,构建基于DQN的角度捕获网络和距离捕获网络,分别实现对战机偏离角调整策略和距离趋近策略的拟合.两网络在作战态势的引导下由逻辑控制部分协调运作.当战机偏离角α过大时,角度捕获网络支撑战机决策,依据态势进行机动,对战机航向进行调整;当α满足要求时,A进入锥形空域,距离捕获网络支撑战机决策,使战机向攻击区域机动.
|
图 4 双网络智能决策方法原理 Fig. 4 Diagram of dual network intelligent decision method |
基于DQN的角度捕获网络.在训练阶段,以均匀分布概率在空间Ω内随机抽取坐标作为A样本,利用战机向A样本机动过程中,与环境产生的交互信息(s, a, r, s′)作为网络拟合偏离角调整策略的训练样本,如2.2节中图 2所示.在工作阶段,态势信息输入到角度捕获网络,输出动作控制决策,使偏离角α减小.
基于DQN的距离捕获网络,在训练阶段与角度捕获网络类似,只是交互空间为锥形空间Ωt,网络拟合的是距离趋近策略.在工作阶段,态势信息输入到距离捕获网络,输出动作指令,实现向A机动.
逻辑控制部分在态势信息的引导下,对角度捕获网络和距离捕获网络进行切换.当α>β时,使用角度捕获网络,对战机航向进行调整,减小偏离角α.当α≤β且d>d′时,则使用距离捕获网络支撑战机向A机动.在使用距离捕获网络的过程中,设置容错角度γ,当α>γ时,启用角度捕获网络进行纠正.当d < d′时认为战机进入A,逻辑控制部分终止此次机动决策过程.基于DQN的双网络智能决策方法伪代码如算法1所示:
算法1 基于DQN的多网络协同决策方法
Input:Airspace range, Conical space range, Attack area.
Output:the successful times
Forepisode=1, M
Initialize state
WhileTrue
While (d>d′andα>β)
count1+=1
action←AngleNetDQN(state)
statenext←step(action)
Ifcount1>SetTime1
break
While(d>d′andα < γ)
count2+=1
action←DistanceNetDQN(state)
statenext←step(action)
Ifcount2>SetTime2
break
If(d>d′and count1+count2 < SetTime)
break
Return:the successful times
3.2 双网络智能决策方法理论分析针对利用DRL解决战机向攻击区域A进行机动决策的问题.想定中战机为固定翼飞机,与四轴全向无人机不同,其各向探索能力分布并不均匀.因此,在规定了步数、动作库等先决条件下,战机在活动空域Ω内存在探索盲区,而机动至盲区的策略并不存在.对网络进行训练的样本(s, a, r, s′),产生于战机向A机动时与环境的交互.A在交互空间内依均匀概率分布随机出现.当A出现在战机探索盲区时,由于机动至A的策略不存在,交互产生的数据样本对神经网络进行策略拟合是无效的,并且对经验回放池中数据产生污染,进而策略拟合难度增加,决策效果变差.若将Ω直接作为利用DRL的交互空间,应根据战机各向探索能力分布,对A分布进行设置,避免产生过多的无效数据样本对经验回放池形成污染.然而,对A分布进行研究难度较大,且战机探索能力的改变直接对A分布产生影响,泛化能力较差.
因此并未沿袭传统思路直接引入DRL,而是结合战机探索能力特性、交互空间特性以及DRL的训练方式,设计了双网络智能决策方法.
距离捕获网络的作用是拟合战机向A机动的策略.为降低A出现在战机探索盲区的几率,减少经验回放池中的无效数据.在战机正前方设置以飞机速度为轴线的锥形空间Ωt,作为训练距离捕获网络的交互空间.由于飞机前向探索能力强,Ωt的探索盲区相对减少,样本A出现在探索盲区数量降低,交互产生的无效数据减少,且Ωt < Ω,压缩了交互空间,减小了战机面临态势,可有效提升网络对策略的拟合效率和质量.
角度捕获网络的作用是减小战机偏离角α.由于角α的范围为[0°,180°],交互空间非常有限,探索盲区少,产生的无效数据不影响对角度搜索策略的拟合效率和质量.
角度捕获网络支撑战机决策完成偏离角调整后,A则进入到战机正前方的锥形空间Ωt,进而利用距离捕获网络支撑战机向A趋近的机动决策.两网络相互配合,支撑战机向攻击区域自主机动.
4 仿真及分析 4.1 仿真条件设置对战机活动空域进行设置主要考虑,战机对随机目标进行捕获时,要有充分的动作空间,以满足对算法的训练及测试.设置战机活动空域Ω长48 km,宽20 km,高度5 km.战机速度为200~400 m/s,每2 s战机进行一次机动决策,设其攻击区域A为距攻击中心点C 3 km以内区域.机动动作包括:匀速平飞、加速平飞、减速平飞、爬升、俯冲、水平左转、水平右转7个基本动作.由战机根据态势自主进行动作选择.战机以300 m/s沿对角线穿过该空域的时间为174 s,其决策时间间隔为2 s,目标随机出现,满足战机充分动作的空间要求.
在对神经网络结构参数进行设置时,主要考虑的因素是网络模型容量[25].网络模型容量增大,可以拟合更加复杂的策略,但同时会带来计算量增加、梯度消失、梯度爆炸等问题.结合网络处理的态势信息已具有相对速度、相对位置等人为抽取特征.角度捕获网络设置了包含7节点的输入层和输出层以及一个包含20节点的隐藏层.输入和输出层的节点数由态势信息维度和基本动作数决定.由于在距离上对目标捕获的难度要远远大于角度上捕获,所以构建距离捕获网络时,适当增加了网络深度和隐藏节点数目,以增加网络模型的容量.距离捕获网络的输入层、输出层同样为7个节点,隐藏层一为20个节点,隐藏层二为30个节点.角度捕获网络和距离捕获网络均采用全连接网络.角度捕获网络和距离捕获网络的学习率设为0.001,折扣因子为0.9,网络参数更新一次在经验回放池中抽取的小批量数据量为500,经验回放池容量为10 000,激活函数选择ReLu函数.
在设置空域内,C点坐标按均匀分布随机抽样决定,模拟战机获取到攻击区域坐标并向该区域机动的背景想定.在训练阶段,战机的初始位置位于设置空域的中心,初始速度、航迹倾斜角和航迹偏转角随机初始化,以使战机对状态获得更加充分的探索.训练样本来源于战机与环境进行交互产生的态势信息和奖惩反馈,并存储至经验回放池中,且随交互数据的产生持续更新,直至算法收敛;在测试阶段,战机的初始位置将不在固定,并对随机出现的C点进行捕获,捕获成功率为算法性能的衡量标准.
4.2 仿真内容及分析为验证角度捕获网络和距离捕获网络有效性与锥形空间的关系,及双网络智能决策方法的有效性,设置仿真试验内容为:研究锥形空间与角度捕获网络捕获率的关系;研究锥形空间与距离捕获网络捕获率的关系;研究双网络智能决策方法有效性与时间限制的关系;研究双网络智能决策方法有效性与容错角度的关系;进行案例仿真,进一步验证双网络智能决策方法的有效性.
试验一 锥形空间顶角与角度捕获网络对攻击区域中心C捕获率的关系.
设置顶角2β为20°、60°、120°,垂线长度为9 km的3个锥形空间Ω′t、Ω″t、Ω'''t,分别进行角度捕获网络训练,其中Ω'''t>Ω″t>Ω′t.
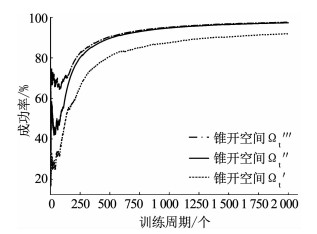
仿真结果如图 5所示,随着训练周期增加,角度捕获网络的捕获率不断上升最后趋于平稳.锥形空间顶角从20°变为60°,训练效果有明显提升.从60°增大至120°时,收敛过程更短,但收敛后的捕获率较60°条件下并无明显优势.
|
图 5 训练周期与角度捕获成功率关系 Fig. 5 Relationship between training episodes and angle capture success rate |
角度捕获的作用是,将战机偏转角α校正到小于β,使A进入锥形空间.当锥形空间顶角2β增大时,实现角度捕获的难度随之降低,成功率增高.从3.2节可知,战机的运动特性造成其存在捕获盲区,捕获率达不到百分之百与实际情况相符.
试验二 锥形空间顶角与距离捕获网络对攻击区域A捕获率的关系.
取锥形空间Ω′t和Ω″t,顶角分别为20°和60°,垂线长度为9 km,Ω″t>Ω′t.分别将Ω′t和Ω″t作为交互空间,对距离捕获网络进行训练.收敛后在各自空间内分别进行1 000次测试实验.
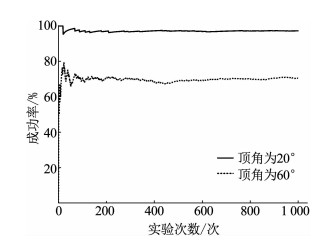
仿真结果如图 6所示.锥形空间顶角为20°时,成功进入A的几率为97.2%,顶角为60°时成功进入A的几率为70.4%.随着Ωt增大,战机成功进入攻击区域的几率明显下降.主要原因是战机的探索性能从其正前方向两侧衰减,随着Ωt的增大,3.2节提到的战机探索盲区更多的扩大到Ωt里,均匀分布的攻击区域A,出现在探索盲区的数量增多,进而交互产生的无效数据增多,影响了网络拟合策略的效果,进入攻击区域的成功率下降.
|
图 6 不同顶角时距离捕获成功率 Fig. 6 Success rate of distance capture under different vertex angles |
试验三 对双网络智能决策方法的有效性进行验证分析.
设置锥形空间顶角为60°,分别对角度捕获网络和距离捕获网络进行训练.
1) 双网络决策方法成功率与时间限制的关系.
在两个网络收敛后,容错角度设置为30°,分别在时间限制设置为100 s、140 s、180 s、240 s、280 s时,各做1 000次试验.
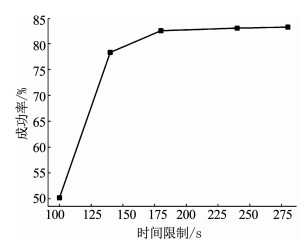
仿真结果如图 7所示,时间限制从100 s~140 s,其成功率从50.2%~78.3%,共提升了28.3%;时间限制从140 s~180 s其成功率从78.3%~82.5%,共提升了4.2%;从180 s~240 s其成功率从82.5%~83%,仅提升了0.5%;从240 s~280 s其成功率从83%~83.2%,仅提升了0.2%.
|
图 7 成功率随时间限制的变化 Fig. 7 Tendency of success rate over set time |
随着限制时间延长,战机向攻击区域机动决策的成功率不断提升,但提升幅度从最开始的28.3%降到了0.2%.
战机取平均速度300 m/s时,穿过Ω对角线的时间为174 s,结合仿真中成功率在时间限制为180 s前,提升幅度大的状况.从100 s~180 s其成功率提升了32.5%,此过程中限制成功率提升的因素是时间,即战机没有足够的时间机动至距离较远的攻击区域.从180 s~280 s其成功率提升了0.7%,此过程中制约成功率提升的是双网络决策方法的性能,继续延长时间限制成功率不再有明显提升.
2) 双网络智能决策方法成功率与容错角度的关系.
时间限制为180 s,容错角度取30°、36°、45°、60°、90°时,各做1 000次试验.
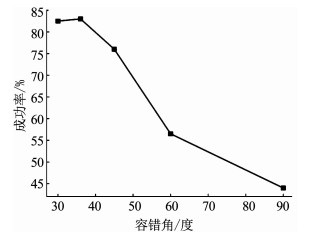
仿真结果如图 8所示,容错角度从30°提升到36°时,飞机进入攻击区域的成功率从82.5%提升到了83%.但是此后,随容错角度的增加,进入攻击区域的成功率不断下降.
|
图 8 成功率随容错角度的变化 Fig. 8 Tendency of success rate over fault-tolerant angle |
主要原因是,增加容错角度,延长了战机无效机动时间,使战机没有充足时间到达攻击区域.
试验四 案例仿真
为进一步验证双网络自主决策方法的有效性,设计仿真案例为,固定翼战机的出发位置为O点,设置3个不同的攻击区域,依次为A1、A2和A3.战机在O点位置获取A1情报,自主机动至A1,获取A2情报,自主机动至A2后获取A3坐标情报,最后机动至A3区域.坐标情报可按时有效获取,不考虑情报源(如指挥中心、自身传感器等)影响.
仿真结果如图 9所示,战机完成了自主向攻击区域机动的任务.红色轨迹代表距离捕获网络进行机动决策,黑色轨迹代表角度捕获网络进行机动决策,两个网络通过逻辑控制部分协调决策,实现了战机向攻击区域的自主机动.案例仿真结果更加直观地表明,双网络决策方法有效的解决了战机向己方攻击区域自主机动决策的问题.

|
图 9 战机机动轨迹示意 Fig. 9 Diagram of maneuvering trajectories for fighter |
从试验一和试验二的结果可得,对于角度捕获网络和距离捕获网络,通过改变锥形空间参数的方法提升其中一方的性能,则必然造成另外一方性能下降.平衡角度捕获网络和距离捕获网络两者之间的矛盾,设计适中的锥形空间影响着该决策方法的性能.从试验三结果可以看出,战机自主向攻击区域机动的成功率最高达到了83%,充分证明了双网络智能决策方法的有效性;充足的机动时间是双网络智能决策方法性能发挥的保证;容错角度过大会增加战机无效机动时间,降低决策方法性能.试验四案例直观表明,该方法有效解决了基于DRL的战机自主趋近攻击区域的问题.
5 总结针对基于DRL战机向攻击区域自主机动决策的问题,结合战机机动的探索能力特性、交互空间特性以及DRL的训练方式,设计了双网络智能决策方法.通过对该方法的理论分析和仿真试验得出了以下结论.
1) 双网络智能决策方法有效压缩了利用DRL的交互空间,降低了构建态势与机动指令映射关系的难度.
2) 双网络智能决策方法通过设置锥形空间,充分利用了战机较强的前向探索性能,避免了其探索性能各向分布不均带来的A样本分布设计问题.
3) 锥形空间顶角变化对角度捕获网络和距离捕获网络性能产生相反影响,容错角度过大增加战机无效机动时间,合理设置锥形空间和容错角度影响着双网络决策方法性能.
4) 双网络智能决策方法有效解决了利用DRL使战机向己方攻击区域自主机动的决策问题.
本文的研究重点是在战机作战机动决策中,基于DRL向攻击区域自主机动的问题.在下步工作中,将在此基础上,利用DRL方法解决战机自主避障、多机协同攻击等复杂战场环境下的决策问题.
| [1] |
RAIVIO T. Capture set computation of an optimally guided missile[J]. Journal of Guidance, Control and Dynamics, 2001, 24(6): 1167. DOI:10.2514/2.4832 |
| [2] |
EHTAMO H, RAIVIO T. On applied nonlinear and bilevel programming or pursuit-evasion games[J]. Journal of Optimization Theory and Applications, 2001, 108(1): 65. DOI:10.1023/A:1026461805159 |
| [3] |
周思羽, 吴文海. 基于随机决策的改进影响图决策方法[J]. 北京理工大学学报, 2013, 33(3): 296. ZHOU Siyu, WU Wenhai. Improved multistage influence diagram maneuvering decision method based on stochastic decision criterions[J]. Transactions of Beijing Institute of Technology, 2013, 33(3): 296. DOI:10.3969/j.issn.1001-0645.2013.03.017 |
| [4] |
KARELAHTI J, KAI V, RAIVIO T, et al. Modelingair combat by a moving horizon influence diagram game[J]. Journal of Guidance Control & Dynamics, 2004, 29(5): 1080. DOI:10.2514/1.17168 |
| [5] |
VIRTANE K, RAIVIO T, HAMALAINEN R P. Modeling pilot's sequential maneuvering decisions by a multistage influence diagram[J]. Journal of Guidance, Control, and Dynamics, 2004, 27(4): 665. DOI:10.2514/1.11167 |
| [6] |
SMITH R E, DIKE B A, MEHRA R K, et al. Classifier systems in combat: two-sided learning of maneuvers for advanced fighter aircraft[J]. Computer Methods in Applied Mechanics and Engineering, 2000, 186(2): 421. DOI:10.1016/S0045-7825(99)00395-3 |
| [7] |
NICHOLAS E, SCHUMACHER D, COHEN K, et al. Genetic fuzzy trees and their application towards autonomous training and control of a squadron of unmanned combat aerial vehicles[J]. Unmanned Systems, 2015, 3(3): 185. DOI:10.1142/S2301385015500120 |
| [8] |
SATHYAN A, NICHOLAS E, COHEN K, et al. An efficient genetic fuzzy approach to UAV swarm routing[J]. Unmanned Systems, 2016, 04(2): 117. DOI:10.1142/S2301385016500011 |
| [9] |
ROGER W S, ALANE B. Neural network models of air combat maneuvering[D]. New Mexico: New Mexico State University, 1992
|
| [10] |
HORIE K, CONWAY B A. Optimal fighter pursuit-evasion maneuvers found via two-sided optimization[J]. Journal of Guidance, Control and Dynamics, 2006, 29(1): 105. DOI:10.2514/1.3960 |
| [11] |
VIRTANEN K, KARELAHTI J, RAIVIO T. Modeling air combat by a moving horizon influence diagram game[J]. Journal of Guidance, Control, and Dynamics, 2006, 29(5): 1080. DOI:10.2514/1.17168 |
| [12] |
NICHOLAS E, COHEN K, SCHUMACHER D. Collaborative tasking of UAVs using a genetic fuzzy approach[C]//51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition. Grapevine: AIAA, 2013: 1032. DOI: 10.2514/6.2013-1032
|
| [13] |
SILVER D, HUANG A, MADDISON C, et al. Mastering the game of Go with deep neural networks and tree search[J]. Nature, 2016, 529(7587): 484. DOI:10.1038/nature16961 |
| [14] |
傅莉, 谢福怀, 孟光磊, 等. 基于滚动时域的无人机空战决策专家系统[J]. 北京航空航天大学学报, 2015, 41(11): 1994. FU Li, XIE Fuhuai, MENG Guanglei, et al. An UAV air-combat decision expert system based on receding horizon control[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(11): 1994. DOI:10.13700/j.bh.1001-5965.2014.0726 |
| [15] |
曹晖, 王瑾, 李寰宇, 等. 基于改进粒子群算法的对地攻击最优航迹规划[J]. 空军工程大学学报(自然科学版), 2013, 14(1): 2. CAO Hui, WANG Jin, LI Huanyu, et al. Air to ground attack route planning by using method of PSO[J]. Journal of Air Force Engineering University (Natural Science Edition), 2013, 14(1): 2. DOI:10.3969/j.issn.1009-3516,2013.01.005 |
| [16] |
陈侠, 魏晓明, 徐光延. 多无人机模糊态势的分布式协同空战决策[J]. 上海交通大学学报, 2014, 48(07): 907. CHEN Xia, WEI Xiaoming, XU Guangyan. Distributed cooperative air combat decision making for fuzzy situation of multi-UAV[J]. Journal of Shanghai Jiaotong University, 2014, 48(07): 907. DOI:10.16183/j.cnki.jsjtu.2014.07.003 |
| [17] |
马耀飞, 龚光红, 彭晓源. 基于强化学习的航空兵认知行为模型[J]. 北京航空航天大学学报, 2010, 36(4): 379. MA Yaofei, GONG Guanghong, PENG Xiaoyuan. Cognition behavior model for air combat based on reinforcement learning[J]. Journal of Beijing University of Aeronautics and Astronautics, 2010, 36(4): 379. DOI:10.13700/j.bh.1001-5965.2010.04.021 |
| [18] |
陈廷楠. 飞机飞行性能品质与控制[M]. 1版. 北京: 国防工业出版社, 2007: 20. CHEN Tingnan. Aircraft flight performance quality and control[M]. 1st ed. Beijing: National Defense Industry Press, 2007: 20. |
| [19] |
FRED A, GIRO C, MICHAEL F. Automated maneuvering decisions for air to air combat: AIAA PAPER 87-2393[R]. Washington, D.C.: nasa, 1987
|
| [20] |
SUTTON R S, BARTO A G. Reinforcement learning: An introduction[M]. 1st ed. Cambridge: MIT Press, 1998: 37.
|
| [21] |
左家亮, 杨任农, 张滢, 等. 基于启发式强化学习的空战机动智能决策[J]. 航空学报, 2017, 38(10): 212. ZUO Jialiang, YANG Rennong, ZHANG Ying, et al. Intelligent decision-making in air combat maneuvering based on heuristic reinforcement learning[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(10): 212. |
| [22] |
ARULKUMARAN K, DEISENROTH M P, BRUNDAGE M, et al. A brief survey of deep reinforcement learning[J/OL]. (2017-08-19)[2019-03-20]. https://arxiv.org/abs/1708.05866
|
| [23] |
MNIH V, KAVUKCUOGLU K, SILVER D, et al. Playing Atari with deep reinforcement learning[C/OL]. (2013-12-19)[2019-03-20]. https://arxiv.org/abs/1312.5602
|
| [24] |
LILLICRAP T P, HUNT J J, PRITZEL A, et al. Continuous control with deep reinforcement learning[J/OL]. (2015-09-9)[2019-03-20].https://arxiv.org/abs/1509.02971
|
| [25] |
LECUN Y, BENGIO Y, HINTON G. Deep learning[J]. Nature, 2015, 521(7553): 436. DOI:10.1038/nature14539 |
 2019, Vol. 51
2019, Vol. 51


