近年来兴起的压缩感知理论[1-2],能以远低于奈奎斯特采样定理的测量数据实现对原始信号的重构,在基于直达波的目标波达方向估计[3-4]中表现出良好的性能.但浅海波导中由于水体环境的不稳定及海面、海底边界的存在,多途效应严重[5],极易导致目标空间的稀疏性降低甚至遭到破坏,基于压缩感知的DOA估计性能将严重下降.
时间反转理论[6-7]是近年来信号检测领域广泛研究的课题,其将“海洋自身”与信号处理相结合,利用信道的多途特性实现目标的自适应空时聚焦.基于此,近年来逐渐有学者将其应用在阵列信号处理,但自身都有不足.其中,付永庆等[8-10]通过对时反聚焦点的位置搜索实现了通信电台的被动测向,但计算复杂度较高;Foroozan等[11-13]分析了时反在MIMO雷达参数估计中的应用,但并未考虑探测信号与目标之间的多途效应;杨伏洲等[14]建立了基于被动时反的非均匀线列阵模型,但对模拟信道要求较高;荆海霞等[15]分析了基于主动时反Capon算法的水下DOA估计,但并未分析水下目标的空间稀疏性.
综上,本文提出了一种基于时反-压缩感知的浅海目标DOA估计算法,建立了基于主动时反理论的浅海目标DOA估计模型,实现了多径对信道稀疏性干扰的抑制,并通过仿真验证了该算法的优越性.
1 基于CS的浅海目标DOA估计水下环境的复杂性极大的限制了声信号有效、稳定的传输,对常规阵列信号处理方法产生了严重的影响.而基于稀疏信号的压缩感知理论可以从少量数据中高概率的恢复原信号,在小快拍、低信噪比环境的水声信号处理中展现出独有的优越性.压缩感知对信号的稀疏性有一定的要求,但实际的海洋环境是复杂多变的,尤其是存在上下边界的浅海波导,不同的介质、声速和温度,以及环境中存在的多种散射体,均会引起不同的折射反射,导致复杂的多径声传播,进而产生多个不同于原始目标的虚拟位置,对信道稀疏性产生干扰,影响了浅海目标的DOA估计性能.
1.1 常规浅海多径DOA估计模型首先建立多径环境下的目标DOA估计模型.设某一均匀浅海波导如图 1所示.假定波导中介质密度ρ、声速c均为常数.波导中有一均匀垂直收发合置阵(source-receive array,SRA)和目标R,其中阵列阵元数为P,阵元间距为d.各阵元与目标间受多途效应的影响,均为多途信道.根据射线理论[16],阵元接收信号可表示为不同入射角度(这里仅考虑俯仰角)信号的叠加.图中以其中三条传播路径为例,其对应的入射角分别为θ1,θ2,θ3.

|
图 1 均匀浅海多径DOA估计模型 Fig. 1 Multipath DOA estimation model for homogeneous shallow water |
假定该浅海信道的多径数目为N,则阵元j与目标R之间的信道传输函数为
| $ h_{j}(t)=\sum\limits_{n=1}^{N} c_{j n} \delta\left(t-\tau_{j n}\right). $ | (1) |
式中cjn、τjn为第j个阵元与目标R之间第n条传播路径的幅度衰减和传播时延.由于目标经过相同路径n到达各个阵元的幅度衰减相差甚微,可认为该幅度衰减与阵元无关,即:cjn=cn.所以,信道传输函数可以改写为
| $ h_{j}(t)=\sum\limits_{n=1}^{N} c_{n} \delta\left(t-\tau_{j n}\right). $ | (2) |
令SRA的P个阵元发射如下探测信号
| $f(t)=s(t) \mathrm{e}^{\mathrm{j} \omega_{\mathrm{c}} t}. $ | (3) |
式中s(t)、ωc为基带信号和载波发射频率.
则目标散射信号为
| $ \begin{aligned} X(t) &=\sum\limits_{j=1}^{P} f(t) \otimes h_{j}(t) \\ &=\sum\limits_{j=1}^{P} \sum\limits_{n=1}^{N} c_{n} f\left(t-\tau_{j n}\right) .\end{aligned} $ | (4) |
式中⊗为卷积运算符.
目标散射信号经过信道传输到达接收阵列,则第k个阵元的接收信号为
| $ \begin{array}{*{20}{l}} {{y_k}(t) = X(t) \otimes {h_k}(t) + {n_k}(t) = }\\ {\sum\limits_{m = 1}^M {{c_m}} X\left( {t - {\tau _{km}}} \right) + {n_k}(t) = }\\ {\sum\limits_{m = 1}^M {\sum\limits_{j = 1}^P {\sum\limits_{n = 1}^N {{c_m}} } } {c_n}f\left( {t - {\tau _{jn}} - {\tau _{km}}} \right) + {n_k}(t)}. \end{array} $ | (5) |
考虑阵列接收信号为远场窄带信号,上式可改写为
| $ \begin{array}{l}{y_{k}(t) \approx \sum\limits_{m=1}^{M} \sum\limits_{j=1}^{P} \sum\limits_{n=1}^{N} c_{m} c_{n} s(t) \mathrm{e}^{\mathrm{j} \omega_{\mathrm{c}}\left(t-\tau_{j n}-\tau_{k m}\right)}+n_{k}(t)=} \\ {\sum\limits_{m=1}^{M} \sum\limits_{j=1}^{P} \sum\limits_{n=1}^{N} c_{m} c_{n} s(t) \mathrm{e}^{\mathrm{j} \omega_{\mathrm{c}}\left(t-\tau_{j n}-\tau_{1 m}-\Delta \tau_{k m}\right)}+n_{k}(t)=} \\ {\sum\limits_{m=1}^{M} c_{m} \mathrm{e}^{-\mathrm{j} \omega_{\mathrm{c}} \tau_{1m}} \cdot \mathrm{e}^{-\mathrm{j} \omega_\text{c} \Delta \tau_{k m}} \sum\limits_{j=1}^{P} \sum\limits_{n=1}^{N} c_{n} \mathrm{e}^{-\mathrm{j} \omega_\text{c} \tau_{j n}} \cdot f(t)+n_{k}(t)}.\end{array} $ | (6) |
式中:τ1m为目标经过第m条路径到达阵元1的参考时延,Δτkm为相比于参考时延,目标经第m条路径到达阵元k的相对时延.
所以矢量形式的阵列接收信号为
| $ \boldsymbol{Y}(t)=\boldsymbol{A} \boldsymbol{C B} \sum\limits_{j=1}^{P} \boldsymbol{D}_{j} \boldsymbol{F}(t)+\boldsymbol{N}(t). $ | (7) |
式中:A = [a(θ1) a(θ2) … a(θM)]表示阵列接收信号的阵列流型矩阵,如式(8)所示;C=diag[c1 c2 … cM]表示各路径的幅度衰减矩阵;B=[e-jωcτ11 e-jωcτ12 … e-jωcτ1M]T表示各路径到达参考阵列的时延矩阵;Dj=A(j, :) CB第j个阵元的发射信号到达目标处所通过的信道传输矩阵;F(t)=s(t)ejωct表示发射信号矩阵;N(t)=[n1(t)n2(t)…nP(t)]T表示噪声矩阵.
| $ \boldsymbol{A}=\left[\begin{array}{cccc}{\mathrm{e}^{-\mathrm{j} \omega_{\mathrm{c}} \Delta \tau_{11}}} & {\mathrm{e}^{-\mathrm{j} \omega_{\mathrm{c}} \Delta \tau_{12}}} & {\cdots} & {\mathrm{e}^{-\mathrm{j} \omega_{\mathrm{c}} \Delta \tau_{1 M}}} \\ {\mathrm{e}^{-\mathrm{j} \omega_{\mathrm{c}} \Delta \tau_{21}}} & {\mathrm{e}^{-\mathrm{j} \omega_{\mathrm{c}} \Delta \tau_{22}}} & {\cdots} & {\mathrm{e}^{-\mathrm{j} \omega_{\mathrm{c}} \Delta \tau_{2 M}}} \\ {\vdots} & {\vdots} & {\vdots} & {\vdots} \\ {\mathrm{e}^{-\mathrm{j} \omega_{\mathrm{c}} \Delta \tau_{P 1}}} & {\mathrm{e}^{-\mathrm{j} \omega_\text{c} \Delta \tau_{P 2}}} & {\cdots} & {\mathrm{e}^{-\mathrm{j} \omega_{\mathrm{c}} \Delta \tau_{P M}}}\end{array}\right]. $ | (8) |
压缩感知是指利用信号在某个变换域上的稀疏性,在采样的同时对数据进行压缩,最后通过重构算法从少量的观测数据中恢复出原始信号.可从数学的角度描述如下:
假设空间中存在的某一维离散时间信号x = [x1 x2 … xN]T可由式(9)表示,则称信号x是稀疏的.
| $ \boldsymbol{x}=\sum\limits_{i=1}^{N} \boldsymbol{\psi}_{i} \boldsymbol{\alpha}_{i}=\boldsymbol{\psi} \boldsymbol{\alpha}. $ | (9) |
式中:ψ为基向量
采用满足一定条件的某一测量矩阵Φ∈RM×N(M≪N)对信号进行“感知”,可以得到观测信号
| $\boldsymbol{ y}=\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} \boldsymbol{ x}. $ | (10) |
式中y是M ×1维的观测向量.
将式带入式可得
| $ \boldsymbol{y}=\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} \boldsymbol{x}=\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} \boldsymbol{\psi} \boldsymbol{\alpha}=\mathit{\boldsymbol{ \boldsymbol{\varTheta} }} \boldsymbol{\alpha}. $ | (11) |
式中Θ = Φψ为M×N维矩阵,是测量矩阵与稀疏表示矩阵的乘积,称为感知矩阵.
E.Candes等[1-2]证明,如果信号α稀疏,且感知矩阵Θ满足任意2K列都是线性无关的条件,则可以通过一定重构算法求解α.
在压缩感知框架下进行浅海目标的DOA估计时,可将声呐感知的二维平面离散为L个方位角,入射信号即为有M(L≫M)个非零项的空域稀疏信号,将对应的阵列流型矩阵作为测量矩阵即可实现对稀疏信号的压缩采样.所以基于压缩感知的DOA估计实际是对空域稀疏信号的重构,通过所重构稀疏信号中非零元素的位置与入射角度{θ1 θ2 … θL}的一一对应关系可确定空间目标的角度信息.
感知矩阵选取扩展后的阵列流型矩阵A(L)=[a(θ1) a(θ2) … a(θL)],则阵列接收信号可以表示为
| $ \boldsymbol{Y}(t)=\boldsymbol{A}^{(L)} \boldsymbol{S}^{(L)}(t)+N(t). $ | (12) |
式中:
重构的空间稀疏信号S(L)(t)可以由下式得到
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{\widehat S}}^{(L)}} = {\mathop{\rm argmin}\nolimits} {\left\| {{\mathit{\boldsymbol{S}}^{(L)}}} \right\|_0};\\ \ \ s.t\ \ {\left\| {\mathit{\boldsymbol{Y}} - {\mathit{\boldsymbol{A}}^{({\rm{L}})}}{\mathit{\boldsymbol{S}}^{(L)}}} \right\|_2} \le \sigma. \end{array} \right. $ | (13) |
式中:‖S(L)‖0为S(L)的l0范数,‖Y-A(L)S(L)‖2为Y-A(L)S(L)的l2范数,σ为可能的噪声水平估计.
2 基于TR-CS的浅海目标DOA估计 2.1 时反理论的空时聚焦特性时间反转理论是针对声波在不均匀介质中的传播失真提出的,能够在介质先验信息未知的条件下实现对海洋中多途效应的补偿.其特有的空时聚焦特性由Fink等[17]通过数值理论分析首次验证,并经过了Kuperman等的多次浅海实验考证.图 2给出了时反处理的示意图.

|
图 2 时反处理示意 Fig. 2 Schematic diagram of time reversal processing |
可以看出,时反处理分为前向传播和后向传播两个阶段.首先,声波由于海面和海底的反射,经由3条前向传播路径以不同的传播时延先后到达阵列.其次,对接收信号做时间反转处理,遵循“先到后发,后到先发”的原则,阵元首先沿着远的路径发射最后一个到达波,再沿着近的路径发射第2个到达波,最后发射第一个到达波.由于波在传播过程中具有互易性及时反不变性,3条后向传播路径将会同时到达初始声源处,并且相干叠加,形成聚焦点.目标处的到达信号相当于初始发射信号的时间反转形式.
设声源发射信号为x(t),前向传播的信道冲激响应函数为h1(t),后向传播的信道冲激响应函数为h2(t),先忽略本地噪声的影响,则阵列接收信号为
| $ y(t)=x(t) \otimes h_{1}(t). $ | (14) |
对接收信号做时间反转处理,则后向传播信道的输出为
| $ z(t)=x(-t) \otimes h_{1}(-t) \otimes h_{2}(t). $ | (15) |
当前后向传播信道相同时,即h1(t)=h2(t),上式可改写为
| $ z(t)=x(-t) \otimes h_{1}(-t) \otimes h_{1}(t). $ | (16) |
所以时间反转信道为
| $h_{\mathrm{TR}}(t)=h_{1}(-t) \otimes h_{1}(t). $ | (17) |
可以看出,时反信道为信道冲激函数的自相关函数,在t=0时可取得主峰峰值,此时信号在目标处形成空时聚焦,为
| $ z(t)=x(-t) \otimes R_{h}(0). $ | (18) |
在t不等于0的时刻或信道不匹配时,其值远远小于聚焦点强度.
2.2 基于时反理论的多径DOA估计模型根据时反理论的空时聚焦特性,可以将浅海环境下的接收信号做时间反转处理,并再次送入信道,此时信号在目标处将形成聚焦点,目标信号的增益得以提高,多途效应也得到抑制.
令二次发射信号与首次发射的信号功率相同,取能量归一化系数
| $ g_{k}=\sqrt{\left(\|f(t)\|^{2}\right) /\left(\left\|y_{k}(t)\right\|^{2}\right)}. $ | (19) |
所以目标的二次散射信号为:
| $Z(t)=\sum\limits_{k=1}^{P} g_{k} y_{k}(-t) \otimes h_{k}^{\prime}(t). $ | (20) |
假设信道环境理想,声场满足时不变性和互易性,即h′k(t)=hk(t),则此时多径信号经过时反处理后同时到达目标处,并相干叠加,在目标处形成空时聚焦,即
| $ Z(t)=\sum\limits_{k=1}^{P} g_{k} \sum\limits_{m=1}^{M} c_{m} y_{k}(-t) \mathrm{e}^{j \omega_\text{c} \tau_{k m}}. $ | (21) |
所以,阵列第l个阵元的接收信号为
| $\begin{array}{l}{\quad r_{t}(t)=Z(t) \otimes h_{t}(t)+\zeta_{t}(t)=} \\ {\sum\limits_{m=1}^{M} c_{m} Z\left(t-\tau_{m}\right)+\zeta_{l}(t)=} \\ {\sum\limits_{m=1}^{M} c_{m} \mathrm{e}^{\mathrm{j} \omega_\text{c} \tau _{m1}} \mathrm{e}^{\text{j} \omega_\text{c} \Delta \tau _{ml}} \sum\limits_{k=1}^{P} g_{k} \sum\limits_{m=1}^{M} c_{m} \mathrm{e}^{\mathrm{j} \omega_\text{c} \tau_{km}} y_{k}(-t)+\zeta_{1}(t)}.\end{array} $ | (22) |
矢量形式的全部阵元的二次接收信号为
| $ \boldsymbol{R}(t)=\boldsymbol{A}^{*} \boldsymbol{C B}^{*} \sum\limits_{k=1}^{P} g_{k} \boldsymbol{D}_{k}^{*} y_{k}(-t)+\boldsymbol{\zeta}(t). $ | (23) |
式中:Dk*= A*(k, :) C B*为阵元k发送的时反信号的时延补偿矩阵,*为共轭,ζ(t)=[ζl(t) ζ2(t) … ζP(t)]T 为二次接收噪声矩阵.
2.3 基于TR-CS的浅海目标DOA估计根据式所示,对时反处理后的二次接收信号做基于压缩感知的DOA估计,感知矩阵选取A*(L)=[a*(θ1) a*(θ2) … a*(θL)],则阵列接收信号为
| $ \boldsymbol{R}(t)=\boldsymbol{A}^{*(L)} \boldsymbol{S}_{\mathrm{tr}}^{(L)}+\boldsymbol{\zeta}(t). $ | (24) |
式中:
所以,重构的空间稀疏信号Str(L)(t)可以由下式得到
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\widehat S}}_{{\rm{tr}}}^{(L)} = {\mathop{\rm argmin}\nolimits} {\left\| {\mathit{\boldsymbol{S}}_{{\rm{tr}}}^{(L)}} \right\|_0}, \\ s.t\ \ {\rm{ }}{\left\| {\mathit{\boldsymbol{R}} - {\mathit{\boldsymbol{A}}^{*(L)}}\mathit{\boldsymbol{S}}_{{\rm{tr}}}^{(L)}} \right\|_2} \le \sigma. \end{array} \right. $ | (25) |
式中:‖Str(L)‖0为Str(L)的l0范数,‖R-A*(L)Str(L)‖2为R-A*(L)Str(L)的l2范数,σ为可能的噪声水平估计.
本文在此选取OMP算法进行空间信号的稀疏重构.
相对于常规浅海多径环境中基于压缩感知的目标DOA估计,增加的时反处理步骤利用了多径这一特征,将多径信号聚焦于目标处,相当于在目标来波方向上实现了波束形成,增强了真实目标处的散射能量,实现了接收信号能量的重新分配,提高了接收信号的稀疏性,增强了该DOA估计方法在复杂浅海环境中的适应性及估计性能.
2.4 TR-CS算法的计算量分析计算量是衡量阵列测向方法性能的一项重要指标,通常以算法所需的复数乘法次数来评价.标准的基于压缩感知的DOA估计算法的计算量主要包括相关处理和最小二乘求解,所以总的计算复杂度为O{[KNs+K(K+1)/2]PT},式中K,Ns,P,T分别代表入射信号的稀疏度、空间角度网格划分的方位角点数、阵元数以及快拍数.对于本文所提出的TR-CS算法,运行时间还包括了阵列对首次接收信号的时反处理及再次的信道传输,尽管相比标准CS算法有所增加,但相对于本文算法对多途效应的抑制及性能的提高,这一计算量的增加在可接受范围内.
3 仿真研究 3.1 参数设置利用bellhop仿真工具箱建立图 1所示的均匀等声速(Pekeris)浅海波导环境.具体参数设置如下:浅海深度为200 m,其中传播声速c1=1 500 m/s,密度ρ1=1.0 g/cm3;海底声速为2 000 m/s,其中密度ρ2=1.8 g/cm3;SRA为阵元数P=8的垂直均匀阵列,阵元间距为λ/2,其中距离海面最近的阵元位于水深70 m处;目标位于距离海面130 m的水深处,且与阵元水平相距1 km;假设阵列发射的探测信号为1 kHz频率的CW信号,快拍数为10.
选取仿真模型中的部分路径信息建立DOA估计模型,具体路径具体参数如表 1和表 2所示:
| 表 1 3条多径传播信道参数 Tab. 1 Parameters of three multipath propagation channels |
| 表 2 5条多径传播信道参数 Tab. 2 Parameters of five multipath propagation channels |
其中,多径1和多径2分别表示经由海面或海底一次反射的多径信号,多径3与多径4分别表示经由海底和海面各一次反射的多径信号.本次仿真以3条多径传播信道表示仅存在海面或海底一次反射的浅海环境,以5条多径传播信道表示存在两次反射的浅海环境,较3条多径环境更为复杂.
由于实际浅海环境的复杂性,具体路径数需根据具体环境再做分析.本次仿真选取的路径参数仅针对浅海环境的一般路径特征做概括描述,可验证本文算法在浅海环境中的普遍适用性.
假设本文所提TR-CS算法与传统CS算法仿真环境一致,即:时反信号的发射功率与首次发射信号的功率相同,且阵列二次接收信号引入与首次接收信号相同的噪声.
3.2 评价指标本次试验均基于1 000次蒙特卡洛仿真,以均方根误差(RMSE)与信噪比(SNR)的关系曲线来表示算法的DOA估计性能,其定义分别如下:
| $ R_{\mathrm{RMSE}}=\frac{1}{I} \sum\limits_{i=1}^{I} \sqrt{\frac{1}{J} \sum\limits_{j=1}^{J}\left(\hat{\theta}_{i j}-\theta_{i}\right)^{2}}. $ | (26) |
| $R_{\mathrm{sn}}=\frac{\sum\limits_{i=1}^{N} \sum\limits_{j=1}^{P} E\left\{\left|s_{i j}(t)\right|^{2}\right\}}{\sum\limits_{i=1}^{N} \sum\limits_{j=1}^{P} E\left\{\left|n_{i j}(t)\right|^{2}\right\}}. $ | (27) |
式中:I为信号源总个数,J为蒙特卡洛实验次数,θij为第i个信号源经第j次蒙特卡洛实验得到的估计角度,θi为第i个信号源的真实角度,N为快拍数,P为阵元个数,sij为第j个阵元接收的第i个快拍的信号,nij为第j个阵元接收第i个快拍信号时引入的信道噪声.
3.3 实验分析实验一:仿真对比多途环境下TR-CS算法与CS算法的DOA估计性能
图 3表示不同多径环境下传统CS算法[18]的DOA估计性能.可以看出,文献[18]中基于OMP的目标DOA估计算法在信噪比低于0 dB时,其性能随着信噪比的降低明显下降,所以传统CS算法在一定的低信噪比下并没有良好的性能.并且,相比仅存在直达波的理想环境,多径环境下目标DOA估计的RMSE明显增加,并且随着多径数目的增多,RMSE的值更大.这表明浅海环境中的多途效应对目标的DOA估计产生了严重影响,使得其性能明显下降.

|
图 3 不同多径环境下CS算法的DOA估计RMSE分析 Fig. 3 RMSE of DOA estimation for CS algorithm in different multipath environments |
图 4表示不同多径环境下TR-CS算法与CS算法的DOA估计性能比较.其中,图 4(a)表示直达波环境下的性能分析,可以看出,直达波环境下两种算法的RMSE极为相近,TR-CS算法并没有体现出优越性;图 4(b)和图 4(c)分别表示3条多径和5条多径环境下的性能分析,可以看出,在多途效应严重的浅海环境中,TR-CS算法的RMSE明显低于CS算法,在低信噪比时RMSE的下降程度更为明显,且5条多径环境下性能提高更为显著.所以本文所提TR-CS算法适用于多途效应严重的浅海环境.

|
图 4 不同多径环境下TR-CS算法与CS算法的DOA估计RMSE分析 Fig. 4 RMSE of DOA estimation for TR-CS algorithm and CS algorithm in different multipath environments |
实验二:仿真对比多途环境下信噪比为-5 dB时TR-CS算法与CS算法的DOA估计误差分布
定义第j次蒙特卡洛实验对第i个信号源的估计误差为
| $ \left|\hat \theta _{i j}-\theta_{i}\right|. $ | (28) |
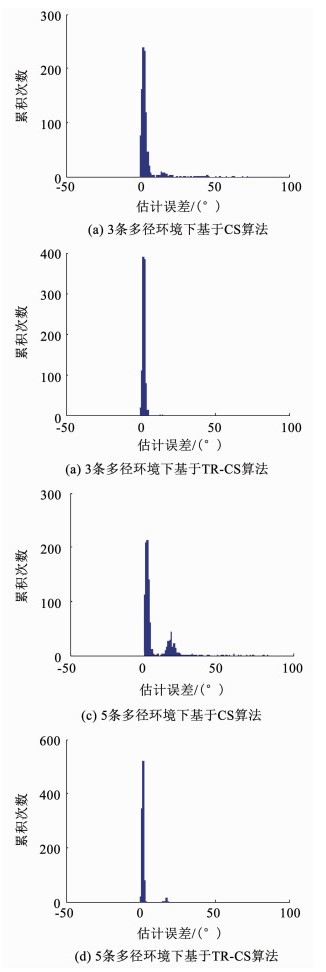
则多途环境下的误差分布如图 5所示,其中图 5(a)、(b)为3条多径环境下的误差分布,图 5(c)、(d)为5条多径环境下的误差分布.可以看出,多径环境下传统CS算法的误差大多在0°~50°以内,分布范围较为分散,并且5条多径下的误差在20°附近仍有较高峰值,分布范围明显大于3条多径环境.而改进后的TR-CS算法误差明显集中在0°附近,分布较为集中,峰值尖锐.这进一步证明了本文所提TR-CS算法减小了多途效应对DOA估计所造成的误差,更能体现出TR-CS算法的优越性.
|
图 5 不同多径环境下TR-CS算法与CS算法的DOA估计误差分布 Fig. 5 Error distribution of DOA estimation for TR-CS and CS in different multipath environments |
表 3为基于上述仿真条件不变的情况下,3条多径和5条多径环境下传统CS算法与本文所提TR-CS算法的归一化旁瓣幅度Amp_cs、Amp_trcs及其差值Differ=Amp_cs-Amp_trcs的分析.可以看出,5条多径环境的旁瓣幅度明显大于3条多径,表明多途效应干扰了信道的稀疏性.而算法改进前后的旁瓣幅度差值为正,则证明本文所提的TR-CS算法明显抑制了杂波幅度,提高了信道的稀疏性,改善了目标的DOA估计性能.
| 表 3 时反处理前后不同多径环境下的旁瓣幅度差异 Tab. 3 Sidelobe amplitude difference in different multipath environments after TR |
实验三:仿真对比不同快拍数下TR-CS算法和CS算法的性能
图 6表示在复杂度为3条多径的浅海环境中,本文所提TR-CS算法与传统CS算法在快拍数分别为10、20、50、100时的DOA估计性能分析.可以看出,随着快拍数的增加,TR-CS算法与CS算法的估计性能均有所提高,且TR-CS算法性能优于CS算法.随着快拍数的增加,CS算法在低信噪比下的性能逐渐提高.所以,TR-CS算法在低信噪比、少快拍的条件下更能体现其优势.

|
图 6 不同快拍数下TR-CS算法与CS算法的DOA估计RMSE分析 Fig. 6 RMSE of DOA estimation for TR-CS algorithm and CS algorithm under different snapshot numbers |
在上述相同仿真环境下,以运行时间为度量,可以比较本文所提TR-CS算法与传统CS算法的计算量.计算TR-CS算法和CS算法平均每次的运行时间,结果如表 4所示.可以看出,随着快拍数的增加,两类算法的运算时间均逐渐增大,并且在相同快拍数下,TR-CS算法的运行时间均大于CS算法.所以本文所提TR-CS算法是以计算量的增加为代价,实现了对多途效应的抑制,提高了浅海目标的DOA估计性能.
| 表 4 CS算法与TR-CS算法的运行时间比较 Tab. 4 Comparison of running time between CS algorithm and TR-CS algorithm |
| 表 5 时反处理后不同多径环境下的接收信噪比增益 Tab. 5 Receiving in different multipath environments after TR |
实验四:仿真对比多途环境下TR-CS算法与CS算法的接收信噪比增益(GSNR)
表 4为3条多径和5条多径环境下算法改进前后的接收信噪比.可以看出,TR-CS算法相比CS算法,在不同多径环境下的接收信噪比均有提高.其中3条多径环境下提高了4.2 dB,而5条多径环境下提高了6.2 dB,优于三条多径环境2 dB.所以本文所提TR-CS算法由于时反理论的引入,使得信号在目标处的增益提高,阵列信号的接收信噪比也相应提高,这是算法性能改善的重要因素.并且多途效应越严重,本文所提TR-CS算法的优越性越能得到体现.
虽然阵列将时反前的接收信号和噪声一起做了时反处理并再次送入信道,在一定程度上造成了信噪比的损失,但只要时反的聚焦增益足够高,噪声的影响可以忽略不计.
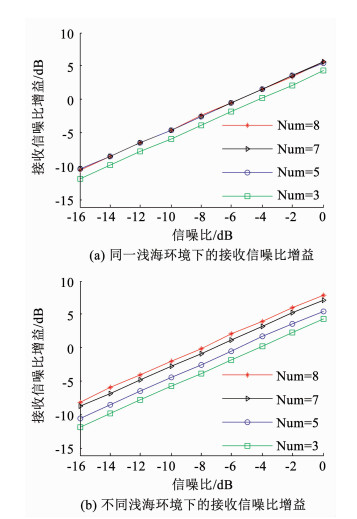
进一步增加多径数目,本文所提TR-CS算法的接收信噪比增益如图 7所示.其中图 7(a)表示同一浅海环境下的增益,图 7(b)表示不同浅海环境下的增益.
|
图 7 接收信噪比与多径数目的关系 Fig. 7 Relationship between received RSN and multipath numbers |
可以看出,同一环境下随着可分析多径数目Num的增加,经过多次反射的信号也被考虑在内.但是由于边界损耗,经过多次反射后的信号幅度极小,其对时反聚焦的贡献可以忽略不计,所以同一环境下本文算法随着多径数目的增加性能趋于平稳.但对于因为环境复杂性提高而引起的多径数目的增加,有效路径数也会相应增加,目标处的聚焦增益将会增强,本文所提算法性能进一步提高.
4 结论本文研究了复杂浅海环境中多径效应对目标DOA估计的影响,结合时间反转理论的空时聚焦特性,提出了一种基于时反-压缩感知的浅海目标DOA估计算法,并通过数值仿真分析了其估计性能.仿真结果表明:在小快拍、低信噪比的条件下,相比于传统基于压缩感知的目标DOA估计理论,本文所提算法利用了时反理论对多途效应的适应性,实现了对多途畸变的修正,使得多径来波信号在目标处聚焦并抑制了杂波的幅度,增加了信道的稀疏性,同时提高了接收信号的信噪比,估计性能明显改善,并且在多途效应越严重的环境中,该算法的性能优势越为突出.
| [1] |
BARANIUK R G, CANDES E, NOWAK R, et al. Compressive sampling[J]. Signal Processing Magazine IEEE, 2008, 25(2): 12. DOI:10.1109/MSP.2008.915557 |
| [2] |
CANDES E. Compressive sampling[C]//International Congress of Mathematics, Madrid, Spain, 2006: 1433. DOI: 10.1109/MSP.2007.914731
|
| [3] |
王永良, 陈辉, 彭应宁, 等.空间谱估计估计理论与算法[M].清华大学出版社, 2004 WANG Yongliang, CHEN Hui, PENG Yingning, et al. The theory and algorithm of Spatial spectrum estimation[M]. Tsinghua University Press, 2004 |
| [4] |
LIAO Bin, HUANG Lei, GUO Chongtao, et al. New approaches to direction-of-arrival estunation with sensor arrays in unknown nonunifonn noise[J]. IEEE Sensors Journal, 2016, 16(24): 982. DOI:10.1109/JSEN.2016.2621057 |
| [5] |
ETTER P C. Underwater acoustic modeling and simulation[M]. Taylor & Francis, 2003
|
| [6] |
KIM J S, SONG H C, KUPERMAN W A. Adaptive time-reversal mirror[J]. Journal of the Acoustical Society of America, 2001, 109(1): 1817. DOI:10.1121/1.1358299 |
| [7] |
HEINEMANN M, LARRAZA A, SMITH K B. Experimental studies of applications of time-reversal acoustics to noncoherent underwater communications[J]. Journal of the Acoustical Society of America, 2003, 113(6): 3111. DOI:10.1121/1.1570832 |
| [8] |
李敬蕊.基于虚拟时反理论的通信电台被动测向方法研究[D].哈尔滨: 哈尔滨工程大学, 2014 LI Jingrui. The research of passive DOA estimation method for communication station based on virtual time reversal theory[D]. Harbin: Harbin Engineering University, 2014 http://cdmd.cnki.com.cn/Article/CDMD-10217-1017245179.htm |
| [9] |
FU Yongqing, LIU Wei, BAI Ruijie, et al. A novel virtual time reversal method for passive direction of arrival estimation[J]. Mathematical Problems in Engineering, 2015, 1. DOI:10.1155/2015/613692 |
| [10] |
田金龙.虚拟时反被动测向辐射源信号的研究与应用[D].哈尔滨: 哈尔滨工程大学, 2017 TIAN Jinlong. The research and application on emitter source signal used in virtual time reversal passive direction finding[D]. Harbin: Harbin Engineering University, 2017 http://cdmd.cnki.com.cn/Article/CDMD-10217-1018081443.htm |
| [11] |
FOROOZAN F, ASIF A. Time reversal direction of arrival estimation with Cramér-Rao bound analysis[C]//2010 IEEE Global Telecommunications Conference. Piscataway: IEEE, 2010: 1. DOI: 10.1109/GLOCOM.2010.5683345
|
| [12] |
FOROOZAN F, ASIF A. Time reversal MIMO radar for angle-Doppler estimation[C]//2012 IEEE Statistical Signal Processing Workshop. Piscataway: IEEE, 2012: 860. DOI: 10.1109/SSP.2012.6319843
|
| [13] |
SAJJADIEH M H S, ASIF A. Compressive sensing time reversal MIMO radar: Joint direction and Doppler frequency estimation[J]. IEEE Signal Processing Letters, 2015, 22(9): 1283. DOI:10.1109/LSP.2015.2396650 |
| [14] |
杨伏洲, 王海燕, 申晓红, 等. 基于时间反转的非均匀线列阵超指向性阵元分布模型[J]. 上海交通大学学报, 2013, 47(12): 1907. YANG Fuzhou, WANG Haiyan, SHEN Xiaohong, et al. Super-directional element distribution model of NLA based on TR[J]. Journal of Shanghai Jiaotong University, 2013, 47(12): 1907. DOI:10.16183/j.cnki.jsjtu.2013.12.016 |
| [15] |
荆海霞, 王海燕, 刘郑国, 等. 基于主动时反的浅海目标DOA估计优化算法[J]. 西北工业大学学报, 2018, 36(2): 270. JING Haixia, WANG Haiyan, LIU Zhengguo, et al. Optimization algorithm for DOA estimation of a shallow sea target based on active time reversal[J]. Journal of Northwestern Polytechnical University, 2018, 36(2): 270. DOI:10.3969/j.issn.1000-2758.2018.02.010 |
| [16] |
JENSEN F B, KUPERMAN W A, PORTER M B, et al. Computational Ocean Acoustics[M]. New York: Springer, 2011.
|
| [17] |
FINK M. An overview of time-reversal coustics[J]. The Journal of the Acoustical Society of America, 2008, 123(5): 3183. DOI:10.1121/1.2933288 |
| [18] |
黄祖镇.基于压缩感知的阵列DOA估计[D].哈尔滨: 哈尔滨工业大学, 2013 HUANG Zuzhen. Array DOA estimation based on compressed sensing[D]. Harbin: Harbin Institute of Technology, 2013 http://cdmd.cnki.com.cn/Article/CDMD-10701-1014325126.htm |
 2019, Vol. 51
2019, Vol. 51


