堆芯稳态核设计软件是反应堆设计的重要组成部分之一,其软件质量影响整个核电站的设计,运行和维护的安全性和经济性.软件验证与确认(Verification & Validation,V&V)是保证软件质量的必经步骤[1].
基准题验证是核电软件测试的主要方法之一,该方法是测试人员运行核电软件执行基准题计算,通过比较计算结果与基准题结果是否吻合,从而判断计算程序是否存在错误[2-3].基准题即为核电软件验证的测试用例,其来源主要有三方面:一是参与国际科研机构研发基准题;二是实验获取或者购买基准题数据,三是电厂实际运行数据.这些数据来源成本都相对较高,且数量较有限.为了确保我国自主化核电软件的质量,需要大量的基准题用于测试.而基准题存在研发成本高,周期长等问题.
为了解决上述问题,利用现有的基准题来生成更多的测试用例,开展基准题衍生技术研究是降低测试成本的研究方向.其中,蜕变测试技术是一种值得借鉴的方法[4-5].蜕变测试是通过验证一组测试用例所对应的输出是否满足特定的关系(蜕变关系)来测试程序的技术,而每一组测试用例包含了已有的测试用例(原始测试用例)和由它们根据蜕变关系构造的新测试用例(衍生测试用例).该技术已经广泛应用于计算机软件测试领域[5].
近年来,已有研究者将蜕变测试技术应用于测试用例生成.在非核电软件领域,例如文献[6]分别利用特殊值和随机值作为原始测试用例生成新的测试用例,进而对测试效果做了比较研究.文献[7]考虑到特殊值用例的不充分性和随机值用例的盲目性,将蜕变测试技术与迭代测试方法相结合,提出了一种迭代生成测试用例的算法.文献[8]将蜕变测试技术与路径分析技术结合,建立3种不同的路径覆盖测试准则,提出相应的测试用例集生成算法,可以避免生成测试用例的盲目性和冗余.文献[9]针对二元蜕变关系,提出2种迭代的蜕变测试算法,上述研究针对特定领域以简单程序为例进行理论研究为主,提出的理论方法是否适用于实际的工程应用程序验证尚待进一步研究.
基于蜕变测试技术的测试用例自动化生成工具研发方面,相关研究者开发相应的蜕变测试工具,比如文献[10]设计的Amsterdam,该工具集成衍生用例的自动化生成;文献[11]提出一种基于蜕变测试的编译器测试技术,实现了一个自动化测试工具Metto.目前文献调研分析来看,基于蜕变测试技术的测试用例自动化生成工具尚不多,处于前期探索阶段.
在核电软件验证测试方面,本文作者将蜕变测试技术应用于一个堆芯燃料元件计算程序验证,进行前期探索研究[12];针对中子扩散程序提出了一种基于基准题的蜕变测试验证方法,并以一维计算程序进行实例验证[13].但是上述研究工作只是提出了基于基准题的蜕变测试验证方法以及基本流程,但是对于基准题如何衍生、如何求解的相关问题没有详细展开论述.由于堆芯核设计程序是与普通的计算机软件不同,具有其特殊性:除了集成大量的数值计算程序之外,程序的输入方式是固定格式的输入卡,其数据来源于基准题,在程序验证时,不同的测试用例对应于不同的输入卡.输入卡中数据涉及堆芯计算的几何构型、材料、模块运算等变量参数.数值程序越复杂,相应的变量越多.若以人工方式来实现测试用例的生成,效率低且容易造成输入出错.而目前基于蜕变测试技术的测试用例生成技术研究尚没有考虑到上述特征.
目前我国核电软件验证技术研究主要依靠自主化,适应于核电软件基准题衍生的自动化工具市面上尚少见.因此,基准题衍生技术研究,以及自动衍生工具的设计与开发对于提高测试效率,降低成本具有实际工程意义.
本文提出一种基准题衍生技术,首先对衍生技术的基本原理进行描述,然后提出基准题衍生技术的基本框架,设计基准题自动衍生算法,实现基准题衍生工具的研发,为证明衍生基准题有效性,并以蒙特利尔大学开发的DONJON程序进行实例展示.
1 基准题衍生技术 1.1 定义定义1 蜕变关系[4].假设程序用来计算函数f(x),x1、x2是x的两次运行值,若x1、x2之间满足关系r时,f(x1)、f(x2)满足关系R,即r(x1, x2)→ R(f(x1), f(x2)),则称MR(r, R)是程序的蜕变关系.
蜕变关系是待测程序的多次测试执行的输入关系与输出关系之间的蕴含式[13-16].比如测试cos(x)函数计算程序,从函数性质cos(x-π)=-cos(x)可得一条蜕变关系,数学表达式为
| $ \begin{aligned} r\left\{x_{1}, x_{2} | x_{2}=x_{1}-\pi\right\} & \rightarrow R\left\{\cos x_{1}, \cos x_{2} | \cos x_{2}=\right.\\ &\left.-\cos x_{1}\right\} .\end{aligned} $ | (1) |
如果程序违背了上述蜕变关系,则该程序有缺陷.再者,如果已知测试用例(x1, T(x1)),依据蜕变关系式计算可得到新的测试用例(x2, T(x2)),可知,蜕变关系既是判断程序计算结果正确与否的重要根据,又是生成新的测试用例的依据.
定义2 原始测试用例/衍生测试用例[17].使用蜕变关系MR(r, R)测试待测程序时,起初给定的测试用例称为原始测试用例;由原始测试用例根据关系r计算出的用例是原始用例基于蜕变关系的衍生测试用例.
以计算cos(x)函数的程序测试为例,展示衍生测试用例原理,如图 1所示.

|
图 1 衍生测试用例原理 Fig. 1 Schematic diagram of derivative test case |
基准题是一类用于核电软件测试的测试用例,类似定义2,给出原始基准题和衍生基准题的定义.
定义3 原始基准题/衍生基准题.设待测程序已有的验证基准题,称为原始基准题.由原始基准题跟据待测程序某条蜕变关系计算得出的基准题,称为衍生基准题.
1.2 基准题衍生技术国际研究机构包括国际原子能组织,西屋,美国自然科学研究院等发布了一系列的核电软件验证基准例题,基准例题数据获取通常需要做多次实验,成本较高,而利用蜕变关系,在已有的一次实验获取的基准题数据基础上,根据蜕变关系的输入关系r和输出关系的R,生成新的基准题数据.显然,实验次数减少,成本降低.
堆芯核设计程序验证时,程序输入采用固定格式的输入卡,一个输入卡对应一个测试用例,其数据来源于基准题,基准题即为验证的测试用例.程序越复杂涉及的参变量越多,基准题衍生越难;再者,核电软件的蜕变关系表达式也涉及多个变量之间的关系,解析这些关系也较繁琐.若按照传统的人工方式生成测试用例,耗时费力效率低, 首先提出一种基准题衍生技术框架,再设计基准题自动衍生算法,并研发和实现出自动衍生工具.
1.2.1 基准题衍生技术框架本文基于蜕变测试技术,提出一种基准题衍生技术框架,主要思想是根据蜕变关系的参变量及关系式,直接对于原始基准题的相关输入和输出参变量进行计算求解,生成用于验证的衍生基准题,将大幅提高测试效率.基准题衍生技术框架关键步骤如下:
1) 分析找出蜕变关系表达式中输入关系变量及输出关系变量,并进行标记.
2) 找出原始基准题中涉及蜕变关系表达式中标记的变量.
3) 根据蜕变关系的输入关系r,输出关系R,计算得到衍生基准题的输入及输出值.
4) 比较原始基准题和衍生基准题的计算结果是否符合蜕变关系式.
5) 如符合,则输出衍生基准题.否则,退出.
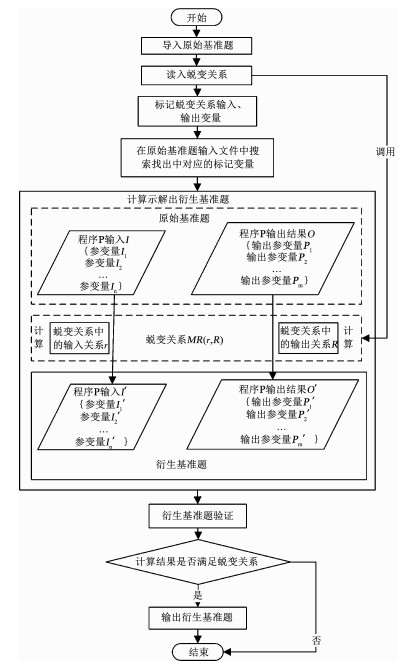
具体流程如图 2所示.
|
图 2 基准题衍生技术框架流程图 Fig. 2 Flow chart of benchmark derivation techniques |
图 2中,假设原始基准题的所有的输入用向量集合I=(I1, I2, …, In),输出结果用向量集合O=(P1, P2, …, Pm),其中I1, I2, …, In为不同的输入参变量,例如,某基准题的输入,I1为堆芯燃料富集度的值,I2为泠却剂的初始温度值等.P1, P2, …, Pn为不同的输出参变量,比如P1为堆芯出口温度的值,P2为堆芯压力值等.
1.2.2 基准题自动衍生算法该算法目的是实现从原始基准题输入卡自动生成衍生基准题输入卡,直接可被待测程序调用(见图 3).

|
图 3 原始基准题输入卡与衍生基准题输入卡 Fig. 3 Input card for original benchmark and input card for derivative benchmark |
基准题自动衍生算法1,如下.
算法1 基准题自动衍生算法
输入:原始基准题输入卡test_x2m.txt,选择蜕变关系
输出:衍生基准题输出卡test2_x2m.txt
步骤:
1) 初始化
var test_x2m=read("test_x2m.txt"); //读取原始基准题test_x2m.txt
var mt1=read("y=ax+b"); //读取蜕变关系y=ax+b
List<string>listX2m=test_x2m.Readline(); //将test_x2m.txt的每行保存到listX2m的每一项
List<string>listMt1 //将已有的蜕变关系保存到listMt1
List<string>list2X2m //将衍生结果的每一行保存到list2X2m
2) 获取蜕变关系的输入
foreach(var p in listMt1) //遍历listMt1找出对应所选蜕变关系
if(p.Name =="y=ax+b"))
Read("y=ax+b"); //解析蜕变关系式
var a = read(); //输入参数a变量
var b = read(); //输入参数b变量
3) 根据蜕变关系表达式计算得到衍生基准题.
foreach(var p in listX2m) //遍历listX2m找出关键字,映射map中对应的关系式
{
var line=p;
foreach(var t in map) //遍历Map
{
if(p.Contains(t.Key))
{
list=p.Split(" ");
var index=list.IndexOf(t.Key);
list[index+1]=t.Value.Caculate
(list[index+1]); //根据y=ax+b蜕变关系计算
list[index+2]=t.Value.Caculate
(list[index+2]); //根据y=ax+b蜕变关系计算
line=list.toString();
}
}
list2X2m.Add(line); //保存计算结果
}
4) 输出衍生基准题
write(list2X2m)=>test2_x2m.txt //将list2X2m写入文件
算法1的主要步骤:1)初始化.原始基准输入卡和蜕变关系的读取.为了便于说明算法思想,这里以一个线性的蜕变关系为例.2)解析蜕变关系式及参数设置.若生成多个衍生基准题,则可以采用随机方法生成参数组.3)求解衍生基准题.从原始基准题输入卡中标记出蜕变关系涉及的变量,然后根据蜕变关系式进行求解,保存计算结果.4)输出衍生基准题.
1.2.3 基准题自动衍生工具设计与实现考虑到核电软件测试的实际需求,根据基准题衍生技术框架,结合基准题自动衍生算法,为了提升基准题衍生效率,设计一款基准题自动衍生工具(Benchmark Driver, BD).该工具使用Java语言在Windows 7环境下编写完成,可实现原始基准题和蜕变关系的导入和读取,并自动生成衍生基准题,且衍生基准题是可以直接被程序计算调用,然后通过可对比原始基准题和衍生基准题的计算结果,判断是否满足蜕变关系式.最后通过测试结果分析,可生成结果分析报表.
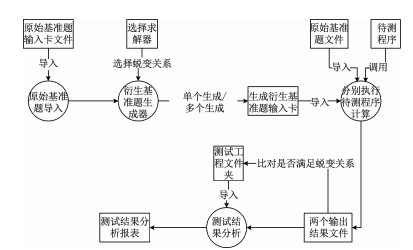
该工具的主要业务功能包括:原始基准题导入模块、衍生基准题生成器模块、执行蜕变测试模块、测试结果分析模块.工具的功能结构如下图 4所示.
|
图 4 基准题自动衍生工具功能结构 Fig. 4 Functional structure diagram of Benchmark Driver |
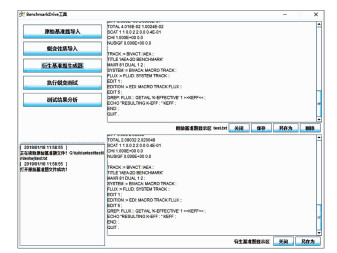
基准题衍生工具(Benchmark Driver)界面如图 5所示.
|
图 5 基准题衍生工具 Fig. 5 Benchmark derivation techniques tool |
为验证本文提出的基准题衍生技术及算法,实验以堆芯稳态设计程序验证的二维、三维原始基准例题为例.其中,二维基准题为国际原子能机构(IAEA)发布的二维双群压水堆问题基准题(IAEA_2D_2G基准题,详细描述见文献[18-19]),三维基准题为加拿大原子能科研机构发布的三维XYZ几何双群重水堆问题(PHWR_3D_2G基准题,具体描述见文献[20]),这两类基准题是堆芯核设计程序的数值验证常用基准题.
为了检验衍生基准题的有效性,因此需要验证其是否满足数学推导的蜕变关系式,为此选取了加拿大蒙特利尔理工大学开发的一款进行全堆芯扩散计算的核设计程序—DONJON程序[21].由于此程序已经历多年工程验证,具有较好的易用性以及良好的计算性能,计算结果精度高,常用作其他新开发的核设计软件的对标程序.
2.1 堆芯稳态核设计程序的蜕变关系从堆芯稳态核设计程序求解的多群中子扩散方程中导出蜕变关系.方程模型为
| $ \begin{array}{l} - \nabla {D_{\rm{g}}}(r)\nabla {\varphi _{\rm{g}}}(r) + {\sum _{{\rm{t}}, {\rm{g}}}}(r)\varphi (r) - \\ \sum\limits_{{\rm{g}} = 1}^G {{\Sigma _{{\rm{g'}} \to {\rm{g}}}}} {\varphi _{{\rm{g'}}}}(r) = \frac{1}{{{k_{{\rm{eff}}}}}}{\chi _{\rm{g}}}(r)\sum\limits_{{\rm{g'}} = 1}^G {{{\left( {\upsilon {\sum _{\rm{f}}}} \right)}_{{\rm{g'}}}}{\varphi _{{\rm{g'}}}}(r), } \\ g = 1,2, \cdots ,G. \end{array} $ | (2) |
式中:Dg为g群扩散系数;∑t, g为g群宏观总截面;∑g′→g为g′群向g群转移截面;χg为g群裂变中子谱;υ为平均裂变中子数;∑f, g′为g′群宏观裂变截面,G为总能群数目.keff为有效增殖因子.
根据方程(2)的线性齐次性,文献[6]通过数学推导,得到该方程的一条蜕变关系,如下式
| $ \ \ \ \ \ \ \ \ \ \ \ MR(r, R) : r\left\{\boldsymbol{M}_{1}, \boldsymbol{F}_{1}, \boldsymbol{M}_{2}, \boldsymbol{F}_{2} | \boldsymbol{M}_{2}=\alpha \boldsymbol{M}_{1}, \boldsymbol{F}_{2}=\right.\\\left.\beta \boldsymbol{F}_{1}\right\} \rightarrow R\left\{k_{\mathrm{eff}}, k_{\mathrm{eff}}^{\prime} | k_{\mathrm{eff}}^{\prime}=\frac{\beta}{\alpha} k_{\mathrm{eff}}\right.\} , $ | (3) |
式中:M1、F1,M2、F2分别为求解式(2)程序的不同输入矩阵,keff,k′eff分别为有效增殖因子的不同输出结果,α、β为常数.输入矩阵涉及的输入变量有扩散系数D,宏观总截面∑t, g,转移截面∑g′→g,裂变中子谱χ,平均裂变中子数υ与宏观裂变截面∑f的乘积.输出变量为有效增殖因子keff.该蜕变关系可作为本论文实验例子中基准题衍生的计算依据.
2.2 实验过程实验环境:Intel Core(TM) i5-4570 CPU @ 3.20GHz 3.2GHz.
实验软件:基准题衍生工具(Benchmark Driver)
1) 读取原始基准题.IAEA_2D_2G基准题的程序输入卡文件为IAEA_2D_2G.x2m,输入卡信息包含DONJON程序的输入变量参数,以及有效增殖因子keff的预期输出结果参数.PHWR_3D_2G基准题输入卡文件为PHWR_3D_2G.x2m.
2) 读入DONJON程序的蜕变关系输入文件MT1.txt,文件内容是式(3)的具体表达,并标记相应输入和输出变量,其中本实验设定α=1,β=2(也可以根据情况需要设定其他的值).
3) 利用基准题衍生算法,分别求解衍生基准题.
4) 调用DONJON程序执行文件,验证衍生基准题是否满足数学推导的蜕变关系式.
2.3 实验结果与讨论本实验得出的二维,三维衍生基准题结果分别如下.
2.3.1 IAEA_2D_2G衍生基准题此二维双群衍生基准题具体描述.输入参数:1)堆芯、组件几何及材料布置参数,边界条件参数与原始基准题(IAEA_2D_2G基准题[19])相同.2)组件均匀化参数见表 1.输出变量及参数:有效增殖因子k′eff,根据式(3),其理论参考值为其文献[19]参考值的1/2倍,等于0.514 917 5.
| 表 1 IAEA_2D_2G衍生基准题组件均匀化参数 Tab. 1 Cross-section data for the derived benchmark by IAEA_2D_2G |
此三维衍生基准题具体描述,输入变量及参数值:1)堆芯、组件几何及材料布置参数;边界条件参数与原始基准题(PHWR_3D_2G基准题[20])相同.2)组件均匀化参数见表 2.输出变量及参数:有效增殖因子k′eff,根据式(3),其理论参考值为其文献[20]参考值的1/2倍,等于0.501 8.
| 表 2 PHWR_3D_2G衍生基准题组件均匀化参数 Tab. 2 Cross-section data for the derived benchmark by PHWR_3D_2G |
利用DONGJON计算程序,分别执行原始基准题和其衍生基准题计算,计算结果见表 3、4;衍生基准题验证结果见表 5.
| 表 3 原始基准题计算结果 Tab. 3 Results of the original benchmarks |
| 表 4 衍生基准题计算结果 Tab. 4 Results of the derived benchmarks |
| 表 5 衍生基准题验证结果 Tab. 5 Verification results of the derived benchmarks |
表 3中,二维原始基准题(IAEA_2D_2G)的有效增殖因子keff参考值为1.032 0,见文献[19],三维原始基准题(PHWR_3D_2G)的有效增殖因子k′eff参考值为1.003 6,见文献[20].DONJON程序分别执行二维、三维原始基准题计算,得到有效增殖因子的计算结果,并与参考值作比较,其绝对误差分别为3.896×10-3,3.152×10-3,由表 3可知,计算结果跟参考值吻合较好,表明实现所选择的程序计算精度高,为衍生基准题的计算结果提供了参考.表 4为DONJON程序分别执行二维、三维衍生基准题计算,得出的有效增殖因子的结果与参考值的比较,其绝对误差分别为8.536×10-3,4.342×10-4,其计算精度表明,Benchmark Driver工具生成的衍生基准题数据准确无误,且由表 5的结果表明,衍生基准题计算结果满足数学推导的蜕变关系式,具有有效性,进一步表明了由本文所提出的基准题衍生技术,以及基于该技术开发的自动衍生工具很好地实现了二维,三维基准题衍生.
表 6展示的是批量生成衍生基准题的结果,对论文实验所使用的线性蜕变关系式的常系数α,β采用随机算法分别生成100组,1 000组参数,对应生成的衍生基准题分别为100个,1 000个.这里的常系数α,β跟实际的物理参数意义及范围有关,此实验α,β设置的范围为[1, 10].根据等价类覆盖准则[6],α/β≈1则表示生成的衍生基准题跟原始基准题是同一等价类,视为不可用基准题,或者当α/β≈0的情况生成的衍生基准题也视为不可用的基准题.表 6的实验结果表明,其生成不可用的基准题的概率比较低,导致的主要原因有:参数选取跟参数的实际物理意义和测试充分性准则相关.
| 表 6 批量衍生基准题结果 Tab. 6 Batch derivative benchmark results |
此外,从基准题衍生工具效率方面来看,基准题自动衍生算法1由上往下执行,当原始基准题的文本行数为60行,蜕变关系的个数为3个,总共需要的时间为4 ms;当原始基准题文本行数为200行,蜕变关系的个数为10个,总共需要的时间为5 ms.则代码的时间复杂度为O(n2).算法中整个辅助空间为(n+n+n),则代码的空间复杂度为O(n).表 6表明批量衍生基准题的时间效率高.从算法复杂度和执行时间上,Benchmark Driver工具都比测试人员手动生成衍生基准题效率高很多倍,而且不会带入人为的输入错误.特别是对于是大批量、更复杂程序的基准题的衍生,显然基准题衍生工具的效率远远高于人工效率.
3 结论针对堆芯稳态核设计软件验证测试需要大量基准题,而通过实验获取基准题数据存在周期长、成本高的问题,同时,考虑到堆芯核设计程序验证输入的特点,以及基准题数据复杂的实际需求,本文提出一种基准题衍生技术.该技术利用原始基准题数据,基于蜕变测试技术原理提出基准题衍生框架,为了提升衍生效率,设计基准题自动衍生算法及工具.以堆芯计算程序的二维、三维基准题为例,实验结果表明,本文所提出的基准题衍生技术及研发的工具自动地实现二维,三维基准题衍生,生成数据准确,效率高.该技术是一种成本较低的基准题衍生方法.
该技术后续将结合测试充分性准则及蜕变关系选择策略,对算法进行优化,提高衍生基准题的测试覆盖率,可以进一步拓展该技术在核电软件验证测试中的应用.
| [1] |
卢宗健, 李庆, 刘东, 等. NESTOR软件包工程应用适用性强化设计[J]. 核动力工程, 2018, 39(1): 161. LU Zongjian, LI Qing, LIU Dong, et al. Engineering applicability strengthening design and practice of NESTOR software package[J]. Nuclear Power Engineering, 2018, 39(1): 161. DOI:10.13832/j.jnpe.2018.01.0161 |
| [2] |
吕牛, 夏兆东, 朱庆福, 等. APA-H程序应用于田湾核电站1号机组堆芯物理参数计算验证[J]. 原子能科学技术, 2017, 51(5): 817. LV Niu, XIA Zhaodong, ZHU Qingfu, et al. Validation of APA-H code calculation based on core physical parameter for Tianwan NPP Unit 1[J]. Atomic Energy Scienceand Technology, 2017, 51(5): 817. DOI:10.7538/yzk.2017.51.05.0817 |
| [3] |
秦瑶, 余慧, 全国萍, 等. 基于VERA基准题的cosRMC程序验证[J]. 强激光与粒子束, 2017, 29(12): 161. QIN Yao, YU Hui, QUAN Guoping, et al. Verification of Monte Carlo code cosRMC based on VERA core physics benchmark[J]. High Power Laser and Particle Beams, 2017, 29(12): 161. DOI:10.11884/HPLPB201729.170221 |
| [4] |
CHEN T Y, CHEUNG S C, YIU S M. Metamorphic testing: A new approach for generating next test cases. Technical Report HKUST-CS98-01[R]. Hong Kong: University of Science and Technology, 1998
|
| [5] |
S EGURA S, FRASER G, SANCHEZ A, et al. A survey on metamorphic testing[J]. IEEE Transactions on Software Engineering, 2016, 42(9): 1. DOI:10.1109/TSE.2016.25328 |
| [6] |
阳小华, 闫仕宇, 李萌, 等. 基于基准题的中子扩散程序蜕变测试验证方法[J]. 原子能科学技术, 2017, 51(7): 12393. YANG Xiaohua, YAN Shiyu, LI Meng, et al. Verification method of metamorphic test on neutron diffusion program based on benchmark problem[J]. Atomic Energy Science and Technology, 2017, 51(7): 1239. DOI:10.7538/yzk.2017.51.07.1239 |
| [7] |
闫仕宇, 阳小华, 李萌, 等. 基于蜕变测试的热传导程序的验证测试研究[J]. 核科学与工程, 2017, 37(3): 380. YAN Shiyu, YANG Xiaohua, LI Meng, et al. Research of verification test for heat transfer program based on metamorphic testing[J]. Nuclear Science and Engineering, 2017, 37(3): 380. DOI:10.3969/j.issn.0258-0918.2017.03.007 |
| [8] |
PENG Wu, SHI Xiaochun, TANG Jianjun, et al. Metamorphic testing and special case testing: A case study[J]. Journal of Software, 2005, 16(7): 1210. DOI:10.1360/jos161210 |
| [9] |
PENG Wu. Iterative metamorphic testing[C]//Computer Software and Applications Conference, USA: IEEE, 2005, 1: 19
|
| [10] |
董国伟, 聂长海, 徐宝文. 基于程序路径分析的有效蜕变测试[J]. 计算机学报, 2009, 32(5): 1002. DONG Guowei, NIE Changhai, XU Baowen. Effectively metamorphic testing based on program path analysis[J]. Chinese Journal of Computers, 2009, 32(5): 1002. DOI:10.3724/SP.J.1016.2009.01002 |
| [11] |
董国伟, 郭涛, 张普含, 等. 基于路径分析和迭代蜕变测试的Bug检测[J]. 清华大学学报(自然科学版), 2015, 54(1): 60. DONG Guowei, GUO Tao, ZHANG Puhan, et al. Bug detection methods based on path analyses and iterative metamorphic testing[J]. Journal of Tsinghua University (Science and Technology), 2015, 54(1): 60. DOI:10.16511/j.cnki.qhdxxb.2014.01.012 |
| [12] |
TAO Qiuming, WU Wei, ZHAO Chen, et al. An automatic testing approach for compiler based on metamorphic testing technique[C]//Asia Pacific Software Engineering Conference. IEEE Computer Society, USA: IEEE, 2010: 270. DOI: 10.1109/APSEC.2010.39
|
| [13] |
CHEN T Y, TSE T H, ZHOU Z Q. Fault-based testing without the need of oracles[J]. Information & Software Technology, 2003, 45(1): 1. DOI:10.1016/S0950-5849(02)00129-5 |
| [14] |
MURPHY C, SHEN K, KAISER G. Automatic system testing of programs without test oracles[C]//Proceedings of The Eighteenth International Symposium on software Testing and Analysis. USA: ACM, 2009: 189. DOI: 10.1145/1572272.1572295
|
| [15] |
CHEN T Y, HO J W, LIU H, et al. An innovative approach for testing bioinformatics programs using metamorphic testing[J]. BMC Bioinformatics, 2009, 10(1): 24. DOI:10.1186/1471-2105-10-24 |
| [16] |
KANEWALA U, BIEMAN J M, BENHUR A. Predicting metamorphic relations for testing scientific software: a machine learning approach using graph kernels[J]. Software Testing, Verification and Reliability, 2016, 26(3): 245. DOI:10.1002/stvr |
| [17] |
董国伟, 徐宝文, 陈林, 等.蜕变测试技术综述[J].计算机科学与探索, 2009, 3(2): 130. DOI:1673-9418/2009/03(02)-0130-14 DONG Guowei, XU Baowen, CHEN Lin, et al. Survey of metamorphic testing[J]. Journal of Frontier of Computer Science & Technology, 2009, 3(2): 130. DOI:1673-9418/2009/03(02)-0130-14 |
| [18] |
HĚBERT A. Application of the Hermite method for finite element reactor calculations[J]. Nuclear Science & Engineering, 1985, 91(1): 34. DOI:10.13182/NSE85-A17127 |
| [19] |
THELER G, BONETTO F J, CLAUSSE A. Solution of the 2D IAEA PWR benchmark with the neutronic code milonga[J]. Actas de la Reunión Anual de la Asociación Argentina de Tecnología Nuclear, XXXVⅢ, 2011. |
| [20] |
JUDD R A, ROUBEN B. Three dimensional kinetics benchmark problem in a heavy water reactor, AECL-7236[R]. Canada: Atomic Energy Canada Limited, 1981
|
| [21] |
HĚBERT A, SEKKI D. A user guide for TRIVAC version 4[J]. Institut De Génie Nucléaire, 2007, 13: 112. |
 2019, Vol. 51
2019, Vol. 51


