传统的视频通信系统根据奈奎斯特-香农采样定理对每帧采集一组大量的信号样本，采样率要求不小于视频信号带宽的两倍，随后进行高复杂度的压缩编码，以消除像素之间存在的冗余.压缩感知(CS)技术的兴起提供了一种新型的信号采集与重构方法，根据CS理论，系统只需通过将信号投射到随机基上以获得少量的测量值，在某一变换域中具有稀疏或近稀疏表示的信号就可以通过这些测量值得到高可靠性的重构^[1-3].

在初期的压缩感知文献中，测量端对视频帧采用直接观测，但由于视频帧的信息量较大，在进行重构时对计算资源有着非常高的要求.为减少计算复杂度，文献[4]提出了分块压缩感知(BCS)框架及其重构算法，即先对视频帧进行分块测量，之后再利用投影Landweber迭代重构，并在迭代过程中执行维纳滤波以消除重构中的块效应.BCS框架稳定了视频压缩感知的重构质量，大大降低了重构计算的复杂度，被认为是图像/视频压缩感知的典型框架，在图像/视频压缩感知研究中广泛使用.基于BCS框架，文献[5]提出了在离散双树小波变换(DDWT)域进行图像重构的算法，由于这类重构算法没有借鉴传统图像编码中对块间相关性的充分利用，其重构效果并不理想.

对于视频压缩感知，研究人员已经提出在重建端通过块匹配进行运动估计和补偿^[6-7]，即将相邻帧作为参考帧，从参考帧中选取匹配块作为当前块的一个预测.文献[8]提出通过稀疏化当前帧与其运动补偿帧之间的残差进行重构^[9-10]，这是因为残差通常比原始信号具有更大的稀疏性.多假设预测是目前视频压缩感知重构的主流技术^[11].在变换域多假设预测的研究中，文献[12]对文献[5]进行了改进，采用多假设(MH)预测的线性组合来估计变换域中的运动补偿帧，在重构质量与复杂度两方面取得了较好的性能折中.对于多个匹配块的权值分配问题，文献[13]提出通过增加Tikhonov正则化项来求解最优权值；文献[14]则提出在l₂正则化项中加入权重调整函数；文献[15]通过联合lasso模型中的l₁范数正则化与回归模型中的l₂正则化，求解最优权值.

在匹配块的选取方面，文献[16]提出多参考帧假设集合的优化算法，增加匹配块数目以扩大假设选择范围；文献[17]则提出基于菱形快速搜索的双匹配算法，即利用菱形快速搜索方式确定当前解码块的前景/背景的运动矢量，获得两个最佳搜索窗，从中搜索匹配块.这些挑选匹配块的方法均从最小化每个匹配块与原始块均方误差的角度进行考虑，没有对挑选的匹配块进行整体结构质量的衡量，同时这些挑选匹配块的方法存在复杂度过高的问题.

文献[18]在文献[12]的基础上进一步利用了视频序列的时空相关性，提出了一种基于判别加权残差稀疏性(RSS)的视频重构算法，该RSS算法首先对每帧图像进行高质量的独立恢复，随后执行帧间的运动估计，对非关键帧进行预测.RSS算法建模了信号间残差的稀疏性而不是信号内的稀疏性，对不同残差系数的稀疏性进行判别加权，并对权重进行迭代更新.RSS算法在现有视频重构算法中具有相对突出的重构性能，本文试图在增加一定复杂度的情形下进一步提升其重构质量.此外，现有重构算法均只是试图去最小化块间的均方误差，没有考虑视频整体结构相似性(SSIM)的最大化.在某些情况下，均方误差的最小化并不能得到满意的重构效果.因此，本文提出基于SSIM和动态多模式匹配的视频压缩感知三步重构算法，以期进一步提升视频压缩感知的重构质量.

1 视频压缩感知 1.1 多假设预测

压缩感知理论认为，如果一个信号在某变换域中足够稀疏，那么该信号可以从少量的测量值中恢复.若$ \boldsymbol{x} \in \mathscr{R}^{N} $为N维信号，$ \mathit{\boldsymbol{\varphi }} \in \mathscr{R}^{M \times N}$代表一个测量矩阵，则BCS框架的测量过程为

$ \mathit{\boldsymbol{y}} = \mathit{\boldsymbol{\varphi x}}\mathit{\boldsymbol{.}} $

(1)

式中: y ∈ $\mathscr{R} $^M为得到的测量值.测量值的个数M通常比原始信号中的数据个数N小得多，因此该重构恢复问题是欠定的.采样率定义为M/N.一个视频序列表示为{x¹, x², …, x^t, …}，其中x^t为即将进行重构的当前帧信号，$ \hat{\boldsymbol{x}} $表示相应的重构帧.

$ \hat{\boldsymbol{x}} $^p为重构帧$ \hat{\boldsymbol{x}} $通过前一次迭代后获得的重构结果，p为前一次重构.在式(1)的基础上，为有效消除潜在的块效应，常将$ \hat{\boldsymbol{x}} $^p拆分成D个重叠的块：$ \hat{\boldsymbol{x}} $_k^p∈ $ \mathscr{R} $^S2，1≤k≤D，其中S²是重叠块的大小.上述的拆分过程为

$ \hat{\boldsymbol{x}}_{\mathrm{k}}^{\mathrm{p}}=\boldsymbol{E}_{\mathrm{k}} \hat{\boldsymbol{x}}^{\mathrm{p}} $

式中E_k∈ $ \mathscr{R} $^S2×N为矩阵算子，以交叉重叠块的方式从$\mathit{\boldsymbol{\hat x}} $^p中获取重构块$ \mathit{\boldsymbol{\hat x}} $_k^p，对于拆分获得的每个块，从指定的参考帧中挑选与该块$ \mathit{\boldsymbol{\hat x}} $_k^p具有高度相似性的匹配块.一般地，块与块之间的像素相似性可用均方误差(MSE)衡量，具体的表达式为

$ M_{\mathrm{se}}\left(\hat{\boldsymbol{x}}_{\mathrm{k}}^{\mathrm{p}}, \hat{\boldsymbol{x}}_{\mathrm{ref}, i}\right)=\frac{1}{S^{2}}|| \hat{\boldsymbol{x}}_{\mathrm{k}}^{p}-\hat{\boldsymbol{x}}_{\mathrm{ref}, i}||_{2}^{2} $

(2)

式中: $ \mathit{\boldsymbol{\hat x}} $_{ref, i}为在某个参考帧中的一个S²大小的块，该块在以块$ \mathit{\boldsymbol{\hat x}} $_k^p为中心的L×L搜索窗内.基于式(2)挑选C个匹配块，也就是均方误差较小的C个匹配块，将它们定义为v_ki，1≤i≤C.上述的C个块，将视为重构块$ \mathit{\boldsymbol{\hat x}} $_k^p的多假设匹配块.

1.2 加权残差稀疏模型

当前块x_k的残差R(x_k)是块原始值与多个匹配块线性组合之间的差值，该差值表示为

$R\left( {{\mathit{\boldsymbol{x}}_{\rm{k}}}} \right) = {\mathit{\boldsymbol{x}}_{\rm{k}}} - \sum\limits_{1 \le i \le C} {{\mathit{\boldsymbol{\alpha }}_{{k_i}}}} {\mathit{\boldsymbol{v}}_{{k_i}}}. $

式中: α_ki为某匹配块的权重，将影响块匹配的预测精度.一般而言，匹配块如果和当前块相似性更高，那么该匹配块将赋予较大的权重；匹配块与当前块的相似性不高，赋予该匹配块一个较小的权重.因此，权重应与匹配块和当前块的均方误差值成反比关系.可以选取指数函数来计算不同匹配块的残差权重，由于原始块x_k无法获取，我们利用前一次的重构结果$ \mathit{\boldsymbol{\hat x}} $_k^p进行如下计算

$ \boldsymbol{\alpha}_{k_{i}}=\frac{\exp \left(-\operatorname{MSE}\left(\hat{\boldsymbol{x}}_{\mathrm{k}}^{\mathrm{p}}, \boldsymbol{v}_{k_{i}}\right) / h\right)}{\sum\nolimits_{1 \leq j \leq C} \exp \left(-\operatorname{MSE}\left(\hat{\boldsymbol{x}}_{\mathrm{k}}^{\mathrm{p}}, \boldsymbol{v}_{k_{j}}\right) / h\right)}. $

式中：h为一常数，MSE(·)为计算均方误差的公式.变换域内信号残差的稀疏性已经被广泛运用.因此，可采用DDWT对残差进行稀疏化.残差R(x_k)的DDWT变换系数表示为

$ {{R}_{\Psi }}\left( {{\boldsymbol{x}}_{\text{k}}} \right)={{\mathit{\Psi} }^{\text{T}}}R\left( {{\boldsymbol{x}}_{\text{k}}} \right)={{\widetilde{\boldsymbol{x}}}_{\text{k}}}-\sum\limits_{1\le i\le c }{\boldsymbol{\alpha }_{{k_i}}}{{\widetilde{\boldsymbol{v}}}_{{{k}_{i}}}}. $

式中：Ψ为DDWT基，Ψ^T为其转置，并且$ {{\boldsymbol{\tilde{x}}}_{\text{k}}}={{\mathit{\Psi} }^{\text{T}}}{{\boldsymbol{x}}_{\text{k}}} $，$ {{\widetilde{\boldsymbol{v}}}_{{{k}_{i}}}}={\mathit{\Psi}^{\text{T}}}{{\boldsymbol{v}}_{{{k}_{i}}}} $.不同系数为0的概率存在区别，所以可以对残差稀疏度进行加权.加权残差稀疏模型表示为.

$F\left(\boldsymbol{x}_{\mathrm{k}}\right)=\boldsymbol{W}_{\mathrm{k}} \boldsymbol{R}_{\Psi}\left(\boldsymbol{x}_{\mathrm{k}}\right) $

式中：W_k为一个对角阵，对角线上元素为w_{k, 1}, …, w_{k, s²}，其余位置为0.w_{k, 1}, …, w_{k, s²}是残差系数的权重，每个值反映了对应系数为0的概率.利用对于F(x_k)的稀疏化，并得到一个加权的l₁范数问题

$ \mathit{\boldsymbol{\hat x}} = \arg \mathop {\min }\limits_x \sum\limits_{1 \le k \le D} | |F\left( {{\mathit{\boldsymbol{E}}_{\rm{k}}}\mathit{\boldsymbol{x}}} \right)|{|_1}{\rm{s}}.{\rm{t}}.\mathit{\boldsymbol{y}} = \mathit{\boldsymbol{\varphi x}}. $

式中: x_k= E_kx.通过求解上式可获得当前帧的重构$ \mathit{\boldsymbol{\hat x}} $.当前重构获得的帧$ \mathit{\boldsymbol{\hat x}} $相较于前一次迭代获取的重构帧$ \mathit{\boldsymbol{\hat x}} $^p具有显著的质量改进.所提算法将不断迭代进行多假设预测的块匹配，构建加权残差稀疏模型进行重构，获得最终重构结果.

2 三步重构算法

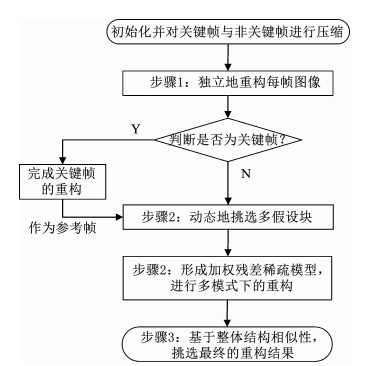
为控制计算复杂度和内存需求，测量端逐帧地采用基于BCS框架的随机测量进行视频信号的采集^{[5, 19]}.视频序列由若干图像组构成，每个图像组由一个关键帧和后面的一些非关键帧组成.关键帧使用相对较高的采样率进行测量，而非关键帧使用较低的采样率进行测量.接下来，着重介绍本文提出的基于SSIM和动态多模式匹配的视频压缩感知三步重构算法，所提算法的整体流程如图 1所示，主要包括三大步骤：首先对于序列中的每帧进行独立的重构；其次非关键帧利用第一步中重构的关键帧进行多假设预测的块匹配，在挑选匹配块总个数时进行动态分配；最后通过整体结构相似性的最大化，获取最终的重构结果.

步骤1：视频序列中每帧均通过帧内模型独立恢复.这一步采用基于多假设预测的残差重构算法，匹配块从每帧自身进行挑选.一般而言，采样率越高的帧重构质量越好，采样率越低的帧重构质量越差.受传统视频压缩编解码的启发，所提算法采用具有较高采样率的帧作为参考帧.

步骤2：重构非关键帧.非关键帧可从相邻的两参考帧获得匹配块，由于参考帧在步骤1后得到了较好的重构结果，不需要进一步处理.如前所述，对于每个非关键帧，应该考虑从前面参考帧和后面参考帧选取匹配块的个数.所提算法采用动态多模式挑选匹配块.基于每一非关键帧与前后两帧的距离决定从两参考帧挑选匹配块的个数，而不是固定每一帧从某参考帧中获取块个数.也就是，如果当前的非关键帧距离前向参考帧较近，从前向参考帧中将挑选更多的匹配块而从后向参考帧中挑选的匹配块将相应减少.

为降低计算复杂度，基于帧距离挑选匹配块总数量的机制，可简化为：假定从两个参考帧中挑选的总匹配块个数为M，不失一般性，M为偶数，可设置三组模式进行动态挑选：1、从前后两参考帧各挑选M/2块；2、从距离较近的参考帧挑选M/2+1块，从距离较远的参考帧挑选M/2-1块；3、从距离较近的参考帧挑选M/2+2块，从距离较远的参考帧挑选M/2-2块.在获得上述匹配块之后，对于1 2 3每种模式，计算每块与对应的匹配块线性组合之间残差.然后，根据残差系数为零的概率对残差系数进行加权，得到一个加权的l₁最小化问题，根据Split Bregman迭代算法解决该问题，从而完成一帧的重构.例如，当M设置为10时，从前后两个参考帧中基于帧距离挑选匹配块的个数分配如表 1所示.

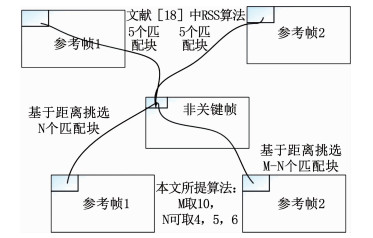
文献[18]的RRS算法挑选匹配块的模式较为固定，所提算法根据视频帧之间的时域相关性，采用了多种模式动态地挑选匹配块，两者的对比如图 2所示.

步骤3：挑选最终的重构结果.由于在某些情况下最小化均方误差并不会得到满意的效果，因此本步骤基于整体结构相似性从模式1~3中挑选最终的重构结果.为降低复杂度，设置一阈值T(0 < T < 1)，可依据重构质量需求自动调节所提算法的复杂度.视频序列中的每个非关键帧按照模式1~3的顺序依次执行残差重构，并在每种模式重构完成后计算其与参考帧的SSIM，若某种模式下对应的SSIM大于T，则重构完成，该模式对应的重构结果为最终结果；否则，接着执行其余的模式；若三种模式下得到的SSIM均小于阈值T，则从三种模式中挑选较大的SSIM对应的重构结果为最终重构结果.

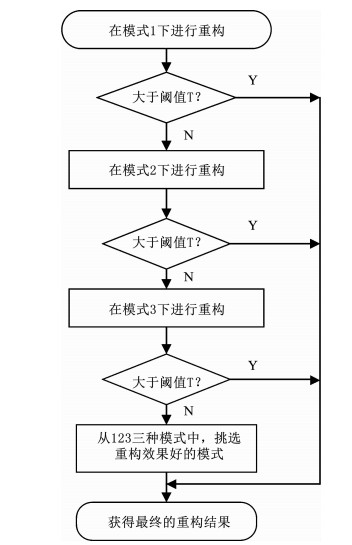
从大量实验可以分析得出，阈值T的合理设置决定了最终的重构质量以及算法的复杂度：若阈值过小，则最终的重构质量效果不好；相反若阈值过大，重构时间较长，算法复杂度较高，甚至在耗费很长的计算时间之后还是达不到高阈值情况下所期望的重构效果.一般情况下，阈值T在0.9左右时所提算法在重构效果和复杂度方面均能取得较好的性能，因此本文在实验结果部分设置阈值T=0.9进行所提算法的性能评估.在步骤3中挑选最终重构结果的详细算法流程图如图 3所示.

相比于现有固定挑选匹配块的模式，所提算法挑选匹配块的模式更加灵活，实现了多模式的动态挑选.同时，在基于整体结构相似性的考虑下，所提算法可以从总体上衡量每个视频帧的质量，进一步消除了块效应，在增加一定复杂度的情况下有效地提升了视频压缩感知的重构质量.

3 实验结果

提出算法的实验仿真与分析，以验证所提算法的性能.以下的实验过程均在装有MATLAB R2018a软件的Lenovo Y430p计算机上进行，具体硬件配置如下：CPU型号为Intel酷睿i7 4710MQ、CPU主频为2.5 GHz、内存容量4 GB、显存容量2 GB，该计算机的操作系统是64位的Windows 8.1.

所提算法需要进行一些参数设置：搜索窗大小L×L、从前后两参考帧挑选匹配块的总个数C、重叠块的大小S²、每个匹配块权重的参数常量h、阈值T.基于算法复杂度的考虑，实验中的参数值选取如下：S²=8×8、C=10、h=8、T=0.9.由于所提算法的目标是从整体质量上改进视频重构的效果，本文选取SSIM作为算法性能的主要评价指标，同时辅以峰值信噪比(PSNR)进行指标分析.

结合式(2)与峰值信噪比PSNR的定义，可得

$ P_{\mathrm{PSNR}}=20 \log _{10}\left(\frac{\mathrm{MAX}}{\sqrt{\operatorname{MSE}\left(\hat{x}_{\mathrm{k}}^{\mathrm{p}}, \hat{x}_{\mathrm{ref}, i}\right)}}\right) $

式中:MAX为常数，如果每个像素用8位表示，那么其值为255.从式中可看出PSNR与MSE成反比，而MSE表征了重构图像与原始图像的最小均方误差，其值越小表明重构效果越好.基于以上分析可得出PSNR值越大，均方误差意义上的重构质量越高.

为方便叙述，规定如下：文献[12]中的算法为多假设(MH)算法，文献[18]中的算法为RRS算法，本文所提算法(Proposed)主要与这两种代表性的算法作对比.

在进行匹配块的选取过程中，可发现当按照多种分配从前后两个参考帧中挑选匹配块时，不同分配会在SSIM与PSNR上产生区别，基于帧距离的匹配块选择机制的实验示例如图 4所示.图中的“前”“后”表示从前后两个参考帧挑选的匹配块的个数，例如“前4后6”表明当前重构块从前向参考帧中挑选4个匹配块、而从后向参考帧中挑选6个匹配块.从图中可看出，图 4(a)中的两曲线相差较大，图 4(b)中的两曲线基本重合，这表明两种挑选匹配块的配置导致重构PSNR基本一致，但在SSIM上却有较大的差别.一般而言，SSIM值越大，重构视频在整体质量会越好.因此，所提算法可基于帧距离的匹配块选择机制，利用多模式重构动态地挑选匹配块.

由于本文算法从MSE与SSIM两方面全面考虑了视频重构的质量，通过增加一定的复杂度进行了更为精细的预测，从理论上可以预期所提算法在PSNR与SSIM上均会有较好的表现；同时，在进行大量CIF格式视频序列实验的基础上，本文挑选了3个具有代表性的Foreman、Akiyo与Container视频序列在多种采样率下依次执行MH算法、RRS算法与本文所提算法，得出的实验结论基本一致.

在实验中，每种序列选取连续的17帧，其中第1、9、17选用较高的采样率并作为参考帧，其余的各帧为非关键帧.使用三种算法对应的重构结果如表 2、表 3所示.其中，表 2展示重构结果的PSNR平均值；表 3展示重构结果的SSIM平均值.对于两表中的联合采样率，逗号前为参考帧采样率，逗号后的为非关键帧的采样率.从表 2可以看出，在(0.4, 0.3)、(0.6, 0.4)、(0.7, 0.2)、(0.5, 0.4)4种联合采样率下，RRS算法在PSNR方面相对MH算法有所改进，在3个序列各采样率下提高大概1~2dB，而本文所提算法在PSNR方面基本与RRS算法基本持平，甚至在某些采样率下有较小的改善.由表 3可以看出，在整体结构相似性上，MH与RRS两种算法的性能基本一致，本文算法对于上述两种算法在多种采样率下具有较好的改进.所提算法在3个视频序列上的SSIM平均值相较于RRS算法提高大约10%.

本文算法与MH算法、RRS算法从原理上进行简单的比较，MH算法利用多假设的方法进行重构，只进行了一次重构；RRS重构分为两个阶段，第一阶段基于MH算法进行初步的重构，在第二阶段进一步进行重构.上述两种方法均采用分块的方法进行重构，并通过MSE度量重构质量，因此在PSNR质量上表现较好，但在SSIM度量上欠缺考虑.本文算法从MSE与SSIM两方面进行度量，因此在整体重构质量上有更好的表现.

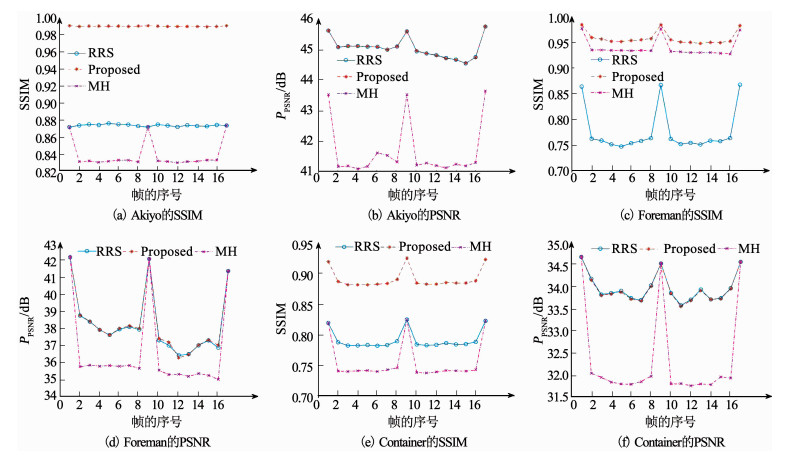
为更加直观地比较所提算法的性能，依次挑选Akiyo序列在(0.5, 0.4)联合采样率下、Foreman序列在(0.5, 0.2)联合采样率下、Container在(0.4, 0.3)联合采样率下分别执行三种重构算法.图 5分别给出了三种重构算法的SSIM与PSNR对比图.由各图中可看出，所提算法在SSIM指标上远高于MH算法和RRS算法，也就是在视频重构的整体质量上，所提算法具有较好的效果；在PSNR指标方面，本文算法与RRS算法基本一致，都远高于MH算法.对于所选取的Foreman序列，在SSIM与PSNR指标方面也有同样的实验结果.综上所述，本文算法在保持较高PSNR质量的同时，对于SSIM质量具有较为显著的改善.

基于以上分析，可以得出本文所提算法相较于MH算法，无论从PSNR还是SSIM两方面均取得较大性能的提升，图像的重构质量得到明显的提升；与RRS算法相比较，虽然在PSNR上改进的效果不是特别明显，但是在SSIM方面却有较大的改善，可以得出从整体重构质量方面，本文算法相较于RRS也有一定程度上的改善.同非压缩感知系统相比，压缩感知系统的相对优势是测量端简单、重建端复杂，可将测量端的复杂度向重建端转移，适合于无线多媒体传感应用.一般而言，重建端具有充足的计算资源，其核心难题是如何提升重构质量.本文算法通过适当增加重建端的复杂度，在现有方法的基础上进一步提升了视频信号的重构质量.

提出算法的复杂度主要由挑选匹配块的过程所决定.所提算法在极端情况下才达到RRS算法的3倍复杂度，因此重构每帧的算法复杂度大概为O(N).基于前文所述实验平台的具体软硬件条件以及实验参数的设置，对于本文所使用的CIF格式的视频序列，所提算法重构每帧图像平均大约花费5~6分钟；相较于RRS与MH算法的3~4分钟，所提算法在增加一定算法复杂度的情况下，重构效果得到了改进.由于硬件并行计算的发展，上述复杂的计算问题将得到一定程度的解决.

4 结论

现有的压缩感知重构算法基于均方误差的基础上，进行重构，存在一定的弊端.本文提出了一种基于动态多模式挑选匹配块的视频压缩感知重构算法，在迭代重构中有效融合了均方误差与结构相似准则，通过多模式视频重构获取最终的重构结果.所提算法充分利用了视频帧的时空相关性，提高了重构视频的整体质量，在PSNR与SSIM性能指标方面相比于当前代表性的算法均有所改善，无论在重构图像的细节和整体质量上都有提升.但本文所提算法复杂度有一定提升，对计算硬件要求较高.