工程岩体是一种不连系、非均质的天然地质体,在长期的地质作用和各种成岩环境下[1],其内.部形成了大量随机分布微裂隙、微孔洞及节理等地质缺陷,这些缺陷的存在影响着岩体的力学性质,也影响应力波在岩体内的传播.由于人工扰动(如矿山钻爆开采)、岩爆和地震等引起的动应力波以围岩为介质向四周传播,当动应力波穿越这些地质缺陷时,会受其物理力学性质及其在岩体内空间展布状态的影响,使得动应力波在节理岩体内传播更加复杂.因此,精确地表征节理接触面积及其空间几何分布形态,进而量化应力波在岩体内传播规律的影响,对实现深部金属矿的诱导开采和岩爆、围岩失稳等动力灾害的研究均有重要意义.
关于节理对应力波传播的影响,相关学者开展了大量的研究.根据研究方法的不同,可以将理论模型大致分为3类,即波散射模型[2-3]、等效介质模型[4]和位移不连系模型[5].此后,R.Miller等[6-8]基于位移不连系模型发现应力波穿过节理面时波幅值衰减、时间延迟及中心频率降低,且随入射角度变化波形和频率均发生变化.但由于节理的形成及其物理力学性质具有明显的随机性、复杂性,而且应力波穿越节理时会受到节理面基本特征(有效接触面积、几何分布、粗糙度及填充材料等)的影响[9-15]发生波型变换和多次透反射问题,因此,上述建立的理论模型很难精确地描述应力波在节理岩体内的传播.为此,部分学者从简单的单节理或有规律的多节理出发,将有效接触面积、几何分布及粗糙度等作为单因素进行研究,进而逐步地揭示节理面对应力波传播的影响.例如,S.Kahraman等[11]在岩石表面沿不同方向进行锯切刻槽模拟节理的粗糙系数(FRC),试验数据用最小二乘法进行拟合发现P波速度随FRC值的增加而减小.赵坚[12]定义两个节理面相接触的面积占总节理面面积的比值为节理吻合系数(CJM),用以描述两个节理面的“匹配”或“咬合”情况.在此基础上,陈昕等[13]和Li J C等[14]将表面纵横切槽不同程度的岩块与完整岩块组合得到不同的节理吻合系数组合试样,探讨了节理吻合系数(CJM)对应力波透射系数及节理动态力学响应的影响.戎立帆等[15]从能量的角度研究节理面对应力波的波动性和能量耗散的影响.
通过上述文献分析发现,当前关于节理吻合系数(CJM)对波传播的试验研究主要通过在岩石表面刻画不同数量的人工切槽来实现.这种方案虽然能很好地剔除了节理粗糙度的影响,但不同的节理接触面积通过改变凹槽数量实现,即在节理接触面积改变的同时节理的几何分布也发生改变,这难于反映节理有效接触面积作为单一变量对应力波的影响研究.因此,通过预制凹凸相间的扇形节理试样,试验时通过将两个人工节理分布形态相同的组合试样旋转不同角度获得不同节理接触面积,实现在不改变节理的几何分布下改变节理吻合系数.由于复杂图样加工技术难于实现,加之处于弹性阶段的材料并不影响波传播规律的获取,基于相似理论选择水泥砂浆材料作为相似材料模拟岩石试样.采用分离式霍普金森压杆(SHPB)系统对不同节理形态的水泥砂浆组合试样进行冲击试验,探究节理形态及其接触面积比对应力波的影响.
1 试验 1.1 试样制作天然岩体内节理表面形态复杂,若用其加工试样进行试验,加工难而且离散性大,因此,试验基于相似理论并参考现有岩石模拟试验领域的研究,选择水泥砂浆材料模拟岩石.杨阳等[16]通过改变水泥砂浆配比模拟不同强度的岩石试件,本文在此基础上选择水泥砂浆比为:m(水): m(水泥): m(砂)=1: 2: 6,其中所用水泥为P.O 42.5,砂直径<0.012 5 mm.
试验所用模具主要包括:可以制作尺寸为Φ50 mm×50 mm圆柱体的模具和尺寸为Φ50 mm×1 mm并带有扇形凹凸相间(凹面下沉高度为1 mm)的薄圆柱体模具,其中凹面扇形夹角分别为36°,45°,60°,90°和180°,试验模具如图 1,2所示.试验时将带有扇形的模具置于Φ50 mm×50 mm的圆柱体模具底部,用于制作不同节理分布形态的水泥砂浆试样.试验用扇形凹面数量描述节理分布形态,即节理聚散程度.试验时对试样所含凹面数量进行统计并编号,结果见表 1.

|
图 1 制备水泥砂浆试样模具 Fig. 1 Preparation of cement mortar sample mold |

|
图 2 制备扇形凹凸相间节理模具 Fig. 2 Preparation of fan-shaped concave and convex joint mold |
| 表 1 水泥砂浆试样含凹面数量 Tab. 1 Concave quantities in cement mortar specimens |
按相关规范、标准,制作两端面光滑水泥砂浆试样和一端面光滑一端面带有不同扇形夹角的水泥砂浆试样,如图 3所示.光滑节理组合试样由两个两端面均光滑的水泥砂浆试样组合而成;不同节理分布形态组合试样由两个凹面数相同的试样组合而成.试验通过将两个节理分布形态相同的试样旋转不同角度获得不同接触面积的组合试样,组合试样示意如图 4所示.组合试样的扇形节理角度相对于试样截面等角度,因此,只需考虑上下接触的单个扇形节理接触面情况,即在图 4中只需考虑区域A、B、C、D相对面积变化.区域C为两节理面接触区域,区域A和B分别为上下试样扇形节理没有接触部分,区域D面积变化与区域C相同.两相接触的节理面面积AS为区域C面积4倍,两节理面总面积A为区域A、B、C、D面积总和的4倍.

|
图 3 不同扇形角度的水泥砂浆试样 Fig. 3 Cement mortar specimens with different fan-shaped angles |

|
图 4 相同节理几何分布组合试样示意 Fig. 4 Schematic diagram of composite specimens with the same joint geometry distribution |
节理接触面积比(CJM)为两相接触的节理面面积AS与总节理面面积A之比[12],即
| $ C_{\mathrm{JM}}=\left(A_{\mathrm{s}} / A\right) \times 100 \%. $ | (1) |
按试验要求设计了5种不同扇形角度和4种不同接触面积比试样,经统计试验过程中所用的水泥砂浆组合试验的表面参数如表 2所示.
| 表 2 水泥砂浆试样表面参数 Tab. 2 Surface parameters of cement mortarspecimens |
试验采用分离式霍普金森压杆装置(SHPB),该系统主要由空气炮、纺锤形子弹、激光测速仪、入射杆、透射杆、吸收杆、超动态采集仪、示波器组成.纺锤形子弹、入射杆、透射杆和吸收杆均为高强度合金钢,其弹性模量E=250 GPa,密度ρ=7 787 kg/m3,波速c=5 189 m/s.纺锤形子弹长360 mm,入射杆、透射杆和吸收杆直径均为50 mm,长度为2 000 mm,试验装置如图 5(a)所示.

|
图 5 SHPB试验装备 Fig. 5 SHPB experimental device |
在冲击试验前,将试件和压杆的接触端面均匀涂抹凡士林,然后将试样夹在入射杆和透射杆之间.试验时组合试样在两压杆中放置如图 6所示.每次试验均应该保证入射杆在相同位置,确保每次获得相同的子弹冲击速度.冲击过程中,子弹在高压氮气推动下撞击入射杆产生一维P波,当一维P波传播至压杆和试样界面时,由于压杆和试样材料波阻抗不同,在界面处产生透反射效应,其中反射波折回入射杆中,透射波沿入射波传播方向继续传播进入透射杆,应力波传播原理如图 5(b)所示.在入射杆和透射杆上各自贴上一对应变片,分别编号为1#,2#.试验过程中应变片上采集的数据通过LabVIEW平台进行记录和储存.

|
图 6 SHPB冲击示意 Fig. 6 Schematic diagram of SHPB impact |
假定在SHPB试验中满足以下两个假设条件[17]:1)一维弹性波理论,即子弹撞击入射杆产生的波为一维应力波,使试样为一维加载状态;2)均匀性假设,即试样内部的应力场、应变场是均匀的.把入射杆和透射杆与试样的交界面分别记为编号1和2,则根据应力波理论端面1和端面2处端面力和端面质点移动速度分别为
| $ {\nu _1} = {c_0}\left[ {{\sigma _i}(t) + {\sigma _r}(t)} \right]/E, $ | (2) |
| $ \nu_{2}=c_{0} \sigma_{t}(t) / E, $ | (3) |
| $ F_{1}(t)=A_{0}\left[\sigma_{i}(t)+\sigma_{r}(t)\right], $ | (4) |
| $ F_{2}(t)=A_{0} \sigma_{t}(t). $ | (5) |
式中:v1(t)和v2(t)分别为端面1和端面2质点移动速度;F1(t)和F2(t)分别为端面1和端面2端面力;σi(t)和σr(t)分别为端面1的入射时程应力波和反射时程应力波;σt(t)为端面2的透射时程应力波;c0为压杆波速,m/s;A0为压杆横截面面积,mm2.
试样应变率为
| $ \dot{\varepsilon}(t)=\left(\nu_{1}(t)-\nu_{2}(t)\right) / l_{0}. $ | (6) |
试样平均应力为
| $ \sigma(t)=\left(F_{1}(t)+F_{2}(t)\right) / 2 A. $ | (7) |
将式(2)~(5)代入式(6)、(7)有
| $ \sigma(t)=\left(\sigma_{t}(t)+\sigma_{r}(t)+\sigma_{i}(t)\right) / 2, $ | (8) |
| $ \dot{\varepsilon}(t)=\frac{1}{\rho c_{0} l}\left[\left(\sigma_{i}(t)-\sigma_{r}(t)+\sigma_{t}(t)\right)\right]. $ | (9) |
对式(9)进行时间积分可以获得应变
| $ \varepsilon(t)=\frac{1}{\rho c_{0} l} \int_{0}^{t}\left[\sigma_{i}(t)-\sigma_{r}(t)-\sigma(t)\right] \mathrm{d} t. $ | (10) |
假定试样应力-应变曲线为线弹性关系,则
| $ \varepsilon=\sigma / E. $ | (11) |
式中:σ为应力;ε为应变;E为弹性模量.
依据文献[18]所提节理等效刚度为
| $K_{n}=\sigma A_{0} /\left(\varepsilon l_{0}\right). $ | (12) |
式中:A0为压杆横截面面积,mm2;l0为试样高度,mm.
将式(11)代入式(12)可得
| $K_{n}=E A_{0} / l_{0}. $ | (13) |
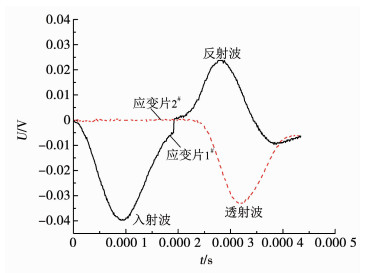
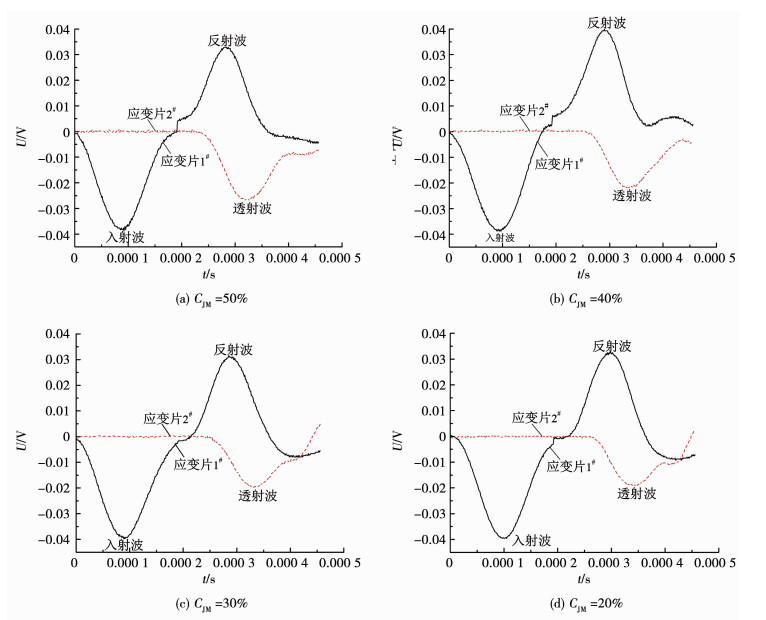
受篇幅所限,选择由凹面扇形夹角为60°构成的节理分布形态组合试样(即SH-3组试样)的试验结果作为典型示意.图 7为光滑节理组合试样的波形图.图 8为SH-3组试样试验数据,即凹面扇形夹角为60°,节理接触面积分别为50%,40%,30%和20%的组合试样做SHPB冲击试验时,在入射杆和透射杆上应变片测得的电压波.其中,光滑节理试样表示两个试件接触端面是平整不存在凹凸面的试件组合;接触面积比50%表示两个节理分布相同的试样节理面完全正对;接触面积小于50%表示根据需求通过两个节理分布相同试样旋转不同角度获得不同的节理面接触面积比.由图 7可以看出,纺锤形子弹撞击入射杆产生正弦式应力波,当该波给试样加载时,入射波波形经过滤波后没有明显的振荡.入射波加载至波峰时间约95 μs,足够使应力波在试样内来回反射3.1次,大于均匀性2~3次来回反射[19],说明试件内部达到应力-应变的均匀化.
|
图 7 光滑节理组合试样的波形 Fig. 7 Waveform diagram of a smooth joint sample |
|
图 8 SH-3组试样的波形 Fig. 8 Waveform diagram of group SH-3 specimens |
由图 8对比分析可知,相同冲击速率,各试样入射波波形与振幅相同,透射波、反射波波形相似.但透射波振幅均小于入射波,而且随着接触面积的减小,呈非线性减小趋势变化,这与文献[20]结果相同.说明试样在相同加载条件下,穿越不同节理面接触面积时发生不同程度的透反射效应,即光滑节理组合和非光滑节理在应力波作用下产生不同程度的非弹性变形,使得应力波产生不同程度衰减.
2.2 岩体的应力-应变关系分析利用式(8)~(10)计算应力波数据,得到SH-3组试样(扇形夹角60°)的应力-应变关系曲线,如图 9所示.可以看出,在相同的一维应力波加载条件下,试样在应力峰前的应变随应力的增加而呈非线性增加,且试样的峰值应变随着节理吻合系数减小而逐渐增大.此外,含光滑节理试样在加载段只发生线弹性变形,而不同的节理吻合系数试样在加载前期有下凹变形之后再逐渐向线性过渡,最后在峰值强度附近出现强度硬化,使整个峰前阶段呈S型变化.同时,通过对比发现,试样加载初期的下凹变形随节理吻合系数减小而愈加明显.这是因为在入射条件相同下,根据SHPB系统的动量守恒σ=ρcv(式中ρ为试样密度,c为应力波波速,v为质点振动速度),压杆对试样的作用荷载F0=σA0相同,当节理接触面积AS越小时,节理受到应力越大,产生的法向位移量也越大.试验在卸载过程中,含光滑节理试样近似呈线性形式下降,不同节理吻合系数试样均呈非线性变化.节理试样下降曲率随节理吻合系数增大而增大,且卸载曲线与加载曲线不重合,这是节理发生塑性变形所致.试样在同等应力水平下,加载段应变均大于卸载段应变,通过对比发现随着节理吻合系数减小,试样残余应变越大,说明试样在卸载过程中节理闭合量增大而产生应变恢复滞后.

|
图 9 SH-3组试样的应力-应变关系曲线 Fig. 9 Stress-strain curves of group SH-3 specimens |
为了定量描述节理对应力波传播规律的影响,定义透射波和入射波应变峰值的比值为透射系数,其计算式为
| $ T=\max =\left|\varepsilon_{t}\right| / \max \left|\varepsilon_{i}\right|. $ | (14) |
式中:εt、εi分别为透射波和入射波的应变值.
运用式(14)可以得到应力波穿越不同节理试样的透射系数.图 10显示不同节理吻合系数及几何分布对透射系数的影响及其相应的拟合曲线.

|
图 10 节理分布和CJM与透射系数的关系 Fig. 10 Correlation of joint distribution and CJM with transmission coefficient |
本文选用节理扇形凹面数量作为反映节理分布形态的参量,记节理扇形凹面数量为n.由图 10可以看出,不同节理吻合系数(CJM)的试样透射系数均小于1,说明在穿越节理面时应力波均产生波幅衰减.当节理分布形态相同时,应力波透射系数随接触面积比增大呈线性增大.表明在相同试验条件下(子弹速率和节理分布形态相同),节理吻合系数(CJM)越大应力波衰减越小,透射波振幅越大,即节理接触情况越好透射系数越大.另外,随着接触面积增大,不同节理凹面数的透射系数间差值越大,说明节理分布越分散对应力波传播越明显.当节理吻合系数(CJM)相同时,节理凹面数越多透射系数越大,但由于透射系数间差值均在一定误差范围内,难于精确地客观描述节理分布对透射系数的影响,这也进一步说明了节理接触面积对波透射系数影响比节理分布大.
2.4 节理分布及CJM对等效刚度的影响等效刚度通常用来描述节理的动态力学行为,所以,通过式(13)求得试验试样的等效刚度比.图 11为节理吻合系数和节理分布形态对节理等效刚度的影响.可以看出,当节理分布形态相同时,节理动态等效刚度随接触面积增大呈线性增大.例如,凹面扇形夹角为60°的节理,接触面积比从20%增加到50%时,节理等效刚度比分别为16.8,29.7,39.1,48.9和92.1 GPa/m.当节理接触面积相同时,节理凹面数越多节理等效刚度越大,说明了节理分布离散的等效刚度比节理分布紧凑的刚度大,即节理越聚合,试样受力越不均匀,节理的抵抗变形能力越弱,导致节理刚度越小.

|
图 11 节理分布和CJM与等效刚度的关系 Fig. 11 Correlation of joint distribution and CJM with equivalent stiffness |
1) 节理面的接触面积大小明显影响节理试样的应力-应变曲线.当节理分布形态相同时,试样应力-应变曲线在加载初期的非线性随节理接触面积减小逐渐增大,说明在相同入射应力波条件下,节理接触面积越小节理受到应力越大,产生节理闭合量越大.
2) 应力波的透射系数与节理接触面积比密切相关.相同冲击速率下,节理几何分布形态相同时透射系数与节理接触面积呈线性正相关,而且节理几何分布越分散的透射系数随接触面积变化影响越明显.
3) 对试验所得的等效刚度进行曲线拟合发现,相同节理形态组合试样的节理等效刚度和节理接触面积比呈线性正相关.而在相同面积下,节理几何分布越分散比节理分布紧凑的等效刚度大,且随接触面积增大几何分布形态作用影响愈明显.
| [1] |
孙广忠. 工程地质与地质工程[M]. 北京: 地震出版社, 1993: 14. SUN Guangzhong. Engineering geology and geoengineering[M]. Beijing: Seismological Press, 1993: 14. |
| [2] |
CHATTERJEE A K, MAL A K, KNOPOFF L, et al. Attenuation of elastic waves in a cracked, fluid-saturated solid[J]. Mathematical Proceedings of the Cambridge Philosophical Society, 1980, 88(3): 547. DOI:10.1017/S0305004100057832 |
| [3] |
ACHENBACH J D, LI Z L. Propagation of horizontally polarized transverse waves in a solid with a periodic distribution of cracks[J]. Wave Motion, 2016, 8(4): 371. DOI:10.1016/0165-2125(86)90016-8 |
| [4] |
BIOT M A. Theory of propagation of elastic waves in a fluid-saturated porous solid. Ⅰ. Low-frequency range[J]. Journal of the Acoustical Society of America, 2005, 28(2): 179. DOI:10.1121/1.1908239 |
| [5] |
SCHOENBERG M. Elastic wave behavior across linear slip interfaces[J]. Journal of the Acoustical Society of America, 1980, 68(5): 1516. DOI:10.1121/1.385077 |
| [6] |
MILLER R K. An approximate method of analysis of the transmission of elastic waves through a frictional boundary[J]. Journal of Applied Mechanics, 1977, 44(4): 652. DOI:10.1115/1.3424152 |
| [7] |
PYRAK-NOLTE L J, MYER L R, COOK N G W. Transmission of seismic waves across single natural fractures[J]. Journal of Geophysical Research, 1990, 95(B6): 8617. DOI:10.1029/JB095iB06p08617 |
| [8] |
Zhu Jianbo, PERINO A, Zhan Gaofang, et al. Seismic response of a single and a set of filled joints of viscoelastic deformationalbehaviour[J]. Geophysical Journal International, 2011, 186(3): 1315. DOI:10.1111/j.1365-246x.2011.05110.x |
| [9] |
INDRARATNA B, JAYANATHAN M, BROWN T. Shear strength model for overconsolidated clay-infilled idealised rock joints[J]. Geotechnique, 2008, 58(1): 55. DOI:10.1680/geot.2008.58.1.55 |
| [10] |
INDRARATNA B, OLIVEIRA D A F, BROWN E T, et al. Effect of soil-infilled joints on the stability of rock wedges formed in a tunnel roof[J]. International Journal of Rock Mechanics and Mining Science, 2010, 47(5): 739. DOI:10.1016/j.ijrmms.2010.05.006 |
| [11] |
KAHRAMAN S. The effects of fracture roughness on P-wave velocity[J]. Engineering Geology, 2002, 63(3): 347. DOI:10.1016/S0013-7952(01)00089-8 |
| [12] |
赵坚. 岩石节理吻合系数及其对节理特性的影响[J]. 岩石力学与工程学报, 1997, 16(6): 514. ZHAO Jian. Joint match coefficient and effects to behavior of rock joint[J]. Chinese Journal of Rock Mechanics and Engineering, 1997, 16(6): 514. DOI:10.1007/BF02029074 |
| [13] |
陈昕, 李建春, 任奋华, 等. JMC对应力波透射系数和节理比刚度影响的实验研究[J]. 岩石力学与工程学报, 2016, 35(5): 957. CHEN Xin, LI Jianchun, REN Fenhua, et al. Experimental research of JMC effect on stress wave propagation and joint specific stiffness[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(5): 957. DOI:10.13722/j.cnki.jrme.2015.1717 |
| [14] |
LI Jianchun, LI Nana, LI Haibo, et al. An SHPB test study on wave propagation across rock masses with different contact area ratios of joint[J]. International Journal of Impact Engineering, 2017, 105: 109. DOI:10.1016/j.ijimpeng.2016.12.011 |
| [15] |
戎立帆, 李建春, 李海波, 等. 基于能量法测量节理岩体品质因子的实验研究[J]. 岩石力学与工程学报, 2017, 36(10): 2474. RONG Lifan, LI Jianchun, LI Haibo, et al. Measurement of seismic quality factor of jointed rock based on stress wave energy[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(10): 2474. DOI:10.13722/j.cnki.jrme.2017.0372 |
| [16] |
杨阳, 杨仁树, 王建国. 节理厚度对岩石动力特性影响的模拟试验[J]. 中国矿业大学学报, 2016, 45(2): 211. YANG Yang, YANG Renshu, WANG Jianguo. Simulation material experiment on dynamic mechanical properties of jointed rock affected by joint thickness[J]. Journal of China University of Mining and Technology, 2016, 45(2): 211. DOI:10.13247/j.cnki.jcumt.000474 |
| [17] |
王礼立. 应力波基础[M]. 2版. 北京: 国防工业出版社, 2010: 39. WANG Lili. Foundation of stress waves[M]. 2nd ed. Beijing: National Defense Industry Press, 2010: 39. |
| [18] |
李娜娜, 李建春, 李海波, 等. 节理接触面对应力波传播影响的SHPB试验研究[J]. 岩石力学与工程学报, 2015, 34(10): 1994. LI Nana, LI Jianchun, LI Haibo, et al. SHPB experiment on influence of contact area of joints on propagation of stress wave[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(10): 1994. DOI:10.13722/j.cnki.jrme.2015.0419 |
| [19] |
李夕兵. 岩石动力学基础与应用[M]. 北京: 科学出版社, 2014: 67. LI Xibing. Rock dynamics fundamentals and applications[M]. Beijing: Science Press, 2014: 67. |
| [20] |
刘婷婷, 李建春, 李海波, 等. 接触面积对波传播规律及节理力学特性影响[J]. 岩石力学与工程学报, 2014, 33(9): 1749. LIU Tingting, LI Jianchun, LI Haibo, et al. Effects of contact area on stress wave propagation and joint mechanical properties[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(9): 1749. DOI:10.13722/j.cnki.jrme.2014.09.003 |
 2019, Vol. 51
2019, Vol. 51


