随着纳米技术的发展,微机电系统(Micro Electro Mechanical Systems,MEMS)逐步向纳机电系统(Nano Electro Mechanical Systems,NEMS)过渡,从微米到纳米,不仅是尺寸的改变而且是本质的跃迁[1].由于缺少对纳米材料器件工作过程中变形机理的研究,尤其是纳米材料变形过程中材料缺陷演生过程及材料内应力传递方式等方面的研究,未能有效分析纳米材料器件失效的微观原因,NEMS的应用受到限制,仍处于一种“能看不能用,能用不能动”的状态[2].因此,研究多晶纳米材料的变形机理对提升纳米材料性能具有重要意义[3-7].大量学者[8-20]针对纯金属多晶材料力学特性进行研究,包括晶粒度、位错形核、位错演生、变形机制、晶界结构等方面,并针对合金材料力学特性进行研究,包括溶质作用、晶界强化、偏析现象、弹性模量、晶界滑移与耦合、位错密度等方面.此外,大量研究结果表明合金元素可提高多晶材料晶界结构稳定,赵等[21]研究了元素比例对铜铅合金内部应力的影响;Babicheva等[22]研究了第二相元素对铝基合金拉伸变形的作用,发现Co、Fe的加入对晶界具有强化作用,能够提高多晶合金的屈服应力;Rupert[23]研究了铜基二元合金的溶质作用,随着Ni含量的增加,合金的的强度增加,随着Pb含量的增加,合金的强度下降;Purohit等[24]建立了双晶铝模型,选择一定比例铅原子替换模型中的铝原子,得到稳定的铝铅合金,研究表明模型中的铅原子会优先偏析到晶界位置.
由于纳米压痕,原子力显微镜法,扫描电镜法,透射电镜法,聚焦粒子束法及X射线衍射法等实验方法[25-30]在不同程度上受到实验条件及测试尺度的限制,而分子动力学方法[31-32](molecular dynamics,MD)能够从原子尺度解释材料变形机理及力学特性,被广泛用于材料的纳米加工机理研究中.
铜铅合金由于铜的高塑性、高强度以及铅的自润滑功能,显现出优良的抗磨性,是经过实践检验证明的优良减磨材料,广泛应用于精密机械和航空航天领域中.本工作基于Poisson-Voronoi和Inverse Monte Carlo法建立大规模多晶铜分子动力学模型,并采用hybrid MC/MD方法将不同比例分数的金属铅混入多晶铜模型,建立不同铅含量的铜铅合金分子动力学模型.通过MD模拟对比了多晶铜及铜铅合金的力学特性,研究了合金元素比例对铜铅合金材料位错演生的影响,研究了力学特性、位错形核与扩展、内应力、原子势能分布的影响.对合金元素作用机制及晶界结构进行了分析,以期为铜铅合金材料纳米拉伸的变形机理提供一些理论依据.
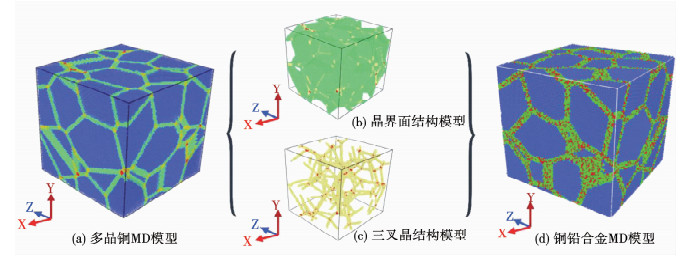
1 建模与模拟 1.1 模型的建立图 1为多晶铜及铜铅合金MD模型,多晶铜及铜铅合金模型尺寸均为41.5×41.5×41.5 nm3,包含约6.10×106个原子,晶粒度为10.74 nm.其中多晶铜模型采用Poisson-Voronoi和Inverse Monte Carlo法建立,包括晶粒内部与晶界两种结构,如图 1a所示.本工作中多晶体模型晶界结构根据维度数的差异被进一步划分为晶界面(2维)、三叉晶界(1维)及顶点团(0维)等微观结构,具体过程请参考本课题组前期工作[33-34].微观结构划分简要过程为:1)建立Voronoi胞拓扑结构模型并保证Voronoi胞具有与实际晶粒相近的尺寸,使Voronoi胞尺寸满足Monte Carlo分布;2)建立单晶材料的晶体结构模型用于填充Voronoi胞;3)通过识别Voronoi胞拓扑模型中各微观结构与2)中原子结构模型原子位置的对应关系,晶界被进一步划分为三类微观结构[35].本工作研究的铜铅合金模型具有与多晶铜模型相同的Voronoi胞,采用hybrid MC/MD方法将铅原子逐步加入多晶铜模型[36-37],采用半巨正则系综方法定位模型中溶质原子[38],并基于铜铅合金势函数最终获得具有不同比例分数的一系列铜铅合金模型,具体建模方法请参考本课题组前期工作[21].本工作研究的多晶铜及铜铅合金模型沿三个轴方向均采用周期性边界条件以消除仿真中尺寸效应的影响.
|
图 1 多晶铜及铜铅合金拉伸分子动力学模拟模型 Fig. 1 Molecular dynamics simulation model of polycrystalline copper and copper-lead alloy |
初始模型采用共轭梯度法实现能量最小化并在等温等压系综(NPT系综)通过Nose-Hoover热浴法在300 K下完成弛豫,弛豫时间为100 ps.弛豫后的模型在正则系综(NVT系综)进行拉伸MD模拟.本文采用EAM势模拟多晶铜和铜铅合金拉伸变形过程,只需此势函数便可以计算铜铅合金中铜-铜、铜-铅、铅-铅之原子间的相互作用力,EAM势表达式为
| $ {E_i} = {F_\alpha }\left( {\sum\limits_{j \ne i} {{\rho _\beta }} \left( {{r_{ij}}} \right)} \right) + \frac{1}{2}\sum\limits_{j \ne i} {{\varphi _{\alpha \beta }}} \left( {{r_{ij}}} \right) $ |
式中:Fα为嵌入能,ρβ为原子的电子云密度,φαβ为元素αβ的原子对势.
模拟时间步长为1 fs,远小于铅原子与铜原子间的振荡频率.MD模拟的真实拉伸速率为0.2% ps-1,最大应变量为20%,期间每隔0.5%记录一次数据,以测量系统在该拉伸速率下各原子的坐标及应力、原子势能等模拟参数.
多晶铜及铜铅合金拉伸过程是对其晶粒内部稳定的fcc晶体结构的破坏过程,该过程位错在晶界处大量形核并滑移,模型应变量不累积并产生显着的塑性变形.利用ovitio软件,采用共近邻分析法(local crystalline structure, CNA)追踪识别模拟拉伸过程中位错原子的形核及扩散,并分析材料内应力、原子势能(potential energy,PE)的变化规律.为简化应力分析,消除微观尺度上晶粒的取向不同造成的应力各向异性的影响,本文采用静水压力(hydrostatic stress,HY)与Mises等效应力(von Mises stress,VM)表征应力,静水压力与Mises等效应力的计算方法,请参考本课题组前期工作[39].
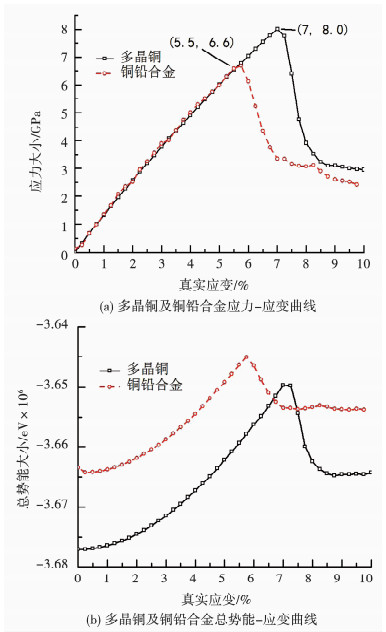
2 结果与讨论 2.1 多晶铜与铜铅合金力学特性对比图 2为多晶铜及铜铅合金拉伸应力、总势能-应变曲线,其中铜铅合金中铅原子比例为3.2%.发现材料塑性变形过程中当应变量为0~5.5%时,两种材料应力变化趋势一致,随后铜铅合金应力曲线迅速下降,而多晶铜应变量为7%时应力曲线开始下降.根据系统势能变化曲线,发现势能曲线的转折点与应力曲线转折点一致,这是由于裂纹生长过程材料的应力及势能均开始下降.由于加入铅原子导致系统势能增加,铜铅合金的势能曲线高于多晶铜势能曲线.铜铅合金的极限强度小于多晶铜,而且铜铅合金产生裂纹早于多晶铜,其材料塑性相比多晶铜显著降低.
|
图 2 多晶体及铜铅合金应力、总势能随应变量变化 Fig. 2 The stress-true strain and total potential energy-true strain curves of polycrystalline copper and copper-lead alloy |
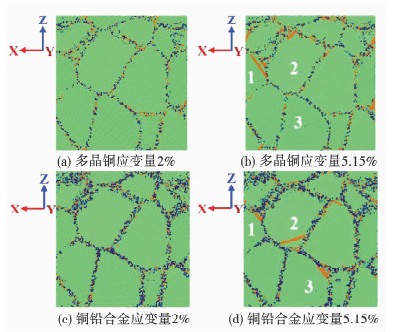
图 3为多晶铜及铜铅合金在不同应变时刻的位错形核及扩展过程.由于铅原子比例较小,两模型在塑性变形时的缺陷分布差别不明显.对比图 3 (b)和(d),发现少量铅原子的加入导致材料晶界结构不规则度进一步增大.此外,多晶铜和铜铅合金在1号晶粒顶点团区域均产生了位错,铜铅合金3号晶粒虽然出现了位错核,但始终没有向晶粒内部扩展,这是由于该晶粒的{111}晶面与晶界面结构相交,晶界面阻碍了位错的扩展.铜铅合金3号晶界存在位错形核与堆积,此时晶界原子应力较高,晶界将高应力传递到相邻的2号晶界从而在2号晶粒内部产生新的位错层.
|
图 3 多晶铜及铜铅合金位错形核与扩展 Fig. 3 The defect nucleation and propagation process in polycrystalline copper and copper-lead alloy |
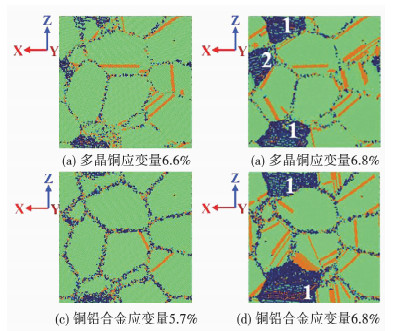
随着多晶铜及铜铅合金应变量进一步累积,当应力增大到材料能承受的最大应力时,材料出现裂纹,此时的最大应力为材料的极限强度,模型总势能也达到最大值,如图 4所示.发现铜铅合金出现裂纹早于多晶铜,其中多晶铜和铜铅合金分别为8.02 GPa、6.76 GPa.此时,多晶铜和铜铅合金晶粒内部存在大量的堆垛层错,由于部分晶粒强度较弱、晶粒变形严重,晶粒内部出现多个平行的位错层,部分晶粒内部出现平行层错、交叉层错及孪晶层.对比多晶铜和铜铅合金的缺陷分布发现,同一时刻铜铅合金的HCP原子比例低于多晶铜,铅元素加入抑制了缺陷结构的形核与扩展.此外,多晶铜和铜铅合金均为沿晶断裂,即裂纹在晶界面产生并扩展到其他晶界位置.裂纹扩展阶段多晶铜在晶界位置产生了1、2两个空位,两空位沿晶界扩展并相遇,加快了裂纹扩展进程.铜铅合金在相同位置产生了相同的空位1,而空位2并没有形成,空位1裂纹沿晶界面扩展到相邻晶界面处,相比多晶铜的扩展速度慢.
|
图 4 多晶铜及铜铅合金内部缺陷分布 Fig. 4 The defect distribution in polycrystalline copper and copper-lead alloy with large plastic deformation |
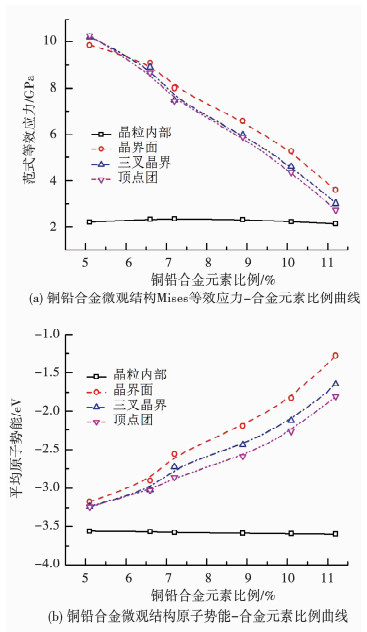
为了更好地分析合金元素铅的比例对铜铅合金力学性能的影响,采用比例分别为5.1%、6.6%、7.2%、8.9%、10.1%、11.2%的铜铅合金进行拉伸MD模拟.图 5为铜铅合金微观结构应力及势能随合金铅元素比例变化,对比各微观结构的Mises等效应力,发现其大小降序为晶界面、三叉晶界、顶点团,这说明虽然三叉晶界和顶点团在局部区域应力集中,但晶界面原子普遍承受着较高的剪应力.根据图 5(b),发现铜铅合金平均原子势能随铅元素比例的增加而增加,这是由于铅的结合能高于铜原子.晶粒势能基本保持不变,约等于铜的结合能;晶界势能随铅元素比例的增加线性升高,铜铅合金的势能大小也呈现晶界面、三叉晶界、顶点团、晶粒的递减趋势.表明铜铅合金材料的晶界面原子最不稳定,对材料本身特性的影响最大.
|
图 5 铜铅合金微观结构应力及势能随铅元素比例变化 Fig. 5 The variations of von Mises stress and atomic potential energy with fraction of lead for microstructural components in copper-lead alloy |
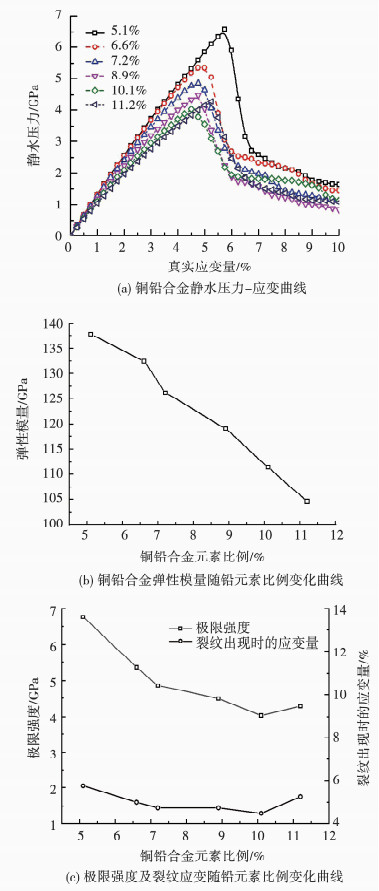
图 6为铅元素比例对铜铅合金力学性能的影响,图 6(a)中,发现铜铅合金的应力应变曲线均呈现先线性上升后急速下降再缓慢下降的特点,与多晶铜的应力变化特点一致.图 6(b)中,随着铅比例的增加,应力上升速度逐渐减小,铜铅合金的弹性模量逐渐降低,这是由于铅的弹性模量小于铜,当向多晶铜中加入铅原子使得整体材料的弹性模量降低,纳米级铜铅合金的这一特性与宏观尺度下的铜铅合金是相同的.应力上升到最大值时,材料强度达到最大.此外,图 6(c)中,铜铅合金的极限强度在加入少量的铅原子就表现出明显的减弱现象,后随着铅比例的增加表现出轻微的先减小后增加的特点.极限强度对应的应变即为材料产生裂纹的时刻,可以看出,随着铅比例的增加,铜铅合金出现裂纹的时刻先提前后推迟,由于产生裂纹的时间代表着材料的塑性强弱,因此铜铅合金塑性由于铅原子的作用表现出先减弱后增强的特性.
|
图 6 铅元素比例对铜铅合金力学性能的影响 Fig. 6 Fraction of lead in copper-lead alloy effects on the mechanical properties |
图 7为铜铅合金晶粒内部及晶界静水压力随真实应变量变化曲线.发现不同铜铅合金的变化趋势相同,晶粒内部总势能随应变量增大先升高后降低,晶界势能随应变的增加先降低后升高.根据图 7(a),发现铜铅合金晶粒内部势能曲线随含铅量高的先升高后降低.随铅原子比例的增大,铜铅合金拉伸过程累积的最大势能逐渐降低.根据图 7(b),发现铜铅合金晶粒内部势能曲线均呈现先降低后升高的趋势,且随着晶界处铅原子的增多,晶界势能变化量更大,材料产生裂纹前相同应变量时,晶界势能随含铅量高的升高而降低,产生裂纹后相同应变量时的晶界势能含铅量高的升高而升高,其中晶界全部为铅原子时的晶界势能在材料塑性阶段的变化量很大,表明铜铅合金中晶界原子在塑性变形中的作用大于晶粒内部原子的作用.

|
图 7 铜铅合金晶粒内部及晶界静水压力随应变变化 Fig. 7 The variations of hydrostatic stress of the grain cell and grain boundary interface with true strain in copper-lead alloy |
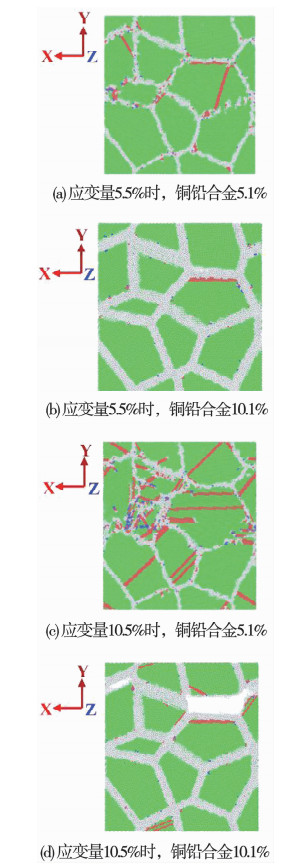
图 8为铅元素比例对铜铅合金位错分布的影响.根据原子的CNA分析,发现当应变为5.5%时,图 8(a)、(b)的应力仍在增加,即前两个模拟模型仍在塑性变形阶段,通过对比铜铅合金在不同应变条件下的位错分布,发现当铅比例较低时,铜铅合金抵抗变形的能力较弱,在塑性变形阶段晶粒内部已经位错层,位错一般在晶界位置产生;铅元素比例较高时,铜铅合金在塑性变形阶段的裂纹是缺陷产生的驱动因素,裂纹周围出现多个位错层.当应变为10%时,所有的铜铅合金模型都产生了大量的裂纹.此外,随着铅比例的增加,缺陷原子明显减少,晶界内部原子排列有序度增加,这表明铅原子在材料拉伸过程中可以减小材料内部缺陷,有效抑制位错的形成与扩展.
|
图 8 铅元素比例对铜铅合金位错分布的影响 Fig. 8 The fraction of lead effects on defect distribution in copper-lead alloy |
图 9为铜铅合金HCP原子比例变化曲线.发现铜铅合金弹性变形阶段各模型HCP原子数均保持不变,铅比例高的模型在弹性阶段的HCP相对要少,这是因为铅原子的增多导致晶界原子无序度增加,从而增加了未知结构的原子数目,HCP原子比例减少.随着拉伸应变量累积,铜铅合金原子晶格的较小增量变化无法满足外加载荷导致的应变量,材料进入塑性变形阶段,材料开始出现小部分HCP原子,位错核增多.当应力上升到材料能承受的最大强度时,晶界面区域出现裂纹,随着裂纹沿晶界面的扩展,材料局部变形严重,裂纹周围的位错核向晶粒内部扩展形成位错层,HCP原子比例开始明显增多.位错扩展阶段的HCP曲线能明显看出铅比例高的铜铅合金HCP原子比例少,即合金铅元素比例的增大导致缺陷结构形核受到抑制.

|
图 9 铜铅合金HCP原子比例变化曲线 Fig. 9 The variation of fraction of HCP atoms with true strain in copper-lead alloy |
本工作表明,铜铅合金力学特性及塑性变形过程与合金元素比例密切相关,合金元素主要通过改变合金材料晶界结构来改变合金材料性能.由于晶界结构可根据维度数不同,进一步划分为晶界面、三叉晶界及顶点团结构,合金元素对不同微观结构的作用机制有待进一步研究.此外,为了进一步提高多晶材料的机械加工性能,可将合金元素定向加入多晶材料不同的微观结构,从而定量的研究合金元素对多晶材料力学特性的影响机制,我们将在后续的工作中进一步研究微观结构对合金材料加工特性及变形机理.
3 结论本文针对多晶铜和加入少量铅原子的铜铅模型进行拉伸MD模拟,通过分析模型应力、势能、配位数、原子结构等获取了铅原子对多晶铜材料力学特性与变形机理的影响,得到以下结论:
1) 铜铅合金和多晶铜的静应力分布相似,铜铅合金晶界的Mises等效应力、CNA和势能均高于多晶铜,由于二者晶粒内部应力、CNA、势能值基本相等,表明铅元素的加入主要影响合金的晶界性能.
2) 铜铅合金在拉伸过程中具有的应力、势能、原子配位数等变化规律与多晶铜拉伸过程各参数变化规律相似,铜铅合金的弹性模量和极限强度均小于多晶铜,此外,铅原子能够抑制合金材料晶界处位错形核与扩展,从而获得稳定的晶界结构.
3) 当不同铅原子比例的铜铅合金模型的晶界体积分数相同时,弛豫结果表明铅比例对静水压力影响较小,不同微观结构的Mises等效应力随合金铅元素比例的增加呈线性降低,势能随合金铅元素比例的增加呈线性增长.
4) 随着铅原子比例的增加,晶粒内部缺陷明显减少,铜铅合金的弹性模量呈线性下降,极限强度和断裂时间均呈现先减小后略有增加.铜铅合金的势能和应力应变曲线相似,晶粒和晶界的势能变化特点完全不同,晶界结构在材料的塑性变形过程中具有重要作用.
| [1] |
LOH O Y, ESPINOSA H D. Nanoelectromechanical contact switches[J]. Nature Nanotechnology, 2012, 7(5): 283. DOI:10.1038/NNANO.2012.40 |
| [2] |
CHEN Changyao, HONE J. Graphene nanoelectromechanical systems[J]. Proceedings of the IEEE, 2013, 101(7): 1766. DOI:10.1109/JPROC.2013.2253291 |
| [3] |
LIN Yenhung, CHEN Teichen. A molecular dynamics study of phase transformations in mono-crystalline si under nanoindentation[J]. Applied Physics A, 2008, 92(3): 571. DOI:10.1007/s00339-008-4633-9 |
| [4] |
XU Baoxing, YUE Zhufeng, CHEN Xi. Numerical investigation of indentation fatigue on polycrystalline copper[J]. Journalof Materials Research, 2009, 24(3): 1007. DOI:10.1557/jmr.2009.0107 |
| [5] |
HOU X D, BUSHBY A J, JENNETT N M. Study of the interaction between the indentation size effect and hal-lcpetch effect with spherical indenters on annealed polycr-ystalline copper[J]. Journal of Physics D: Applied Physic-s, 2008, 41(7): 074006. DOI:10.1088/0022-3727/41/7/074006 |
| [6] |
XU Baoxing, YUE Zhufeng, WANG Jin. Indentation fatigue beh-aviour of polycrystalline copper[J]. Mechanics of Materials, 2007, 39(12): 1066. DOI:10.1016/j.mechmat.2007.06.001 |
| [7] |
CHEN Jian, SHEN Yuanfang, LIU Wenlin, et al. Effects of loading rate on development of pile-up during indentation creep of polycrystalline copper[J]. Materials Science and Engineering: A, 2016, 656: 216. DOI:10.1016/j.msea.2016.01.042 |
| [8] |
LUCCA D A, HERRMANN K, KLOPFSTEIN M J. Nanoindentation: Measuring methods and applications[J]. CIRP annals, 2010, 59(2): 803. DOI:10.1016/j.cirp.2010.05.009 |
| [9] |
MICIC M, KLYMYSHYN N, SUH Y D, et al. Finite element method simulation of the field distribution for afm tip-enhanced surface-enhanced raman scanning microscopy[J]. The Journal of Physical Chemistry B, 2003, 107(7): 15749. DOI:10.1021/jp022060s |
| [10] |
FANG Fengzhou, LIU Bing, XU Zongwei. Nanome-tric cutting in a scanning electron microscope[J]. Precision Engineering, 2015, 41: 145. DOI:10.1016/j.precisioneng.2015.01.009 |
| [11] |
YAN Jiwang, ASAMI T, HARADA H, et al. Fundamental investigation of subsurface damage in single crystalline silicon caused by diamond machining[J]. Precision Engineering, 2009, 33(4): 378. DOI:10.1016/j.precisioneng.2008.10.008 |
| [12] |
VOLKERT C A. Focused ion beam microscopy and micromaching[J]. MRS bulletin, 2007, 32(5): 389. DOI:10.1557/mrs2007.62 |
| [13] |
PELLICER E, VAREA A, PANE S, et al. Nanocrystalline electroplated cu-ni: Metallic thin films with enhanced mechanical properties and tunable magnetic behavior[J]. Advanced Functional Materials, 2010, 20(6): 983. DOI:10.1002/adfm.200901732 |
| [14] |
CASALS O, OCENASEK J, ALCALA J. Crystal plasticity finite element simulations of pyramidal indentation in copper single crystals[J]. Acta Materialia, 2007, 55(1): 55. DOI:10.1016/j.actamat.2006.07.018 |
| [15] |
ZHANG Kai, WEERTMAN J R, EASTMAN J A. The influence of time, temperature, and grain size on indentation creep in high-purity nanocrystalline and ultrafine grain copper[J]. Applied Physics Letters, 2004, 85(22): 5197. DOI:10.1063/1.1828213 |
| [16] |
JANG S, PUROHIT Y, IRVING D L, et al. Molecular dynamics simulations of deformation in nanocrystalline Al-Pb alloys[J]. Materials Science and Engineering: A, 2008, 493(1-2): 53. DOI:10.1016/j.msea.2007.05.130 |
| [17] |
JANG S, PUROHIT Y, IRVING D L, et al. Influence of Pb segregation on the deformation of nanocrystalline Al: Insights from molecular simulations[J]. Acta Materialia, 2008, 56(17): 4750. DOI:10.1016/j.actamat.2008.05.024 |
| [18] |
SCHAFER J, STUKOWSKI A, ALBE K. Plastic defo-rmation of nanocrystalline Pd–Au alloys: On the interplay of grain boundary solute segregation, fault energies and grain size[J]. Acta Materialia, 2011, 59(8): 2957. DOI:10.1016/j.actamat.2011.01.036 |
| [19] |
SCHAFER J, ALBE K. Influence of solutes on the competition between mesoscopic grain boundary sliding and coupled grain boundary motion[J]. Scripta Materialia, 2012, 66(5): 315. DOI:10.1016/j.scriptamat.2011.11.031 |
| [20] |
SCHAFER J, ALBE K. Plasticity of nanocrystalline alloys with chemical order: on the strength and ductility of nanocrystalline Ni-Fe[J]. Beilstein Journal of Nanotechnology, 2013, 4: 542. DOI:10.3762/bjnano.4.63 |
| [21] |
ZHAO Pengyue, GUO Yongbo. Element proportion effect on internal stress from interfaces and other microstr-uctural components in Cu-Pb alloys[J]. Molecular Simulati-on, 2019, 45: 815. DOI:10.1080/08927022.2019.1602868 |
| [22] |
BABICHEVA R I, DMITRIEV S V, Zhang Ying, et al. Effect of grain boundary segregations of Fe, Co, Cu, Ti, Mg and Pb on small plastic deformation of nanocrystalline Al[J]. Computational Materials Science, 2015, 98: 410. DOI:10.1016/j.commatsci.2014.11.038 |
| [23] |
RUPERT T J. Solid solution strengthening and softening due to collective nanocrystalline deformation physics[J]. Scripta Materialia, 2014, 81: 44. DOI:10.1016/j.scriptamat.2014.03.006 |
| [24] |
PUROHIT Y, SANG J, IRVING D L, et al. Atomistic modeling of the segregation of lead impurities to a grain boundary in an aluminum bicrystalline solid[J]. Materials Science and Engeering: A, 2008, 493(1-2): 97. DOI:10.1016/j.msea.2007.05.128 |
| [25] |
SCHIOTZ J, VEGGE T. Atomic-scale Simulations of the Mechanical deformation of nanocrystalline metals[J]. Physical Review B, 1999, 82(60): 11971. DOI:10.1103/PhysRevB.60.11971 |
| [26] |
VAN S H, DERLET P M, FROSETH A G. Nucleati-on and extension of dislocations in nanocrystalline fcc metals[J]. Acta Materialia, 2006, 54(7): 1975. DOI:10.1016/j.actamat.2005.12.026 |
| [27] |
BITZEK E, BRANDL C, DERLET P M, et al. Dis-location cross-slip in nanocrystalline fcc metals[J]. Physical Review Letters, 2008, 100(23): 235501. DOI:10.1103/PhysRevLett.100.235501 |
| [28] |
YAMAKOV V, WOLF D, PHILLPOT S R, et al. Dislocation processes in the defor-mation of nanocrystalline aluminium by molecular-dynamics simulation[J]. Nature Materials, 2002, 1: 45. DOI:10.1038/nmat700 |
| [29] |
SHABIB I, MILLER R E. Deformation characteristics and stress-strain response of nanotwinned copper via molecular dynamics simulation[J]. Acta Materialia, 2009, 57(15): 4364. DOI:10.1016/j.actamat.2009.05.028 |
| [30] |
RUPERT T J. Solid solution strengthening and softening due to collective nanocrystalline deformation physics[J]. Scripta Materialia, 2014, 81: 44. DOI:10.1016/j.scriptamat.2014.03.006 |
| [31] |
BABICHEVA R I, DMITRIEV S V, ZHANG Y, et al. Effect of grain boundary segregations of Fe, Co, Cu, Ti, Mg and Pb on small plastic deformation of nanocrystalline Al[J]. Computational Materials Science, 2015, 98: 410. DOI:10.1016/j.commatsci.2014.11.038 |
| [32] |
PUROHIT Y, SANG J, IRVING D L, et al. Atomisticmodeling of the segregation of lead impurities to a grain boundary in an aluminum bicrystalline solid[J]. Materials Science and Engineering: A, 2008, 493(1-2): 97. DOI:10.1016/j.msea.2007.05.128 |
| [33] |
GUO Yongbo, XU Tao, LI Mo. Generalized type iii internal stress from interfaces, triple junctions and other microstructural components in nanocrystalline materials[J]. Acta Materialia, 2013, 61: 4974. DOI:10.1016/j.actamat.2013.04.048 |
| [34] |
GUO Yongbo, XU Tao, LI Mo. Hierarchical dislocati-on nucleation controlled by internal stress in nanocrystalline copper[J]. Appl. Phys. Lett., 2013, 102(24): 241910. DOI:10.1063/1.4811791 |
| [35] |
LI Mo, XU Tao. Topological and atomic scale characterization of grain boundary networks in polycrystalline and nanocrystalline materials[J]. Progress in Materials Science, 2011, 56(6): 864. DOI:10.1016/j.pmatsci.2011.01.011 |
| [36] |
VO N Q, SCHAFER J, AVERBACK R S, et al. Reaching theoretical strengths in nanocrystalline Cu by grain boundary doping[J]. Scripta Materialia, 2015, 65(8): 660. DOI:10.1016/j.scriptamat.2011.06.048 |
| [37] |
CARO A, FARKAS D, BRINGA E M, et al. Effects of microalloying on the mobility and mechanical response of interfaces in nanocrystalline Cu[J]. Materials Science Forum, 2009, 633-634(6): 21. |
| [38] |
PAREIGE C, DOMAIN C, OLSSON P. Short-and long-range orders in Fe-Cr: A Monte Carlo study[J]. Journal of Applied Physics, 2009, 106(10): 104906-1. DOI:10.1063/1.3257232 |
| [39] |
GUO Yongbo, XU Tao, LI Mo. Atomistic calculation-f internal stress in nanoscale polycrystalline materials[J]. Philos. Mag. A, 2012, 92(24): 3064-3083. DOI:10.1080/14786435.2012.685963 |
 2019, Vol. 51
2019, Vol. 51


