多重信号分类(Multiple Signal Classification,MUSIC)是应用于测向系统中信号波达方向(direction-of-arrival,DOA)估计的著名算法[1-2],该算法基于已知的信号源个数,利用噪声与信号子空间的正交性构造具有“超分辨力”的空间谱函数[3-4],并通过谱峰搜索获取DOA.通常,谱峰搜索的计算量异常庞大[5],因此MUSIC算法的工程应用效果并不是十分理想[6-8].为降低计算量,学者提出了求根MUSIC(root-MUSIC)算法[9],该算法是高效派生算法的典型代表[10-11],具有良好的分辨性能.后来,一种利用酉变换对协方差矩阵进行实值分解的方法被提出[12].此方法在实值DOA估计中被广泛采用,但由于算法所构造的是复系数多项式,在阶次较高的情况下,获取信源DOA的求根过程中涉及复数运算,计算复杂度较高[13-14].在root-MUSIC算法的基础之上,文献[15]基于阵列的范德蒙结构,提出了一种利用接收数据构造多项式并求根的方法,保证了在快拍数较少的情况下也能正常工作.
本文提出的基于实系数多项式闭式求根的DOA估计(Real-Coefficient root-MUSIC,RC-root-MUSIC)算法则利用变换域的思想,进一步将复系数的求根多项式转化为同阶次的实系数求根多项式,降低了计算复杂度.最后在利用实值运算进行信源DOA的求解时,运用了Bairstow快速算法[16],在保证计算精度的前提下提高了计算效率,从而为root-MUSIC算法的工程化推进提供了理论依据.
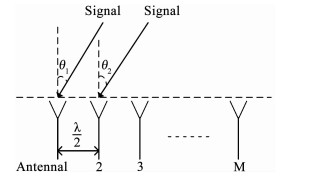
1 信号模型及相关算法 1.1 信号模型假设XOY平面存在M个相互独立的阵元,以半波长等间距放置并组成均匀线阵(uniform linear array,ULA)模型.考虑空间中存在N个远场窄带信号并且通道附加高斯白噪声,定义DOA为信号与阵列法线的夹角[2],如图 1所示.则阵列接收数据为
|
图 1 阵列模型 Fig. 1 Array model |
| $ \boldsymbol{X}(t)=\boldsymbol{A}({\theta}) \boldsymbol{S}(t)+\boldsymbol{N}(t), $ |
式中:
| $ \mathit{\boldsymbol{\alpha }}\left( {{\theta _i}} \right) = {\left[ {1, {{\rm{e}}^{{\rm{ - j}}{{\rm{ \mathsf{ τ} }}_{{\rm{1i}}}}}}, \cdots , {{\rm{e}}^{{\rm{ - j}}{{\rm{ \mathsf{ τ} }}_{{\rm{Mi}}}}}}} \right]^{\rm{T}}}, i \in [1, N]. $ |
式中
| $ {{\rm{ \mathsf{ τ} }}_{{\rm{ki}}}} = \frac{{2{\rm{ \mathsf{ π} }}({\rm{k}} - 1){\rm{d}}\sin {{\rm{ \mathsf{ θ} }}_i}}}{\lambda }. $ |
式中:d=λ/2,λ为入射信号的波长.
| $\boldsymbol{R}=E\left[X X^{\mathrm{H}}\right]=\boldsymbol{A} \boldsymbol{R}_{\mathrm{s}} \boldsymbol{A}^{\mathrm{H}}+\boldsymbol{\sigma}_{\mathrm{n}}^{2} \boldsymbol{I}.$ |
式中: Rs为信号协方差矩阵,σn2为高斯白噪声功率.对R进行特征值分解,可得
| $ \mathit{\boldsymbol{R}} = \sum\limits_{{\rm{i}} = 1}^N {{\lambda _{\rm{i}}}} {\mathit{\boldsymbol{e}}_{\rm{i}}}\mathit{\boldsymbol{e}}_{\rm{i}}^{\rm{H}} + \sum\limits_{{\rm{j}} = N + 1}^M {{\lambda _{\rm{j}}}} {\mathit{\boldsymbol{e}}_{\rm{j}}}\mathit{\boldsymbol{e}}_{\rm{j}}^{\rm{H}}. $ |
式中:λi, i=1, 2, …, N为矩阵R的N个大特征值,λj, j=N+1, …, M为(M-N)个小特征值,由λi和λj分别对应的特征向量ei和ej构成了矩阵
| $\left\{\begin{array}{l}{\boldsymbol{U}_{\mathrm{s}} \triangleq\left[\boldsymbol{e}_{1}, \boldsymbol{e}_{2}, \cdots, \boldsymbol{e}_{\mathrm{N}}\right]}, \\ {\boldsymbol{U}_{\mathrm{n}} \triangleq\left[\boldsymbol{e}_{\mathrm{N}+1}, \boldsymbol{e}_{\mathrm{N}+2}, \cdots, \boldsymbol{e}_{\mathrm{M}}\right]}.\end{array}\right.$ |
则Us和Un的列向量分别张成了信号子空间和噪声子空间,并且span(Us)⊥span(Un)以及span(Us)=span(A).
1.2 MUSIC算法根据信号与噪声两者子空间的正交性,在信号DOA方向有aH(θ)Un=0,进一步可以通过‖aH(θ)Un‖得到MUSIC空间谱函数
| $ {f_{{\rm{MSUIC}}}}(\theta ) = \frac{1}{{{\alpha ^{\rm{H}}}(\theta ){\mathit{\boldsymbol{U}}_{\rm{n}}}\mathit{\boldsymbol{U}}_{\rm{n}}^{\rm{H}}\alpha (\theta )}}. $ | (1) |
通过在[-π/2, π/2]进行遍历搜索,找出式(1)的极大值点θ即为信源DOA.
1.3 root-MUSIC算法根据上述阵列和信号模型,root-MUSIC算法定义如下多项式
| $ f_{\text {root }}(z)=\boldsymbol{p}^{\mathrm{H}}(z) \boldsymbol{U}_{\mathrm{n}} \boldsymbol{U}_{\mathrm{n}}^{\mathrm{H}} \boldsymbol{p}(z). $ |
式中z=ejw,导向矢量p(z)为
| $\boldsymbol{p}(z)=\left(1, z, z^{2}, \cdots, z^{\mathrm{M}-1}\right)^{\mathrm{T}}, $ |
对froot(z)求根即可求得信号DOA.考虑到式中含有z*项,做如下修正
| $f_{\text {root }}(z)=z^{\mathrm{M}-1} \boldsymbol{p}^{\mathrm{T}}\left(z^{-1}\right) \boldsymbol{U}_{\mathrm{n}} \boldsymbol{U}_{\mathrm{n}}^{\mathrm{H}} \boldsymbol{p}(z).$ | (2) |
此时,多项式froot(z)的阶数为2(M-1).由于具有埃尔米特属性,则其具有关于单位圆对称的M-1对共轭根,这M-1对根中有N对根分布在单位圆上.在实际应用中,考虑误差的存在,再得到N对靠近单位圆的根后,可按式(3)求解信号DOA
| $ {\theta _{\rm{i}}} = \arcsin \left( {\frac{\lambda }{{2{\rm{ \mathsf{ π} d}}}}\arg \left( {{z_{\rm{i}}}} \right)} \right), i \in [1, N]. $ | (3) |
root-MUSIC以多项式求根代替谱峰搜索,求解过程计算量减小.
2 实系数多项式闭式求根的快速DOA估计 2.1 实系数多项式RC-root-MUSIC算法在root-MUSIC算法中,根据式(2)令froot(z)=0并求根即可获得信号DOA.但多项式展开后涉及复数计算,复杂度较高.为方便计算,先对式(2)进行移项处理
| $f_{\text {root }}(z)=\boldsymbol{p}^{\mathrm{H}}(z) z^{\mathrm{M}-1} \boldsymbol{U}_{\mathrm{n}} \boldsymbol{U}_{\mathrm{n}}^{\mathrm{H}} \boldsymbol{p}(z).$ |
然后令pH(z)zM-1=pT(z)J,其中变换矩阵J为
| $\boldsymbol{J}=\left[\begin{array}{ccccc}{0} & {0} & {\cdots} & {0} & {1} \\ {0} & {0} & {\cdots} & {1} & {0} \\ {\vdots} & {\vdots} & {} & {\vdots} & {\vdots} \\ {0} & {1} & {\cdots} & {0} & {0} \\ {1} & {0} & {\cdots} & {0} & {0}\end{array}\right]_{\mathrm{M} \times \mathrm{M}}.$ | (4) |
此时,root-MUSIC算法的表达式可等价为
| $f_{\text {root }}(z)=\boldsymbol{p}^{\mathrm{T}}(z) \boldsymbol{J} \boldsymbol{U}_{\mathrm{n}} \boldsymbol{U}_{\mathrm{n}}^{\mathrm{H}} \boldsymbol{p}(z).$ | (5) |
由于式(5)为复系数表达式,直接进行求根运算,计算相当复杂.考虑到如果能够将复系数表达式实值化,那么将为降低root-MUSIC算法的计算量提供了可能.基于此分析,引入新的变量u来进行坐标系的转换,为后续的系数实值化进行预处理.变量u定义如下
| $ u(z) = - {\rm{j}}\frac{{z - {\rm{j}}}}{{z + {\rm{j}}}}. $ | (6) |
该变换将root-MUSIC谱函数froot(z)从传统的z域转换到u域,其反变换为
| $ z(u) = - {\rm{j}}\frac{{u - {\rm{j}}}}{{u + {\rm{j}}}}. $ | (7) |
显然,对于给定的z域DOA有唯一的u域DOA与其对应,则以u域和以z域得到的DOA具有相同的物理意义.
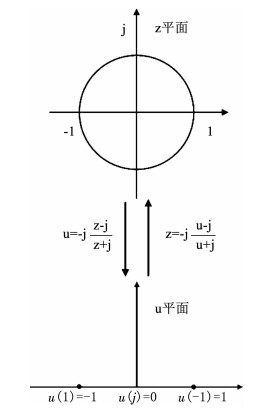
对于半波长ULA,w=π sin (θ).当θ∈[0, π/2]时,根据z=ejw及欧拉公式ejw=cos(w)+jsin(w)可知,z∈[1, -1],对应z平面的上半圆,根据式(6)映射到u平面实轴上对应u∈[-1, 1].同理当θ∈[-π/2, 0]时,u平面上映射区间为u∈(-∞, -1]∪[1, +∞),如下图 2所示.
|
图 2 坐标轴的转换关系 Fig. 2 Coordinate transformation relationship |
为进一步将复系数表达式转换为实系数表达式,将式(7)代入导向矢量p(z)中,可以得到u域中p(u)|z(u)的每一个元素
| $\boldsymbol{p}_{\mathrm{m}}(u)=z^{\mathrm{m}-1}=(-\mathrm{j})^{\mathrm{m}-1}\left(\frac{u-\mathrm{j}}{u+\mathrm{j}}\right)^{\mathrm{m}-1}, m \in[1, M].$ |
定义新的变量φ(u)
| $\begin{array}{c}{\varphi_{\mathrm{m}}(u)=p_{\mathrm{m}}(u) \times(u+\mathrm{j})^{\mathrm{M}-1}=} \\ {A \times(u-\mathrm{j})^{\mathrm{m}-1}(u+\mathrm{j})^{M-\mathrm{m}}}.\end{array}$ | (8) |
式中A=(-j)m-1.可以看出由φm(u), m∈[1, M]组成的φ(u)为M-1阶多项式,式(9)将φ(u)用矩阵简化为
| $ \varphi (u) = \mathit{\boldsymbol{Cv}}(u). $ | (9) |
式中:C为M×N维系数矩阵.对于半波长ULA阵列,C可以一次计算获得.v(u)为范德蒙向量
| $ \boldsymbol{v}_{\mathrm{m}}(u)=u^{\mathrm{m}-1}. $ | (10) |
根据式(8)中φ(u)和导向矢量p(u)的关系,p(u)可进一步表示为
| $ \boldsymbol{p}(u)=(u+\mathrm{j})^{1-\mathrm{M}} \boldsymbol{C} \boldsymbol{v}(u). $ | (11) |
将式(11)代入式(4)中可得u域中的root-MUSIC谱函数fRC-root(u)
| $ \begin{array}{c}{f_{\mathrm{RC}-\text { root }}(u)=\boldsymbol{p}^{\mathrm{T}}(u) \boldsymbol{JU}_{\mathrm{n}} \boldsymbol{U}_{\mathrm{n}}^{\mathrm{H}} \boldsymbol{p}(u)=} \\ {(u+\mathrm{j})^{2(1-\mathrm{M})} \times \boldsymbol{v}^{\mathrm{T}}(u) \times \boldsymbol{C}^{\mathrm{T}} \boldsymbol{J} \boldsymbol{U}_{\mathrm{n}} \boldsymbol{U}_{\mathrm{n}}^{\mathrm{H}} \boldsymbol{C} \boldsymbol{v}(u)}.\end{array} $ |
此时,当u=-j时fRC-root(u)=0.根据式(7)可知z=-∞,故舍去.从而获得修正后的fRC-root(u)
| $ f_{\mathrm{RC}-\text { root }}(u)=\boldsymbol{v}^{\mathrm{T}}(u) \boldsymbol{C}^{\mathrm{T}} \boldsymbol{J} \boldsymbol{U}_{\mathrm{n}} \boldsymbol{U}_{\mathrm{n}}^{\mathrm{H}} \boldsymbol{C} \boldsymbol{v}(u). $ | (12) |
可以看出式(12)是一个关于u的2(M-1)阶多项式.根据多项式求根的性质,一个2(M-1)阶多项式有2(M-1)个根,这些根可能为实根或复根.如果这个多项式是实系数多项式或虚系数多项式,那么它的复根将以共轭根对的形式呈现.
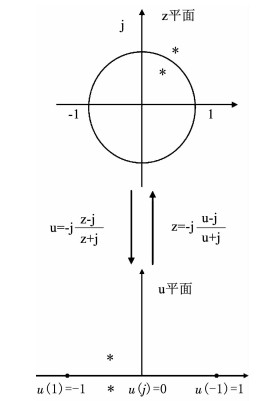
而在传统root-MUSIC算法中,多项式的根关于单位圆镜像对称,根据式(6)中z域和u域的转换关系可知,z域的单位圆映射到u域后为实轴.因此,在u域中这些多项式的根关于实轴呈共轭对称,如图 3所示.由此可以推出,式(12)中fRC-root(u)为实系数多项式或虚系数多项式.
|
图 3 不同坐标系下根的分布情况 Fig. 3 Roots distribution in different coordinate systems |
为进一步讨论fRC-root(u)中系数的实虚问题,根据根的分布情况,式(12)可做如下变换:
| $ \begin{array}{c}{\boldsymbol{Y}=\boldsymbol{C}^{\mathrm{T}} \boldsymbol{J} \boldsymbol{U}_{\mathrm{n}} \boldsymbol{U}_{\mathrm{n}}^{\mathrm{H}} \boldsymbol{C}}, \\ {f_{\mathrm{RC}-\mathrm{root}}(u)=\boldsymbol{v}^{\mathrm{T}}(u) \boldsymbol{Y} \boldsymbol{v}(u).}\end{array} $ | (13) |
以下根据M的奇偶性,可分两种情况对式(13)进行化简.
情况1:阵元数M为奇数时,Y为
| $ \mathit{\boldsymbol{Y}} = {\left( {\begin{array}{*{20}{c}} {{y_{11}} + {\rm{j}}{z_{11}}}& \cdots &{{y_{{\rm{ \mathsf{ ξ} \mathsf{ η} }}}} + j{z_{{\rm{ \mathsf{ ξ} \mathsf{ η} }}}}}\\ \vdots & \ddots & \vdots \\ {{y_{{\rm{ \mathsf{ η} \mathsf{ ξ} }}}} + {\rm{j}}{z_{{\rm{ \mathsf{ η} \mathsf{ ξ} }}}}}& \cdots &{{y_{{\rm{MM}}}} + {\rm{j}}{z_{{\rm{MM}}}}} \end{array}} \right)_{{\rm{M}} \times {\rm{M}}}}. $ | (14) |
式中:zξξ=0, ξ∈[1, M],yξη=yηξ,zξη=-zηξ.由于在计算中式(14)的虚部被抵消,v(u)为实向量,此时式(12)中fRC-root(u)为实系数多项式.为减少计算量,式(12)可简写为
| $ f_{\mathrm{RC}-\mathrm{root}}(u)=\boldsymbol{v}^{\mathrm{T}}(u) \operatorname{Re}\left\{\boldsymbol{C}^{\mathrm{T}} \boldsymbol{J} \boldsymbol{U}_{\mathrm{n}} \boldsymbol{U}_{\mathrm{n}}^{\mathrm{H}} \boldsymbol{C}\right\} \boldsymbol{v}(u), $ | (15) |
情况2:阵元数M为偶数时,Y为
| $ \mathit{\boldsymbol{Y}} = {\left( {\begin{array}{*{20}{c}} {{y_{11}} + {\rm{j}}{z_{11}}}& \cdots &{{y_{{\rm{ \mathsf{ ξ} \mathsf{ η} }}}} + {\rm{j}}{z_{{\rm{ \mathsf{ ξ} \mathsf{ η} }}}}}\\ \vdots & \ddots & \vdots \\ {{y_{{\rm{ \mathsf{ η} \mathsf{ ξ} }}}} + {\rm{j}}{z_{{\rm{ \mathsf{ η} \mathsf{ ξ} }}}}}& \cdots &{{y_{{\rm{MM}}}} + {\rm{j}}{z_{{\rm{MM}}}}} \end{array}} \right)_{{\rm{M}} \times {\rm{M}}}}. $ |
式中:yξξ=0, ξ∈[1, M],yξη=-yηξ,zξη=zηξ.由上述变换同理可知,式(12)中fRC-root(u)为虚系数多项式.对等式两遍取虚部
| $ f_{\mathrm{RC}-\mathrm{root}}(u)=\boldsymbol{v}^{\mathrm{T}}(u) \operatorname{Im}\left\{\boldsymbol{C}^{\mathrm{T}} \boldsymbol{J} \boldsymbol{U}_{\mathrm{n}} \boldsymbol{U}_{\mathrm{n}}^{\mathrm{H}} \boldsymbol{C}\right\} \boldsymbol{v}(u). $ | (16) |
此时,式(16)为实系数多项式,具有和式(13)相同的解,并且式(15)和式(16)均为2(M-1)阶.至此,z域中的复系数多项式在经过坐标轴变换后全部转化为u域中实系数多项式.最后根据式(17)可以得到传统的角度域和u域的关系
| $ w=(-\mathrm{j}) \times \ln \left(-\mathrm{j} \times \frac{u-\mathrm{j}}{u-\mathrm{j}}\right). $ | (17) |
如前文所述,RC-root-MUSIC的中心思想就是将复数运算转化为同阶次的实数运算,极大减少了计算量.而在实际应用中可以继续利用Bairstow快速求根法对实系数多项式进行求解.
2.2 实系数多项式求解的Bairstow算法RC-root-MUSIC算法虽然减少了计算量,但是所构造的实系数多项式具有和复系数多项式相同的阶数.当2(M-1)较大时,求根运算依旧十分复杂.考虑到实系数多项式具有关于实轴对称的根,而Bairstow算法通过利用收敛的二次因子可以对实系数多项式进行快速求根.由此分析,假设:x1=α+jβ和x2=α-jβ是RC-root-MUSIC中关于实轴对称的共轭根,则可构造一个二次因子x2+μx+ν,使x1, x2为二次因子的两个解.设n阶实系数多项式为
| $ P(x) = \sum\limits_{k = 0}^n {{a_{\rm{k}}}} {x^{\rm{k}}}. $ |
通常,实系数多项式除以一个二次因子时余项为一个线性项,即多项式可以改写为
| $ \begin{aligned} P(x)=& \sum\limits_{k=0}^{n} a_{{\rm k}} x^{{\rm k}}=\left(x^{2}+\mu x+\nu\right) Q(x)+R(x)=\\ &\left(x^{2}+\mu x+\nu\right)\left(\sum\limits_{k=0}^{n-2} b_{{\rm k}} x^{{\rm k}}\right)+R(x). \end{aligned} $ | (18) |
式中:Q(x)为P(x)除以二次因子x2+μx+ν的商,R(x)=Cx+D为余数.同时,式中各系数关系[16]可通过式(19)至式(22)求出:
| $ b_{\mathrm{n}}=b_{\mathrm{n}-1}=0, $ | (19) |
| $ b_{\mathrm{k}}=a_{\mathrm{k}+2}-\mu b_{\mathrm{k}+1}-\nu b_{\mathrm{k}+2}, $ | (20) |
| $ C=a_{1}-\mu b_{0}-\nu b_{1}, $ | (21) |
| $ D=a_{0}-\nu b_{0}. $ | (22) |
从上述公式可以看出,若给定μ和ν的值,则可求得C和D.因此,可把C和D看作μ和ν的函数,即定义C=C(μ, ν),D=D(μ, ν).Baristow法就是利用牛顿法求解μ和ν,即构造雅克比矩阵求解其偏导数.为得到μ和ν中偏导数项,对P(x)关于变量μ求导,有
| $ \frac{\partial P}{\partial \mu}=\left(x^{2}+\mu x+\nu\right) \frac{\partial Q}{\partial \mu}+x Q+\frac{\partial C}{\partial \mu} x+\frac{\partial D}{\partial \mu}=0. $ |
为方便化简进行移项,可得
| $ -x Q=\left(x^{2}+\mu x+\nu\right) \frac{\partial Q}{\partial \mu}+\frac{\partial C}{\partial \mu} x+\frac{\partial D}{\partial \mu}. $ | (23) |
同理对P(x)关于变量ν求导
| $ \frac{\partial P}{\partial \nu}=\left(x^{2}+\mu x+\nu\right) \frac{\partial Q}{\partial \nu}+Q+\frac{\partial C}{\partial \nu} x+\frac{\partial D}{\partial \nu}=0. $ |
并进行移项,可得
| $ -Q=\left(x^{2}+\mu x+\nu\right) \frac{\partial Q}{\partial \nu}+\frac{\partial C}{\partial \nu} x+\frac{\partial D}{\partial \nu}. $ | (24) |
为求解出系数再次用Q(x)除以二次因子x2+μx+ν
| $ Q(x) = \left( {{x^2} + \mu x + \nu } \right)\left( {\sum\limits_{i = 0}^{n - 4} {{f_i}} {x^i}} \right) + (Gx + H). $ | (25) |
利用待定系数法将式(24)与式(25)联立,可得其系数的内部关系如下:
| $ \begin{array}{l}{\frac{\partial C}{\partial \nu}=-G}, \\ {\frac{\partial D}{\partial \nu}=-H}.\end{array} $ |
由假设可知,x1, x2是x2+μx+ν=0的两个解,将其带入式(25)可进一步化简为
| $ Q\left(x_{1, 2}\right)=G x_{1, 2}+H. $ | (26) |
将式(26)代入式(23)中得:
| $ -x_{1}\left(G x_{1}+H\right)=\frac{\partial C}{\partial \mu} x_{1}+\frac{\partial D}{\partial \mu}. $ | (27) |
| $ -x_{2}\left(G x_{2}+H\right)=\frac{\partial C}{\partial \mu} x_{2}+\frac{\partial D}{\partial \mu}. $ | (28) |
由二次多项式根与系数的性质,得知:
| $ x_{1}+x_{2}=-\mu, $ | (29) |
| $ x_{1} x_{2}=\nu. $ | (30) |
将式(27)至式(30)联立并求解方程组,可将C和D中所有关于μ和ν的偏导数全部求出,结论如下:
| $ \begin{array}{c}{\frac{\partial C}{\partial \mu}=\mu G-H}, \\ {\frac{\partial D}{\partial \mu}=\nu G}.\end{array} $ |
由于Bairstow法仅限于实值运算并且每次仅求解多项式的一对共轭根,因此将其应用于RC-root-MUSIC算法中将具有重要的工程意义.根据上述性质,借助实系数多项式求根的方法可以快速估计信号DOA,这就是本文提出的RC-root-MUSIC算法,具体实施步骤如下
步骤一:对阵列协方差矩阵R进行特征值分解,得到信号子空间和噪声子空间;
步骤二:根据式(5)构造矩阵J,并根据式(9)至式(10)构造矩阵C以及范德蒙向量v;
步骤三:根据式(15)或(16)构造实系数多项式并利用Bairstow算法对其求根;
步骤四:从所有根中找出接近实轴的N对共轭对称根,根据式(17)求解出对应w的值;
步骤五:根据w与θ的对应关系,求解信号的波达角;
3 计算量分析首先分析经典MUSIC和root-MUSIC算法的计算量.由于这两种算法均包含协方差矩阵计算和特征值分解的步骤,两者的实值总计算量共为4×M2(N+M)[4],其中ο(·)为实数运算.通过文献[5]可知,复数的运算量通常是实数的4倍,因此,总计算量为4×M2(N+M).再分别考虑不同经典算法进行求解DOA时的不同计算量,MUSIC算法是通过谱峰搜索获得信源DOA,其计算量与在角度范围[-π/2, π/2]内的搜索总点数J成正比(一般情况下,J≫M3).而root-MUSIC则是通过多项式求根代替谱峰搜索,计算量与多项式的阶数成正比.
接下来考虑所提出的RC-root-MUSIC,协方差矩阵的计算和特征值分解均已考虑,这里不再详细赘述.RC-root-MUSIC的计算量主要体现在求根多项式的构建上,以奇阵元为例.式(24)中J和C可以通过离线求得,单元ο(6M3-6NM2)给出了构造RC-root-MUSIC算法中的实系数多项式的计算量.对算法所构造的2(M-1)阶多项式进行求根,其计算量为ο((2M-2)3).可以得出结论见表 1.
| 表 1 不同算法的计算量分析 Tab. 1 Computational complexity analysis of different algorithms |
通过RC-root-MUSIC与root-MUSIC的计算量分析可以看出,RC-root-MUSIC的计算量远小于root-MUSIC.当阵元数M较大时,RC-root-MUSIC计算量的优势更加突出.
4 仿真及分析 4.1 root-MUSIC和RC-root-MUSIC效率对比为进一步确认RC-root-MUSIC相比于root-MUSIC性能的优越性,本实验主要比较不同阵元数下两种算法的仿真时间.假设采用ULA阵型,两个入射信号的方向为10°和45°,信噪比SNR为15 dB,快拍数为300.
root-MUSIC与RC-root-MUSIC的200次蒙特卡洛实验运行总时长的对比如下表 2所示.为准确比较算法的运算速度,两种算法中均包含的协方差矩阵R以及特征分解不在考虑范围之内.由表 2可以看出,RC-root-MUSIC算法运算速度在大阵元情况下明显优于root-MUSIC算法.
| 表 2 运算速度对比表 Tab. 2 Comparison of calculation speed |
本实验主要验证root-MUSIC和RC-root-MUSIC在不同坐标系下根的分布情况.假设采用8阵元的ULA阵型,两个入射信号的方向为10°和45°,SNR为15 dB,快拍数为300.
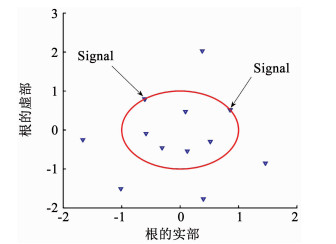
图 4为z域中root-MUSIC所构造多项式的根分布情况.由式(10)可知阵元数为8的情况下应拥有M-1=7对根,并且每对共轭根关于单位圆呈镜像对称,含有DOA信息的根位于单位圆附近.
|
图 4 z域中root-MUSIC根的分布 Fig. 4 Roots distribution map for root-MUSIC in the z domain |
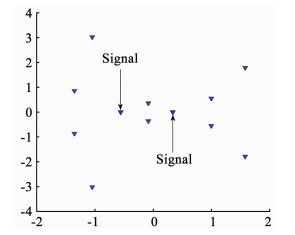
图 5为u域中RC-root-MUSIC所构造多项式的根分布情况.由式(31)可知有M-1=7对关于实轴对称的根,含有DOA信息的根位于实轴附近,因此RC-root-MUSIC算法可以准确估计信号源的个数.
|
图 5 u域中RC-root-MUSIC根的分布 Fig. 5 Roots distribution map for RC-root-MUSIC in the u domain |
本实验用于分析信噪比和快拍数在不同范围内对估计精度的影响.假设采用8阵元的ULA阵列,两个入射信号的方向为10°和45°,蒙特卡洛试验次数为200次.实验中采用均方根误差RMSE来描述角度估计的精度RRMSE为
| $ {R_{{\rm{RMSE}}}} = \sqrt {\frac{1}{{200}}\sum\limits_{{\rm{i}} = 1}^{200} {{{\left( {{\theta _i} - \theta } \right)}^2}} } . $ |
式中θi代表第i次蒙特卡洛实验得到的角度估计值.同时,引入MUSIC算法、求根MUSIC算法、酉求根MUSIC算法、ESPRIT算法[18]、实值求根MUSCI算法(RV-root-MUSIC)[19]以及非限制克拉美罗下界(Unconditional Cramer-Rao Lower Bound,CRLB)[17]来衡量估计的性能.其中,RV-root-MUSIC算法利用协方差矩阵实虚部分离原理,构建了一个2(M-1)阶实系数求根多项式,由于和本文所提出的RC-root-MUSIC算法具有相似性,因此作为性能仿真中的对比算法.
由图 6和图 7可见,本文提出的RC-root-MUSIC和经典的root-MUSIC算法具有相同的估计精度.原因在于RC-root-MUSIC算法采用的是坐标系变换的方法,其核心是坐标映射的关系.将式(15)改写为u=f(z),即u可以看作是z的函数.在RC-root-MUSIC算法中,先对u进行求解,然后将结果反带回z,因此可以得出RC-root-MUSIC和root-MUSIC具有相同的解的结论,从而两者具有相同的估计精度.
|
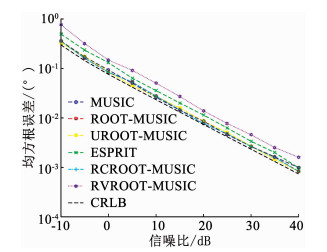
图 6 θ1信噪比对估计精度的影响 Fig. 6 Influence of SNR θ1 on estimate accuracy |
|
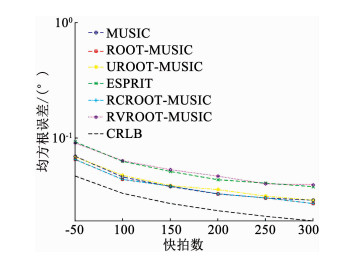
图 7 θ1快拍数对估计精度的影响 Fig. 7 Influence of snapshots number θ1 on estimate accuracy |
图 6中当信噪比在20 dB~40 dB的时候,root-MUSIC、RC-root-MUSIC,U-root-MUSIC和MUSIC的RMSE呈直线下滑的趋势4种算法的RMSE优于ESPRIT算法和RV-root-MUSIC算法并且均逐渐趋近于CRLB.而图 7中可以得到相同的结论,root-MUSIC和RC-root-MUSIC两种算法的RMSE相同并趋近于CRLB.从性能图中可以看出,本文所提出的RC-root-MUSIC算法具有和传统求根类算法相同的估计精度,同时优于新颖的RV-root-MUSIC算法.
5 结语本文在分析了高效超分辨算法中典型代表root-MUSIC算法的优缺点之后,先提出实系数多项式root-MUSIC算法,即RC-root-MUSIC算法,利用变换矩阵以及坐标系之间的映射,将复系数求根多项式转化为实系数求根多项式进行求解.再利用Bairstow算法,把一个复杂的实系数多项式逐步分解为多个一元二次多项式,实现了降次从而加快了求根的效率.最后通过计算机仿真,证明了所提出的算法保持了相同的DOA估计精度,降低了计算复杂度,并极大减少了计算时间,为root-MUSIC算法在工程应用中提供了强有力的理论依据.
| [1] |
SCHMIDIT R O. Multiple emitter location and signal parameter estimation[J]. IEEE Trans. on Antennas and Propagation, 1986, 34(3): 243. DOI:10.1109/TAP.1986.1143830 |
| [2] |
王永良. 空间谱估计理论与算法[M]. 北京: 清华大学出版社, 2004: 18. WANG Yongliang. Theory and algorithm of spatial spectrum estimation[M]. Peking: Tsinghua University Press, 2004: 18. |
| [3] |
YAN Fenggang, JIN Ming, QIAO Xiaolin. Low-complexity DOA estimation based on compressed MUSIC and its performance analysis[J]. IEEE Trans. on Signal Processing, 2013, 61(8): 1915. DOI:10.1109/TSP.2013.2243442 |
| [4] |
YAN Fenggang, LIU Shuai, WANG Jun, et al. Real-valued root-MUSIC for DOA estimation with reduced-dimension EVD/SVD computation[J]. Signal Processing, 2018, 152: 1. DOI:10.1016/j.sigpro.2018.05.009 |
| [5] |
YAN Fenggang, CAO Bin, LIU Shuai, et al. Reduced-complexity direction of arrival estimation with centro-symmetrical arrays and its performance analysis[J]. Signal Processing, 2018, 142: 388. DOI:10.1109/TSP.2013.2243442 |
| [6] |
徐丽琴, 李勇. 单基MIMO雷达低复杂度求根MUSIC角度估计方法[J]. 系统工程与电子技术, 2017, 39(11): 2434. XU Liqin, LI Yong. Low-complexity root-MUSIC algorithm for angle estimation in monostatic MIMO radar[J]. Systems Engineering and Electronics, 2017, 39(11): 2434. DOI:10.3969/j.issn.1001-506X.2017.11.07 |
| [7] |
LIU Mingqian, ZHANG Junlin, TANG Jie, et al. 2-D DOA robust estimation of echo signals based on multiple satellites passive radar in the presence of alpha stabledistribution noise[J]. IEEE Access, 2019, 7: 16032. DOI:10.1109/ACCESS.2019.2894997 |
| [8] |
闫锋刚, 沈毅, 刘帅, 等. 高效超分辨波达方向估计算法综述[J]. 系统工程与电子技术, 2015, 37(7): 1465. YAN Fenggang, SHEN Yi, LIU Shuai, et al. Overview of efficient algorithms for super-resolution DOA estimation[J]. Systems Engineering and Electronics, 2015, 37(7): 1465. DOI:10.3969/j.issn.1001-506X.2015.07.01 |
| [9] |
BARABELL A. Improving the resolution performance of eigenstructure-based direction finding algorithms[C]. IEEE Conference on Acoustics, Speech and Signal Processing, Boston, 1983: 336. DOI: 10.1109/ICASSP.1983.1172124
|
| [10] |
JENS S, FLORIAN R, MARTIN H, et al. Performance analysis of multi-dimensional ESPRIT-type algorithms for arbitrary and strictly non-circular sources with spatial smoothing[J]. IEEE Trans. on Signal Processing, 2017, 65(9): 2262. DOI:10.1109/TSP.2017.2652388 |
| [11] |
SHU Feng, QIN Yaolu, LIU Tingting, et al. Low-complexity and high-resolution DOA estimation for hybrid analog and digital massive MIMO receive array[J]. IEEE Trans. on Communications, 2018, 66(6): 2487. DOI:10.1109/TCOMM.2018.2805803 |
| [12] |
MARIUS P, ALEX B, MARTIN H. Unitary root-MUSIC with a real-valued eigen-decomposition: A theoretical and experimental performance study[J]. IEEE Trans. on Signal Processing, 2000, 5(48): 1306. DOI:10.1109/78.839978 |
| [13] |
QIAN Cheng, HUANG Lei. Improved unitary root-MUSIC for DOA estimation based on pseudo-noise resampling[J]. IEEE Signal Processing Letters, 2014, 21(2): 140. DOI:10.1109/LSP.2013.2294676 |
| [14] |
LI Jianfeng, LI Dong, JIANG Defu, et al. Extended-aperture unitary root-MUSIC based DOA estimation for coprime array[J]. IEEE Communications Letters, 2018, 22(4): 752. DOI:10.1109/LCOMM.2018.2802491 |
| [15] |
何子远, 龚耀寰, 杨峰. 多项式求根法估计来波DOA[J]. 电波科学学报, 2008, 23(3): 407. HE Ziyuan, GONG Yaohuan, YANG Feng. DOA estimation based on polynomial rooting method[J]. Journal of Radio Science, 2008, 23(3): 407. DOI:10.3969/j.issn.1005-0388.2008.03.004 |
| [16] |
郑士明. 同时求解多项式所有二次因子的迭代法[J]. 计算数学, 1980, 2(3): 229. ZHENG Shiming. An iteration methodfor finging all quadratic factors of polynomial simultaneously[J]. Journal of Computational Mathematics, 1980, 2(3): 229. |
| [17] |
Stoica P, Nehorai A. Performance study of array signal processing research: the parametric approach[J]. IEEE Signal Processing Magazine, 1996, 13: 67. DOI:10.1109/79.526899 |
| [18] |
Roy R, Kailath T. ESPRIT-estimation of signal paramaters via rotational invariance techniques[J]. IEEE Trans. on Signal Processing, 1989, 37(7): 984. DOI:10.1109/29.32276 |
| [19] |
YAN Fenggang, SHEN Yi, JIN Ming. Fast DOA estimation based on a split subspace decomposition on the array covariance matrix[J]. Signal Processing, 2015, 115: 1. DOI:10.1016/j.sigpro.2015.03.008 |
 2019, Vol. 51
2019, Vol. 51


