对于不同的地质体,其地震剖面图像[1]的纹理会有所不同.一般情况下,地震剖面图像的纹理结构发生突变表示该地质结构发生变化.这些常识性信息应用较广,如石油勘探,天然气探勘,考古挖掘等.因此,如何充分利用地质结构数据的丰富信息,如何有效地对地震图像进行去噪和纹理分析,成为解决实际问题的关键.
对于纹理的描述,至今没有一个公认准确的定义[2].由于地震剖面图具有明显的纹理方向性,文献[3]利用二维方向滤波来提取纹理特征,并分割地震剖面图.他选择了一组初始相角分别为0°,45°,90°和135°的8对方向滤波器对图像进行了滤波,并由它们组成了一个特征向量,由此来对纹理特征值进行提取.为了进一步增强地震图像纹理细节信息,文献[4]提出了脉冲耦合神经网络(Pulse Coupled Neural Network PCNN)和多分辨率分析的地震图像增强算法.该算法对PCNN进行改进,将图像像素的局部梯度值作为PCNN的链接强度系数,在动态阈值函数中加入侧抑制信号,对分解后的高频分量图进行细节增强[4].然而,局部梯度信息无法概括变化多端的剖面纹理信息.文献[5]提出一种针对地震纹理的图像增强方法,根据地震数据的全变分L1分解模型,把地震图像信息分解为结构与纹理分量,基于偏微分方程分别对结构和纹理分量进行加强,提高空间分辨率.但对于结构和纹理分量的区别并不明确,因为地震剖面图像的纹理有很多是线性结构.文献[6]在地震纹理分析中使用了纹理模型回归分析,介绍了地震构造解释和储层特征预测.文献[7]基于方向性对数变差函数的纹理分析模型,提取非下采样轮廓变换(Non-down Sampling Contourlet Transform NSCT)空间中不同尺度上的图像纹理差异特征,利用模糊C均值聚类方法来对差异特征进行分类.总体方法较为复杂,且在变换域进行了多次计算.文献[8]以单个体元为标准, 以奇数对称为准则, 修改了地震数据标准化, 实现了对道内振幅变化及小断层细节纹理的清晰刻画.为了保持地震图像的地质特征,以及抑制采集和处理伪影,文献[9]对Sobel滤波器进行修改,开发了平面波Sobel属性,使用平面波沿地震结构定向滤波,达到增强地震图像纹理的效果.文献[10]采用标准化全梯度(Normalized Full Gradient NFG)方法,对地震影像中的盐边界进行探测,并利用NFG方法对地震图像的道进行处理.结果表明,与希尔伯特变换相比,该方法的地震包络线的垂直分辨率有所提高,整体分辨率更高.在众多纹理分析方法中,还可采用如下的纹理特征提取方法:灰度共生矩阵[11](Gray-level Co-occurrence Matrix GLCM)方法、分形理论[12]、小波变换方法[13]等,但这些方法不一定都适合地震剖面图像.
对于地震剖面图像,相邻图像的各个相邻点之间存在不同的运动速度.分形理论等空域方法难以解决纹理边缘和流速不连续处的计算问题;NSCT等频率方法会模糊纹理的线性结构,而这些线性纹理结构是地震解释的重要信息依据.因此,有必要研究一种适合于地震图像线性结构的纹理分析方法,本文提出一种适合于地震图像纹理分析的综合算法,该算法包括基于高斯金字塔的改进光流法和纹理平滑滤波两部分,取得了较好的处理效果,提高了地震数据解释效率.
1 地震图像的纹理基元及属性 1.1 纹理基元的引入和灰度共生矩阵的构建地震资料灰度共生矩阵的构建基础是纹理基元,纹理基元是纹理图像中引起视觉感知的基本单元,其形态多样.如将地震纹理图像定义为地震数据体的反射振幅[14].本文以体、剖面和道表示纹理基元,具体如图 1所示.
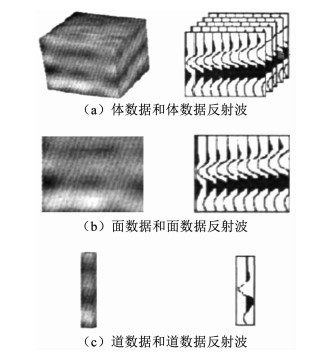
|
图 1 地震纹理基元示意 Fig. 1 Sketch map of seismic texture elements |
在地震图像纹理基元基础上,引入灰度共生矩阵(GLCM),其形式如下
| $ \begin{array}{c}{p(i, j, \alpha, \beta)=\sum\left\{\left(g\left(x_{1}, y_{1}, z_{1}\right)=i, g\left(x_{2}, y_{2}, z_{2}\right)=j\right)\right\}} \\ {i, j=0, 1, 2, \cdots, L-1}.\end{array} $ | (1) |
式中:g(x, y, z)为纹理基元体中x, y, z点的灰度值;(x1, y1, z1)和(x2, y2, z2)为距离δ的两个像素点;α,β为方向(如图 2所示);∑{.}为距离δ的任意两个像素点满足以上条件的概率统计.特殊情况下,α=90°,β=0°对应X轴方向;α=0°,β=0°对应Y轴方向;β=90°对应Z轴方向;L表示灰度值的级数.
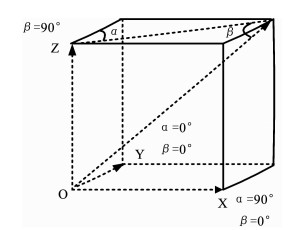
|
图 2 纹理基元的不同方向 Fig. 2 Differentdirections of texture elements |
纹理属性与纹理基元关系紧密.对于图 2的纹理基元方向,当灰度共生矩阵中的元素分布集中在主对角线附近时,对于纹理变化缓慢的图像(粗纹理),其对角线上的数值较大;对于纹理变化较快(细纹理)的图像,其对角线上的数值较小,且对角线两侧上的元素值增大.本文在灰度共生矩阵的基础上计算纹理能量、纹理熵和纹理对比度等属性.为了方便后面计算,下面给出这些属性的定义.
纹理能量TEne(Ene-Energy, 能量)反映了灰度分布均匀程度和纹理粗细度,其定义如下
| $ {T_{{\rm{Ene }}}} = \sum\limits_{i = 0}^{L - 1} {\sum\limits_{j = 0}^{L - 1} {{P^2}} } (i, j). $ |
纹理熵TEnt(Ent-Entropy, 熵)用于度量纹理的随机性
| $ {T_{{\rm{Ent}}}} = \sum\limits_{i = 0}^{L - 1} {\sum\limits_{j = 0}^{L - 1} P } (i, j)\lg P(i, j). $ |
纹理对比度TCon(Con-Contrast, 对比度)是灰度共生矩阵主对角线附近的惯性矩,用于度量矩阵值的分布和局部变化,可反映清晰度和纹理的沟纹深浅
| $ {T_{{\rm{Con}}}} = \sum\limits_{i = 0}^{L - 1} {\sum\limits_{j = 0}^{L - 1} {{{(i - j)}^2}} } P(i, j). $ |
这些属性对于研究地震图像,识别断层和裂缝具有重要的研究价值.值得一提,与以往灰度共生矩阵法不同,本文不是选择一种恒定的模板对所有区域进行处理,而是根据地震图像的纹理复杂度,选用不同的模板.首先根据不同的纹理特征设定其权重,并计算地震剖面图像的纹理复杂度作为判定阈值,对于复杂度小于阈值的纹理区域选择矩形模板,用滤波模板的均值代替模板点的灰度值;对于复杂度大于阈值的纹理区域,使用线性模板,计算8个线性模板灰度的均值和方差,将方差最小的模板作为滤波模板.实验结果证明,这种纹理平滑滤波方法可以增强地震图像相同方向轴的连续性,因此,能有效的保存地震纹理图像的边缘信息.
2 改进的光流法分析地震图像纹理由于相邻地震图像可能包含相同的或不同的地质体,且各个地质体的倾向不同,使得相邻点在相邻图像的位移是变化的,即:相邻图像的各个相邻点之间存在不同的运动速度.利用地震图像的这一特点,本文引入光流算法进行地震剖面图像的纹理分析,并利用高斯金字塔改进原光流法.
2.1 梯度约束方程及其不适定性设g(x, y, t))为t时刻一像点的灰度值,在时刻(t+dt)时,这一点的相邻点是(x+dx, y+dy),其灰度值为g(x+dx, y+dy, t+dt),根据图像灰度在有限区间内保持恒定的假设,有
| $ g(x+\mathrm{d} x, y+\mathrm{d} y, t+\mathrm{d} t)=g(x, y, t). $ | (2) |
将式(2)左边用泰勒公式展开,简化后得
| $ \frac{\partial g}{\partial x} \cdot \frac{\partial x}{\partial t}+\frac{\partial g}{\partial y} \cdot \frac{\partial y}{\partial t}+\frac{\partial g}{\partial t}=0 $ |
令
| $ \frac{\partial g}{\partial x} \cdot u+\frac{\partial g}{\partial y} \cdot v+\frac{\partial g}{\partial t}=0, $ |
即
| $ g_{x} \cdot u+g_{y} \cdot v+g_{t}=0. $ | (3) |
上式是光流分析法的基本方程,也即梯度约束方程[15],写成矢量形式为
| $ \nabla g \cdot u+g_{t}=0. $ | (4) |
式中:∇为梯度算子,U=(u, v)T为二维流速,gx, gy, gt分别为像点处沿x、y、t3个方向的偏导数.
由于光流场的基本方程具有不适定性,是“病态”的.因此,需要引入附加约束条件对方程进行正则化.对于存在遮挡和运动不连续的图像序列是不合适的,显然对地震图像也是不合适的.因为地震图像反映地下地质结构,长期的沉积和各种作用力的挤压,使得同一地质体的相邻点产生很大的位移,从而导致实际相邻的地震图像间相邻点的位移较大.因此,本文对其进行改进.
2.2 本文改进的光流算法模型利用高斯图像金字塔能够实现对流速由粗到细的计算,但是,这种计算存在着一个不足:如果光流估计在低分辨率层中有错误,那么该错误在高分辨率层不但不能被纠正,而且还会传播,因此需要提高每一分辨率层流速计算的准确性,减小误差传播.
假设f(x, y, t)是t时刻图像上(x, y)处的灰度值,在dt时间间隔内该像素点沿x, y方向的流速为(u, v),定义U=(u, v)T,其估计值设为
| $ \begin{array}{c}{f_{t}=(f(x, y, t+\mathrm{d} t)-f(x, y, t)) / \mathrm{d} t=} \\ {(f(x, y, t+\mathrm{d} t)-f(x+\tilde{u} \mathrm{d} t, y+\tilde{v} \mathrm{d} t, t+\mathrm{d} t)+} \\ {f(x+\tilde{u} \mathrm{d} t, y+\tilde{v} \mathrm{d} t, t+\mathrm{d} t)-f(x, y, t)) / \mathrm{d} t.}\end{array} $ | (5) |
上式的第一项和第二项由泰勒级数展开,并忽略二次和二次以上项,有:
| $ f(x, y, t+\mathrm{d} t) \approx f+f_{t} \mathrm{d} t. $ | (6) |
| $ f(x+\tilde{u} \mathrm{d} t, y+\tilde{v} \mathrm{d} t, t+\mathrm{d} t) \approx f+\tilde{u} f_{x} \mathrm{d} t+\tilde{v} f_{y} \mathrm{d} t+f_{t} \mathrm{d} t. $ | (7) |
令e为“亮度恒定假设误差”,梯度约束方程变为
| $ e=f_{x} u+f_{y} v+f_{t}. $ | (8) |
如果亮度恒定假设成立,则e为零.将式(5)~(7)带入式(8),得到梯度约束方程为
| $ e=f_{x} \Delta u+f_{y} \Delta v+\frac{f(x+\tilde{u} \mathrm{d} t, y+\tilde{v} \mathrm{d} t, t+\mathrm{d} t)-f(x, y, t)}{\mathrm{d} t}, $ | (9) |
| $ \Delta u=(u-\tilde{u}) ; \Delta v=(v-\tilde{v}). $ | (10) |
式中:Δu和Δv为实际流速与估计流速之间的误差(两个方向).上述过程将上一次迭代的流速估值引入到当前迭代的时间梯度计算中,当估计值越准确,则Δu和Δv越小.因此,帧间亮度恒定假设误差越小,光流的计算越精确.
在改进的梯度约束方程式(9)中,可令
| $ \begin{array}{c}{f_{t}(\tilde{u}, \tilde{v})=-f_{x} \tilde{u}-f_{y} \tilde{v}+} \\ {\frac{f_{t}(x+\tilde{u} \mathrm{d} t, y+\tilde{v} \mathrm{d} t, t+\mathrm{d} t)-f(x, y, t)}{\mathrm{d} t}}, \end{array} $ |
在此基础上,引入Nagel的方向平滑约束[16],即:
| $ \begin{array}{*{20}{c}} {{\mathop{\rm trace}\nolimits} \left( {{{(\nabla U)}^{\rm{T}}}W(\nabla U)} \right) \Rightarrow \min , }\\ {\mathit{\boldsymbol{W}} = \left\{ {\left( {\begin{array}{*{20}{c}} {{f_y}}\\ { - {f_x}} \end{array}} \right){{\left( {\begin{array}{*{20}{c}} {{f_y}}\\ { - {f_x}} \end{array}} \right)}^{\rm{T}}} + {b^2}\left( {\begin{array}{*{20}{c}} {{f_{yy}}}&{ - {f_{xy}}}\\ { - {f_{xy}}}&{{f_{xx}}} \end{array}} \right){{\left( {\begin{array}{*{20}{c}} {{f_{yy}}}&{ - {f_{xy}}}\\ { - {f_{xy}}}&{{f_{xx}}} \end{array}} \right)}^{\rm{T}}}} \right\}.} \end{array} $ |
则流速计算可以归结为求解如下方程
| $ \begin{aligned} \iint\left[\left(f_{x} u+f_{y} v+f_{t}(\tilde{u}, \tilde{v})\right)^{2}+\lambda\right.\cdot\\\left.\operatorname{trace}\left((\nabla U)^{\mathrm{T}} W(\nabla U)\right)\right] \mathrm{d} x \mathrm{d} y &=\min \end{aligned} $ | (11) |
在权矩阵W中,忽略图像函数的二次偏导数,则上式可写为
| $ \begin{array}{l} \int\!\!\!\int \left[ {{{\left( {{f_x}u + {f_y}v + {f_t}(\tilde u, \tilde v)} \right)}^2} + \lambda } \right. \cdot \\ \left. {{\mathop{\rm trace}\nolimits} \left( {{{(\nabla U)}^{\rm{T}}}\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over W} (\nabla U)} \right)} \right]{\rm{d}}x{\rm{d}}y = \min . \end{array} $ | (12) |
式(12)中的
| $ \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over W}=\frac{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over W}+I \gamma}{\operatorname{trace}(\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over W}+I \gamma)}. $ | (13) |
式中:I为2×2的单位矩阵;γ为方向平滑约束的权重;如果γ=0,则为全局均匀平滑性约束.权重矩阵
| $ \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over W}=\frac{1}{g}\left[\begin{array}{cc}{f_{y}^{2}+\gamma} & {-f_{x} f_{y}} \\ {-f_{x} f_{y}} & {f_{x}^{2}+\gamma}\end{array}\right]. $ | (14) |
式中g=(fx2+fy2+2γ).由变分法得到式(12)的两个欧拉方程如下
| $ \left\{\begin{array}{l}{\lambda \cdot \operatorname{div}(\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over W} \nabla u)-f_{x}\left(f_{x} u+f_{y} v+f_{t}(\tilde{u}, \tilde{v})\right)=0}, \\ {\lambda \cdot \operatorname{div}(\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over W} \nabla u)-f_{y}\left(f_{x} u+f_{y} v+f_{t}(\tilde{u}, \tilde{v})\right)=0}.\end{array}\right. $ | (15) |
由于式(15)包含扩散项,根据扩散理论,可以在式(15)的欧拉方程中引入P-M扩散方程,通过计算抛物线型方程组的渐进形式(t→∞)来计算欧拉方程组,从而得到
| $ \left\{\begin{array}{l}{\frac{\partial u}{\partial t}=\lambda \cdot \operatorname{div}\left(c_{u} \nabla u\right)-f_{x}\left(f_{x} u+f_{y} v+f_{t}(\tilde{u}, \tilde{v})\right)}, \\ {\frac{\partial v}{\partial t}=\lambda \cdot \operatorname{div}\left(c_{v} \nabla v\right)-f_{y}\left(f_{x} u+f_{y} v+f_{t}(\tilde{u}, \tilde{v})\right)}.\end{array}\right. $ | (16) |
式中扩散系数
| $ \begin{array}{l} u_{m, n}^{k + 1} = u_{m, n}^k + \frac{{\Delta t \cdot \lambda }}{2} \cdot \left[ {\left( {c_{um, n}^k + c_{um + 1, n}^k} \right)\left( {u_{m + 1, n}^k - u_{m, n}^k} \right) + } \right.\\ \left( {c_{um - 1, n}^k + c_{um, n}^k} \right)\left( {u_{m - 1, n}^k - u_{m, n}^k} \right) + \left( {c_{um, n + 1}^k + c_{um, n}^k} \right)\\ \left( {u_{m, n + 1}^k - u_{m, n}^k} \right)\left. { + \left( {c_{mn, n - 1}^k + c_{um, n}^k} \right)\left( {u_{m, n - 1}^k - u_{m, n}^k} \right)} \right] - \\ \Delta t \cdot {f_{1, x}}\left( {{f_{2, t}}\left( {m + n_{m, n}^k, n + v_{m, n}^k} \right) - {f_{1, t}}} \right), \\ v_{m, n}^{k + 1} = v_{m, n}^k + \frac{{\Delta t \cdot \lambda }}{2} \cdot \left[ {\left( {c_{vm, n}^k + c_{vm + 1, n}^k} \right)\left( {v_{m + 1, n}^k - v_{m, n}^k} \right) + } \right.\\ \left( {c_{vm - 1, n}^k + c_{vm, n}^k} \right)\left( {v_{m - 1, n}^k - v_{m, n}^k} \right) + \left( {c_{vm, n + 1}^k + c_{vm, n}^k} \right)\\ \left. {\left( {v_{m, n + 1}^k - v_{m, n}^k} \right) + \left( {c_{vm, n - 1}^k + c_{vm, n}^k} \right)\left( {v_{m, n - 1}^k - v_{m, n}^k} \right)} \right]\\ - \Delta t \cdot {f_{1, y}}\left( {{f_{2, t}}\left( {m + u_{m, n}^k, n + v_{m, n}^k} \right) - {f_{1, t}}} \right). \end{array} $ |
上述改进的光流模型引入了纹理平滑滤波[17]的思想,在连续平滑区域可以有效地对流速进行平滑,而在图像边界处可以有效地保护流速的变化,改善对边缘和流速不连续处的计算,提高整个流速场的计算精度.
2.3 所提方法的地震图像纹理分析过程通过以上分析,本文将高斯金字塔多尺度描述与光流算法模型结合构成适合地震图像序列的多尺度光流算法,首先将输入的相邻两帧地震图像f1(x, y)和f2(x, y)作为最高分辨率层的原图像,根据高斯金字塔法,按分辨率递减的规律生成不同分辨率层次的图像f0j, f1j, fnj, …, fNj(j=1, 2, 0≤n≤N);在设置最大迭代次数的情况下,为了提高计算速度,当相邻两次迭代结果残差‖Un(k)-Un(k-1)‖的均方根εu和εv很小时,可以终止当前分辨率层的迭代计算,因此,设置门限ε,当均方根小于门限值时结束迭代.并且设置映射因子为2,令低分辨率层计算得到的流速的2倍作为高一分辨率层图像流速的初始值.在这些设置完成后,执行纹理平滑滤波算法,其具体步骤如下:
1) 令n=N,迭代次数k=0,给定初始流速矢量场Un0;
2) 令K=K+1;在相应层次分辨率图像上计算矢量速度Unk;
3) 判断相邻两次迭代结果残差的均方根是否小于设定的门限值,如果小于,则继续;否则,返回步骤(2);
4) 判断,如果n>0,则根据设定的映射因子,计算高一分辨率层的流速矢量场初值2Un(k)→Un-10,并且令n=n-1, k=0,返回步骤(2);否则,继续.
5) 输出Unk.首先,构建一个地震子剖面,剖面中心是分析点,然后,根据下面两个公式计算该剖面的随机性与均一性:
| $ H=\sum\limits_{i=1}^{m} \sum\limits_{j=1}^{n}[E(i, j)]^{2}, $ | (17) |
| $ R = \sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n E } (i, j)lg E(i, j). $ | (18) |
式中:E(i, j)为共生矩阵.式(17)用于计算纹理均一性,式(18)用于计算纹理随机性.
6) 计算该地震子剖面的纹理复杂度
| $ C=\omega_{1} * H+\omega_{2} * R. $ |
7) 如果上述区域的纹理复杂度小于阈值β, 则转向式(9);如果纹理复杂度大于等于阈值β,则转向式(8).
8) 计算获得方差最小的线性模板Tmin,将其作为滤波模板Tfil.
9) 计算获得滤波模板灰度的均值Afil,将该灰度值作为目标点的灰度值,即Atar;然后,对下一个地震道作相同操作.
3 仿真实验与分析实验分为3组,第1组是所提算法与光流法的比较实验.第2组实验通过谱结构分析,来比较改进算法与均值滤波的结果.第3组实验是纹理分析,以及模板的讨论,包括模板的大小和模板的选取.
3.1 实验1:与原光流法比较在实验1中,金字塔分级4层,设置最大迭代次数为40次,残差门限ε=0.02.选择不同的参数λ对地震图像进行实验,每级图像计算光流场实际的迭代次数在表 1中给出,可以看出,随着λ由40逐步减小到0.2,各级的迭代次数逐渐越少,即,计算速度逐渐加快.实验结果如图 3所示,其中,图 3(a)和(b)是相邻两帧的地震剖面,带有随机噪声,图 3(c)是经过纹理平滑处理后的地震图像;图 3(d)是λ=1时图 3(a)到(b)的光流场;图 3(e)是λ=40时图 3(a)到(b)的光流场,图 3(c)是经过算法处理后的地震图像.可以看出图 3(c)的噪声更小,同相轴的连续性更强,反射特征保留得较好.
| 表 1 设置不同λ时的迭代次数 Tab. 1 Number of iterations with different λ |
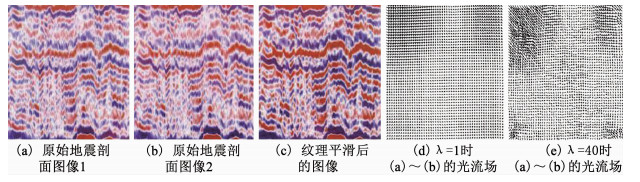
|
图 3 本文改进算法的实验结果 Fig. 3 Experimental results of the improved algorithm in this paper |
选取不同信噪比地震剖面图像,对实际的地震图像序列作了大量的实验,并计算了处理后信噪比的增加与信号能量保持,表 2给出了3幅图像的评价结果,其中信噪比、处理时间和能量保持百分比的最优数值用加粗形式显示.首先,所提算法在信噪比方面提升较大,这主要得益于高斯金字塔多尺度描述与光流算法的结合,获得了纹理平滑滤波的效果,在图像边界处可以有效地保护流速的变化,改善了对边缘和流速不连续处的计算.其次,运行时间更短,这说明利用相邻两次迭代结果的均方根可以明显提高计算速度.由于地震剖面图像的细节得到较多保存,噪声也得到抑制,其信号能量则更高.图 4和图 5分别给出了与一般光流法+均值滤波的效果对比图,其中图 5是地震剖面图纹理截取的一部分,可以看出剖面断层和褶皱的部分.由于在所提方法中引入了纹理平滑滤波,可以看出,处理后的信噪比增加了7~10 dB,而信号能量均保持在80%左右.处理结果说明:高斯金字塔多尺度描述与光流算法结合,并通过纹理平滑滤波后,具有良好的性能.不但能够较好地抑制噪声,而且能较好地保持信号能量,同相轴清晰,剖面断层位置清楚,处理效果较明显.褶皱前翼部分如图 5(c)所示,可以看出,该部分连续性较好,边界的信号较为完整,噪声也得到了一定程度的压制.
| 表 2 改进算法与原光流法的性能比较 Tab. 2 Performance comparison between improved algorithm and original optical flow method |

|
图 4 整个地震剖面图像实验结果(滤波采用7×7窗口) Fig. 4 Experimental results of the whole seismic profile image |
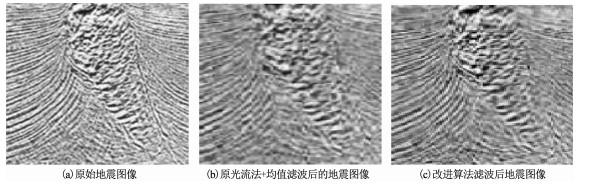
|
图 5 截取的地震剖面图像实验结果(滤波采用5×5窗口) Fig. 5 Experimental results of intercepted seismic profile images (filtering using 5 *5 window) |
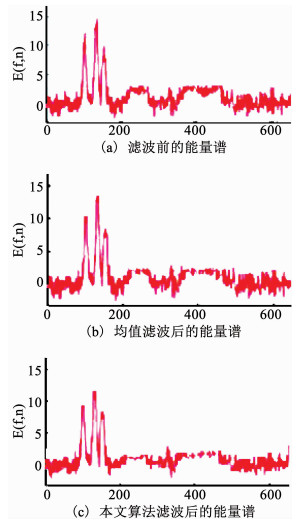
第2组实验是通过能谱结构分析,来衡量比较改进算法与均值滤波的结果,其参数设置与实验1相同.按照第2.3节给出的能量分析方法,对盐67长6的2 401.17横测线的215-265道号的某幅地震剖面原图进行频谱分析,并与两种不同算法的滤波后结果进行比较分析.滤波前后能谱对比图如图 6所示,图中纵坐标E(f, n)为地震剖面道的能量谱密度,f为频率,n为地震剖面数据第n列.由图 6可以看出,均值滤波并不能完全保持原始信号的频谱结构,其信号的能量损失较大,而本文算法处理后,其能量损失轻微.因此,从能谱结构分析看,本文算法更优.
|
图 6 滤波前后的能谱 Fig. 6 Energy spectrum before and after filtering |
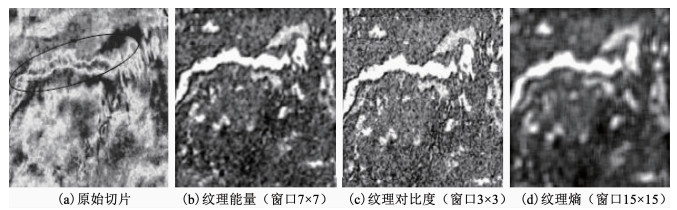
第3组实验是纹理属性的对比分析,以及关于模板的讨论.高斯金字塔分为4层,设置最大迭代次数为40次,残差门限ε取值0.02,λ取值0.2.图 7(a)为某工区的沿层振幅切片,为了检测断层,实验采用16级灰度级和9×9×9的三维滑动窗提取纹理体属性,然后,抽取沿层切片进行对比分析.高振幅能量的河道如图 7(a)中的划线区域所示,实验中的窗口尺寸设定为三种:3×3、7×7和15×15.提取三种纹理特征:角二阶矩、对比度和熵,其结果如图 7(b)~(d)所示.对比图 7中3种纹理属性可以发现,窗口尺寸的设定会直接影响到纹理有效信息的多少.由上述结果可以看出,窗口尺寸越大,所丢失的纹理信息越多,反之则越少.从图 7可以看出,使用3×3和7×7的窗口尺寸所获得的图像纹理较为清晰自然,而15×15的窗口尺寸会带来较为模糊的边缘.
|
图 7 纹理属性对比 Fig. 7 Comparison of texture properties |
此外,纹理窗口的选取也会对纹理信息的提取产生重要影响.纹理平滑滤波算法[17]不是选择一种恒定的模板对应所有的区域进行卷积运算,而是根据地震图像的纹理复杂程度,选用不同的模板.首先根据不同的纹理特征设定其权重,并计算地震剖面图像的纹理复杂度作为阈值的判定标准,如果区域的纹理复杂度小于阈值,则选择矩形模板,用滤波模板的均值代替模板点的灰度值;如果区域的纹理复杂度不小于阈值,则使用线性模板.这样可有效地保存地震数据的边缘信息,增强地震图像同相轴的连续性.
可以看出,采用高斯金字塔与光流算法结合的改进方法,并通过纹理平滑滤波,能够较好地消除随机噪声,使处理后的地震图像信噪比有很大提高,地质结构更加清晰,未出现任何假象,通过设置迭代结果残差的均方根的门限值,减少迭代次数,缩短了处理时间.在实际操作中,可以根据地震图像剖面纹理复杂度,选用不同的模板,能够有效的保存地震数据的边缘信息,增强地震图像同相轴的连续性.
3.4 与其他先进方法的比较为了分析所提方法的性能,本文与文献[9]和文献[10]两个先进方法进行比较.其中,文献[9]对Sobel滤波器进行了修改,开发了平面波Sobel属性,使用平面波沿地震结构定向滤波.且该方法的实验仅采用3×3窗口.文献[10]采用标准化全梯度(NFG)方法,对地震影像中的盐边界进行探测,并利用NFG方法对地震图像的道进行处理.本文通过处理30幅不同地震剖面图像(300×300 dpi),计算平均处理时间,平均能量保持量,以及信噪比提高情况.
综合比较情况如表 3所示.由于不同的硬件平台、软件实现方式和算法设计方法都会影响最终的实验结果,因此,表 3的实验数据仅供参考.可以看出,平面波Sobel[9]的平均处理时间最短,这主要是因为平面波Sobel[9]是Sobel滤波的改进形式,其计算框架和过程较为简单.NFG[10]处理效果较好,但计算过程相当复杂,需要进行大量的偏微分计算.本文方法各方面适中,较为优秀.
| 表 3 各方法的综合比较 Tab. 3 Comparison of the methods |
本文将高斯金字塔多尺度描述与光流算法结合,构成适合地震图像纹理分析的多尺度改进光流算法,在此基础上,结合纹理平滑滤波,构成一种综合改进算法.该算法利用光流分析法得到图像帧间位移,进而校准图像,利用多尺度高斯金字塔解决大流速的计算问题.此外,通过设置迭代结果残差的均方根门限值,减少了迭代次数,缩短了处理时间.通过对地震图像的信噪比和能量分析,实验结果证明,该算法能够有效提高信噪比,较好地保持原图像纹理结构和能量,减少处理时间,提高地震资料解释的效率.
| [1] |
陈凤, 李金宗, 黄建明, 等. 提高地震剖面图像信噪比的二维沿层滤波方法[J]. 哈尔滨工业大学学报, 2005, 37(5): 667. CHEN Feng, LI Jinzong, HUANG Jianming, et al. 2-D tracing horizon filtering method to increase signal to noise ratio of seismic section image[J]. Journal of Harbin Institute of Technology, 2005, 37(5): 667. DOI:10.3321/j.issn:0367-6234.2005.05.027 |
| [2] |
君顶, 毋小省. 纹理谱描述符及其在图像检索中的应用[J]. 计算机辅助设计与图形学学报, 2010, 22(3): 516. JUN Ding, WU Xiaosheng. Content-based image retrieval based on texture spectrum descriptors[J]. Journal of Computer-Aided Design & Computer Graphics, 2010, 22(3): 516. |
| [3] |
HUANG X, GRIFFITHS C M, LIU J. Recent development in stratigraphic forward modeling and its application in petroleum exploration[J]. Australian Journal of Earth Sciences, 2015, 62(8): 903. DOI:10.1080/08120099.2015.1125389 |
| [4] |
杨雪.融合多分辨率分析与PCNN的地震剖面图像增强算法研究[D].西安: 西安石油大学, 2016 YANG Xue. Research on seismic profile image enhancement algorithms based on fusion of multiple-resolution analysis and PCNN[D]. Xi'an: Xi'an Shiyou University, 2016 http://cdmd.cnki.com.cn/Article/CDMD-10705-1016089126.htm |
| [5] |
杨宁, 杨威. TV-L~1分解模型下的地震图像增强方法研究[J]. 地球物理学进展, 2016, 31(6): 100. YANG Ning, YANG Wei. Enhancement of seismic image based on seismic data decomposition by the TV-L1 model[J]. Progress in Geophysics, 2016, 31(6): 100. |
| [6] |
ZHANG Pengzhi, LI Lanbin. The research progress of seismic texture analysis attribute in oil and gas exploration[J]. Geophysical & Geochemical Exploration, 2013, 37(3): 61. DOI:10.11720/j.issn.1000-8918.2013.3.16 |
| [7] |
刘洋.基于NSCT纹理信息分析的地震图像变化检测[D].长沙: 长沙理工大学, 2016 LIU Yang. Seismic image change detection based on texture information analysis of NSCT[D]. Changsha: Changsha University of Science & Technology, 2016 http://cdmd.cnki.com.cn/Article/CDMD-10536-1017301110.htm |
| [8] |
吕凤华, 舒宁, 龚龑, 等. 利用多特征进行航空影像建筑物提取[J]. 武汉大学学报(信息科学版), 2017, 42(5): 656. LV Fenghua, SHU Ning, GONG Yan, et al. Regular building extraction from high resolution image based on multilevel-features[J]. Geomatics and Information Science of Wuhan University, 2017, 42(5): 656. DOI:10.13203/j.whugis20140781 |
| [9] |
PHILLIPS M, FOMEL S. Plane-wave Sobel attribute for discontinuity enhancement in seismic images[J]. Geophysics, 2017, 82(6): 1. DOI:10.1190/geo2017-0233.1 |
| [10] |
SOLEIMANI M, AGHAJANI H, HEYDARI-NEJAD S. Salt dome boundary detection in seismic image via resolution enhancement by the improved NFG method[J]. Acta Geodaetica et Geophysica, 2018, 53(3): 463. DOI:10.1007/s40328-018-0222-3 |
| [11] |
吴昊.利用灰度共生矩阵提取纹理属性的研究以及沉积相划分[D].荆州: 长江大学, 2014 WU Hao. The study of texture attributes extracting and sedimentary facies using gray level co-occurrence matrix[D]. Jingzhou: Yangtze University, 2014 http://cdmd.cnki.com.cn/Article/CDMD-10489-1016201186.htm |
| [12] |
FLORINDO J B, BRUNO O M. Fractal descriptors based on Fourier spectrum applied to texture analysis[J]. Physica A Statistical Mechanics and Its Applications, 2012, 391(20): 4909. DOI:10.1016/j.physa.2012.03.039 |
| [13] |
杨雪, 刘天时, 李湘眷. 融合小波变换与改进PCNN的图像增强算法研究[J]. 计算机工程与应用, 2016, 52(8): 163. YANG Xue, LIU Tianshi, LI Xiangjuan. Study on image enhancement algorithm merged wavelet transform and improved PCNN[J]. Computer Engineering and Applications, 2016, 52(8): 163. DOI:10.3778/j.issn.1002-8331.1508-0248 |
| [14] |
SHABELANSKY A H, MALCOLM A, FEHLER M. Data-driven estimation of the sensitivity of target-oriented time-lapse seismic imaging to source geometry[J]. Geophysics, 2013, 8(2). DOI:10.1190/geo2012-0175.1 |
| [15] |
马龙, 王鲁平, 陈小天, 等. 噪声环境下光流场估计方法[J]. 信号处理, 2012, 8(1): 87. MA Long, WANG Luping, CHEN Xiaotian, et al. Determining optical flow field in the presence of noise[J]. Signal Processing, 2012, 8(1): 87. DOI:10.3969/j.issn.1003-05302012.01.013 |
| [16] |
MITANI S, YAMAKAWA H. Continuous-thrust transfer with control magnitude and direction constraints using smoothing techniques[J]. Journal of Guidance, Control, and Dynamics, 2013, 36(1): 163. DOI:10.2514/1.56882 |
| [17] |
CHO H, LEE H, KANG H, et al. Bilateral texture filtering[J]. ACM Transactions on Graphics, 2014, 33(4): 1. DOI:10.1145/2601097.2601188 |
 2019, Vol. 51
2019, Vol. 51


