统计表明,包括飞机、车辆、桥梁和吊车梁等在内的金属结构中,约80%~90%的破坏与疲劳断裂有关[1].结构钢疲劳破坏是结构钢在反复荷载作用下损伤累积产生初始微裂纹,裂纹反复扩展、闭合,直至净截面强度不足而瞬间断裂的破坏过程.一般说来,结构钢的疲劳破坏可分为3个阶段:初始微裂纹形成、裂纹稳定扩展和裂纹失稳扩展.在反复荷载作用下,位错或孔穴运动、聚合导致结构钢晶界或滑移带开裂,或在大尺寸夹杂物或其他缺陷周边因应力集中与结构钢基本相界面分离或夹杂物本身断裂形成初始微裂纹.初始微裂纹形成后,裂尖形成高度应力集中,即便在名义应力不高于结构钢断裂强度甚至低于屈服强度时,裂尖真实应力场达到结构钢断裂临界值而开裂,在反复荷载作用下,裂纹反复扩展、闭合,即为裂纹稳定扩展阶段.当裂纹稳定扩展到一定长度,试件承载截面面积削弱过多,最后因净截面承载强度不足而瞬间拉裂,为裂纹失稳扩展阶段.疲劳断裂面相应地形成贝纹状的裂纹稳定扩展区和粗糙的裂纹失稳扩展区.
钢结构不存在裂纹形成阶段[1-2],因钢结构在制作和构造上不可避免地存在缺陷,如焊接结构中存在的气孔、欠焊、夹渣,非焊接结构中存在的刻痕、分层、凹凸点、轧钢缺陷及冲孔、剪切、气割处存在的微裂纹等,这些缺陷就是初始裂纹(起裂源).考虑到疲劳裂纹失稳扩展是瞬间断裂的,因此,本文偏于保守地约定结构钢试件的疲劳寿命不计疲劳裂纹失稳扩展阶段的循环加载次数,即:对于有初始裂纹或缺陷的结构钢试件,疲劳裂纹从初始裂纹根部或初始缺陷周边开始稳定扩展阶段的循环加载次数为其疲劳寿命;对于经超声波等检测无初始裂纹或缺陷的结构钢试件,疲劳微裂纹形成阶段和疲劳裂纹稳定扩展阶段的循环加载次数之和为其疲劳寿命.
由于对结构钢疲劳裂纹的形成、扩展以至断裂这一过程的极限状态及有关影响因素的研究还不足,现行《钢结构设计标准》[3]采用允许应力法和应力幅准则计算钢结构的疲劳寿命,前规范《钢结构设计规范》[4]则采用最大应力准则验算钢结构的疲劳破坏.当前,结构钢的疲劳破坏虽然积累了丰富的试验资料,也能通过计算预估疲劳寿命,但仍较多地依赖经验,理论上并未真正解决[2].
本文以结构钢的椭球面断裂模型为开裂判据,基于结构钢疲劳裂纹随加载次数加速扩展的试验事实,假定结构钢圆杆的疲劳裂纹稳定扩展速率是循环加载次数的单调递增幂函数,由结构钢圆杆疲劳裂纹的裂尖真实应力场,推导出结构钢圆杆的疲劳破坏模型.对Q345B圆钢杆进行了疲劳试验,考察了相对应力幅和名义最大应力对其疲劳寿命的影响规律,标定了Q345B圆钢杆的疲劳破坏模型参数,验证了建议的结构钢圆杆的疲劳破坏模型精度.
1 结构钢圆杆的疲劳破坏模型 1.1 疲劳裂纹失稳扩展面积为计算结构钢圆杆的疲劳裂纹失稳扩展面积An,需选用能描述结构钢在复杂应力状态下的断裂判据,并求解裂尖真实应力场.王万祯[5]建议的结构钢椭球面断裂模型及耦联的椭球面屈服模型分别为:
| $ {\left( {{\sigma _{{\rm{seq}}}}/r} \right)^2} + {\left( {{\sigma _{\rm{m}}}/q} \right)^2} = 3\tau _{\rm{y}}^2, $ | (1) |
| $ \sigma _{{\rm{seq}}}^2 + {\left( {{\sigma _{\rm{m}}}/q} \right)^2} = 3\tau _{\rm{y}}^2. $ | (2) |
式中:
王万祯等[6]对刻槽圆钢杆的研究表明,尖锐刻槽根部的应力场接近固接约束状态,即:σ2=μσ1,σ3=μσ1.把结构钢圆杆的疲劳裂纹看作无限尖锐刻槽,裂尖处于固接约束应力状态,疲劳裂纹失稳扩展时裂尖真实应力场计算如下:
| $ {\sigma _1} = {P_{\max }}/{A_{\rm{n}}} = {\sigma _{\max }} \cdot A/{A_{\rm{n}}}, $ | (3) |
| $ {\sigma _2} = {\sigma _3} = \mu {\sigma _1}, $ | (4) |
| $ {\sigma _{\rm{m}}} = \left( {{\sigma _1} + {\sigma _2} + {\sigma _3}} \right)/3 = \left( {1 + 2\mu } \right){\sigma _{\max }} \cdot A/3{A_{\rm{n}}}, $ | (5) |
| $ \begin{array}{*{20}{c}} {{\sigma _{{\rm{seq}}}} = \sqrt {\frac{1}{2}\left[ {{{\left( {{\sigma _1} - {\sigma _2}} \right)}^2} + {{\left( {{\sigma _2} - {\sigma _3}} \right)}^2} + {{\left( {{\sigma _3} - {\sigma _1}} \right)}^2}} \right]} = }\\ {\left( {1 - \mu } \right){\sigma _{\max }} \cdot A/{A_{\rm{n}}}.} \end{array} $ | (6) |
式(3)~(6)中:σ1、σ2、σ3分别为第一、第二、第三主应力,σmax和Pmax分别为疲劳试验名义最大应力和名义最大载荷.
将式(3)~(6)计算的疲劳裂纹裂尖应力场代入式(1)建议的结构钢椭球面断裂模型,得
| $ {A_{\rm{n}}} = \frac{{\sqrt {9{q^2}{{\left( {1 - \mu } \right)}^2} + {{\left( {1 + 2\mu } \right)}^2}{r^2}} \cdot {\sigma _{{\rm{max}}}}A}}{{3\sqrt 3 qr \cdot {\tau _\text{y}}}}. $ | (7) |
由式(7)求得结构钢圆杆的疲劳裂纹失稳扩展面积An,则包含初始裂纹或缺陷尺寸a0效应的疲劳裂纹稳定扩展面积Af=A-An.
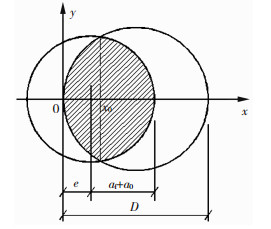
图 1结构钢圆杆疲劳裂纹扩展示意图中,e为起裂点距圆杆边缘的距离,0≤e≤D/2.为叙述简洁,本文约定:当e=0时,为边缘裂纹;当0 < e < D/2时,为内部裂纹;当e=D/2时,为中心裂纹.
|
图 1 结构钢圆杆的疲劳裂纹扩展示意 Fig. 1 Sketch of fatigue crack propagation of round bar made from constructional steel |
假设疲劳裂纹稳定扩展阶段以起裂点为中心向四周呈辐射状扩展,可解得包含初始裂纹或缺陷尺寸a0效应的疲劳裂纹稳定扩展面积Af和疲劳裂纹稳定扩展长度af间的函数关系,求得疲劳裂纹稳定扩展长度af.
当0≤e < D/2时,解得疲劳裂纹扩展圆与杆件截面圆交点坐标
| $ \begin{array}{*{20}{c}} {{A_{\rm{f}}} = A - {A_{\rm{n}}} = 2\int_0^{{x_0}} {\sqrt {\frac{{{D^2}}}{4} - {{\left( {x - \frac{D}{2}} \right)}^2}} } {\rm{d}}x + }\\ {2\int_{{x_0}}^{{a_{\rm{f}}} + {a_0} + e} {\sqrt {{{\left( {{a_{\rm{f}}} + {a_0}} \right)}^2} - {{\left( {x - e} \right)}^2}} {\rm{d}}x} = }\\ {\left( {{x_0} - \frac{D}{2}} \right)\sqrt {{x_0}D - x_0^2} + \frac{{{\rm{ \mathsf{ π} }}{D^2}}}{8} + \frac{{{\rm{ \mathsf{ π} }}{{\left( {{a_{\rm{f}}} + {a_0}} \right)}^2}}}{2} - }\\ {\left( {{x_0} - e} \right)\sqrt {{{\left( {{a_{\rm{f}}} + {a_0}} \right)}^2} - {{\left( {{x_0} - e} \right)}^2}} + }\\ {\frac{{{D^2}}}{4}\arcsin \frac{{2{x_0} - D}}{D} - {{\left( {{a_{\rm{f}}} + {a_0}} \right)}^2}\arcsin \frac{{{x_0} - e}}{{{a_{\rm{f}}} + {a_0}}}.} \end{array} $ | (8) |
特别地,当e≥af+a0或e=D/2时
| $ {A_{\rm{f}}} = A - {A_{\rm{n}}} = {\rm{ \mathsf{ π} }}{\left( {{a_{\rm{f}}} + {a_0}} \right)^2}. $ | (9) |
疲劳裂纹扩展速率是决定结构钢疲劳寿命的关键因素,受到广泛研究[7-11].
Paris-Erdogan模型[7]定量描述了结构钢的疲劳裂纹扩展速率;Forman等[8]建议的疲劳裂纹扩展速率方程考虑了高ΔK范围内的应力比效应;Elber[9]提出了考虑裂纹张开效应的疲劳裂纹扩展速率方程.
赵永翔等[10]指出,Paris-Erdogan模型[7]不能表征门槛值ΔKth和断裂韧度ΔKIC附近的疲劳裂纹扩展规律,Forman等[8]建议的疲劳裂纹扩展速率方程不能表征门槛值ΔKth附近的疲劳裂纹扩展规律,Elber[9]提出的疲劳裂纹扩展速率方程不能表征高应力强度因子范围的疲劳裂纹扩展规律.
以往建议的结构钢疲劳裂纹扩展模型[7-11],多是基于断裂力学原理(如应力强度因子、COD理论和J积分等)建立的,适用于含初始裂纹或缺陷的结构钢试件,模型参数强烈敏感于初始裂纹尺寸及形状.《钢结构工程施工质量验收规范》[12]明确规定,按一级和二级质量检测的钢结构及焊缝不得存在裂纹等缺陷.因此,应用以往建议的结构钢疲劳裂纹扩展模型时,需引入人为设定的初始裂纹(或缺陷)尺寸a0,与《钢结构工程施工质量验收规范》[12]对钢结构质量的要求不符,且人为设定的初始裂纹尺寸具有很大的不确定性.
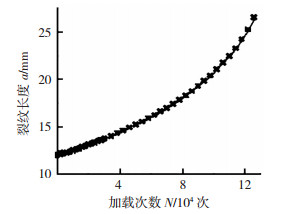
图 2为含初始裂纹的WNQ570桥梁钢的疲劳试验结果[13],可见,结构钢的疲劳裂纹稳定扩展长度增速随加载次数逐渐增大.在疲劳裂纹稳定扩展阶段,随着裂纹扩展,试件净截面面积减小,裂尖真实应力增加,裂纹加速扩展,即第N次循环加载时的裂纹扩展长度大于第(N-1)次循环加载.疲劳裂纹失稳扩展本质上也是裂纹扩展过快以致最后一次循环加载中裂纹瞬间穿透试件剩余截面的破坏过程.
|
图 2 WNQ570钢的疲劳试验结果 Fig. 2 Fatigue test results of WNQ570 steel |
本文根据唯象理论假定结构钢圆杆的疲劳裂纹稳定扩展速率va(包括疲劳裂纹形成阶段)是循环加载次数N的单调递增幂函数,即
| $ {v_{\rm{a}}} = b \cdot {N^c} + d. $ | (10) |
由初始条件va|N=0=0,得d=0.
式(10)简化为
| $ {v_{\rm{a}}} = b \cdot {N^c}. $ | (11) |
即双对数坐标系下疲劳裂纹扩展速率va是循环加载次数N的单调递增线性函数:
| $ \log {v_{\rm{a}}} = c \cdot \log N + \log b. $ | (12) |
对式(12)积分,得疲劳裂纹稳定扩展长度:
| $ {a_{\rm{f}}} = \frac{b}{{c + 1}} \cdot N_{\rm{f}}^{c + 1}. $ | (13) |
式中:Nf为疲劳裂纹形成和稳定扩展阶段的循环加载总次数,即疲劳寿命.
令
| $ {a_{\rm{f}}} = \xi \cdot N_{\rm{f}}^\eta . $ | (14) |
由式(14)得结构钢圆杆的疲劳破坏模型:
| $ {N_{\rm{f}}} = {\left( {\frac{{{a_{\rm{f}}}}}{\xi }} \right)^{\frac{1}{\eta }}}. $ | (15) |
式中:参数ξ、η是试件类别和相对应力幅RA=(σmax-σmin)/σmax的函数,由疲劳试验数据拟合标定;af由式(8)~(9)计算,Af=A-An,An由式(7)计算.
式(7)~(9)、(15)和图 1表明,其他条件(材质、几何形状、荷载参数等)相同的试件,其全截面面积A和疲劳裂纹失稳扩展面积An相同,进而疲劳裂纹稳定扩展面积Af也相同.单向扩展模式的边缘裂纹(e=0),其疲劳裂纹稳定扩展长度af和疲劳寿命Nf大于双向扩展模式的内部裂纹(0 < e < D/2)和中心裂纹(e=D/2).初始裂纹位置参数e和初始裂纹长度a0越大的试件,疲劳裂纹扩展长度af和疲劳寿命Nf越小.初始裂纹位置和初始裂纹长度取决于材质缺陷位置和缺陷大小,同批次试件的材质缺陷大小相差不大,但缺陷位置是随机分布的.随机分布的初始缺陷位置不同,导致其他参数相同的试件的疲劳寿命不同,较好解释了结构钢疲劳试验数据离散性大的试验结果[13],不能简单地完全归因于试验误差.
式(15)建议的结构钢圆杆的疲劳破坏模型较好地解释了下述疲劳试验现象[1]:1)构件的名义最大应力较小时,疲劳裂纹稳定扩展区面积占比大;反之,疲劳裂纹稳定扩展区面积占比小.构件的名义最大应力小,试件发生净截面强度不足而拉断(裂纹失稳扩展)面积An占比小,疲劳裂纹稳定扩展区面积占比大.2)疲劳裂纹稳定扩展区断面光滑,且愈近裂源愈光滑.疲劳裂纹扩展速率是循环加载次数的单调增函数,愈靠近裂源区,疲劳裂纹扩展愈缓慢,循环加载磨合次数愈多,断面愈光滑.
2 Q345圆钢杆疲劳试验 2.1 材性试验为确定式(1)建议的结构钢椭球面断裂模型参数(fy、fu和μ等)和Q345B圆钢杆疲劳试验加载参数(σmax和σmin),疲劳试验前需进行材性试验.
按照《金属材料拉伸试验第1部分:室温试验方法》[14]的规定,制作了与疲劳试验试件同批次的Q345B钢材性试件3根.材性试验测得其泊松比μ=0.272,弹性模量E=2.09×106 MPa,工程应力强度值和真实应力强度值列于表 1,前者用于计算疲劳试验加载参数,因疲劳载荷是按试件原始截面计算的,后者用于计算疲劳裂纹失稳扩展面积An,因式(1)建议的结构钢椭球面断裂模型是基于裂尖真实应力场计算的.
| 表 1 Q345B钢材性试验结果 Tab. 1 Test results of Q345B steel's mechanical properties |
计算得式(1)建议的Q345B钢椭球面断裂模型参数,即式(7)计算疲劳裂纹失稳扩展面积所用参数:
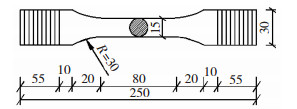
根据《金属材料疲劳试验轴向力控制方法》[15]对疲劳试验试样要求,加工了图 3和表 2所示的Q345B圆钢杆疲劳试验试件,两端部55 mm范围内刻制螺纹,以便和内设丝扣的疲劳试验机套筒夹头固接,图 4为部分试件照片.参照《钢及钢产品力学性能试验取样位置及试样制备》[16]取样要求,圆钢杆疲劳试验试件由直径为35 mm的Q345B圆钢机械加工而成,经检查,试件外观无微裂纹等加工缺陷.
|
图 3 Q345B圆钢杆的几何尺寸 Fig. 3 Geometric dimension of Q345B steel round bars |
| 表 2 疲劳试验加载参数 Tab. 2 Loading parameters of fatigue test |

|
图 4 Q345B圆钢杆照片 Fig. 4 Photo of Q345B steel round bars |
疲劳试验设备为QBG-400高频疲劳试验机(图 5),由主机系统、控制系统和数据输出系统组成.疲劳试验的交变荷载波形为正弦等幅交变荷载,加载频率约为107.7 Hz.

|
图 5 疲劳试验照片 Fig. 5 Photo of fatigue test |
图 6为Q345B圆钢杆的疲劳试验破坏照片,宏观疲劳断口位于过渡圆弧末端与中间平行段交界处,疲劳裂纹起始于交界处外表面.过渡圆弧末端虽相切于平行段,但交界处外形尺寸有变化,造成轻微应力集中,边缘应力幅值略大于心部,应力状态较中间平行段不利.

|
图 6 Q345B圆钢杆的疲劳试验破坏照片 Fig. 6 Fatigue test photos of Q345B steel round bars |
图 6(c)所示的宏观疲劳断口清晰地分为裂纹稳定扩展区(垂直于轴向的光滑断面)和裂纹失稳扩展区(粗糙的纤维状拉断区),二者交界线为外凸于裂纹失稳扩展区的圆弧,证明了疲劳裂纹是以起裂点为中心向四周呈放射状扩展.在疲劳裂纹稳定扩展区,愈靠近裂源,裂纹纹理愈细密,断口愈光滑,说明愈靠近裂源,疲劳裂纹扩展愈缓慢,循环加载次数愈多,证明了前文关于疲劳裂纹扩展速率是循环加载次数单调递增幂函数的假定合理性.
图 6(d)所示的疲劳断口电镜扫描照片显示,疲劳裂纹起源于靠近试件表面的夹杂物周边,该处材料和几何不连续,存在应力集中,说明初始疲劳裂纹对应力集中非常敏感.
表 3汇总的各试件疲劳寿命试验值Nf, t显示,Q345B圆钢杆的疲劳寿命虽有一定离散度,但仍呈现出明显的规律:当相对应力幅RA相同时,疲劳寿命随名义最大应力σmax的降低而增加,如试件SP1~SP5、SP6~SP10、SP11~SP15;当名义最大应力σmax相同时,疲劳寿命随相对应力幅RA的降低而增加,如试件SP5、SP9、SP13.
| 表 3 疲劳试验结果和参数标定 Tab. 3 Fatigue tests results and parameters calibration |
表 3中,Nf, s为按《钢结构设计标准》[3]建议的疲劳寿命计算式计算的各试件的疲劳寿命, 相对试验值的误差
本文建议的结构钢圆杆的疲劳破坏模型认为,名义最大应力σmax决定了疲劳裂纹失稳扩展面积An和稳定扩展面积Af,其和初始裂纹位置参数e、初始裂纹长度a0决定了疲劳裂纹扩展长度af;疲劳裂纹扩展速率va取决于相对应力幅RA;可由疲劳裂纹扩展长度af和扩展速率va计算的疲劳寿命Nf则是名义最大应力σmax、相对应力幅RA、初始裂纹位置参数e和初始裂纹长度a0的函数.
《钢结构设计标准》[3]建议的结构钢疲劳寿命计算式,假定结构钢母材光滑试件的疲劳寿命仅是应力幅Δσ=σmax-0.7σmin的函数,和名义最大应力σmax、相对应力幅RA、初始裂纹位置参数e和初始裂纹长度a0无关,过于简单化.
3 疲劳破坏模型参数标定由式(7)计算各试件的疲劳裂纹失稳扩展面积An,则疲劳裂纹稳定扩展面积Af=A-An,A为试件全截面面积(见表 2).采用牛顿-拉斐逊迭代方法按式(8)解得疲劳裂纹稳定扩展长度af,其中,初始裂纹(起裂点)位置参数e=0(疲劳裂纹起源于试件表面).各试件的参数An、Af和af的计算结果列于表 3.
按前述假设,式(15)建议的结构钢圆杆的疲劳破坏模型中,参数ξ、η是相对应力幅RA的函数,即相对应力幅RA相同的试件,参数ξ、η相同,则参数ξ、η可由相对应力幅RA相同的同组试件的疲劳试验结果拟合标定.
将式(15)建议的结构钢圆杆的疲劳破坏模型改写为双对数坐标,并取a0=0(疲劳试验前检查,试件表面无微裂纹等缺陷),得
| $ \log {N_{\rm{f}}} = \frac{1}{\eta }\log {a_{\rm{f}}} - \frac{1}{\eta }\log \xi . $ | (16) |
对表 3中各组试件的疲劳寿命试验值Nf, t和疲劳裂纹稳定扩展长度af按式(16)的拟合结果见图 7,标定的参数ξ、η列于表 3.参数η随相对应力幅RA变化不大,η=1.620~1.625,平均值ηm=1.622.参数ξ敏感于相对应力幅RA,随相对应力幅RA的增加而增加.
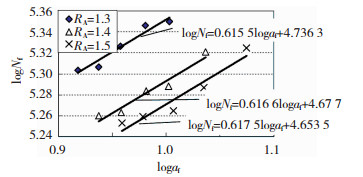
|
图 7 疲劳裂纹稳定扩展长度和疲劳寿命的拟合函数 Fig. 7 Fitting functions of stable propagation length of fatigue crack and fatigue life |
取η=1.622,将式(16)减去各试件1.645倍的标准差s,得式(17).对表 3中各试件疲劳寿命试验值Nf, t和疲劳裂纹稳定扩展长度af按式(17)重新拟合,得95%保证率的Q345B圆钢杆的疲劳破坏模型参数ξ0.95,列于表 3.
| $ \log {N_{\rm{f}}} = \frac{1}{\eta }\log {a_{\rm{f}}} + \frac{1}{\eta }\log {\xi _{0.95}} - 1.645\ s. $ | (17) |
参考刘艳萍等[17]对结构钢疲劳裂纹扩展行为的研究结果,假设疲劳破坏模型参数ξ0.95是相对应力幅RA的幂函数,即
| $ {\xi _{0.95}} = u \cdot R_{\rm{A}}^v + w. $ | (18) |
当相对应力幅RA=0时,为单调静载情况,试件的疲劳寿命Nf=∞,由式(15)得ξ0.95=0,即
| $ {\left. {{\xi _{0.95}}} \right|_{{R_{\rm{A}}} = 0}} = 0 $ |
代入式(18)得w=0.则式(18)简化为
| $ {\xi _{0.95}} = u \cdot R_{\rm{A}}^v. $ | (19) |
将式(19)建议的疲劳破坏模型参数ξ0.95和相对应力幅RA的幂函数改写为双对数坐标,得
| $ \log {\xi _{0.95}} = v \cdot \log {R_{\rm{A}}} + \log u. $ | (20) |
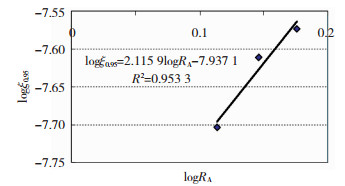
对表 3所列的各组试件的疲劳破坏模型参数ξ0.95和相对应力幅RA按式(20)拟合(图 8),得:
| $ \log {\xi _{0.95}} = 2.116 \times \log {R_{\rm{A}}} - 7.937, $ | (21) |
| $ {\xi _{0.95}} = 1.156 \times {10^{ - 8}} \times R_{\rm{A}}^{2.116}. $ | (22) |
|
图 8 参数ξ0.95和相对应力幅RA的拟合函数 Fig. 8 Fitting functions of fatigue failure model parameter ξ0.95 and relative stress amplitude RA |
将式(22)标定的参数ξ0.95代入式(15)建议的结构钢圆杆的疲劳破坏模型,并取参数η=1.622,Q345圆钢杆的疲劳破坏模型量化为
| $ {N_{\rm{f}}} = {\left( {\frac{{{a_{\rm{f}}}}}{{1.156 \times {{10}^{ - 8}} \times R_{\rm{A}}^{2.116}}}} \right)^{\frac{1}{{1.622}}}}. $ | (23) |
按式(23)计算的各试件的疲劳寿命Nf, c和相对试验值的误差εc-t列于表 3中,其中,各试件的相对应力幅参数RA和疲劳裂纹稳定扩展长度af分别取自表 2和表 3中数据,且取a0=0.可见,式(23)计算的各试件的疲劳寿命略偏于保守,误差为-5.5%~-1.0%.
4 结论以结构钢的椭球面断裂模型为判据,假设结构钢疲劳裂纹稳定扩展速率是循环加载次数的单调递增幂函数,从理论上推导了结构钢圆杆的疲劳破坏模型.对Q345圆钢杆进行了疲劳试验,考察了相对应力幅和名义最大应力对其疲劳寿命的影响规律,标定了建议的结构钢圆杆的疲劳破坏模型参数.所得结论如下:
1) 建议的结构钢圆杆的疲劳破坏模型表明,结构钢圆杆的疲劳寿命Nf是名义最大应力σmax、相对应力幅RA、初始裂纹位置参数e和初始裂纹长度a0的复杂函数,不能简单化为仅是应力幅Δσ的函数.
2) Q345圆钢杆的疲劳寿命随名义最大应力σmax和相对应力幅RA的降低而增加.
3) 量化的结构钢圆杆的疲劳破坏模型,对预测Q345B圆钢杆的疲劳寿命略偏于保守,误差为-5.5%~-1.0%.
| [1] |
陈绍蕃, 顾强. 钢结构(上册)钢结构基础[M]. 北京: 中国建筑工业出版社, 2003: 306. CHEN Shaofan, GU Qiang. Steel structures (Volume Ⅰ): Basic theory of steel structures[M]. Beijing: China Architecture & Building Press, 2003: 306. |
| [2] |
沈祖炎, 陈扬骥, 陈以一. 钢结构基本原理[M]. 北京: 中国建筑工业出版社, 2005: 29. SHEN Zuyan, CHEN Yangji, CHEN Yiyi. Basic principle of steel structures[M]. Beijing: China Architecture & Building Press, 2005: 29. |
| [3] |
钢结构设计标准: GB 50017—2017[S].北京: 中国建筑工业出版社, 2017 Standard for design of steel structures: GB 50017—2017[S]. Beijing: China Architecture & Building Press, 2017 |
| [4] |
钢结构设计规范: TJ 17—74[S].北京: 中国建筑工业出版社, 1975 Code for design of steel structures: TJ 17—74[S]. Beijing: China Architecture & Building Press, 1975 |
| [5] |
王万祯. 结构钢开裂准则及断裂试验分析[J]. 工程力学, 2008, 26(5): 27. WANG Wanzhen. Crack criterion and fracture tests of structural steel[J]. Engineering Mechanics, 2008, 26(5): 27. |
| [6] |
王万祯, 顾强, 孙玉萍. 延性金属在应力三轴空间的裂纹形成准则[J]. 建筑结构, 2007, 37(6): 71. WANG Wanzhen, GU Qiang, SUN Yuping. Crack formation criterion of ductile metal in stress triaxiality space[J]. Building Structure, 2007, 37(6): 71. DOI:10.19701/j.jzjg.2007.06.024 |
| [7] |
PARIS P C, ERDOGAN F. A critical analysis of crack growth laws[J]. Journal of Basic Engineering, 1963, 85(3): 528. |
| [8] |
FORMAN R G, KEARNEY V E, ENGLE R M. Numerical analysis of crack propagation in cyclic-loaded structure[J]. Journal of Basic Engineering, 1967, 89(3): 459. DOI:10.1115/1.3609637 |
| [9] |
ELBER W. The significance of fatigue crack closure[C]//Damage tolerate in aircraft structures, ASTM STP 486. Philadophia: American Society for Testing and Material, 1971: 230
|
| [10] |
赵永翔, 杨冰, 张卫华. 一种疲劳长裂纹扩展率新模型[J]. 机械工程学报, 2006, 42(11): 120. ZHAO Yongxiang, YANG Bing, ZHANG Weihua. New model for long fatigue crack growth rate[J]. Chinese Journal of Mechanical Engineering, 2006, 42(11): 120. DOI:10.3321/j.issn:0577-6686.2006.11.019 |
| [11] |
罗斌, 林琳, 钟诗胜. 一种结合UKF的疲劳结构剩余寿命预测方法[J]. 哈尔滨工业大学学报, 2018, 50(7): 38. LUO Bin, LIN Lin, ZHONG Shisheng. Remaining useful life prediction based on UKF for aircraft structure with fatigue crack[J]. Journal of Harbin Institute of Technology, 2018, 50(7): 38. DOI:10.11918/j.issn.0367-6234.201709020 |
| [12] |
钢结构工程施工质量验收规范: GB 50205—2001[S].北京: 中国标准出版社, 2002 Code for acceptance of construction quality of steel structures: GB 50205—2001[S]. Beijing: China Standards Press, 2002 |
| [13] |
施刚, 张建兴. 高强度钢材Q460C及其焊缝的疲劳性能试验研究[J]. 建筑结构, 2014, 44(17): 1. SHI Gang, ZHANG Jianxing. Fatigue performance test study on high strength steel Q460C and its welded connection[J]. Building Structure, 2014, 44(17): 1. DOI:10.19701/j.jzjg.2014.17.001 |
| [14] |
金属材料拉伸试验第1部分: 室温试验方法: GB/T 228.1—2010[S].北京: 中国计划出版社, 2010 Metallic materials—tensile testing—part 1: Method of test at room temperature: GB/T 228.1—2010[S]. Beijing: China Planning Press, 2010 |
| [15] |
金属材料疲劳试验轴向力控制方法: GB/T 3075—2008[S].北京: 中国标准出版社, 2009 Metallic materials fatigue testing axial force controlled method: GB/T 3075—2008[S]. Beijing: China Standards Press, 2009 |
| [16] |
钢及钢产品力学性能试验取样位置及试样制备: GB/T 2975—1998[S].北京: 中国标准出版社, 1998 Steel and steel products-location and preparation of test piece for mechanical testing: GB/T 2975—1998[S]. Beijing: China Standards Press, 1998 |
| [17] |
刘艳萍, 陈传尧, 李建兵, 等. 14MnNbq焊接桥梁钢的疲劳裂纹扩展行为研究[J]. 工程力学, 2008, 25(4): 209. LIU Yanping, CHEN Chuanyao, LI Jianbing, et al. Fatigue crack growth behavior for the welded heat-affected zone of 14MnNbq bridge steel[J]. Engineering Mechanics, 2008, 25(4): 209. |
 2019, Vol. 51
2019, Vol. 51


