Mehta等[1]将具有高强度、高耐久性、高工作性能的混凝土称为高强高性能混凝土.随着经济社会的快速发展,建筑物不断向高层、巨型、地下等方向发展,实际工程对混凝土的要求越来越高.而超高强混凝土对减少材料用量、节约资源和保护环境等方面均具有重要意义,因此在工程中得到广泛的应用.
混凝土是一种多相复合材料,粗骨料一般占混凝土体积的50%~70%,对混凝土的力学性能有重要影响.目前国内外关于粗骨料类型对超高强混凝土力学性能影响的研究,主要集中在单轴应力状态下.Wu等[2]、Ozturan等[3]研究了不同岩石骨料对不同强度等级混凝土单轴力学性能的影响;戴朝阳等[4]通过研究5~20 mm的4种不同骨料(石灰石、熟料、陶粒和碎砖)对不同强度混凝土力学性能的影响,发现骨料强度对高强混凝土力学性能的影响较普通混凝土显著;杨再富等[5]研究了粗骨料强度对混凝土抗压强度的影响,认为只有骨料强度与基体强度相互协调时,才能更好地发挥骨料和基体的作用.在超高强混凝土的常规三轴试验中,大多集中在对单一粗骨料超高强混凝土的研究上,而针对粗骨料类型对超高强混凝土力学性能影响的研究尚不多见.Xie等[6]利用最大粒径为14 mm连续级配的石英岩粗骨料配制60、90、120 MPa的高强高性能混凝土并进行常规三轴试验;Candappa等[7]用玄武岩粗骨料制备强度等级为40~100 MPa的混凝土,取芯加工成圆柱体试样并测得围压为4、8、12 MPa时的力学响应,建立了等围压下混凝土的破坏准则.这些试验研究均表明,随着围压的增大,混凝土的强度和延性均有明显的改善.
本文分别采用3种不同岩石骨料、同一配合比制备超高强混凝土,与其基体砂浆试样进行六档围压下的常规三轴试验,研究围压和粗骨料对超高强混凝土抗压性能的影响.
1 试验概况 1.1 试验材料及试样制备用于制备超高强混凝土的原材料如下:
1) 水泥:大连小野田公司生产的普通硅酸盐水泥P·Ⅱ52.5R;
2) 硅灰:埃肯国际贸易(上海)有限公司生产的微硅粉,平均粒径约为0.1~0.3 μm;
3) 石英砂:粒径为20~40目和40~80目的石英砂,按质量1: 1混合均匀;
4) 石英粉:平均粒径约为200目的石英粉;
5) 粗骨料:3~10 mm连续粒径的玄武岩、石英岩和大理岩碎石,清洗干净并晾晒至饱和面干状态;
6) 减水剂:西卡公司生产的3301MH型聚羧酸减水剂;
7) 消泡剂:混凝土液体消泡剂;
8) 水:北京市自来水.
本文制备的超高强混凝土配合比见表 1,含粗骨料超高强混凝土的制备是在基体砂浆RPC中加入相同质量、不同类型的粗骨料,不同粗骨料超高强混凝土配合比之间的差异仅在于粗骨料的类型.制备过程如下:将上述材料放入卧式搅拌机搅拌均匀,浇筑至300 mm×250 mm×180 mm的自制木模具和70.7 mm的立方体钢制模具中,在振动台振捣密实.混凝土表面覆盖保鲜膜后放入标准养护室养护2 d,拆模后再移入养护室继续养护,2 d后放置在90 ℃高温养护箱中养护,6 d后取出在室内存放,60 d后开始加工试样.考虑到粗骨料的最大粒径为10 mm和加载时端部效应的影响,将芯样加工成Φ48×145 mm,长径比为3的圆柱体试样.
| 表 1 超高强混凝土配合比 Tab. 1 Mix proportion of UHSC |
本试验共制备4种不同类型、两种形状(70.7 mm的立方体试样和Φ48×145 mm的圆柱体试样)的超高强混凝土,分别用不同编号表示:XW、SY、DL分别代表含玄武岩、石英岩和大理岩碎石的超高强混凝土,三者仅粗骨料种类不同;RPC代表上述3种超高强混凝土中的基体砂浆,其配合比符合活性粉末混凝土的要求;UHSC代表XW、SY、DL和RPC的总称;含粗骨料UHSC代表XW、SY和DL的总称.UHSC的立方体试样仅在2.3节和2.6.2节进行研究.
1.2 试验设备和试验方法试验采用长春新特XTR01型微机控制电液伺服岩石三轴试验机,其轴向荷载的最大量程为2 000 kN,围压的量程为0~100 MPa.试验机的三轴室具有自平衡功能,即液压油作用在柱塞上的合力为零,这是因为三轴室和柱塞采用了特殊的结构形式.试样在三轴室内受到的轴向压应力σ1=p+q=p+F/A,其中:p为液压油施加的围压;q为柱塞施加给试样的偏差应力;F为荷载传感器测得的荷载,等于柱塞受到的轴向荷载;A为试样的横截面面积.试样受力见图 1.

|
图 1 UHSC试样受力简图 Fig. 1 Force diagram of the UHSC specimen |
本试验的上压头(带球铰)和下压头的直径分别为50 mm和53 mm,试样与压头直接接触.采用轴向和径向引伸计来测量试样的变形,见图 2.由于引伸计尺寸的限制,轴向引伸计的上、下端分别固定在试样的上部和下压头上,所测变形包括115 mm的试样变形和35 mm的下压头变形,径向引伸计测量试样中部两个互相垂直方向的位移.使用武汉优泰uT7816动静态应变仪作为外接采集系统,采样频率设置为5 Hz.

|
图 2 引伸计布置图 Fig. 2 Placement of extensometers |
试验中轴压采用位移控制,围压采用应力控制.试验时,首先开始数据采集,再对试样进行轴向预压,通过球铰的调整使上压头端面与柱塞端面平行接触.随后以0.1~0.2 MPa/s的速率施加围压至设计值,保持围压不变至变形稳定,释放掉热缩套和试样的黏塑性变形.然后以0.004~0.005 mm/s的恒定速率施加轴向位移,当峰后曲线出现一段水平段后开始卸载.轴向位移以0.01 mm/s的速率卸载至荷载F为0后再以0.1~0.2 MPa/s卸掉围压,最后停止数据采集.
对于试样表面存在的孔洞等缺陷,采用快硬水泥进行修补,防止试验过程中液压油将热缩套压入孔洞中使其破裂.相同类型的UHSC试样均钻取于同一个UHSC大试块,选用0、5、10、20、40和70 MPa共6档围压.在每档围压下对2块相同类型的试样进行加载,2块试样的峰值偏差应力qmax之差小于两者平均值的7%.当试验中出现漏油或其他原因造成数据不理想时,再增加试样块数.
2 试验结果及分析 2.1 应力-应变曲线规定应力和应变均以压缩为正,拉伸为负.轴向应变用ε1表示,径向应变平均值εr =(ε2+ε3)/2,其中ε2和ε3分别为试样中部同一高度处两个相互垂直方向的径向应变.如前所述,由于释放掉了热缩套和试样的黏塑性变形,所以径向引伸计所测变形即为试样的径向变形.轴向引伸计所测变形需减去35 mm的下压头变形,下压头的弹性模量为206 GPa.
图 3是不同围压下UHSC的轴向(径向)应力-应变曲线,在不同围压下UHSC的q-εr, q-ε1曲线形状基本相似.当围压较低时,加载到试样的应力峰值点后荷载立即下降,变形突然增大,此过程在一瞬间发生并发出巨大的响声,这是由于压力机刚度不足造成的.此过程发生的时间小于数据采集的间隔导致未采集到数据,从试样的破坏形态中可以看到在峰后段贯通形成的斜向主裂缝,应力-应变曲线有明显的尖点;而在70 MPa的高围压下,上述过程发展的十分缓慢,荷载在峰值点附近波动一段时间后缓慢下降,变形缓慢增大.整个过程并没有发出响声,应力-应变曲线变得光滑连续,试样没有形成斜向主裂缝.此后,应变继续增长而应力基本不变,在应力-应变曲线上呈现一段平台区.这是由于围压的作用,试样破坏面间存在摩擦力,从破坏试样的剪切面上可以看到由于摩擦而产生的粉末.

|
图 3 UHSC试样的q-εr, q-ε1曲线 Fig. 3 q-εr and q-ε1 curves of UHSC specimens |
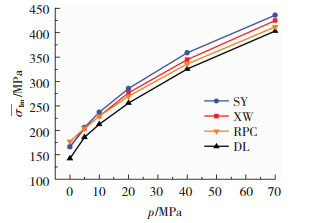
UHSC试样的峰值应力平均值σ1m=qmax+p,其中qmax为相同围压下同一类型的两个试样峰值偏差应力的平均值,p为围压,图 4为UHSC试样的σ1m-p曲线.
|
图 4 UHSC试样的σ1m-p曲线 Fig. 4 σ1m-p curves of UHSC specimens |
对于普通混凝土,由于基体砂浆及其与骨料界面的黏结强度都较低,混凝土的峰值应力由两者的强度决定.而在超高强混凝土中,基体砂浆及其与骨料界面的黏结强度均得到提高,荷载产生的裂缝可能穿越骨料而引起混凝土破坏,此时骨料对混凝土的强度起到了控制作用.
由图 4可知:1)在单轴加载条件下,含粗骨料UHSC的强度低于其基体砂浆RPC的强度;2)随着围压的升高,含石英岩和玄武岩UHSC的强度明显高于RPC,而含大理岩UHSC的强度略低于RPC;3)RPC的峰值应力随着围压的升高有显著的提高,而粗骨料的掺入使得含粗骨料UHSC的增长速率在低围压下明显高于其基体砂浆RPC;4)不同类型UHSC峰值应力的增长速率随围压的升高逐渐变慢,在40~70 MPa下基本趋于同一速率.
围压的大小、粗骨料的类型共同影响UHSC的峰值应力.在单轴加载条件下,圆柱体试样的中部几乎为单向应力状态,随着荷载的增大,在试样中产生横向拉应变.岩石在破碎成粗骨料碎石的过程中会在粗骨料上产生微裂缝,粗骨料受拉时容易先从裂缝处发生开裂,这将导致含粗骨料UHSC的单轴抗压强度小于RPC.而在三轴条件下,围压的约束作用能够推迟甚至防止骨料开裂,使得含粗骨料UHSC的强度随围压大幅增长.由于石英岩、玄武岩的强度高于大理岩,因此XW、SY的峰值应力高于RPC,而DL略低于RPC.王冲等[8]研究发现混凝土中的粗集料对混凝土的单轴抗压强度不利,与含粗集料混凝土相比,混凝土中无粗集料时的强度明显较高,从而说明了活性粉末混凝土的合理性,这与本文所得结论一致.
2.3 圆柱体与立方体试样的单轴抗压强度表 2给出了UHSC立方体与圆柱体的单轴抗压强度及它们之间的换算系数,可看到:1)同一类型UHSC的立方体单轴抗压强度高于圆柱体;2)含粗骨料UHSC的换算系数明显小于基体砂浆RPC.产生1)的原因为端部约束的影响致使立方体单轴受压时实际破裂面与真实破裂面不重合,导致测得的抗压强度比真实值偏大,引起了形状效应[9].而对于长径比为3的圆柱体试样,其破坏发生在试样中部的近似单轴应力区,削弱了端部约束的影响,测得的抗压强度更接近材料的真实值.对2)的原因讨论如下:由于端部效应的影响产生由试样端面的四周指向圆心的切向力,切向力由骨料和砂浆从试样的两端向中部传递并逐渐减小.与RPC相比,粗骨料在混凝土中由于相互咬合、镶嵌、搭接等作用增加了混凝土的整体性,更有利于切向力向中部传递,增大了端部约束的影响.端部约束如同围压的作用,如上节所述,提高了抗压强度.
| 表 2 UHSC立方体与圆柱体的单轴抗压强度 Tab. 2 Uniaxial compressive strength of UHSC cubes and cylinders |
由图 3可以看到UHSC试样在不同围压下的应力-应变曲线在峰值点前直线段的斜率大致相等,因此,UHSC的弹性模量受围压的影响不大.在低围压下,UHSC直到破坏前几乎一直为线性,因而可以确定一个常数作为弹性模量.而在高围压下仅在很小的应力范围内表现为线性,因此在不同阶段联系应力-应变关系的材料模量是一个变值,称为变形模量,变形模量更能表现出围压的影响.本文取应力-应变曲线的原点至85%峰值偏差应力点之间的割线来定义变形模量Ef,取应力-应变曲线的直线段来定义弹性模量E.
由表 3可见,UHSC的弹性模量受围压的影响不大,与所含粗骨料的弹性模量有关,粗骨料的加入明显提高了UHSC的弹性模量.这是因为荷载由UHSC中的基体砂浆和粗骨料共同承担,由于粗骨料的弹性模量大于基体砂浆,在相同应力下粗骨料的变形小于基体砂浆.因此粗骨料的加入减小了含粗骨料UHSC的变形,提高了弹性模量.陈兵等[10]研究发现在基体砂浆基本相同的情况下,混凝土所含骨料对其弹性模量的影响很大,这与本文所得结论一致.变形模量大致呈现随围压的升高而减小的趋势,这是由于UHSC在应力峰值点前应力的增长速率远小于应变的增长速率.围压越大,弹性模量与变形模量的差值越大.
| 表 3 UHSC的弹性模量和变形模量 Tab. 3 Elastic modulus and deformation modulus of UHSC |
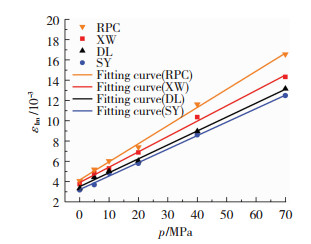
图 5为5 MPa围压下UHSC试样的q-εr, q-ε1曲线,这里仅给出UHSC试样在5 MPa围压下的应力-应变曲线,在其他围压下有相同的规律.从图 5可知,在相同轴向应力下含粗骨料UHSC的变形均小于RPC,这是因为含粗骨料UHSC的弹性模量高于RPC.图 6为UHSC试样峰值点的轴向应变ε1m与围压p的关系,由于围压的存在阻碍了裂缝的产生与扩展,使得UHSC的变形能力得到提高.对于RPC,在70 MPa围压下ε1m从单轴时0.004 1增长到0.016 6,增长了近4.1倍.随着围压的增大,UHSC试样峰值点的轴向应变呈线性增长,拟合关系式:

|
图 5 5 MPa围压下UHSC试样的q-εr, q-ε1曲线 Fig. 5 q-εr and q-ε1 curves of UHSC specimens under 5 MPa confinement |
|
图 6 UHSC试样的ε1m-p曲线 Fig. 6 ε1m-p curves of UHSC specimens |
ε1m=A+Bp,
对于XW: A=3.9×10-3, B=1.513 7×10-4, R2=0.998 3;
对于SY: A=3.2×10-3, B=1.330 4×10-4, R2=0.997 8;
对于DL:A=3.5×10-3, B=1.372 2×10-4, R2=0.997 6;
对于RPC:A=4.2×10-3, B=1.786 9×10-4, R2=0.997 6.
相关系数均大于0.99,线性关系良好.
2.6 破坏形态 2.6.1 围压的影响图 7为不同围压下UHSC的破坏形态:在单轴条件下,UHSC试样类似劈裂破坏,破坏均发生在试样的中部,破坏后有多条中间宽两端细的竖向裂缝,形成多个破碎块.在围压为5~40 MPa时,试样的破坏形态变为剪切破坏,呈现一条或两条斜向主裂缝和多条次裂缝.随着围压的增大,斜裂缝与水平方向的夹角大致呈减小趋势,次裂缝逐渐消失,剪切面上附有因摩擦而产生的粉末.在围压为70 MPa时,破坏后的试样仍为一个整体,但试样中部或两端鼓胀明显,表面有多条不规则的微细裂缝,表现出一定的挤压流动特征.

|
注:在围压为5~40 MPa的试样图片中,左侧为原始图片,右侧在原始图片中标注了裂缝. 图 7 不同围压下UHSC的破坏形态 Fig. 7 Failure modes of UHSC specimens under different confinements |
图 8为UHSC试样的破坏详图,这里仅以含石英岩和大理岩UHSC为例,对破坏试样表面的裂缝走向进行汇总,研究粗骨料的影响,含玄武岩UHSC的裂缝走向与石英岩相似.骨料在混凝土破坏过程中的作用主要表现在对裂缝扩展的影响,即产生和阻挡裂缝.根据能量最小原理,裂缝总是选择耗能小的路径前进.由表 4可知,不同骨料对裂缝扩展呈现不同的作用.当裂缝扩展至骨料时,对于石英岩,裂缝多是绕行骨料;而对于大理岩,裂缝多是穿越骨料.

|
注:图中红色箭头代表裂缝穿越粗骨料,蓝色箭头代表裂缝绕行粗骨料. 图 8 UHSC试样的破坏形态详图 Fig. 8 Detailed failure modes of UHSC specimens |
| 表 4 含石英岩、大理岩UHSC试样裂缝走向 Tab. 4 Fracture trends of UHSC specimens containing quartz and marble |
如图 7所示,不同类型UHSC的破坏形态在相同围压下基本一致.在70 MPa围压下,含粗骨料UHSC试样的裂缝多出现在试样的中部而RPC试样多出现在两端.由图 9可知,UHSC立方体试样的破坏形态近似呈现正倒相接的四角锥形.

|
图 9 UHSC立方体试样破坏形态 Fig. 9 Failure modes of UHSC cubes |
综上所述,围压和粗骨料对试样的破坏形态均有影响:围压占主要作用,影响试样的宏观破坏形态,0围压时类似劈裂破坏,5~40 MPa下呈现剪切破坏,70 MPa时表现出一定的挤压流动特征.粗骨料起次要作用,影响试样的细观破坏形态,在不同围压下裂缝按不同的破坏形态扩展.当裂缝遇到粗骨料时,粗骨料仅在局部影响裂缝的走向,而裂缝的总体走向不变.
2.7 抗压强度准则分别采用Mohr-Coulomb准则和Ansari准则来描述UHSC试样的抗压强度规律.
Mohr-Coulomb准则可表示为
| $ \frac{\sigma_{\max }}{f_{\mathrm{c}}}=1+\frac{k \sigma_{3}}{f_{\mathrm{c}}}. $ | (1) |
式中:σmax为三轴抗压强度(σmax=qmax+p),fc为单轴抗压强度,σ3为围压(σ3=p),k为Mohr-Coulomb准则的参数,其大小代表混凝土的强度随围压的增长速度,取值在2.6~5.3之间并与混凝土材料等因素有关[11],而本文得到的不同UHSC试样的k值也在此范围内.
表 5为Mohr-Coulomb准则拟合结果,拟合效果不理想,当UHSC中含大理岩时,相关系数R2仅为0.891 18,因此需要进行改良.Ansari等[12]提出将线性公式改为非线性公式:
| $ \frac{\sigma_{\max }}{f_{\mathrm{c}}}=1+k\left(\frac{\sigma_{3}}{f_{\mathrm{c}}}\right)^{a} $ | (2) |
| 表 5 Mohr-Coulomb准则拟合结果 Tab. 5 Fitting result by using Mohr-Coulomb criterion |
式中a为Ansari准则的参数,其他参数同式(1).
表 6为Ansari准则拟合结果,R2均大于0.99,具有较高的吻合度.从图 10 (a)可看到,Mohr-Coulomb准则能大致反映试验数据的变化趋势,当围压较低时,低估了UHSC的强度,而在围压较高时高估了UHSC的强度.图 10 (b)表明Ansari准则较Mohr-Coulomb准则更精确地反映混凝土强度随围压的变化趋势.
| 表 6 Ansari准则拟合结果 Tab. 6 Fitting result by using Ansari criterion |

|
图 10 拟合结果与试验数据的比较 Fig. 10 Comparison between fitting results and experimental data |
1) 围压的大小、粗骨料的类型共同影响UHSC的抗压强度:在单轴受压条件下,含粗骨料UHSC的强度低于其基体砂浆RPC;随着围压的升高,含石英岩和玄武岩UHSC的强度高于RPC;含粗骨料UHSC峰值应力的增长速率在低围压下明显高于RPC.
2) UHSC的弹性模量与所含粗骨料的弹性模量有关,与围压大小几乎无关.
3) UHSC峰值点的轴向应变与围压呈线性关系;由于粗骨料的弹性模量高于基体砂浆RPC,在相同轴向应力下含粗骨料UHSC的变形明显小于RPC.
4) 围压不同,UHSC的破坏形态不同:0围压时类似劈裂破坏,5~40 MPa围压下呈现剪切破坏,70 MPa围压时表现出一定的挤压流动特征;不同骨料对裂缝的扩展呈现不同的阻挡作用,对于石英岩,裂缝多是绕行骨料,而对于大理岩,裂缝多是穿越骨料.
5) Ansari准则较Mohr-Coulomb准则更精确地反映混凝土强度随围压的变化趋势.
| [1] |
MEHTA P K, AITCIN P C. Principles underlying production of high-performance concrete[J]. Cement Concrete & Aggregate, 1990, 12(2): 70. DOI:10.1520/CCA10274J |
| [2] |
WU Keru, CHEN Bing, WU Yao, et al. Effect of coarse aggregate type on mechanical properties of high-performance concrete[J]. Concrete, 2001, 31(10): 1421. DOI:10.1016/S0008-8846(01)00588-9 |
| [3] |
OZTURAN T, CENEN C. Effect of coarse aggregate type on mechanical properties of concretes with different strengths[J]. Cement & Concrete Research, 1997, 27(2): 165. DOI:10.1016/S0008-8846(97)00006-9 |
| [4] |
戴朝阳, 陆洪建, 陈兵. 集料与混凝土力学性能关系研究[J]. 江西建材, 2000(1): 13. DAI Chaoyang, LU Hongjian, CHEN Bing. Study on the relationship between aggregate and mechanical properties of concrete[J]. Jiangxi Building Materials, 2000(1): 13. |
| [5] |
杨再富, 钱觉时, 唐祖全, 等. 粗集料强度对混凝土抗压强度影响的试验研究[J]. 混凝土, 2004(12): 23. YANG Zaifu, QIAN Jueshi, TANG Zuquan, et al. Experimental study about effect of coarse aggregate strength on compressive strength of concrete[J]. Concrete, 2004(12): 23. DOI:10.3969/j.issn.1002-3550.2004.12.008 |
| [6] |
XIE J, ELWI A E, MACGREGOR J G. Mechanical properties of three high-strength concretes containing silica fume[J]. ACI Materials Journal, 1995, 92(2): 135. |
| [7] |
CANDAPPA D C, SANIAYAN J G, SETUNG S. Complete triaxial stress-strain curves of high-strength concrete[J]. Journal of Materials in Civil Engineering, 2001, 13(3): 209. DOI:10.1061/(ASCE)0899-1561(2001)13:3(209) |
| [8] |
王冲, 蒲心诚, 刘芳, 等. 150 ~ 200 MPa超高性能混凝土的配制[J]. 工业建筑, 2005, 35(1): 20. WANG Chong, PU Xincheng, LIU Fang, et al. The preparation of 150-200 MPa super high strength & high performance concrete[J]. Industrial Construction, 2005, 35(1): 20. DOI:10.15986/j.1006-7930.2018.02.008 |
| [9] |
康亚明, 贾延, 罗玉财. 立方体测混凝土抗压强度时的破裂形态与机制[J]. 西安建筑科技大学学报(自然科学版), 2018(2): 202. KANG Yaming, JIA Yan, LUO Yucai. Fracture morphology and mechanism of concrete cube test blocks subjected to compression failure[J]. Journal of Xi'an University of Architecture & Technology (Natural Science Edition), 2018(2): 202. DOI:10.15986/j.1006-7930.2018.02.008 |
| [10] |
陈兵, 张立新, 刘娟育. 集料对高性能混凝土力学性能影响研究[J]. 混凝土, 2000(4): 26. CHEN Bing, ZHANG Lixin, LIU Juanyu. Effect of coarse aggregate type on mechanical properties of high performance concrete[J]. Concrete, 2000(4): 26. |
| [11] |
FARNAM Y, MOOSAVI M, SHEKARCHI M, et al. Behaviour of Slurry Infiltrated Fibre Concrete (SIFCON) under triaxial compression[J]. Cement and Concrete Research, 2010, 40(11): 1579. DOI:10.1016/j.cemconres.2010.06.009 |
| [12] |
ANSARI F, LI Qingbin. High-strength concrete subjected to triaxial compression[J]. ACI Materials Joumal, 1998, 95(6): 752. |
 2019, Vol. 51
2019, Vol. 51


