土体变形具有明显的流变性质。为了理论和数值模拟土体的流变特性,岩土学者已建立了许多土体流变模型。但这些模型主要侧重于研究饱和土的应变速率效应[1-6],有关非饱和土的流变模型则相对较少[7-8]。Gennaro等[7]率先开展非饱和土率相关本构模型的研究工作.他们把净应力和吸力作为状态变量[9],根据非饱和土等应变速率压缩线提出了屈服净应力与应变速率之间的关系式,建立了非饱和土弹黏塑性模型.李冬等[8]把土骨架平均应力和有效吸力作为状态变量[10-11],建立了非饱和土弹黏塑性模型.他们在非饱和土流变模型上的开创性工作,有力地推动了非饱和土流变力学的发展.但这些非饱和土流变模型在描述速率效应对屈服应力的影响时,认为总体应变速率(等于弹性应变速率和黏塑性应变速率之和)影响非饱和土的屈服应力.而现代连续介质力学认为[3, 12-13],弹性变形属于可恢复变形,其速率不会对引起不可恢复变形的屈服应力产生影响.因此采用黏塑性应变速率而不是总应变速率来建立屈服应力流变方程,更符合热力学规律.其次,非饱和土具有两种塑性机制.一个是净应力加载引起的塑性体积变形,采用LC屈服面来描述;另一个是吸力加载引起的塑性体积变形,采用SI屈服面来反映其变形特征.但现有的非饱和土流变模型只考虑LC屈服面的变形特性,对非饱和土流变特性的研究还欠全面.因此有关非饱和土流变模型的研究还有待日臻完善.
本文借鉴巴塞罗那非饱和土弹塑性模型[9],以净应力和吸力作为建模应力变量,根据等效时间法[4],分别获得LC和SI两个屈服面的弹黏塑性方程,建立了非饱和土双屈服面流变模型.“净应力和吸力”与“土骨架平均应力和有效吸力”成一一对应关系,故“净应力和吸力”是与“土骨架平均应力和有效吸力”等效的非饱和土本构模型应力变量,采用“净应力和吸力”双变量来建模同样具有热力学意义上的合理性.
1 非饱和土流变模型非饱和土弹塑性模型存在两个屈服面,一个是LC屈服面,另一个是SI屈服面.根据弹黏塑性流变模型理论,双屈服面的总应变可以表示为弹性应变和两个屈服面的黏塑性应变之和:
| $ {{\dot \varepsilon }_{\rm{v}}} = \dot \varepsilon _{\rm{v}}^{\rm{e}} + \dot \varepsilon _{\rm{v}}^{{\rm{Lvp}}} + \dot \varepsilon _{\rm{v}}^{{\rm{svp}}}, $ | (1) |
| $ {{\dot \zeta }_{ij}} = \dot \zeta _{ij}^{\rm{e}} + \dot \zeta _{ij}^{{\rm{Lvp}}} + \dot \zeta _{ij}^{{\rm{svp}}}. $ | (2) |
式中:εv为体应变,εve为弹性体应变,εvLvp和εvsvp分别是LC和SI屈服面的黏塑性体应变.式(2)中的ζij为偏应变,ζije为弹性偏应变,ζijLvp和ζijsvp分别是LC和SI屈服面的黏塑性偏应变.
1.1 弹性方程非饱和土的弹性本构方程可表示为[9]:
| $ \varepsilon _{\rm{v}}^{\rm{e}} = \frac{\kappa }{{{v_0}}}\frac{{\dot {\bar p}}}{{\bar p}} + \frac{{{\kappa _{\rm{s}}}}}{{{v_0}}}\frac{{\dot s}}{{s + {p_{{\rm{atm}}}}}}, $ | (3) |
| $ \dot \zeta _{ij}^{\rm{e}} = {{\dot S}_{ij}}/\left( {2G} \right). $ | (4) |
式中:p=p-pG为净应力,s=pG-pL为吸力,p、pG和pL分别是总应力,孔隙气体和液体压力,patm为标准大气压,κ和κs为净应力和吸力回弹模量.υ0=1+e0为初始比容,e0为初始孔隙比.Sij为偏应力,G=[1.5(1-2μ)/(1+μ)](p′υ0/κ)为剪切模量,μ为泊松比.
1.2 LC流变屈服方程根据巴塞罗那弹塑性模型,非饱和土的LC屈服方程为
| $ F=q^{2}+M^{2}\left(\bar{p}+\bar{p}_{\mathrm{s}}\right)\left(\bar{p}-\bar{p}_{\mathrm{c}}\right)=0. $ | (5) |
式中:q为广义剪应力,pc为屈服净应力,ps=kas,ka为常数[9].在塑性模型中,屈服净应力的硬化参数是塑性体应变和吸力;而在黏塑性流变模型中,屈服净应力的硬化参数是黏塑性体应变速率、黏塑性体应变和吸力,即屈服净应力的硬化规律可表示为pc=f1(
| $ \dot \varepsilon _{\rm{v}}^{{\rm{Lvp}}} = f\left( {{{\bar p}_{\rm{c}}},s,\varepsilon _{\rm{v}}^{{\rm{Lvp}}}} \right). $ | (6) |
式(6)表明黏塑性体应变速率可唯一地表示为屈服净应力,吸力和黏塑性体应变的函数.
非饱和土试验研究表明,当吸力保持不变时,不同等效时间的黏塑性体应变随屈服净应力的压缩线近似为平行线且随等效时间对数增长[7],见图 1.

|
图 1 吸力相同时黏塑性体应变的等效时间压缩线 Fig. 1 Equivalent-time compression lines of viscoplastic volumetric strain at same suction |
选择tr时刻的等时间压缩线作为参考时间线,tLe为常应力和吸力作用下从参考时间起算的变化到现时黏塑性体应变所需的蠕变时间[4],则非饱和土的黏塑性应变公式可表示为
| $ \varepsilon _{\rm{v}}^{{\rm{Lvp}}} = \varepsilon _{\rm{r}}^{{\rm{Lvp}}}\left( s \right) + \frac{{\lambda \left( s \right) - \kappa }}{{{v_0}}}\ln \frac{{{{\bar p}_{\rm{c}}}}}{{{{\bar p}_{\rm{r}}}}} + \frac{{\psi \left( s \right)}}{{{v_0}}}\ln \frac{{{t_{\rm{r}}} + {t_{{\rm{Le}}}}}}{{{t_{\rm{r}}}}}. $ | (7) |
式中:λ(s)为压缩指数,ψ(s)为次固结系数,pr为参考净应力,υ0为初始比容,εrLvp(s)为吸力s时在参考时间tr线上参考净应力pr所对应的参考黏塑性体应变,本文把εrLvp(s)称为参考时间黏塑性体应变.对式(7)求时间导数得
| $ \dot \varepsilon _{\rm{v}}^{{\rm{Lvp}}} = \psi \left( s \right)/\left[ {{v_0}\left( {{t_{\rm{r}}} + {t_{{\rm{Le}}}}} \right)} \right]. $ | (8) |
令黏塑性指数比β(s)为
| $ \beta \left( s \right) = \psi \left( s \right)/\left[ {\lambda \left( s \right) - \kappa } \right]. $ | (9) |
式(8)中的tLe用式(7)代替后利用式(9)得
| $ \dot \varepsilon _{\rm{v}}^{{\rm{Lvp}}} = \frac{{\psi \left( s \right)}}{{{v_0}{t_{\rm{r}}}}}\exp \left[ {\frac{{\varepsilon _{\rm{r}}^{{\rm{Lvp}}}\left( s \right) - \varepsilon _{\rm{v}}^{{\rm{Lvp}}}}}{{\psi \left( s \right)/{v_0}}}} \right]{\left( {\frac{{{{\bar p}_{\rm{c}}}}}{{{{\bar p}_{\rm{r}}}}}} \right)^{\frac{1}{{\beta \left( s \right)}}}}. $ | (10) |
由于黏塑性体应变速率是关于屈服净应力,吸力和黏塑性体应变的唯一函数.故式(10)必须与式(6)相等.同时,式(10)中的黏塑性体应变速率是通过蠕变时间tLe间接获得的,与文献[4]一样,把tLe称为等效时间.
从式(8)可知,当黏塑性体应变速率相同时,等效时间tLe会随着参考时间tr选择的不同而发生变化,这不利于流变模型参数在不同参考时间之间的转换.故引入绝对等效时间tLa[3, 13],它的定义为参考时间tr与等效时间LLe之和.由式(8)可知,绝对等效时间与黏塑性体应变速率成一一对应关系.由于黏塑性体应变速率是一个客观量,故绝对等效时间也是一个客观量,它不会随着参考时间的不同选择而发生变化,因此工程应用时绝对等效时间比一般等效时间要方便得多.把tLa=tLe+tr代入式(7)可得黏塑性体应变-净应力-绝对等效时间的唯一性关系方程为
| $ \varepsilon _{\rm{v}}^{{\rm{Lvp}}} = \varepsilon _{\rm{r}}^{{\rm{Lvp}}}\left( s \right) + \frac{{\lambda \left( s \right) - \kappa }}{{{v_0}}}\ln \frac{{{{\bar p}_{\rm{c}}}}}{{{{\bar p}_{\rm{r}}}}} + \frac{{\psi \left( s \right)}}{{{v_0}}}\ln \frac{{{t_{{\rm{La}}}}}}{{{t_{\rm{r}}}}}. $ | (11) |
假定LC屈服准则符合相关联流动法则,根据Perzyna过应力势函数理论,由式(5)得
| $ \left( {\dot \varepsilon _{\rm{v}}^{{\rm{Lvp}}}/\dot \varepsilon _{\rm{s}}^{{\rm{Lvp}}}} \right) = {M^2}\left( {2\bar p + {{\bar p}_s} - {{\bar p}_{\rm{c}}}} \right)/\left( {2q} \right), $ | (12) |
式中εsLvp为LC屈服面的广义剪应变.由式(10)、(12)得
| $ \begin{array}{l} \dot \varepsilon _{\rm{s}}^{{\rm{Lvp}}} = \frac{{2q\psi \left( s \right)/\left( {{v_0}{t_{\rm{r}}}} \right)}}{{{M^2}\left( {2\bar p + {{\bar p}_s} - {{\bar p}_{\rm{c}}}} \right)}} \times \\ \;\;\;\;\;\;\exp \left[ {\frac{{\varepsilon _{\rm{r}}^{{\rm{Lvp}}}\left( s \right) - \varepsilon _{\rm{v}}^{{\rm{Lvp}}}}}{{\psi \left( s \right)/{v_0}}}} \right]{\left( {\frac{{{{\bar p}_{\rm{c}}}}}{{{{\bar p}_{\rm{r}}}}}} \right)^{\frac{1}{{\beta \left( s \right)}}}}. \end{array} $ | (13) |
当q=0和净应力p为压时,由式(5)可知pc=p.把pc=p代入到式(10)和式(11)可得:
| $ \dot \varepsilon _{\rm{v}}^{{\rm{Lvp}}} = \frac{{\psi \left( s \right)}}{{{t_{\rm{r}}}}}\exp \left[ {\frac{{\varepsilon _{\rm{r}}^{{\rm{Lvp}}}\left( s \right) - \varepsilon _{\rm{v}}^{{\rm{Lvp}}}}}{{\psi \left( s \right)}}} \right]{\left( {\frac{{\bar p}}{{{{\bar p}_{\rm{r}}}}}} \right)^{\frac{1}{{\beta \left( s \right)}}}}, $ | (14) |
| $ \varepsilon _{\rm{v}}^{{\rm{Lvp}}} = \varepsilon _{\rm{r}}^{{\rm{Lvp}}}\left( s \right) + \frac{{\lambda \left( s \right) - \kappa }}{{{v_0}}}\ln \frac{{\bar p}}{{{{\bar p}_{\rm{r}}}}} + \frac{{\psi \left( s \right)}}{{{v_0}}}\ln \frac{{{t_{{\rm{La}}}}}}{{{t_{\rm{r}}}}}. $ | (15) |
式(14)是等向压缩条件下黏塑性体应变速率公式,式(15)是等向压缩条件下吸力s恒定时黏塑性体应变-净应力-绝对等效时间的唯一性关系方程.鉴于一维完全侧限压缩变形和等向压缩变形的力学机理均为体积压缩变形,因此把式(14)~(15)中的p和pr改为竖向净应力后,可以描述一维完全侧限条件下非饱和土的流变特性.
1.3 LC屈服净应力的硬化规律方程从式(5)、(6)之间的文字说明可看出,黏塑性体应变速率方程和屈服净应力硬化规律方程互为反函数.因此,本节通过LC流变速率方程建立包含黏塑性体应变速率影响的屈服净应力硬化规律.
1) 首先推导黏塑性体应变-净应力-黏塑性体应变速率之间的唯一性关系方程
选择
| $ \varepsilon _{{\rm{vr}}}^{{\rm{Lvp}}} = \varepsilon _{\rm{r}}^{{\rm{Lvp}}}\left( s \right) + \frac{{\psi \left( s \right)}}{{{v_0}}}\ln \frac{{\psi \left( s \right)}}{{{v_0}{t_{\rm{r}}}\varepsilon _{{\rm{vr}}}^{{\rm{Lvp}}}}}. $ | (16) |
利用式(16)把式(10)的tr用
| $ \varepsilon _{\rm{v}}^{{\rm{Lvp}}} = \varepsilon _{{\rm{vr}}}^{{\rm{Lvp}}}\left( s \right) + \frac{{\lambda \left( s \right) - \kappa }}{{{v_0}}}\ln \frac{{{{\bar p}_{\rm{c}}}}}{{{{\bar p}_{\rm{r}}}}} + \frac{{\psi \left( s \right)}}{{{v_0}}}\ln \frac{{\dot \varepsilon _{{\rm{vr}}}^{{\rm{Lvp}}}}}{{\dot \varepsilon _{\rm{v}}^{{\rm{Lvp}}}}}. $ | (17) |
式(17)为黏塑性体应变-净应力-黏塑性体应变速率之间的唯一性关系方程.
2) 其次推导同一屈服面上屈服净应力与吸力和黏塑性体应变速率之间的数学关系式
饱和土的s=0,净应力等于有效应力.设饱和土参考
| $ \frac{{{{\bar p}_{\rm{c}}}}}{{{{\bar p}_{\rm{r}}}}} = \exp \left\{ {\frac{{\varepsilon _{{\rm{vr}}}^{{\rm{Lvp}}}\left( 0 \right) - \varepsilon _{{\rm{vr}}}^{{\rm{Lvp}}}\left( s \right)}}{{\left[ {\lambda \left( s \right) - \kappa } \right]/{v_0}}}} \right\}{\left( {\frac{{\varepsilon _{\rm{v}}^{{\rm{Lvp}}}}}{{\dot \varepsilon _{{\rm{vr}}}^{{\rm{Lvp}}}}}} \right)^{\beta \left( s \right)}}{\left[ {\frac{{{{\bar p}_{{\rm{c}},{\rm{r}}}}\left( 0 \right)}}{{{{\bar p}_{\rm{r}}}}}} \right]^{\frac{{\lambda \left( 0 \right) - \kappa }}{{\lambda \left( s \right) - \kappa }}}}. $ | (18) |
式(18)给出了同一屈服面上s和
| $ {{\bar p}_{\rm{c}}}/{{\bar p}_{{\rm{c}},{\rm{r}}}}\left( s \right) = {\left( {\dot \varepsilon _{\rm{v}}^{{\rm{Lvp}}}/\dot \varepsilon _{{\rm{vr}}}^{{\rm{Lvp}}}} \right)^{\beta \left( s \right)}}. $ | (19) |
式(19)是同一屈服面吸力相同时pc随
3) 最后推导后继屈服面硬化方程
非饱和土LC后继屈服面反映的是屈服净应力随黏塑性体应变发展关系.设饱和土初始黏塑性体应变εv0Lvp=0,在参考
| $ \begin{array}{*{20}{c}} {\frac{{{{\bar p}_{\rm{c}}}}}{{{{\bar p}_{\rm{r}}}}} = \exp \left\{ {\frac{{\varepsilon _{\rm{v}}^{{\rm{Lvp}}} + \varepsilon _{{\rm{vr}}}^{{\rm{Lvp}}}\left( 0 \right) - \varepsilon _{{\rm{vr}}}^{{\rm{Lvp}}}\left( s \right)}}{{\left[ {\lambda \left( s \right) - \kappa } \right]/{v_0}}}} \right\} \times }\\ {{{\left( {\frac{{\dot \varepsilon _{\rm{v}}^{{\rm{Lvp}}}}}{{\dot \varepsilon _{{\rm{vr}}}^{{\rm{Lvp}}}}}} \right)}^{\beta \left( s \right)}}{{\left( {\frac{{{{\bar p}_{{\rm{c}}0}}}}{{{{\bar p}_{\rm{r}}}}}} \right)}^{\frac{{\lambda \left( 0 \right) - \kappa }}{{\lambda \left( s \right) - \kappa }}}}.} \end{array} $ | (20) |
式(20)即是LC后继屈服面的屈服净应力方程.
1.4 等效时间LC屈服流变方程的特色1) LC屈服面硬化方程的退化
假定任何s的εvrLvp(s)相同,即:
| $ \varepsilon _{{\rm{vr}}}^{{\rm{Lvp}}}\left( 0 \right) = \varepsilon _{{\rm{vr}}}^{{\rm{Lvp}}}\left( s \right). $ | (21) |
式(21)表明在εvLvp~pc图中所有s的等
| $ \frac{{{{\bar p}_{\rm{c}}}}}{{{{\bar p}_{\rm{r}}}}} = {\left[ {\frac{{{{\bar p}_{{\rm{c}},{\rm{r}}}}\left( 0 \right)}}{{{{\bar p}_{\rm{r}}}}}} \right]^{\frac{{\lambda \left( 0 \right) - \kappa }}{{\lambda \left( s \right) - \kappa }}}}. $ | (22) |
式(22)与非饱和土巴塞罗那弹塑性模型[9]的屈服方程相同,这表明本文流变屈服方程可以退化为巴塞罗那LC屈服净应力方程.
2) 与Gennaro-Pereira非饱和土流变模型的比较
Gennaro-Pereira[7]通过等速率法建立了非饱和土流变模型,获得的屈服方程为
| $ \frac{{{{\bar p}_{\rm{c}}}}}{{{{\bar p}_{\rm{r}}}}} = \exp \left[ {\frac{{{v_0}\varepsilon _{\rm{v}}^{{\rm{Lvp}}}}}{{\lambda \left( s \right) - \kappa }}} \right]{\left[ {\frac{{\dot \varepsilon _{\rm{v}}^{\rm{e}} + \dot \varepsilon _{\rm{v}}^{{\rm{Lvp}}}}}{{{{\left( {\dot \varepsilon _{\rm{v}}^{\rm{e}} + \dot \varepsilon _{\rm{v}}^{{\rm{Lvp}}}} \right)}_{{\rm{vr}}}}}}} \right]^{\frac{{\lambda \left( 0 \right) - \mathit{\boldsymbol{\kappa }}}}{{\lambda \left( s \right)}}\beta \left( s \right)}}{\left( {\frac{{{{\bar p}_{{\rm{c}}0}}}}{{{{\bar p}_{\rm{r}}}}}} \right)^{\frac{{\lambda \left( 0 \right) - \kappa }}{{\lambda \left( s \right) - \kappa }}}}. $ | (23) |
比较式(20)和式(23)可以发现本文LC屈服面的流变屈服方程和Gennaro-Pereira流变屈服方程之间存在明显差异.(Ⅰ)本文屈服方程式(20)采用黏塑性体应变速率表示,而Gennaro-Pereira屈服方程式(23)采用总体应变速率表示;(Ⅱ)式(20)中黏塑性体应变速率的幂是β(s),而式(23)中总的体应变速率的幂是β(s){[λ(0)-κ]/λ(s)}.由于饱和土的Yin-Graham屈服净应力只与黏塑性体应变速率有关而与弹性体应变速率无关[13-14],故式(23)无法退化到饱和土的Yin-Graham屈服净应力公式.
3) 满足式(21)的
如果式(20)中εvvrLvp(s)和εvvrLvp(0)满足式(21),则LC后继屈服面的净应力方程式会更简单.现证明:最多只有一组(
实际上,假定还存在另一组参考黏塑性体应变速率
| $ \bar p_{\rm{r}}^* = {{\bar p}_{\rm{r}}}{\left( {\dot \varepsilon _{{\rm{vr}}}^{{\rm{Lv}}{{\rm{p}}^*}}/\dot \varepsilon _{{\rm{vr}}}^{{\rm{Lvp}}}} \right)^{\frac{{\psi \left( 0 \right) - \psi \left( s \right)}}{{\lambda \left( 0 \right) - \lambda \left( s \right)}}}}. $ | (24) |
土工试验表明ψ(s)/λ(s)随s发生变化[7],故式(24)等式右边也随s发生变化,但等式左边的pr*对所有的s取同一个值,故式(24)不成立.这就证明了满足式(21)的参考黏塑性体应变速率和参考净应力最多只有一组.故根据土工试验确定唯一满足式(21)的参考黏塑性体应变速率和参考净应力是困难的.在实际应用中只能人为地假定参考黏塑性体应变速率和参考净应力满足式(21),从而不可避免地会带来误差.式(20)不需要满足苛刻条件式(21),因此采用式(20)作为非饱和土的LC流变屈服方程更合理.
1.5 SI流变屈服方程非饱和土除LC屈服面外还存在SI屈服面.SI屈服面的屈服条件为s=sc=constant[9].假定SI屈服面的压缩变形随蠕变时间指数衰减,其表达式为
| $ \varepsilon _{\rm{v}}^{{\rm{svp}}} = \varepsilon _{v0}^{{\rm{svp}}} + \frac{{\lambda _{\rm{s}}^{{\rm{vp}}}}}{{{v_0}}}\ln \frac{{s + {p_{{\rm{atm}}}}}}{{{s_{\rm{c}}} + {P_{{\rm{atm}}}}}}\left[ {1 - \exp \left( { - \frac{{{t_{{\rm{sa}}}}}}{{{\psi _{\rm{s}}}}}} \right)} \right]. $ | (25) |
式中:εv0svp是sc时SI屈服面的黏塑性体应变,λsvp是吸力黏塑性指数,ψs是吸力蠕变系数,tsa为吸力恒定条件下的蠕变时间.对式(25)关于时间求导得
| $ {\psi _{\rm{s}}}\dot \varepsilon _{\rm{v}}^{{\rm{svp}}} = \frac{{\lambda _{\rm{s}}^{{\rm{vp}}}}}{{{v_0}}}\ln \frac{{s + {p_{{\rm{atm}}}}}}{{{s_{\rm{c}}} + {p_{{\rm{atm}}}}}}\exp \left( { - \frac{{{t_{{\rm{sa}}}}}}{{{\psi _{\rm{s}}}}}} \right). $ | (26) |
把式(25)中的tsa代入到式(26)得
| $ {\psi _{\rm{s}}}\dot \varepsilon _{\rm{v}}^{{\rm{svp}}} = \varepsilon _{v0}^{{\rm{svp}}} - \varepsilon _{\rm{v}}^{{\rm{svp}}} + \frac{{\lambda _{\rm{s}}^{{\rm{vp}}}}}{{{v_0}}}\ln \frac{{s + {p_{{\rm{atm}}}}}}{{{s_{\rm{c}}} + {P_{{\rm{atm}}}}}}. $ | (27) |
与LC屈服面的等效时间黏塑性体应变速率性质一样,利用等效时间获得的SI屈服面的黏塑性体应变速率方程式(27)也适用于任何一种应力路径.
Alonso等[9]认为,SI屈服面服从非相关联流动法则,它的黏塑性势函数与剪应力无关,故根据Perzyna理论可知SI屈服面不会产生黏塑性剪应变,即ζijsvp=0,相应的黏塑性广义剪应变为εssvp=0.
1.6 非饱和土弹黏塑性方程根据上面分析,非饱和土弹黏塑性方程包括:(Ⅰ)体应变流变方程,它由式(1)、(3)、(10)和(27)组成;(Ⅱ)偏应变流变方程,它由式(2)、(4)、(13)和ζijsvp=0组成.偏应变流变方程可合写为
| $ \begin{array}{l} {{\dot \zeta }_{ij}} = \frac{{{{\dot S}_{ij}}}}{{2G}} + \dot \lambda \frac{{\partial F}}{{\partial q}}\frac{{\partial q}}{{\partial {S_{ij}}}} = \frac{{{{\dot S}_{ij}}}}{{2G}} + \varepsilon _{\rm{s}}^{{\rm{Lvp}}}\frac{{\partial q}}{{\partial {S_{ij}}}} = \frac{{{{\dot S}_{ij}}}}{{2G}} + \\ \frac{{2\psi \left( s \right)q/\left( {{\mathit{\boldsymbol{v}}_0}{t_{\rm{r}}}} \right)}}{{{M^2}\left( {2\bar p + {{\bar p}_{\rm{s}}} - {{\bar p}_{\rm{c}}}} \right)}}\exp \left[ {\frac{{\varepsilon _{\rm{r}}^{{\rm{Lvp}}}\left( s \right) - \varepsilon _{\rm{v}}^{{\rm{Lvp}}}}}{{\psi \left( s \right)/{v_0}}}} \right]{\left( {\frac{{{{\bar p}_{\rm{c}}}}}{{{{\bar p}_{\rm{r}}}}}} \right)^{\frac{1}{{\beta \left( s \right)}}}}\frac{{\partial q}}{{\partial {S_{ij}}}}. \end{array} $ | (28) |
在三轴试验中,净应力和净应力速率的Lode角均为-π/6,由式(28)可得
| $ \begin{array}{l} {{\dot \zeta }_{\rm{s}}} = \frac{{\dot q}}{{3G}} + \frac{{2\psi \left( s \right)q/\left( {{v_0}{t_{\rm{r}}}} \right)}}{{{M^2}\left( {2\bar p + {{\bar p}_{\rm{s}}} - {{\bar p}_{\rm{c}}}} \right)}} \times \\ \;\;\;\;\;\;\;\;\exp \left[ {\frac{{\varepsilon _{\rm{r}}^{{\rm{Lvp}}}\left( s \right) - \varepsilon _{\rm{v}}^{{\rm{Lvp}}}}}{{\psi \left( s \right)/{v_0}}}} \right]{\left( {\frac{{{{\bar p}_{\rm{c}}}}}{{{{\bar p}_{\rm{r}}}}}} \right)^{\frac{1}{{\beta \left( s \right)}}}}. \end{array} $ | (29) |
此时第1、第2和第3主应变εi(i=1, 2, 3)有:
| $ {{\dot \varepsilon }_1} = \left( {G{{\dot \varepsilon }_{\rm{v}}} + \dot q + 3G{{\dot \zeta }_{\rm{s}}}} \right)/3G, $ | (30) |
| $ {{\dot \varepsilon }_2} = {{\dot \varepsilon }_3} = \left( {2G{{\dot \varepsilon }_{\rm{v}}} - \dot q - 3G{{\dot \zeta }_{\rm{s}}}} \right)/6G. $ | (31) |
试验表明,一些非饱和土的水力和力学之间存在较明显的相互耦合作用[15],表现在土-水特性上,非饱和土的饱和度除与吸力相关外,还与土骨架应变有关.它们之间的本构方程可表示为
| $ {{\dot S}_{\rm{r}}} = \left( {\partial {S_{\rm{r}}}/\partial s} \right)\dot s + \left( {\partial {S_{\rm{r}}}/\partial {\varepsilon _{\rm{v}}}} \right){{\dot \varepsilon }_{\rm{v}}}. $ | (32) |
假定土-水特征曲线满足Genuchten方程[16],则主脱湿和主吸湿方程可表示为:
主脱湿方程
| $ {S_{{\rm{rd}}}} = {\left[ {1 + {{\left( {{s_{\rm{d}}}/{\alpha _{\rm{d}}}} \right)}^m}} \right]^{ - n}},{\rm{d}}{s_{\rm{d}}} > 0; $ | (33) |
主吸湿方程
| $ {S_{{\rm{rw}}}} = {\left[ {1 + {{\left( {{s_{\rm{w}}}/{\alpha _{\rm{w}}}} \right)}^m}} \right]^{ - n}},{\rm{d}}{s_{\rm{w}}} < 0. $ | (34) |
式中:sd和sw分别是主脱湿和主吸湿过程的吸力,Srd和Srw分别是主脱湿和主吸湿过程的饱和度,αd、αw、m和n分别是Genuchten方程参数.
设一般脱湿(或吸湿)过程起始时刻的饱和度和吸力为Sr0和s0,Sr0时在主脱湿和主吸湿曲线上所对应的吸力分别为sd0和sw0.假定饱和度Sr相同时毛细管道的孔喉概率分布特征随孔隙半径r呈rb自相似,b为孔喉结构分形维数.根据Young-Laplace方程可知孔隙半径r与吸力s呈反比,故对于相同饱和度Sr,s与式(33)~(34)中sd和sw的关系:
| $ \left\{ \begin{array}{l} s_0^{ - b} - {s^{ - b}} = s_{{\rm{d}}0}^{ - b} - s_{\rm{d}}^{ - b},{\rm{d}}s > 0\left( {脱湿过程} \right);\\ {s^{ - b}} - s_0^{ - b} = s_{\rm{w}}^{ - b} - s_{{\rm{w}}0}^{ - b},{\rm{d}}s < 0\left( {吸湿过程} \right). \end{array} \right. $ | (35) |
由式(33)~(35)可得式(32)中等式右边的第一项为
| $ \frac{{\partial {S_{\rm{r}}}}}{{\partial s}} = \left\{ {\begin{array}{*{20}{l}} {\left( {\partial {s_{\rm{d}}}/\partial s} \right)\left( {\partial {S_{{\rm{rd}}}}/\partial {s_{\rm{d}}}} \right),{\rm{d}}s > 0\left( {脱湿过程} \right);}\\ {\left( {\partial {s_{\rm{w}}}/\partial s} \right)\left( {\partial {S_{{\rm{rw}}}}/\partial {s_{\rm{w}}}} \right),{\rm{d}}s < 0\left( {吸湿过程} \right).} \end{array}} \right. $ | (36) |
式(32)中等式右边第二项的表达式建议取为
| $ \partial {S_{\rm{r}}}/\partial {\varepsilon _{\rm{v}}} = {S_{\rm{r}}}{\left( {1 - {S_{\rm{r}}}} \right)^{{\alpha _2}}}/n. $ | (37) |
式中n为孔隙率,α2为水力-力学耦合参数.
2 模型算例分析非饱和土三维流变方程涉及的模型参数包括回弹指数κ/υ0,压缩指数λ(s)/υ0,次固结系数ψ(s)/υ0、吸力回弹指数κs/υ0、吸力黏塑性指数λsvp(s)/υ0、吸力蠕变系数ψs(s)、弹性剪切模量G、参数κa和M以及土水特征曲线的αd、αw、α2、b、m和n.上述参数的确定方法见文献[4, 7-9, 16].
冯君[17]对合肥地区非饱和黏土的蠕变特性进行了系统的试验研究,试验土样取自肥东县长临河铁路旁,场区表层1~2 m为第四系松软土,其下为20~25 m厚黏土,属塑性较强的下蜀组黏土,该层黏土的主要物理力学性质指标见表 1[17].
冯君[17]在净压力50~300 kPa和吸力0~200 kPa范围内对黏土进行排水固结蠕变和剪切试验,由此获得参数如下:λ(s)/υ0=[6.03exp(-0.015 s)+2.88]×10-3,εvrLvp(s)=[1.175+6.5exp(-0.018 s)]×10-3,pr=50 kPa,ψ(s)/υ0=[2.12exp(-0.02 s)+3.12]×10-4,tr=1 d,κ/υ0=1.05×10-3,κs/υ0=0.001 56,μ=0.25,ka=0.3,M=1.01.当s≤sc时可不考虑吸力黏塑性压缩影响,故取λsvp=0和ψs=0[9].同时,试验表明土骨架变形对土-水特性的影响较小,为节省篇幅,本算例不对土-水特征曲线做具体分析.利用式(30)~(31)可获得各吸力和蠕变持续时间下的理论预测εv~p曲线,与实测值对比见图 2.

|
图 2 理论预测值和实测值对比 Fig. 2 Comparison diagram between the theoretical predicts and the measured data |
从图 2可看出,随着吸力增大,非饱和黏土的弹塑性压缩线斜率变缓,压缩变形减少.同时次固结系数降低,蠕变变形也相应减小.图中预测值与实测值基本吻合,说明等效时间弹黏塑性模型能够反映该非饱和黏土的流变力学特性.图中还给出了20 a后次固结变形预测值,应变变化量约为0.31%~0.52%,当黏土层厚度达到30~40 m时将产生约9.5~12.4 cm(按0.31%计算)和15.6~20.8 cm(按0.52%计算)的次固结沉降,对于高等级公路的关键部位,如路基和桥头接触处,上述沉降量超过了公路规范规定,因此不可忽略次固结变形对黏土地基工后沉降的影响.
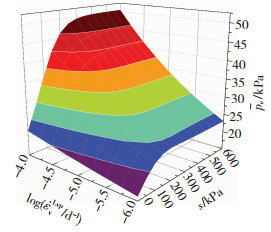
图 3给出了LC屈服净应力pc随吸力s和黏塑性体应变速率
|
图 3
LC屈服净应力随s和 |
从图 3可看出,pc随着s和
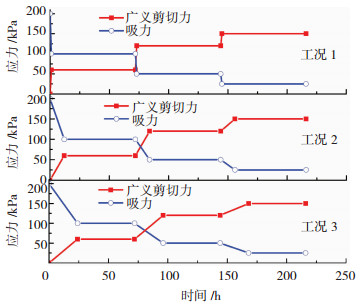
根据非饱和土三维流变模型可以分析一般应力作用下土体应变随时间的变化特性.设土样先在围压σ1=σ2=σ3=100 kPa下固结24 h,把此时应变作为理论分析的起始零应变.然后保持σ2=σ3=100 kPa不变,在σ1方向分三种工况施加荷载.q=σ1-σ3,图 4给出了广义剪应力q和吸力s在三种工况中的加载应力历史.在图 4三种工况中q和s都分三级加载,第一次加载幅值为Δq=60 kPa,Δs=-100 kPa,第二次加载幅值为Δq=60 kPa,Δs=-50 kPa,第三次加载幅值为Δq=30 kPa,Δs=-20 kPa,三次加载后广义剪应力从零增加到150 kPa,吸力从200 kPa减少为25 kPa.三种工况的不同点为,工况1为突然施加广义剪切力和吸力,然而维持72 h保持不变后再施加下级荷载.工况2为线性加载,加载时间12 h,然而维持60 h不变后再施加下级荷载.工况3为线性加载,但加载时间为24 h,然而维持48 h保持不变后再施加下级荷载.
|
图 4 广义剪应力和吸力随时间加载图 Fig. 4 Loading diagram of generalized shear stress and suction with time |
采用4阶Rung-Kutta方法对体应变和广义剪应变进行了编程计算,计算结果见图 5、6.

|
图 5 体应变随时间变化 Fig. 5 Change diagram of volumetric strain with time |

|
图 6 广义剪应变随时间变化 Fig. 6 Change diagram of generalized shear strain with time |
图 5给出了体应变随时间变化图.从图 5可看出,在加载过程和维持恒载的初始阶段,三种加载历史对体应变有明显的影响,工况1的体应变>工况2的体应变>工况3的体应变.但随着维持恒载的时间增长,这三种工况的体应变逐渐接近.这一性质与饱和黏土的流变特性相类似.图 6给出了广义剪应变随时间变化曲线.从图 6可看出,当广义剪应力较小时,这三种加载方式引起的广义剪应变差别不大,但随着广义剪应力逐渐增大,三种加载方式引起的广义剪应变具有明显差别.它们不但在加载过程存在明显不同的增加速率,而且在恒载维持阶段也具有不同的增长幅值.工况1产生的广义剪应变明显大于工况2和工况3的广义剪应变.造成这一情况的主要原因是广义剪应变的增加速率不光与体积流变速率有关,而且还与剪切应力水平密切相关.从式(12)可看出,达到较高应力水平的时间越快,同样体积流变量产生的剪切流变量越大.工况1达到较高应力水平的时间最快,工况2次之,工况3最迟,故对于流变产生的广义剪应变值,工况1>工况2>工况3.这说明在流变模型中,不同加载历史会对剪应变产生较明显的影响.
3 结论1) 根据非饱和土黏塑性体应变-净应力-等效时间关系式,利用等效时间法获得LC屈服面的黏塑性体应变速率方程,建立了LC屈服面的黏塑性广义剪应变速率方程.根据SI屈服面的常吸力压缩蠕变公式,利用等效时间法建立了SI屈服面的黏塑性体应变速率方程,SI屈服面不产生黏塑性剪应变.
2) 当非饱和土退化为饱和土时,本文非饱和土等效时间流变模型退化为饱和土的Yin-Graham流变模型.当不考虑流变特性时,本文非饱和土流变模型能够退化为巴塞罗那非饱和土弹塑性模型.
3) 数值分析了非饱和土一维压缩蠕变特性,研究了三轴不同加载方式作用下非饱和土体应变和广义剪应变随时间变化规律.结果表明,加载方式只对加载期间和恒荷初始阶段的体应变有影响,对长期体应变值影响不大;无论在加载还是在荷载恒定阶段,加载方式均对剪应变产生较明显的影响.
| [1] |
柯文汇, 陈健, 盛谦, 等. 一个描述软黏土时效特性的一维弹黏塑性模型[J]. 岩土力学, 2016, 37(8): 2198. KE Wenhui, CHEN Jian, SHENG Qian, et al. A one-dimensional elasto-viscoplastic model for describing time-dependent behavior of soft clays[J]. Rock and Soil Mechanics, 2016, 37(8): 2198. |
| [2] |
李硕, 王常明, 吴谦, 等. 上海淤泥质黏土固结蠕变过程中结合水与微结构的变化[J]. 岩土力学, 2017, 38(10): 2809. LI Shuo, WANG Changming, WU Qian, et al. Variations of bound water and microstructure in consolidation creep process of Shanghai mucky clay[J]. Rock and Soil Mechanics, 2017, 38(10): 2809. |
| [3] |
胡亚元. 软土的等效时间线剪切流变模型[J]. 哈尔滨工业大学学报, 2018, 50(6): 84. HU Yayuan. An equivalent-time line shear rheological model for soft clay[J]. Journal of Harbin Institute of Technology, 2018, 50(6): 84. |
| [4] |
YIN J H, GRAHAM J. Elastic viscoplastic modelling of the time-dependent stress-strain behaviour of soils[J]. Canadian Geotechnical Journal, 1999, 36(4): 736. DOI:10.1139/t99-042 |
| [5] |
SHI X S, YIN J H, FENG W Q, et al. Creep coefficient of binary sand-bentonite mixtures in oedometer testing using mixture theory[J]. International Journal of Geomechanics, 2018, 18(12): 04018159. DOI:10.1061/(ASCE)GM.1943-5622.0001295 |
| [6] |
ZHU Q Y, YIN Z Y, HICHER P Y, et al. Nonlinearity of one-dimensional creep characteristics of soft clays[J]. Acta Geotechnica, 2016, 11(4): 887. DOI:10.1007/s11440-015-0411-y |
| [7] |
DE GENNARO V, PEREIRA J M. A viscoplastic constitutive model for unsaturated geomaterials[J]. Computers and Geotechnics, 2013, 54(Suppl C): 143. |
| [8] |
李冬, 刘艳. 非饱和土的黏弹塑性本构模型研究[J]. 北京工业大学学报, 2018, 44(3): 321. LI Dong, LIU Yan. Visco-elasto-plasitcconstitutive model for unsaturated soils[J]. Journal of Beijing University of Technology, 2018, 44(3): 321. |
| [9] |
ALONSO E E, GENS A, JOSA A. A constitutive model for partially saturated soils[J]. Geotechnique, 1990, 40(3): 405. DOI:10.1680/geot.1990.40.3.405 |
| [10] |
HOULSBY G T. The work input to an unsaturated granular material[J]. Geotechnique, 1997, 47(1): 193. DOI:10.1680/geot.1997.47.1.193 |
| [11] |
WHEELER S J, SHARMA R S, BUISSON M S R. Coupling of hydraulic hysteresis and stress-strain behaviour in unsaturated soils[J]. Geotechnique, 2003, 53(1): 41. |
| [12] |
HOULSBY G T, PUZRIN A M. Principles of hyperplasticity[M]. London: Springer, 2006: 211.
|
| [13] |
胡亚元. 准塑性的黏弹性模型在黏土中的应用[J]. 岩土工程学报, 2009, 31(3): 353. HU Yayuan. Application of plastic-like visco-elastic model to clay[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(3): 353. DOI:10.3321/j.issn:1000-4548.2009.03.008 |
| [14] |
殷建华. 从本构模型研究到试验和光纤监测技术研发[J]. 岩土工程学报, 2011, 33(1): 1. YIN Jianhua. From constitutive modeling to development of laboratory testing and optical fiber sensor monitoring technologies[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(1): 1. |
| [15] |
孙德安, 陈振新. 非饱和上海软土水力和力学特性耦合弹塑性模拟[J]. 岩土力学, 2012, 33(增刊2): 16. SUN Dean, CHEN Zhenxin. Elastoplastic modelling of coupled hydraulic and mechanical behaviour of unsaturated Shanghai soft clay[J]. Rock and Soil Mechanics, 2012, 33(S2): 16. |
| [16] |
VAN GENUCHTEN M T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J]. Soil Science Society of America Journal, 1980, 44: 892. DOI:10.2136/sssaj1980.03615995004400050002x |
| [17] |
冯君.合肥地区黏性地基土非饱和工程特性试验研究[D].成都: 西南交通大学, 2015: 80 FENG Jun.Experimental study on the unsaturated engineering behavior of the cohesive soil of Hefei area[D]. Chengdu: Southwest Jiaotong University, 2015: 80 http://cdmd.cnki.com.cn/Article/CDMD-10613-1016166561.htm |
 2019, Vol. 51
2019, Vol. 51


