2. 水质科学与水环境恢复工程北京市重点实验室(北京工业大学),北京 100124;
3. 中国水利水电科学研究院,北京 100038;
4. 流域水循环模拟与调控国家重点实验室(中国水利水电科学研究院),北京 100038
2. Key Laboratory of Beijing for Water Quality Science and Water Environment Recovery Engineering (Beijing University of Technology), Beijing 100124, China;
3. China Institute of Water Resources and Hydropower Research, Beijing 100038, China;
4. State Key Laboratory of Simulation and Regulation of Water Cycle in River Basin (China Institute of Water Resources and Hydropower Research), Beijing 100038, China
城市内涝实时预警可以在强降雨来临之前对未来内涝灾害情况进行预测,使得防汛部门提前对灾害采取相应的防治措施.内涝实时预警技术的关键在于具有一定预测精度的前提下,保证足够长的预见期.若预测精度不足,则无法采取正确的防治措施;若预见期过短,则很难保证措施按时完成.预测精度问题通过提高水力模型计算精度已得到很好的解决,而预见期的提前往往会存在一定困难.
目前,较为常用的内涝实时预警方法是基于雨量计的降雨数据实时传输,运用水力模型以实时降雨为输入对管网系统进行实时模拟[1-3].此方法的主要原理是:降雨落到地面-节点溢流形成积水,这一过程需经历一段时间(地表产汇流和管网汇流),若在此时间内完成模拟便能够产生一定的预见期.然而,由于城市发展导致的下垫面硬化愈发严重,产汇流时间往往较短,大大缩短了预见期[4],不利于防汛部门及时决策.
随着雷达预测技术的发展,雷达预测降雨已成功应用到洪水预报中,如周蔚等[5]运用多普勒雷达预测技术,结合水文模型进行流域防洪灾害预警研究,延长了预见期;潘安君等[6]通过对多普勒雷达数据的分析应用,最大程度提高了洪水灾害的预警能力.可见,若能够保证一定时长的降雨预测,便可将预测降雨为输入进行内涝预警模拟,进而得到更长的预见期.因此,本文将雷达预测降雨技术与城市排水管网模型相结合,重点研究城市内涝的实时预警模拟.
1 雷达预测降雨原理雷达对降雨进行临近预报是通过实测雷达反射率因子对未来时刻反射率进行外推,并运用Z-R关系估算出未来时刻的降雨量[7],主要包括雷达外推与降雨定量估算两个过程.
1.1 雷达外推雷达外推常用的方法是交叉相关法(TREC),该方法是对连续两时刻的雷达反射率因子网格通过搜索进行相关系数求解,具有最大相关系数的移动即为预测的反射率因子移动矢量[8],计算公式为
| $ r = \frac{{\sum {{Z_1}\left( i \right){Z_2}\left( i \right)} - {n^{ - 1}}\sum {{Z_1}\left( i \right)} \sum {{Z_2}\left( i \right)} }}{{{{\left[ {\left( {\sum {Z_1^2\left( i \right)} - n\bar Z_1^2} \right)\left( {\sum {Z_2^2\left( i \right)} - n\bar Z_2^2} \right)} \right]}^{\frac{1}{2}}}}}, $ | (1) |
| $ R = {v_{\max }} \times \Delta t. $ | (2) |
式中:r为两个网格矩阵的相关系数,Z1和Z2分别表示T和T+Δt时刻的网格反射率矩阵,n表示矩阵点数,R为搜索半径,vmax为雷达回波最大移动速度,Δt为数据时间间隔.
同时结合两时间层半拉格朗日法得到外推结果[9],即
| $ \hat Z\left( {{t_0} + \Delta t,x} \right) = Z\left( {{t_0},x - \alpha } \right), $ | (3) |
| $ \alpha = \Delta tu\left( {{t_0},x - \alpha /2} \right). $ | (4) |
式中:Z,
在得到雷达矢量场分布后需将预测的反射率因子转换成降雨分布以实现对未来降雨的预测.转换过程根据Z-R相关关系进行计算[10],表达式如下:
| $ Z = A{R^b}. $ | (5) |
式中:Z表示雷达反射率因子(mm3/m6),R表示估算的降雨强度(mm/h),A、b为计算参数.目前中国一直沿用美国WSR-88D的经验公式:Z=300R1.4.
1.2.2 Z-R关系优化Z-R关系在不同区域存在一定差异,因此,经验公式在实际应用中具有一定的局限性,需要依据当地情况对公式优化,确定符合当地雨情的Z-R公式[11].Z-R公式优化可通过目标函数并结合变量的约束范围来构建优化模型,运用优化算法对模型求解,得到最佳参数值.目标函数采用改进的最优化方法准则[12],具体表达式为
| $ {F_{\min }} = \min \left\{ {\sum\limits_{i = 1}^n {{{\left( {{R_i} - {I_i}} \right)}^2}} + \left| {{R_i} - {I_i}} \right|} \right\}. $ | (6) |
式中:n为样本个数,Ri为估算降雨量,Ii为实测降雨量,优化计算时需设置变量约束范围,依据相关文献[13]:A∈(16,1 200),b∈(1,2.87).
1.2.3 Z-R关系误差分析Z-R关系优化后可通过误差分析来评定优化效果,借助式(7)~(10)进行误差计算,以误差值为依据来评估Z-R关系对雨量估算的精度.
| $ {e_1} = \frac{1}{n}\sum\limits_{i = 1}^n {\frac{{\left| {{R_i} - {I_i}} \right|}}{{{I_i}}}} , $ | (7) |
| $ {e_2} = \frac{{\sum\limits_{i = 1}^n {{I_i}} }}{{\sum\limits_{i = 1}^n {{R_i}} }}, $ | (8) |
| $ {e_3} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {{R_i} - {I_i}} \right)}^2}} } , $ | (9) |
| $ {e_4} = \frac{{\sum\limits_{i = 1}^n {\left( {{R_i} - {{\bar R}_i}} \right)\left( {{I_i} - {{\bar I}_i}} \right)} }}{{\sqrt {\sum\limits_{i = 1}^n {{{\left( {{R_i} - {{\bar R}_i}} \right)}^2}} } \sqrt {\sum\limits_{i = 1}^n {{{\left( {{I_i} - {{\bar I}_i}} \right)}^2}} } }}. $ | (10) |
式中:e1为平均相对误差,e2为总雨量比值,e3为均方根误差,e4为相关系数,n为样本总数,Ri和Ii分别为第i个样本的估算降雨量与实测降雨量.
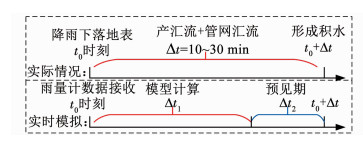
2 基于雷达技术的内涝实时预警 2.1 基于雨量计实时数据的内涝预警方法基于雨量计实时数据传输,通过模型实时模拟是目前城市内涝实时预警的一种常见方法.该方法以实时降雨为输入,运用水力模型在线模拟,得到的模拟结果经分析后可进行内涝实时预警.降雨落在地表后,汇入管网并形成积水这一过程需要经过地表产汇流和管网汇流环节,即降雨发生到管网溢流形成积水的时间间隔为地表产汇流与管网汇流时间总和(10~30 min),只要在这段时间内完成模型的模拟预警,便可提供一定的内涝灾害预见期,如图 1所示.可以看出,此方法的预见期为Δt2=Δt-Δt1,然而模型计算的时间往往需要几分钟,因此,保留的预见期只有5~25 min,若地表硬化、粗糙度较小,则产汇流时间较短,更是大大缩短了预见期,很难满足防汛调度的时间需求.
|
图 1 基于雨量计实时模拟方法 Fig. 1 Real time simulation based on rain station |
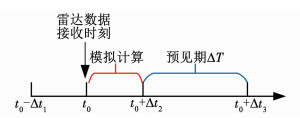
上文介绍了基于雷达外推对未来时段降雨量的预测方法,因此,在城市内涝实时预警中可借助雷达技术,以预测降雨为输入对未来时段的内涝情况进行模拟,如图 2所示.图 2中,t0为雷达数据实时接收时刻,Δt1为雷达数据传输间隔(一般为10 min),Δt2为雷达预测降雨与内涝模型计算时间总和,Δt3为降雨预测时长,ΔT为预见期.从图 2可以看出,以t0和t0-Δt1的雷达数据可预测t0~t0+Δt3时段的降雨,将预测降雨输入到内涝模型中进行模拟,便可得到t0~t0+Δt3时段的内涝积水结果,实现内涝的实时预警.雷达技术在临近降雨预报中,预测时间越长,预测结果越不精确,Δt3往往在1 h内会得到较好预测效果[14].Δt2一般可控制在10 min以内,因此,基于雷达的内涝实时模拟方法可保留预见期ΔT=Δt3-Δt2=50 min.
|
图 2 基于雷达外推实时模拟方法 Fig. 2 Real time simulation based on radar extrapolation |
雷达外推与降雨定量估算得到的每一时刻降雨量是分布在每个雷达网格上的,即每个网格单元均可得到未来时段的降雨过程.在城市排水系统模拟研究中,SWMM(storm water management model)模型已得到广泛应用,选用SWMM进行排水系统的模拟计算[15].SWMM中降雨的输入方式是为每个子汇水区指定一个降雨过程线.因此,可依据雷达网格与每个子汇水区相交的面积权重来提取各个子汇水区的降雨过程作为输入,即
| $ S_i^t = \left( {A_1^i \times I_1^t + A_2^i \times I_2^t + \cdots + A_n^i \times I_n^t} \right)/\sum\limits_{k = 1}^n {A_k^i} . $ | (11) |
式中:Sit为子汇水区i在t时刻的降雨强度,n为与子汇水区i相交的雷达网格数,Aki为与子汇水区i相交的第k个网格的相交面积,Ikt为第k个相交网格在时刻t的降雨强度.可见预测模型每个汇水区的降雨过程是依据对应雷达网格空间位置而输入的,模型不仅能够进行预测模拟,还充分考虑了降雨的空间分布这一因素,使得模拟更加精确.
2.4 内涝实时预警步骤结合雷达外推、降雨定量估算和SWMM模型,进行城市内涝实时预警,具体步骤如下:
1) 依据基础数据构建研究区排水系统SWMM模型.
2) 在t时刻实时接收雷达数据并结合上一时刻t-Δt的数据通过式(1)~(4)进行雷达外推,得到未来1 h内各时刻(间隔Δt)的反射率因子.
3) 将外推结果依据Z-R关系进行降雨定量估算,得到未来1 h内各时刻(间隔Δt)的降雨量.
4) 将预测降雨依据式(11)输入SWMM模型.
5) 若非首次预测,需将上一次预测过程中SWMM模型在t时刻的模拟结果作为本次模拟的初始条件,初始条件的设置包括节点的初始水位和管段的初始流量;若为首次预测,则跳过此步骤.
6) 调用SWMM进行模拟计算,并读取模拟结果.
7) 若步骤1)~6)进行过程中,接收到新雷达数据,则另外并行开启一个新进程,进行步骤2);否则,本次预测结束并等待新雷达数据,返回步骤2).
可见,内涝实时预警模拟是每间隔Δt时间便可更新一次预警结果,进行实时滚动刷新预警.此外,随着时间的推移,当地的气候条件会发生变化而导致雨情发生变化,因此在实时预警进行的同时还要依据不断累积增加的雷达实时数据和降雨实时数据运用Z-R关系优化模型定期对Z-R关系进行优化修正,以保证其能够符合当地的实时雨情.
3 实例研究 3.1 实例1以某市中心城区为研究区域,当地提供的6个雨量站数据(2015—2016年5场分钟降雨数据)和对应时段的雷达反射率因子为基础,进行Z-R关系优化研究.以式(6)为目标函数,运用遗传算法对Z-R关系参数A、b进行优化计算,最终优化得到Z-R关系为
| $ Z = 170.89{R^{1.81}}. $ | (12) |
分别将经验公式和式(12)通过式(7)~(10)进行误差对比分析,如表 1所示.
| 表 1 不同Z-R关系误差对比 Tab. 1 Comparison of different Z-R relationship |
e1和e3越小,表示优化结果越好;e2和e4越接近1,表示估算值与实际值越接近.由表 1可以看出,经优化后的Z-R关系从这4种误差对比上均优于经验公式.因此,通过Z-R关系优化模型可使得降雨定量估算更为精确.
3.2 实例2在研究区6个雨量站5场降雨数据中提取每场最大1 h降雨的起止时间,运用这5个时段的降雨数据和对应时段的雷达反射率数据进行降雨预测研究.以每场雨的两个起始时刻通过式(1)~(4)进行1 h雷达回波外推,运用经验公式和优化得到的式(12)进行雨量计算,得出未来1 h降雨过程,并与实际降雨量进行降雨总量相对误差比较,见式(13),比较结果如表 2所示.
| $ 相对误差 = \left| {{R_n} - {G_n}} \right|/{G_n} \times 100\% . $ | (13) |
| 表 2 预测与实测降雨总量相对误差对比 Tab. 2 Relative error of total rainfall between prediction and measurement |
式中:n为样本数,Rn为1 h雷达预测降雨总量(mm/h),Gn为1 h实测降雨总量(mm/h).
由表 2可以看出,在5个时段6个雨量站的预测过程中经过优化的Z-R关系在应用到降雨预测时,得到的降雨量误差均小于经验公式,因此,通过将Z-R关系优化可提高降雨的预测精度.
3.3 实例3该地区在2015/8/15 02:00—2015/8/15 07:00发生了强降雨事件,其中主城区发生了较为严重的内涝灾害.因此,以该时段进行内涝灾害实时预警仿真模拟,并将预警结果与实际调研情况进行对比验证,评估预测精度.以当地主城区为研究区域构建SWMM模型,模型中管网总长60 km,子汇水区926个,同时依据主城区土地利用数据提取子汇水区产汇流参数,依据管网实测水位、流量数据对模型率定并修正产汇流参数,确保模型参数设置准确.由于SWMM只能模拟出管网溢流量,无法获得溢流水体在地表的淹没范围,本文将SWMM模拟后得到的溢流量借助DEM数据计算淹没范围,从而获得地表的积水情况[16].
模型建立后,以2015/8/15 02:00为仿真起始时间,2015/8/15 07:00为仿真结束时间,按照2.4节的内涝实时预警方法进行实时预警仿真.以间隔10 min读取对应时刻雷达数据的形式来仿真数据实时传输过程(雷达数据时间间隔为10 min).本文仿真采用的雷达数据空间分辨率为300 m×300 m.表 3记录了每次预测过程中各部分的耗时,其中t1为雷达外推和降雨估算时间,t2为汇水区降雨过程提取时间,t3为SWMM模拟计算时间,t4为DEM淹没计算时间.表 3数据显示单次预测总耗时均小于10 min,即在每次雷达数据接收之前便可完成上一次的预测计算,可保留至少50 min的预见期.
| 表 3 各时段单次预测所需时间 Tab. 3 Single prediction time of each period |
据当地排水中心提供的涝情统计资料显示,在2015/8/25 4:00—2015/8/25 5:00期间主城区发生了内涝积水,积水范围约4.76 km2,平均积水深度为0.6 m.将灾害发生时间附近的各个时段预测结果与实际积水情况进行对比,如表 4所示,其中t0为单次预测起始时间,tmax为单次预测的最大淹没时刻,A1为预测的最大淹没面积,A2为预测淹没范围与实测淹没范围相交面积,h为预测淹没范围与实测淹没范围相交区域内模拟的平均水深,eA为A2与实测淹没面积的相对误差,eh为h与实测平均水深的相对误差.
| 表 4 实时内涝预测模拟结果 Tab. 4 Model result of real time urban flooding prediction |
由表 4可以看出,预测的最大淹没时刻在4:40,预测的淹没范围和淹没水深与实际资料的误差分别为10.1%~19.3%和12.2%~22.5%,预测起始时间与最大淹没时刻越接近,预测误差越小,其中最大淹没的1 h临近预报误差在15%以内,基本与实际情况相符.
通过实例1~3可见,将雷达外推、降雨定量估算以及内涝实时模拟技术相结合,可以获得较为准确的内涝实时预警结果.同时,单次预测时间可控制在10 min以内,为防汛调度工作预留50 min以上的预见期.
4 结论1) 采用雷达外推、降雨定量估算与水力模型相结合能够进行城市内涝灾害的实时预警.预警结果与实际调研情况基本相符,具有较高的预测精度,并通过实例进行了验证.
2) 仿真实验证明,本文的实时模拟方法能够预留50 min以上的预见期,与传统的基于雨量计实时模拟方法相比可提高至少25 min的预见期,为防汛部门的调度指挥工作预留了更长的时间.
3) 值得注意的是,基于雨量计实时模拟方法往往依靠单个或多个雨量站数据作为模型输入,不能充分考虑降雨的空间分布.而雷达预测降雨可得到每个雷达网格上的降雨分布过程,充分考虑了降雨的空间分布特性.
| [1] |
黄纪萍.城市排水管网水力模拟及内涝预警系统研究[D].广州: 华南理工大学, 2014: 72 HUANG Jiping. Hydraulic simulation of urban drainage network and waterlogging warning system study[D]. Guangzhou: South China University of Technology, 2014: 72 http://cdmd.cnki.com.cn/Article/CDMD-10561-1014063650.htm |
| [2] |
姜元军, 来丽芳, 李亚丹, 等. 基于GIS的城市内涝预警预报系统设计与实现[J]. 测绘与空间地理信息, 2016, 39(8): 69. JIANG Yuanjun, LAI Lifang, LI Yadan, et al. Design and implementation of early warning and forecasting system for urban water logging based on GIS[J]. Geomatics & Spatial Information Technology, 2016, 39(8): 69. DOI:10.3969/j.issn.1672-5867.2016.08.020 |
| [3] |
DEGRAVE R, SCHOORENS J, LITRICO X. Real-time control of a small urban stormwater network[J]. IEEE International Conference on Networking, 2013, 526. DOI:10.1109/ICNSC.2013.6548794 |
| [4] |
邸苏闯, 刘洪伟, 苏泓菲. 北京城市暴雨预警及应急管理现状与挑战[J]. 中国防汛抗旱, 2016, 26(3): 48. DI Suchuang, LIU Hongwei, SU Hongfei, et al. Current situation and challenges of rainstorm warning system and emergency response management in urban region of Beijing[J]. China Flood & Drought Management, 2016, 26(3): 48. DOI:10.3969/j.issn.1673-9264.2016.03.016 |
| [5] |
周蔚. 小流域防洪预警体系的初步研究——以浙江省为例[J]. 浙江水利科技, 2011(1): 33. ZHOU Wei. Study on small watershed flood warning system: A case study in Zhejiang Province[J]. Zhejiang Hydrotechnics, 2011(1): 33. DOI:10.3969/j.issn.1008-701X.2011.01.011 |
| [6] |
潘安君, 卢江涛, 田富强, 等. 雷达测雨的最优化方法在分布式城市洪水模型中的应用[J]. 中国水利, 2010(23): 54. PAN Anjun, LU Jiangtao, TIAN Fuqiang. Application of radar rainfall data optimization method in the distributed model of urban flooding[J]. China Water Resoures, 2010(23): 54. DOI:10.3969/j.issn.1000-1123.2010.23.021 |
| [7] |
AUSTIN G L, BELLON A. The use of digital weather radar records for short-term precipitation forecasting[J]. Quarterly Journal of the Royal Meteorological Society, 2010, 102(431): 265. DOI:10.1002/qj.49710042612 |
| [8] |
LIANG Qiaoqian, FENG Yerong, DENG Wenjian, et al. A composite approach of radar echo extrapolation based on TREC vectors in combination with model-predicted winds[J]. Advances in Atmospheric Sciences, 2010, 27(5): 1119. DOI:10.1007/s00376-009-9093-4 |
| [9] |
伊凡.基于半拉格朗日方法的雷达图像运动分析[D].山东: 中国海洋大学, 2013: 27 YI Fan. Motion analysis based on semi-Lagrangian in radar images[D]. Shandong: Ocean University of China, 2013: 27 http://cdmd.cnki.com.cn/Article/CDMD-10423-1013368106.htm |
| [10] |
WANG Gaili, LIU liping, DING Yuanyuan. Improvement of radar quantitative precipitation estimation based on real-time adjustments to Z-R relationships and inverse distance weighting correction schemes[J]. Advances in Atmospheric Sciences, 2012, 29(3): 575. DOI:10.1007/s00376-011-1139-8 |
| [11] |
LEE Y, HEE N. Optimization of Z-R relationship in the summer of 2014 using a micro genetic algorithm[J]. Journal of Korean Institute of Intelligent Systems, 2016, 16(1): 1. DOI:10.5391/JKⅡS.2016.26.1.001 |
| [12] |
YUAN Xiaoqing, NI Guangheng, PAN Anjun, et al. NEXRAD Z-R power relationship in Beijing based on optimization algorithm[J]. Journal of China Hydrology, 2010, 30(1): 1. |
| [13] |
RENDON S H, VIEUX B E, PATHAK C S. Deriving radar specific Z-R relationships for hydrologic operations[J]. World Environmental & Water Resources Congress, 2011(414): 4682. DOI:10.1061/41173(414)487 |
| [14] |
王丹.雷达外推预报与暴雨数值模式融合预报降水方法研究[D].北京: 中国气象研究院, 2013: 2 WANG Dan. Analyse of the blending algorithm based on radar-nowcasting and meso-scale numerical weather prediction model[D]. Beijing: Chinese Academy of Meteorological Sciences, 2013: 2 http://cdmd.cnki.com.cn/Article/CDMD-85101-1013212501.htm |
| [15] |
刘子龙, 周玉文, 王强, 等. SWMM产汇流模型参数的设计条件等价优化[J]. 哈尔滨工业大学学报, 2015, 47(8): 92. LIU Zilong, ZHOU Yuwen, WANG Qiang, et al. Optimization of equivalent design conditions for SWMM rain-off model parameters[J]. Journal of Harbin Institute of Technology, 2015, 47(8): 92. DOI:10.11918/j.issn.0367-6234.2015.08.018 |
| [16] |
石赟赟, 万东辉, 陈黎, 等. 基于GIS和SWMM的城市暴雨内涝淹没模拟分析[J]. 水电能源科学, 2014, 32(6): 57. SHI Yunyun, WAN Donghui, CHEN Li, et al. Simulation of rainstorm waterlogging and submergence in urban areas based on GIS and SWMM[J]. Water Resource and Water, 2014, 32(6): 57. |
 2019, Vol. 51
2019, Vol. 51


