随着中国饮用水水源受到日趋广泛的污染,以去除浑浊度和病原微生物为主要目标的常规处理工艺已经不能满足保障饮用水水质安全的需求[1].因此,以预臭氧氧化(预处理),特别是臭氧-生物活性炭等为代表的深度处理工艺发展迅速,在国内的饮用水处理中推广应用日益广泛[2-3].臭氧-生物活性炭深度处理过程的“臭氧”,也叫“后臭氧”,后臭氧化工艺能够消毒和部分降解有机物,并将大分子有机物转化为小分子有机物,以利于后续生物活性炭单元的生物降解[4].后臭氧投加量的不足,可能造成接触氧化的不充分,使生物活性炭生物降解有机物效果不佳;而过量投加一方面会直接导致水厂运行成本的增加,另一方面不利于生物活性炭的吸附,以及影响生物活性炭的使用寿命.更重要的是,随着臭氧投加量的增加,容易带来溴酸盐等臭氧化副产物[5].因此,在含溴水的臭氧化过程中,既要保证臭氧化效能,也要限制溴酸盐生成,后臭氧投加面临如何优化控制的问题.
目前后臭氧投加控制主要采用水流量比例前馈和出水余臭氧质量浓度PID反馈复合控制方法[6].水流量比例前馈控制根据进水流量的变化调整臭氧投加量.出水余臭氧质量浓度PID反馈控制根据出水余臭氧质量浓度的偏差调整臭氧投加量.但是,当进水水质变化时,PID反馈控制由于控制响应过慢而无法快速调整臭氧投加量,极易引起出水水质的波动.模型预测控制(model predictive control,MPC)因对过程未来动态有预测功能而被视作处理大时滞、大惯性和非线性控制问题的有效方法[7].鉴于后臭氧化工艺大时滞、大惯性和非线性的特点,将MPC用于后臭氧投加的反馈控制.
前馈控制根据干扰的测量值对实际干扰进行补偿设计,是最直接最主动的干扰抑制方法[8].然而实际被控过程很多干扰是不可测或很难测,干扰观测器(disturbance observer,DOB)作为一种有效的干扰估计技术广泛应用于前馈控制中[9-10].鉴于后臭氧接触池进水水质和水流量变化对后臭氧化工艺的影响,以及DOB的优越性,将DOB估计结果用于后臭氧投加的前馈控制.
CT(即C和T的乘积,C为水中余臭氧质量浓度,T为臭氧与水接触时间)值是控制臭氧化效能的重要指标[11-12],将CT值保持在理想值能够有效地控制臭氧化效果和溴酸盐生成量.CT值计算方法有出口法、几何平均法和扩展CSTR法等[13].在实际工程应用中,为便于测量和计算,常采用出口法,即出口余臭氧质量浓度C和臭氧与水接触时间T的乘积.本文以臭氧化CT值为控制目标,在水流量比例控制的基础上,提出一种基于DOB和MPC的后臭氧投加复合控制方法.其中MPC用于后臭氧投加的反馈控制,DOB用于估计进水水质和水流量变化对后臭氧化工艺产生的模型失配和外部干扰,并将估计结果用于后臭氧投加的前馈控制中,提高后臭氧化工艺应对进水水质和水流量变化的能力.
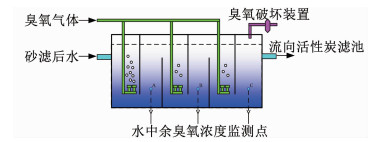
1 后臭氧投加过程某水厂的后臭氧化工艺由两个并行的后臭氧接触池组成,如图 1所示.由于后臭氧接触池复杂的内部结构和水流类型,臭氧在水中的停留时间分布非常不均匀.后臭氧接触池的内部由阻碍墙体将其分成6个单元,水流受到阻碍墙体的阻碍作用在后臭氧接触池内部上下翻滚,一定程度地保证了臭氧在后臭氧接触池内部的停留时间,使臭氧能够与水充分接触.为了提高臭氧的利用效率和降低臭氧化副产物——溴酸盐的生成,一般采用三级投加(研究对象水厂的三级投加比为3: 1: 1)的微孔曝气投加方式.水中余臭氧质量浓度在线检测仪表由图 1中的A、B和C 3个采样点采集水样并实施余臭氧质量浓度在线检测.由于阻碍墙体的作用,随着水流速的下降和臭氧的消耗,采样点C的水中余臭氧质量浓度在线检测值波动相对比较平缓,被用作后臭氧接触池出水余臭氧质量浓度的近似值.
|
图 1 后臭氧化阶段的工艺图 Fig. 1 Process diagram of post-ozonation stage |
取臭氧与水接触时间T的常用值T10,即90%的水通过后臭氧接触池的停留时间.有效停留时间T10的出口法计算如下:
| $ {T_{10}} = {T_{{\rm{HR}}}} \cdot \frac{{{T_{10}}}}{{{T_{{\rm{HR}}}}}}. $ | (1) |
式中:阻碍系数
| $ {T_{{\rm{HR}}}} = \frac{V}{f}. $ | (2) |
式中:V为臭氧接触池内的水体积,f为臭氧接触池的进水流量.
由于T10随着进水流量变化而变化,为了将CT10控制在理想值,C的设定值也随之变化.因此,以CT值为控制目标的臭氧投加控制问题转变成了C设定值的动态跟踪控制问题.
2 DOB-MPC复合控制方案后臭氧化工艺运行中,臭氧消耗一般经历快速消耗和缓慢衰减两个阶段[14].快速消耗阶段在臭氧与水接触的很短时间内完成,在后臭氧化工艺中难以测量,缓慢衰减阶段可近似描述为动力学一阶过程.因此,以出水余臭氧质量浓度为被控变量,臭氧投加量为控制变量,可以用一阶加时滞(first order plus time delay, FOPTD)的形式表示后臭氧投加控制模型[15],其传递函数可以表示为
| $ {G_{\rm{m}}}\left( s \right) = {g_{\rm{m}}}\left( s \right){{\rm{e}}^{ - \tau s}}, $ | (3) |
| $ {g_{\rm{m}}}\left( s \right) = \frac{K}{{Ts + 1}}. $ | (4) |
式中:gm(s)为最小相位部分,e-τs为时滞部分.
放大系数K和时间系数T与实时变化的水质指标和水流量直接相关,可采用多元线性回归的方法进行辨识;时滞时间常数τ与变化的水流量直接相关,可通过线性插值的方法获得[15].因此,后臭氧投加控制模型Gm(s)是随着进水水质和水流量变化而动态变化的.
2.1 MPCMPC通过式(3)所示的控制模型对后臭氧投加过程的输出(水中余臭氧质量浓度)进行预测,并在每个控制周期内通过优化式(5)所示目标函数得出最优的控制增量.
| $ \begin{array}{l} J = \sum\limits_{j = 1}^{{N_{\rm{y}}}} {{{\left[ {{y_{\rm{p}}}\left( {k + j} \right) - {y_{\rm{r}}}\left( {k + j} \right)} \right]}^2}} + \\ \;\;\;\;\;\;\sum\limits_{j = 1}^{{N_{\rm{u}}}} {{\lambda _j}{{\left[ {u\left( {k + j} \right)} \right]}^2}} + \sum\limits_{j = 1}^{{N_{\rm{u}}}} {{{\lambda '}_j}{{\left[ {\Delta u\left( {k + j} \right)} \right]}^2}} . \end{array} $ | (5) |
其约束条件为
| $ {y_{\min }} \le {y_{\rm{p}}}\left( {k + j} \right) \le {y_{\max }},1 \le j \le {N_{\rm{y}}}, $ | (6) |
| $ {u_{\min }} \le u\left( {k + j} \right) \le {u_{\max }},1 \le j \le {N_{\rm{u}}}, $ | (7) |
| $ - \Delta {u_{\max }} \le \Delta u\left( {k + j} \right) \le \Delta {u_{\max }},1 \le j \le {N_{\rm{u}}}. $ | (8) |
式中:yp(k)为预测输出,yr(k)为输出设定值,u(k)为输入变量,Δu(k)为输入变化量,λj和λ′j为输入权重,Ny为预测时域,Nu为控制时域.
为了应对进水水质和流量变化对后臭氧投加的影响,实施在线校正模型策略.通过将反馈误差e(k)=|y(k)-ym(k)|与设定误差emin比较决定是否进行在线校正.其中,y(k)为实际输出,ym(k)为模型输出.为了提高算法的在线学习速度,只对超过设定误差的模型输出进行在线校正.
如果反馈误差e(k) < emin,表明模型精度较高,不需要校正,则式(5)中的第j步预测输出为
| $ {y_{\rm{p}}}\left( {k + j} \right) = {y_{\rm{m}}}\left( {k + j} \right). $ | (9) |
如果反馈误差e(k)≥emin,表明模型失配,需要进行反馈校正,则式(5)中的第j步预测输出为
| $ {y_{\rm{p}}}\left( {k + j} \right) = {y_{\rm{m}}}\left( {k + j} \right) + e\left( k \right). $ | (10) |
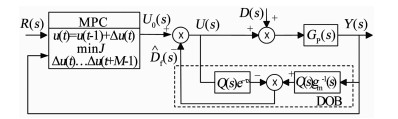
DOB是根据被控变量和控制变量对干扰进行估计的过程,将干扰估计作为前馈可以有效补偿干扰对被控过程的影响,从而达到抑制干扰的目的.对于带有时滞特性的臭氧投加过程,将DOB引入到MPC中,得到如图 2所示的复合控制方案.
|
图 2 DOB-MPC复合控制结构 Fig. 2 Structure of DOB-MPC composite control |
在图 2中,R(s)为被控变量的设定值,U0(s)为MPC控制器输出,Gp(s)为实际被控过程,Y(s)为实际过程输出.虚线框内为干扰观测器,D(s)为实际干扰,
| $ Q\left( s \right) = \frac{1}{{{{\left( {1 + \lambda s} \right)}^r}}}. $ | (11) |
式中:r为滤波器的阶次,λ为滤波器的时间常数.
Q(s)的设计直接决定了干扰观测器的动态特性和系统的鲁棒性.Q(s)的阶次r越高,干扰观测器的响应速度越快,抑制干扰的能力越强.但是随着r的升高,大的相位滞后会使系统产生欠阻尼现象,使控制系统的鲁棒性变差,因而r通常取为控制模型Gm(s)的相对阶次(分母的阶次减去分子的阶次).Q(s)的时间常数λ越大,闭环系统的稳定性越强,λ越小,闭环系统的抗干扰能力越强.因此,Q(s)的参数设计应综合考虑闭环系统的抗干扰性能和鲁棒稳定性[16].
3 验证结果及分析 3.1 仿真验证后臭氧投加过程可近似为参数随进水水质和水流量变化的FOPTD过程,根据文献[15]的后臭氧投加模型构建方法,在仿真验证中取某一进水水质和水流量下的式(12)模型作为后臭氧投加实际过程,其对应的详细进水水质和水流量,以及FOPTD模型的参数如表 1所示.
| $ {G_{\rm{p}}}\left( s \right) = \frac{{0.39}}{{2.35s + 1}}{{\rm{e}}^{ - 7.8s}}. $ | (12) |
| 表 1 FOPTD仿真模型对应的进水水质、水流量和模型参数 Tab. 1 Influent water quality, water flow, and model parameters for the FOPTD simulation model |
以Theil不等系数(Theil’s inequality coefficient, CTI)作为评估建模型的精度指标,即
| $ {C_{{\rm{TI}}}} = \frac{{\sqrt {\sum\nolimits_i {{{\left( {{y_i} - {y_{m,i}}} \right)}^2}} } }}{{\sqrt {\sum\nolimits_i {{y_i}^2} } + \sqrt {\sum\nolimits_i {{y_{m,i}}^2} } }}. $ | (13) |
式中:yi为实际过程输出,ym, i为模型输出.
所构建式(12)模型的TIC为0.019,远小于0.3,说明该模型精度很好[17],可以用于后臭氧投加控制研究中.
为了对比分析所提臭氧投加DOB-MPC复合控制方案的有效性,MPC反馈控制方案也做了仿真验证.分别在模型匹配和模型失配情况下,仿真验证了控制方案的抗干扰性能.在仿真验证过程中,CT10设定值取为3.5 mg/L·min,仿真时间0~500 min,在t=250 min时刻进水水量由4 000 m3/h提高到5 300 m3/h,研究对象水厂的臭氧接触池水体积为1 200 m3,因此,由式(1)和式(2)计算可知T10由11.7 min减小到8.8 min,为了将CT10控制在3.5 mg/L·min,出水余臭氧质量浓度C的设定值也由0.3 mg/L提高到0.4 mg/L,时滞时间常数τ由7.8 min减小到6.8 min,放大系数K和时间常数T也由0.39和2.35分别增大到0.4和2.47.为了验证控制方案的抗干扰性能,在t=400 min时刻施加0.1 mg/L的外部干扰(如图 2中的D(s)处).
为了定量分析两种控制方案的设定点跟踪性能和抗干扰性能,选取超调量、稳定时间和如式(14)所示的绝对误差积分(integral of absolute error, IAE)作为评价控制响应的性能指标, 即
| $ {I_{{\rm{AE}}}}\left( t \right) = \frac{1}{N}\sum\limits_{k = 1}^N {\left| {r\left( k \right) - y\left( k \right)} \right|} . $ | (14) |
式中:r(k)为输出设定值,y(k)为实际过程输出.
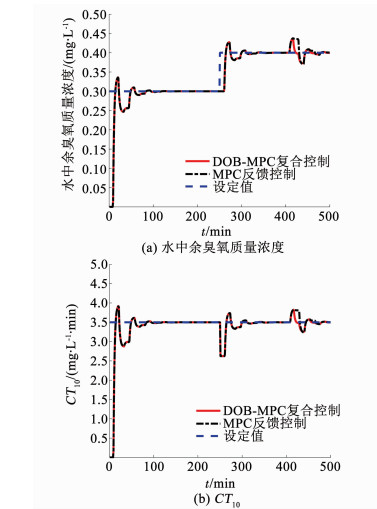
3.1.1 模型匹配情况当所建立的臭氧投加过程控制模型与实际过程匹配时,即Gm(s)=Gp(s),DOB-MPC复合控制与MPC反馈控制的仿真结果如图 3所示.其中图 3(a)为水中余臭氧质量浓度的响应曲线,其对应的性能指标如表 2所示,图 3(b)为CT10的响应曲线.可以看出在0~250 min和251~400 min,由于模型匹配和没有外部干扰,DOB的输出为零,DOB-MPC复合控制与MPC反馈控制的控制效果相同,都能够较好地跟踪变化的水中余臭氧质量浓度设定值,从而较好地将CT10控制在设定值;在401~500 min,施加外部干扰时,基于DOB的干扰估计补偿,使DOB-MPC复合控制具有更好的抗干扰能力.
|
图 3 模型匹配情况的仿真结果 Fig. 3 Simulation results in nominal case |
| 表 2 模型匹配情况仿真结果的水中余臭氧质量浓度控制响应性能指标 Tab. 2 Performance indices of control response of concentration of ozone residual in water for the simulation results in nominal case |
为了验证由进水水质和水流量变化引起的模型失配时,所提控制方案的鲁棒性,将式(12)的放大系数K和时间系数T分别减小30%,得到变化后的臭氧投加过程实际过程如下:
| $ {G_{\rm{p}}}\left( s \right) = \frac{{0.273}}{{1.645s + 1}}{{\rm{e}}^{ - 7.8s}} $ | (15) |
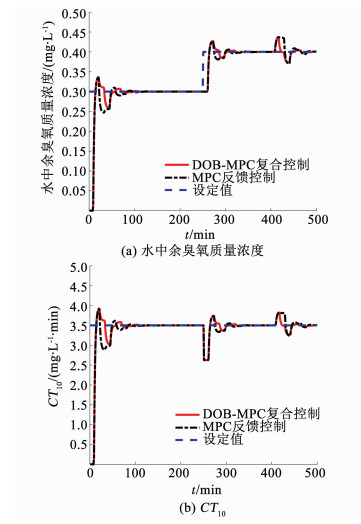
DOB-MPC复合控制和MPC反馈控制参数保持不变,对两种控制方案进行仿真验证,仿真结果如图 4所示.其中图 4(a)为水中余臭氧质量浓度的响应曲线,其对应的控制响应性能指标如表 3所示,图 4(b)为CT10的响应曲线.可以看出在0~250 min和251~400 min,基于DOB对模型失配的前馈估计补偿,使DOB-MPC复合控制能够更好地跟踪变化的水中余臭氧质量浓度设定值,从而更好地将CT10控制在设定值;在401~500 min,施加外部干扰时,基于DOB的干扰估计补偿,使DOB-MPC复合控制具有更好的设定点跟踪和抗干扰能力.由此可见,对于进水水质和水流量变化引起的模型失配和外部干扰,所提后臭氧投加DOB-MPC复合控制方案具有更优异的控制性能和鲁棒稳定性.
|
图 4 模型失配情况的仿真结果 Fig. 4 Simulation results in mismatch case |
| 表 3 模型失配情况仿真结果的水中余臭氧质量浓度控制响应性能指标 Tab. 3 Performance indices of control response of concentration of ozone residual in water for the simulation results in mismatch case |
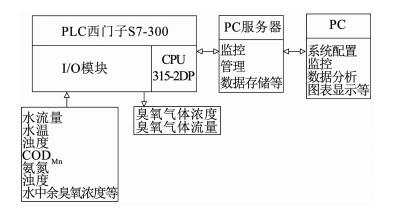
某水厂后臭氧投加分布式控制系统如图 5所示.为了分析测试所提DOB-MPC复合控制方案的实际控制效果,分别将所提后臭氧投加DOB-MPC复合控制和MPC反馈控制方案在水厂西门子SCADA软件Wincc的嵌入式VBA中编程实现,并通过PLC执行对臭氧投加装置的实时控制.两种控制方案的实验验证是在水流量比例投加的基础上实现的,即臭氧投加量(mg/L)与臭氧接触池进水流量(m3/h)的乘积作为向后臭氧接触池进水中投加的臭氧量(kg/h),臭氧发生装置根据实际臭氧需要量实时发生一定质量浓度和流量的臭氧气体.
|
图 5 后臭氧投加分布式控制系统 Fig. 5 Distributed control system for the ozone dosing |
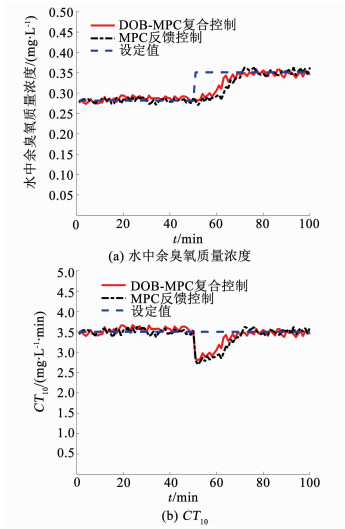
受进厂原水水质和后臭氧化工艺以前各环节的影响,实际的后臭氧接触池进水水质和水流量是时刻变化的,因此,臭氧投加控制存在模型失配和外部干扰的情况比较普遍.本文在相似的进水水质和水流量状况下,分别进行后臭氧投加DOB-MPC复合控制和MPC反馈控制方案的实验验证.CT10设定值取为3.5 mg/L·min,截取实验期间某段100 min内的实验结果,其中在t=50 min时刻因前端提升泵房的水量调度需要使得后臭氧接触池的进水流量变大,根据式(1)和式(2)可知T10变小,为了将CT10控制恒定在3.5 mg/L·min,出水余臭氧质量浓度C的设定值变大,实验结果如图 6所示,其对应的控制响应性能指标如表 4所示.可以看出,所提DOB-MPC复合控制方案具有更好的控制性能和鲁棒稳定性,与理论分析和仿真验证结果相一致.
|
图 6 后臭氧投加控制实验结果 Fig. 6 Experimental results for the control of post-ozone dosing |
| 表 4 实验结果中水中余臭氧质量浓度控制响应性能指标 Tab. 4 Performance indices of control response of concentration of ozone residual in water for the experimental results |
与仿真数据相比,实际运行数据的超调量和稳定时间较小,这是因为实验验证过程中的水流量突变幅度较小,从而水中余臭氧质量浓度C突变幅度也较小,水中余臭氧质量浓度C能够较快地达到稳定状态;与仿真数据相比,实际运行数据的IAE较大,这是因为实际运行过程中的进水水质和水流量是不断变化的,处于模型失配和外部干扰下的后臭氧投加控制要更加复杂,水中余臭氧质量浓度C的波动较大.
4 结语本文以CT值为控制目标,在水流量比例控制的基础上,提出了一种基于扰动观测器和模型预测控制的后臭氧投加复合控制方法.通过模型预测控制实现臭氧投加的反馈控制,通过采用扰动观测器对进水水质和水流量变化引起的模型失配和外部干扰进行前馈补偿.仿真和实验验证结果表明,该方法能够有效提高后臭氧化工艺应对进水水质和水流量变化的能力,稳定和提高了深度处理工艺的出水水质.
| [1] |
王占生, 刘文君, 董丽华. 饮用水深度处理的必要性与发展趋势[J]. 给水排水, 2014, 40(2): 1. WANG Zhansheng, LIU Wenjun, DONG Lihua. Necessity and development trend of advanced drinking water treatment[J]. Water & Wastewater Engineering, 2014, 40(2): 1. DOI:10.3969/j.issn.1002-8471.2014.02.001 |
| [2] |
黎雷, 高乃云, 张可佳, 等. 饮用水臭氧生物活性炭净化效果与传统工艺比较[J]. 同济大学学报(自然科学版), 2010, 38(9): 1309. LI Lei, GAO Naiyun, ZHANG Kejia, et al. Comparison of O3-BAC combination and conventional processes on removal of pollutants for treating drinking water[J]. Journal of Tongji University (Natural Science), 2010, 38(9): 1309. DOI:10.3969/j.issn.0253-374x.2010.09.010 |
| [3] |
崔婧, 温汝青, 何士忠, 等. 北方某水厂臭氧/活性炭深度处理工艺设计[J]. 中国给水排水, 2015, 31(10): 58. CUI Jing, WEN Ruqing, HE Shizhong, et al. Design of ozonation/BAC advanced treatment process in a waterworks in NorthChina[J]. China Water & Wastewater, 2015, 31(10): 58. |
| [4] |
LV L. Fate of organic pollutants in a full-scale drinking water treatment plant using O3-BAC[J]. Ozone Science & Engineering, 2015, 37(3): 257. DOI:10.1080/01919512.2014.997867 |
| [5] |
QI S, MAO Y, LV M, et al. Pathway fraction of bromate formation during O3 and O3/H2O2 processes in drinking water treatment[J]. Chemosphere, 2016, 144: 2436. DOI:10.1016/j.chemosphere.2015.11.022 |
| [6] |
VAN DER HELM A W C. Integrated modeling of ozonation for optimization of drinking water treatment[D]. Delft: Delft University of Technology, 2007
|
| [7] |
MARTINS M A F, YAMASHITA A S, SANTORO B F, et al. Robust model predictive control of integrating time delay processes[J]. Journal of Process Control, 2013, 23(7): 917. DOI:10.1016/j.jprocont.2013.05.002 |
| [8] |
KADRI M B. Disturbance rejection in nonlinear uncertain systems using feedforward control[J]. Arabian Journal for Science & Engineering, 2013, 38(9): 2439. DOI:10.1007/s13369-012-0516-7 |
| [9] |
CHEN S L, LI X, TEO C S, et al. Composite jerk feedforward and disturbance observer for robust tracking of flexible systems[J]. Automatica, 2017, 80: 253. DOI:10.1016/j.automatica.2017.02.024 |
| [10] |
LI X, CHEN S L, TEO C S, et al. Data-based tuning of reduced-order inverse model in both disturbance observer and feedforward with application to tray indexing[J]. IEEE Transactions on Industrial Electronics, 2017, 64(7): 5492. DOI:10.1109/TIE.2017.2674623 |
| [11] |
PAK G, ESPINELI S D, LEE H, et al. Comparison of antibiotic resistance removal efficiencies using ozone disinfection under different pH and suspended solids and humic substance concentrations[J]. Environmental Science & Technology, 2016, 50(14): 7590. DOI:10.1021/acs.est.6b01340 |
| [12] |
VELÃSQUEZ M T O D, NOGUEZ I Y, RODRÃ-GUEZ B C, et al. Effects of ozone and chlorine disinfection on VBNC Helicobacter pylori by molecular techniques and FESEM images[J]. Environmental Technology, 2017, 38(6): 744. DOI:10.1080/09593330.2016.1210680 |
| [13] |
RAKNESS K L, NAJM I, ELOVITZ M, et al. Cryptosporidium log-inactivation with ozone using effluent CT10, geometric mean CT10, extended integrated CT10 and extended CSTR calculations[J]. Ozone: Science & Engineering, 2005, 27(5): 335. DOI:10.1080/01919510500250267 |
| [14] |
ZIMMERMANN S G, WITTENWILER M, HOLLENDER J, et al. Kinetic assessment and modeling of an ozonation step for full-scale municipal wastewater treatment: Micropollutant oxidation, by-product formation and disinfection[J]. Water Research, 2011, 45(2): 605. DOI:10.1016/j.watres.2010.07.080 |
| [15] |
WANG D S, LI S H, ZHOU X P. Control-oriented modeling and real-time control for the ozone dosing process of drinking water treatment[J]. Environmental Science & Technology, 2013, 47(5): 2197. DOI:10.1021/es303408q |
| [16] |
PAN Y R, SHIH Y T, HORNG R H, et al. Advanced parameter identification for a linear-motor-driven motion system using disturbance observer[J]. International Journal of Precision Engineering & Manufacturing, 2009, 10(4): 35. DOI:10.1007/s12541-009-0069-1 |
| [17] |
ZHOU X M. A new method with high confidence for validation of computer simulation models of flight systems[J]. Journal of Systems Engineering & Electronics, 1993, 4(4): 43. |
 2019, Vol. 51
2019, Vol. 51


