围岩抗力系数(k)是隧道衬砌结构设计计算中一个重要的力学参数,反映围岩与衬砌结构共同作用时围岩所能承担荷载的能力,k的取值不同直接影响了衬砌的内力[1].目前,k的确定方法主要包括以下3种:1)根据围岩级别从规范中查询,《铁路隧道设计规范》中给出了不同围岩级别下k的参考值[2],从表中可以看出即使围岩为某一级明确的岩体,设计人员也难以根据自己的经验从一个宽广的范围中选出相对合理的值.2)理论研究,最早是基于弹性理论中厚壁圆筒的Lame经典解答得到的Gallerkin公式.钱令希[3]提出了考虑洞周裂缝区影响的k的计算公式.吕有年[4]根据弹性和塑性理论推导出了通用计算公式.考虑到隧道开挖后围岩所处的真实应力状态,Muir Wood[5]提出了基于Airy应力函数的地层抗力系数计算公式.蔡晓鸿等[6-8]考虑围岩的蠕变效应、中间主应力、剪胀等性质作用下,采用不同的强度准则分别得到了k的计算公式.上述查表和理论研究方法均未考虑围岩各向异性的影响,节理的存在会导致k的各向异性,不少现场试验结果表明k具有各向异性.3)现场试验,常用的方法有千斤顶法和径向液压枕法.刘长庚等[9]在小浪底水库的砂页岩地层,采用径向千斤顶进行试验,得到了k的各向异性特征;李维树[10]利用层状岩体波速的各向异性,给出了层状岩体k的计算公式.唐爱松等[11]在广西岩滩水电站采用径向液压枕法现场试验,分析了k的各向异性与压力的关系;李波等[12]在沪昆高速铁路隧道通过径向液压枕法试验,获得了k的各向异性分布规律.
以上实测结果均表明k存在各向异性,尤其是层状和节理岩体中各向异性明显,但现有研究均未对抗力系数的分布特征及其对隧道支护设计的影响等问题进一步深入探讨.针对节理岩体中围岩抗力系数的各向异性分布特征,以大连地铁2号线兴工街站隧道工程为背景,采用正交试验和离散单元法模拟径向液压枕法测围岩抗力系数,通过81个数值试验,分析各因素综合作用下k的各向异性分布特征,并进行方差分析,确定各因素的影响显著性.为使k适用于不同规模的地下工程,进一步分析了尺寸效应.基于以上分析结果,借助坐标变换理论和力的平衡方程,推导出抗力系数椭圆分布函数的计算公式,通过与数值计算结果的对比,验证了公式的准确性.最后以兴工街站隧道为例,分析了围岩抗力系数各向异性对衬砌内力的影响.
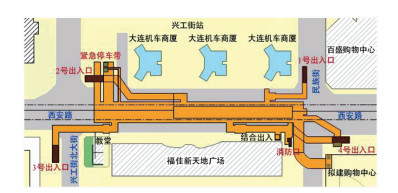
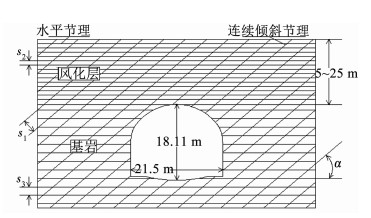
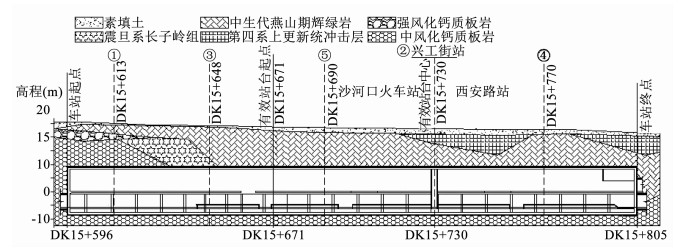
1 工程概况大连地铁2号线兴工街站位于兴工街与西安路交叉口处,西安路的正下方,其东面有机车商厦,西面是福佳新天地广场,建筑物密集,道路交通繁忙,地理位置如图 1所示.隧道总长208.3 m,为地下双层岛式站台车站,车站主体标准断面开挖宽度为21.5 m,高18.11 m,洞顶埋深5~25 m,开挖断面面积为344 m2,横截面如图 2所示.隧道上部为较软弱风化层岩体,由中生代燕山期辉绿岩、震旦系长子岭组、第四系上更新统冲击层等组成,受构造影响严重,呈碎石、角砾、粉末状的断层带;隧道洞身及下部为中风化钙质板岩,地质构造复杂,盖层中褶皱多为紧密线性同斜单元褶皱,层理和节理裂隙发育至极发育,矿物主要为云母、石英、方解石,局部夹石英岩脉.岩体等级为Ⅳ级[13-15],地质纵剖面如图 3所示.s1、s2、s3和α分别为节理间距和节理倾角.岩石和节理的物理力学参数取值如表 1所示.
|
图 1 兴工街站地理位置 Fig. 1 Location of Xinggongjie Station |
|
图 2 兴工街站隧道节理分布 Fig. 2 Joints schematic diagram of Xinggongjie Station Tunnel |
|
图 3 兴工街站隧道地质纵剖面 Fig. 3 Profile showing geological conditions of Xinggongjie Station Tunnel |
| 表 1 兴工街站隧道围岩参数取值范围 Tab. 1 Parameters value scope of Xinggongjie Station Tunnel |
离散单元法(UDEC)模拟节理岩体中的隧道受力与变形时,是通过模拟节理的切割将模型离散成为变形块体,并借助牛顿第二定律进行求解.其在工程上的适用性已经得到了广泛的认可,李英勇等[16]利用离散元UDEC分析了极浅埋连拱隧道中隔墙顶部围岩塌方演化的全过程;莫振泽等[17]运用UDEC建立了滚刀贯切岩石的二维数值系列模型,对TBM滚刀破岩过程进行分析.
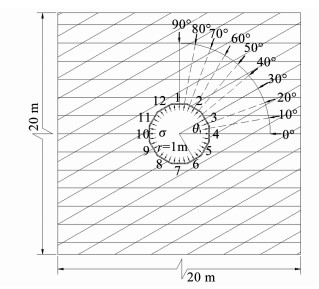
参照《水利水电工程岩石试验规程》[18]中径向液压枕法测围岩抗力系数的相关规定,确定数值计算模型如图 4所示,试验洞半径为1 m,模型边界距隧道中心为10 m,四周边界均采用法向约束支座.兴工街车站隧道围岩主要为Ⅳ级,围岩中含有2组水平层状节理、1组贯通倾斜节理以及一些次生节理.不同组节理的节理间距相差较小,因此,简化为两组等间距节理,节理夹角为0°~90°,将其中1组节理的倾角固定为0°,让另外1组节理倾角由0°到90°变化.其他更为普遍的节理夹角可以通过模型的旋转得到.
|
图 4 径向液压枕法测围岩抗力系数的数值计算模型 Fig. 4 Numerical model of the radial hydraulic pressure pillow testing to measure rock mass resistant coefficient |
依据兴工街站隧道围岩压力的实际监测结果可知地应力均小于0.5 MPa[13],参考现有试验的径向压力值[9-12],试验中作用于隧道内壁上的径向压力取为3.2 MPa,按0.8 MPa的步距逐步施加,并监测记录洞壁12个方向上的变形值.
数值计算中岩石采用线弹性本构,节理采用库伦-滑移模型.由于岩石为线弹性、节理为常刚度,需要进一步判断围岩压力对抗力系数是否会产生影响,以上述兴工街车站隧道的围岩条件进行计算,岩石和节理的物理力学参数取值见表 2.地应力(p0)分别取为0,0.8,1.6,2.4和3.2 MPa,模拟径向液压枕法测围岩抗力系数,得到洞壁位移随径向压力的变化曲线,如图 5所示.
| 表 2 兴工街站隧道围岩参数 Tab. 2 Parameters of Xinggongjie Station Tunnel |
|
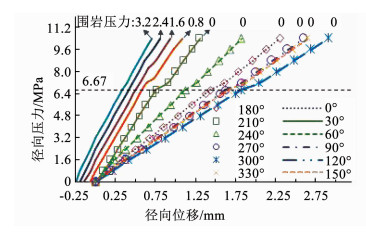
图 5 洞壁径向压力与径向位移的关系 Fig. 5 Relation curves between radial pressure and displacement at the cavity excavation interface |
由图 5可以看出,径向压力p < 6.67 MPa时,曲线均呈直线增加,围岩抗力系数(斜率)不随压力变化,可以称为弹性抗力系数;径向压力p=6.67 MPa时,围岩压力为0的曲线有一个突变,这是因为此时节理发生了剪切滑移,根据库伦剪切滑移理论τ=C+σtan φ,可以计算得到使节理发生剪切滑移的临界径向压力为
| $ p = \frac{C}{{1 - \tan \varphi }}. $ | (1) |
将C=0.8 MPa,φ=35°代入上式可得p=6.67 MPa,与数值计算结果一致.
围岩压力为0时,对比图 5中洞周12个方向的位移曲线,即右边6条曲线和6组数据点所示,可知洞壁位移关于原点中心对称.30°方向的曲线斜率最大,围岩抗力系数最大,该组共轭节理的夹角为60°,说明沿两组节理夹角角平分线方向围岩抗力系数最大,且可以看出垂直于两组节理夹角角平分线方向(120°)围岩抗力系数最小.
考虑围岩压力(p0=0.8,1.6,2.4,3.2 MPa)的影响,如图 5中左边4条曲线所示,当径向压力小于围岩压力时,洞壁的位移向洞内收敛,为负值,随着径向压力的增大,位移逐渐减小,当径向压力等于围岩压力时,洞壁的位移为0.不同围岩压力下的位移曲线与无围岩压力下的位移曲线平行,围岩抗力系数相等,这是由于当岩石采用线弹性本构、节理采用常刚度的库伦滑移模型时,节理发生张开滑移前,围岩压力对围岩抗力系数没有影响,可称为弹性抗力系数.
2.1 正交试验根据现有的理论研究和现场实测结果,选定岩石的弹性模量E和泊松比μ、节理间距s、节理夹角α、节理法向刚度kn、节理切向刚度ks、节理的黏聚力C、摩擦角φ、抗拉强度σtj以及剪胀角ψ共10个因素作为抗力系数的影响因素.岩石弹性模量大小为1~57 GPa,泊松比为0.05~0.45;节理法向刚度和切向刚度均为1~41 GPa;其他因素的取值范围参照《工程岩体分级标准》[19]确定,各因素的水平划分见表 3.采用正交试验设计试验方案,每个因素考虑9个变化水平,10因素9水平需要81次试验.由正交试验表L981(10)可以得出81个试验方案中各因素的取值组合.
| 表 3 正交试验中各参量的水平划分 Tab. 3 Variable levels of factors in orthogonal array testing |
采用统计软件SPSS进行方差分析时需要设立一个对比项,先通过极差分析选出对k影响最小的因素剪胀角作为对比项,再采用方差分析判断各因素影响的显著性.对81个试验结果中0°方向的抗力系数进行方差分析,结果如表 4所示.
| 表 4 方差分析计算结果 Tab. 4 Results of the variance analysis |
根据F分布表可得,F1-0.01(8, 8)=6.03,F1-0.05(8, 8)=3.44,F1-0.10(8, 8)=2.59.因此,可以得出各个因素对围岩抗力系数的影响顺序依次为Fkn > FE > Fs > Fα > F1-0.01(8, 8) > F1-0.05(8, 8) > Fμ > F1-0.10(8, 8) > Fks > Fσtj > FC > Fφ.岩石弹性模量、节理法向刚度、节理间距、节理夹角是对抗力系数影响高度显著的4个因素,岩石泊松比对围岩抗力系数有一定影响,其他因素对围岩抗力系数无显著影响.
3 k的各向异性分布特征根据各个测点的压力-变形曲线的斜率计算出每个方向的围岩抗力系数值.通过对计算结果的分析发现:1)围岩抗力系数分布范围较广,最小值为19 MPa/m,最大值为30 103 MPa/m.节理岩体中隧道围岩抗力系数的影响因素较多,数值变化范围大,工程设计时简单套用规范中不同围岩级别下的抗力系数有一定盲目性,结合岩石的坚硬程度和节理的分布状态及力学性质等综合确定较为合理;2)洞壁不同方向上的围岩抗力系数值并不相同,差异明显,节理岩体中围岩抗力系数有明显的各向异性特征.抗力系数分布曲线可按节理间夹角的大小划分为3种类型,节理夹角为10°,20°,30°时属于第1种类型(椭圆形),节理夹角为40°,50°,60°时属于第2种类型(近似椭圆形),节理夹角为70°,80°,90°时属于第3种类型(圆形),3种分布曲线如图 6所示.

|
图 6 不同节理间距下围岩抗力系数的分布曲线 Fig. 6 Distributing curves of rock mass resistant coefficient under different joint spacing |
围岩抗力系数分布曲线的形状近似于椭圆形,且椭圆关于两组节理夹角角平分线对称,沿两组节理夹角角平分线方向围岩抗力系数最大,垂直于夹角角平分线方向最小.节理夹角分别为30°,60°,90°时,围岩抗力系数分布曲线由椭圆形逐渐变为圆形,随着节理间距的增大,围岩抗力系数呈现出不规则的变化规律,这与岩石弹性模量、节理切向刚度、法向刚度等因素的影响有关.
定义各向异性系数ξ为隧道洞周围岩抗力系数的最大值与最小值之比,各向异性系数接近1.0时,表示各向异性较弱,大于3.0时表示各向异性较强或极强[20].为分析隧道洞径和节理间距对围岩抗力系数分布的影响规律以及抗力系数的尺寸效应,采用各向异性系数代表洞周围岩抗力系数的分布特征,用隧道直径d与节理间距s的比值λ=d/s代表节理岩体中结构体的相对大小[21].
在前述正交试验模型基础上,新增不同节理间距下不同洞径的离散元计算模型.隧道洞径为1~6 m,节理间距为0.2~4 m,模型尺寸均为20×20 m,施加的最大径向压力均为3.2 MPa.不同洞径和节理间距下的各向异性系数计算结果见表 5,整理得出各向异性系数ξ与λ的关系曲线见图 7.
| 表 5 不同隧道洞径和节理间距下围岩的各向异性系数 Tab. 5 Anisotropy coefficient of different tunnel diameter and joints spacing |
|
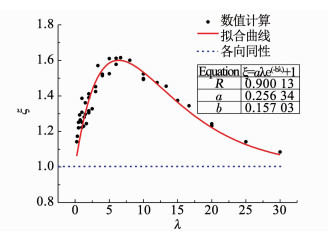
图 7 各向异性系数拟合曲线 Fig. 7 Fitted curve of the anisotropy coefficient |
各向异性系数表现出随相对尺度增大,先增大后减小,并逐渐趋于1的变化规律,当岩体中不含节理时λ=0,岩体为各向同性体;当岩体中存在密集分布的节理时,λ→∞,各向异性系数趋近于1,表示岩体可视作等效各向同性体.即需要满足以下极限条件
| $ \left\{ \begin{array}{l} \mathop {\lim }\limits_{\lambda \to 0} f\left( \lambda \right) = 1,\\ \mathop {\lim }\limits_{\lambda \to \infty } f\left( \lambda \right) = 1. \end{array} \right. $ | (2) |
采用非线性最小二乘法回归分析,拟合得到各向异性系数ξ与相对尺度λ的函数关系为
| $ \xi = f\left( \lambda \right) = 0.256 \cdot \lambda \cdot {{\rm{e}}^{ - 0.157 \lambda}} + 1. $ | (3) |
由上述计算结果可知,含有两组节理的岩体中围岩抗力系数分布曲线为椭圆形,这与小浪底水库[9]、岩滩水电站[11]、沪昆高速铁路隧道[12]工程实测得到的分布曲线十分相似.因此,建立围岩抗力系数的椭圆方程,沿两组节理夹角角平分线方向的围岩抗力系数最大,用kmax表示,为椭圆的长轴方向;垂直于两组节理夹角角平分线方向最小,用kmin表示,为椭圆的短轴方向.
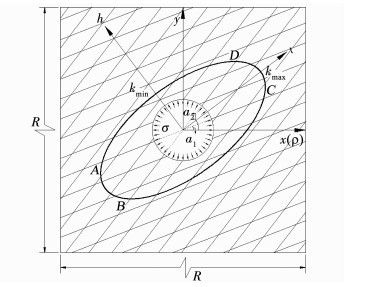
针对任意倾斜的两组节理,其倾角分别为α1、α2(α2>α1),如图 8所示,建立平面直角坐标系xoy和极坐标系ρoθ,同时另一直角坐标系toh,坐标轴分别沿椭圆的长轴与短轴方向.在toh坐标系下椭圆曲线方程为
| $ \frac{{{t^2}}}{{k_{\max }^2}} + \frac{{{h^2}}}{{k_{\min }^2}} = 1. $ | (4) |
|
图 8 围岩抗力系数的椭圆分布模型 Fig. 8 Ovalshape model of rock mass resistant coefficient |
坐标轴x与t之间的夹角δ=(α1+α2)/2,根据坐标变换理论可得
| $ \left( {\begin{array}{*{20}{c}} t\\ h \end{array}} \right) = \left[ {\begin{array}{*{20}{c}} {\cos \delta }&{\sin \delta }\\ { - \sin \delta }&{\cos \delta } \end{array}} \right]\left( {\begin{array}{*{20}{c}} x\\ y \end{array}} \right). $ | (5) |
将其代入式(4)得
| $ \frac{{{{\left[ {x\cos \delta + y\sin \delta } \right]}^2}}}{{k_{\max }^2}} + \frac{{{{\left[ {y\cos \delta - x\sin \delta } \right]}^2}}}{{k_{\min }^2}} = 1. $ | (6) |
为使方程中各变量有明确的物理意义,选用极坐标ρoθ表示上述的椭圆方程,ρ代表围岩抗力系数,用k替换,θ为沿洞周的方向角.根据极坐标与直角坐标之间的转换关系,整理可得极坐标系下围岩抗力系数分布的椭圆方程为
| $ \frac{{{k^2}{{\cos }^2}\left( {\theta - \delta } \right)}}{{k_{\max }^2}} + \frac{{{k^2}{{\sin }^2}\left( {\theta - \delta } \right)}}{{k_{\min }^2}} = 1. $ | (7) |
据此可推导出围岩抗力系数的计算公式为
| $ \frac{1}{k} = {\left[ {\frac{{{{\cos }^2}\left( {\theta - \delta } \right)}}{{k_{\max }^2}} + \frac{{{{\sin }^2}\left( {\theta - \delta } \right)}}{{k_{\min }^2}}} \right]^{\frac{1}{2}}}. $ | (8) |
将各向异性系数ξ=kmax/kmin代入上式得
| $ \frac{1}{k} = \frac{1}{{{k_{\max }}}}{\left[ {{{\cos }^2}\left( {\theta - \delta } \right) + {\xi ^2}{{\sin }^2}\left( {\theta - \delta } \right)} \right]^{\frac{1}{2}}}. $ | (9) |
当ξ=1时,可得k=kmax=kmin,洞周各个方向的围岩抗力系数相等,分布曲线退化为圆形,岩体为各向同性体.由上式可以看出,围岩抗力系数由各向异性系数ξ和最大值kmax决定,ξ代表椭圆的形状,而kmax代表数值的大小.
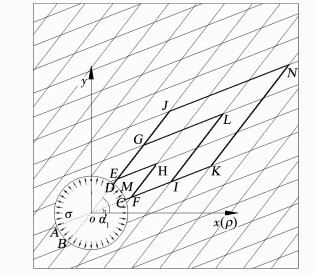
4.2 kmax的计算 4.2.1 节理面上的作用力径向液压枕法试验中圆形隧洞在均布的径向内压作用下,洞周围岩内的应力分布特征为径向受压环向受拉,经过坐标原点的2条对称的节理处于法向受拉状态.选择图 8中右上部分的节理和岩石作为研究对象,建立计算模型如图 9所示.
|
图 9 最大围岩抗力系数计算模型 Fig. 9 Model of the maximal rock mass resistant coefficient |
节理CK和DJ面上没有剪力作用,假设EH与FH、GL与IL、JN与KN节理面上应力均匀分布,由于对称应力分别相等.其中,EH面上的应力为
| $ {\sigma _1} = \frac{{{F_{{{\rm{N}}_{\rm{1}}}}}}}{{\left| {EH} \right|}},{\tau _1} = \frac{{{F_{{{\rm{S}}_{\rm{1}}}}}}}{{\left| {EH} \right|}}. $ | (10) |
式中:FN1、FS1分别为节理EH上的法向力和剪力.
首先对CDEHF块体,求FN1、FS1,块体几何和荷载都关于OH对称,只有2个未知量.先求圆弧CD上径向压力在x轴和y轴方向的分量,在洞周上点(ρ,θ)处取一个微段ρ·dθ.
x方向上力的分量为σρdθcos θ,y方向上力的分量为σρdθsin θ.将θ从α1到α2积分,得到
| $ \int_{{\alpha _1}}^{{\alpha _2}} {\sigma \cdot 1 \cdot \rho {\rm{d}}\theta } \cdot \cos \theta = \sigma r\left[ {\sin {\alpha _2} - \sin {\alpha _1}} \right]. $ | (11) |
σ在y方向产生的力的分量为
| $ \int_{{\alpha _1}}^{{\alpha _2}} {\sigma \cdot 1 \cdot \rho {\rm{d}}\theta } \cdot \sin \theta = \sigma r\left[ {\cos {\alpha _1} - \cos {\alpha _2}} \right]. $ | (12) |
FH边上,x方向分量为
| $ - {F_{{{\rm{N}}_{\rm{1}}}}} \cdot \sin {\alpha _2} - {F_{{{\rm{S}}_1}}} \cdot \cos {\alpha _2}. $ | (13) |
y方向分量为
| $ {F_{{{\rm{N}}_{\rm{1}}}}} \cdot \cos {\alpha _2} - {F_{{{\rm{S}}_1}}} \cdot \sin {\alpha _2}. $ | (14) |
EH边上,x方向分量为
| $ {F_{{{\rm{N}}_{\rm{1}}}}} \cdot \sin {\alpha _1} - {F_{{{\rm{S}}_1}}} \cdot \cos {\alpha _1}. $ | (15) |
y方向分量为
| $ - {F_{{{\rm{N}}_{\rm{1}}}}} \cdot \cos {\alpha _1} - {F_{{{\rm{S}}_1}}} \cdot \sin {\alpha _1}. $ | (16) |
块体CDEHF在x方向的平衡方程为
| $ \begin{array}{*{20}{c}} {\sigma r\left[ {\sin {\alpha _2} - \sin {\alpha _1}} \right] - {F_{{{\rm{N}}_{\rm{1}}}}}\sin {\alpha _2} - }\\ {{F_{{{\rm{S}}_1}}}\cos {\alpha _2} + {F_{{{\rm{N}}_{\rm{1}}}}}\sin {\alpha _1} - {F_{{{\rm{S}}_1}}}\cos {\alpha _1} = 0.} \end{array} $ | (17) |
y方向平衡方程为
| $ \begin{array}{*{20}{c}} {\sigma r\left[ {\cos {\alpha _1} - \cos {\alpha _2}} \right] + {F_{{{\rm{N}}_{\rm{1}}}}}\cos {\alpha _2} - }\\ {{F_{{{\rm{S}}_1}}}\sin {\alpha _2} - {F_{{{\rm{N}}_{\rm{1}}}}}\cos {\alpha _1} - {F_{{{\rm{S}}_1}}}\sin {\alpha _1} = 0.} \end{array} $ | (18) |
式(17)与式(18)等价,需要再建立一个平衡方程,即沿两组节理夹角角平分线上的平衡方程.
σ在OH方向上力的分量为
| $ \begin{array}{*{20}{c}} {\int_{{\alpha _1}}^{\frac{{{\alpha _1} + {\alpha _2}}}{2}} {\sigma \rho {\rm{d}}\theta \cdot \cos \left( {\frac{{{\alpha _1} + {\alpha _2}}}{2} - \theta } \right)} + }\\ {\int_{\frac{{{\alpha _1} + {\alpha _2}}}{2}}^{{\alpha _2}} {\sigma \rho {\rm{d}}\theta \cdot \cos \left( {\theta - \frac{{{\alpha _1} + {\alpha _2}}}{2}} \right)} = 2r\sigma \sin \left( {\frac{{{\alpha _2} - {\alpha _1}}}{2}} \right).} \end{array} $ | (19) |
FN1与OH的夹角为(π+α1-α2)/2,OH方向平衡方程为
| $ \begin{array}{*{20}{c}} {2r\sigma \sin \left( {\frac{{{\alpha _2} - {\alpha _1}}}{2}} \right) - 2\left[ {{F_{{{\rm{N}}_{\rm{1}}}}}\cos \left( {\frac{{{\rm{ \mathsf{ π} }} + {\alpha _1} - {\alpha _2}}}{2}} \right) + } \right.}\\ {\left. {{F_{{{\rm{S}}_{\rm{1}}}}}\sin \left( {\frac{{{\rm{ \mathsf{ π} }} + {\alpha _1} - {\alpha _2}}}{2}} \right)} \right] = 0.} \end{array} $ | (20) |
联立式(10)、(17)和(20)求解得
| $ \left\{ \begin{array}{l} {F_{{{\rm{N}}_{\rm{1}}}}} = r\sigma ,\\ {F_{{{\rm{S}}_{\rm{1}}}}} = 0. \end{array} \right. $ | (21) |
CDGLI块体,边IL上的作用力FN2,FS2,同理可得
| $ \left\{ \begin{array}{l} {F_{{{\rm{N}}_{\rm{2}}}}} = {F_{{{\rm{N}}_{\rm{1}}}}},\\ {F_{{{\rm{S}}_{\rm{2}}}}} = {F_{{{\rm{S}}_{\rm{1}}}}}. \end{array} \right. $ | (22) |
进一步得
| $ \left\{ \begin{array}{l} {F_{{{\rm{N}}_{\rm{1}}}}} = {F_{{{\rm{N}}_{\rm{2}}}}} = {F_{{{\rm{N}}_{\rm{3}}}}} = \cdots = {F_{{{\rm{N}}_n}}},\\ {F_{{{\rm{S}}_{\rm{1}}}}} = {F_{{{\rm{S}}_{\rm{2}}}}} = {F_{{{\rm{S}}_{\rm{3}}}}} = \cdots = {F_{{{\rm{S}}_n}}}. \end{array} \right. $ | (23) |
FH、IL、KN节理面上作用力虽然相同,但作用面积不同,因此应力不同,节理长度
FH边
| $ \left\{ \begin{array}{l} {\sigma _1} = \frac{{{F_{{{\rm{N}}_{\rm{1}}}}}}}{{\left| {FH} \right|}} = \frac{{r\sigma \cdot \sin \left( {{\alpha _2} - {\alpha _1}} \right)}}{s},\\ {\tau _1} = \frac{{{F_{{{\rm{S}}_{\rm{1}}}}}}}{{\left| {FH} \right|}} = 0. \end{array} \right. $ | (24) |
IL边
| $ \left\{ \begin{array}{l} {\sigma _2} = \frac{{{F_{{{\rm{N}}_{\rm{2}}}}}}}{{\left| {IL} \right|}} = \frac{{r\sigma \cdot \sin \left( {{\alpha _2} - {\alpha _1}} \right)}}{{2s}},\\ {\tau _2} = \frac{{{F_{{{\rm{S}}_{\rm{2}}}}}}}{{\left| {FH} \right|}} = 0. \end{array} \right. $ | (25) |
KN边
| $ \begin{array}{*{20}{c}} {\left\{ \begin{array}{l} {\sigma _3} = \frac{{{F_{{{\rm{N}}_{\rm{3}}}}}}}{{\left| {KN} \right|}} = \frac{{r\sigma \cdot \sin \left( {{\alpha _2} - {\alpha _1}} \right)}}{{3s}},\\ {\tau _3} = \frac{{{F_{{{\rm{S}}_{\rm{3}}}}}}}{{\left| {KN} \right|}} = 0. \end{array} \right.}\\ \cdots \end{array} $ | (26) |
第n边
| $ \left\{ \begin{array}{l} {\sigma _n} = \frac{{{F_{{{\rm{N}}_n}}}}}{{\left| {nFN} \right|}} = \frac{{r\sigma \cdot \sin \left( {{\alpha _2} - {\alpha _1}} \right)}}{{ns}},\\ {\tau _n} = \frac{{{F_{{{\rm{S}}_n}}}}}{{\left| {nFN} \right|}} = 0. \end{array} \right. $ | (27) |
如图 9所示,M点为洞壁与两组节理夹角角平分线的交点,该点处围岩抗力系数最大,M点的径向位移为岩石和节理在径向产生的变形之和.
由于岩石被节理切割成棱形块体,且随着节理间距和倾角的变化,棱形岩石块体形状在不断地变化,难以求出岩块的变形,因此,将岩石产生的变形简化为均质岩体条件下的变形[21],根据压力隧洞的Lame解答,可知在径向应力σ作用下洞壁岩石的径向变形为
| $ {u_{\rm{r}}} = \frac{{r\sigma \left( {1 + \mu } \right)}}{E}. $ | (28) |
M点径向方向上,节理产生的变形包括该方向上所有节理法向和切向变形在该方向上的分量之和,节理EH和FH的位移为
| $ \begin{array}{l} {u_{{{\rm{J}}_{\rm{1}}}}} = \frac{{{\sigma _1}}}{{{k_n}}} \cdot \cos \left( {\frac{{{\rm{ \mathsf{ π} }} + {\alpha _1} - {\alpha _2}}}{2}} \right) + \frac{{{\tau _1}}}{{{k_s}}} \cdot \sin \left( {\frac{{{\rm{ \mathsf{ π} }} + {\alpha _1} - {\alpha _2}}}{2}} \right) = \\ \;\;\;\;\;\;\;\frac{{r\sigma }}{{s{k_n}}}\sin \left( {{\alpha _2} - {\alpha _1}} \right)\sin \left( {\frac{{{\alpha _2} - {\alpha _1}}}{2}} \right). \end{array} $ | (29) |
节理GL和IL的位移为
| $ {u_{{{\rm{J}}_{\rm{2}}}}} = \frac{{r\sigma }}{{2s{k_n}}}\sin \left( {{\alpha _2} - {\alpha _1}} \right)\sin \left( {\frac{{{\alpha _2} - {\alpha _1}}}{2}} \right). $ | (30) |
第n条节理的位移为
| $ {u_{{{\rm{J}}_n}}} = \frac{{r\sigma }}{{ns{k_n}}}\sin \left( {{\alpha _2} - {\alpha _1}} \right)\sin \left( {\frac{{{\alpha _2} - {\alpha _1}}}{2}} \right). $ | (31) |
即可得到M点的径向位移为
| $ \begin{array}{l} {u_{\rm{M}}} = {u_{\rm{r}}} + {u_{\rm{J}}} = \frac{{r\sigma \left( {1 + \mu } \right)}}{E} + \frac{{r\sigma }}{{s{k_n}}}\sin \left( {{\alpha _2} - {\alpha _1}} \right) \cdot \\ \;\;\;\;\;\;\;\;\sin \left( {\frac{{{\alpha _2} - {\alpha _1}}}{2}} \right) \cdot \left( {1 + \frac{1}{2} + \frac{1}{3} + \cdots + \frac{1}{n}} \right). \end{array} $ | (32) |
参数n是关于节理间距s和隧道开挖影响范围R的函数,2组等间距节理相互切割产生的棱形边长为
| $ \begin{array}{l} 1 + \frac{1}{2} + \frac{1}{3} + \cdots + \frac{1}{n} = \ln \left( {n + 1} \right) + a = \\ \;\;\;\;\ln \left[ {\frac{{\left( {R - r} \right) \cdot \sin \left( {{\alpha _2} - {\alpha _1}} \right)}}{s} + 1} \right] + a. \end{array} $ | (33) |
式中:a为欧拉常数0.577 215 664 9,R的取值需根据实际情况确定,应大于应力影响半径.
将位移代入
| $ \begin{array}{l} \frac{1}{{{k_{\max }}}} = \frac{{r\left( {1 + \mu } \right)}}{E} + \frac{r}{{s{k_n}}}\sin \left( {{\alpha _2} - {\alpha _1}} \right) \cdot \sin \left( {\frac{{{\alpha _2} - {\alpha _1}}}{2}} \right) \cdot \\ \;\;\;\;\;\;\;\;\;\;\left\{ {\ln \left[ {\frac{{\left( {R - r} \right) \cdot \sin \left( {{\alpha _2} - {\alpha _1}} \right)}}{s} + 1} \right] + a} \right\}. \end{array} $ | (34) |
得到围岩抗力系数的计算公式为
| $ \frac{1}{k} = \frac{{\sqrt {{{\cos }^2}\left( {\theta - \frac{{{\alpha _1} + {\alpha _2}}}{2}} \right) + {\xi ^2}{{\sin }^2}\left( {\theta - \frac{{{\alpha _1} + {\alpha _2}}}{2}} \right)} }}{{{k_{\max }}}}. $ | (35) |
由式(34)可以看出,对节理岩体围岩抗力系数起决定性的因素是岩石弹性模量、节理法向刚度、节理夹角和节理间距,这与前面各因素的显著性分析结果相一致,式中的几何参数是隧道半径r、影响范围R、方向角θ,体现了尺寸效应和椭圆分布规律,表明了理论公式的合理性.若岩体为不含任何节理的均质岩体,即α1=α2=0,ξ=1,将模型边界取为无穷大R→∞,代入式(35)中,式(35)将退化为著名的Gallerkin公式
| $ k = \frac{E}{{r\left( {1 + \mu } \right)}}. $ | (36) |
围岩抗力系数解析公式(35)是依据力的平衡条件推导得出的,与前面的正交试验数值计算结果没有直接的因果关系,因此,可以用正交试验的结果来验证解析公式的准确性,统计出正交试验中81个模型的最大围岩抗力系数,同时通过解析公式计算出每个模型的最大围岩抗力系数,如图 10所示.可以看出,数据点与折线起伏走势几乎一致,接近重合.解析解与数值解的差异均小于14%(#6号试验),且绝大部分试验的差异均小于5%.说明81个模型试验数值计算的结果与解析公式计算的结果一致,证明了最大围岩抗力系数公式的准确性.
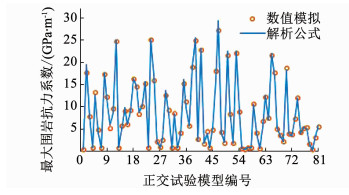
|
图 10 解析公式与数值模拟结果的对比 Fig. 10 Comparisons between the analytical calculation results and the numerical modeling results |
以大连地铁2号线兴工街站隧道工程为例说明本文模型的实际应用,探讨围岩抗力系数各向异性对衬砌内力的影响.工程设计中对地质条件最差的断面DK15+613进行地质勘测,岩体力学参数如表 2所示,并对其围岩压力、变形、支护结构受力进行了监测.将表 2中各参数代入式(3),得到各向异性系数ξ=1.47.由于其他断面地质条件相对较好,根据地质纵剖面图中各断面的破碎程度,将各断面DK15+730、DK15+648、DK15+770、DK15+690的各向异性系数分别取为1.3, 1.2, 1.1, 1.0,将其代入式(35),得到不同断面下围岩抗力系数的分布如图 11所示.
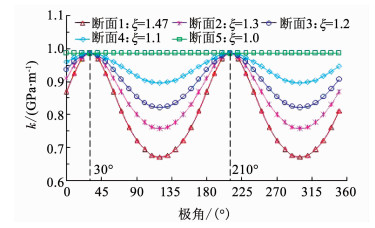
|
图 11 隧道周围围岩抗力系数分布 Fig. 11 Distribution of k around the tunnel |
监测断面DK15+613处初期支护结构上的围岩压力实测值如图 12所示,图中虚线表示缺乏实测数据,采用均匀分布压力.围岩抗力系数分别采用上述断面1,2,3,4和5的计算结果,均采用仅受压地基弹簧模拟.隧道轮廓尺寸如图 2所示,初期支护为钢筋格栅-混凝土结构,钢筋为Φ25HRB335,按间距0.5 m布置,混凝土为C30,弹性模量取为E=31 GPa,重度为γ=25 kN/m3.
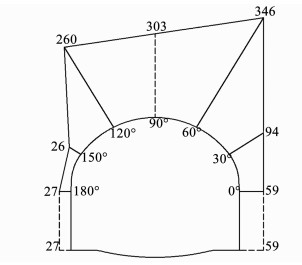
|
图 12 监测断面DK15+613的围岩压力分布(kPa) Fig. 12 Distribution ofstress on section DK15+613 |
采用荷载-结构模型,利用有限元进行建模计算,因为围岩只能受压不能受拉,通过不断地迭代计算删掉受拉弹簧,直到所有弹簧均受压为止.得到5种情况下衬砌的内力,其中,轴力与现场实测结果对比如表 6所示,弯矩随各向异性系数的变化曲线如图 13所示.
| 表 6 现场实测与理论模型轴力对比 kN Tab. 6 Comparisons of axial force bymonitor and model |
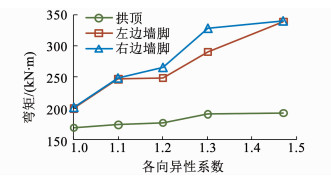
|
图 13 弯矩随各向异性系数变化曲线 Fig. 13 Bending moment vs anisotropy coefficient |
由表 6可以看出,理论模型(断面1)计算结果与现场实测轴力相差不大,最大差异为13.6%,最大轴力均出现拱顶,两者反映的轴力分布趋势一致,进一步证明了本文模型的准确性.
不同断面围岩抗力系数分布下衬砌的轴力相差不大,断面1,2,3,4和5下最大轴力分别为3 599,3 605,3 618,3 620和3 631 kN,轴力的差异小于1%,围岩抗力系数各向异性对衬砌轴力影响不大.围岩抗力系数越大,约束衬砌变形的能力越强,衬砌轴力越大.
由图 13可以看出,围岩抗力系数各向异性对衬砌弯矩的影响显著,各向异性系数对弯矩的影响几乎呈正相关,各向异性系数越大,衬砌所受的弯矩越大.弯矩最大值出现在两边墙墙脚,断面1,2,3,4,5情况下得到的衬砌弯矩最大值分别为341,328,266,249和202 kN·m,断面1和5下的各向异性系数分别为1.47和1,相差32.0%,产生的衬砌弯矩最大值分别为341和202 kN·m,相差40.7%,说明考虑围岩抗力系数的各向异性与否对衬砌弯矩的影响较大,为了能更加真实地描述岩体的围岩抗力系数,应充分考虑节理对围岩抗力系数各向异性的影响.
7 结论1) 当岩石为线弹性体、节理服从库伦滑移本构模型时,节理岩体围岩抗力系数不受围岩压力和径向液压力的影响,可称为弹性抗力系数.
2) 岩体中存在两组等间距节理时,围岩抗力系数分布曲线呈椭圆形,沿两组节理夹角角平分线方向围岩抗力系数最大,为椭圆的长轴,垂直于两组节理夹角角平分线方向围岩抗力系数最小,为椭圆的短轴.
3) 岩石弹性模量、节理法向刚度、节理间距和节理夹角对围岩抗力系数有显著影响,岩石泊松比对围岩抗力系数有一定影响,其他因素对围岩抗力系数无显著影响.
4) 隧道直径与节理间距的比值是影响围岩抗力系数尺寸效应的主要因素,比值接近于0时,可以认为围岩是均质体,比值趋于无穷大时,可以将围岩当作等效各向同性体,并用数学函数描述这一物理现象,得到了各向异性系数的表达式.
5) 推导出了围岩抗力系数的计算公式,并论证了公式的准确性,工程实例计算表明,围岩抗力系数各向异性对衬砌轴力的影响较小,对弯矩的影响显著.
6) 本文模型适用于岩石坚硬、节理填充物较少的围岩,对于软岩和节理填充物复杂的岩体工程需要采用不同的本构模型,是下一步的研究重点.
| [1] |
MASHIMO H, ISHIMURA T. Evaluation of the load on shield tunnel lining in gravel[J]. Tunnelling and Underground Space Technology, 2003, 18(2): 233. DOI:10.1016/S0886-7798(03)00032-4 |
| [2] |
铁路隧道设计规范: TB 10003-2016[S].北京: 中国铁道出版社, 2016 Code for design on tunnel of railway: TB 10003-2016[S]. Beijing: China Railway Publishing House, 2016 |
| [3] |
钱令希. 关于水工有压隧洞计算中的弹性抗力系数"k"[J]. 土木工程学报, 1955, 2(4): 369. QIAN Lingxi. Calculation method of elastic resistant coefficient "k" in hydraulic pressure tunnel[J]. China Civil Engineering Journal, 1955, 2(4): 369. DOI:10.15951/j.tmgcxb.1955.04.002 |
| [4] |
吕有年. 水工有压隧洞岩石抗力系数"K"的一个新公式[J]. 岩土工程学报, 1981, 3(1): 70. LV Younian. A new formula of rock resistant factor "K" in hydraulic pressure tunnel[J]. Chinese Journal of Geotechnical Engineering, 1981, 3(1): 70. DOI:10.3321/j.issn:1000-4548.1981.01.007 |
| [5] |
MUIR WOOD A M. The circular tunnel in elastic ground[J]. Geotechnique, 1975, 5(1): 115. DOI:10.1680/GEOT.1975.25.1.115 |
| [6] |
蔡晓鸿. 圆形压力隧洞岩石抗力系数K的理论和计算[J]. 工程力学, 1988, 5(3): 100. CAI Xiaohong. The theories and computation of the rock resistant factor K in circular pressure tunnel[J]. Engineering Mechanics, 1988, 5(3): 100. |
| [7] |
徐栓强, 俞茂宏. 考虑中间主应力效应的隧洞岩石抗力系数的计算[J]. 岩石力学与工程学报, 2004, 23(s1): 4303. XU Shuanqiang, YU Maohong. Calculation of rock resistant factor in tunnel considering intermediate principal stress effect[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(s1): 4303. DOI:10.3321/j.issn:1000-6915.2004.z1.005 |
| [8] |
唐葭, 邓宗伟, 蒋建清. 考虑蠕变影响的隧道围岩抗力系数计算方法[J]. 中南大学学报(自然科学版), 2014, 45(4): 1281. TANG Jia, DENG Zongwei, JIANG Jianqing. Calculation on rock resistant coefficient of tunnel considering creep effect[J]. Journal of Central South University (Science and Technology), 2014, 45(4): 1281. |
| [9] |
刘长庚, 孙民伟.小浪底水库围岩径向变形试验[C]//岩石力学理论与工程实践.中国岩石力学与工程学会青年工作委员会, 1997: 6 LIU Changgeng, SUN Minwei. Radial deformation test of rock mass in Xiaolangdi Hydropower Station[C]//Rock Mechanics Theory and Engineering Practice. Youth Work Committee of China Society of Rock Mechanics and Engineering. 1997: 6 |
| [10] |
李维树.围岩弹性抗力试验方法及k0参数取值研究[C]//第八次全国岩石力学与工程学术大会论文集.中国岩石力学与工程学会, 2004: 6 LI Weishu. Studies on the test methods of elastic resistance for surrounding rock mass and the selection of parameter k0[C]//Proceedings of the Eighth National Conference on Rock Mechanics and Engineering. Chinese Society of Rock Mechanics and Engineering, 2004: 6 |
| [11] |
唐爱松, 李敦仁, 钟作武, 等. 岩滩电站岩体弹性抗力系数试验研究[J]. 岩石力学与工程学报, 2005, 24(20): 3761. TANG Aisong, LI Dunren, ZHONG Zuowu, et al. Experimental research on rock mass elasticity resisting coefficient in Yantan Hydropower Station[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(20): 163. DOI:10.3321/j.issn:1000-6915.2005.20.025 |
| [12] |
李波, 吴立, 邓宗伟, 等. 高速铁路隧道围岩抗力系数现场试验与理论研究[J]. 岩土力学, 2015, 36(2): 532. LI Bo, WU Li, DENG Zongwei, et al. Field test and theoretical study of rock resistant coefficient in high-speed railway runnel[J]. Rock and Soil Mechanics, 2015, 36(2): 532. DOI:10.16285/j.rsm.2015.02.032 |
| [13] |
宋超业, 涂洪亮, 乔春生. 大连地铁2号线兴工街站浅埋大跨隧道双层初期支护组合形式及合理参数分析[J]. 隧道建设, 2015, 35(6): 491. SONG Chaoye, TU Hongliang, QIAO Chunsheng. Analysis on combination mode and parameters of primary support of shallow-buried large-span tunnel: Case study on Xinggongjie Station Tunnel on No. 2 Line of Dalian Metro[J]. Tunnel Construction, 2015, 35(6): 491. DOI:10.3973/j.issn.1672-741X.2015.06.001 |
| [14] |
王志伟, 乔春生, 宋超业. 上软下硬岩质地层浅埋大跨隧道松动压力计算[J]. 岩土力学, 2014, 35(8): 2342. WANG Zhiwei, QIAO Chunsheng, SONG Chaoye. Calculation method of relaxation pressure of shallow large span tunnel in up-soft/low-hard rock stratum[J]. Rock and Soil Mechanics, 2014, 35(8): 2342. DOI:10.16285/j.rsm.2014.08.028 |
| [15] |
WANG Z W, QIAO C S, SONG C Y, et al. Upper bound limit analysis of support pressures of shallow tunnels in layered jointed rock strata[J]. Tunnelling and Underground Space Technology, 2014, 43: 171. DOI:10.1016/j.tust.2014.05.010 |
| [16] |
李英勇, 冯现大, 李术才, 等. 极浅埋连拱隧道中隔墙顶部岩体塌方演化过程分析[J]. 岩土力学, 2011, 32(9): 2747. LI Yingyong, FENG Xianda, LI Shucai, et al. Analysis of evolution process of rock collapse on top of middlewall in an extremely shallow double arch tunnel[J]. Rock and Soil Mechanics, 2011, 32(9): 2747. DOI:10.3969/j.issn.1000-7598.2011.09.031 |
| [17] |
莫振泽, 李海波, 周青春, 等. 基于UDEC的隧道掘进机滚刀破岩数值模拟研究[J]. 岩土力学, 2012, 33(4): 1196. MO Zhenze, LI Haibo, ZHOU Qingchun, et al. Research on numerical simulation of rock breaking using TBM disc cutters based on UDEC method[J]. Rock and Soil Mechanics, 2012, 33(4): 1197. DOI:10.3969/j.issn.1000-7598.2012.04.035 |
| [18] |
水利水电工程岩石试验规程: DLJ204-81, SLJ2-81, 1982[S].北京: 水利出版社, 1982 Standard for rock testing of water conservancy and hydropower engineering: DLJ204-81, SLJ2-81, 1982[S]. Beijing: China Water Press, 1982 |
| [19] |
工程岩体分级标准: GB/T 50218-2014[S].北京: 中国计划出版社, 2014 Standard for engineering classification of rock mass: GB/T 50218-2014[S]. Beijing: China Planning Press, 2014 |
| [20] |
王思敬. 论岩石的地质本质性及其岩石力学演绎[J]. 岩石力学与工程学报, 2009, 28(3): 433. WANG Sijing. Geological nature of rock and its deduction for rock mechanics[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(3): 433. DOI:10.3321/j.issn:1000-6915.2009.03.001 |
| [21] |
张占荣, 赵新益, 刘庆辉, 等. 节理岩体变形模量的结构效应研究[J]. 岩石力学与工程学报, 2011, 30(s2): 4158. ZHANG Zhanrong, ZHAO Xinyi, LIU Qinghui, et al. Study of structure effect of jointed rock mass deformation modulus[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(s2): 4158. |
 2019, Vol. 51
2019, Vol. 51


