对于混凝土等脆性材料,其抗拉伸强度往往远小于其抗压缩强度[1].正是因为混凝土材料的这种性质,导致其在实际工程中拉裂破坏很常见,而在现行的设计规范中,对混凝土的抗拉强度重视尚有不足.已有研究多集中于中低强度混凝土或者特殊骨料的混凝土材料,胡时胜等[2]研究发现,混凝土材料流动应力的变化对应变率效应十分敏感;吴胜兴等[3]提出了基于微观结构特征的混凝土动态抗拉强度提高机理;胡俊等[4]证实了EPS(聚苯乙烯)混凝土中存在粒径尺寸效应,王志亮等[5-6]指出钢纤维的体积分数是钢纤维混凝土(SFRC)力学性能的主要影响因素.尽管混凝土具有比静强度更高的动强度,但仍缺少高强度混凝土在中高加载率下的拉伸强度数据.
动态劈裂试验是在静态巴西圆盘的基础上,结合应力波理论,获得混凝土等脆性材料在高应变率下的动态拉伸强度.在对于劈裂公式的推导过程中,很多学者应用Griffith理论和有限元模拟的方法得到圆盘端部集中力过大[7],甚至质疑巴西圆盘试验的可靠性[8].随着对分离式霍普金森杆(SHPB)的深入研究[9],异形冲头技术[10]、平台巴西圆盘[11]以及弧形垫块[4]等方法在动态劈裂试验中也获得了较好的应用.由于直接拉伸的局限性[12],动态劈裂在测试混凝土等脆性材料拉伸强度的方法中依然被广泛采用.
本文在静态劈裂理论解法基础上,应用MATLAB软件将圆盘内部应力等值区域进行可视化,为巴西圆盘的可靠性提供理论依据.此外,还基于一维应力波理论,对常见的C75高强混凝土进行了动态劈裂拉伸试验,并结合试验中出现的现象开展系列数值模拟和分析,力求得出具有参考价值的结论,以期指导工程实践.
1 试验测试原理由于直接拉伸强度测试的局限性,脆性材料的动态抗拉强度测试最常用的方法是巴西圆盘劈裂试验.该方法是基于静态巴西劈裂试验,即圆盘试样的直径方向上受到一对等值的线荷载,试件沿着受力方向的直径裂开成两个半圆盘.若将试样简化为均质脆性材料,用弹性力学中对心受压圆盘的平面应力问题解析解[13],可以求出巴西试验中用于测试脆性材料抗拉强度.
Griffith准则[14]能从理论上解释岩石内部裂纹扩展现象,可较好地描述岩石破坏的机理,其强度判据为
| $ \left\{ \begin{array}{l} {\sigma _1} + 3{\sigma _3} \le 0,{\sigma _{\rm{t}}} = - {\sigma _3},\\ {\sigma _1} + 3{\sigma _3} > 0,{\sigma _{\rm{t}}} = \frac{{{{\left( {{\sigma _1} - {\sigma _3}} \right)}^2}}}{{8\left( {{\sigma _1} + {\sigma _3}} \right)}}. \end{array} \right. $ | (1) |
其中:σ1、σ3分别为最大、最小主应力,其值可以根据二维应力张量分析得到.根据Griffith理论,岩石单轴抗压强度是其抗拉强度的8倍,而对于一般的混凝土材料,抗压强度约为抗拉强度的10倍[12],与式(1)略有差别.不少学者根据式(1)推导出从圆盘中心到加载点其Griffith等效应力值逐渐增加,加载端应力集中明显会最先开裂的结论[7-8],而现有的高速摄影技术显示,静态以及动态巴西圆盘劈裂试验中,裂纹的确是由中心起裂然后向两端扩展[10, 15-16],这样就造成了理论与试验现象相悖.
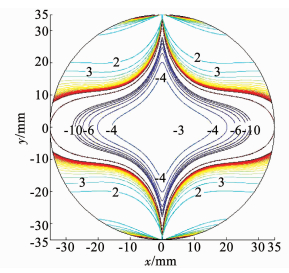
在二维受力条件下,采用MATLAB软件将圆盘试样中两个主应力之比用等势线表示出来(如图 1),圆盘试样的σ1/σ3等值线近似呈封闭的菱形四边形.在集中荷载作用处,压应力集中现象十分明显,圆盘中心点O的压、拉应力分别为:σy=6P/(πD0L),σx= -2P/(πD0L).此时,圆盘中心处压应力为拉应力的3倍.
|
图 1 最大与最小主应力之比等值线 Fig. 1 Contours of ratio of maximum to minimum principal stress |
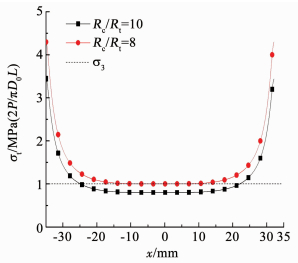
根据Griffith理论的判别条件,仅中心点处有σ1+3σ3=0,其他区域满足σ1+3σ3>0.若压拉比调整为10,修正公式(1)后得到的等效应力,其受压方向上等效应力值如图 2所示.当计算系数采用压拉比Rc/Rt=10时,等效应力与Rc/Rt=8时的变化趋势相同,但其在中心点附近的值已经小于σ3,此时中心点处依然满足σ1+3σ3=0的判别条件,得到的等效应力值为σ3,这就形成了中心点为其邻域内的极大值.此外,将修正后的等效应力σt与σ3作差比较,其等值线如图 3所示,由此可以得到圆盘内由拉应力控制区域.在实际试验进行中,圆盘处于三维受力状态,其加载端原生裂纹尖端的应力集中程度随着塑性区的形成和扩展而比弹性理论计算得到的应力集中程度小,故中心起裂在原理上依然可以保证.
|
图 2 不同压拉比下圆盘受压直径上等效应力值 Fig. 2 Equivalent stresses along the diameter of disc under different Rc/Rt |

|
图 3 等效应力σt与σ3差值等值线 Fig. 3 Contours of difference between σt and σ3 |
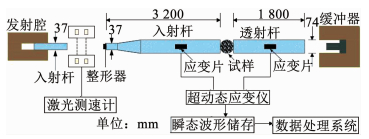
试样原材料选用上海金山水泥厂的万安牌P.Ⅱ42.5水泥、细度模数为2.65的中砂、粒径5~10 mm的石子、自来水以及减水效率为25%的萘系高效减水剂.水灰比采用0.38,砂率48%,减水剂掺量为水泥质量1%.混凝土各组分的比为m(水泥):m(水):m(砂):m(石):m(减水剂)=1:0.38:2.41: 2.61: 0.01.将配好的混凝土装入试模内,然后用小型振动棒捣实,直到出浆为止,再抹平表面.试件成型后用薄膜覆盖,在室温环境中静置24 h后脱模,放入温度为(20±2)℃、相对湿度为90%以上的标准养护室中养护28 d,所研究的C75混凝土基本物理力学参数见表 1.根据国际岩石力学学会建议的巴西试验测试规范[17],将混凝土材料尺寸加工成Φ70×35 mm的圆盘试样,且两端面的不平整度控制在0.05 mm以内.本次试验是在Φ74 mm变截面SHPB上完成(图 4),进行了5组不同应变率劈裂试验.
| 表 1 混凝土基本物理力学参数 Tab. 1 Basic parameters ofthe concrete tested |
|
图 4 试验装置示意 Fig. 4 Schematic of experiment set-up |
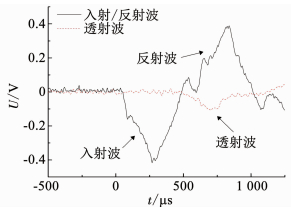
试验中,混凝土试样被夹在入射杆和透射杆之间(如图 5),子弹以初速度v撞击入射杆,在入射杆中产生入射波εi(t)沿杆向前传播,入射波到达试样时,试样开始变形并产生反射波εr(t)和透射波εt(t),见图 6.

|
图 5 SHPB试验中圆盘试样的夹持状态 Fig. 5 State of disc specimen during SHPB test |
|
图 6 SHPB试验中原始波形图 Fig. 6 Recorded curves of waveform in SHPB test |
基于一维应力假设和均匀性假定,通过试验过程中的应力波形可以计算得到试件两端受力:
| $ F\left( t \right) = \frac{{\pi D_1^2}}{8}{E_1}[{\varepsilon _{\rm{i}}}\left( t \right) + {\varepsilon _{\rm{r}}}\left( t \right) + {\varepsilon _{\rm{t}}}\left( t \right)]. $ | (2) |
式中:D1和E1分别表示霍普金森压杆的直径和弹性模量,εi(t)、εr(t)和εt(t)分别为入射杆和透射杆上应变片测到的入射波、反射波和透射波信号.
根据静态劈裂公式,试件中心处的拉应力应为
| $ {\sigma _{\rm{t}}}\left( t \right) = \frac{{2F(t)}}{{\pi {D_0}L}}. $ | (3) |
式中:D0和L分别表示试样的直径和厚度.试样中心点应力σt(t)的最大值即为动态劈裂强度ftd.
对于岩石类脆性材料,在冲击荷载下,试样呈中心双向拉-压应力状态,当应力超过一定阈值时,试样呈现出拉应力失效导致的试件中心开裂.因此,可以用混凝土内脆性材料的劈裂强度作为其抗拉强度.
3 试验结果及分析 3.1 应力平衡分析为了使SHPB试验中测试系统记录的应力波形图真实可靠,所获得的数据与其试件的实际行为相吻合,对于动态劈裂试验中的应力平衡假设,必须对试验过程中的应力平衡情况进行校验[17].
若试件内部应力均匀化实现,即应力平衡假设成立,则入射端和透射端应力相等,有
| $ {\varepsilon _{\rm{i}}}\left( t \right) + {\varepsilon _{\rm{r}}}\left( t \right) = {\varepsilon _{\rm{t}}}\left( t \right). $ | (4) |
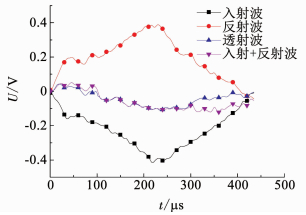
图 7为混凝土劈裂试验中得到的波形曲线,可以看出在透射波到达峰值之前,试样两端应力基本达到平衡(入射波和反射波叠加值与透射波曲线重合),即在试件破坏之前,应力已经达到均匀,这满足了动态劈裂试验中的均匀性假定,故试验数据的可靠有效性能得到保证.
|
图 7 试验过程中应力平衡校验图(v0=5.9 m/s) Fig. 7 Check of stress equilibrium during test (v0=5.9 m/s) |
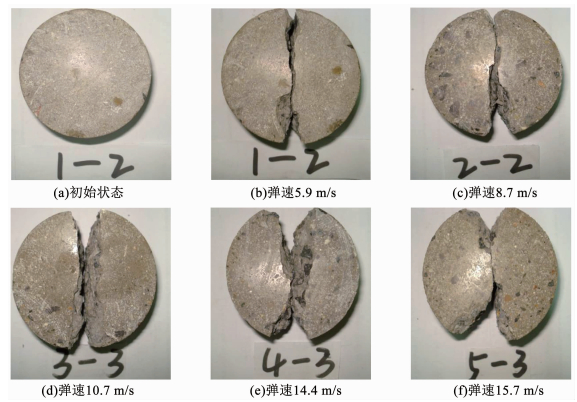
图 8为试验中试样典型破坏形式,C75混凝土的动态破坏模式完全不同于静态劈裂破坏.在弹速较低时,试件基本呈对称开裂,即沿直径方向破裂成较完整的两块;随着弹速的增加,试样仍可以沿中心裂开,但试件上下两端出现明显的三角形破碎区域.结合中应力平衡图的分析,对各组试验结果进行验证,发现在图 8(f)中入射端(试样下方)的破坏区域明显大于透射端(试样上方),且对应的表 2中5-3组数据不满足应力平衡要求,因此,在分析应变率效应时将其剔除.
|
图 8 不同弹速下试样破坏比较 Fig. 8 Comparison of fracturing modes of specimens under different impact velocities |
| 表 2 混凝土劈裂试验结果 Tab. 2 Results of dynamic splitting tests |
在动载荷条件下,混凝土的力学行为与静态下有很大差异,材料的应变率是反映混凝土动态力学的重要指标.本次试验,应变率定义为
| $ \dot \varepsilon = \frac{{{f_{{\rm{td}}}}}}{{{E_{\rm{t}}}\tau }}. $ | (5) |
式中:Et为混凝土的拉伸模量,τ为透射波从起始点到峰值所经历的时间.应力率[16]和解析解[18]的方法常被用来表征加载率效应,由式(3)、(5)可得动态劈裂试验的动态劈裂强度和应变率,各组试验结果见表 2.
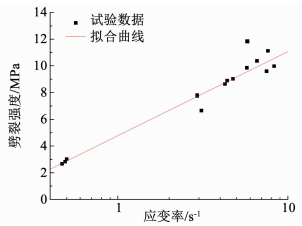
研究表明,随着应变率的增大,材料动态强度随着增加[2, 19].为了研究C75混凝土的“率”效应,将应变率和动态劈裂强度在对数坐标下进行拟合,相关系数R2=0.93,见图 9所示.
| $ {f_{{\rm{td}}}} = 4.78 + 6.49\lg \dot \varepsilon . $ | (6) |
|
图 9 劈裂强度和应变率关系 Fig. 9 Relationship between splitting strength and strain rate |
由此可见,动态劈裂强度与其对应的应变率在对数坐标下呈良好的线性相关.
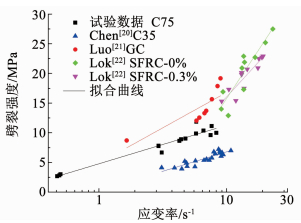
3.4 C75混凝土拉伸强度特点近年来,不少学者对中等应变率下(10-4 s-1 <
|
图 10 不同混凝土劈裂强度与应变率关系比较 Fig. 10 Comparisons of splitting strength with strain rate for different concretes |
普通水泥混凝土是一种由砂石骨料、水泥、水及其他外加材料混合而形成的非均质脆性材料,由于其存在脆性高、耐久性差等缺点,已有研究表明可以将减水剂、废旧轮胎橡胶粒子、聚合物乳液、硅灰、膨润土和钢纤维等添加到普通水泥混凝土对其进行改性,而成为一种新型的混凝土材料.
3.5 混凝土应变率效应的物理机制目前,对于混凝土应变率效应产生的机制说法很多,主要有如下几种:黏性效应[23](Stenfan效应)、惯性效应[24]和裂纹演化机理[25].其中,黏性效应可以解释应变率较低时的动态单轴拉伸和压缩强度的增长情况,惯性效应可以解释高应变率下单轴压缩强度增长现象,而裂纹演化机理效应可以解释高应变率下动态拉伸强度增长的原因.
在本文试验中,可以用裂纹增长机制解释应变率效应:混凝土试样的破坏往往沿着强度最低的骨料-砂浆界面扩展;而在动态试验中,裂纹来不及在薄弱界面充分扩展,断裂就发生了,或者说断裂不一定沿着骨料-砂浆界面传播.试验后观察也发现断面处的粗骨料有时会直接被劈开,断口面呈平滑状.这种现象使得混凝土在应变率增加的过程中,其抗拉强度也随之增大.
4 数值模拟及破碎模式研究随着计算机技术的发展,有限元模拟已经成为研究混凝土内部损伤和动力学特性的一种重要手段[7-8, 26].上述动态劈裂试验现象表明,混凝土在高应变率下两端会产生三角形粉碎区域,其主要原因是:试样端部存在严重的应力集中(图 2),并且受压区破碎时,还存在少量的摩擦力作用.圆盘试样端部受到集中应力和少量弯矩(摩擦力形成)的双重作用,这种力与力矩的协同作用使得岩样在破裂时不仅仅存在沿直径方向的一条主裂纹,更导致局部压缩破坏形成端部的三角形压碎区域.
在动力分析中,混凝土有限元模型选用ANSYS/LS-DYNA分析程序中的solid164单元,该单元是8节点六面体单元.在模拟中接触定义为面面接触,在接触算法中采用罚函数法,接触刚度比例因子对接触力的控制起关键作用,其程序默认值为0.1,调整接触刚度可以避免由接触界面应力过度集中引起的结果数据振荡.建立SHPB杆件模型,其中入射杆和透射杆密度为7 900 kg/m3,弹性模量为210 GPa,泊松比为0.3,试样采用黏塑性本构模型,基本参数取值密度为2 318 kg/m3,弹性模量为42.93 GPa,泊松比为0.2.由于入射杆和透射杆材质均匀,选择等分的映射网格划分,其中变截面网格划分如图 11(a)所示,在试样受拉力破坏时,其裂纹主要产生在与杆件接触的两端和中心部分,故采用非等分网格划分,其单元划分示意如图 11(b)示.

|
图 11 数值模拟中单元网格划分 Fig. 11 Element meshing in numerical simulation |
在数值模拟中,选取Cowper-Symonds黏塑性本构模型[27]考虑高强混凝土力学性能,LS-DYNA关键字MAT_PLASTIC_KINEMATIC,该模型可以提供材料的塑形变形模量,还能通过应变率因子考虑动态加载下的应变率效应,其本构方程为
| $ {\sigma _{\rm{d}}} = ({\sigma _0} + {E_{\rm{p}}}{{\bar \varepsilon }_{\rm{p}}})\left[ {1 + {{\left( {\dot \varepsilon /C} \right)}^{1/p}}} \right]. $ | (7) |
式中:σ0为静态屈服应力;Ep为塑性硬化模量,
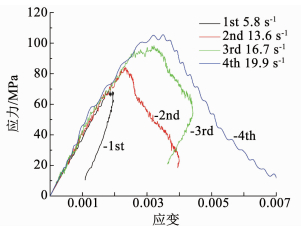
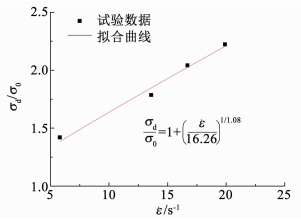
为了测量试样的动态压缩弹性模量,在同批次的C75混凝土试验中做了动态冲击压缩试验,相关结果如图 12所示.根据图中同批次试样的动态压缩试验数据,拟合得到C=16.26,p=1.08;其拟合曲线如图 13所示,相关系数R2=0.98.
|
图 12 混凝土试样动态应力-应变曲线 Fig. 12 Dynamic stress-strain curves of concrete specimens |
|
图 13 Cowper-Symonds本构中参数拟合曲线 Fig. 13 Fitted curves of C-S constitutive parameters |
采用Cowper-Symonds黏塑性本构模型进行数值模拟时,参照静态巴西圆盘的应力状态,使用第一主应力破坏准则作为单元失效准则,关键字为*MAT_ADD_EROSION,用来模拟冲击荷载作用下C75混凝土试样的裂纹起裂以及破坏形态.图 14展示了低弹速5.9 m/s时裂纹起裂以及扩展的过程.从模拟结果可以看出,试样中心先产生裂纹,随后裂纹向两端(注上端为透射端,与透射杆接触)扩展直至贯穿试样,最终造成轴对称破裂.

|
图 14 低弹速5.9 m/s下裂纹起裂以及扩展的过程 Fig. 14 Initiation and propagation of cracks at low projectile velocity (5.9 m/s) |
动态加载的过程中,在应力达到平衡之前,试样轴线附近靠近入射杆方向出现拉应力区域,且该拉伸区范围随弹速增加而增加,当弹速超过某临界值时,产生的拉应力峰值将超过材料拉伸强度,试样的最终破碎模式呈现出不对称.图 15给出了弹速10.7 m/s下混凝土破坏模拟结果.数值模拟显示高弹速下裂纹扩展的先后顺序如下:中心起裂→入射端压碎→裂纹扩展→透射端压碎和入射端三角区域形成→透射端三角形区域形成→试样破碎,可见下方(入射端)破坏区域明显大于上方(透射端).本文模拟的断裂过程以及断裂形态与文[10, 15-16]中采用高速摄影得到试验结果吻合度较高,且与前述的10.7 m/s弹速试验结果(图 8(d))非常相近,从而也验证了考虑应变率效应的Cowper-Symonds本构在模拟混凝土拉伸破坏时的可行性以及拟合参数选取的合理性.

|
图 15 高弹速时裂纹起裂以及扩展过程v=10.7 m/s) Fig. 15 Initiation and propagation of cracks at high projectile velocity (v=10.7 m/s) |
1) 二维受力状态下,巴西圆盘试样的最大与最小主应力之比(σ1/σ3)等值线近似呈封闭的菱形,其比值在圆盘的中心处达到最大值,若按Griffith准则计算试样内等效应力,采用10倍的压拉比,可以从理论上保证圆盘试样中心处最先发生拉裂破坏.
2) 冲击载荷下,C75混凝土试样沿径向呈对称开裂;随着弹速的增加,试样受载端出现明显的三角形破碎区且靠近入射端破碎较严重.在100~101/s应变率范围内,试样动态劈裂强度与应变率对数呈现出良好的线性相关性.
3) 黏塑性本构Cowper-Symonds能够较好地表征本文所研究的混凝土动力学行为,基于其模拟出的试样动态劈裂效果与破裂过程与试验观测到结果吻合度非常高,能逼真地展示该混凝土材料动态损伤破裂的全过程.
| [1] |
梅塔.混凝土微观结构、特性和材料[M].欧阳东, 译.北京: 中国建筑工业出版社, 2016 METHAP K. Concrete: Microstructure, properties, and materials[M]. OUYANG Dong, trans. Beijing: China Architecture & Building Press, 2016 |
| [2] |
胡时胜, 王道荣, 刘剑飞. 混凝土材料动态力学性能的实验研究[J]. 工程力学, 2001, 18(5): 115. HU Shisheng, WANG Daorong, LIU Jianfei. Experimental study of dynamic mechanical behavior of concrete[J]. Engineering Mechanics, 2001, 18(5): 115. DOI:10.3969/j.issn.1000-4750.2001.05.015 |
| [3] |
吴胜兴, 周继凯, 陈厚群. 基于微观结构特征的混凝土动态抗拉强度提高机理及其统一模型[J]. 水利学报, 2010, 41(4): 419. WU Shengxing, ZHOU Jikai, CHEN Houqun. Unified model and mechanism for dynamic tensile strength increase of concrete base on its microstructure characteristics[J]. Journal of Hydraulic Engineering, 2010, 41(4): 419. |
| [4] |
胡俊, 丁克伟, 韦璐. EPS混凝土静态压缩和劈裂性能[J]. 建筑材料学报, 2015, 18(5): 737. HU Jun, DING Kewei, WEI Lu. Compressive and splitting behavior of eps concrete under static loading[J]. Journal of Building Materials, 2015, 18(5): 737. DOI:10.3969/j.issn.1007-9629.2015.05.004 |
| [5] |
WANG Z L, SHI Z M, WANG J G. On the strength and toughness properties of SFRC under static-dynamic compression[J]. Composites Part B Engineering, 2011, 42(5): 1285. DOI:10.1016/j.compositesb.2011.01.027 |
| [6] |
WANG Z L, WU L P, WANG J G. A study of constitutive relation and dynamic failure for SFRC in compression[J]. Construction & Building Materials, 2010, 24(8): 1358. DOI:10.1016/j.conbuildmat.2009.12.038 |
| [7] |
巫绪涛, 耿宁宁, 李和平. 动态SCB实验技术的数值模拟研究[J]. 应用力学学报, 2013(6): 899. WU Xutao, GENG Ningning, LI Heping. Numerical simulation of dynamic SCB testing[J]. Chinese Journal of Applied Mechanics, 2013(6): 899. DOI:10.11776/cjam.30.06.B005 |
| [8] |
喻勇. 质疑岩石巴西圆盘拉伸强度试验[J]. 岩石力学与工程学报, 2005, 24(7): 1150. YU Yong. Questioning the validity of the Brazilian test for determining tensile strength of rocks[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2005, 24(7): 1150. DOI:10.3321/j.issn:1000-6915.2005.07.011 |
| [9] |
KOLSKY H. Stress waves in solids[M]. UK: Clarendon Press, Oxford, 1953.
|
| [10] |
ZHOU Z, LI X, ZOU Y, et al. Dynamic Brazilian tests of granite under coupled static and dynamic loads[J]. Rock Mechanics & Rock Engineering, 2014, 47(2): 495. DOI:10.1007/s00603-013-0441-4 |
| [11] |
WANG Q Z, LI W, XIE H P. Dynamic split tensile test of flattened Brazilian disc of rock with SHPB setup[J]. Mechanics of Materials, 2009, 41(3): 252. DOI:10.1016/j.mechmat.2008.10.004 |
| [12] |
沈明荣, 陈建峰. 岩体力学[M]. 上海: 同济大学出版社, 2006. SHEN Mingrong, CHEN Jianfeng. Rock mechanics[M]. Shanghai: Tongji University Press, 2006. |
| [13] |
MUSKHELISHVILI N I. Some basic problems of the mathematical theory of elasticity[M]. Groningen-Holland: P Noordhoff Ltd, 1953.
|
| [14] |
布洛克.工程断裂力学基础[M].王克仁, 译.北京: 科学出版社, 1980 BROEK D. Elementary engineering fracture mechanics[M]. WANG Keren, trans. Beijing: Science Press, 1980 |
| [15] |
XIA K W, YAO W. Dynamic rock tests using split Hopkinson (Kolsky)bar system: A review[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2015, 7(1): 27. DOI:10.1016/j.jrmge.2014.07.008 |
| [16] |
YIN T, LI X, CAO W, et al. Effects ofthermal treatment on tensile strength of Laurentian granite using Brazilian test[J]. Rock Mechanics & Rock Engineering, 2015, 48(6): 2213. DOI:10.1007/s00603-015-0712-3 |
| [17] |
ZHOU Y X, XIA K, LI X B, et al. Suggested methods for determining the dynamic strength parameters and model-Ⅰ: Fracture toughness of rock materials[J]. International Journal of Rock Mechanics and Mining Science, 2012, 49: 105. DOI:10.1016/j.ijrmms.2011.10.004 |
| [18] |
宫凤强, 李夕兵. 巴西圆盘劈裂试验中拉伸模量的解析算法[J]. 岩石力学与工程学报, 2010, 29(5): 881. GONG Fengqiang, LI Xibing. Analytical algorithm to estimate tensile modulus in Brazilian disk splitting tests[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2010, 29(5): 881. |
| [19] |
MALVAR L J, ROSS C A. A review of strain rate effects for concrete in tension[J]. ACI Materials Journal, 1998, 95(6): 735. |
| [20] |
CHEN X, WU S, ZHOU J. Experimental study on dynamic tensile strength of cement mortar using split Hopkinson pressure bar technique[J]. Journal of Materials in Civil Engineering, 2014, 26(6): 150. DOI:10.1061/(ASCE)MT.1943-5533.0000926 |
| [21] |
LUO X, XU J. Dynamic splitting-tensile testing of highly fluidised geopolymer concrete[J]. Magazine of Concrete Research, 2013, 65(14): 837. DOI:10.1680/macr.12.00172 |
| [22] |
LOK T S, ZHAO P J, LU G. Using the split Hopkinson pressure bar to investigate the dynamic behaviour of SFRC[J]. Magazine of Concrete Research, 2003, 55(2): 183. DOI:10.1680/macr.2003.55.2.183 |
| [23] |
ROSSI P. Strain rate effects in concrete structures: The LCPC experience[J]. Materials & Structures, 1997, 30(1): 54. DOI:10.1007/BF02539277 |
| [24] |
RAGUENEAU F, GATUINGT F. Inelastic behavior modelling of concrete in low and high strain rate dynamics[J]. Computers & Structures, 2003, 81(12): 1287. DOI:10.1016/S0045-7949(03)00043-9 |
| [25] |
张磊.混凝土层裂强度的研究[D].合肥: 中国科学技术大学, 2006 ZHANG Lei. Study on spalling strength of concrete[D]. Heifei: University of Science and Technology of China, 2006 http://cdmd.cnki.com.cn/Article/CDMD-10358-2006102750.htm |
| [26] |
吴顺川, 张晓平, 刘洋. 基于颗粒元模拟的含软弱夹层类土质边坡变形破坏过程分析[J]. 岩土力学, 2008, 29(11): 2899. WU Shunchuan, ZHANG Xiaoping, LIU Yang. Analysis of failure process of similar soil slope with weak intercalated layer based on particle flow simulation[J]. Rock and Soil Mechanics, 2008, 29(11): 2899. DOI:10.3969/j.issn.1000-7598.2008.11.003 |
| [27] |
王震, 胡可, 赵阳. 考虑Cowper-Symonds黏塑性材料本构的向量式有限元三角形薄壳单元研究[J]. 建筑结构学报, 2014, 35(4): 71. WANG Zhen, HU Ke, ZHAO Yang. Study on triangular thin-shell element of vector form intrinsic finite element considering Cowper-Symonds viscoplastic constitutive model[J]. Journal of Building Structures, 2014, 35(4): 71. |
 2019, Vol. 51
2019, Vol. 51


