2. 中国建筑第七工程局有限公司,郑州 450004;
3. 中铁十一局集团第五工程有限公司,重庆 400037
2. China Construction Seventh Engineering Division Co., Ltd., Zhengzhou 450004, China;
3. The 5th Engineering Ltd. of the 11th Engineering Bureau of China Railway, Chongqing 400037, China
岩溶区发生的地震一般震级不大,且震源较浅,但烈度普遍较高,存在明显的“低震级,高烈度”现象.岩石在动力荷载的作用下,其破坏强度和弹性模量相较于静力荷载作用时都有所提高,且岩石的破坏特征与荷载的加载速率、频率、持续时间以及地震波形都有很大关系[1].研究表明,岩体中采空区的存在可以阻碍地震波的传递,起到一定的隔震效果[2].中国基础设施建设飞速发展,桥梁桩基作用于溶洞顶板的情况屡见不鲜,桩基作用下溶洞顶板最小安全厚度的研究也取得了丰富的成果[3-4],不少学者对岩溶区嵌岩桩承载性能的影响因素也进行了系统研究[5-6].近年来, 由于中国地震频发,振动台模型试验越来越得到重视,因其可模拟多维数振动状态下的反应状态,成为目前研究地震作用对结构破坏模式的有效手段.Kagawa等[7-10]采用分层剪切箱和Kasumingaura砂进行了砂土液化下的振动台桩-土作用模型试验,观察完全液化的砂土层对桩的力学特性,试验结果与数值分析结果基本吻合.Meymand[11]利用大型振动台,采用圆筒形模型箱,铝管为模型桩,高岭土、斑脱岩等混合物为模型土,研究了自由场、单桩、群桩模型在软黏土中桩-土上部结构的相互作用.冯士伦等[12]通过振动台模型相似试验,对饱和砂土中的桩基振动特性进行了研究,并且对砂土液化后距模型桩不同位置处的砂土动力p-y曲线和API推荐做法得到的静力p-y曲线进行了对比分析,指出了饱和砂土液化对模型桩的横向承载能力有降低作用.叶海林等[13]利用大型振动台输入3种不同的地震波,并不断加大地震波幅值,对桩后土压力、边坡坡面加速度和位移进行监测,研究了地震荷载作用下边坡抗滑桩的抗震性能.Lei Su等[14]通过振动台模型试验,探讨了中密和密实砂液化场地混凝土承台群桩和地基动力响应的差异.由上述研究可以看出,由于动力问题本身的复杂性和特殊性,现有岩溶区桩基稳定性的试验研究还只停留在静载阶段,而采用振动台试验开展地震动力荷载下的桩-土相互影响研究虽然成果较为丰富但没有考虑岩溶这一特殊地质.
针对以上问题,采用分离相似方法设计并制作岩溶桩基模型,利用室内小型振动台开展地震动力特性模型试验,对桩端荷载及地震共同作用下岩溶顶板的动力特性及破坏特征进行研究.
1 模型的分离相似设计与实施方案 1.1 分离相似设计概念及试验相似参数相似理论是进行缩尺模型试验的基础,对于大部分的模型试验来说,原型和模型之间的相似关系都是基于量纲分析法[15]和控制方程法建立的[16-19],但量纲分析法参数众多而不可能完全满足各部分的相似要求,控制方程法也不能区别同一方程中各参数对模型设计的重要程度.文献[20]结合以上问题提出了模型试验的分离相似设计办法,可分别对模型内部各种材料以及地震波进行相似设计,优先满足了关键参数的相似关系,并在此基础上尽可能地满足其他参数的相似要求.
本文试验中的模型包括桩、模型土、模型岩、地震波,其相关参数包括几何尺寸L、密度ρ、重力加速度g、正应力σ、应变ε、剪应力τ、剪切模量G、变形模量E、横截面积A、抗弯刚度EI、剪应变γ、阻尼比λ、剪切波速vs、动黏聚力c、动内摩擦角φ、力F、弯矩M、质量m、加速度a、位移u、时间t、频率ω.考虑到加载采用的WS-Z30-50型振动台系统,其振动台台面尺寸516 mm×380 mm(如图 1),因此,结合依托工程渝黔铁路复线周家湾大桥的实际情况,选定几何相似比CL作为一个主控因素,并明确CL=100;模型和原型同处于一个自重应力场,选定重力相似比Cg=1作为另一个主控因素,并在此基础上控制密度相似比Cρ的大小,以达到较好模拟试验自重应力场的目的.考虑到振动台面的实际承载能力有限,选定Cρ=1.2作为第3个主控参数[21].

|
图 1 振动台系统 Fig. 1 Shaking table system |
当几何尺寸相似比、密度相似比和重力加速度相似比作为主控因素确定之后,便可得到模型试验的一级特征方程:
| $ \begin{array}{l} f(L,\rho ,g/\tau ,\sigma ,E,I,A,G,\gamma ,\varepsilon ,\lambda ,{v_s},c,\varphi ,u,F,\\ M,m,a,t,\omega ). \end{array} $ | (1) |
方程自变量中,竖线之前的变量为控制参数,之后的变量为待确定参数,根据桩、模型土、模型岩、地震波各自的相关参数,可以将式(1)进行二次分离,求得二级特征方程:
| $ {{f'}_{{\rm{rock}}}}\left( {L,\rho ,g/\sigma ,\varepsilon ,\tau ,E,\gamma ,\lambda ,{v_s},c,\varphi ,u,F,m,a} \right) = 0, $ | (2) |
| $ {{f'}_{{\rm{pile}}}}\left( {L,\rho ,g/\sigma ,\varepsilon ,\tau ,EI,\gamma ,M} \right) = 0, $ | (3) |
| $ {{f'}_{{\rm{wave}}}}\left( {L,\rho ,g/a,t,\omega } \right) = 0. $ | (4) |
二级特征方程中给出了模型不同部分与之相关的参数,其中式(4)中几何尺寸、密度、重力加速度只作为推导地震波待确定参数的控制参数,对地震波本身没有影响.式(2)、(3)虽然给出了满足模型岩和模型桩的各自相关参数,但是同时满足二级特征方程推导得到的所有相似常数仍然比较困难.考虑到并非所有参数都对试验设计起到决定性的作用,且模型试验旨在通过模型某些关键部位的特性来精确预测原型的性质,有必要对其进行进一步的简化设计.对于模型试验整体而言,主要考虑重力场相似,因此,几何尺寸L、密度ρ、重力加速度g作为模型设计的控制参数;对于结构面相似材料模型岩的设计,选择莫尔-库伦模型准则可确定主要参数为结构面抗剪强度τ,黏聚力c,变形模量E,内摩擦角φ;对于模型桩的设计,主要考虑桩的抗弯,其主要参数为抗弯刚度EI,弯矩M.根据以上分析,模型试验以几何尺寸L、密度ρ、重力加速度g为控制参数,把对试验各部分起重要作用的参数从二级特征方程中分离出来,定义为主要参数,则可得出三级特征方程[21]:
| $ {{f''}_{{\rm{rock}}}}\left( {L,\rho ,g/\tau ,E,c,\varphi } \right) = 0, $ | (5) |
| $ {{f''}_{{\rm{pile}}}}\left( {L,\rho ,g/EI,M} \right) = 0, $ | (6) |
| $ {{f''}_{{\rm{wave}}}}\left( {L,\rho ,g/a,t,\omega } \right) = 0. $ | (7) |
由三级特征方程便可得到控制参数和各主要参数的相似常数,如表 1所示.
1.2 模型箱的设计及相似材料的配比考虑到振动台承载以及模型的可视性,本次试验采用中心对称模型进行设计,模型箱采用有机玻璃制作,根据振动台台面的大小及原型尺寸,确定箱子的内部几何尺寸为20 cm×24 cm×25 cm,利用提前打好孔的42 cm×36 cm×0.8 cm的有机玻璃板作为连接平台,配合振动台面预留的螺栓孔与振动台连接,如图 2所示.

|
图 2 模型制作 Fig. 2 Making process of the model |
由勘测资料可知,周家湾大桥所处区域地质结构复杂,桩基下部溶洞分布广泛且极为发育,其地层厚度为20~25 m,上部存在3.5 m深的红黏土,下部为白云质灰岩,桥位地区地震动峰值加速度小于0.05g,地震动反应谱特征周期为0.35 s.通过钻孔探测,桩基下部溶洞极为发育,分布复杂,溶洞层数多达5层,给施工造成很大麻烦.本次试验主要研究溶洞顶板岩层的动力特性,根据模型相似常数,可得岩质材料的相似关系如表 2所示.
根据表 2可对试验所需的模型岩质材料进行配比,配比试验选用铁精粉、重晶石粉、石英砂为骨料,松香酒精溶液为胶结剂,石膏为调节剂[22].采用正交试验方法设置4因素4水平共16组试验方案,通过称重、直剪仪和万能试验机对每组配比下的密度、黏聚力、内摩擦角以及变形模量进行反复测试,并分析每种材料对各参数大小的影响程度,在此次试验的基础上再进行3组二次细化试验,得到最佳配合比为:m(铁精粉)/m(重晶石粉)=0.4、m(石英砂)/m(重金石粉+铁精粉)=0.3、m(石膏)/ m(骨料)=0.02、m(松香)/m(松香+酒精)=0.24,且得到试验匹配参数如表 2所示.
1.3 边界的处理将模型箱用螺栓固定于振动台上,确保其整体稳定,箱体内部突出的螺帽在模型填充之后与其连为一个整体,可阻止模型的相对滑移.振动台试验过程中,地震波会在模型箱边界处发生反射,从而对试验的结果产生影响;与此同时,模型材料与箱体之间的摩擦力会使得模型岩土不能产生自由变形,因此,在试验开始之前必须对模型箱的边界进行处理,最大限度地减少边界效应的影响.
岩土工程振动台试验过程中,常见的边界处理方式有4种[23]:①内侧加聚苯乙烯泡沫板(适用于刚性模型箱);②内侧加橡胶膜(适用于层状剪切模型箱);③采用柔性容器;④采用黏滞液体人工阻尼边界.根据文献[21],图 2所示的有机玻璃模型箱属于刚性模型箱,因此,模型填充时在其长边方向(即振动方向)放置了1 cm厚的聚苯乙烯泡沫板,防止震动过程中地震波的反射;而在箱子另两侧与模型岩土直接接触的有机玻璃面上涂抹凡士林,减少两者间的摩擦.
2 振动台模型试验过程 2.1 传感器的选取及布置试验主要通过加速度计和应变片分别对模型各测点的加速度值和溶洞顶板的应变情况进行测试.以顶板厚度2倍桩径、溶洞直径为4倍桩径为例,加速度计和应变片的布置如图 3,4所示.
|
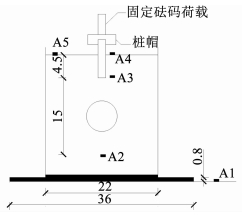
图 3 加速度计的布置(cm) Fig. 3 Placement of accelerometer(cm) |
|
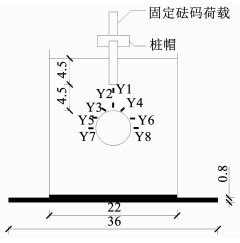
图 4 应变片的布置(cm) Fig. 4 Placement of strain gauge(cm) |
1) 加速度计的布置.其中A2~A4沿溶洞中轴线从下而上布置(其间隔与溶洞的大小有关),用于测试不同高程加速度的变化规律,同时观察溶洞对地震波的影响,A5与A4均设置于模型表面,且A5距离A4较远,主要用于对比下部有无溶洞对地震波传递的影响,台面上A1主要是检测模型的振动加速度与地震波的激励加速度是否一致,用以判断试验的有效性.
2) 应变片的布置.模型试验的重点在于测试岩溶顶板的动力特性与破坏特征,因此,应变片主要布置于岩溶顶板,待预置溶洞干燥后进行.由于应变片体积较小,粘贴较为不易,在粘贴之前采用环氧树脂对模型表面进行处理.
2.2 地震波的选取及加载工况模型试验在选择地震波时,主要考虑地震强度、地震动频谱特性和地震持续时间3个主要因素.为了尽可能全面且真实地反映地震作用下岩溶桩基的破坏以及便于比较,本次试验选取了常用的EL-Centro波、汶川波以及人工地震波,并采用水平单向输入,每组试验前后输入白噪声激振.
根据《建筑抗震设计规范》(GB50011—2001)规定的抗震设防烈度和设计基本地震加速度取值的对应关系[24],试验先进行0.05g地震波的加载,之后依次进行0.1g、0.2g、0.3g的地震波加载.具体加载工况如表 3.
| 表 3 模型试验加载工况 Tab. 3 Loading conditions of model tests |
动载模型试验是在静载试验的基础上,先确定每种工况下的允许荷载强度值(试验取桩基静载试验过程中沉降0.5 mm时所对应的荷载值),之后依照静载试验步骤对模型进行荷载,达到该工况允许荷载强度值时停止加载.待模型稳定之后,依据表 3开始依次施加地震波,随着地震波加速度幅值的增大对所有测点进行动力数据监测,并观察溶洞顶板的渐进破坏特征.
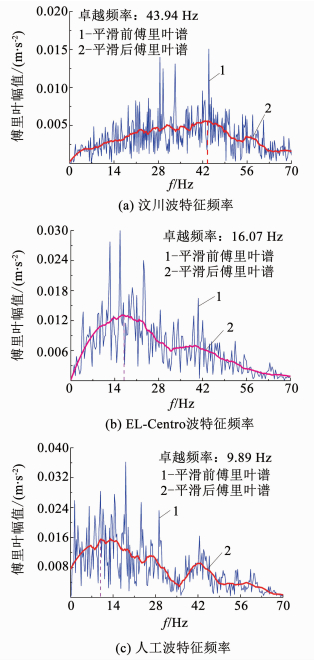
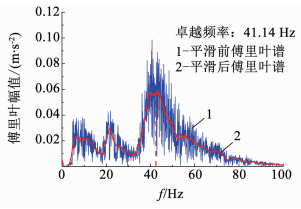
3 地震动力特性测试结果分析 3.1 不同测点频域特征分析试验进行了不同顶板厚度及溶洞尺寸下的多组模型测试,以0.3g汶川波作用下的“顶板厚度为2倍桩径,溶洞大小为4倍桩径”模型为例,由图 5可知,汶川波的主频为43.94 Hz,EL-Centro波的主频为16.07 Hz,人工波的主频为9.89 Hz.图 6给出了0.3g白噪声作用下模型A2测点频率41.14 Hz时振幅达到峰值,可知模型的基频在41 Hz左右.以下主要对模型A2~A5测点采集数据进行傅里叶变换,并采用传递函数方法,分析不同位置频谱的变化规律.
|
图 5 地震波特征频率 Fig. 5 Characteristic frequency of different seismic waves |
|
图 6 0.3g加速度白噪声 Fig. 6 White noise of 0.3g acceleration |
采用SeismoSignal软件对A2~A5测点的采集数据进行滤波处理,排除干扰因素,之后对其进行傅里叶变换,并分析曲线的变化规律,如图 7所示.1)A2~A5各测点在41 Hz附近的频谱幅值明显增大,说明地震波与模型产生了共振,使得该频率成分被明显放大.2)A2和A3测点的傅里叶变换图在形状上有了一些变化,整体幅值有微弱下降,溶洞的存在对地震波的向上传递起到了阻碍作用;处于地表的A4和A5测点幅值明显比有一定埋深的A2和A3要大,说明地震传播频谱幅值随着埋深的减小而增大,传至地表时达到极大值;A4和A5傅里叶变换图在形状上没有明显的区别,A4的幅值比A5偏小,说明溶洞的存在对波的能量传递有一定的消散作用,此外,溶洞顶板在桩端荷载和地震共同作用下产生的裂隙,也会造成其整体幅值的下降.3)当地震波穿过溶洞之后,20 Hz附近的频率有小幅上升,说明溶洞的存在对局部的基频也会产生影响.

|
图 7 0.3g加速度条件下A2~A5测点的加速度傅里叶变换图 Fig. 7 Acceleration Fourier transform of A2-A5 under 0.3g acceleration |
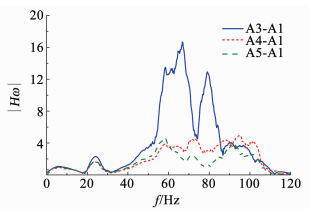
A3、A4、A5对输入波A1的传递函数频响幅值谱如图 8所示.由A3A1可知,地震波通过溶洞后,60 Hz左右的频率传递影响较明显,而A4、A5点各频率成分基本保持不变.
|
图 8 传递函数曲线 Fig. 8 Transfer function curve |
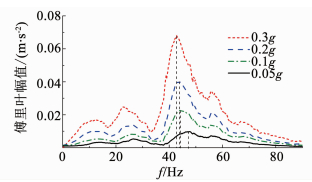
为了研究地震强度对模型结构频谱的影响,选用不同加速度大小的汶川波作用下,A2~A5测点采集数据的加速度傅里叶频谱进行比较分析,图 9~12所示为A2~A5测点在0.05g,0.1g,0.2g,0.3g汶川波作用下的傅里叶变换图,对比分析可知:
|
图 9 汶川波不同幅值作用下A2点的傅里叶变换图 Fig. 9 Fourier transform of A2 with different amplitude of Wenchuan wave |
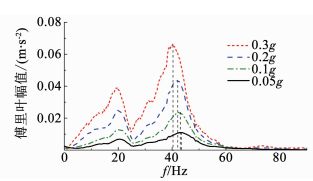
|
图 10 汶川波不同幅值作用下A3点的傅里叶变换图 Fig. 10 Fourier transform of A3 with different amplitudes of Wenchuan wave |
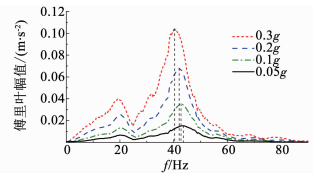
|
图 11 汶川波不同幅值作用下A4点的傅里叶变换图 Fig. 11 Fourier transform of A4 with different amplitudes of Wenchuan wave |
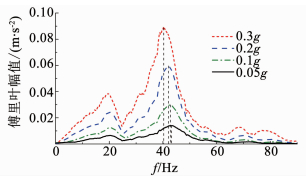
|
图 12 汶川波不同幅值作用下A5点的傅里叶变换图 Fig. 12 Fourier transform of A5 with different amplitudes of Wenchuan wave |
1) 随着地震波加速度幅值的增大,各测点的频谱图形、频谱成分未发生变化,仅幅值随着加速度的增大而增大.此外,模型的主频会随着加速度的增加而产生小幅的下降,原因有两个方面:①随着振动幅度的不断增大,模型整体出现松动,内部岩体的动剪切强度和动剪切模量随之下降,模型岩体内部裂纹增多,使得其主频随之降低;②随着振动的继续,地震波的能量不断被消耗,模型的阻尼比逐渐增大,同样会造成频率的降低.
2) 测点A4和A5之间的频谱没有发生变化,只是幅值略有不同,同样说明溶洞对波传递能量的消耗作用.但A2与A3之间的差异不仅体现在幅值上,频谱的成分也有了变化,20 Hz附近的频率有了小幅度的增长,且在A4~A5上也有体现,说明溶洞的存在对模型局部基频产生了影响,且该部分的基频在20 Hz左右;此外,在上部桩基荷载的作用下,溶洞顶板产生的细微裂纹随着时间的增长进一步扩大,导致模型应力集中区的剪切强度降低,基频也随之减小.
3.3 地震动特征频率的影响分析不同地震波对应的特征频率有所区别,对模型结构的频谱特性也存在不同的影响.因此,以顶板厚度2倍桩径、溶洞大小4倍桩径的模型为例,选用EL-Cenrto波、人工波、汶川波在0.3g加速度的作用下A2、A3和A4处的加速度傅里叶变换频谱图进行对比分析.由图 13~15可知,模型底部、溶洞顶板以及模型表面的加速度频谱曲线相比,同种波之间仅幅值差别较大,其他方面没有明显区别.如图 14所示,3种地震波在穿过溶洞之前,其第一主频均在41 Hz左右,与模型基频保持一致;当地震波穿过溶洞之后,其第一主频的位置就发生了变化,其中汶川波的第一主频仍为41 Hz,而EL波和人工波的第一主频的位置则处于10~15 Hz,与两种地震波自身的频率比较接近.结合上文可知溶洞附近的基频为20 Hz,地震波穿过溶洞之后,20 Hz左右的频率得以放大,在EL波和人工波作用下,该处发生共振效应,图 15同样证明了这一结论,也说明了不同种地震波之间频谱分布的差别与波本身的频率有关.
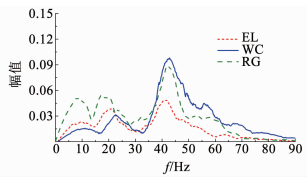
|
图 13 不同地震波作用下A2点采集波傅里叶变换图 Fig. 13 Fourier transform of collection waves of A2 with different seismic waves |
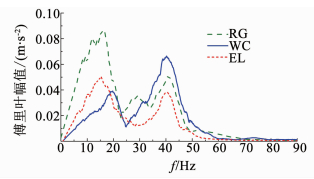
|
图 14 不同地震波作用下A3点采集波傅里叶变换图 Fig. 14 Fourier transform of collection waves of A3 with different seismic waves |
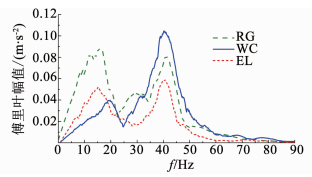
|
图 15 不同地震波作用下A4点采集波傅里叶变换图 Fig. 15 Fourier transform of collection waves of A4 with different seismic waves |
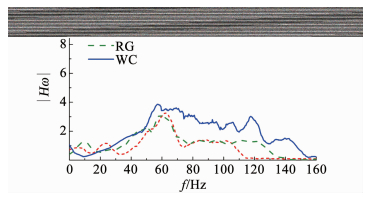
不同地震波作用下测点A4~A1的传递函数图如图 16所示.从模型底部到模型表面,不同波的传递函数之间没有明显差异,在60 Hz频段传递效果较好,增益较大,说明波的传递与模型结构本身有很大关系,与地震波本身无关.
|
图 16 不同地震波作用下A4-A1的传递函数图 Fig. 16 Transfer function of A1 to A4 under different seismic waves |
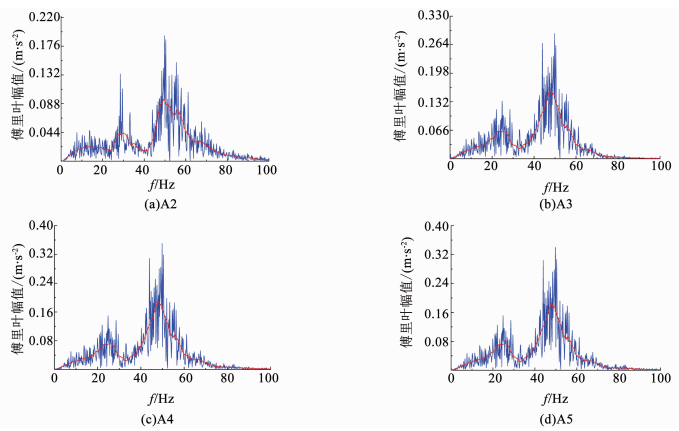
为分析溶洞顶板在地震作用下,桩端荷载对顶板动力特性的影响程度,可对相同模型在无外荷载时输入相同地震波,然后对测点采集数据进行傅里叶变换,结果如图 17所示.该图显示了顶板厚度2倍桩径、溶洞大小4倍桩径模型在0.3g加速度条件下,A2、A3、A4和A5测点数据的傅里叶变换,红色部分为趋势线.可以看出,A3~A5的傅里叶变换结果主要体现在幅值上,说明频谱的变化与上部荷载关系不大.而A3与A2对比,其频谱曲线形状存在较大差异,特别是在20 Hz处A3测点的幅值有较大提升,同样说明溶洞的存在对局部基频产生了影响,顶板的破坏也引起了基频的变化.
|
图 17 无荷载模型在0.3g加速度条件下A2-A5测点的采集数据傅里叶变换图 Fig. 17 Fourier transform results of the vibration wave of A2-A5 in the unload model under 0.3g acceleration |
针对性地对溶洞顶板、溶洞两侧及侧上方位置粘贴应变片,测试其应变大小变化.试验开始前,将周边土体对应变片的影响清零,以满足试验精度要求.由图 4可知,应变片的粘贴为对称分布,因此,以Y1、Y2、Y3、Y5、Y7 5个测点为基准,以不同加速度汶川波作用下的模型测点数据为例进行分析,如图 18所示.同时对比0.05g加速度条件不同地震波对模型应变的影响情况,如图 19所示.

|
图 18 汶川波作用下测点应力峰值 Fig. 18 Peak stress of measuring point under Wenchuan waves |
|
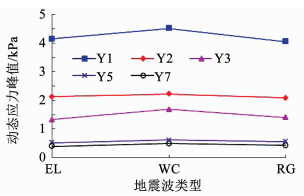
图 19 地震波在0.05g加速度下各测点应力峰值 Fig. 19 Peak stress of measuring points with 0.05g acceleration seismic wave |
各测点的应变均随着地震峰值的增加而增大,变化规律十分相似,受地震烈度大小的影响很明显.溶洞正上方的岩体,应变值较大,离桩越近应变越大,说明应力集中越显著.分析相同加速度下不同地震波作用的应力峰值曲线可知,汶川波较另外两种波的应力峰值都大,可见由于汶川波基频与模型基频相近,模型振动相对较大.
4 模型的破坏形态分析图 20, 21给出了顶板厚度为2倍桩径、溶洞直径分别为2倍和4倍桩径的模型在地震波作用下的渐进性破坏结果.地震波施加之前的静载阶段,溶洞顶板逐渐被上部荷载压密,出现应力集中区,该区域与周围岩体出现明显的差异;随着地震波的施加与加速度峰值的加大,溶洞正上方顶板开始出现竖向和环向裂纹,并逐渐相交、贯通,如图 20(a)所示;当地震波进一步加大,裂纹逐渐发展为裂缝,顶板发生显著的剪切错动并最终脱落,模型最终发生剪切破坏,如图 20(b)所示.
|
图 20 溶洞直径为2d时地震波作用下2d厚度的顶板破坏形态 Fig. 20 Failure mode of the roof with 2d thickness under the seismic waves action when the karst cave is 2d in diameter |
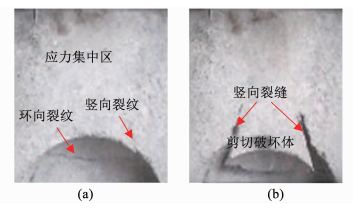
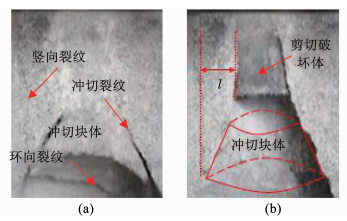
由图 21可知,当溶洞直径增大至4倍桩径时,在上部荷载和地震波的共同作用下,溶洞顶板出现冲切和竖向裂缝,其中冲切裂缝角度与水平方向呈45°左右.而竖向裂缝与桩之间的距离L为0.5倍桩径左右,如图 21(a)所示,该条竖向裂缝是地震初期桩体嵌固作用使桩-岩形成咬合整体的结果.随着地震波的增强,溶洞顶板破坏加剧,左右两侧冲切裂缝不断增大,而竖向裂缝则基本保持不变,最终出现如图 21(b)所示的冲切破坏体.
|
图 21 溶洞直径为4d时地震波作用下2d厚度的顶板破坏形态 Fig. 21 Failure mode of the roof with 2d thickness under the seismic waves action when the karst cave is 4d in diameter |
1) 基于分离相似设计方法,得出了岩质材料的主要参数为结构面抗剪强度τ、黏聚力c、变形模量E、内摩擦角φ;模型桩的主要参数为抗弯刚度EI、弯矩M;地震波的主要参数为加速度a、时间t、频率ω.通过19组配比试验最终得到振动台试验用的岩体相似模型材料成分配比,参数匹配效果较好.
2) 地震波通过溶洞之后,部分波段产生较大增益,随着波在岩土体中继续传递,各频率成分基本保持不变,趋于稳定状态.而不经过溶洞部分的地震波,振动频率成分保持稳定.溶洞的存在对地震波的传递起到了阻碍及能量消散作用,对模型局部的基频也产生了影响.此外,波的频谱变化与上部荷载大小无直接关系,而溶洞顶板在桩端荷载和地震的共同作用下产生的桩端裂隙,造成了地震波整体幅值的下降,引起了模型基频的变化.
3) 随着地震波加速度的增大,测点的频谱形状和频谱成分不变,但振动幅值增大;随着振动的增强,模型内部出现松动,岩体的动剪切强度和动剪切模量随之下降,内部裂纹不断地增多使其阻尼比逐渐增大,地震波传播过程中的能量不断被消耗,导致其主频随之下降.不同地震波作用下,与模型主频相近的波段频率有所提高,对模型结构的频谱特性产生不同程度的影响,主频与模型相近的汶川波,其破坏效果最为明显;分析溶洞底部、顶板以及地表的加速度频谱曲线,表明相同类型地震波之间仅幅值有所差别,而不同类型地震波之间的频谱分布差异较大,且仅与波本身的频率相关.
4) 各测点的应变均随着地震峰值的增加而增大,受地震烈度大小的影响明显,溶洞正上方的岩体应力集中显著,离桩越近应变越大.地震荷载的作用下,溶洞直径较小时,顶板临空面处发生剪切破坏;当溶洞直径较大,临空面处易发生冲切破坏,并同时驱动桩端处岩体的剪切失稳,整体表现为冲-剪破坏.
| [1] |
梁庆国, 韩文峰, 谌文武, 等. 岩体地震动力破坏问题研究[J]. 岩石力学与工程学报, 2003, 22(s2): 2783. LIANG Qingguo, HAN Wenfeng, CHEN Wenwu, et al. Discussion on rock mass failure under seismic load[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(s2): 2783. DOI:10.3321/j.issn:1000-6915.2003.z2.052 |
| [2] |
刘书贤, 王春丽, 魏晓刚, 等. 煤矿采空区的地震动力响应及其对地表的影响[J]. 地震研究, 2014, 37(4): 642. LIU Shuxian, WANG Chunli, WEI Xiaogang, et al. Analysis on seismic dynamic response of coal mine gob area and its influence on ground surface[J]. Journal of Seismological Research, 2014, 37(4): 642. DOI:10.3969/j.issn.1000-0666.2014.04.023 |
| [3] |
赵明华, 雷勇, 张锐. 岩溶区桩基冲切破坏模式及安全厚度研究[J]. 岩土力学, 2012, 33(2): 524. ZHAO Minghua, LEI Yong, ZHANG Rui. Study of punching failure mode and safe thickness of pile foundation in karst region[J]. Rock and Soil Mechanics, 2012, 33(2): 524. DOI:10.3969/j.issn.1000-7598.2012.02.032 |
| [4] |
柏华军. 考虑溶洞顶板自重时桩端持力岩层安全厚度计算方法[J]. 岩土力学, 2016(10): 2945. BAI Huajun. A method for calculating the safety rock thickness of pile bearing strata with considering deadweight of karst cave roof[J]. Rock and Soil Mechanics, 2016(10): 2945. DOI:10.16285/j.rsm.2016.10.028 |
| [5] |
张慧乐, 马凛, 张智浩, 等. 岩溶区嵌岩桩承载特性影响因素试验研究[J]. 岩土力学, 2013, 34(1): 92. ZHANG Huile, MA Lin, ZHANG Zhihao, et al. Test research on factors influencing bearing capacity of rock-socketed piles in karst area[J]. Rock and Soil Mechanics, 2013, 34(1): 92. DOI:10.16285/j.rsm.2013.01.042 |
| [6] |
张智浩, 张慧乐, 马凛, 等. 岩溶区嵌岩桩的破坏模式与工程设计探讨[J]. 岩石力学与工程学报, 2013, 32(s2): 4130. ZHANG Zhihao, ZHANG Huile, MA Lin, et al. Discussion on failure mode and engineering design of rock-socketed pile in karst area[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(s2): 4130. |
| [7] |
SATO M. A new dynamic geotechnical centrifuge and performance of shaking table tests[C]//Proc Int Conf on Centrifuge. Rotterdam, 1994: 157
|
| [8] |
KAGAWA T, SATO M, MINOWA C, et al. Centrifuge simulations of large-scale shaking table tests: Case studies[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2004, 130(7): 663. DOI:10.1061/(ASCE)1090-0241(2004)130:7(663) |
| [9] |
KAGAWA T. Dynamic model testing in geotechnical engineering[C]//Proc 1st Int Conf on Geotechnical Earthquake Engineering. Tokyo, 1995: 1435
|
| [10] |
KAGAWA T, MINOWA C, ABE A, et al. Shaking-table tests on and analyses of piles in liquefying sands[C]//Earthquake Geotechnical Engineering: Proceedings of the First International Conference. IS-Tokyo, 1995: 699
|
| [11] |
MEYMAND P J. Shaking table scale model tests of nonlinear soil-pile-superstructure interaction in soft clay[D]. Berkeley: University of California, 1998
|
| [12] |
冯士伦, 王建华, 郭金童. 液化土层中桩基抗震性能振动台试验研究[J]. 土木工程学报, 2005, 38(7): 92. FENG Shilun, WANG Jianhua, GUO Jintong. A shake table test on the seismic resistance of pile foundation in liquefied soil[J]. China Civil Engineering Journal, 2005, 38(7): 92. DOI:10.3321/j.issn:1000-131X.2005.07.018 |
| [13] |
叶海林, 郑颖人, 李安洪, 等. 地震作用下边坡抗滑桩振动台试验研究[J]. 岩土工程学报, 2012, 34(2): 251. YE Hailin, ZHENG Yingren, LI Anhong, et al. Shaking table tests on stabilizing piles of slopes under earthquakes[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(2): 251. |
| [14] |
SU L, TANG L, LING X, et al. Responses of reinforced concrete pile group in two-layered liquefied soils: Shake-table investigations[J]. Journal of Zhejiang University-Science A (Applied Physics & Engineering), 2015, 16(2): 93. DOI:10.1631/jzus.A1400093 |
| [15] |
KANA D D, BOYCE L, BLANEY G W. Development of a scale model for the dynamic interaction of a pile in clay[J]. Journal of Energy Resources Technology, 1986, 108(3): 254. DOI:10.1115/1.3231274 |
| [16] |
LAI S. Similitude for shaking table tests on soil-structure-fluid model in 1g gravitational field[J]. Soils and Foundations, 1989, 29(1): 105. DOI:10.3208/sandf1972.29.105 |
| [17] |
BATHURST R J, ZARNANI S, GASKIN A. Shaking table testing of geofoam seismic buffers[J]. Soil Dynamics and Earthquake Engineering, 2007, 27(4): 324. DOI:10.1016/j.soildyn.2006.08.003 |
| [18] |
LIN M L, WANG K L. Seismic slope behavior in a large-scale shaking table model test[J]. Engineering Geology, 2006, 86(2): 118. DOI:10.1016/j.enggeo.2006.02.011 |
| [19] |
林皋, 朱彤, 林蓓. 结构动力模型试验的相似技巧[J]. 大连理工大学学报, 2000, 40(1): 1. LIN Gao, ZHU Tong, LIN Bei. Similarity technique for dynamic structural model test[J]. Journal of Dalian University of Technology, 2000, 40(1): 1. DOI:10.3321/j.issn:1000-8608.2000.01.001 |
| [20] |
王志佳, 张建经, 付晓, 等. 模型试验的分离相似设计方法--以锚索格构加固边坡模型试验为例[J]. 岩土力学, 2016(9): 2617. WANG Zhijia, ZHANG Jianjing, FU Xiao, et al. Isolated similar design method for a scaled model test and its application to slope-anchor cable-lattice beam system[J]. Rock and Soil Mechanics, 2016(9): 2617. DOI:10.16285/j.rsm.2016.09.025 |
| [21] |
黄明, 付俊杰, 陈福全, 等. 桩端荷载与地震耦合作用下溶洞顶板的破坏特征及安全厚度计算[J]. 岩土力学, 2017, 38(11): 3154. HUANG Ming, FU Junjie, CHEN Fuquan, et al. Damage characteristics of karst cave roof and its safety thickness calculation under the coupling effect of pile-tip load and seismic wave[J]. Rock and Soil Mechanics, 2017, 38(11): 3154. DOI:10.16285/j.rsm.2017.11010 |
| [22] |
江松, 黄明, 付俊杰, 等. 岩溶桩基振动台试验中岩体相似材料的配比研究[J]. 工程地质学报, 2017, 25(3): 671. JIANG Song, HUANG Ming, FU Junjie, et al. Experiment study on similarity ratio of similar material of rock mass for shaking table test of pile in karst region[J]. Journal of Engineering Geology, 2017, 25(3): 671. DOI:10.13544/j.cnki.jeg.2017.03.012 |
| [23] |
刘晓敏, 盛谦, 陈健, 等. 大型地下洞室群地震模拟振动台试验研究(Ⅱ):试验方案设计[J]. 岩土力学, 2015, 36(6): 1683. LIU Xiaomin, SHENG Qian, CHEN Jian, et al. Seismic shaking table test for large-scale underground cavern group(Ⅱ): Test scheme[J]. Rock and Soil Mechanics, 2015, 36(6): 1683. DOI:10.16285/j.rsm.2015.06.021 |
| [24] |
中华人民共和国住房和城乡建设部. GB 50011-2010建筑抗震设计规范[S].北京: 中国建筑工业出版社, 2010
|
 2019, Vol. 51
2019, Vol. 51


