2. 城市与工程安全减灾省部共建教育部重点实验室 (北京工业大学),北京 100124;
3. 上海大学 土木工程系,上海 200072
2. Key Laboratory of Urban Security and Disaster Engineering (Beijing University of Technology), Beijing 100124, China;
3. Department of Civil Engineering, Shanghai University, Shanghai 200072, China
桩基纵向振动特性研究作为岩土工程和固体力学的热点问题[1-3],对桩基抗震、防震设计及动力测桩技术发展具有重要的理论意义和实际应用价值.桩基施工会引起桩周土体产生挤土、松弛现象,即径向非均质效应[4-5],基于此,诸多国内外学者做了较多相关研究.Novak等[6-7]考虑桩周土体单层内部扰动,基于滞回阻尼平面应变模型推导了存在单层软化区域土体的桩基纵向、扭转动力阻抗解析解答,并就桩周土体非均质性对桩-土耦合振动特性的影响规律进行了初步分析.Nogami等[8-9]基于平面应变模型考虑远场区域土体作用,近场区域土体则采用非线性Winkler模型,并将两者作用相互串联考虑桩周土体径向非均质性,对径向非均质桩周土中桩基纵向振动特性进行分析.进一步地,EI Naggar[10]将桩周围土体沿径向分为内部扰动区和外部未扰动区,内部区域划分为多个同心圆,首先计算各圈层的复刚度,并将其串联以考虑桩周土的径向非均质特性,分析了径向多圈层土中桩基纵向振动特性.王奎华和杨冬英等[11-12]研究发现EI Naggar所提出的模型在理论上不严谨,计算结果与实测结果存在较大误差.在此基础上,Wang和Yang等[13-14]基于径向复刚度传递,土体材料阻尼采用滞回阻尼模型,提出了多圈层平面应变模型,建立了能更为合理地考虑施工扰动引起的桩周土径向非均质效应的桩-土耦合纵向振动简化力学模型,并对桩顶动力阻抗影响因素进行参数化分析.
以上研究均对象均为实体桩,而针对大直径管桩的相关研究较为少见.刘汉龙等[15]基于径向不变假定,不考虑桩周土体作用探讨了管桩桩顶动力响应及平截面假定的影响深度问题.在此基础上,丁选明等[16]以Winkler模型模拟桩周土和桩芯土作用,祛除“径向不变假定”,建立了任意段变阻抗薄壁管桩动力响应波动方程,分析了变截面桩和变模量的动力响应特性.进一步地,丁选明等[17]基于平面应变模型, 土体阻尼采用黏性阻尼,推导出了均质土中管桩动力响应的频域解析表达式.郑长杰等[18]则基于三维轴对称模型,考虑土体材料的滞回阻尼和桩周土-桩-桩芯土耦合振动,对均质黏弹性地基中现浇大直径管桩纵向振动频域特性进行理论研究.Zheng等[19]基于三维轴对称模型同时考虑土体纵向位移和径向位移,土体材料阻尼选用滞回阻尼模型,求解了均质地基中管桩纵向振动频域解析解.吴文兵等[20]基于平面应变模型,土体材料阻尼采用滞回阻尼,桩底支承采用虚土桩模型,以附加质量考虑土塞,研究了均质地基中土塞效应对管桩纵向振动特性的影响.刘林超等[21]将桩周土、桩芯土和管桩视为一个整体,不考虑径向位移和环向位移,基于三维轴对称模型,利用桩-土接触面的连续条件得到均质土中管桩纵向振动解析解.管桩在施工过程中同样会扰动桩周土体,因此,Li等[22]考虑土体双向成层特性,土体材料阻尼采用滞回阻尼模型,解析求解了复杂非均质土中管桩纵向振动特性.
综上,考虑桩周土体施工扰动影响的成果多针对实体桩展开,且土体材料阻尼均采用滞回阻尼模型.瞬态激振作用下土阻尼力与应变速率相关,土体滞回阻尼模型会引起概念上的矛盾,此时应用黏性阻尼模型则较合理[23-28].基于此点考虑,本文基于黏性阻尼模型考虑土体材料阻尼,考虑施工扰动引起的桩周土体径向非均质性,利用多圈层径向复刚度传递,研究考虑施工扰动效应的管桩纵向振动特性.
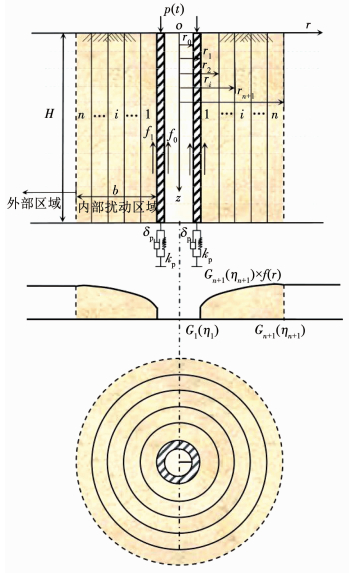
1 定解问题力学模型建立 1.1 计算简图基于平面应变模型,对任意激振下黏弹性支承管桩-径向多圈层土体纵向耦合振动特性进行研究,力学简化模型如图 1所示.桩顶作用任意激振力p(t),桩芯土和桩周土对桩身产生的切应力分别为f0和f1,桩长、内半径、外半径、桩身密度、弹性模量和桩底黏弹性支承常数分别为H、r0、r1、ρp、Ep和δp、kp,桩周第i圈层土的密度、剪切模量、黏性阻尼系数分别为ρi、Gi、ηi,桩芯土的密度、剪切模量、黏性阻尼系数分别为ρ0、G0、η0.
|
图 1 桩土系统纵向耦合振动力学简化模型 Fig. 1 Simplified model of vertical vibration of pile-soil system |
基本假定如下:
1) 桩周土和桩芯土为一系列相互独立的薄层,忽略土层间相互作用;
2) 桩周土体分为内部区域和外部区域,内部区域划分任意圈层,各圈层土体均质,土体材料阻尼采用黏性阻尼模型;
3) 各圈层土界面两侧位移连续、应力平衡,且桩土系统振动为小变形,桩土界面完全接触,无脱开和滑移[29];
4) 桩身混凝土为线弹性,应力波在桩身中的传播满足平截面假定.
1.2 多圈层参数确定假设内部区域径向厚度为b,内外部区域界面处的半径为rn+1,内部区域第j圈层土体的剪切模量和黏性阻尼系数Gi、ηi根据该圈层内边界半径ri,按式(1)和式(2)确定:
| $ G\left( r \right) = \left\{ \begin{array}{l} {G_1} \to r = {r_1},\\ {G_{n + 1}}f\left( r \right) \to {r_1} < r < {r_{n + 1}},\\ {G_{n + 1}} \to r \ge {r_{n + 1}}, \end{array} \right. $ | (1) |
| $ \eta \left( r \right) = \left\{ \begin{array}{l} {\eta _1} \to r = {r_1},\\ {\eta _{n + 1}}f\left( r \right) \to {r_1} < r < {r_{n + 1}},\\ {\eta _{n + 1}} \to r \ge {r_{n + 1}}, \end{array} \right. $ | (2) |
式中:G1、η1、Gn+1、ηn+1分别为桩土、内外区域界面处土体剪切模量、黏性阻尼系数,f(r)参照文献[20]采用二次函数描述桩周土内部区域土体性质变化.
1.3 定解问题设桩周第i圈层土体位移为ui(r,t),桩芯土体位移为u0(r,t),本文工程背景基于现浇大直径管桩,因此,桩芯土为满布.平面应变条件下桩周、桩芯土体振动方程如下:
桩周土体
| $ \begin{array}{*{20}{c}} {{G_i}\frac{{{\partial ^2}{u_i}\left( {r,t} \right)}}{{\partial {r^2}}} + {\eta _i}\frac{{{\partial ^3}{u_i}\left( {r,t} \right)}}{{\partial t\partial {r^2}}} + \frac{{{G_i}}}{r}\frac{{\partial {u_i}\left( {r,t} \right)}}{{\partial r}} + }\\ {\frac{{{\eta _i}}}{r}\frac{{{\partial ^2}{u_i}\left( {r,t} \right)}}{{\partial t\partial r}} = {\rho _i}\frac{{{\partial ^2}{u_i}\left( {r,t} \right)}}{{\partial {t^2}}}.} \end{array} $ | (3) |
桩芯土体
| $ \begin{array}{*{20}{c}} {{G_0}\frac{{{\partial ^2}{u_0}\left( {r,t} \right)}}{{\partial {r^2}}} + {\eta _0}\frac{{{\partial ^3}{u_0}\left( {r,t} \right)}}{{\partial t\partial {r^2}}} + \frac{{{G_0}}}{r}\frac{{\partial {u_0}\left( {r,t} \right)}}{{\partial r}} + }\\ {\frac{{{\eta _0}}}{r}\frac{{{\partial ^2}{u_0}\left( {r,t} \right)}}{{\partial t\partial r}} = {\rho _0}\frac{{{\partial ^2}{u_0}\left( {r,t} \right)}}{{\partial {t^2}}}.} \end{array} $ | (4) |
设桩身位移为up(z,t),则符合平截面假定的桩身纵向振动基本方程为
| $ \frac{{{\partial ^2}{u_{\rm{p}}}\left( {z,t} \right)}}{{\partial {z^2}}} - \frac{{2{\rm{ \mathit{ π} }}{r_0}{f_0}}}{{{E_{\rm{p}}}{A_{\rm{p}}}}} - \frac{{2{\rm{ \mathit{ π} }}{r_1}{f_1}}}{{{E_{\rm{p}}}{A_{\rm{p}}}}} = \frac{{{\rho _{\rm{p}}}}}{{{E_{\rm{p}}}}}\frac{{{\partial ^2}{u_{\rm{p}}}\left( {z,t} \right)}}{{\partial {t^2}}}. $ | (5) |
边界条件
1) 桩芯土
当r=0时,位移为有限值,即
| $ \mathop {\lim }\limits_{r \to 0} {u_0}\left( {r,t} \right) = 有限值. $ | (6) |
桩芯土与桩位移及力连续条件
| $ {u_0}\left( {{r_0},t} \right) = {u_{\rm{p}}}\left( {{r_0},t} \right), $ | (7) |
| $ {f_0} = {\tau _0}\left( r \right)\left| {_{r = {r_0}}} \right.. $ | (8) |
其中剪应力顺时针为正.
2) 桩周土
当r=∞时,位移为零,即
| $ \mathop {\lim }\limits_{r \to \infty } {u_{n + 1}}\left( {r,t} \right) = 0. $ | (9) |
式中un+1(r, t)代表外部区域土体位移.
桩周土与桩位移及力连续条件
| $ {u_1}\left( {{r_1},t} \right) = {u_{\rm{p}}}\left( {{r_1},t} \right), $ | (10) |
| $ {f_1} = - {\tau _1}\left( r \right)\left| {_{r = {r_1}}} \right.. $ | (11) |
3) 桩身
桩顶作用力为p(t),即
| $ {E_{\rm{p}}}{A_{\rm{p}}}\frac{{\partial {u_{\rm{p}}}\left( {z,t} \right)}}{{\partial z}}\left| {_{z = 0}} \right. = p\left( t \right). $ | (12) |
桩端处边界条件
| $ {E_{\rm{p}}}\frac{{\partial {u_{\rm{p}}}\left( {z,t} \right)}}{{\partial z}}\left| {_{z = H}} \right. = - \left( {{k_{\rm{p}}}{u_{\rm{p}}}\left( {z,t} \right) + {\delta _{\rm{p}}}\frac{{\partial {u_{\rm{p}}}\left( {z,t} \right)}}{{\partial t}}} \right). $ | (13) |
对方程(3)进行Laplace变换得
| $ \begin{array}{*{20}{c}} {{G_i}\frac{{{\partial ^2}{U_i}\left( {r,s} \right)}}{{\partial {r^2}}} + {\eta _i}s\frac{{{\partial ^2}{U_i}\left( {r,s} \right)}}{{\partial {r^2}}} + \frac{{{G_i}}}{r}\frac{{\partial {U_i}\left( {r,s} \right)}}{{\partial r}} + }\\ {\frac{{{\eta _i}s}}{r}\frac{{\partial {U_i}\left( {r,s} \right)}}{{\partial r}} = {\rho _i}{s^2}{U_i}\left( {r,s} \right).} \end{array} $ | (14) |
式中:Ui(r, s)为ui(r, t)的Laplace变换,进一步整理式(14)可得
| $ \frac{{{\partial ^2}{U_i}\left( {r,s} \right)}}{{\partial {r^2}}} + \frac{1}{r}\frac{{\partial {U_i}\left( {r,s} \right)}}{{\partial r}} = q_i^2{U_i}\left( {r,s} \right). $ | (15) |
式中
方程(15)的通解为
| $ {U_i}\left( {r,s} \right) = {A_i}{K_0}\left( {{q_i}r} \right) + {B_i}{I_0}\left( {{q_i}r} \right). $ | (16) |
式中:I0(q, r)、K0(qir)分别为零阶第一类、第二类修正Bessel函数,Ai、Bi为待定系数.
对式(9)进行Laplace变换,代入式(16)可得Bn+1=0,因此,有
| $ {U_{n + 1}}\left( {r,s} \right) = {A_{n + 1}}{K_0}\left( {{q_{n + 1}}r} \right). $ | (17) |
则外部区域土体任意点的竖向剪切应力为
| $ \begin{array}{l} {\tau _{n + 1}} = \left( {{G_{n + 1}} + {\eta _{n + 1}}s} \right)\frac{{\partial {U_{n + 1}}\left( {r,s} \right)}}{{\partial r}} = \\ \;\;\;\;\;\;\;\;\;\; - \left( {{G_{n + 1}} + {\eta _{n + 1}}s} \right){q_{n + 1}}{A_{n + 1}}{K_1}\left( {{q_{n + 1}}r} \right). \end{array} $ | (18) |
内、外部区域分界面处,内部区域受到外部区域的竖向剪切刚度为
| $ \begin{array}{l} K{K_{n + 1}} = - \frac{{2{\rm{ \mathit{ π} }}{r_{n + 1}}{\tau _{n + 1}}\left( {{r_{n + 1}}} \right)}}{{{U_{n + 1}}\left( {{r_{n + 1}},s} \right)}} = \\ \;\;\;\;\;\;\;2{\rm{ \mathit{ π} }}{r_{n + 1}}\left( {{G_{n + 1}} + {\eta _{n + 1}}s} \right){q_{n + 1}}\frac{{{K_1}\left( {{q_{n + 1}}{r_{n + 1}}} \right)}}{{{K_0}\left( {{q_{n + 1}}{r_{n + 1}}} \right)}}. \end{array} $ | (19) |
内部区域圈层i中任意点处的竖向剪切力为
| $ \begin{array}{l} {\tau _i} = \left( {{G_i} + {\eta _i}s} \right)\frac{{\partial {U_i}\left( {r,s} \right)}}{{\partial r}} = \\ \;\;\;\;\;\;\;\; - \left( {{G_i} + {\eta _i}s} \right){q_i}\left[ {{A_i}{K_1}\left( {{q_i}r} \right) - {B_i}{I_1}\left( {{q_i}r} \right)} \right]. \end{array} $ | (20) |
则i圈层的外边界(r=ri+1)和内边界(r=ri)处的竖向剪切刚度为
| $ \begin{array}{l} K{K_{i + 1}} = - \frac{{2{\rm{ \mathit{ π} }}{r_{i + 1}}{\tau _i}\left( {{r_{i + 1}}} \right)}}{{{U_i}\left( {{r_{i + 1}},s} \right)}} = \\ 2{\rm{ \mathit{ π} }}{r_{i + 1}}{q_i}\left( {{G_i} + {\eta _i}s} \right)\frac{{{A_i}{K_1}\left( {{q_i}{r_{i + 1}}} \right) - {B_i}{I_1}\left( {{q_i}{r_{i + 1}}} \right)}}{{{A_i}{K_0}\left( {{q_i}{r_{i + 1}}} \right) + {B_i}{I_0}\left( {{q_i}{r_{i + 1}}} \right)}}. \end{array} $ | (21) |
| $ \begin{array}{l} K{K_i} = - \frac{{2{\rm{ \mathit{ π} }}{r_i}{\tau _{i\left( {{r_i}} \right)}}}}{{{U_i}\left( {{r_i},s} \right)}} = \\ \;\;\;\;\;\;\;2{\rm{ \mathit{ π} }}{r_i}{q_i}\left( {{G_i} + {\eta _i}s} \right)\frac{{{A_i}{K_1}\left( {{q_i}{r_i}} \right) - {B_i}{I_1}\left( {{q_i}{r_i}} \right)}}{{{A_i}{K_0}\left( {{q_i}{r_i}} \right) + {B_i}{I_0}\left( {{q_i}{r_i}} \right)}}. \end{array} $ | (22) |
由此可得基于黏性阻尼的多圈层平面应变模型,土层剪切刚度递推公式
| $ K{K_i} = 2{\rm{ \mathit{ π} }}{r_i}{q_i}\left( {{G_i} + {\eta _i}s} \right)\frac{{{C_i} + {E_i}K{K_{i + 1}}}}{{{D_i} + {F_i}K{K_{i + 1}}}}. $ | (23) |
式中:
| $ \begin{array}{l} {C_i} = 2{\rm{ \mathit{ π} }}{r_{i + 1}}{q_i}\left( {{G_i} + {\eta _i}s} \right)\left[ {{I_1}\left( {{q_i}{r_{i + 1}}} \right){K_1}\left( {{q_i}{r_i}} \right) - } \right.\\ \left. {{K_1}\left( {{q_i}{r_{i + 1}}} \right){I_1}\left( {{q_i}{r_i}} \right)} \right], \end{array} $ | (24) |
| $ \begin{array}{l} {D_i} = 2{\rm{ \mathit{ π} }}{r_{i + 1}}{q_i}\left( {{G_i} + {\eta _i}s} \right)\left[ {{I_1}\left( {{q_i}{r_{i + 1}}} \right){K_1}\left( {{q_i}{r_i}} \right) + } \right.\\ \left. {{K_1}\left( {{q_i}{r_{i + 1}}} \right){I_0}\left( {{q_i}{r_i}} \right)} \right], \end{array} $ | (25) |
| $ {E_i} = {I_0}\left( {{q_i}{r_{i + 1}}} \right){K_1}\left( {{q_i}{r_i}} \right) + {K_0}\left( {{q_i}{r_{i + 1}}} \right){I_1}\left( {{q_i}{r_i}} \right), $ | (26) |
| $ {F_i} = {I_0}\left( {{q_i}{r_{i + 1}}} \right){K_0}\left( {{q_i}{r_i}} \right) - {K_0}\left( {{q_i}{r_{i + 1}}} \right){I_0}\left( {{q_i}{r_i}} \right). $ | (27) |
对方程(4)进行Laplace变换可得
| $ \begin{array}{*{20}{c}} {{G_0}\frac{{{\partial ^2}{U_0}\left( {r,s} \right)}}{{\partial {r^2}}} + {\eta _0}s\frac{{{\partial ^2}{U_0}\left( {r,s} \right)}}{{\partial {r^2}}} + \frac{{{G_0}}}{r}\frac{{\partial {U_0}\left( {r,s} \right)}}{{\partial r}} + }\\ {\frac{{{\eta _0}s}}{r}\frac{{\partial {U_0}\left( {r,s} \right)}}{{\partial r}} = {\rho _0}{s^2}{U_0}\left( {r,s} \right).} \end{array} $ | (28) |
式中,U0(r, s)为u0(r, t)的Laplace变换,进一步整理式(28)可得
| $ \frac{{{\partial ^2}{U_0}\left( {r,s} \right)}}{{\partial {r^2}}} + \frac{1}{r}\frac{{\partial {U_0}\left( {r,s} \right)}}{{\partial r}} = q_0^2{U_0}\left( {r,s} \right). $ | (29) |
式中
方程(29)的通解为
| $ {U_0}\left( {r,s} \right) = {A_0}{K_0}\left( {{q_0}r} \right) + {B_0}{I_0}\left( {{q_0}r} \right). $ | (30) |
对式(6)进行Laplace变换,代入式(30)可得A0=0,因此,有
| $ {U_0}\left( {r,s} \right) = {B_0}{I_0}\left( {{q_0}r} \right). $ | (31) |
由式(7)和(31)可得管桩内壁受到桩芯土体的剪切刚度为
| $ K{K_0} = - \frac{{2{\rm{ \mathit{ π} }}{r_0}{\tau _0}\left( {{r_0}} \right)}}{{{U_{\rm{p}}}}} = - 2{\rm{ \mathit{ π} }}{r_0}\left( {{G_0} + {\eta _0}s} \right){q_0}\frac{{{I_1}\left( {{q_0}{r_0}} \right)}}{{{I_0}\left( {{q_0}{r_0}} \right)}}. $ | (32) |
对式(5)进行Laplace变换,并将由式(23)递推所得桩周最内层土体与桩接触面上剪切刚度KK1和式(32)代入可得
| $ \frac{{{\partial ^2}{U_{\rm{p}}}\left( {z,s} \right)}}{{\partial {z^2}}} - {\alpha ^2}{U_{\rm{p}}}\left( {z,s} \right) = 0. $ | (33) |
式中:
方程(33)的通解为
| $ {U_{\rm{p}}}\left( {z,s} \right) = C{{\rm{e}}^{\alpha z}} + D{{\rm{e}}^{ - \alpha z}}. $ | (34) |
式中C、D为由边界条件确定的待定系数.
进一步对式(12)、(13)进行Laplace变换,并将式(34)代入后可得
| $ C = \frac{{\xi P\left( s \right)}}{{\alpha \left( {\xi - 1} \right){E_{\rm{p}}}{A_{\rm{p}}}}}, $ | (35) |
| $ D = \frac{{P\left( s \right)}}{{\alpha \left( {\xi - 1} \right){E_{\rm{p}}}{A_{\rm{p}}}}}. $ | (36) |
式中
将式(35)、(36)代入(34)可得
| $ {U_{\rm{p}}}\left( {z,s} \right) = \frac{{\left( {\xi {{\rm{e}}^{\alpha z}} + {{\rm{e}}^{ - \alpha z}}} \right)}}{{\alpha \left( {\xi - 1} \right){E_{\rm{p}}}{A_{\rm{p}}}}}P\left( s \right). $ | (37) |
式中:令s=iω,则Laplace变换相当于单边的Fourier变换,因此, 可以得到管桩位移频域响应函数为Up(z, iω).由此可得桩顶复动刚度
| $ {K_{\rm{d}}} = \frac{{P\left( {{\rm{i}}\omega } \right)}}{{{U_{\rm{p}}}\left( {z,{\rm{i}}\omega } \right)}}\left| {_{z = 0}} \right. = \frac{{\alpha \left( {\xi - 1} \right){E_{\rm{p}}}{A_{\rm{p}}}}}{{\left( {\xi + 1} \right)}} = \frac{{{E_{\rm{p}}}{A_{\rm{p}}}}}{H}{{K'}_{\rm{d}}}, $ | (38) |
| $ {{K'}_{\rm{d}}} = \frac{{\bar \alpha \left( {\xi - 1} \right)}}{{\left( {\xi + 1} \right)}}. $ | (39) |
式中:α =αH,P(iω)为p(t)的傅里叶变换,Kd′为无量纲复刚度.令Kd′=Kr+iKi,其中Kr代表动刚度,Ki代表动阻尼.
3 算例分析基于图 1所示径向非均质黏弹性土体中管桩耦合振动力学模型,采用前述推导求解所得管桩纵向振动动力阻抗解析解答,如无特殊说明,具体土层参数取值如下:桩长6 m,外直径1.0 m,壁厚0.12 m,桩身混凝土弹性模量25 GPa,密度2 500 kg/m3;桩周土和桩芯土参数相同,剪切模量为5 MPa,密度为2 000 kg/m3,黏性阻尼系数为η=10 kN · s/m2,桩底刚度系数kp=1 000 kN/m3,阻尼系数δp=100 kN/m3.
当桩周土体径向圈层数大于20时[11],径向圈层的数目对计算结果的影响是可以忽略的.因此,随后的分析将桩周围土体的内部区域划分20个圈层.假定外部区域剪切波速
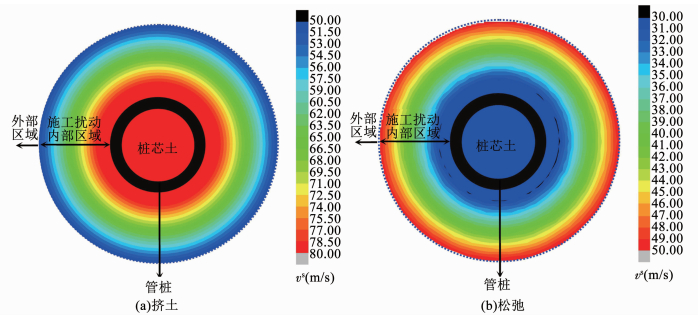
|
图 2 管桩施工扰动示意 Fig. 2 Diagram ofpipe pile under construction disturbance |
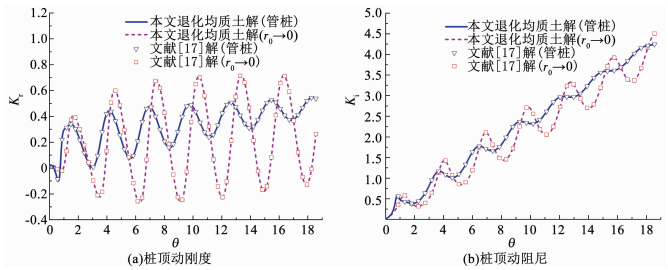
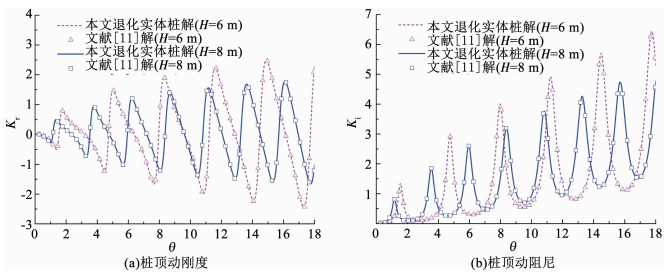
为了验证本文所推导的径向非均质土中管桩纵向振动动力阻抗解析解答的合理性,桩周围非均质土退化为均质与文献[17]中给出的解析解比较见图 3.此外,管桩退化为实体桩(阻尼系数取0),与文献[11]已有解析解进行对比验证,如图 3,4所示.图中无量纲频率θ为以特征频率为单位的频率计量,其中特征频率为ωc=vP/H,vP=
|
图 3 管桩桩顶动力阻抗本文退化解与文献[17]解对比 Fig. 3 Comparison of the dynamic impedance of pipe pile with the solution in Ref.[17] |
|
图 4 本文管桩退化到实体桩所得桩顶动力阻抗与文献[11]解对比 Fig. 4 Comparison of the dynamic impedance of pipe pile with Wang's solution in Ref.[11] |
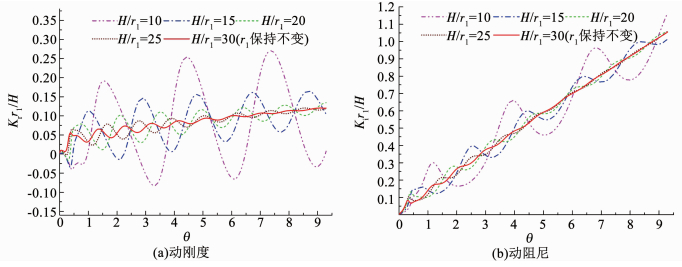
图 5为管桩长径比对桩顶动力阻抗的影响.桩长径比一般控制在50以内,此处取长径比10,15,20,25,30进行对比分析.可以看出,管桩长径比对桩顶动力阻抗曲线影响较大.管桩内外壁侧摩阻力随管桩长径比增加而增大,这就使得桩顶动力阻抗曲线振幅、共振频率均有所减小.桩长径比变化对桩顶动力阻抗影响呈现衰减趋势,当其达到一定幅值后此种影响效应趋于稳定.
|
图 5 桩顶动力阻抗曲线随长细比变化 Fig. 5 Variation of dynamic impedance of pipe pile with length diameter ratio of pipe pile |
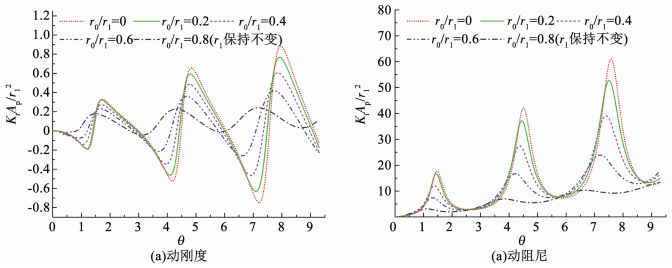
图 6为管桩顶动力阻抗随管桩内外径变化情况.可以看出,动力阻抗曲线的振幅、共振频率均随着管桩内外径比减小而增大.且当r0/r1=0(实体桩)时,桩顶动力阻抗曲线振幅最大,由此可知桩芯土能对管桩桩体起到减振作用.
|
图 6 桩顶动力阻抗曲线随管桩内外径比的变化 Fig. 6 Variation of dynamic impedance of pipe pile with the outer and inner diameters |
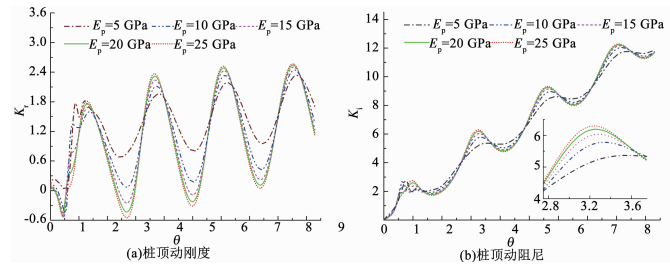
图 7为桩弹性模量对桩顶动力阻抗曲线的影响.可以看出,随着管桩弹性模量的增加,管桩桩顶动力阻抗曲线振幅均逐步增大,且管桩弹性模量对管桩动刚度影响较动阻尼更为显著.不同地,管桩弹性模量增大仅引起桩顶动阻尼共振频率小幅减小.管桩弹性模量变化对桩顶动刚度和动阻尼的影响程度逐步衰减,当其达到一定幅值后此种影响趋于稳定.
|
图 7 管桩桩顶动力阻抗随管桩弹性模量变化 Fig. 7 Effect of pipe pile elastic modulus on dynamic impedance at the pile head |
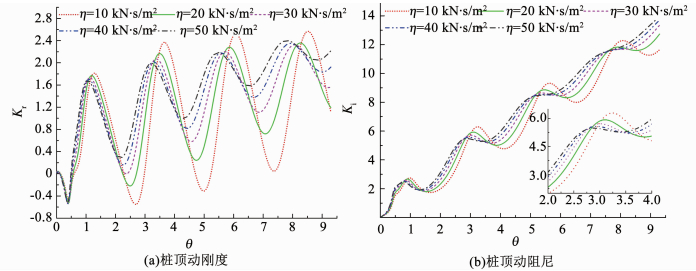
图 8为桩周土体黏性阻尼系数对桩顶动力阻抗的影响.可以看出,桩顶动刚度和动阻尼振幅和共振频率均随桩周土体黏性阻尼系数增加而显著减小,且桩周土体黏性阻尼系数变化对桩顶动刚度和动阻尼的影响程度随其增加而逐步衰减.
|
图 8 管桩桩顶动力阻抗随土体黏性阻尼系数变化 Fig. 8 Variation of dynamic impedance of pipe pile with the soil damping coefficient |
桩身施工扰动会引起原土质较松散或不够密实的砂土、粉土在靠近桩身的内部区域土体硬化.不同地,原土质为密实的砂土、粉土以及高灵敏度黏土、软土时,靠近桩身的内部区域土体在桩身施工扰动影响下则产生软化效应.基于此,对管桩施工扰动引起的桩周土体软化、硬化对桩顶动力阻抗的影响进行分析.
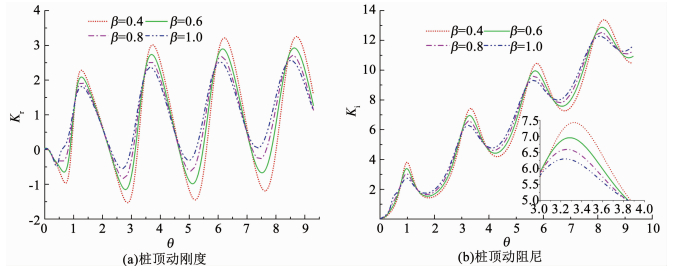
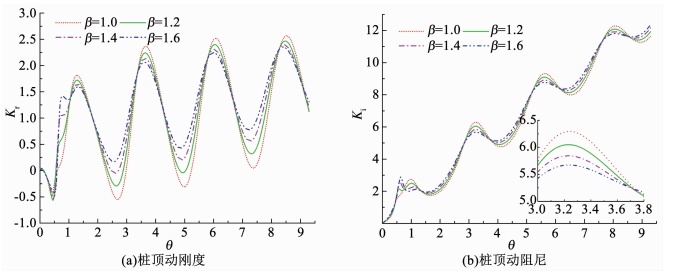
图 9,10分别为桩周土软化、硬化程度对桩顶动力阻抗曲线的影响.可以看出,桩周土的软化和硬化程度对桩顶动力阻抗曲线的幅值有明显的影响,即动力阻抗曲线振幅随桩周土体软化程度升高而增大,随桩周土体硬化程度升高而减小.但桩周土软化、硬化程度对桩顶动力阻抗共振频率影响较小.
|
图 9 管桩桩顶动力阻抗随桩周土软化程度变化 Fig. 9 Variation of dynamic impedance of pipe pile with the soil softening degree |
|
图 10 管桩桩顶动力阻抗随桩周土硬化程度变化 Fig. 10 Variation of dynamic impedance of pipe pile with the soil hardening degree |
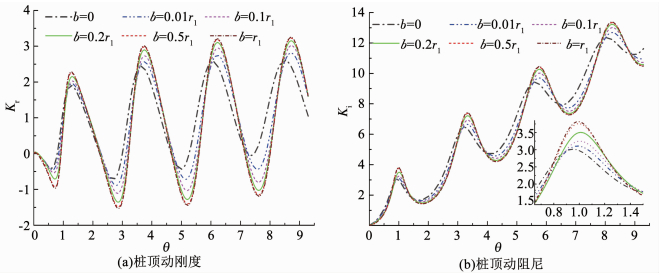
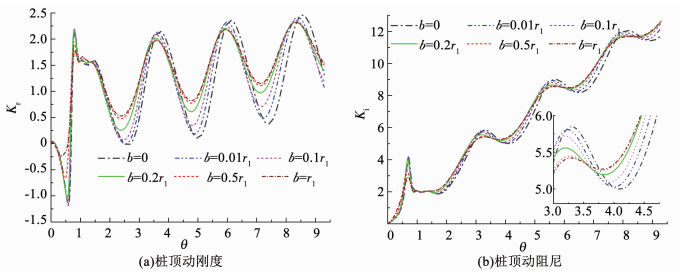
图 11,12分别为土体软化和硬化范围对桩顶动力阻抗的影响.可以看出,土体软化和硬化范围对桩顶动力阻抗曲线的幅值有明显影响,振幅随桩周土软化范围增加而增大,随桩周土体硬化范围增加而减小.但与实体桩不同,此种影响由于桩芯土的存在仅在近桩小范围内较为明显,超出该范围即大幅衰减至稳定.
|
图 11 管桩桩顶动力阻抗随桩周土软化范围变化(β=0.4) Fig. 11 Variation of dynamic impedance of pipe pile with the softening range |
|
图 12 管桩桩顶动力阻抗随桩周土硬化范围变化(β=2.0) Fig. 12 Variation of dynamic impedance of pipe pile with the hardening range |
1) 桩顶动力阻抗曲线振幅、共振频率均随管桩长径比的增加而减小,且桩长径比变化对桩顶动力阻抗特性影响随其增加而呈现衰减趋势.
2) 桩顶动力阻抗曲线的振幅和共振频率随内外径比的减小而增大,由此可知桩芯土能对管桩桩体起到减振作用.
3) 桩顶动力阻抗曲线振幅随桩身弹性模量的增加而增大,随着桩的弹性模量的增加,这种影响程度逐渐减弱.
4) 管桩桩顶动力阻抗振幅、共振频率随桩周土体黏性阻尼系数的增加均显著减小,且桩周土体黏性阻尼系数变化对桩顶动力阻抗特性影响程度随其增加而逐步衰减.
5) 桩周土体的软(硬)化程度越高,桩顶动力阻抗曲线振幅越大(小).相对而言,桩周土软(硬)化程度对桩顶动力阻抗共振频率影响程度较小.
6) 管桩桩顶动力阻抗振幅水平随桩周土软(硬)化范围增加而增大(减小),此种影响由于桩芯土的存在仅在近桩小范围内较为明显,超出该范围即大幅衰减至稳定.不同地,桩周土施工扰动范围改变对桩顶动力阻抗共振频率影响很小.
| [1] |
崔春义, 张石平, 杨刚, 等. 考虑桩底土层波动效应的饱和黏弹性半空间中摩擦桩竖向振动[J]. 岩土工程学报, 2015, 37(5): 878. CUI Chunyi, ZHANG Shiping, YANG Gang, et al. Vertical vibration of floating piles in saturated viscoelastic half-space considering wave effect of subsoil under pile bottom[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(5): 878. DOI:10.11779/CJGE201505014 |
| [2] |
CUI C Y, ZHANG S P, YANG G, et al. Vertical vibration of a floating pile in a saturated viscoelastic soil layer overlaying bedrock[J]. Journal of Southeast University, 2016, 23(1): 220. DOI:10.1007/s11771-016-3065-5 |
| [3] |
吴文兵, 王奎华, 杨冬英, 等. 成层土中基于虚土桩模型的桩基纵向振动响应[J]. 中国公路学报, 2012, 25(2): 73. WU Wenbing, WANG Kuihua, YANG Dongying, et al. Longitudinal dynamic response to the pile embedded in layered soil based on fictious soil pile model[J]. China Journal of Highway and Transport, 2012, 25(2): 73. DOI:10.19721/j.cnki.1001-7372.2012.02.011 |
| [4] |
HAN Y, VAZIRI H. Dynamic response of pile groups under lateral loading[J]. Soil Dynamics & Earthquake Engineering, 1992, 11(2): 87. |
| [5] |
WU W B, JIANG G S, DOU B, et al. Vertical dynamic impedance of tapered piles considering compacting effects[J]. Mathematical Problems in Engineering, 2013(2): 1. |
| [6] |
NOVAK M, SHETA M. Approximate approach to contact problems of piles[C]//Proceedings of the Geotechnical Engineering Division, American Society of Civil Engineering National Convention. Florida, 1980: 53
|
| [7] |
NOVAK M, HAN Y C. Impedances of soil layer with boundary zone[J]. Journal of Geotechnical Engineering, 1990, 116(6): 1008. DOI:10.1061/(ASCE)0733-9410(1990)116:6(1008) |
| [8] |
NOGAMI T, KONAGAI K. Dynamic response of vertically loaded nonlinear pile foundations[J]. Journal of Geotechnical Engineering, 1987, 113(2): 147. DOI:10.1061/(ASCE)0733-9410(1987)113:2(147) |
| [9] |
NOGAMI T, KONAGAI K. Time domain flexural response of dynamically loaded single piles[J]. Journal of Engineering Mechanics, ASCE, 1988, 114(9): 1512. DOI:10.1061/(ASCE)0733-9399(1988)114:9(1512) |
| [10] |
EI NAGGAR M H. Vertical and torsional soil reactions for radially inhomogeneous soil layer[J]. Structural Engineering & Mechanics, 2000, 10(4): 299. |
| [11] |
王奎华, 杨冬英, 张智卿, 等. 基于复刚度传递多圈层平面应变模型的桩动力响应研究[J]. 岩石力学与工程学报, 2008, 27(4): 825. WANG Kuihua, YANG Dongying, ZHANG Zhiqing. Study on dynamic response of pile based on complex stiffness transfer model of radial multizone plane strain[J]. Chinese Journal of Rock Mechanics & Engineering, 2008, 27(4): 825. DOI:10.3321/j.issn:1000-6915.2008.04.024 |
| [12] |
杨冬英, 王奎华. 任意圈层径向非均质土中桩的纵向振动特性[J]. 力学学报, 2009, 41(2): 243. YANG Dongying, WANG Kuihua. Vertical vibration of pile in radially inhomogeneous soil layers[J]. Chinese Journal of Theoretical & Applied Mechanics, 2009, 41(2): 243. DOI:10.3321/j.issn:0459-1879.2009.02.014 |
| [13] |
WANG K H, YANG D Y, ZHANG Z Q, et al. A new approach for vertical impedance in radially inhomogeneous soil layer[J]. International Journal for Numerical & Analytical Methods in Geomechanics, 2012, 36(6): 697. |
| [14] |
YANG D Y, WANG K H, ZHANG Z Q, et al. Vertical dynamic response of pile in a radially heterogeneous soil layer[J]. International Journal for Numerical & Analytical Methods in Geomechanics, 2009, 33(8): 1039. |
| [15] |
刘汉龙, 丁选明. 现浇薄壁管桩在低应变瞬态集中荷载作用下的动力响应解析解[J]. 岩土工程学报, 2007, 29(11): 1611. LIU Hanlong, DING Xuanming. Analytical solution of dynamic response of cast-in-situ concrete thin-wall pipe piles under transient concentrated load with low strain[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(11): 1611. DOI:10.3321/j.issn:1000-4548.2007.11.003 |
| [16] |
丁选明, 刘汉龙. 低应变下变阻抗薄壁管桩动力响应频域解析解[J]. 岩土力学, 2009, 30(6): 1793. DING Xuanming, LIU Hanlong. Analytical solution in frequency domain of dynamic response of thin-wall pipe piles with variable wave impedance under low strain transient concentrated load[J]. Rock & Soil Mechanics, 2009, 30(6): 1793. DOI:10.3969/j.issn.1000-7598.2009.06.046 |
| [17] |
丁选明, 陈磊. 粘弹性地基中管桩的纵向振动特性研究[J]. 长江科学院院报, 2009, 26(3): 32. DING Xuanming, CHEN Lei. Study on Vertical vibration characteristics of pipe piles in viscoelastic soil[J]. Journal of Yangtze River Scientific Research Institute, 2009, 26(3): 32. DOI:10.3969/j.issn.1001-5485.2009.03.009 |
| [18] |
郑长杰, 丁选明, 黄旭, 等. 滞回阻尼土中大直径管桩纵向振动响应解析解[J]. 岩石力学与工程学报, 2014(s1): 3284. ZHENG Changjie, DING Xuanming, HUANG Xu, et al. Analytical solution of vertical vibration response of large diameter pipe pile in hysteretic damping soil[J]. Chinese Journal of Rock Mechanics & Engineering, 2014(s1): 3284. DOI:10.13722/j.cnki.jrme.2014.s1.097 |
| [19] |
ZHENG C J, DING X M, SUN Y F. Vertical vibration of a pipe pile in viscoelastic soil considering the three-dimensional wave effect of soil[J]. International Journal of Geomechanics, 2015, 16(1): 1. |
| [20] |
吴文兵, 蒋国盛, 王奎华, 等. 土塞效应对管桩纵向动力特性的影响研究[J]. 岩土工程学报, 2014, 36(6): 1129. WU Wenbing, JIANG Guosheng, WANG Kuihua, et al. Influence of soil plug effect on vertical dynamic response of pipe piles[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(6): 1129. DOI:10.11779/CJGE201406019 |
| [21] |
刘林超, 闫启方, 王颂, 等. 基于轴对称模型的管桩竖向振动研究[J]. 岩土力学, 2016, 37(1): 119. LIU Linchao, YAN Qifang, WANG Song, et al. Vertical vibration of pipe pile based on axisymmetric model[J]. Rock & Soil Mechanics, 2016, 37(1): 119. DOI:10.16285/j.rsm.2016.01.014 |
| [22] |
LI Z Y, WANG K H, WU W B, et al. Vertical vibration of a large-diameter pipe pile considering the radial inhomogeneity of soil caused by the construction disturbance effect[J]. Computers & Geotechnics, 2017, 90. |
| [23] |
胡昌斌, 王奎华, 谢康和. 桩与黏性阻尼土耦合纵向振动时桩顶时域响应研究[J]. 振动工程学报, 2004, 17(1): 72. HU Changbin, WANG Kuihua, XIE Kanghe. Time domain axial response of dynamically loaded pile in viscous damping soil layer[J]. Journal of Vibration Engineering, 2004, 17(1): 72. DOI:10.16385/j.cnki.issn.1004-4523.2004.01.018 |
| [24] |
NOGAMI T, NOVAK M. Soil-pile interaction in vertical vibration[J]. Earthquake Engineering & Structural Dynamics, 1976, 4(3): 277. |
| [25] |
MILITANO G, RAJAPAKSE R K N D. Dynamic response of a pile in a multi-layered soil transient torsional and axial loading[J]. Géotechnique, 1999, 49(1): 91. DOI:10.1680/geot.1999.49.1.91 |
| [26] |
胡海岩. 结构阻尼模型及系统时域动响应[J]. 应用力学学报, 1993(1): 8. HU Haiyan. Structural damping model and system dynamic response at time domain[J]. Chinese Journal of Applied Mechanics, 1993(1): 8. |
| [27] |
廖振鹏. 工程波动理论导论[M]. 北京: 科学出版社, 2002. LIAO Zhenpeng. Introduction to engineering wave theory[M]. Beijing: Science Press, 2002. |
| [28] |
赵会杰.径向非均质粘弹性单相土中管桩纵向振动特性分析[D].大连: 大连海事大学, 2017 ZHAO Huijie. Study on vertical vibration characteristics of pipe piles in viscoelastic single-phase soil[D]. Dalian: Dalian Maritime University, 2017 http://cdmd.cnki.com.cn/Article/CDMD-10151-1017054140.htm |
| [29] |
胡昌斌, 王奎华, 谢康和. 考虑桩土耦合作用时弹性支承桩纵向振动特性分析及应用[J]. 工程力学, 2003, 20(2): 146. HU Changbin, WANG Kuihua, XIE Kanghe. Soil-pile interaction in vertical vibrations of a pile with elastic bottom boundaries and its applications[J]. Engineering Mechanics, 2003, 20(2): 146. DOI:10.3969/j.issn.1000-4750.2003.02.028 |
 2019, Vol. 51
2019, Vol. 51


