目前,针对高压工况,如注浆泵高压压注水泥浆液、发动机油泵喷洒高压雾化油、液压系统给液压杆提供高压力等,大多使用往复泵,以活塞泵为主[1];针对大流量工况,如农作物灌溉、城市排水、消防供水等,大多使用叶片泵,其中离心泵最为常见[2].而针对高压、大流量工况需求时,如深层矿井排水、液体介质长距离输送、大涌水量注浆治理等情况时,传统的泵类结构很难达到要求.
活塞泵的基本运动是靠曲轴旋转带动连杆机构完成活塞在缸体内的往复运动.其密封系统比较完善,能够产生较高的压力,但是活塞的往复工作方式带来的惯性力矩、惯性力的不平衡性造成活塞泵结构中支撑件的惯性负荷加剧,容易引起设备整体的不稳定震动与噪声[3-5].离心泵是利用叶轮的高速旋转运动使液体介质在离心泵腔体内一起高速旋转,在离心力的作用下排出泵体.离心泵的高速旋转结构能实现较大的流量,但其叶轮结构密封性差,很难产生较大压力,多级离心泵效率较低[6-8].为了解决上述问题,近年来,多位学者进行了传统设备的结构改进,叶素娣等[9]对模数大、齿数少的齿轮泵进行了增效设计,一定程度上减小了在高压作用下的间隙泄漏和黏滞摩擦损失;张琛等[10]研制了高压大流量柱塞泵,并设计了性能测试台进行了性能测试;多级离心泵的出现解决了许多高压大流量的工况,不过多级泵容积效率低,能量损失较为严重,且在第一级泵体进口叶片反面低压处易发生气蚀现象[8, 11];Seok-Yun Jeon等提出一种优化设计方法来提高叶轮泵的性能[12].
为解决高压大流量类型泵的选择难问题,设计了一种将往复泵做成旋转运动方式的挤压式偏心回转泵,吸取了往复泵高压力和离心泵大流量的优点,以旋转挤压的形式完成泵送工作.为充分测试挤压式偏心回转泵的性能特点,将泵体内部零件进行分析和优化,并针对CN-1.5S型号测试泵进行不同转速和出口直径下的测试,运用对相似性能泵体参数分析方法[11, 13-15],对监测元件收集到的数据进行分析计算,得到测试泵的流量、压力、效率等性能参数的变化规律.挤压式偏心回转泵可以归类于转子泵,与转子泵结构也有很多共同点,但由于腔体密封性差,转子泵中大部分容积效率较低[16-19].
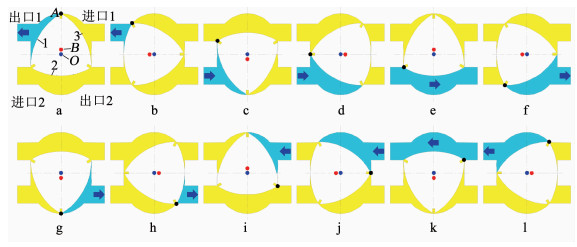
1 原理新型挤压式偏心回转泵是通过转子在缸体内做偏心回转运动改变泵工作腔的腔体容积,从而完成吸入和排出工作,工作原理如图 1所示,浅色零件为缸体,白色零件为转子,深色部分代表工作腔体内的介质,点B为转子的形心,点O为缸体的形心,同时也是曲轴(图 6)主轴颈的轴线投影.为了避免泵吸入和排出时的相互干涉,缸体的两个进口和两个出口各设有一个单向阀.图中,点A为转子的一个顶点,转子的3个侧面分别编号为1、2、3,转子的3个顶点与侧面把缸体分为3个工作腔,工作腔体容积发生变化从而完成吸入和排出工作.转子运动过程是一个复合运动,包括转子截面形心B围绕缸体截面形心O的逆时针转动(曲轴的连杆颈围绕主颈的旋转),以及转子围绕其截面形心B的顺时针转动(转子围绕曲轴连杆颈的自转,可观察点A与点B的相对运动),其转速比为3: 2.图中过程a到l再回到a为转子的一个运动周期,A点回到原位,转子侧面1相邻的工作腔共完成了两次吸入和排出工作,所以, 3个工作腔共完成6次工作.
|
图 1 新型挤压式偏心回转泵工作原理 Fig. 1 Principle of the extrusive eccentric rotary pump |
主要零件有转子、缸体、曲轴、齿轮座、轴承座等,图 2为双缸泵结构图.其中,定齿轮通过齿轮座固定在前封板上,与缸体相对静止;曲轴主轴颈通过深沟球轴承与齿轮座配合,并与定齿轮同心;连杆颈通过滚针轴承与转子配合,并与转子同心;内齿圈通过螺栓紧固在转子上,并与定齿轮啮合,齿数比为3: 2.

|
图 2 新型挤压式偏心回转泵结构示意 Fig. 2 Extrusive eccentric rotary pump structure |
当动力装置驱动曲轴主轴颈转动时,曲轴旳连杆颈使得转子上的内齿圈与定齿轮啮合运动,同时转子绕连杆颈自转运动,所以,转子在刚体内的复合运动包括转子的自转运动与转子中心绕曲轴主轴颈中心的公转运动,其中转子公转转速与转子自转转速比为3: 2,曲轴主轴颈转动3圈,3个独立腔体分别完成两次吸入与排出工作.即曲轴主轴颈转动一圈,单一缸体完成两个腔体的吸排工作.
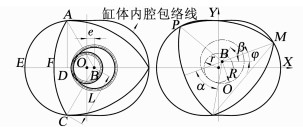
2.1 缸体内腔包络线新型挤压式偏心回转泵缸体的内腔截面线为双弧外次摆线,也是转子3个顶点运动轨迹的包络线,如图 3所示.
|
图 3 缸体内腔包络线 Fig. 3 Inner enveloping line of the cylinder |
定齿轮中心O与转子中心B的中心距为e,转子中心到其顶点的距离为L.图 3中定齿轮分度圆半径为r,转子内齿圈分度圆半径为R,左图到右图过程中转子中心B转过的角度为β,其中一个顶点M转过φ角,定齿轮分度圆与内齿圈分度圆内切点变化的过程中出现两段长度相等的圆弧,α·R等于β·r,即α/β=r/R=2/3,又因为β=α+φ,有β=3φ[20].
转子任一顶点P在X-Y坐标系中的坐标即腔体轮廓线可以表示为
| $ \left\{ \begin{array}{l} X = e\cos \beta + L\cos \varphi ,\\ Y = e\sin \beta + L\sin \varphi . \end{array} \right. $ | (1) |
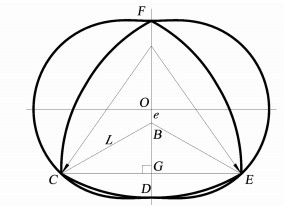
当转子内齿圈固定不动,定齿轮带动缸体型线沿着内齿圈转动,就形成了缸体型线的包络线,即转子的3条边, 由于转子型线的包络线难以准确加工, 可用3条当量圆弧代替,如图 4所示,其中一条当量圆弧为转子的两个顶点C、E与缸体上点D 3点所确定的圆弧,圆弧的圆点为F,其半径FC可以表示为
|
图 4 转子型线 Fig. 4 Rotor profile |
| $ FC = \sqrt {F{G^2} + C{G^2}} = \frac{{{{\left( {L - e} \right)}^2} + 3{e^2}}}{{L - 4e}}. $ | (2) |
由于缸体3个独立腔体中任意一个在一个循环内完成两次泵送工作,新型挤压式偏心回转泵单缸体设计有两个进口与两个出口,如图 1所示,c~h与i~b即为转子侧面1所在工作腔1所完成的两次泵送工作.
以c~h为例,工作腔1的体积由小变大,再由大变小从而完成一次泵送工作.经过计算,体积最大位置即在中间位置e处.
进出口的大小与尺寸直接影响泵体的工作性能与效率,下面对进出口的位置与尺寸进行分析优化.首先将转子在缸体内运动的过程确定出4种特征位置,如图 1所示a~d 4种位置情况分别为:工作腔2体积最大(a)、工作腔1体积最小(b)、工作腔3体积最大(c)、工作腔2体积最小(d).本文中的过程演示均是以4种特征位置来表示,只是其他过程为不同工作腔的特征位置.可以看出,工作腔体积最小与最大的临界位置即工作腔吸入与排出过程的转变位置,所以,进出口位置要根据转子的4种特征位置来选定.
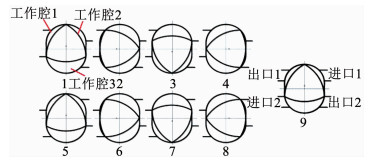
根据转子的4种特征位置也就确定了进口与出口的两种极限位置,图 5中1~4过程与5~8过程分别为进出口的两种极限位置.以进口1为例,图中过程1为工作腔2体积最大位置,随着转子的转动,工作腔2由吸入变为排出,而转子恰好转过进口1,所以,1~4过程中进口1的位置设定为进口的上限位置;图中过程6为工作腔1的体积最小位置,随着转子的转动,工作腔1由排出变为吸入,而恰好进口1进入到工作腔1中开始吸入工作,所以,设定5~8过程中进口1的位置设定为进口的下限位置.同样分析出口1的极限位置,过程2为工作腔1由排出变为吸入,随着转子的转动转子恰好转过出口1,1~4过程中出口1的位置设定为出口的上限位置;过程7为工作腔3由吸入变为排出,随着转子的转动恰好出口1进入到工作腔3中开始排出工作,所以,5~8过程中出口1的位置设定为出口的下限位置.若进出口的位置超过了上下限,将会失去其本身的作用,所以,将进出口设定在极限位置之内,但新型挤压式偏心回转泵的工作腔又有连通性,即进出口设定在极限位置之内任意位置、任意尺寸的情况下都会出现介质倒流现象.例如图中过程1进口1位置下移时,随着转子的转动,工作腔2排出的过程中仍与进口1联通,出口同样会有这种情况,这样就需要在进口、出口处设置单向阀.为了减小缸体内的压力积聚,上下限即设定为进出口的尺寸,如过程9中所示.
|
图 5 进出口设计 Fig. 5 Imports and exports design |
由2.3可知,图 3中转子运转到左图位置时,AECF所包围截面所在腔体体积变为最大,AECF所包围的面积SAECF为
| $ {S_{AECF}} = 2{S_{AEF}} = 2\left( {{S_{AED}} - {S_{AFD}}} \right). $ |
由式(1)可得
| $ {S_{AED}} = \int_{\rm{ \mathsf{ π} }}^{\frac{{2{\rm{ \mathsf{ π} }}}}{3}} {\left( {e\sin 3\varphi + L\sin \varphi } \right) \cdot {{\left( {e\cos 3\varphi + L\cos \varphi } \right)}^\prime }{\rm{d}}\varphi } . $ |
由图 3中几何关系可得
| $ {S_{AFD}} = \left( {\frac{{\rm{ \mathsf{ π} }}}{4} - \frac{{3\sqrt 3 }}{8}} \right){L^2}. $ |
得到SAECF的表达式为
| $ {S_{AECF}} = {\rm{ \mathsf{ π} }} \cdot {e^2} + \frac{{3\sqrt 3 eL}}{2} - \left( {\frac{{\rm{ \mathsf{ π} }}}{6} - \frac{{\sqrt 3 }}{2}} \right){L^2}. $ |
由挤压式偏心回转泵的工作原理可知,主轴转动一圈,完成两个腔体容积介质的吸入和排出,若缸体的厚度为s,则输入轴转速为n时单缸挤压式偏心回转泵的流量Q为
| $ Q = 2ns{S_{AECF}} = 2ns{\rm{ \mathsf{ π} }} \cdot {e^2} + 3\sqrt 3 eLns\left( {\frac{{\rm{ \mathsf{ π} }}}{3} - \sqrt 3 } \right){L^2}ns. $ | (3) |
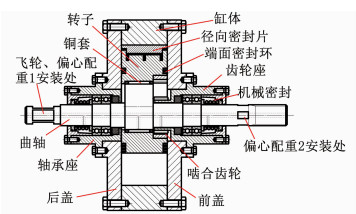
以CN-1.5S单缸挤压式偏心回转泵为例介绍其结构,如图 6所示. CN-1.5S内齿圈与定齿轮模数取2,齿数分别为36与24.
|
图 6 单缸泵结构 Fig. 6 Structure of the new pump |
由于工作状态下曲轴主要受径向力,曲轴的主轴颈两端由两列深沟球轴承支撑,依靠两端端盖定位,深沟球轴承分别放在齿轮座和轴承后座的中心孔内.发动机或电机驱动曲轴转动,带动转子挤压液体介质,曲轴是整个装置中受载荷最大的零件,而且所承受的动载荷方向和大小均时刻变化,所以,曲轴要有足够的强度、刚度以及抗疲劳强度.首先曲轴在选材上要恰当,选取几种常用的轴用材料进行比对,如表 1所示,为了达到CN-1.5S的最佳性能,选取20CrMnMo渗碳处理.
| 表 1 不同曲轴材料性能 Tab. 1 Performance of different crankshaft materials |
图 6所示曲轴的主轴颈穿过定齿轮的中心孔,所以,定齿轮处的主轴颈直径要小于定齿轮的内孔直径,该型号泵的定齿轮齿根圆直径为43 mm,根据实验及强度计算,定齿轮齿底到中心孔的距离不小于7 mm,主轴颈与中心孔由于相互运动关系还要留有一定间隙(0.5 mm),所以, 此处主轴颈直径最大为28 mm.根据曲轴最大有效直径,可以计算其动力端的许用功率:
| $ {P_0} \le {\left( {\frac{d}{C}} \right)^3}n. $ | (4) |
式中:P0为动力端功率,d为轴直径,C为计算常数,n为轴的转速.其中C根据20CrMnMo查表取98,可以得到转速不同情况下CN-1.5S的动力端许用功率,以及不同转速下的理论流量、出口直径不变时的理论压力值, 见表 2.
| 表 2 CN-1.5S理论性能 Tab. 2 Theoretical performance of CN-1.5S |
在CN-1.5S运转过程中,转子和曲轴的连杆颈在旋转过程中会产生离心力,当转子旋转到图 1中位置e时,转子与连杆颈的离心力方向相同,合力作用方向竖直向上,此时也是工作腔1的工作状态由吸入变为排出,介质对转子的压力方向同样竖直向上,并由转子传递给曲轴. CN-1.5S所设计的最大工作压力为6.325 MPa,轴的弹性模量渗碳后取1.8E11,泊松比0.27,用ANSYS对曲轴进行受力分析,如图 7所示.可以看出,在最大工作压力下曲轴的挠曲变形最大值为0.020 5 mm,在曲轴的承受范围内.

|
图 7 曲轴受力分析 Fig. 7 Force analysis of crankshaft |
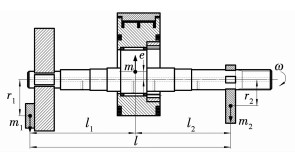
为了平衡曲轴上转子及连杆颈高速旋转时带来的旋转惯性力,需要在曲轴的两端各加一个偏心配重块,来平衡转子偏心运动带来的振动,如图 8中的偏心配重1与偏心配重2.
|
图 8 曲轴平衡分析 Fig. 8 Crankshaft balance analysis |
为了达到曲轴转动过程的向心力和力矩平衡,需满足以下两式:
| $ me{\omega ^2} = {m_1}{r_1}{\omega ^2} + {m_2}{r_2}{\omega ^2}, $ | (5) |
| $ {m_1}{r_1}{l_1} = {m_2}{r_2}{l_2}. $ | (6) |
式中:m为转子与连杆颈的质量,ω为曲轴的角速度,m1为偏心配重1的质量,r1为偏心配重1质心到主轴颈中心线的距离,m2为偏心配重2的质量,r2为偏心配重2质心到主轴颈中心线的距离,l1为偏心配重1质心到转子与连杆颈质心的距离,l2为偏心配重2质心到转子与连杆颈质心的距离.
联立式(5)、(6)可得偏心配重的质量:
| $ {m_1} = \frac{{ma{l_2}}}{{l{r_1}}}, $ | (7) |
| $ {m_2} = \frac{{ma{l_1}}}{{l{r_2}}}. $ | (8) |
式中:l为偏心配重1质心到偏心配重2质心的水平距离.
这样,挤压式偏心回转泵因转子、连杆颈带来的偏心旋转质量可以完全平衡,而活塞式往复泵产生的不平衡往复质量没办法完全解决,所以,挤压式偏心回转泵的运行要比活塞泵平稳得多.
3.2 转子转子为挤压式偏心回转泵将活塞往复挤压结构转为旋转式挤压结构的核心单元,同时也是液体密封系统的核心部件.
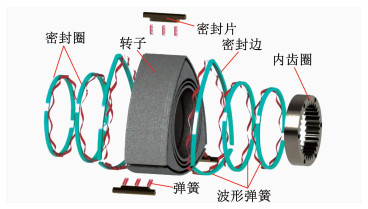
转子部件主要包括转子、内齿圈、密封圈、密封边、密封片、弹簧等零件,如图 9所示.其中由密封片与缸体内壁组成的径向密封与密封圈、密封条与前后封板组成的端面密封是泵体密封性、耐疲劳、效率的关键因素.
|
图 9 转子结构 Fig. 9 Rotor structure |
由于在同一时间3个工作腔体的工作状态不同,安装在转子三角部位的密封片通过弹簧和离心力的共同作用与缸体内壁始终贴合在一起,将3个工作腔体分割开来,其密封度决定了泵体的工作压力.
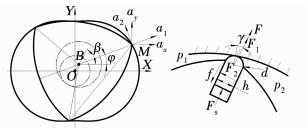
当转子转动到图 10位置时,式(1)对时间t进行微分,带入β=3φ,可以得到P点处密封片的线速度在X轴、Y轴方向的分量:
|
图 10 密封片受力分析 Fig. 10 Force analysis of the of the seals |
| $ \left\{ \begin{array}{l} {v_x} = \frac{{{\rm{d}}x}}{{{\rm{d}}t}} = - e\sin \beta \frac{{{\rm{d}}\beta }}{{{\rm{d}}t}} - \frac{L}{3}\sin \frac{\beta }{3}\frac{{{\rm{d}}\beta }}{{{\rm{d}}t}},\\ {v_y} = \frac{{{\rm{d}}y}}{{{\rm{d}}t}} = e\cos \beta \frac{{{\rm{d}}\beta }}{{{\rm{d}}t}} + \frac{L}{3}\cos \frac{\beta }{3}\frac{{{\rm{d}}\beta }}{{{\rm{d}}t}}. \end{array} \right. $ | (9) |
然后再将式(8)对时间t进行微分可以得P点处密封片的加速度在X轴、Y轴方向的分量:
| $ \left\{ \begin{array}{l} {a_x} = \frac{{{\rm{d}}{v_x}}}{{{\rm{d}}t}} = - e\cos \beta \frac{{{{\rm{d}}^2}\beta }}{{{\rm{d}}{t^2}}} - \frac{L}{9}\cos \frac{\beta }{3}\frac{{{{\rm{d}}^2}\beta }}{{{\rm{d}}{t^2}}},\\ {a_y} = \frac{{{\rm{d}}{v_y}}}{{{\rm{d}}t}} = - e\sin \beta \frac{{{{\rm{d}}^2}\beta }}{{{\rm{d}}{t^2}}} - \frac{L}{9}\sin \frac{\beta }{3}\frac{{{{\rm{d}}^2}\beta }}{{{\rm{d}}{t^2}}}. \end{array} \right. $ | (10) |
式中:
根据图 10中加速度分量的三角函数关系可以得到密封片的径向加速度a1和切向加速度a2,即
| $ \left\{ \begin{array}{l} {a_1} = \cos \frac{\beta }{3}{a_x} + \sin \frac{\beta }{3}{a_y} = - \frac{{L{\omega ^2}}}{9} - e{\omega ^2}\cos \frac{{2\beta }}{3},\\ {a_2} = - \sin \frac{\beta }{3}{a_x} + \cos \frac{\beta }{3}{a_y} = - e{\omega ^2}\sin \frac{{2\beta }}{3}. \end{array} \right. $ | (11) |
由图 14可得密封片受到的介质压力p、径向惯性力F1、切向惯性力F2、侧面摩擦力f分别为
| $ p = \left( {\frac{{hH}}{2} - {r_{\rm{a}}}H\sin \gamma } \right){p_1} + \left( {\frac{{hH}}{2} + {r_{\rm{a}}}H\sin \gamma } \right){p_2}, $ | (12) |
| $ {F_1} = m'{a_1} = - \frac{{L{\omega ^2}m}}{9} - e{\omega ^2}m\cos \frac{{2\beta }}{3}, $ | (13) |
| $ {F_2} = m'{a_2} = - e{\omega ^2}m'\sin \frac{{2\beta }}{3}, $ | (14) |
| $ f = \mu {F_2} = - \mu e{\omega ^2}m'\sin \frac{{2\beta }}{3}. $ | (15) |
式中:h为密封片的厚度,H为密封片的长度,ra为密封片接触面半径,γ为密封片接触点与径向的偏移角,p1、p2为相邻缸体的介质压力,m′为密封片的质量,μ为密封片与侧壁的摩擦系数.
得到密封片的向心合力
| $ F = {F_1} + {F_{\rm{s}}} - p - f. $ | (16) |
在转速一定的情况下,既要保证缸体的密封性,又要防止密封片和缸体内壁磨损严重,这就要求密封片向心合力满足:
| $ 0 < F < F'. $ | (17) |
F′为密封片许用最大向心合力,通过实验获得.所以,得到弹簧弹力的取值区间为
| $ p + f - {F_1} < {F_{\rm{s}}} < F' + p + f - {F_1}. $ | (18) |
径向密封度取决于缸壁、密封片的材质及热处理工艺,还取决于弹簧的弹力,错误的材料或过大的弹力会导致缸体内壁的“波纹损伤”(如图 11所示)或密封片磨耗过快,进而密封性急剧下降.为了避免“波纹损伤”,还要考虑缸体的定位孔不会因为整体热处理发生变形或位置尺寸改变,选用表 3中3种方案.

|
图 11 缸体内壁波纹伤痕 Fig. 11 Ripple damage on the inner wall of the cylinder |
| 表 3 缸体内壁与对应密封片的选材及处理 Tab. 3 Selection and treatment of the inner wall of the cylinder and the seal |
为了确保腔体与转子内的铜套、曲轴两端轴承以及啮合齿轮空间不连通,转子的端面密封由两道密封圈和一道密封条组成,并由波形弹簧施加压力贴合在前盖、后盖上.密封圈与密封条材料选碳纤维聚四氟乙烯,有较好的耐磨、密封性质,有较强的自润滑性能.
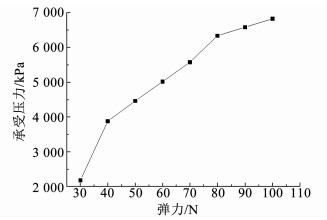
波形弹簧的弹力大小对端面密封起到关键作用,分别测试弹簧弹力在30,40,50,60,70,80,90,100 N下端面密封所能承受的压力值,测试结果如图 12所示,当弹力大于80 N时,满足6.325 MPa的最大压力值.
|
图 12 端面密封性能随波形弹簧弹力的变化 Fig. 12 Sealing properties with the change of the waveform spring elastic force |
该试验测试系统由CN-1.5S测试泵、数据监测元件、数据收集中心、高压管路、储水池、介质搅拌桶(测试悬浊液或其他黏度较大介质时使用)等组成,测试泵体搭载22 kW变频电机,系统装配如图 13所示.

|
图 13 试验布置 Fig. 13 Test system display |
监测元件包括FDDCIIIEP2M3A型电磁流量计,用来采集流量参数,监测量程为0~100 m3/h;FD80/86平模型压力变送器,用来监测进口、出口管路中的介质压力;西门子G120变频器,用来检测瞬时电压、电流及测试泵转速等参数信息.数据监测元件所采集的数据通过NHR-8100/8700彩色无纸记录仪进行实时显示并记录,再由计算机存储数据.
试验系统的控制包括通过变频器对变频电机调速,来实现测试泵输出不同的流量;通过阀门定位器控制气动V型调节球阀来改变出口大小,实现输出不同的压力.
4.2 试验方案1) 通过变频器调节电机转速n为100,200,300,400,500,600,700,800,900,1 000 r/min等10种转速,通过气动V型调节球阀设定出口直径D0由大到小a、b、c、d 4种出口尺寸,分别监测并记录相同时间段内的泵出流量和压力.
2) 在不同转速下,分别由大到小不间断控制a、b、c、d 4种出口直径100 s,根据所收集的试验数据,研究挤压式偏心回转泵的流量、压力的时间曲线,分析其容积效率和工作效率,计算泵的不均匀系数.
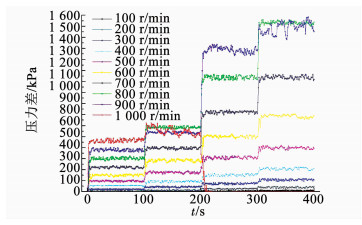
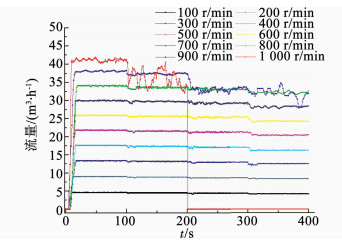
4.3 试验结果及分析根据所检测的CN-1.5S在不同转速、出口直径下的流量与压力数据,可以绘制流量Q与时间t、出口与进口的压力差Δp与时间t的动态变化曲线,如图 14,15所示.
|
图 14 压力随时间变化曲线 Fig. 14 Pressure changes over time |
|
图 15 流量随时间变化曲线 Fig. 15 Flow changes over time |
根据挤压式偏心回转泵的流量、压力变化曲线,可以看出:
1) 在CN-1.5S测试试验中流量Q随时间的变化比较平稳,压力差Δp随时间波动较大.
2) 出口直径越小,Δp和Q波动越明显;电机转速越快,Δp和Q波动越明显.
3) 电机转速在100~800 r/min时,曲线较为平稳,Δp、Q随时间的波动不大;当转速升到900 r/min时,出口直径减小到c时曲线出现轻微波动,出口直径减小到d时曲线波动较大;当转速上升到1 000 r/min时,曲线在出口直径为b时开始有较大波动,泵体运行不稳定,电机出现“丢转”现象,随后关闭电机.
4) 由于在出口直径刚刚变化时流量不稳定,选取每个出口直径16 s之后数据计算CN-1.5S在不同转速、出口直径下的最大流量Qmax、最小流量Qmin、流量平均值Qm统计数据见表 4.
| 表 4 流量特性值 Tab. 4 Flow characteristic value |
测试泵流量曲线的波动性可以用不均匀系数反映,其表达式为
| $ \delta Q = \frac{{{Q_{\max }} - {Q_{\rm{m}}}}}{{{Q_{\rm{m}}}}} \times 100\% . $ | (19) |
式中δQ为不均匀系数.
将表 4中数据带入公式可以得CN-1.5S测试泵的流量不均匀系数,如表 5所示.
| 表 5 不均匀系数 Tab. 5 Non-uniform coefficient |
5) 由表 5可知,CN-1.5S电机时匹配22 kW电机,出口直径为a时,测试泵的最佳测试转速为1 000 r/min,此阶段流量不均匀系数为2.47%,曲线波动小,流量、压力数值较为理想;出口直径为b时,测试泵的最佳测试转速为900 r/min,此阶段流量不均匀系数为0.82%;出口直径为c时,测试泵的最佳测试转速为800 r/min,此阶段流量不均匀系数为2.09%;出口直径为d时,测试泵的最佳测试转速为800 r/min,此阶段流量不均匀系数为2.40%.
6) 容积效率
由各转速下曲线随出口直径减小的变化趋势看,流量随出口直径减小而有所损失,这种损失可以用容积效率ηv来表示,其表达式为
| $ {\eta _{\rm{v}}} = \frac{{{Q_{\rm{m}}}}}{{{Q_{\rm{0}}}}} \times 100\% . $ | (20) |
式中:Q0为理论流量,用所计算的平均流量Qm来表示测试泵的实际流量值.
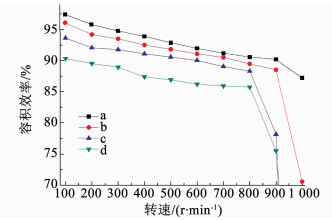
根据2.3中挤压式偏心回转泵的理论流量的计算公式(3)以及CN-1.5S的特性参数可以得到其各转速下的理论流量,如表 6所示,所测得的实际流量比所计算的理论流量值要小一些,并且随着出口直径的减小,流量测试值越来越小,这是由于随着出口直径的减小出口压力变大,工作腔体、单向阀之间的液体泄漏量随之加大,从而容积效率越来越小.结合CN-1.5S的实际流量值进而可以得到测试泵在不同出口直径时的容积效率随转速的变化规律,如图 16所示.
| 表 6 CN-1.5S理论流量与实际流量的对比 Tab. 6 Contradistinction of theoretical and actual flow of CN-1.5S |
|
图 16 容积效率随转速的变化 Fig. 16 Relationship between volume efficiency and rotation speed |
由图 16可以看出:同种出口直径下容积效率随转速的升高有所下降,转速越高,下降幅度越大;同种转速下出口直径越小,容积效率越小;出口直径为a、b时,在转速0~900 r/min内,容积效率保持在88%以上,当转速达1 000 r/min时,容积效率下降幅度较大;出口直径为c、d时,在转速0~800 r/min内,容积效率保持在85%以上,当转速达900 r/min时,容积效率下降幅度较大.
7) 机械效率
泵输入端的转矩与输入端功率的关系式为
| $ {P_0} = \frac{{Tn}}{{9\;550}}. $ |
式中T为泵输入轴的转矩.
电机的输出功率可以表示为
| $ {P_0} = U \cdot I. $ |
式中:U为电压值,I为电流值.
电流值与电压值可由变频器记录,可以计算得到实时的电机输出功率值,发现其与转速成正比关系,这是由于所用电机为恒转矩电机,根据所记录的电流与电压值可以得到.根据以上可以计算出来的参数,按照压差法计算测试泵的机械效率[21],即
| $ {\eta _{\rm{m}}} = \frac{{\Delta p{Q_0}}}{{2{\rm{ \mathsf{ π} }}nT}}. $ | (21) |
式中:ηm为机械效率,T为泵输入轴的转矩.
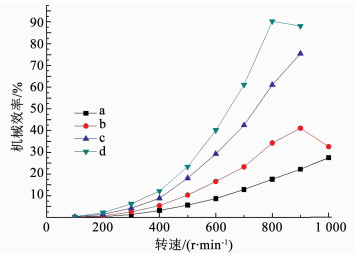
得到测试泵在不同出口直径时的机械效率随转速的变化规律,如图 17所示.
|
图 17 机械效率随转速的变化 Fig. 17 Relationship between mechanical efficiency and rotation speed |
8) 水力效率
根据伯努利方程可以计算得到出口的理论扬程(H0),如表 7所示.
| 表 7 CN-1.5S理论扬程 Tab. 7 H0 of CN-1.5S |
根据试验中进、出口的压力差和流速可以得到测试泵体的扬程表达式:
| $ H = \frac{{\Delta p}}{{\rho g}} + \frac{{{v_2} - {v_1}}}{{2g}}. $ | (22) |
式中:H为CN-1.5S的扬程,ρ为介质密度,g为重力加速度,v2为出口介质流速,v1为进口流速.
进出口流速可以由进出口流量与进出管截面积得到.
水力效率可以表述为实际扬程与理论扬程的比值:
| $ {\eta _{\rm{h}}} = \frac{H}{{{H_0}}}. $ | (23) |
式中ηh为机械效率.
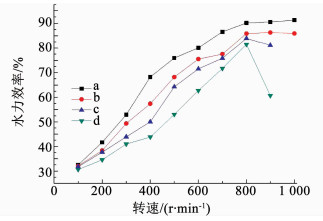
根据计算所得理论扬程值和实际扬程值可以得到测试泵在不同出口直径时的水力效率随转速的变化规律,如图 18所示.
|
图 18 水力效率随转速的变化 Fig. 18 Relationship between hydraulic efficiency and rotation speed |
9) 总效率
泵的总效率为容积效率、机械效率、水力效率的乘积,即
| $ \eta = {\eta _{\rm{v}}} \cdot {\eta _{\rm{m}}} \cdot {\eta _{\rm{h}}}. $ | (24) |
式中η为泵的总效率.
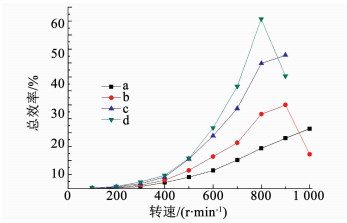
根据上文中所统计的容积效率、机械效率、水力效率的乘积可以得到测试泵在不同出口直径时的总效率随转速的变化规律,如图 19所示.可以看出,根据不同出口直径下实际测试得到的流量和压力所计算的总效率随着转速的加快大致呈增长趋势.根据理论计算结果,流量、压力在转速为1 000 r/min达到最大值,而实际测试结果是在出口直径为d、电机转速为800 r/min时CN-1.5S的总效率达到最大值60.75%,这是由于恒转矩电机转速在900和1 000 r/min时的转矩小于达到此时的流量和压力所需要的转矩,所以在电机功率为17.6 kW(800 r/min)时,CN-1.5S可以达到的流量为32.17 m3/h,压力为1.7 MPa,效率为60.75%.
|
图 19 总效率随转速的变化 Fig. 19 Relationship between overall efficiency and rotation speed |
10) 性能对比
由图 19可以看出,当转速为800 r/min、出口直径为d时泵的总效率最高,为60.75%,此时电机的输出功率为17.6 kW,选取额定功率为18 kW的多级离心泵CDL42-50-2与活塞泵3SNS进行参数的对比,如表 8所示.可以看出,相同功率下与离心泵相比,CN-1.5S的流量与CDL42-50-2的额定流量基本相同,CN-1.5S的压力约为CDL42-50-2额定压力的1.45倍;相同功率下与活塞泵相比,CN-1.5S的流量约为3SNS额定流量的2.6倍,CN-1.5S的压力小于3SNS的额定压力.
| 表 8 同功率泵的性能对比 Tab. 8 Comparison of performance of several identical power pumps |
综上,挤压式偏心回转泵的流量能达到离心泵的流量,且远大于活塞泵,其压力大于离心泵.所以,挤压式偏心回转泵适用于流量要求大,离心泵压力达不到、活塞泵流量值不足的工况,来替代离心泵或活塞泵.
5 结论设计了一种挤压式偏心回转泵,采用转子偏心旋转挤压式结构,可以同时输出较大的流量和压力.提出了新型泵的原理及设计方法,对关键零部件进行了结构尺寸、材质、受力等分析,并以CN-1.5S为例进行了试验测试,获得以下结论:
1) 电机转速为800 r/min、输入功率为17.6 kW时,测试泵的流量达32.17 m3/h,压力达1.7 MPa,与同等输入功率的离心泵相比,流量相近,其压力大于离心泵;与同等功率的活塞泵相比,其流量远大于活塞泵.
2) 转速800 r/min以内时,其流量不均匀系数小于2.4%,容积效率在85%以上;转速为800 r/min、出口直径为d时机械效率达最大值90.23%;水力效率随转速的升高而升高,当转速达800 r/min时开始减缓升高或降低;试泵的总效率在转速为800 r/min、出口直径为d时达最大值60.75%.
3) CN-1.5S使用22 kW恒转矩变频电机在800 r/min转时达到最佳输出状态,需要使用更高功率的电机提高输入端的扭矩测试CN-1.5的最佳性能.
4) 挤压式偏心回转泵具有较好的输出性能,可在需求同时具备大流量和较高压力的工况下推广应用.
| [1] |
LIU S, LI X, SUN T, et al. Calculation of the hydraulic extension limit of an extended-reach well with allowance for the power limitations of the available mud pumps[J]. Chemistry and Technology of Fuels and Oils, 2016, 51(6): 713. DOI:10.1007/s10553-016-0662-9 |
| [2] |
张永学, 陈龙, 周鑫, 等. 高效率离心泵水力设计及BVF诊断[J]. 排灌机械工程学报, 2013, 31(6): 479. ZHANG Yongxue, CHEN Long, ZHOU Xin, et al. Hydraulic design and BVF diagnosis of high efficiency centrifugal pump[J]. Journal of Drainage and Irrigation Machinery Engineering, 2013, 31(6): 479. DOI:10.3969/j.issn.1674-8530.2013.06.005 |
| [3] |
夏江敏, 刘海冰, 张振海, 等. 往复泵曲柄连杆机构振动特性分析[J]. 噪声与振动控制, 2016, 36(3): 151. XIA Jiangmin, LIU Haibing, ZHANG Zhenhai, et al. Vibration analysis of the crank-link mechanism of reciprocating bilge pumps[J]. Noise and Vibration Control, 2016, 36(3): 151. DOI:10.11887/j.cn.201606014 |
| [4] |
闫祥安, 郑炜, 张青, 等. 往复泵输液管道结构振动有限元法分析[J]. 机械工程学报, 1999, 35(6): 74. YAN Xiangan, ZHENG Wei, ZHANG Qing, et al. Finite element analysis on the structural vibration of the discharge pipes for reciprocating pumps[J]. Chinese Journal of Mechanical Engineering, 1999, 35(6): 74. DOI:10.3321/j.issn:0577-6686.1999.06.019 |
| [5] |
吴昊, 童志伟, 陈航, 等. 基于SolidWorks Motion与ADAMS在改进型BW-280/12泥浆泵的动力学仿真[J]. 制造业自动化, 2014, 19(5): 65. WU Hao, TONG Zhiwei, CHEN Hang, et al. Dynamic simulation analysis on improved mud pump BW-280/12 using SolidWorks motion and ADAMS[J]. Manufacturing Automation, 2014, 19(5): 65. DOI:10.3969/j.issn.1009-0134.2014.03(上).19 |
| [6] |
朱相源, 江伟, 李国君, 等. 导叶式离心泵内部流动特性数值模拟[J]. 农业机械学报, 2016, 47(6): 34. ZHU Xiangyuan, JIANG Wei, LI Guojun, et al. Numerical analysis of hydraulic performance in centrifugal pump with vane diffuser[J]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(6): 34. DOI:10.6041/j.issn.1000-1298.2016.06.005 |
| [7] |
吴大转, 许斌杰, 武鹏, 等. 多级离心泵内部间隙流动与泄漏损失[J]. 浙江大学学报(工学版), 2011, 45(8): 1393. WU Dazhuan, XU Binjie, WU Peng, et al. Internal clearance flow and leakage loss in multi-stage centrifugal pump[J]. Journal of Zhejiang University (Engineering Science), 2011, 45(8): 1393. DOI:10.3785/j.issn.1008-973x.2011.08.011 |
| [8] |
王洋, 赵立峰, 刘志超, 等. 多级离心泵水力性能数值预测涡量分析法[J]. 排灌机械工程学报, 2016, 34(7): 561. WANG Yang, ZHAO Lifeng, LIU Zhichao, et al. Numerical prediction of multistage centrifugal pump performance and analysis of vorticity of flow field[J]. Journal of Drainage and Irrigation Machinery Engineering, 2016, 34(7): 561. DOI:10.3969/j.issn.1674-8530.15.0088 |
| [9] |
叶素娣, 徐敬华. 高压大流量齿轮泵混合参数增效设计[J]. 机械科学与技术, 2016, 35(2): 165. YE Sudi, XU Jinghua. Efficiency-improving design of high pressure and large flow gear pump by using hybrid parameters[J]. Mechanical Science and Technology for Aerospace Engineering, 2016, 35(2): 165. DOI:10.13433/j.cnki.1003-8728.2016.0201 |
| [10] |
张琛, 冯世波, 白清鹏, 等. 一种高压大流量液压泵测试台的开发[J]. 液压气动与密封, 2015(7): 82. ZHANG Chen, FENG Shibo, BAI Qingpeng, et al. The development of a test bench for testing the hydraulic pump with high pressure large flow[J]. Hydraulics Pneumatics & Seals, 2015(7): 82. DOI:10.3969/j.issn.1008-0813.2015.07.028 |
| [11] |
江见福, 顾伯勤, 邵春雷. 多级泵内部流动分析及其性能预测[J]. 南京工业大学学报(自然科学版), 2012, 34(5): 94. JIANG Jianfu, GU Boqin, SHAO Chunlei. Analysis of inner flow on multistage pump and its performance prediction[J]. Journal of Nanjing University of Technology(Natural Science Edition), 2012, 34(5): 94. DOI:10.3969/j.issn.1671-7627.2012.05.018 |
| [12] |
JEON S, KIM C, LEE S, et al. Performance enhancement of a pump impeller using optimal design method[J]. Journal of Thermal Science, 2017, 26(2): 119. DOI:10.1007/s11630-017-0919-6 |
| [13] |
XU B, HU X, ZHANG J, et al. Characteristics of volumetric losses and efficiency of axial piston pump with respect to displacement conditions[J]. Journal of Zhejiang University Science A, 2016, 17(3): 186. DOI:10.1631/jzus.A1500197 |
| [14] |
YAN P, LI S, YANG S, et al. Effect of stacking conditions on performance of a centrifugal pump[J]. Journal of Mechanical Science and Technology, 2017, 31(2): 689. DOI:10.1007/s12206-017-0120-6 |
| [15] |
闻德生, 陈帆, 甄新帅, 等. 凸轮转子型双定子叶片泵泄漏与容积效率分析[J]. 西安交通大学学报, 2016, 50(9): 20. WEN Desheng, CHEN Fan, ZHEN Xinshuai, et al. Analysis of leakage and volumetric efficiency for cam-rotor double-stator vane pump[J]. Journal of Xi'an Jiaotong University, 2016, 50(9): 20. DOI:10.7652/xjtuxb201609003 |
| [16] |
宋如钢, 张宝欢, 杨延相. 新型摆线转子泵啮合特性的研究[J]. 粉末冶金技术, 2007, 25(2): 99. SONG Rugang, ZHANG Baohuan, YANG Yanxiang. Study on the meshing characteristic of a new cycloidal pump[J]. Powder Metallurgy Technology, 2007, 25(2): 99. DOI:10.19591/j.cnki.cn11-1974/tf.2007.02.005 |
| [17] |
任洪勇, 张生昌, 王宗槐, 等. 新型偏心蠕动式转子泵的特性及流量分析[J]. 轻工机械, 2011, 29(2): 14. REN Hongyong, ZHANG Shengchang, WANG Zonghuai, et al. Analysis of the characteristics and flow rate of a new eccentric and squirmy rotor pump for cleaning machine[J]. Light Industry Machinery, 2011, 29(2): 14. DOI:10.3969/j.issn.1005-2895.2011.02.005 |
| [18] |
李玉龙, 刘焜, 彭骏华. 转子泵设计与建模的参数化集成[J]. 农业机械学报, 2006, 37(12): 109. LI Yulong, LIU Kun, PENG Junhua. Research and development on integrative parameterization design with its solid model for cycloid pump[J]. Transactions of the Chinese Society for Agricultural Machinery, 2006, 37(12): 109. DOI:10.3969/j.issn.1000-1298.2006.12.027 |
| [19] |
陈作炳, 邹远志, 江智, 等. 转子与泵体间隙对转子泵性能影响的数值模拟[J]. 噪声与振动控制, 2017, 37(2): 62. CHEN Zuobing, ZOU Yuanzhi, JIANG Zhi, et al. Numerical simulation of the effect of the gap between rotor and pump on the performance of the rotor pump[J]. Noise and Vibration Control, 2017, 37(2): 62. DOI:10.3969/j.issn.1006-1355.2017.02.013 |
| [20] |
辛动. 三角转子发动机[M]. 北京: 科学出版社, 1981: 12. XIN Dong. Delta rotor engine[M]. Beijing: Science Press, 1981: 12. |
| [21] |
宋岩. 煤矿用乳化液泵机械效率的研究[J]. 煤矿机械, 2010, 31(3): 59. SONG Yan. Study on mechanical efficiency of emulsion pump for coal mine[J]. Coal Mine Machinery, 2010, 31(3): 59. DOI:10.3969/j.issn.1003-0794.2010.03.023 |
 2019, Vol. 51
2019, Vol. 51


