近年来,车辆保有量上升、交通拥堵情况日趋严重.城市轨道交通作为运量大、速度快的高效运输工具,自建设以来一直受到出行者的广泛青睐.而随着城市轨道交通的大力发展,轨道交通线路逐渐扩张,客源分布也随之扩散,导致轨道交通在人们的日常出行方式中占比趋高,由此引发的轨道交通需求增长,对现有地铁运营提出了挑战.城市轨道交通突发大客流疏导的核心在于缓解网络供给能力与客流需求之间的矛盾,降低突发大客流对于城市轨道交通系统运营产生的影响,使得客流运营能够按照正常和均衡的态势运行.疏导策略主要从提高区间运输能力和限制区间运量两方面着手[1],但在区间运输能力基本达到极限的情况下,对相关车站进行客流控制成为了有效措施.客流组织与控制的关键在于采用各种措施,使得车站站内的通过能力与线路运输能力相协调,确保客流状态的安全有序,提高系统的整体疏散效率并降低事故风险.
针对城市轨道交通突发大客流的形成与客流组织已有一定的研究,而专门针对突发大客流的研究相对较少.在大客流组织方面,张伦等对大客流进行分类,探讨地铁车站客流组织的影响因素,从客流预测、车站客流组织、列车运能、票务组织等方面提出地铁车站大客流的具体运营措施[2];刘莲花等基于广州地铁的实际案例出发,提出了相关的限流措施[3];Xu Xinyue提出了在客流需求不确定情况下地铁车站客流组织的问题[4];Sigurd对纽约地铁、轻轨在内的轨道交通路网的运输组织进行了分析,形成了包含运营模式、客流组织、运能、开行方案等方面的运营管理理论体系[5].在协调限流的研究上,赵鹏等针对路网某条线路利用优化控流率来提高运力利用率[6-7].刘晓华等针对该问题提出一种面向重点车站的流量控制模型,通过对重点车站相邻的上游车站进行限流以实现对重点车站的能力预留[8];姚向明等提出了客流需求与输送能力匹配度最大为目标的多站协同限流模型[9].Jin J G等考虑通过公交网络与地铁线路的配合,完成大量通勤人流的疏散[10].
文章基于对轨道交通车站突发大客流事件的界定与分类,采用定性定量相结合的方法深入分析突发大客流事件形成的内在机理,并以此为基础,所提出的协调限流模型借鉴LP控制方法[11]的思想,兼顾地铁运营商和乘客的利益,以车站进站量为变量,通过协调各车站各时段进站量,达到缓解车站客流压力和有效分线路运输能力的目的.
1 突发大客流分类及形成机理 1.1 突发大客流的分类突发大客流是指在某一时间段中,车站到达的乘客时间集中,且流量超过车站正常客运设施或客运组织所能承担的客流[12].不同于早晚高峰大客流,突发大客流的诱发因素复杂,发生时间、持续时长、影响范围具有不确定性.
通过调查分析得到,城市轨道交通大客流产生的原因主要有以下几个方面:
1) 节假日大客流,主要是指由于元旦、劳动节、国庆节等国家法定假日期间引起本地和外地市民的旅游需求和出行的大幅提高,往往会造成全线各站客流普遍大幅上升.
2) 大型活动大客流,主要指城市大型文化体育活动、商业会展、博览会等大型活动的举办引发轨道交通客流爆发.大型活动出行目的地单一,客流呈现“多起点单聚集地”的出行特性[13],而在进场和散场阶段会产生方向性极不均匀的客流.
3) 恶劣天气大客流,主要指由于恶劣天气下,较多市民从其他运输方式转移到地铁或进人地铁车站避雨雪,而造成地铁各个车站客流上升.
4) 轨道交通系统发生紧急事件引发大客流,地铁车站发生紧急事件,如火灾、大面积停电、列车延误时,会导致车站客流持续积压.一般而言,此类大客流直接影响范围较小但波及范围较大.
1.2 突发大客流形成机理一般地,乘客通过车站出入口通道到站厅购票,经过闸机进入付费区,通过升降设备到达站台候车,地铁按照既定运营计划完成运输乘客的任务.然而当车站发生大客流事件时,大量的乘客通过站内设施到达站台候车,由于列车输送能力的限制,不能一次性服务全部的排队乘客,部分乘客需等待下一班列车,从而出现乘客滞留——“留乘”,留乘的持续累积使车站滞留乘客持续增加,进而超过车站的容许客流量.
站台是乘客候车、上下车的重要场所,是关键的安全控制点之一[14].站台是一个客流积累的空间区域,对于一般站台,客流积累量主要由乘客进站流量、乘客出站流量、乘客下车流量和乘客上车流量共同决定,见图 1.

|
图 1 客流积累过程 Fig. 1 Passenger flow accumulation process |
因此,站台积累客流量的数学表达式为
| $ Q\left( t \right) = \int\limits_0^t {\left[ {{q_{{\rm{xc}}}}\left( t \right) - {q_{{\rm{sc}}}}\left( t \right) + {q_{{\rm{jz}}}}\left( t \right) - {q_{{\rm{cz}}}}\left( t \right)} \right]{\rm{d}}t} . $ | (1) |
式中:Q(t)为站台积累客流量,qxc(t)为乘客下车客流量,qsc(t)为乘客上车客流量,qjz(t)为乘客进站客流量,qcz(t)为乘客出站客流量(人/min),t为调控时刻.
地铁站台的容纳能力是大客流事件形成的决定因素之一,当站台客流量超过所能承受的极限能力时,大客流事件形成,站台容易引发踩踏等危险状况.文献通过釆集轨道交通车站重点区域的客流密度来反映突发大客流的等级,根据一定的客流密度函数,将客流分成五层等级[15],该文献的研究结果是将2.5人/m2的客流密度视为大客流的下界.因此,选用2.5人/m2和地铁站站台的有效面积S作为判定依据,可以得到大客流事件是否发生的条件,表达式如下:
1) 当Q(t) < (2.5×S)时,地铁系统内的客流量在站台有效区域的容纳范围之内,大客流事件尚未形成.
2) 当Q(t)≥(2.5×S)时,地铁系统内的客流量达到或超过站台有效区域的容纳能力,大客流事件形成.
2 协调限流优化模型构建 2.1 问题描述为解决地铁线路上某个或某些车站突发大客流问题,对地铁线路的站点采取协调限流.为了便于模型定量描述,定义如下变量:J为车站集合共有m个车站;T为客流控制时段集合共有n个时段;L为相邻车站的区间集合共有m-1个.乘客因为共同的目的集聚,这使得数量以及进入B站的客流去向可预测.考虑流量Z的突发大客流发生在一个方向上.大客流突发站点B之前有b个站,在1至B站采取措施控制客流量.虽然列车剩余运力能够满足前b个站的客流需求,为了避免B站大客流的长时间淤积,采取协调限流措施.B站客流控制强度则由剩余运输能力决定.协调限流示意图见图 2.
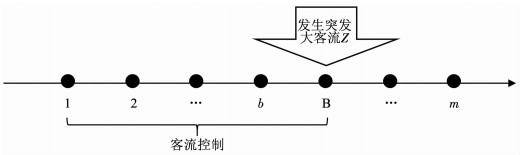
|
图 2 协调限流示意 Fig. 2 Coordinated passenger-flow limit diagram |
线路协调限流策略的实施时间段为突发大客流在站点集聚的时间点与客流疏散完成时间点之间的时段.文本策略优化核心在于在时间段T下,考虑地铁运营商成本投入的同时,减少线路客流的人均延误,加速突发大客流的疏散.为构建模型,对相关影响因素作如下假设:
1) 通过对类似事件引发大客流的历史数据进行分析,可以对该大客流的OD以及进站客流的分流比例做出准确的推断.
2) 模型中的列车运行参数来自列车运行图.假设列车完全按照运行图行驶,忽略运行干扰因素对模型造成偏误.
3) 节假日及大型活动期间整体客流需求在一段时间内较稳定,客流弹性损失可忽略不计.
4) 尽管突发大客流可能在双向或多线路发生,但以单条线路的单个方向为基础建立客流控制模型的构建思路仍具有推广意义.
在假设的基础上,协调限流优化模型构建思路见图 3.

|
图 3 模型构建思路 Fig. 3 Idea of model building |
基于最优化的方法构建模型,使得协调限流模型满足多目标优化的需求.从地铁运营商的角度来看,通过协调限流策略应尽量充分利用列车的运能,在保证安全运营的基础上,提高列车运能的利用率,从而降低企业的运营成本;从乘客的角度来看,在突发大客流背景下,提高乘客的服务质量在于减少乘客的延误时间,通过协调限流的措施应让线路上的乘客尽可能多而快地乘车离站,从而降低线路乘客的人均延误.因此,通过人均延误时间衡量乘客的利益,通过各相邻区间列车满载率之和衡量地铁运营商的利益,目标函数表达式为
| $ \min {T^a} = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^m {\frac{{\left( {{U_{ij}} - U_{ij}^C} \right) \times \Delta t}}{{{D_{ij}}}}} } , $ | (2) |
| $ \max \theta = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^m {\frac{{\left( {\sum\limits_{l \in L} {U_{ij}^C \times p_{i,j}^l} } \right)}}{{{C_{l,\max }}}}} } . $ | (3) |
式中:Ta为人均延误时间,θ为各区间满载率之和,n为突发大客流控制时段T内的时间间隔数量,Uij为第i个时间间隔下第j个车站的乘客需求量,UijC为第i个时间间隔下第j个车站的最佳进站量,Δt为突发大客流控制时段T内的时间间隔长度,Dij为第i个时间间隔下第j个车站的到达乘客数;pi, jl为第i个时间间隔下车站j对第l区间的客流贡献率,Cl, max为列车最大载客量.
2.3 约束条件在城市轨道交通系统中,线路、车站以及交通设施的能力都有自身的限制,城市轨道交通客流控制中必须要求在不超过设施能力限制的条件下进行控制管理,因此,需要加入约束条件对优化函数加以约束.本文约束条件主要考虑5个方面,分别为客流需求约束、站内设施通过能力约束、区间运输能力约束、客流控制强度约束和站台安全约束.
2.3.1 客流需求约束控制时间段T内,每个时间间隔的进站客流需求量由新到达客流量和前一个时间间隔滞留客流两部分组成;而滞留客流量则为前一个时间间隔的客流需求量与控制进站客流量的差值.客流需求约束方程为
| $ {U_{i,j}} = {D_{i,j}} + {S_{i - 1,j}},\forall i \in T,\forall j \in J, $ | (4) |
| $ {S_{i - 1,j}} = {U_{i - 1,j}} - U_{i - 1,j}^C,\forall i \in T,\forall j \in J, $ | (5) |
| $ {U_{i,j}} = {D_{i,j}},i = 1,\forall j \in J. $ | (6) |
式中Si, j为第i个时间间隔下第j个车站滞留客流量.
2.3.2 区间运输能力约束区间运输能力约束是模型最重要的约束,当控制在最佳进站量下,在区间上的客流量不大于区间的运输能力.区间客流量Q等于在时段i下,各个车站所控制的最佳进站流量UijC与最佳流量经过区间l比例pi, jl的乘积的累加之和.pi, jl表示无运能约束下UijC经过区间l的比例,可以通过客流OD结构推算.区间运输能力约束公式为
| $ \sum\limits_{l \in L} {\left( {U_{ij}^C \times p_{i,j}^l} \right)} \le {C_{l,\max }} \times \Delta t \times \gamma . $ | (7) |
式中γ为列车满载系数.
2.3.3 客流控制强度约束客流控制强度约束是指最佳进站人数不能超出实际客流需求,同时,在非极端大客流情况下不会采取封站措施,故最佳进站人数还需要满足最低进站客流量要求.即
| $ 0 \le \frac{{{U_{i,j}} - U_{i,j}^C}}{{{U_{i,j}}}} \le \varphi ,\forall i \in T,\forall j \in J. $ | (8) |
式中φ为最大控流率.
2.3.4 站内设施通过能力约束单位时间内容许进站客流量不仅与线路运输能力有关,还受到车站基础设施通过能力的制约,因此,将车站闸机、通道、升降设备等设施通过能力的最小值作为车站通过能力.在大客流背景下,为保障运营安全设定车站通过能力折减系数,其值采取经验折减系数.根据哈尔滨市地铁历史客流数据,对比节假日车站通过能力和正常状态下车站通过能力,以大客流状态与正常状态之间车站通过能力比值作为折减系数,即
| $ U_{i,j}^C \le \delta \times E_J^{\max },\forall i \in T,\forall j \in J. $ | (9) |
式中:δ为突发大客流状态下车站通过能力折减系数(在此设为0.8),EJmax为车站通过能力.
2.3.5 站台安全约束客流密度是反应客流安全情况的重要监测指标[10],站台是关键的风险控制点.当客流达到一定密度时,乘客难以移动,造成冲突不断,极易引发踩踏等群体安全事故.根据一般车站乘客先下后上的原则,列车乘客下车时,站台人数将达到该时段的最大值,因此,要控制此时的客流人数不得超过安全阈值,即
| $ \frac{{U_{i,j}^C + {f_i}\left( l \right) \times {r_{ij}}}}{{{S_j}}} \le \sigma ,\forall i \in T,\forall j \in J,\forall l \in L. $ | (10) |
式中:Sj为车站j的站台有效面积,σ为站台安全阈值(通常取2.5人/m2),fi(l)为i时段区间l的载客量,rij为i时段车站j的下车率.
2.4 模型求解文章中所建立的客流协调控制模型为多目标线性规划模型.由于多个目标之间既有一定的相关性,又有矛盾性,要求所有的目标同时达到最优的可能性较小,在实际求解过程中往往是求其次优解.本文采用理想点法,首先对各个目标函数单独求解,而后采用理想点法对模型求解进而得到最终解.
考虑Lingo11求解器在模型求解上的优越性及操作简便性,模型利用Lingo11求解器进行求解.对于文章所建的优化模型,Lingo11求解器能够发挥很好的作用,且求解结果保证全局最优.Lingo11操作界面见图 4.

|
图 4 Lingo11操作界面 Fig. 4 Operation interface of Lingo11 |
某城市轨道交通Y线自南向北,共有10座车站(称为A1、A2…A10),开通以来客流持续增长,节假日期间乘客滞留车站情况突出.选取本线上行方向为对象进行实际计算,协调限流控制阶段为节假日高峰时段.算例采用等间隔发车,发车间隔为5 min.
表 1为每个发车间隔内车站客流需求量,从表 1可以看出,各站客流需求量严重不均衡:车站A1、A5、A6需求量巨大;不同时段间客流需求量也存在较大差异.客流时空不均衡的特点极易导致列车在前方区间运能被快速占用,导致后方车站乘客大量滞留.因此,需要采取限流措施,避免后方车站客流不断堆积,车站拥堵引发踩踏等意外事故.
| 表 1 分时段车站进站客流量 Tab. 1 Inbound traffic flow at every period |
根据进站客流量数据和OD对客流比例数据,可以推算出每个时段每个车站的进站客流量,对各个区间的贡献率.该系数是模型中最重要的参数,部分数据见表 2.
| 表 2 某时段车站客流量对区间贡献率 Tab. 2 Station's contribution to the interval during a certain period |
表 3为模型构建的具体参数,包含车辆型号、列车编组等信息.
| 表 3 模型参数 Tab. 3 Parameters of the model |
采用数学优化软件Lingo对所构建模型进行求解,得到各车站分时段最佳进站客流量及车站控流率.定义的控流率为控制时段内不能满足的客流需求与实际客流需求的比值.为便于结果分析,选取车站控流率和滞留人次两个指标对协调限流和不采取协调限流措施两种情况进行对比.其中,不采取协调限流措施指仅满足区间运输能力约束条件下,乘客按时间和空间的先后顺序乘车,前方车站的乘客具有优先权,求解时采用逐次递推的方法即可求解各区间通过客流量及车站滞留客流量;协调限流措施则考虑了前后车站间的协调,以均匀分配运力,提高运输效率.因此,模型求解时需要同时进行.
表 4为计算得到的协调限流下车站分时段控流率;表 5为计算得到的不采取协调限流下车站分时段控流率.从受限流的车站可以看出,结果与协调限流的思路一致:A5、A6是大客流发生站,虽然列车经过A3、A4的剩余运力满足其客流需求,但是为了给A5、A6预留更大的剩余运力,模型对A3、A4实施了限流措施;对比两种情况下的车站控流率的数值可以看出,采用协调限流模型,由于受模型最大控流率的约束,A5、A6的控流率有多个时段达到50%,这说明车站受大客流压力很大;不进行协调限流,而是直接对大客流发生站进行限流,有多个时段的车站控流率超过50%,甚至达到61%,这将严重降低A5、A6乘客的服务质量.
| 表 4 协调限流下车站分时段控流率 Tab. 4 The controlled flow rate at stations at every period under current-limiting |
| 表 5 不采取协调限流下车站分时段控流率 Tab. 5 The controlled flow rate at stations at every period without current-limiting |
表 6给出了控制时段内协调限流与实际限流的车站滞留人数.滞留人数是每个时段实际客流与进站客流的差值,是衡量车站客流积压严重程度最直观的数据.通过对比采取协调限流和不采取两种情况,可以得到各站滞留乘客的增量,通过加总协调限流后各车站滞留乘客的增量,可知协调限流后,减少总体滞留人数160人次,节约800 min的等候时间.再者,在某些时段的站点,如(5,7)、(6,10)等,不采取协调限流的车站A5的滞留客量从时段3开始累加,到时段7已超过500人,相对于车站A5的站台面积而言,车站A5存在爆发群体事故的风险;而采取协调限流措施可以有效地控制风险,避免发生险情,因此,通过车站间的协调限流,能够将拥挤压力分散到多个车站,降低单个车站过度拥挤带来的分析.
| 表 6 协调限流和实际限流下车站分时段滞留人数对比 Tab. 6 Comparison of detained passenger's number under coordinated current limit and actual current limit |
1) 根据产生原因将突发大客流分成4类:节假日大客流、大型活动大客流、恶劣天气大客流和地铁故障大客流.以车站站台为控制点,研究站台客流量的动态变化,分析突发大客流形成的内在机理,为后续模型研究提供基础.
2) 构建了线路上的多车站协调限流优化模型,以人均延误最小和各区间运力满载率之和最大为目标,完善了最大控流率、车站安全约束等相关约束条件,为大客流疏散提供可量化依据.
3) 通过协调限流模型的算例分析,计算了采取协调限流和不采取两个情况下的车站控流率和滞留人数,结果表明:通过协调限流,对部分非拥堵车站提前进行客流控制,为拥堵车站提供更大的剩余运力的策略,可以从系统角度降低人均延误,提高运输效率.
| [1] |
苗沁. 城市突发大客流的轨道交通解决方案[J]. 都市快轨交通, 2015, 28: 62. MIAO Qin. How to solve unexpected large passenger flow with metro[J]. Urban Rapid Rail Transit, 2015, 28: 62. DOI:10.3969/j.issn.1672-6073.2015.04013 |
| [2] |
张伦, 陈扶崑. 地铁车站大客流运营组织探讨[J]. 城市轨道交通研究, 2011, 14(5): 87. ZHANG Lun, CHEN Fukun. Research on large passenger flow operating organizations at metro station[J]. Urban Mass Transit, 2011, 14(5): 87. DOI:10.3969/j.issn.1007-869X.2011.05.022 |
| [3] |
刘莲花, 蒋亮. 城市轨道交通网络客流控制方法研究[J]. 铁道运输与经济, 2011, 33(5): 51. LIU Lianhua, JIANG Liang. Research on passenger flow control method of urban rail transit network[J]. Railway Transport and Economy, 2011, 33(5): 51. DOI:10.3969/j.issn.1003-1421.2011.05.014 |
| [4] |
XU X Y, LIU J, LI H Y, et al. Capacity-oriented passenger flow control under uncertain demand: Algorithm development and real-world case study[J]. Transportation Research Part E, 2016, 87: 130. DOI:10.1016/j.tre.2016.01.004 |
| [5] |
GRAVA S. Urban transportation systems[M]. New York: IBT Global, 2003.
|
| [6] |
赵鹏, 姚向明, 禹丹丹. 高峰时段城市轨道交通线路客流协调控制[J]. 同济大学学报(自然科学版), 2014, 42(9): 1340. ZHAO Peng, YAO Xiangming, YU Dandan. Cooperative passenger inflow control of urban mass transit in peak hours[J]. Journal of Tongji University (Natural Science), 2014, 42(9): 1340. DOI:10.3969/j.issn,0253-374x.2014,09,006 |
| [7] |
潘寒川, 刘志钢, 邹承良, 等. 城市轨道交通网络协调限流优化研究[J]. 重庆交通大学学报(自然科学版), 2018, 37(5): 77. PAN Hanchuan, LIU Zhigang, ZOU Chengliang. Optimization of cooperative passenger flow control in urban rail transit network[J]. Journal of Chongqing Jiaotong University (Natural Sciences), 2018, 37(5): 77. DOI:10.3969/J.ISSN.1674-0696.2017 |
| [8] |
刘晓华. 城市轨道交通线路客流协同控制[J]. 城市轨道交通研究, 2014(5): 106. LIU Xiaohua. Cooperative passenger inflow control of urban mass transit[J]. Urban Mass Transit, 2014(5): 106. |
| [9] |
姚向明, 赵鹏, 乔珂, 等. 城市轨道交通网络客流协同控制模型[J]. 中南大学学报(自然科学版), 2015(1): 342. YAO Xiangming, ZHAO Peng, QIAO Ke. Coordinated passenger inflow control model of urban rail transit network[J]. Journal of Central South University (Natural Science), 2015(1): 342. DOI:10.1187/j.issn.1672-7207.2015.01.046 |
| [10] |
JIN J G, TANG L C, SUN L, et al. Enhancing metro network resilience via localized integration with bus services[J]. Transportation Research Part E Logistics & Transportation Review, 2014, 63(2): 17. |
| [11] |
杨晓光. 考虑进出口匝道排队约束的城市快速道路交通系统动态控制方法[J]. 长安大学学报(自然科学版), 1999(2): 20. YANG Xiaoguang. An approach to dynamic traffic control system for urban expressway with constraint of queue length of on-ramp & off-ramp[J]. Journal of Xi'an Highway University (Natural Science), 1999(2): 20. DOI:10.19721/j.cnki.167-8879.1999.02.007 |
| [12] |
周玮腾.拥塞条件下的城市轨道交通网络流量分配演化建模及疏导策略研究[D].北京: 北京交通大学, 2016 ZHOU Weiteng. Modeling passenger flow assignment and evolution in urban rail transit network with dispersion strategy research under congestion conditions[D]. Beijing: Beijing Jiaotong University, 2016 http://cdmd.cnki.com.cn/Article/CDMD-10004-1016059131.htm |
| [13] |
李倩.城市轨道交通大型活动客流网络传播规律研究[D].北京: 北京交通大学, 2016 LI Qian. Study of the network propagation law of urban rail transit passenger flow during the end of big event[D]. Beijing: Beijing Jiaotong University, 2016 |
| [14] |
宋利明. 地铁线网大客流应对措施探讨[J]. 城市轨道交通研究, 2011, 14(8): 49. SONG Liming. Measures for large passenger flow organization in metro[J]. Urban Mass Transit, 2011, 14(8): 49. DOI:10.16037/j.1007-869x.2011.08.019 |
| [15] |
王静, 刘剑锋, 马毅林, 等. 北京市轨道交通车站客流时空分布特征[J]. 城市交通, 2013, 11(6): 18. WANG Jing, LIU Jianfeng, MA Yilin. Temporal and spatial passenger flow distribution characteristics at rail transit stations in Beijing[J]. Urban Transport of China, 2013, 11(6): 18. DOI:10.13813/j.cn11-5141/u.2013.06.004 |
 2019, Vol. 51
2019, Vol. 51


