UCAV编队作战是近年来的研究热点,UCAV编队作战可充分利用有限单机资源,共同执行复杂任务[1],如协同侦查、协同搜救、态势感知与评估、多目标打击等[2]. UCAV编队队形优化是研究UCAV编队控制的前提与关键,合理有效的队形设计可以延长无人机编队飞行距离、节省燃料消耗、增加编队灵活性,提高其安全性与任务完成率[3].由于不同型号的UCAV,其通信能力、协同能力、作战能力等性能也存在差异.队形优化是指,在满足环境、任务需求等约束条件的前提下,以作战损耗和收益为性能指标,为每个任务优化出UCAV编队队形以及UCAV在编队中的站位.
目前,关于UCAV编队研究主要集中在任务分配[4]、航迹规划[5]以及跟踪控制[6]等方面,队形优化相关研究成果较少.南京航空航天大学钱斌等[7]采用遗传算法(genetic algorithm,GA)解决大规模直升机编队队形优化问题,有效克服了传统方法的局限性.西北工业大学夏庆军等[8]在采用市场机制完成任务分配的基础上,提出了利用自适应GA完成大规模无人机编队协同空战队形优化,提高了编队作战的效能.英国肯特大学SPANOGIANOPOULOS等[9]提出一种改进的粒子群优化(particle swarm optimization, PSO)算法,用于优化编队中无人机站位问题,相比其他PSO算法,该算法有更快的收敛性.
双层规划模型是一种具有主从分层结构的数学模型[10],广泛应用在火力分配、物流优化等领域.空军工程大学余丽山等[11]针对导弹战斗部结构设计与优化问题,建立双层规划模型,采用模拟退火(simulated annealing,SA)算法求解,有效解决了算法求解过程易陷入局部极小值的问题.空军工程大学Fan等[12]针对反导火力分配问题,建立双层规划模型,提出了改进PSO算法,仿真结果表明基于双层规划模型的算法具有较强的全局搜索能力和更快的收敛速度,能有效解决大规模火力分配问题.北京交通大学Sun[13]针对运输网络设计优化问题,建立双层规划模型,采用GA求解,有效解决了物流运输问题.
对于求解复杂约束环境下的组合优化问题,离散粒子群优化(discrete particle swarm optimization, DPSO)算法存在收敛速度慢、精度低[14],易陷入局部极值等缺点. SA算法寻优效果好[15],能够克服DPSO算法的缺陷.但是基于单层规划的算法对于解决十分复杂约束的组合优化问题迭代后期收敛速度慢,且易陷入局部最优.
本文在文献[4]的研究基础上,设计双层规划模型,解决复杂约束环境下的大规模UCAV编队队形优化问题.针对改进DPSO-SA算法求解队形优化问题存在迭代后期收敛速度慢且易陷入局部极值的问题,提出双层规划模型,有效解决大规模UCAV编队队形优化问题.
1 双层规划模型双层规划模型主要用来研究两个具有相互作用的不同目标函数之间的关系.上层目标函数优先于下层目标函数,下层目标函数随上层目标函数的变化而不断变化[16].由于上下层迭代过程中策略的选取会相互干扰影响,并且上下层中一方的选择又不能完全影响另一方的选择,所以上层目标函数要根据下层目标函数的选择规划出最有利于自己的结果[10].
双层规划模型是由相互关联的上层规划模型(Up)和下层规划模型(Lo)组成,其数学模型可以表示为
| $ \left\{ \begin{array}{l} \left( {{\rm{Up}}} \right)\;\;\;\;\;\;\max F\left( {x,y} \right),\\ {\rm{subject}}\;{\rm{to:}}G\left( {x,y} \right) \le 0;\\ \left( {{\rm{Lo}}} \right)\;\;\;\;\;\;\max f\left( {x,y} \right),\\ {\rm{subject}}\;{\rm{to:}}g\left( {x,y} \right) \le 0. \end{array} \right. $ | (1) |
式中:F(x, y)和G(x, y)分别代表上层规划模型的性能指标和约束指标,f(x, y)和g(x, y)分别代表下层规划模型的性能指标和约束指标.
以大规模UCAV编队空对地饱和打击作战为背景,建立大规模UCAV协同作战编队队形优化问题描述.
1.1 约束指标1) 燃料约束.燃料约束是确保UCAV能够执行任务的前提.燃料消耗与UCAV飞行长度和单位距离燃料消耗密切相关,可以表示为
| $ {f_i} = 2 \cdot {f_{{\rm{u}},i}} \cdot {d_{i,j}}, $ | (2) |
| $ {d_{i,j}} = \sqrt {{{\left( {p_{{\rm{u}},i}^{\rm{x}} - p_{{\rm{t}},j}^{\rm{x}}} \right)}^2} + {{\left( {p_{{\rm{u}},i}^{\rm{y}} - p_{{\rm{t}},j}^{\rm{y}}} \right)}^2}} . $ | (3) |
式中:di, j为第i个UCAV与第j个任务目标之间的长度,fu, i为第i个UCAV的单位燃料消耗,pu, ix和pu, iy分别为第i个UCAV的横纵坐标位置,pt, jx和pt, jy分别为第j个任务的横纵坐标位置.
为了确保完成任务后UCAV安全返回基地,要求自身携带燃料能够大于自身消耗的燃料,可以表示为
| $ {f_i} \le {f_{{\rm{c}},i}}. $ | (4) |
式中fc, i为第i个UCAV携带的燃料容量.
2) 编队作战能力约束.编队作战能力约束是上层队形规划的关键约束. au, ij为第i个UCAV的第j种能力,其中i=1, ..., U, U为UCAV的数目,j=1, ..., 5, 5种能力分别为防御、预警侦查、通讯协同、火力打击和电子干扰[17]. UCAV成本可能从几百美元(一次性火力支援弹药)到数十万美元(持续飞行战斗成员)不等,故用vui表示第i个UCAV的成本.根据编队内UCAV作战能力及其成本,执行第k个任务的编队第j种实际作战能力,可以表示为
| $ a_{{\rm{r}},k}^j = 1 - \prod\limits_{i = 1}^{{l_{{\rm{r}},k}}} {\left( {1 - a_{{\rm{u}},i}^j} \right) \cdot v_{\rm{u}}^i} . $ | (5) |
式中lr, k为执行第k个任务的实际UCAV数目.
根据编队实际作战能力,编队执行第i个任务目标时保护能力与实际防御、预警侦查和通信协同有关,可以表示为
| $ D_{\rm{o}}^i = a_{{\rm{r}},i}^1 \cdot \left( {a_{{\rm{r}},i}^2 + a_{{\rm{r}},i}^3} \right). $ | (6) |
根据编队实际作战能力,编队执行第i个任务目标的打击能力与实际预警侦查、通信协同、火力打击和电子干扰能力有关,可以表示为
| $ A_{\rm{o}}^i = \left( {a_{{\rm{r}},i}^2 + a_{{\rm{r}},i}^3} \right) \cdot \left( {a_{{\rm{r}},i}^4 + a_{{\rm{r}},i}^5} \right). $ | (7) |
3) UCAV数目约束.UCAV数目约束是确保每个任务都有合适数量的UCAV来执行.根据UCAV编队饱和作战模式,由多个UCAV打击一个任务目标.每个任务目标所需UCAV数目有上下限,可以表示为
| $ l_i^1 \le {l_{{\rm{r}},i}} \le l_i^2,i = 1,2, \cdots ,T. $ | (8) |
式中:li2、li1分别为第i个任务所需UCAV的上、下限,T为任务的数目.要求编队中的每个UCAV都需要执行任务且只执行一个任务,可以表示为
| $ \sum\limits_{j = 1}^T {{\delta _{i,j}}} = 1,i = 1,2, \cdots ,U. $ | (9) |
4) 编队队形站位约束.编队队形站位约束是下层站位规划的关键约束.编队战斗队形是指航空兵遂行战斗任务时在空中的UCAV部署及其编队形态.按形态分为梯队、菱队、V队(楔队)、纵队、蛇形队、横队、箭队和三角队等队形.选择合理有效的战斗队形,能增加编队灵活性,提高其安全性与作战效能.不同的编队队形,能够处理的任务类型不同.如菱队常用于打击点线状目标[18];梯队常用于火力攻击;V队常用于出航、巡逻和轰炸[19];环队常用于协同探测与防御[20];横队(纵队)常用于协同突防攻击一体化[21],其中横队还常用于正面搜索;箭队常用于携带核武器;三角队常用于超低空飞行协同突防攻击一体化[21];蛇形队常用于大规模编队出航.针对现有的UCAV编队队形,建立9种编队队形及其站位库,如图 1所示.其中,编队中UCAV站位编号遵循从左至右,从上至下的排列顺序.

|
图 1 不同编队队形的UCAV站位编号 Fig. 1 UCAV location number of different formations |
第k种编队中第i个站位的UCAV的保护能力与站位影响因子、UCAV的防御、预警侦查和通信协同有关,可以表示为
| $ D_{{\rm{u}},k}^i = L_{i,k}^1 \cdot a_{{\rm{u}},i}^1 \cdot \left( {L_{i,k}^2 \cdot a_{{\rm{u}},i}^2 + L_{i,k}^3 \cdot a_{{\rm{u}},i}^3} \right). $ | (10) |
式中Li, kj为第k种编队中第i个站位的UCAV第j种能力的影响因子,其中j=1, ..., 5.
第k种编队中第i个站位的UCAV的打击能力与站位影响因子、UCAV的预警侦查、通信协同、火力打击和电子干扰能力有关,可以表示为
| $ A_{{\rm{u}},k}^i = \left( {L_{i,k}^2 \cdot a_{{\rm{u}},i}^2 + L_{i,k}^3 \cdot a_{{\rm{u}},i}^3} \right) \cdot \left( {L_{i,k}^4 \cdot a_{{\rm{u}},i}^4 + L_{i,k}^5 \cdot a_{{\rm{u}},i}^5} \right). $ | (11) |
1) 任务代价指标.任务代价函数主要UCAV执行任务自身的毁伤代价和燃料消耗代价两个部分.执行任务毁伤代价s通过UCAV编队执行任务目标时的被毁伤概率和UCAV编队防御能力综合得到,可以表示为
| $ s = \sum\limits_{i = 1}^T {\left( {A_{\rm{t}}^i/D_{\rm{o}}^i} \right)} . $ | (12) |
式中Ati为第i个任务的打击能力.燃料消耗代价f可以表示为
| $ f = \sum\limits_{i = 1}^U {{f_i}} . $ | (13) |
2) 任务收益指标.任务收益指标与UCAV编队对任务目标的毁伤概率、任务目标的防御能力以及任务目标的重要程度密切相关,可以表示为
| $ g = \sum\limits_{i = 1}^T {\left( {A_{\rm{o}}^i/D_{\rm{t}}^i \cdot v_{\rm{t}}^i} \right)} . $ | (14) |
式中:Dit为第i个任务的保护能力,vti为第i个任务的重要程度.
3) 罚函数.为便于求解,采用罚函数把约束条件转化到性能指标中.将UCAV数量约束条件转化到代价指标中,式(9)可以转化为
| $ {q_1} = \left\{ \begin{array}{l} \sum\limits_{i = 1}^T {\left| {l_i^1 - {l_{{\rm{r}},i}}} \right|} ,l_i^1 > {l_{{\rm{r}},i}};\\ \sum\limits_{i = 1}^T {\left| {l_i^2 - {l_{{\rm{r}},i}}} \right|} ,l_i^2 < {l_{{\rm{r}},i}};\\ 0,其他. \end{array} \right. $ | (15) |
将执行任务目标时UCAV编队队形约束转化到代价指标中,可以表示为
| $ {q_2} = \sum\limits_{i = 1}^T {\sum\limits_{j = 1}^5 {\left| {a_{{\rm{d}},{O_i}}^j - a_{{\rm{r}},{O_i}}^j} \right|} } $ | (16) |
式中:Oi为执行第i个任务的编队队形,ajd, oi为第i个编队的第j种能力.
4) 综合性能指标.上层队形性能指标主要包含任务代价指标、任务收益指标以及罚函数三部分,可以表示为
| $ \begin{array}{l} \max {J_1} = {\omega _1} \cdot g - {\omega _2} \cdot s - {\omega _3} \cdot f - {\omega _4} \cdot {q_1} - {\omega _5} \cdot {q_2},\\ {\rm{subject}}\;{\rm{to}}:\\ \;\;\;\;\;\;\;\begin{array}{*{20}{c}} {\sum\limits_{i = 1}^T {{\delta _{i,j}}} = 1,\forall j = 1, \cdots ,U,{\delta _{i,j}} \in \left\{ {0,1} \right\},}\\ {{f_i} \le {f_{{\rm{c}},i}}.} \end{array} \end{array} $ | (17) |
式中:J1为上层规划的适应度,ω1、ω2、ω3、ω4、ω5分别为收益、毁伤、油耗、执行任务所需UCAV数量罚函数以及队形罚函数的权重系数.
1.3 下层规划性能指标下层站位性能指标主要包含UCAV的保护能力和打击能力两部分,可以表示为
| $ \max {J_2} = - {c_1} \cdot \sum\limits_{i = 1}^T {\sum\limits_{j = 1}^{{l_{{\rm{r}},i}}} {D_{{\rm{u}},{O_i}}^{S_j^i}} } + {c_2} \cdot \sum\limits_{i = 1}^T {\sum\limits_{j = 1}^{{l_{{\rm{r}},i}}} {A_{{\rm{u}},{O_i}}^{S_j^i}} } . $ | (18) |
式中:J2为下层规划的适应度值,Sij为上层规划的编队队形优化结果,c1、c2分别为UCAV的保护能力和打击能力的权重系数.
2 编码方式粒子解使用结构体表示,结构体中的变量使用多维整数向量编码表示.上层规划中Tp.x表示UCAV执行任务的编号,Tp.x的下标表示UCAV编号;Tp.o表示执行任务的UCAV编队队形编号;下层规划中Up, i.x表示执行第i个任务的UCAV编号,Up, i.x的下标表示UCAV在编队中的站位编号.如图 2所示,上层规划中粒子解Tp.x为3-3-2-1-2-1-3-3-1-2,Tp.o为3-7-6,表示UCAV4、UCAV6、UCAV9执行任务1,其形成的编队队形为3;UCAV3、UCAV5、UCAV10执行任务2,其形成的编队队形为7;UCAV1、UCAV2、UCAV7、UCAV8执行任务3,其形成的编队队形为6.下层规划中Up, 1.x为9-6-4,表示执行任务1的UCAV编队中,UCAV9在编队中1号位置,UCAV6在编队中2号位置,UCAV4在编队中3号位置.
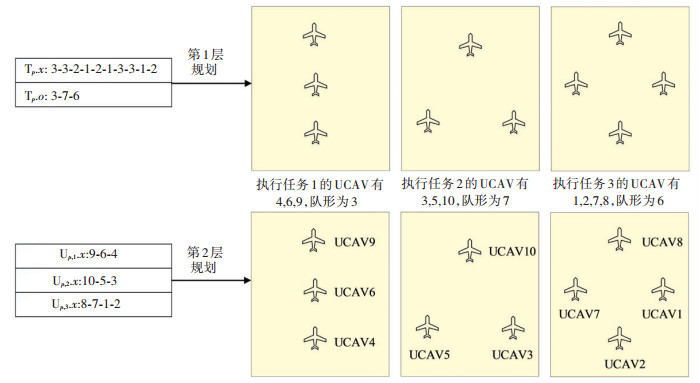
|
图 2 粒子编码方式示意图 Fig. 2 Schematic diagram of particle encoding mode |
目前,对于求解组合优化问题主要有3种DPSO算法:PSO直接离散化、重定义速度位置搜索模型以及基于GA思想的方法[14].本文采用基于GA思想的DPSO算法,引入GA求解组合优化问题时的变异与交叉算子,通过交叉算子向个体极值和全局极值进行学习;通过变异算子对粒子自身进行变异.
SA算法中的Metropolis准则虽然提高了算法的收敛精度,但也存在收敛速度慢的缺陷.为提高SA算法的收敛速度,引入动态温度衰减因子[4].动态温度衰减因子的选取可以表示为
| $ r\left( k \right) = 0.099 \cdot \left( {\frac{{{{\rm{e}}^{0.05\left( { - k + \frac{K}{2}} \right)}}}}{{1 + {{\rm{e}}^{0.05\left( { - k + \frac{K}{2}} \right)}}}} + 9} \right). $ |
式中K为总迭代次数,函数曲线如图 3所示.
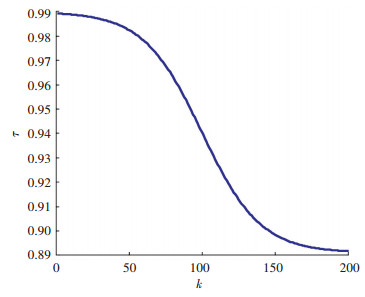
|
图 3 温度衰减因子r和迭代次数k关系曲线 Fig. 3 r-k curves of specimens |
在SA算法的初期,温度衰减因子的值较大,温度Te减小的速度较慢,则SA算法接受较差解的概率e(-Δf/Te)就会较大,使得粒子能够在全局范围内寻优.在SA算法的后期,温度衰减因子的值较小,温度Te减小的速度较快,则SA算法接受较差解的概率e(-Δf/Te)就会较小,使得粒子能够收敛到最优值,提高了SA算法后期的收敛速度.
将DPSO算法和改进SA算法相结合,提出了改进的DPSO-SA算法.
3.2 基于双层规划模型的算法基于单层规划模型的优化算法,如DPSO-SA算法,求解复杂约束问题收敛速度慢且易陷入局部极值.双层规划通过分层迭代思想,即在上层规划和下层规划之间反复迭代[10],可以提高算法的收敛速度和求解精度.上层规划需要为每个任务分配UCAV并优化出编队队形,约束复杂,而DPSO-SA算法非常适应于复杂约束环境中优化问题的求解,故上层规划采用DPSO-SA算法.下层规划针对执行每个任务的编队队形,优化出每个UCAV在编队中的位置,无约束条件,通过简单的交叉倒置等操作即可优化,故下层规划采用GA.如图 4所示,描述了基于双层规划模型的算法流程,详细步骤如下所述.
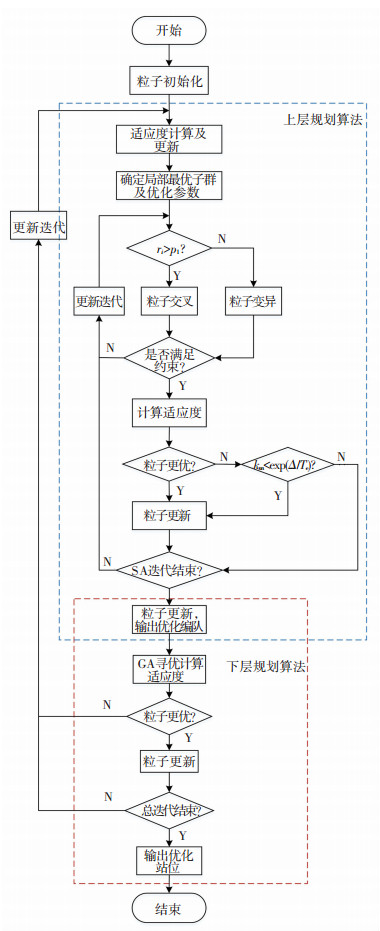
|
图 4 基于双层规划模型的算法 Fig. 4 Algorithm based on bi-level programming model |
步骤1 参数设置以及种群初始化.参考文献[4],设置算法的相关参数,并根据种群大小随机产生粒子,跳转到步骤6.
步骤2 上层规划适应度计算.根据粒子计算上层规划适应度并完成更新,上层规划适应度通过式(17)中上层队形性能指标计算得到.
步骤3 上层规划产生新粒子.对每个粒子进行SA邻域搜索,并产生新的粒子.在区间[0, 1]生成一个随机数ri,如果这个随机数大于学习选择概率p1,那么进行交叉操作;否则进行变异操作.
1) 交叉操作时,在全局最优粒子、局部最优粒子以及随机粒子中确定交叉操作的对象,可以表示为
| $ {P_{\rm{o}}} = \left\{ \begin{array}{l} {P_1},{r_j} < {p_2}\;且\;k < {K_{{\rm{th}}}};\\ {P_g},{r_j} < {p_2}\;且\;k \ge {K_{{\rm{th}}}};\\ {P_{\rm{r}}},其他. \end{array} \right. $ |
式中:Pg为全局最优粒子,Pl为局部最优粒子,Pr为随机粒子,rj为在区间[0, 1]生成一个随机数,p2为学习选择概率,Kth为迭代次数阈值.
2) 变异操作时,从当前粒子中随机选择两个基因,将其之间的基因翻转.
步骤4 判断是否接受新粒子.计算新粒子的适应度,如果适应度比更新前好,接受新粒子;否则,根据Metropolis机制确定是否接受.
步骤5 上层规划是否终止.判断SA过程是否结束,如果结束,输出上层规划结果;否则,跳到步骤3.
步骤6 下层规划新粒子.根据上层规划结果对粒子初始化,选择遗传算子,更新产生新粒子.
步骤7 下层规划适应度计算.计算新粒子下层规划适应度,下层规划适应度是通过式(18)中下层站位性能指标计算得到.如果优于遗传操作前粒子的适应度,则更新该粒子;否则不更新,跳转到步骤2.
步骤8 判断总迭代次数是否结束,如果结束,输出下层规划结果;否则,跳到步骤2.
4 仿真与分析为了验证所设计模型的有效性,基于MATLAB2014a环境进行仿真分析.
4.1 队形优化数据设置粒子数量n=100,r1=20,K=200,L=5,SA初始温度Te=8,性能指标适应度值权重ω1=10, ω2=1, ω3=0.000 5, ω4=1 000, ω5=10, c1=10, c2=10.其中,收益指标在100数量级上,损失指标、UCAV的保护能力指标和打击能力指标在101数量级上,油耗指标在105数量级上,以上权重系数使各项指标在同一数量级上,为使任务能够满足所需UCAV数量约束,执行任务所需UCAV数量罚函数权重系数ω4取值相对较大一些.
仿真验证场景如图 5所示,为1 000 km×1 000 km的空间.设置U=50,T=5,UCAV基地与任务目标在战场环境中的分布如图 5所示,编号为1~25的UCAV在1,编号为26~50的UCAV在基地2.任务性能参数见表 1.不同编队队形作战能力不同,参数见表 2.为简化约束,假设所有UCAV单位燃料消耗均为1,则燃料容量约束可以简化为航程长度表示的代价性能指标,因为UCAV数目过多,UCAV性能参数以及UCAV在编队队形中站位影响因子数据过大,这里不再赘述.

|
图 5 仿真场景分布 Fig. 5 Distribution of simulation environment |
| 表 1 任务属性 Tab. 1 Task attributes |
| 表 2 队形作战能力参数 Tab. 2 Operational capability parameters of formations |
如图 6所示,上层规划模型中引入改进前后的SA算法.其中,适应度为双层规划模型的适应度,是通过上层和下层规划的适应度相加得到. 图 6表明,与包含静态温度衰减因子的DPSO-SA算法相比,引入动态温度衰减因子的DPSO-SA算法收敛速度更快,精度更高.

|
图 6 DPSO-SA中动态和静态温度衰减因子对比 Fig. 6 Comparison of dynamic and static temperature attenuation factors in DPSO-SA |
基于双层规划模型的算法、单层规划模型DPSO算法以及单层规划模型DPSO-SA算法3种算法对比仿真,运行结果如图 7所示,其中基于双层规划模型的算法的平均适应度为-10.39,运行时间为32.92 s;单层规划模型DPSO算法的平均适应度为-12.48,运行时间为52.41 s;单层规划模型DPSO-SA算法的平均适应度为-11.11,运行时间为55.72 s.单层规划模型的适应度是通过综合上层和下层规划适应度值得到的,单层规划模型采用的性能指标参数与双层规划模型的相同.
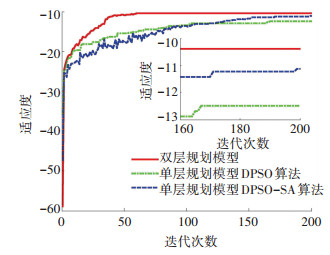
|
图 7 3种算法对比 Fig. 7 Comparison of three algorithms |
可以看出,和单层规划模型相比,采用双层规划模型平均最优适应度更高且求解时间更快,表明改进算法在迭代过程中有利于粒子跳出局部最优值,快速找到优化解.由图 7可以看出,相比单层规划模型,基于双层规划模型的算法在迭代70次左右就能收敛且收敛精度较高,验证了双层规划模型能有效提高收敛速度和收敛精度.
采用基于双层规划模型的算法进行求解,优化结果见表 3.
| 表 3 编队队形优化结果 Tab. 3 Formation optimization results |
为验证所设计算法处理大规模UCAV编队队形优化问题的效能,采用不同数量的UCAV仿真验证,UCAV数量为20、40、60、80、120、160、200时,其运行时间分别为20、26、35、41、53、66、77 s.将这些数据进行拟合,绘制算法运行时间随UCAV数目变化的曲线,如图 8所示.由图 8可知,设计算法的运行时间随UCAV数目近似线性变化.

|
图 8 运行时间t与UCAV数目U关系曲线 Fig. 8 t-U curves of specimens |
1) 针对大规模UCAV编队队形优化问题,建立编队作战队形优化双层规划模型,上层规划采用DPSO-SA算法求解,得到执行每个任务的UCAV编号及其最优编队队形;下层规划采用GA求解,得到UCAV在编队队形中的位置.
2) 针对求解大规模UCAV编队队形优化问题,DPSO算法存在后期收敛速度慢的缺陷,融合改进的SA算法,提出了DPSO-SA算法.
3) 仿真结果表明,相比单层模型的求解算法,基于双层规划模型的求解算法对于求解大规模编队队形优化问题收敛速度更快,寻优效果更好.基于双层规划模型算法的运行时间随UCAV数目线性增加,可以有效解决大规模编队队形优化问题.设计UCAV航迹规划算法以及把算法嵌入UCAV编队平台将是下一步的研究工作.
| [1] |
邱华鑫, 段海滨, 范彦铭. 基于鸽群行为机制的多无人机自主编队[J]. 控制理论与应用, 2015, 32(10): 1298. QIU Huaxin, DUAN Haibin, FAN Yanming. Multiple unmanned aerial vehicle autonomous formation based on the behavior mechanism in pigeon flocks[J]. Control Theory & Applications, 2015, 32(10): 1298. DOI:10.7641/CTA.2015.50314 |
| [2] |
SCHOERLING D, KLEECK C V, FAHIMI F, et al. Experimental test of a robust formation controller for marine unmanned surface vessels[J]. Autonomous Robots, 2010, 28(2): 213. DOI:10.1007/s10514-009-9163-6 |
| [3] |
宗群, 王丹丹, 邵士凯, 等. 多无人机协同编队飞行控制研究现状及发展[J]. 哈尔滨工业大学学报, 2017, 49(3): 1. ZONG Qun, WANG Dandan, SHAO Shikai, et al. Research status and development of multi UAV coordinated formation flight control[J]. Journal of Harbin Institute of Technology, 2017, 49(3): 1. DOI:10.11918/j.issn.0367-6234.2017.03.001 |
| [4] |
宗群, 秦新立, 张博渊, 等. 基于DPSO-GT-SA算法的大规模UCAV协同任务分配[J]. 天津大学学报(自然科学与工程技术版), 2018, 51(10): 1005. ZONG Qun, QIN Xinli, ZHANG Boyuan, et al. Cooperative task allocation of large-scale UCAV based on DPSO-GT-SA algorithm[J]. Journal of Tianjin University (Science and Technology), 2018, 51(10): 1005. DOI:10.11784/tdxbz201711069 |
| [5] |
张博渊, 宗群, 鲁瀚辰, 等. 基于hp自适应伪谱法的四旋翼无人机编队轨迹优化[J]. 中国科学:技术科学, 2017, 35(7): 69. ZHANG Boyuan, ZONG Qun, LU Hanchen, et al. Trajectory optimization of quad-rotor UAV formation using hp-adaptive pseudospectral method[J]. Science & Technology Review, 2017, 35(7): 69. DOI:10.3981/j.issn.1000-7857.2017.07.008 |
| [6] |
WANG D, ZONG Q, TIAN B, et al. Neural network disturbance observer-based distributed finite-time formation tracking control for multiple unmanned helicopters[J]. Isa Transactions, 2018. DOI:10.1016/j.isatra.2017.12.011 |
| [7] |
钱斌, 姜长生. 遗传算法在直升机空战编队优化中的应用[J]. 电光与控制, 2008, 15(1): 6. QIAN Bin, JIANG Changsheng. On air combat formation of helicopters based on genetic algorithm[J]. Electronics Optics & Control, 2008, 15(1): 6. DOI:10.3969/j.issn.1671-637X.2008.01.002 |
| [8] |
夏庆军, 张安, 张耀中. 大规模编队空战队形优化算法[J]. 控制理论与应用, 2010, 27(10): 1418. XIA Qingjun, ZHANG An, ZHANG Yaozhong. Formation optimizing algorithm for large-scale air combat[J]. Control Theory & Applications, 2010, 27(10): 1418. DOI:10.7641/j.issn.1000-8152.2010.10.CCTA090692 |
| [9] |
SPANOGIANOPOULOS S, ZHANG Q, SPURGEON S. Fast formation of swarm of UAVs in congested urban environment[J]. IFAC-PapersOnLine, 2017, 50(1): 8031. DOI:10.1016/j.ifacol.2017.08.1228 |
| [10] |
赵志刚, 顾新一, 李陶深. 求解双层规划模型的粒子群优化算法[J]. 系统工程理论与实践, 2007, 27(8): 92. ZHAO Zhigang, GU Xinyi, LI Taoshen. Particle swarm optimization for bi-level programming problem[J]. Systems Engineering Theory & Practice, 2007, 27(8): 92. DOI:10.12011/1000-6788(2007)8-92 |
| [11] |
余丽山, 李彦彬, 金学科, 等. 双层规划模型在导弹破片杀伤战斗部优化设计中的应用[J]. 弹箭与制导学报, 2017, 37(2): 71. YU Lishan, LI Yanbin, JIN Xueke, et al. Application of bi-level programming model in optimization design of missile fragmenting warhead[J]. Journal of Projectiles Rockets Missiles & Guidance, 2017, 37(2): 71. DOI:10.15892/j.cnki.djzdxb.2017.02.017 |
| [12] |
FAN C L, XING Q H, FU Q, et al. Bi-level programming modeling and hierarchical hybrid algorithm for antimissile dynamic firepower allocation problem with uncertain environment[J]. Pattern Analysis & Applications, 2017, 20(1): 287. DOI:10.1007/s10044-016-0562-y |
| [13] |
SUN Z. Continuous transportation network design problem based on bi-level programming model[J]. Procedia Engineering, 2016, 137: 277. DOI:10.1016/j.proeng.2016.01.259 |
| [14] |
郑东亮, 薛云灿, 杨启文, 等. 基于Inver-Over算子的改进离散粒子群优化算法[J]. 模式识别与人工智能, 2010, 23(1): 97. ZHENG Dongliang, XUE Yuncan, YANG Qiwen, et al. Modified discrete particle swarm optimization algorithm based on Inver-Over operator[J]. Pattern Recognition and Artificial Intelligence, 2010, 23(1): 97. DOI:10.16451/j.cnki.issn1003-6059.2010.01.013 |
| [15] |
BANK M, GHOMI S M T F, JOLAI F, et al. Application of particle swarm optimization and simulated annealing algorithms in flow shop scheduling problem under linear deterioration[J]. Advances in Engineering Software, 2012, 47(1): 1. DOI:10.1016/j.advengsoft.2011.12.001 |
| [16] |
GUO H, LI J, HONG G. A survey of bilevel programming model and algorithm[C]//Fourth International Symposium on Computational Intelligence and Design. Hangzhou: IEEE, 2011: 199. DOI: 10.1109/ISCID.2011.151 https://www.researchgate.net/publication/221261291_A_Survey_of_Bilevel_Programming_Model_and_Algorithm
|
| [17] |
常一哲, 李战武, 寇英信, 等. 不确定信息条件下空战接敌队形选择方法[J]. 系统工程与电子技术, 2016, 38(11): 2552. CHANG Yizhe, LI Zhanwu, KOU Yingxin, et al. Method for formation selection in air combat under uncertain information condition[J]. Systems Engineering and Electronics, 2016, 38(11): 2552. DOI:10.3969/j.issn.1001-506X.2016.11.16 |
| [18] |
朱旭.基于信息一致性的多无人机编队控制方法研究[D].西安: 西北工业大学, 2014 ZHU Xu.Research on multi-UAV formation control based on information consensus[D]. Xi'an: Northwestern Polytechnical University, 2014 |
| [19] |
欧超杰.多无人机编队控制技术研究[D].南京: 南京航空航天大学, 2015 OU Chaojie.UAVs formation flight control[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2015 |
| [20] |
ZHU S, WANG D, LOW C B. Cooperative control of multiple UAVs for moving source seeking[C]//International Conference on Unmanned Aircraft Systems. Atlanta: IEEE, 2013. DOI: 10.1109/ICUAS.2013.6564690 https://link.springer.com/article/10.1007/s10846-013-9899-2
|
| [21] |
王芳.导弹编队协同突防-攻击一体化队形优化设计及最优控制研究[D].哈尔滨: 哈尔滨工业大学, 2016 WANG Fang. Formation optimal design and optimal control method for integrative penetration and attack of missile formation cooperation[D]. Harbin: Harbin Institute of Technology, 2016 |
 2019, Vol. 51
2019, Vol. 51


