2. 系统控制与信息处理教育部重点实验室(上海交通大学),上海 200240;
3. 上海交通大学 机器人研究所,上海 200240
2. Key Laboratory of System Control and Information Processing (Shanghai Jiao Tong University), Ministry of Education, Shanghai 200240, China;
3. Research Institute of Robotics, Shanghai Jiao Tong University, Shanghai 200240, China
在智能交通系统中,磁钉导航是一种有着广泛应用前景的导航方法.相比于基于GPS、视觉或激光雷达等传感器的方法,磁钉导航有着不易受天气影响、可以在多种环境下工作的优点.在1996年的日本AHS项目[1]、1997年的美国加州PATH项目[2]以及2009年的上海交通大学CyberC3实验室的研究项目[3]中,磁钉导航都获得了成功的应用.
早期的磁钉导航项目仅仅依赖于磁钉间的航位推算和车辆经过磁钉时检测到的横向偏差来控制车辆,这是一个无前瞻的look-down系统,不仅给车辆控制算法的设计带来了很大的困难,而且只能适用于曲率变化很小的道路场景(高速公路).为了克服无前瞻的问题,文献[4-5]提出使用RTK-GPS来建立磁钉地图,从而获得无限的前瞻,使得磁钉导航可以适用于任何道路场景.文献[3]对该方法进行了成功的应用.但是,这种建图方法需要采用RTK-GPS对地图中的磁钉逐点测量坐标,不仅成本高,而且费时费力,对于磁钉数量很多的大场景地图显然是不可行的.另外,GPS信号容易受遮挡也限制了这种方法的应用.近些年来,一些研究人员开始尝试用新的方法来建立磁钉地图.文献[6-8]提出了曲率地图的概念,将相邻磁钉间的相对位置关系描述为曲率地图,在导航过程中,通过磁钉计数来查询曲率地图,获取前方道路的曲率信息,从而提供有效前瞻,完成导航.这种方法建图简单快捷,但其建立的曲率地图不含有全局信息,且依赖于磁钉计数导致其仅适用于单环路的磁钉地图,如果地图中有磁钉轨迹交叉的路口,则无法完成计数.文献[9]针对曲率地图无法提供全局信息的问题,创新性地提出使用图优化的思想来建立磁钉地图.对于单环路磁钉地图,人工驾驶数据采集车沿着磁钉环路跑多圈,通过磁钉计数识别多圈间的同一磁钉,建立闭环约束.再使用图优化方法优化整张图,进而得到磁钉地图.这种方法可以得到全局信息,但仍依赖磁钉计数,无法解决有磁钉轨迹交叉的磁钉地图的建图问题.而且其图优化方法对错误闭环的鲁棒性差,很容易优化失败.
为了方便描述,本文将有路口、有磁钉轨迹交叉的磁钉地图定义为多路口磁钉地图.针对多路口磁钉地图的建图问题,本文提出了利用磁钉段特征创建磁钉地图的新方法.利用磁钉段特征建立闭环约束,这避免了磁钉计数的缺陷.在图优化过程中,为优化函数引入约束项和附加项,并将动态因子应用于信息矩阵,构成改进的图优化方法,解决了相似磁钉段间容易引入错误闭环约束的问题,提高了算法的鲁棒性.真实道路环境下的实验验证了本文方法的有效性和适用性.
1 磁钉段特征 1.1 磁钉段的定义在磁钉地图中,磁钉段是人为划分的若干个连续磁钉组成的序列,满足条件:1)磁钉段中磁钉的个数不少于两个;2)有明显的标志点标识磁钉段的起点和终点;3)磁钉段和磁钉段之间通过标志点连接.
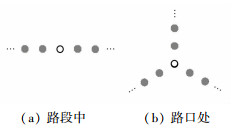
对于条件2,标志点的设定有多种方式,比如利用极性变化的磁钉作为标志点,或者利用两个并排的磁钉作为标志点等等,本文的实验使用了极性变化的磁钉作为标志点.对于条件3,路段中和路口处略有不同,如图 1所示,图中黑色和白色分别代表磁钉的不同极性.
|
图 1 磁钉段的连接 Fig. 1 Link between magnetic segments |
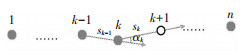
假设道路中存在一个磁钉段,其磁钉个数为n(n≥2),如图 2所示,则磁钉段特征定义为:1)磁钉个数n;2)磁钉极性序列(p1, …, pk-1, pk, pk+1, …, pn);3)磁钉间距序列(s1, …, sk-1, sk, sk+1, …, 0);4)磁钉偏角序列(0, …, αk-1, αk, αk+1, …, 0).其中p为磁钉的极性,由磁尺(磁传感器)测量得到,黑色和白色代表磁钉的不同极性,s、α分别为相邻磁钉的间距与相邻3颗磁钉之间的连线偏角.每个磁钉段的最后一颗磁钉的s为0,第1颗磁钉和最后1颗磁钉的α为0,其他的将由下文方法求取.
|
图 2 磁钉段 Fig. 2 Magnetic segment |
定义世界坐标系的原点为车辆在零时刻本体坐标系的原点,X轴方向为车辆的朝向,并设采样周期为T.在kT时刻,车辆的位姿为(xkv, ykv, θkv)T,从kT时刻到(k+1)T时刻,里程计的增量为ΔSk,航向角的增量为Δθk,利用航位推算,可以得到车辆位姿的递推公式[3-4]为
| $ \left\{ \begin{array}{l} x_{k + 1}^{\rm{v}} = x_k^{\rm{v}} + \Delta {S_k}\cos \left( {\theta _k^{\rm{v}} + \frac{{\Delta {\theta _k}}}{2}} \right),\\ y_{k + 1}^{\rm{v}} = y_k^{\rm{v}} + \Delta {S_k}\sin \left( {\theta _k^{\rm{v}} + \frac{{\Delta {\theta _k}}}{2}} \right),\\ \theta _{k + 1}^{\rm{v}} = \theta _k^{\rm{v}} + \Delta {\theta _k}. \end{array} \right. $ | (1) |
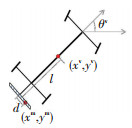
磁尺安装在车辆的后方,距离车辆中心为l,当磁尺运动到磁钉的正上方时,设此时车辆的位姿为(xv, yv, θv),磁钉在磁尺上的横向偏移为d,如图 3所示.
|
图 3 磁钉坐标推导 Fig. 3 Magnet coordinate calculation |
设磁钉的坐标为(xm, ym),由坐标变换,可以求得磁钉在世界坐标系下的坐标为
| $ \left\{ \begin{array}{l} {x^{\rm{m}}} = {x^{\rm{v}}} - l \cdot \cos {\theta ^{\rm{v}}} + d \cdot \sin {\theta ^{\rm{v}}},\\ {y^{\rm{m}}} = {y^{\rm{v}}} - l \cdot \sin {\theta ^{\rm{v}}} - d \cdot \cos {\theta ^{\rm{v}}}. \end{array} \right. $ | (2) |
有了所有磁钉在世界坐标系下的坐标之后,就可以根据磁钉坐标求解前文提到的sk、αk,进而求得磁钉段特征.
设第k颗磁钉的坐标为(xkm, ykm),第k+1颗磁钉的坐标为(xk+1m, yk+1m),有
| $ {s_k} = \sqrt {{{\left( {x_{k + 1}^{\rm{m}} - x_k^{\rm{m}}} \right)}^2} + {{\left( {y_{k + 1}^{\rm{m}} - y_k^{\rm{m}}} \right)}^2}} , $ | (3) |
| $ \begin{array}{l} \cos {\beta _1} = \left( {x_k^{\rm{m}} - x_{k - 1}^{\rm{m}}} \right)/{s_{k - 1}};\sin {\beta _1} = \left( {y_k^{\rm{m}} - y_{k - 1}^{\rm{m}}} \right)/{s_{k - 1}},\\ \cos {\beta _2} = \left( {x_{k + 1}^{\rm{m}} - x_k^{\rm{m}}} \right)/{s_k};\sin {\beta _2} = \left( {y_{k + 1}^{\rm{m}} - y_k^{\rm{m}}} \right)/{s_k},\\ {\alpha _k} = \arcsin \left( {\cos {\beta _1} \cdot \sin {\beta _2} - \sin {\beta _1} \cdot \cos {\beta _2}} \right). \end{array} $ | (4) |
对每个磁钉段进行如上操作,就可以求得磁钉段特征.
2 图的构建基于图优化的SLAM问题通常分为前端和后端两部分.前端负责图的构建,后端负责图的优化估计[10-12].构建图的核心工作是确定优化点的形式和求出优化所需的边.在通常的机器人SLAM问题中,优化点是机器人在某些时刻的位姿的估计值,边是传感器对周围环境的测量求得的闭环约束.而在本文中,优化点是磁钉的全局坐标估计,边是通过磁钉段特征的匹配求得的闭环约束.
利用航位推算可以求得磁钉的坐标估计值,如式(1)、(2),由此可以得到图中的优化点.
有了前文求出的磁钉段特征以后,就可以通过对磁钉段特征进行匹配来建立磁钉段之间的闭环约束.匹配就是求两个磁钉段特征的相似性,满足一定相似性要求则认为是匹配成功,在匹配成功的两个磁钉段之间建立闭环约束.匹配的方法有余弦距离法和欧氏距离法,相比于欧氏距离法,余弦距离法具有固定的取值为[0, 1],更容易进行数值判断,且能够更多地体现两个向量在方向上的差异,因此本文使用余弦距离法进行磁钉段特征的匹配.
设有两个磁钉段,分别为S1、S2,其对应磁钉段特征分别为:1)磁钉个数n1、n2;2)磁钉极性序列
对两组向量,求解余弦距离,得
| $ \left\{ {\begin{array}{*{20}{c}} {\cos p = {{\vec p}_1} \cdot {{\vec p}_2}/\left( {\left| {{{\vec p}_1}} \right| \cdot \left| {{{\vec p}_2}} \right|} \right),}\\ {\cos s = {{\vec s}_1} \cdot {{\vec s}_2}/\left( {\left| {{{\vec s}_1}} \right| \cdot \left| {{{\vec s}_2}} \right|} \right),}\\ {\cos \alpha = {{\vec \alpha }_1} \cdot {{\vec \alpha }_2}/\left( {\left| {{{\vec \alpha }_1}} \right| \cdot \left| {{{\vec \alpha }_2}} \right|} \right),} \end{array}} \right. $ | (5) |
利用如下条件进行相似性判断:
if(n1=n2) & & (cosp>0.8) & &
(cos s>0.8) & & (cos α>0.8)
S1和S2为同一磁钉段;
构建闭环约束.
end
以上条件是对闭环约束的初步构建.其中0.8的阈值是相似度的最低要求.在多路口的磁钉地图中,由于漏检的存在和地图的复杂性,很可能出现两个不同的磁钉段的特征非常相似,满足上述条件而构建了错误闭环约束的情况,这种情况是无法通过阈值的设定来进行限制的.因此,为了使图优化过程对错误的闭环约束具有足够的鲁棒性,本文利用式(5)的结果构成动态信息矩阵,并对图优化算法进行了改进.
3 改进图优化图优化是SLAM问题的后端.在常规图优化算法中,图的因子图表达如图 4所示.其中xi为机器人在i时刻的位姿,ui, j为约束边,ui, j(j=i+1)为里程计约束,通常由航位推算获得,ui, j(j≠i+1)为闭环约束,通常由其他方式获得,比如点云匹配、图像特征匹配[13]等,在本文中,闭环约束通过磁钉段特征匹配得到.

|
图 4 图的因子图表达 Fig. 4 Factor graph representation of a graph |
优化过程本质上是一个利用最小二乘法不断迭代求解优化函数的过程.常规图优化算法不区分里程计约束和闭环约束,在优化的过程中将两者统一考虑,其优化函数为
| $ {X^ * } = \mathop {\arg \min }\limits_X \left[ {\sum\limits_{i,j} {{{\left\| {f\left( {{x_i},{u_{i,j}}} \right) - {x_j}} \right\|}^2}} \cdot {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_{i,j}}} \right]. $ | (6) |
其中Ωi, j为信息矩阵.
实际上,里程计约束一般由航位推算得到,通常误差很小,而闭环约束在发生错误匹配的情况下,误差会很大.对整张图来说,闭环约束是对优化结果起决定作用的,错误的闭环约束将会使优化结果和真实情况相去甚远.因此,更鲁棒的方法是将两者分开,构造新的优化函数[14],即
| $ \begin{array}{l} {X^ * },{S^ * } = \mathop {\arg \min }\limits_{X,S} \left[ {\sum\limits_{i,i + 1} {{{\left\| {f\left( {{x_i},{u_{i,i + 1}}} \right) - {x_{i + 1}}} \right\|}^2}} \cdot } \right.\\ \;\;\;\;\;{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_{i,i + 1}} + \sum\limits_{ij,j \ne i + 1} {{{\left\| {{s_{ij}} \cdot \left( {f\left( {{x_i},{u_{i,j}}} \right) - {x_j}} \right)} \right\|}^2}} \cdot {{\mathit{\boldsymbol{ \boldsymbol{\varOmega} '}}}_{i,j}} + \\ \;\;\;\;\;\left. {\sum {{w_{ij}} \cdot {{\left\| {1 - {s_{ij}}} \right\|}^2}} } \right]. \end{array} $ | (7) |
其中:sij为转换变量,控制闭环约束对优化过程的影响,其本身也是优化变量;wij为附加项,避免sij=0导致正确的闭环约束误差被完全消除;Ωi, j′为动态信息矩阵;Ωi, j为基础信息矩阵.
在常规图优化算法中,Ωi, j取决于传感器精度,对于一个确定的系统,Ωi, j为固定值.然而,当测量的置信度不同时,使用相同的信息矩阵进行优化会让优化结果变差.因此,本文提出利用余弦距离构建动态信息矩阵,即
| $ {{\mathit{\boldsymbol{ \boldsymbol{\varOmega} '}}}_{i,j}} = \cos p \cdot \left[ {\begin{array}{*{20}{c}} {\cos s}&{\cos s}&{\cos \alpha } \end{array}} \right] \cdot {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_{i,j}}. $ | (8) |
式中cos p修正整个信息矩阵的权值,cos s、cos s、cos α分别修正Ωi, j在对角线上的3个值,这3个值对应的是优化目标xi的3个分量的自相关系数的逆.
通过对X, S的联合优化,可以使得正确的闭环约束起作用,而错误的闭环约束的作用被抑制,从而使得优化过程更为鲁棒.
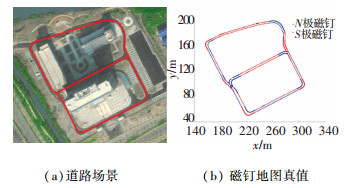
4 实验结果与分析为了验证提出的方法,本文在真实道路环境下进行了建图实验.实验场景如图 5所示,图 5(a)为道路场景,大小约为100 m×120 m,车道均为双向车道. 图 5(b)为磁钉地图的真值,图中共有680颗磁钉,磁钉之间的间距大多在1~2 m之间,个别磁钉间距超过2 m.相同极性的磁钉构成1个磁钉段.
|
图 5 实验场景 Fig. 5 Experimental scenario |
本文使用的数据采集车如图 6所示.采集车上安装的传感器有惯导、里程计和磁尺,惯导和里程计用来推算车辆的位姿,磁尺用来测量磁钉相对于车的位置.采集车由人驾驶在磁钉地图中随意沿轨迹行驶,每个磁钉都至少经过1次.

|
图 6 数据采集车 Fig. 6 Data collection vehicle |
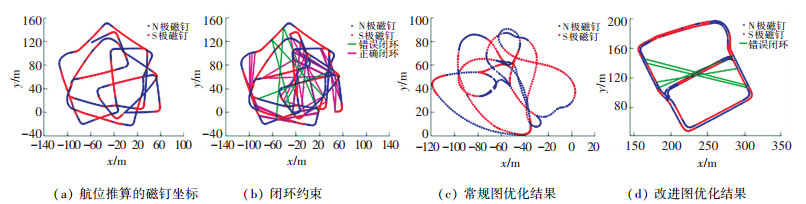
利用航位推算可以求得磁钉坐标,如图 7(a).从图中可以看出,由于航位推算的累积误差,车辆多次经过同一磁钉段时,推算得到的磁钉位置完全不同.整张图也已经看不出地图的形状,这样的地图无法应用于下一步的路径规划和导航.
|
图 7 实验过程 Fig. 7 Experimental process |
利用本文提出的磁钉段特征,寻找图 7(a)中存在的闭环约束,见图 7(b).图中,正确的闭环约束,其连接的两个磁钉是同一磁钉,两个磁钉之间的磁钉段是同一磁钉段;错误的闭环约束,其连接的两个磁钉不是同一磁钉,对应磁钉段特征相似,但并非同一磁钉段.
对含有错误闭环约束的图,常规图优化算法会优化失败,优化结果如图 7(c)所示.可以看到,由于含有错误的闭环约束,常规图优化是失败的,整张图已经和真值完全偏离.
使用本文前述的改进图优化算法,可以得到对错误闭环鲁棒性较好的优化结果,如图 7(d)所示,可以看出,改进图优化算法对于错误闭环约束有很好的鲁棒性,可以大大降低错误闭环约束的影响.
利用ICP算法,将本文建立的磁钉地图和真值地图进行匹配,从而进行对比,如图 8所示.

|
图 8 和真值地图的对比 Fig. 8 Comparison with a true value map |
可以看到,本文方法建立的磁钉地图和真值地图有很好的相似性,多数磁钉段的重复性都比较好,全局一致性良好.但是仍然可以看到,建立的磁钉地图比真值地图略大了一圈,这在SLAM建图中是一种常见的现象[15].航位推算所带来的惯导和里程计的误差累积,会使得地图中路段的长度比真实长度略长,闭环约束和图优化只能减少这部分误差,但无法完全消除.另外,本文的实验场景较大,但图中能建立的闭环约束相对较少,这也使得图优化的效果受到了一定的限制.如果地图中能够有更多的磁钉段提供闭环约束,优化结果会更好.
文献[6-8]得出了磁钉地图的局部精度对于导航更为重要,比较磁钉地图的局部精度更有意义的结论.因此,为了验证本文建立的地图的精度,本文使用RPE(relative pose error)值[16-18]衡量算法结果和真实数据的差距.
用s表示磁钉段中两颗相邻磁钉的间距,α表示相邻磁钉连线相对于世界坐标系的偏角,则对磁钉i和磁钉i+1,在真值地图中,有
| $ \left\{ \begin{array}{l} {s_i} = \sqrt {{{\left( {{x_{i + 1}} - {x_i}} \right)}^2} + {{\left( {{y_{i + 1}} - {y_i}} \right)}^2}} ,\\ {\alpha _i} = \arctan \left( {\frac{{{y_{i + 1}} - {y_i}}}{{{x_{i + 1}} - {x_i}}}} \right). \end{array} \right. $ |
在本文方法建立的地图中,有
| $ \left\{ \begin{array}{l} {{\hat s}_i} = \sqrt {{{\left( {{{\hat x}_{i + 1}} - {{\hat x}_i}} \right)}^2} + {{\left( {{{\hat y}_{i + 1}} - {{\hat y}_i}} \right)}^2}} ,\\ {{\hat \alpha }_i} = \arctan \left( {\frac{{{{\hat y}_{i + 1}} - {{\hat y}_i}}}{{{{\hat x}_{i + 1}} - {{\hat x}_i}}}} \right). \end{array} \right. $ |
则RPE值的计算式为
| $ \left\{ \begin{array}{l} \Delta {s_i} = \left| {{s_i} - {{\hat s}_i}} \right|,\\ \Delta {\alpha _i} = \left| {{\alpha _i} - {{\hat \alpha }_i}} \right|. \end{array} \right. $ |
|
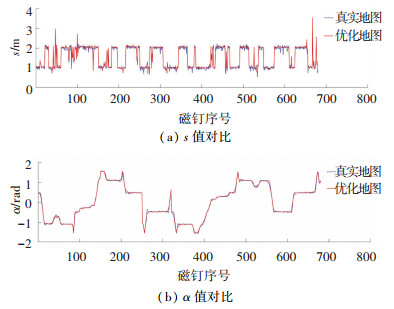
图 9 s、α的比较 Fig. 9 Comparison of s and α |
|
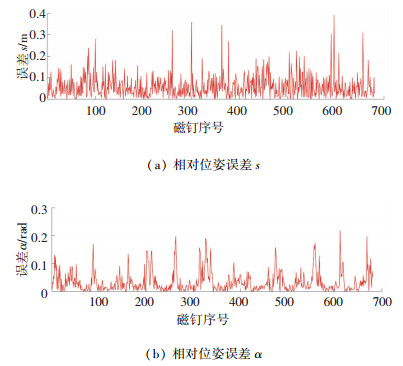
图 10 相对位姿误差 Fig. 10 RPE (relative pose error) |
对上图进行分析可以得到,本文方法建立的地图,95%以上的磁钉的局部精度在15 cm和6°以内,可以满足磁钉导航的需求,基于真实环境的导航实验验证了本文建立的地图的可用性.但同时,在个别位置局部精度并不够好,这是由于在这些位置路面起伏较大,测量受到影响的缘故.如果能够将路面起伏考虑进地图中,建图结果将会更好.
5 结论1) 提出了磁钉段和磁钉段特征的概念,给出了磁钉段的定义和磁钉段特征的求取方法,并利用磁钉段特征的匹配来构建闭环约束,同时利用匹配结果构建了动态信息矩阵.
2) 针对常规图优化算法鲁棒性差的问题,引入了改进图优化算法,并利用动态信息矩阵对该算法进行了进一步的改进.实验结果证明,改进算法对错误闭环有着很强的鲁棒性.
3) 引入了RPE值来衡量建图误差,误差分析显示,利用磁钉段特征创建磁钉地图,建图精度较高,全局一致性良好,真实道路的导航试验证明了地图的可用性.
4) 利用磁钉段特征创建磁钉地图的新方法解决了多路口磁钉地图的创建问题.进一步的研究将致力于如何提高地图的精度以及如何利用该地图进行导航.
| [1] |
ASAOKA A, UEDA S. An experimental study of a magnetic ruler in an automated highway system[C]//Proceedings of Conference on Intelligent Vehicles. Tokyo: IEEE, 1996: 373
|
| [2] |
TAN S H, GULDNER J, PATWARDHAN S, et al. Development of an automated steering vehicle based on roadway magnets-A case study of mechatronic system design[J]. IEEE/ASME Transactions on Mechatronics, 1999, 4(3): 258. DOI:10.1109/3516.789684 |
| [3] |
XU Haigui, YANG Ming, WANG Chunxiang, et al. Magnetic sensing system design for intelligent vehicle guidance[J]. IEEE/ASME Transactions on Mechatronics, 2010, 15(4): 652. DOI:10.1109/TMECH.2009.2029572 |
| [4] |
BENTO L C, NUNES U, MOITA F, et al. Sensor fusion for precise autonomous vehicle navigation in outdoor semi-structured environments[C]//Proceedings of Intelligent Transportation Systems. Vienna: IEEE, 2005: 245 http://www.academia.edu/23855218/Sensor_fusion_for_precise_autonomous_vehicle_navigation_in_outdoor_semi-structured_environments
|
| [5] |
LOPES A C, MOITA F, NUNES U, et al. An outdoor guidepath navigation system for AMRs based on robust detection of magnetic markers[C]//Conference on Emerging Technologies and Factory Automation. Patras: IEEE, 2007: 989 https://www.researchgate.net/publication/4304953_An_outdoor_guidepath_navigation_system_for_AMRs_based_on_robust_detection_of_magnetic_markers
|
| [6] |
ZHU Gang, YANG Ming, WANG Bing, et al.A new approach for autonomous vehicle navigation in urban scenarios based on roadway magnets[C]//Intelligent Vehicles Symposium Proceedings. Dearborn: IEEE, 2014: 432 https://www.researchgate.net/publication/269294127_A_new_approach_for_autonomous_vehicle_navigation_in_urban_scenarios_based_on_roadway_Magnets
|
| [7] |
ZHU Gang, YANG Ming, LI Hao, et al. Curvature map-based magnetic guidance for automated vehicles in an urban environment[J]. IEEE Transactions on Intelligent Transportation Systems, 2016, 17(12): 3541. DOI:10.1109/TITS.2016.2557066 |
| [8] |
朱刚.面向城市环境的无人驾驶车辆磁导航方法研究[D].上海: 上海交通大学, 2015 ZHU Gang. Research on magnetic guidance for automous vehicles in urban environment[D]. Shanghai: Shanghai Jiao Tong University, 2015 http://cdmd.cnki.com.cn/Article/CDMD-10248-1015806587.htm |
| [9] |
YU Yuan, GUO Lindong, YANG Ming, et al.Graph-based SLAM based magnet map generation for magnetic guidance[C]//International Conference on Robotics and Biomimetics. Bali: IEEE, 2014: 2661 http://or.nsfc.gov.cn/bitstream/00001903-5/143621/1/1000009126543.pdf
|
| [10] |
GRISETTI G, KUMMERLE R, STACHNISS C, et al. A tutorial on graph-based SLAM[J]. IEEE Intelligent Transportation Systems Magazine, 2010, 2(4): 31. DOI:10.1109/MITS.2010.939925 |
| [11] |
王忠立, 赵杰, 蔡鹤皋. 大规模环境下基于图优化SLAM的后端优化方法[J]. 哈尔滨工业大学学报, 2015, 47(7): 20. WANG Zhongli, ZHAO Jie, CAI Hegao. Back-end optimization method based on graph-optimization SLAM in large-scale environment[J]. Journal of Harbin Institute of Technology, 2015, 47(7): 20. DOI:10.11918/j.issn.0367-6234.2015.07.002 |
| [12] |
梁明杰, 闵华清, 罗荣华. 基于图优化的同时定位与地图创建综述[J]. 机器人, 2013, 35(4): 500. LIANG Mingjie, MIN Huaqing, LUO Ronghua. Graph-based SLAM:a survey[J]. Robot, 2013, 35(4): 500. DOI:10.3724/SP.J.1218.2013.00500 |
| [13] |
权美香, 朴松昊, 李国. 视觉SLAM综述[J]. 智能系统学报, 2016, 11(6): 768. QUAN Meixiang, PU Songhao, LI Guo. An overview of visual SLAM[J]. CAAI Transactions on Intelligent Systems, 2016, 11(6): 768. DOI:10.11992/tis.201607026 |
| [14] |
SÜNDERHAUFN, PROTZEL P. Switchable constraints for robust pose graph SLAM[C]//International Conference on Intelligent Robots and Systems. Vilamoura: IEEE, 2012: 1879 https://www.tu-chemnitz.de/etit/proaut/publications/IROS12-switchableConstraints.pdf
|
| [15] |
KIM J, CHENG J, SHIM H. Efficient Graph-SLAM optimization using unit dual-quaternions[C]//International Conference on Ubiquitous Robots and Ambient Intelligence. Goyang: IEEE, 2015: 34 Efficient Graph-SLAM optimization using unit dual-quaternions
|
| [16] |
CARLONE L, CENSI A, DELLAERT F. Selecting good measurements via $ell $1 relaxation: a convex approach for robust estimation over graphs[C]//International Conference on Intelligent Robots and Systems. Chicago: IEEE, 2014: 2667
|
| [17] |
KÜMMERLE R, STEDER B, DORNHEGE C, et al. On measuring the accuracy of SLAM algorithms[J]. Auton Robot, 2009, 27: 387. DOI:10.1007/s10514-009-9155-6 |
| [18] |
STURM J, ENGELHARD N, ENDRES F, et al. A benchmark for the evaluation of RGB-D SLAM systems[C]//International Conference on Intelligent Robots and Systems. Vilamoura: IEEE, 2012: 573
|
 2019, Vol. 51
2019, Vol. 51


