2. 九江职业技术学院 机械工程学院,江西 九江 332007
2. College of Mechanical Engineering, Jiujiang Vocational and Technical College, Jiujiang 332007, Jiangxi, China
自主水下航行器(AUV)在民用和军事等众多领域都具有很高的实用价值.由于AUV对路径和轨迹的精确跟踪能力是其完成各种作业任务和避障的关键技术,所以AUV的路径和轨迹跟踪控制问题一直是研究的热点.但是,目前仍存在一些困难使得AUV控制器的设计变得非常棘手[1].例如,出于节能和提高可靠性等方面的考虑,大部分AUV都被设计为欠驱动的形式,一般只配置推进器、方向舵和水平舵,缺少横向和垂向的驱动,从而在横向和垂向运动受到限制.另外,AUV的工作环境中存在海浪、海流等干扰以及AUV六自由度运动存在非线性和耦合性、水动力参数存在不确定性,导致AUV的运动模型很难精确建模.
AUV的路径和轨迹跟踪控制一般分为运动学和动力学两个层面.文献[2-3]分别基于视线法(LOS)和向量场法(VF)导引律,设计了欠驱动船舶的路径跟踪控制器.文献[4]通过引入了趋近角和虚拟向导建立跟踪误差方程,然后基于李雅普诺夫(Lyapunov)理论和反步法设计了水平面路径跟踪控制器.但是当存在海流等干扰时,基于传统的LOS和VF导引律的路径跟踪会产生稳态误差.为了解决这个问题,文献[5]提出了一种积分视线法(ILOS)导引律,并得到了广泛的应用.针对欠驱动AUV的路径跟踪动力学控制器的设计,也有大量的研究.文献[6]应用ILOS导引律和PID控制器实现了海流干扰下欠驱动AUV的水平面路径跟踪控制.文献[7]采用反馈线性化方法设计了水平面路径跟踪控制器.针对AUV的垂直面路径跟踪问题,文献[8]采取解耦方式,分别采用S面控制方法和反步法设计了航速控制器和深度控制器.为了提高系统的鲁棒性,文献[9-10]分别针对水平面和垂直面路径跟踪设计了自适应控制器和滑模控制器.以上文献只是考虑了AUV在水平面或垂直面的路径跟踪问题.文献[11]应用线性稳定理论和反步法设计了欠驱动AUV的三维轨迹跟踪控制器,但未考虑参数的不确定性.文献[12]针对欠驱动AUV三维路径跟踪设计了鲁棒自适应控制器.文献[13]采用滤波反步法设计了三维路径跟踪控制器.但以上三维路径跟踪控制器都未考虑海流的影响.文献[14]针对欠驱动AUV模型不确定性和海流干扰,将三维路径跟踪分解为水平面和垂直面跟踪控制问题,设计了航向和纵倾鲁棒控制器,但仅实现了对三维直线路径的跟踪控制.
本文针对存在海流干扰和模型不确定性情况下欠驱动AUV的三维路径跟踪控制问题,基于Serret-Frenet坐标系引入了虚拟向导并建立了三维路径跟踪误差模型.设计了具有自适应律的虚拟向导并提出了一种改进的积分视线法(ILOS)导引律.基于反步自适应滑模控制(BASMC)理论和AUV与流体的相对速度设计动力学控制器,并应用sigmoid函数设计滑模项,保证了系统的稳定性和鲁棒性、有效地削弱了抖振,而且更便于工程应用.仿真结果验证了该控制器的有效性.
1 AUV六自由度运动方程本文研究的欠驱动AUV浮力与重力配置相等,尾部装有一个螺旋桨、一对水平舵、一对方向舵分别用来控制航速、纵倾和航向. AUV的运动及受力分析需要用到两种坐标系,分别是运动坐标系{B}:O-xyz和固定坐标系{I}:E-ξηζ.本文将运动坐标系的原点O选取在AUV的浮心处,各坐标轴均符合右手系. AUV在六自由度上受到的力和力矩如图 1所示,所有符号均采用国际拖拽水池会议(ITTC)所推荐的符号. AUV的运动学和动力学模型可以分别简化为
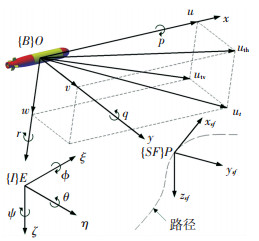
|
图 1 三维路径跟踪示意图 Fig. 1 Schematic diagram of 3D path-following |
| $ \mathit{\boldsymbol{\dot \eta }} = \mathit{\boldsymbol{J}}\left( \mathit{\boldsymbol{\eta }} \right){\mathit{\boldsymbol{v}}_r} + {\left[ {\begin{array}{*{20}{c}} {{v_\xi }}&{{v_\eta }}&{{v_\zeta }}&0&0&0 \end{array}} \right]^{\rm{T}}}, $ | (1) |
| $ \mathit{\boldsymbol{M}}{{\mathit{\boldsymbol{\dot v}}}_r} + \mathit{\boldsymbol{C}}\left( {{\mathit{\boldsymbol{v}}_r}} \right){\mathit{\boldsymbol{v}}_r} + \mathit{\boldsymbol{D}}\left( {{\mathit{\boldsymbol{v}}_r}} \right){\mathit{\boldsymbol{v}}_r} + \mathit{\boldsymbol{g}}\left( \mathit{\boldsymbol{\eta }} \right) = \tau + \mathit{\boldsymbol{d}}. $ | (2) |
式中:η =[ξ η ζ ϕ θ ψ]T,其中ξ、η、ζ为AUV在固定坐标系中的坐标,ϕ、θ、ψ分别为横摇角、纵摇角和艏摇角;J (η)为{B}到{I}的旋转变换矩阵,即
| $ \mathit{\boldsymbol{J}}\left( \mathit{\boldsymbol{\eta }} \right) = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{J}}_1}\left( \mathit{\boldsymbol{\eta }} \right)}&{{{\bf{0}}_{3 \times 3}}}\\ {{{\bf{0}}_{3 \times 3}}}&{{\mathit{\boldsymbol{J}}_2}\left( \mathit{\boldsymbol{\eta }} \right)} \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{J}}_1}\left( \mathit{\boldsymbol{\eta }} \right) = \left[ {\begin{array}{*{20}{c}} {\cos \psi \cos \theta }&{\cos \psi \sin \theta \sin \varphi - \sin \psi \cos \varphi }&{\cos \psi \sin \theta \cos \varphi + \sin \psi \sin \varphi }\\ {\sin \psi \cos \theta }&{\sin \psi \sin \theta \sin \varphi + \cos \psi \cos \varphi }&{\sin \psi \sin \theta \cos \varphi - \cos \psi \sin \varphi }\\ { - \sin \theta }&{\cos \theta \sin \varphi }&{\cos \theta \cos \varphi } \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{J}}_2}\left( \mathit{\boldsymbol{\eta }} \right) = \left[ {\begin{array}{*{20}{c}} 1&{\sin \varphi \tan \theta }&{\cos \varphi \tan \theta }\\ 0&{\cos \varphi }&{ - \sin \varphi }\\ 0&{\sin \varphi /\cos \theta }&{\cos \varphi /\cos \theta } \end{array}} \right]; $ |
vr= vB- vcB=[ur vr wr p q r]T为AUV与流体的相对速度,其中ur、vr、wr分别为纵向、横向和垂向相对速度;AUV的绝对速度定义为vB = [u v w p q r]T, 其中u、v、w分别为纵向、横向和垂向绝对速度,p、q、r分别为横摇、纵摇和艏摇角速度;vcB=[uc vc wc 0 0 0]T为海流在{B}中的速度分量;[uc vc wc]T= J1T(η) vcI, 其中vcI= [vξ vη vζ]T为海流在{I}中的速度分量,假设海流是无旋的且满足vξ+2vη2+vζ2 < Vmax2;M、C (vr)、D (vr)分别为质量矩阵、哥氏力矩阵和阻尼矩阵;g (η)=[0 0 0 KHS MHS 0]T为重力和浮力产生的恢复力矩,本文研究的AUV的重心位于浮心正下方,在横摇和纵摇两个自由度存在恢复力矩分别为KHS=-zgGcos θsin ϕ、MHS=-zgGsin θ, 其中zg、G分别为AUV的稳心高和重力;τ = [Xτ 0 0 0 Mτ Nτ]T为控制力和力矩,其中Xτ、Mτ、Nτ分别为螺旋桨、水平舵和方向舵产生的推力、纵倾力矩和艏摇力矩;d为模型不确定性.
为了便于动力学控制器的设计,可以将动力学模型(2)展开为如下微分方程组的形式:
| $ \left\{ \begin{array}{l} {{\dot u}_r} = {F_u}{u_r} + {F_X}{X_\tau } + {d_u},\\ {{\dot v}_r} = {F_v}{v_r} + {d_v},\\ {{\dot w}_r} = {F_w}{w_r} + {d_w},\\ \dot p = {F_p}p + {d_p},\\ \dot q = {F_q}q + {F_M}{M_{{\rm{HS}}}} + {F_M}{M_\tau } + {d_q},\\ \dot r = {F_r}r + {F_N}{N_\tau } + {d_r}. \end{array} \right. $ | (3) |
式中:
| $ {F_u} = \frac{{{X_{u\left| u \right|}}\left| {{u_r}} \right|}}{{m - {X_{\dot u}}}},{F_X} = \frac{1}{{m - {X_{\dot u}}}},{F_v} = \frac{{{Y_{v\left| v \right|}}\left| {{v_r}} \right|}}{{m - {Y_{\dot v}}}}, $ |
| $ {F_w} = \frac{{{Z_{w\left| w \right|}}\left| {{w_r}} \right|}}{{m - {Z_{\dot w}}}},{F_p} = \frac{{{K_{p\left| p \right|}}\left| p \right|}}{{{I_{xx}} - {K_{\dot p}}}}, $ |
| $ {F_q} = \frac{{{M_{q\left| q \right|}}\left| q \right| + {M_{uq}}{u_r}}}{{{I_{yy}} - {M_{\dot q}}}},{F_M} = \frac{1}{{{I_{yy}} - {M_{\dot q}}}}, $ |
| $ {F_r} = \frac{{{N_{r\left| r \right|}}\left| r \right| + {N_{ur}}{u_r}}}{{{I_{zz}} - {N_{\dot r}}}},{F_N} = \frac{1}{{{I_{zz}} - {N_{\dot r}}}}, $ |
m为AUV的质量,Ixx、Iyy、Izz为AUV的惯性矩,X{.}、Y{.}、Z{.}、K{.}、M{.}、N{.}为水动力系数,F{.}采用名义值,模型不确定性包含在d{.}中.
2 三维路径跟踪运动学误差模型欠驱动AUV三维路径跟踪原理见图 1~3,为了建立跟踪误差模型引入了{SF}: P-xsfysfzsf坐标系,{SF}坐标系的原点P即为期望路径上被AUV跟踪的虚拟向导.定义cc、ct分别为路径的曲率和挠率,从路径起点开始沿路径的广义弧长为s,虚拟向导的速度为uF,{SF}坐标系的纵摇和艏摇角速度分别为qF、rF,则

|
图 2 水平面路径跟踪示意图 Fig. 2 Horizontal plane of path-following |

|
图 3 垂直面路径跟踪示意图 Fig. 3 Vertical plane of path-following |
| $ \mathit{\boldsymbol{R}}_F^I = \left[ {\begin{array}{*{20}{c}} {\cos {\psi _F}\cos {\theta _F}}&0&0\\ {\sin {\psi _F}\cos {\theta _F}}&0&0\\ { - \sin {\theta _F}}&0&0\\ 0&1&0\\ 0&0&{1/\cos {\theta _F}} \end{array}} \right]. $ |
为了便于跟踪误差模型的推导,以AUV的合成速度ut为纵轴定义{W}坐标系,由{B}坐标系沿y轴旋转α再沿z轴旋转β,即为{W}坐标系.忽略横摇的影响,基于{W}定义PO=[ξO ηO ζO θW ψW]T为O在{I}中的位置和姿态,其中θW=θ+α,ψW=ψ+β,α、β分别为攻角和漂角,α=-tan-1(w/u),β=tan-1(v/u).定义在{SF}中的跟踪误差为Pe=[xeye ze θeW ψeW]T= RIF(PO-PP),其中RIF是从{I}到{SF}的旋转变换矩阵,即
| $ \mathit{\boldsymbol{R}}_I^F = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{R}}_1}}&{{{\bf{0}}_{3 \times 2}}}\\ {{{\bf{0}}_{2 \times 3}}}&{{\mathit{\boldsymbol{R}}_2}} \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{R}}_1} = \left[ {\begin{array}{*{20}{c}} {\cos {\psi _F}\cos {\theta _F}}&{\sin {\psi _F}\cos {\theta _F}}&{ - \sin {\theta _F}}\\ { - \sin {\psi _F}}&{\cos {\psi _F}}&0\\ {\cos {\psi _F}\sin {\theta _F}}&{\sin {\psi _F}\sin {\theta _F}}&{\cos {\theta _F}} \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{R}}_2} = \left[ {\begin{array}{*{20}{c}} 1&0\\ 0&{\cos {\theta _F}} \end{array}} \right]. $ |
矩阵R1和R2具有以下性质:
| $ {{\mathit{\boldsymbol{\dot R}}}_1} = {\mathit{\boldsymbol{S}}_1}{\mathit{\boldsymbol{R}}_1},{{\mathit{\boldsymbol{\dot R}}}_2} = {\mathit{\boldsymbol{S}}_2}{\mathit{\boldsymbol{R}}_2},{\chi ^{\rm{T}}}{\mathit{\boldsymbol{S}}_1}\chi = 0,\chi \in {\mathit{\boldsymbol{R}}^3}, $ |
| $ {\mathit{\boldsymbol{S}}_1} = \left[ {\begin{array}{*{20}{c}} 0&{{r_F}}&{ - {q_F}}\\ { - {r_F}}&0&{ - {r_F}\tan {\theta _F}}\\ {{q_F}}&{{r_F}\tan {\theta _F}}&0 \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{S}}_2} = \left[ {\begin{array}{*{20}{c}} 0&0\\ 0&{ - {q_F}\tan {\theta _F}} \end{array}} \right]. $ |
定义PO1=[ξO ηO ζO]T,PP1=[ξP ηP ζP]T,Pe1=[xe ye ze]T,则位置误差为Pe1=[xe ye ze]T= R1(Po1-PP1),对Pe1求导并左乘Pe1T,得
| $ \begin{array}{l} \mathit{\boldsymbol{P}}_{e1}^{\rm{T}}{{\mathit{\boldsymbol{\dot P}}}_{e1}} = \mathit{\boldsymbol{P}}_{e1}^{\rm{T}}\left[ {{{\mathit{\boldsymbol{\dot R}}}_1}\left( {{\mathit{\boldsymbol{P}}_{O1}} - {\mathit{\boldsymbol{P}}_{P1}}} \right) + {\mathit{\boldsymbol{R}}_1}\left( {{{\mathit{\boldsymbol{\dot P}}}_{O1}} - {{\mathit{\boldsymbol{\dot P}}}_{P1}}} \right)} \right] = \\ \;\;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{P}}_{e1}^{\rm{T}}{\mathit{\boldsymbol{S}}_1}{\mathit{\boldsymbol{R}}_1}\left( {{\mathit{\boldsymbol{P}}_{O1}} - {\mathit{\boldsymbol{P}}_{P1}}} \right) + \mathit{\boldsymbol{P}}_{e1}^{\rm{T}}{\mathit{\boldsymbol{R}}_1}\left( {{{\mathit{\boldsymbol{\dot P}}}_{O1}} - {{\mathit{\boldsymbol{\dot P}}}_{P1}}} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{P}}_{e1}^{\rm{T}}{\mathit{\boldsymbol{S}}_1}{\mathit{\boldsymbol{P}}_{e1}} + \mathit{\boldsymbol{P}}_{e1}^{\rm{T}}{\mathit{\boldsymbol{R}}_1}\left( {{{\mathit{\boldsymbol{\dot P}}}_{O1}} - {{\mathit{\boldsymbol{\dot P}}}_{P1}}} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{P}}_{e1}^{\rm{T}}{\mathit{\boldsymbol{R}}_1}\left( {{{\mathit{\boldsymbol{\dot P}}}_{O1}} - {{\mathit{\boldsymbol{\dot P}}}_{P1}}} \right), \end{array} $ |
消去上式两边的Pe1T,得
根据关系式:
| $ {\mathit{\boldsymbol{R}}_1}{{\mathit{\boldsymbol{\dot P}}}_{O1}} = \left[ {\begin{array}{*{20}{c}} {\cos \psi _e^W\cos \theta _e^W}&{ - \sin \psi _e^W}&{\cos \psi _e^W\sin \theta _e^W}\\ {\sin \psi _e^W\cos \theta _e^W}&{\cos \psi _e^W}&{\sin \psi _e^W\sin \theta _e^W}\\ { - \sin \theta _e^W}&0&{\cos \theta _e^W} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{u_t}}\\ 0\\ 0 \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{R}}_1}{{\mathit{\boldsymbol{\dot P}}}_{P1}} = {\left[ {\begin{array}{*{20}{c}} {{u_F}}&0&0 \end{array}} \right]^{\rm{T}}}, $ |
可得
| $ {{\mathit{\boldsymbol{\dot P}}}_{e1}} = \left[ {\begin{array}{*{20}{c}} {{{\dot x}_e}}\\ {{{\dot y}_e}}\\ {{{\dot z}_e}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{u_t}\cos \psi _e^W\cos \theta _e^W - {u_F}}\\ {{u_t}\sin \psi _e^W\cos \theta _e^W}\\ { - {u_t}\sin \theta _e^W} \end{array}} \right]. $ | (4) |
但是误差模型(4)中的ut、θeW、ψeW不便于测量和应用,所以还需要作进一步处理.定义
| $ \mathit{\boldsymbol{P}}_{O2}^B = {\left[ {\begin{array}{*{20}{c}} \theta &\psi \end{array}} \right]^{\rm{T}}}, $ |
| $ \mathit{\boldsymbol{P}}_{O2}^W = {\left[ {\begin{array}{*{20}{c}} {{\theta _W}}&{{\psi _W}} \end{array}} \right]^{\rm{T}}} = \mathit{\boldsymbol{P}}_{O2}^B + {\left[ {\begin{array}{*{20}{c}} \alpha &\beta \end{array}} \right]^{\rm{T}}}, $ |
| $ {\mathit{\boldsymbol{P}}_{P2}} = {\left[ {\begin{array}{*{20}{c}} {{\theta _F}}&{{\psi _F}} \end{array}} \right]^{\rm{T}}}, $ |
姿态误差:
| $ \mathit{\boldsymbol{P}}_{e2}^B = {\left[ {\begin{array}{*{20}{c}} {\theta _e^B}&{\psi _e^B} \end{array}} \right]^{\rm{T}}} = {\mathit{\boldsymbol{R}}_2}\left( {\mathit{\boldsymbol{P}}_{O2}^B - {\mathit{\boldsymbol{P}}_{P2}}} \right), $ |
| $ \begin{array}{l} \mathit{\boldsymbol{P}}_{e2}^W = {\left[ {\begin{array}{*{20}{c}} {\theta _e^W}&{\psi _e^W} \end{array}} \right]^{\rm{T}}} = {\mathit{\boldsymbol{R}}_2}\left( {\mathit{\boldsymbol{P}}_{O2}^W - {\mathit{\boldsymbol{P}}_{P2}}} \right) = \mathit{\boldsymbol{P}}_{e2}^B + \\ \;\;\;\;\;\;\;\;{\left[ {\begin{array}{*{20}{c}} \alpha &{\beta \cos {\theta _F}} \end{array}} \right]^{\rm{T}}}. \end{array} $ |
将
| $ {{\mathit{\boldsymbol{\dot P}}}_{e1}} = \left[ {\begin{array}{*{20}{c}} {{u_r}\cos \psi _e^B\cos \theta _e^B - {u_F} + {d_x}}\\ {{k_y}{u_r}\cos \theta _e^B\sin \psi _e^B + {k_y}{u_r}\cos \theta _e^B\cos \psi _e^B\beta }\\ { - {k_u}{u_r}\sin \theta _e^B - {k_u}{u_r}\cos \theta _e^B\alpha } \end{array}} \right]. $ | (5) |
对姿态误差Pe2B求导,可得
| $ \begin{array}{l} \mathit{\boldsymbol{\dot P}}_{e2}^B = {{\mathit{\boldsymbol{\dot R}}}_2}\left( {\mathit{\boldsymbol{P}}_{O2}^B - {\mathit{\boldsymbol{P}}_{P2}}} \right) + {\mathit{\boldsymbol{R}}_2}\left( {\mathit{\boldsymbol{\dot P}}_{O2}^B - {{\mathit{\boldsymbol{\dot P}}}_{P2}}} \right) = \\ \;\;\;\;\;\;\;\;{\mathit{\boldsymbol{S}}_2}\mathit{\boldsymbol{P}}_{e2}^B + {\mathit{\boldsymbol{R}}_2}\left( {\mathit{\boldsymbol{\dot P}}_{O2}^B - {{\mathit{\boldsymbol{\dot P}}}_{P2}}} \right) = \\ \;\;\;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}} {q - {q_F}}\\ { - {q_F}\psi _e^B\tan {\theta _F} + \frac{{\cos {\theta _F}}}{{\cos \theta }}r - {r_F}} \end{array}} \right]. \end{array} $ | (6) |
本文路径跟踪控制的目的是使AUV收敛到期望路径,并使AUV的纵向相对速度ur保持恒定.所以控制目标为
| $ \left\{ \begin{array}{l} \mathop {\lim }\limits_{t \to \infty } {u_r}\left( t \right) = {u_{rd}};\\ \mathop {\lim }\limits_{t \to \infty } {x_e}\left( t \right) = 0,\mathop {\lim }\limits_{t \to \infty } {y_e}\left( t \right) = 0,\mathop {\lim }\limits_{t \to \infty } {z_e}\left( t \right) = 0;\\ \mathop {\lim }\limits_{t \to \infty } \theta _e^W\left( t \right) = 0,\mathop {\lim }\limits_{t \to \infty } \psi _e^W\left( t \right) = 0. \end{array} \right. $ |
1) 镇定xe.定义
| $ {{\dot V}_1} = {x_e}\left( {{u_r}\cos \psi _e^B\cos \theta _e^B - {u_F} + {{\hat d}_x}} \right) + {{\tilde d}_x}\left( {{x_e} - \frac{1}{{{k_1}}}{{\dot {\hat d}}_x}} \right). $ |
设计虚拟向导和自适应控制律为
| $ \left\{ \begin{array}{l} {u_F} = {u_r}\cos \psi _e^B\cos \theta _e^B + {k_2}{x_e} + {{\hat d}_x},{k_2} > 0;\\ {{\dot {\hat d}}_x} = {k_1}{x_e},{k_1} > 0. \end{array} \right. $ | (7) |
可得
2) 镇定ye和ze.要实现对ye和ze的镇定,需要选择合适的导引律,如果使用传统的LOS导引律
| $ \theta _{ed}^B = {\tan ^{ - 1}}\left( {\frac{{{z_e}}}{{{\Delta _\theta }}}} \right),\psi _{ed}^B = - {\tan ^{ - 1}}\left( {\frac{{{y_e}}}{{{\Delta _\psi }}}} \right),{\Delta _\theta } > 0,{\Delta _\psi } > 0, $ |
其中θedB、ψedB分别为θeB、ψeB的期望值,将θeB=θedB, ψeB=ψedB代入误差模型(4),可得
| $ {{\dot y}_e} = - {u_t}\cos \theta _e^W\left[ {\frac{{{y_e}\cos \left( {\beta \cos {\theta _F}} \right)}}{{\sqrt {\Delta _\psi ^2 + y_e^2} }} - \frac{{{\Delta _\psi }\sin \left( {\beta \cos {\theta _F}} \right)}}{{\sqrt {\Delta _\psi ^2 + y_e^2} }}} \right], $ |
| $ {{\dot z}_e} = - {u_t}\left[ {\frac{{{z_e}}}{{\sqrt {\Delta _\theta ^2 + z_e^2} }}\cos \alpha + \frac{{{\Delta _\theta }}}{{\sqrt {\Delta _\theta ^2 + z_e^2} }}\sin \alpha } \right]. $ |
令
| $ \left| {{y_{ess}}} \right| = {\Delta _\psi }\left| {\tan \left( {\beta \cos {\theta _F}} \right)} \right| \le {\Delta _\psi }\left| {\tan \bar \beta } \right| \approx {\Delta _\psi }\left| {\bar \beta } \right|, $ |
| $ \left| {{z_{ess}}} \right| = {\Delta _\theta }\left| {\tan \alpha } \right| \le {\Delta _\theta }\left| {\tan \bar \alpha } \right| \approx {\Delta _\theta }\left| {\bar \alpha } \right|. $ |
式中α、β分别为α、β的上界.显然,如果α、β不为零,ye、ze会存在稳态误差.为了消除稳态误差,设计ILOS导引律为
| $ \left\{ \begin{array}{l} \theta _{ed}^B = {\tan ^{ - 1}}\left( {\frac{{{z_e} - {\alpha _c}}}{{{\Delta _\theta }}}} \right),\\ \psi _{ed}^B = - {\tan ^{ - 1}}\left( {\frac{{{y_e} + {\beta _c}}}{{{\Delta _\psi }}}} \right). \end{array} \right. $ | (8) |
定义
| $ {V_2} = \frac{1}{2}z_e^2 + \frac{1}{2}y_e^2 + \frac{{{k_u}}}{{2{k_3}}}{{\tilde \alpha }^2} + \frac{{{k_y}}}{{2{k_4}}}{{\tilde \beta }^2}, $ |
令ur=urd, θeB=θedB, ψeB=ψedB,根据式(5)、(8)对V2求导得
| $ \begin{array}{l} {{\dot V}_2} = {z_e}\left( { - \frac{{{k_u}{u_{rd}}\left( {{z_e} - {\alpha _c}} \right)}}{{\sqrt {\Delta _\theta ^2 + {{\left( {{z_e} - {\alpha _c}} \right)}^2}} }} - \frac{{{k_u}{u_{rd}}{\Delta _\theta }}}{{\sqrt {\Delta _\theta ^2 + {{\left( {{z_e} - {\alpha _c}} \right)}^2}} }}\dot \alpha } \right) - \\ \;\;\;\;\;\;\tilde \alpha {k_u}\left( {\frac{1}{{{k_3}}}\dot {\hat \alpha} + \frac{{{u_{rd}}{\Delta _\theta }}}{{\sqrt {\Delta _\theta ^2 + {{\left( {{z_e} - {\alpha _c}} \right)}^2}} }}{z_e}} \right) + \\ \;\;\;\;\;\;{y_e}\left( { - \frac{{{k_y}{u_{rd}}\cos \theta _e^B\left( {{y_e} + {\beta _c}} \right)}}{{\sqrt {\Delta _\psi ^2 + {{\left( {{y_e} + {\beta _c}} \right)}^2}} }} + \frac{{{k_y}{u_{rd}}\cos \theta _e^B{\Delta _\psi }}}{{\sqrt {\Delta _\psi ^2 + {{\left( {{y_e} + {\beta _c}} \right)}^2}} }}\hat \beta } \right) + \\ \;\;\;\;\;\;\tilde \beta {k_y}\left( {\frac{{{u_{rd}}\cos \theta _e^B{\Delta _\psi }}}{{\sqrt {\Delta _\psi ^2 + {{\left( {{y_e} + {\beta _c}} \right)}^2}} }}{y_e} - \frac{1}{{{k_4}}}\dot {\hat \beta} } \right). \end{array} $ |
设计控制律和自适应律为
| $ \left\{ \begin{array}{l} {\alpha _c} = {\Delta _\theta }\hat \alpha ;\\ \dot {\hat \alpha} = - {k_\alpha }\frac{{{k_3}{u_{rd}}{\Delta _\theta }}}{{\sqrt {\Delta _\theta ^2 + {{\left( {{z_e} - {\alpha _c}} \right)}^2}} }}{z_e},\\ \;\;\;\;\;\;\;{k_3} > 0,{k_\alpha } = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} 0,\\ 1, \end{array}&\begin{array}{l} \left| {{z_e}} \right| > {\Delta _z},\\ \left| {{z_e}} \right| \le {\Delta _z}; \end{array} \end{array}} \right.\\ {\beta _c} = {\Delta _\psi }\hat \beta ;\\ \dot {\hat \beta} = {k_\beta }\frac{{{k_4}{u_{rd}}\cos \theta _e^B{\Delta _\psi }}}{{\sqrt {\Delta _\psi ^2 + {{\left( {{y_e} + {\beta _c}} \right)}^2}} }}{y_e},\\ \;\;\;\;\;\;\;{k_4} > 0,{k_\beta } = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} 0,\\ 1, \end{array}&\begin{array}{l} \left| {{y_e}} \right| > {\Delta _y},\\ \left| {{y_e}} \right| \le {\Delta _y}. \end{array} \end{array}} \right. \end{array} \right. $ |
式中:Dz、Δy为边界层厚度,当AUV位于边界层以外时kα=0, kβ=0,式(8)退化为LOS导引律,这样可以减少超调,当AUV位于边界层以内时启动积分项消除稳态误差.只要设置Δy>| yess|,Δz> |zess |就可以保证AUV进入边界层以内,最终可得
| $ {{\dot V}_2} = - \frac{{{k_u}{u_{rd}}}}{{\sqrt {\Delta _\theta ^2 + {{\left( {{z_e} - {\alpha _c}} \right)}^2}} }}z_e^2 - \frac{{{k_y}{u_{rd}}\cos \theta _e^B}}{{\sqrt {\Delta _\psi ^2 + {{\left( {{y_e} + {\beta _c}} \right)}^2}} }}y_e^2 \le 0. $ |
1) 镇定ure.定义误差变量为
| $ \left\{ \begin{array}{l} {u_{re}} = {u_r} - {u_{rd}},\\ \tilde \psi _e^B = \psi _e^B - \psi _{ed}^B,\\ \tilde \theta _e^B = \theta _e^B - \theta _{ed}^B. \end{array} \right. $ | (9) |
因为urd为常值,根据式(3)、(9)可得
| $ {{\dot u}_{re}} = {{\dot u}_r} - {{\dot u}_{rd}} = {F_u}{u_r} + {F_X}{X_\tau } + {d_u}X. $ |
定义
| $ {{\dot V}_3} = {u_{re}}\left( {{F_u}{u_r} + {F_X}{X_\tau } + {{\hat d}_u}} \right) + {{\tilde d}_u}\left( {{u_{re}} - \frac{1}{{{k_5}}}{{\dot {\hat d}}_u}} \right). $ |
设计控制律和自适应律为
| $ \left\{ \begin{array}{l} {X_\tau } = \frac{1}{{{F_X}}}\left[ { - {F_u}{u_r} - {{\hat d}_u} - {k_6}{u_{re}} - {\varepsilon _1}{\rm{sig}}\left( {{u_{re}}} \right)} \right],\\ {\rm{sig}}\left( {{u_{re}}} \right) = \frac{{1 - {e^{ - {k_7}{u_{re}}}}}}{{1 + {e^{ - {k_7}{u_{re}}}}}} = {\mathop{\rm sgn}} \left( {{u_{re}}} \right)\left| {\frac{{1 - {e^{ - {k_7}{u_{re}}}}}}{{1 + {e^{ - {k_7}{u_{re}}}}}}} \right|,\\ {{\dot {\hat d}}_u} = {k_5}{u_{re}},{k_5} > 0,{k_6} > 0,{k_7} > 0,{\varepsilon _1} > 0. \end{array} \right. $ | (10) |
可得
2) 镇定
| $ {{\dot V}_4} = \tilde \psi _e^B\dot {\tilde \psi} _e^B = \tilde \psi _e^B\left( { - {q_F}\psi _e^B\tan {\theta _F} + \frac{{\cos {\theta _F}}}{{\cos \theta }}r - {r_F} - \dot \psi _{ed}^B} \right). $ |
设计r的期望值为
| $ {r_d} = \frac{{\cos \theta }}{{\cos {\theta _F}}}\left( {\dot \psi _{ed}^B + {q_F}\psi _e^B\tan {\theta _F} + {r_F} - {k_8}\tilde \psi _e^B} \right),{k_8} > 0, $ |
定义误差变量re=r-rd,得
| $ \begin{array}{l} {{\dot V}_5} = - {k_8}{\left( {\tilde \psi _e^B} \right)^2} + \frac{{\cos {\theta _F}}}{{\cos \theta }}\tilde \psi _e^B{r_e} + \\ \;\;\;\;\;{r_e}\left( {{F_r}r + {F_N}{N_\tau } + {{\hat d}_r} - {{\dot r}_d}} \right) + {{\tilde d}_r}\left( {{r_e} - \frac{1}{{{k_9}}}{{\dot {\hat d}}_r}} \right), \end{array} $ |
设计控制律和自适应律为
| $ \left\{ \begin{array}{l} {N_\tau } = \frac{1}{{{F_N}}}\left[ {{{\dot r}_d} - {F_r}r - \frac{{\cos {\theta _F}}}{{\cos \theta }}\tilde \psi _e^B - {{\hat d}_r} - {k_{10}}{r_e} - {\varepsilon _2}{\rm{sig}}\left( {{r_e}} \right)} \right],\\ {\rm{sig}}\left( {{r_e}} \right) = \frac{{1 - {e^{ - {k_7}{r_e}}}}}{{1 + {e^{ - {k_7}{r_e}}}}} = {\mathop{\rm sgn}} \left( {{r_e}} \right)\left| {\frac{{1 - {e^{ - {k_7}{r_e}}}}}{{1 + {e^{ - {k_7}{r_e}}}}}} \right|,\\ {{\dot {\hat d}}_r} = {k_9}{r_e},{k_9} > 0,{k_{10}} > 0,{\varepsilon _2} > 0. \end{array} \right. $ | (11) |
可得
| $ {{\dot V}_5} = - {k_8}{\left( {\tilde \psi _e^B} \right)^2} - {k_{10}}r_e^2 - {\varepsilon _2}\left| {{r_e}} \right|\left| {\frac{{1 - {e^{ - {k_7}{r_e}}}}}{{1 + {e^{ - {k_7}{r_e}}}}}} \right| \le 0. $ |
3) 镇定
根据式(3)对qe求导,可得
| $ {{\dot q}_e} = \dot q - {{\dot q}_d} = {F_q}q = {F_M}{M_{{\rm{HS}}}} + {F_M}{M_\tau } + {d_q} - {{\dot q}_d}, $ |
定义
| $ \begin{array}{*{20}{c}} {{{\dot V}_7} = - {k_{11}}{{\left( {\tilde \theta _e^B} \right)}^2} + \tilde \theta _e^B{q_e} + {{\tilde d}_q}\left( {{q_e} - \frac{1}{{{k_{12}}}}{{\dot {\hat d}}_q}} \right) + }\\ {{q_e}\left( {{F_q}q + {F_M}{M_{HS}} + {F_M}{M_\tau } + {{\hat d}_q} - {{\dot q}_d}} \right).} \end{array} $ |
设计控制律和自适应律为
| $ \left\{ \begin{array}{l} {M_\tau } = \frac{1}{{{F_M}}}\left[ {{{\dot q}_d} - {F_q}q - {F_M}{M_{HS}} - \tilde \theta _e^B - {{\hat d}_q} - {k_{13}}{q_e} - } \right.\\ \;\;\;\;\;\;\;\;\left. {{\varepsilon _3}{\rm{sig}}\left( {{q_e}} \right)} \right],\\ {\rm{sig}}\left( {{q_e}} \right) = \frac{{1 - {e^{ - {k_7}{r_e}}}}}{{1 + {e^{ - {k_7}{r_e}}}}} = {\mathop{\rm sgn}} \left( {{q_e}} \right)\left| {\frac{{1 - {e^{ - {k_7}{r_e}}}}}{{1 + {e^{ - {k_7}{r_e}}}}}} \right|,\\ {{\dot {\hat d}}_q} = {k_{12}}{q_e},\;\;\;\;{k_{12}} > 0,{k_{13}} > 0,{\varepsilon _3} > 0. \end{array} \right. $ | (12) |
可得
| $ {{\dot V}_7} = - {k_{11}}{\left( {\tilde \theta _e^B} \right)^2} - {k_{13}}q_e^2 - {\varepsilon _3}\left| {{q_e}} \right|\left| {\frac{{1 - {e^{ - {k_7}{r_e}}}}}{{1 + {e^{ - {k_7}{r_e}}}}}} \right| \le 0. $ |
控制律(10)~(12)分别得到的是螺旋桨和舵产生的推力和力矩,螺旋桨转速n,水平舵角δS,方向舵角δR的水动力方程计算公式为
| $ n = \sqrt {\frac{{{X_\tau }}}{{{K_{\rm{T}}}\rho D_{\rm{p}}^4}}} ,{\delta _S} = \frac{{{M_\tau }}}{{{x_{{\rm{fin}}}}{k_{\rm{L}}}}},{\delta _R} = \frac{{{N_\tau }}}{{{x_{{\rm{fin}}}}{k_{\rm{L}}}}}. $ |
式中ρ、KT、DP、KL、xfin分别为流体密度、螺旋桨推力系数、螺旋桨直径、舵升力系数、舵力臂.
3.3 闭环系统的稳定性分析在前面运动学控制器设计中假设ur=urd, θeB=θedB, ψeB=ψedB,但由于系统动力学特性的影响,ur、θeB、ψeB达到期望值需要响应时间.接下来对运动学和动力学组成的闭环系统的稳定性进行分析.定义误差变量
| $ {{\mathit{\boldsymbol{\dot P}}}_{e1}} = \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{P}}_{e1}} + \mathit{\boldsymbol{Be}}. $ | (13) |
式中:
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {{A_{11}}}&0&0\\ 0&{{A_{22}}}&0\\ 0&0&{{A_{33}}} \end{array}} \right], $ |
| $ \mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_1}}\\ {{\mathit{\boldsymbol{B}}_2}}\\ {{\mathit{\boldsymbol{B}}_3}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{B_{11}}}&0&0&0&0&0\\ 0&0&{{B_{23}}}&{{B_{24}}}&0&{{B_{26}}}\\ 0&{{B_{32}}}&0&{{B_{34}}}&{{B_{35}}}&0 \end{array}} \right], $ |
| $ {A_{11}} = - {k_2},{A_{22}} = - \frac{{{k_y}{u_{rd}}\cos \theta _e^B}}{{\sqrt {\Delta _\psi ^2 + {{\left( {{y_e} + {\beta _c}} \right)}^2}} }}, $ |
| $ {A_{33}} = - \frac{{{k_u}{u_{rd}}}}{{\sqrt {\Delta _\theta ^2 + {{\left( {{z_e} - {\alpha _c}} \right)}^2}} }}, $ |
| $ {B_{11}} = 1,{B_{23}} = \frac{{{k_y}{u_{rd}}\cos \theta _e^B{\Delta _\psi }}}{{\sqrt {\Delta _\psi ^2 + {{\left( {{y_e} + {\beta _c}} \right)}^2}} }}, $ |
| $ {B_{24}} = {k_y}\cos \theta _e^B\sin \psi _e^B + {k_y}\cos \theta _e^B\cos \psi _e^B\beta , $ |
| $ \begin{array}{l} {B_{26}} = \left( \begin{array}{l} {k_y}{u_{rd}}\cos \theta _e^B\sin \psi _{ed}^B + \\ \;\;\;\;\;\;\;{k_y}{u_{rd}}\beta \cos \theta _e^B\cos \psi _{ed}^B \end{array} \right)\frac{{\left( {\cos \tilde \psi _e^B - 1} \right)}}{{\tilde \psi _e^B}} + \\ \;\;\;\;\;\;\;\;\left( {{k_y}{u_{rd}}\cos \theta _e^B\cos \psi _{ed}^B - {k_y}{u_{rd}}\cos \theta _e^B\sin \psi _{ed}^B} \right)\\ \;\;\;\;\;\;\;\;\frac{{\sin \tilde \psi _e^B}}{{\tilde \psi _e^B}},{B_{32}} = - \frac{{{k_u}{u_{rd}}{\Delta _\theta }}}{{\sqrt {\Delta _\theta ^2 + {{\left( {{z_e} - {\alpha _c}} \right)}^2}} }}, \end{array} $ |
| $ {B_{34}} = - \left( {{k_u}\sin \theta _e^B + {k_u}\cos \theta _e^B\alpha } \right), $ |
| $ \begin{array}{l} {B_{35}} = \left( {{k_u}{u_{rd}}\alpha \sin \theta _{ed}^B - {k_u}{u_{rd}}\cos \theta _{ed}^B} \right)\frac{{\sin \tilde \theta _e^B}}{{\tilde \theta _e^B}} - \\ \;\;\;\;\;\left( {{k_u}{u_{rd}}\sin \theta _{ed}^B + {k_u}{u_{rd}}\alpha \cos \theta _{ed}^B} \right)\frac{{\left( {\cos \tilde \theta _e^B - 1} \right)}}{{\tilde \theta _e^B}}. \end{array} $ |
可以认为系统(13)是名义系统
| $ {\left\| {{\mathit{\boldsymbol{B}}_1}} \right\|_1} = \left| {{B_{11}}} \right| = 1, $ |
| $ \begin{array}{l} {\left\| {{\mathit{\boldsymbol{B}}_2}} \right\|_1} = \left| {{B_{23}}} \right| + \left| {{B_{24}}} \right| + \left| {{B_{26}}} \right| \le {k_y}{u_{rd}} + \\ \;\;\;\;\;\;\;\;\;\;{k_y}\left( {1 + 2{u_{rd}}} \right)\left( {1 + \left| \beta \right|} \right), \end{array} $ |
| $ \begin{array}{l} {\left\| {{\mathit{\boldsymbol{B}}_3}} \right\|_1} = \left| {{B_{32}}} \right| + \left| {{B_{34}}} \right| + \left| {{B_{35}}} \right| \le {k_u}{u_{rd}} + \\ \;\;\;\;\;\;\;\;\;\;{k_u}\left( {1 + 2{u_{rd}}} \right)\left( {1 + \left| \alpha \right|} \right). \end{array} $ |
可知B也是有界的.所以根据非线性级联系统理论可得系统(13)是渐进稳定的.
4 仿真结果与分析本文采用美国Hydroid公司的REMUS-100作为仿真模型,具体参数可详见文献[15].期望速度urd=1 m·s-1,海流速度vcI= [0.2 m·s-1 0.2 m·s-1 0 m·s-1]T.控制器的设计参数分别为k1=0.1, k2=0.2, k3=0.02, k4=0.05, k5=0.1, k6=1, k7=25, k8=0.1, k9=0.1, k10=1, k12=0.1, k12=0.1, k13=1, Δθ=6, Δψ=6, Δz=2, Δy=2, ε1=0.3, ε2=0.1, ε3=0.1.期望路径是基于表 1所列的路径点生成,第一段路径为螺旋线,半径和螺距分别为20、40 m,其余路径由直线和圆弧组成,圆弧半径为10 m.仿真采用了两种控制方法进行对比,方法1采用本文提出的控制方法,方法2的运动学控制器采用文献[5]提出了ILOS导引律,动力学控制器采用PID控制器.为了验证控制器的鲁棒性,仿真时段0~120 s水动力参数相对于名义参数增加20%,120~240 s采用名义水动力参数,240~350 s水动力参数相对于名义参数减小20%. AUV的初始状态为0,期望路径的初始位置和方向为PP(0)=[0 -20 5 -tan-1(1/π) 0]T.
| 表 1 路径点 Tab. 1 Waypoints |
仿真结果见图 4~8,图 4为三维路径跟踪曲线和在水平面、垂直面的投影,可以清晰的看出在存在海流和模型不确定性的情况下,两种控制方法都能实现路径的良好跟踪,但通过对比也可看出方法1的超调量要小的多;图 5为跟踪误差曲线,通过图 5(a)、5(b)可以看出位置误差和姿态误差虽然在路径切换时会出现一定的波动,但很快能够稳定下来并全部趋于零. 图 5(c)、5(d)分别为纵倾角和艏摇角误差曲线,纵倾角和艏摇角误差在初始阶段会迅速增大,从而可以有效的减少位置误差,随着位置误差趋于稳定,姿态误差也趋于稳定,应该注意因为要对漂角进行补偿克服海流的影响,艏摇角误差并没有趋于零.
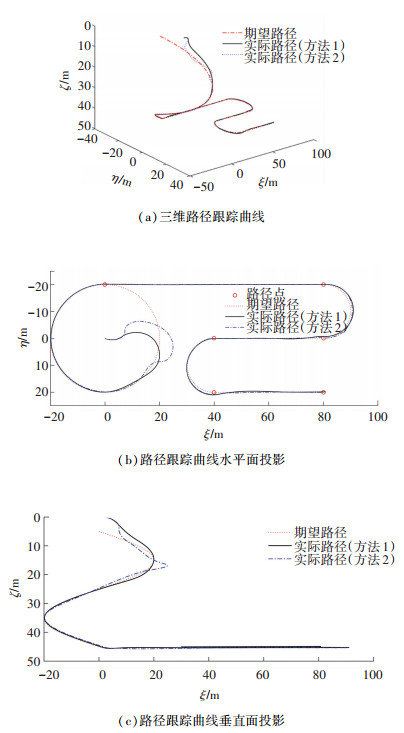
|
图 4 路径跟踪曲线 Fig. 4 Curves of path-following |

|
图 5 路径跟踪误差曲线 Fig. 5 Error curves of path-following |
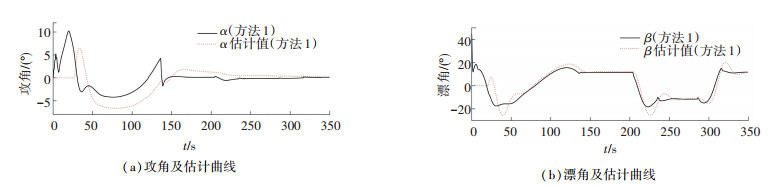
|
图 6 攻角和漂角曲线 Fig. 6 Curves of attack and sideslip angles |

|
图 7 控制输入曲线 Fig. 7 Curves of control inputs |

|
图 8 速度和速度误差曲线 Fig. 8 Curves of velocities and velocity errors |
图 6为攻角、漂角和它们估计值曲线,能够看出自适应律可以较好的实现对攻角、漂角的估计. 图 7为控制输入曲线,可以看到在路径切换时控制输入会产生波动,原因是路径切换时路径曲率不连续,但方法1的控制输入更加平稳一些,抖振也比较小. 图 8为速度和速度误差曲线,通过图 8(a)可以看到AUV的相对速度能很好的收敛到期望值,AUV的绝对速度由于受海流的影响,顺流时会增大,逆流时会减小,虚拟向导的速度能很好的收敛到AUV的绝对速度.通过图 8(b)、8(c)可以看到,纵倾角速度和艏摇角速度都能收敛到期望值.通过图 8(d)~8(f)可以看到纵向速度误差、纵倾角速度误差和艏摇角速度误差均收敛到零.
5 结论1) 基于Serret-Frenet坐标系引入了虚拟向导并建立了三维路径跟踪误差模型.
2) 在运动学控制中设计了具有自适应律的虚拟向导并提出了一种改进的积分视线法(ILOS)导引律.
3) 基于反步自适应滑模控制(BASMC)理论设计了动力学控制器,并应用Sigmoid函数设计滑模项,保证了系统的稳定性和鲁棒性、有效的削弱了抖振.
4) 应用非线性级联理论证明了整个控制系统的闭环稳定性,从而解决了存在海流干扰和模型不确定性情况下欠驱动AUV的三维路径跟踪控制问题.
5) 控制器的设计是基于AUV与流体的相对速度,由于相对速度更便于测量,所以与基于绝对速度的控制方法相比,更便于工程应用.
| [1] |
王芳, 万磊, 李晔, 等. 欠驱动AUV的运动控制技术综述[J]. 中国造船, 2010, 51(2): 227. WANG Fang, WAN Lei, LI Ye, et al. A survey on development of motion control for underactuated AUV[J]. Shipbuilding of China, 2010, 51(2): 227. DOI:10.3969/j.issn.1000-4882.2010.02.030 |
| [2] |
LEKKAS A M, FOSSEN T I. A time-varying lookahead distance guidance law for path following[J]. IFAC Proceedings Volumes, 2012, 45(27): 398. DOI:10.3182/20120919-3-IT-2046.00068 |
| [3] |
XU H, SOARES C G. Vector field path following for surface marine vessel and parameter identification based on LS-SVM[J]. Ocean Engineering, 2016, 113: 151. DOI:10.1016/j.oceaneng.2015.12.037 |
| [4] |
LAPIERRE L, SOETANTO D. Nonlinear path-following control of an AUV[J]. Ocean Engineering, 2007, 34(11): 1734. |
| [5] |
CAHARIJA W, PETTERSEN K Y, BIBULI M, et al. Integral line-of-sight guidance and control of underactuated marine vehicles: theory, simulations, and experiments[J]. IEEE Transactions on Control Systems Technology, 2016, 24(5): 1623. DOI:10.1109/TCST.2015.2504838 |
| [6] |
FOSSEN T I, PETTERSEN K Y, GALEAZZI R. Line-of-sight path following for Dubins paths with adaptive sideslip compensation of drift forces[J]. IEEE Transactions on Control Systems Technology, 2015, 23(2): 820. DOI:10.1109/TCST.2014.2338354 |
| [7] |
CAHARIJA W, PETTERSEN K Y, SØRENSEN A J, et al. Relative velocity control and integral line of sight for path following of autonomous surface vessels: merging intuition with theory[J]. Proceedings of the Institution of Mechanical Engineers, 2014, 228(2): 180. DOI:10.1177/0954407013502951 |
| [8] |
李岳明, 万磊, 孙玉山, 等. 水下机器人高度信息融合与欠驱动地形跟踪控制[J]. 控制理论与应用, 2013, 30(1): 118. LI Yueming, WAN Lei, SUN Yushan, et al. Altitude information fusion and bottom-following control for underactuated autonomous underwater vehicle[J]. Control Theory & Applications, 2013, 30(1): 118. |
| [9] |
FOSSEN T I, LEKKAS A M. Direct and indirect adaptive integral line-of-sight path-following controllers for marine craft exposed to ocean currents[J]. International Journal of Adaptive Control and Signal Processing, 2017, 31(4): 445. DOI:10.1002/acs.2550 |
| [10] |
边信黔, 程相勤, 贾鹤鸣, 等. 基于迭代滑模增量反馈的欠驱动AUV地形跟踪控制[J]. 控制与决策, 2011, 26(2): 289. BIAN Xinqian, CHENG Xiangqin, JIA Heming, et al. A bottom-following controller for underactuated AUV based on iterative sliding and increment feedback[J]. Control and Decision, 2011, 26(2): 289. |
| [11] |
LI Ye, WEI Cong, WU Qi, et al. Study of 3 dimension trajectory tracking of underactuated autonomous underwater vehicle[J]. Ocean Engineering, 2015, 105: 270. DOI:10.1016/j.oceaneng.2015.06.034 |
| [12] |
葛晖, 敬忠良, 高剑. 自主式水下航行器三维路径跟踪的神经网络H∞鲁棒自适应控制方法[J]. 控制理论与应用, 2012, 29(3): 317. GE Hui, JING Zhongliang, GAO Jian. Neural network H-infinity robust adaptive control for autonomous underwater vehicle in 3-dimensional path following[J]. Control Theory & Applications, 2012, 29(3): 317. |
| [13] |
王宏健, 陈子印, 贾鹤鸣, 等. 基于滤波反步法的欠驱动AUV三维路径跟踪控制[J]. 自动化学报, 2015, 41(3): 631. WANG Hongjian, CHEN Ziyin, JIA Heming, et al. Three-dimensional path-following control of underactuated autonomous underwater vehicle with command filtered back-stepping[J]. Acta Automatica Sinica, 2015, 41(3): 631. |
| [14] |
李娟, 边信黔, 熊华胜, 等. AUV的精确航迹跟踪系统的鲁棒控制[J]. 哈尔滨工业大学学报, 2013, 45(1): 112. LI Juan, BIAN Xinqian, XIONG Huasheng, et al. Robust control research for AUV trajectory control system[J]. Journal of Harbin Institute of Technology, 2013, 45(1): 112. |
| [15] |
PRESTERO T. Verification of a six-degree of freedom simulation model for the REMUS autonomous underwater vehicle[D]. Cambridge: Massachusetts Institute of Technology, 2001 https://dspace.mit.edu/handle/1721.1/65068
|
 2019, Vol. 51
2019, Vol. 51


