2. 河南城建学院 土木与交通工程学院, 河南 平顶山 467036
2. School of Civil and Traffic Engineering, Henan University of Urban Construction, Pingdingshan 467036, Henan, China
航空器冲突是指在某一时间内,航空器与特定目标(另一航空器、限制空域、地面障碍物等)之间的距离小于两者之间规定的最小间隔,以至于如果任何一方不改变其运动状态,并采取有效的避险措施,就有可能发生碰撞危险的现象[1].由于空域是有限的资源,航空器之间对空域资源的争夺势必产生矛盾,带来冲突.
航空器冲突规避是指通过预测航空器在未来一段时间内发生冲突的可能性,提前采取速度调整、航迹改变等措施避让潜在冲突,是确保空中交通安全的关键.航空器冲突概率是对航空器发生冲突的可能性的量化,是冲突规避的核心.计算冲突概率时需要综合考虑各种不确定因素带来的误差.现行的空中交通管理下,在无特殊情况下航空器必须按照指定的航路开展飞行活动,因此,误差大部分来源于风、导航、制导等各种不确定因素.对于冲突概率的计算,国内外研究者已展开了大量研究.文献[2-4]通过规定两架飞机在相遇过程中的航迹误差联合协方差为定值,建立预测航迹误差方程,近似求出两架飞机相遇过程中总的冲突概率.文献[5-7]提出了计算飞行冲突概率的随机化方法;文献[8]提出了基于航迹预测的位置预测模型,使用概率分布函数估计法估计冲突概率.后续诸多研究主要是在这几种模型基础上进行修正和改进[9-13].文献[1]使用蒙特卡罗方法计算了3维坐标系下的冲突概率并分析了一系列参数对冲突概率的影响;文献[14-15]提出了基于位置空间离散化思想的快速算法来计算冲突概率.并在此基础上,提出了一种基于三维布朗运动,使用坐标变换和Bachelier-Levy定理来估算冲突概率的方法.现有的冲突概率计算方法能够适应现阶段应用并取得较好地预测精度.为了应对航空运输量的持续增长给现行空管系统带来的挑战,新一代空中交通运输系统提出了基于四维航迹运行的理念.为了提高空域的利用率,保障航空公司的利益[16-17],新一代空中交通运输系统不再限制航空器沿特定航路飞行,而是允许航空器驾驶员在满足经过的航路点和各航路点到达时间的限制下,根据时变的环境和航空公司的运营目标,自由地选择航迹.
然而,航空器驾驶员自主航迹规划自由度的增加大大提高了冲突发生的可能性,飞行安全受到了极大威胁.因此,驾驶员意图不确定给航空器位置预测带来的影响不可忽略.通过上文对研究现状的调查,现有的冲突规避的研究缺少对驾驶员意图的考虑,不能有效地适应新一代空中交通运输系统运行模式的需求.
本研究提出一种新的航空器冲突规避模型.该模型通过描述受四维飞行计划限制下的航空器可达域的方式,将驾驶员意图的不确定性考虑在内.在此基础上,根据可达域约束下航空器位置预测概率分布模型,分别提出航空器与限制空域冲突概率、航空器对之间冲突概率的计算方法,以及该方法下的冲突概率等级划分及相应的冲突规避策略.
1 考虑驾驶员意图的航空器位置预测模型航空器冲突概率估算的基础是对航空器在未来一段时间内的位置进行预测.航空器位置预测的本质是分析建模各种不确定因素对位置分布概率方差的影响,建立航空器位置预测模型.本研究主要针对航空器的航路飞行阶段,研究航空器与限制空域之间及航空器对之间的冲突.
由于驾驶员意图是时变的,且不确定性较大,因此可将考虑驾驶员意图的航空器飞行过程视作无规则的布朗运动.由于在新一代航空运输系统下,航空器完成飞行任务所需要经过的航路点,以及经过各航路点的时间是在飞行计划中提前确定的同时考虑到航空器可达域的限制,即航空器位于可达域之外的概率应为0.因此,本文应用一种截断分布来反映可达域的限制.截断分布是通过限制概率分布的域而产生的条件分布.具体地,正态分布的定义域为(-∞, +∞),可以认为是不进行任何截断的.对X的取值加入范围限制之后,带有限制条件的X服从截断正态分布.由于任何密度函数曲线下方的面积均为1,因此,截断并不意味着直接把原始密度函数两边去掉一部分,而是截断后概率密度函数曲线会有一些变化,使得截断范围内总面积仍为1,截断范围外函数值为0.假设一个随机变量X,其概率密度函数为f(x),累积分布函数为F(x),定义域均为无限集.在定义域限制在一定范围内(例如a < x≤b)时,该随机变量的概率分布[18]为
| $ T\left( x \right) = f\left( {x\left| {a < x \le b} \right.} \right) = \frac{{g\left( x \right)}}{{F\left( b \right) - F\left( a \right)}}, $ | (1) |
| $ g\left( x \right) = \left\{ \begin{array}{l} f\left( x \right),a \le x \le b;\\ 0,x < a\;或\;x > b. \end{array} \right. $ | (2) |
假设某航空器计划于ti时刻经过航路点i,坐标为(xi, yi),于tj时刻经过航路点j,坐标为(xj, yj).由于航空器完成飞行任务所需要经过的航路点,以及经过各航路点的时间是在飞行计划中提前确定的.因此,为保证航班满足到达各航路点的时间要求,航空器在两航路点之间飞行过程中的可达域受到一定限制,可达域是个随时间变化的空间范围,如图 1所示,其计算可参照文献[19-20].根据式(1)、(2),可以得出在可达域限制下任意时刻t(t∈[ti, tj])的航空器位置分布为
| $ L\left( {x\left( t \right)} \right) = \frac{{\varphi \left( {x\left( t \right)} \right)}}{{\varphi \left( {{U_X}\left( t \right)} \right) - \varphi \left( {{L_X}\left( t \right)} \right)}}, $ | (3) |
| $ L\left( {y\left( t \right)\left| {x \sim \left( t \right)} \right.} \right) = \frac{{\varphi \left( {y \sim \left( t \right)} \right)}}{{\varphi \left( {{U_Y}\left( t \right)} \right) - \varphi \left( {{L_Y}\left( t \right)} \right)}}. $ | (4) |

|
图 1 t时刻可达域示意图 Fig. 1 Illustration of aircraft reachable domain at moment t |
式中:UX(t)、LX(t)分别为可达域在x方向的上界和下界;UY(t)、LY(t)分别为可达域在y方向的上界和下界;UX(t)、LX(t)、UY(t)、LY(t)的值也是随时间变化的,如图 1所示,其计算可参照文献[21];φ(x(t))、φ(
| $ {\sigma ^2}{\left( t \right)^\prime } = {\left( {{V_m} - \bar V} \right)^2} \times \left( {t - {t_i}} \right) \times \left( {{t_j} - t} \right). $ | (5) |
由此,航空器在可达域限制下于t时刻位于位置
| $ p\left( {\tilde x\left( t \right),\tilde y\left( t \right)} \right) = L\left( {x\left( t \right)} \right) \times L\left( {y\left( t \right)\left| {\tilde x\left( t \right)} \right.} \right). $ | (6) |
由于航空器的可达域是随时间不断变化的,因此在每一时刻,航空器的位置预测概率分布模型也是不同的.在后续计算中,本研究通过将时间维度离散化的手段,在计算出各时刻航空器的位置预测概率分布的基础上,将各时刻视作均匀分布,得到航空器于任意时刻位于任意位置的概率为
| $ p\left( {x,y,t} \right) = p\left( {\tilde x\left( t \right),\tilde y\left( t \right)} \right) \times \frac{1}{{{t_j} - {t_i}}}. $ | (7) |
在得到航空器在可达域内的位置预测概率分布的基础上,可以估算得到航空器的冲突概率.航空器的冲突概率包括两种类型:航空器与限制空域的冲突、航空器对之间的冲突.
2.1 航空器与限制空域的冲突概率本研究中所指的限制空域包括危险区、军事限制区、禁区,以及一些由于极端天气必须绕飞的区域.限制空域的范围及开放随时间变化,航空器的飞越和进入受时间和高度等条件限制.限制空域的主要信息包括时间信息和空间信息.其中空间信息代表限制空域的范围,可以用多边形、圆形、椭圆等近似地进行描述[22].时间信息反映限制空域随时间变化及发展过程.航空器与限制空域的冲突概率,即航空器进入限制空域的概率,可表示为
| $ {P_{\rm{r}}} = \int {\int {\int {p\left( {{x_i},{y_i},{t_i}} \right){\rm{d}}x{\rm{d}}y{\rm{d}}t} } } . $ | (8) |
由于限制空域的边界不一定是规则形状,且其位置可能会随时间发生移动,式(8)的积分域难以用函数表示,且计算极其复杂,耗时巨大,不适用于实时冲突探测.因此,本文通过将空域进行离散化的方式近似估计航空器的冲突概率.方法计算效率高,适合在线冲突概率计算.选取合适的离散化参数将限制空域离散化为n个点,则航空器与该限制空域的冲突概率Pr可表达为
| $ {P_{\rm{r}}} = \sum\limits_{i = 1}^n {p\left( {{x_i},{y_i},{t_i}} \right)} . $ | (9) |
Pr可以作为反映航空器与限制空域的冲突风险的指标.在确定航空器在未来一段时间内与限制空域的冲突概率的基础上,可以对冲突概率进行等级划分:1)Pr=0,无冲突概率;2)0 < Pr≤PT,安全无保障;3)Pr > PT,高冲突概率.其中PT为划分高、低冲突风险的冲突概率阈值.
假设航空器A计划于13:00:00时经过航路点i(150 km, 125 km),于13:09:00时经过航路点j (250 km, 175 km).途中会受到风暴区W的影响,风暴区范围用圆形表示,其中心位于k (280 km, 150 km),初始半径为30 km.影响时间从13:04:00时持续至13:09:40时,随时间推移,其影响范围不断扩大,直至半径达到100 km,如图 2所示.
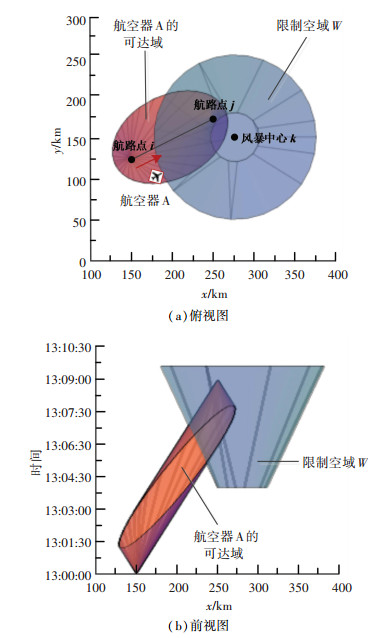
|
图 2 航空器与限制空域冲突示意图 Fig. 2 Illustration of the conflict between aircraft and restricted airspace |
通过计算可以得出随时间变化的冲突概率,如图 3所示.航空器A与风暴区W最初处于无冲突概率状态,于13:05:10时开始产生冲突概率,至13:07:05时达到最大瞬时冲突概率,最大冲突概率值为0.586 1,之后冲突概率不断降低直至于13:09:00时完成该航段飞行任务.

|
图 3 冲突概率随时间变化 Fig. 3 Variation of conflict probability with time |
对于两架及以上航空器之间的潜在冲突,本文将两两航空器可达域形成的交集定义为潜在冲突区(Z),即进入潜在冲突区的航空器有发生冲突的可能,飞行在潜在冲突区外的航空器不具备发生冲突的可能.
当两架航空器同时进入潜在冲突区内且其间距小于一定的安全距离D时,可认为航空器会发生冲突.因此,航空器A与航空器B之间的冲突概率可计算为
| $ {P_{{\rm{A}} - {\rm{B}}}} = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {p\left( {i,j} \right)} } ,i,j \in {Z_{A - B}}. $ | (10) |
其中
| $ \left\{ \begin{array}{l} p\left( {i,j} \right) = {p_{\rm{A}}}\left( {{x_i},{y_i},{t_i}} \right) \times {p_{\rm{B}}}\left( {{x_j},{y_j},{t_j}} \right),{\mathit{\boldsymbol{X}}_i} - {\mathit{\boldsymbol{X}}_j}\left| { \le D} \right.;\\ p\left( {i,j} \right) = 0,\left| {{\mathit{\boldsymbol{X}}_i} - {\mathit{\boldsymbol{X}}_j}} \right| > D. \end{array} \right. $ | (11) |
在未来一段时间内,航空器A的总冲突概率统计为航空器A与所有在同一空域的航空器之间冲突概率之和,记作PA. PA可以作为反映任意航空器冲突风险的指标.在确定下每个航空器在未来一段时间内的总冲突概率后,可以对总冲突概率进行等级划分,以航空器A为例:1)PA=0,无冲突概率;2)0 < PA≤PT,安全无保障;3)PA > PT,高冲突概率.
假设两架航空器,其中航空器A计划于13:00:00时经过航路点i(150 km, 125 km),于13:09:00时经过航路点j(250 km, 175 km),航空器B计划于13:00:00时经过航路点m(225 km, 100 km),于13:09:00时经过航路点n(175 km, 200 km),如图 4所示. 图 5描绘了在此次飞行过程中,两航空器的可达域及冲突情况的示意.
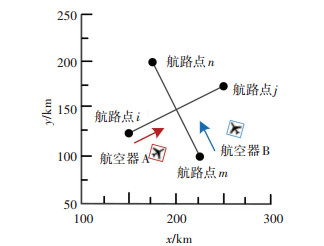
|
图 4 航班计划 Fig. 4 Flight plans of two aircrafts |
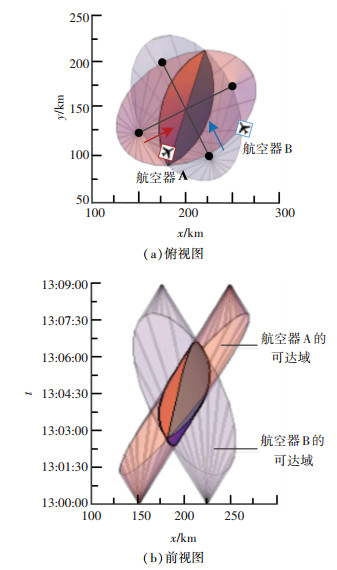
|
图 5 两航空器冲突示意图 Fig. 5 Illustration of the conflict betweentwo aircrafts |
通过计算可以得到航空器A与航空器B之间随时间变化的冲突概率,如图 6所示.航空器A与航空器B最初处于无冲突概率状态,于13:02:40时开始产生冲突概率,至13:04:30时达到最大瞬时冲突概率,最大冲突概率值为0.343 5,之后冲突概率降低直至于13:06:20时后回到无冲突概率状态.
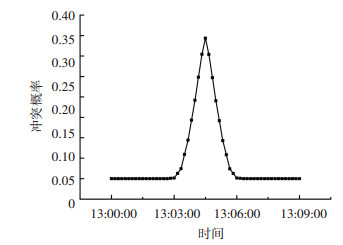
|
图 6 冲突概率随时间变化 Fig. 6 Variation of conflict probability with time |
根据冲突概率的计算过程可推测:无论是航空器与限制空域的冲突,还是航空器之间的冲突,航空器可达域与限制空域的交集,或两两航空器可达域之间交集的大小决定了冲突概率的大小.通过对冲突概率计算过程的分析可知,影响两航空器可达域交集的大小的因素包括:两航班计划飞行航路间距,用航路中点之间的距离来衡量;两航班计划在时间上的接近程度,用航班计划重合时间长短来反映;各航班计划所飞航路段长度;及各航班飞行计划用时.
为了分析各因素对冲突概率值的影响,本文设计了4组影响因素变化:保持航空器A的参数不变,改变航空器B经过的起止航路点坐标及经过起止航路点的时间,从而分别改变4个影响因素的值,并计算相应的冲突概率.绘制相应的冲突概率随影响因素变化曲线,如图 7~10所示.
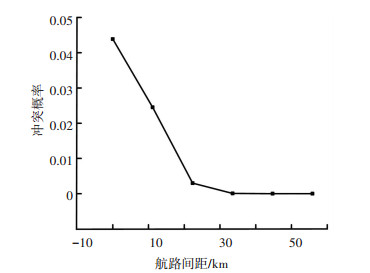
|
图 7 冲突概率随航路间距变化 Fig. 7 Variation of conflict probability with the distance between flight routes |

|
图 8 航空器与限制空域冲突示意图冲突概率随航班计划时间重合度变化 Fig. 8 Variation of conflict probability with the overlapping time of flight plans |
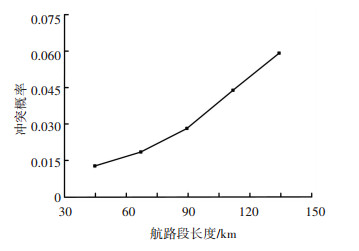
|
图 9 冲突概率随航路段长度变化 Fig. 9 Variation of conflict probability with the length of flight route |
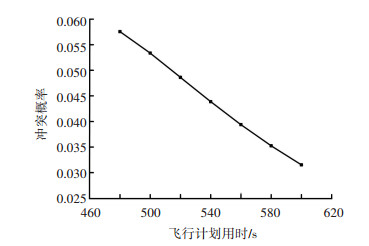
|
图 10 冲突概率随飞行计划用时变化 Fig. 10 Variation of conflict probability with the time of flight plan |
由图 7~10分析可知:1)两航空器飞行航路的间距和冲突概率负相关,当飞行航路间距达到一定阈值时,冲突概率降为0. 2)两航空器航班计划的重合时间和冲突概率正相关,当重合时间减小到某一值后,冲突概率持续为0. 3)飞行航路段长度与冲突概率负相关. 4)飞行计划用时与冲突概率线性正相关.
3.2 航空器冲突规避策略针对上文划分的不同冲突概率等级,提出了相应的冲突规避措施:1)对于无冲突概率的航空器,无需考虑冲突规避.航空器驾驶员可以根据航空公司的目标和周围环境的变化自由地选择可达域内的任意航迹完成飞行任务,无需担心会与其他航空器发生冲突;管制员可降低对该航空器的监视等级. 2)对于安全无保障的航空器,冲突规避任务由航空器驾驶员和管制员协商完成.航空器驾驶员可以自主确定航迹,但需要反馈给管制员,由管制员根据其他航空器反馈信息及周围环境信息判断驾驶员提交的航迹的可行性.在得到管制员许可的情况下可按照该航迹飞行;管制员也必须将该航空器的航迹信息共享给周围航空器,同时提高对该航空器的监视等级. 3)对于高冲突概率的航空器,需要通过自主航空器冲突探测与解脱系统自动发出预警,并提供给航空器驾驶员及管制员可行的冲突规避方案.航空器驾驶员必须按照管制员规定的航迹或给出的指示开展飞行活动,不可自主选择航迹;管制员需高度密切关注航空器的飞行状态.
4 结论1) 针对新一代空中交通运输系统带来的驾驶员意图不确定性给航空器飞行安全带来的隐患,提出了考虑驾驶员意图的航空器冲突规避模型.首先,考虑航空器可达域的限制改进了航空器位置预测模型.其次,定义了航空器与空域之间冲突、航空器对之间冲突,并提出了相应的冲突概率估算模型,等级划分方法.
2) 挖掘并分析了冲突概率大小的4个重要影响因素,发现两航空器飞行航路段间距,各航班计划飞行航路段长度与冲突概率值负相关,两航空器航班计划时间重合度,各航班飞行计划用时与冲突概率正相关.并在此基础上提出了各冲突概率等级相应的冲突规避策略.
3) 改进的系统通过计算冲突概率量化冲突风险,提供自动报告及预警来辅助管制员尽早地发现和解决可能的冲突.管制员可以将更多的精力转移到对航空器的监视上,这将很大程度上降低管制员工作负荷,对保障空中交通安全、提高空域利用率具有重要意义.
4) 提出的冲突规避模型适用于航空器巡航飞行阶段.航空器进场、离场阶段由于涉及高度变更,需要对本研究提出的模型中的部分参数进行修改.进一步研究将探索适用于航空器进、离场阶段的航空器位置预测模型、相应的冲突概率估算方法及冲突规避策略.
| [1] |
梁海军, 杨红雨, 肖朝, 等. 3维坐标系下的飞行冲突探测算法[J]. 四川大学学报(工程科学版), 2013, 3(45): 88. LIANG Haijun, YANG Hongyu, XIAO Zhao, et al. Flight conflict detection algorithm based on the three dimensional coordinate system[J]. Journal of Sichuan University (Engineering Science Edition), 2013, 3(45): 88. |
| [2] |
PAIELLI R A, ERZBERGER H. Conflict probability estimation for free flight[J]. Journal of Guidance, Control, and Dynamics, 1997, 20(3): 588. DOI:10.2514/2.4081 |
| [3] |
PAIELLI R, ERZBERGER H. Conflict probability estimation generalized to non-level flight[J]. Air Traffic Control Quarterly, 1999, 7(3): 1. |
| [4] |
ERZBERGER H, PAIELLI R A, ISAACSON D R, et al. Conflict detection and resolution in the presence of prediction error[C]//1st USA/Europe Air Traffic Management Research and Development Seminar. Saclay, France: NASA Ames Research Center, 1997
|
| [5] |
PRANDINI M, LYGEROS J, NILIM A, et al. Randomized algorithms for probabilistic aircraft conflict detection[C]// Proceedings of the 38th IEEE Conference on Decision and Control.Berkeley, CA, USA: IEEE, 1999, 3: 2444
|
| [6] |
PRANDINI M, HU J, LYGEROS J, et al. A probabilistic approach to aircraft conflict detection[J]. IEEE Transactions on Intelligent Transportation Systems, 2000, 1(4): 199. DOI:10.1109/6979.898224 |
| [7] |
PRANDINI M, WATKINS O J. Probabilistic aircraft conflict detection[R]. https://pdfs.semanticscholar.org/7ce8/c886bdf7cb175a5d368a9bf8262140d54141.pdf
|
| [8] |
HWANG I, SEAC C E. Intent-based probabilistic conflict detection for the next generation air transportation system[J]. Proceedings of the IEEE, 2008, 96(12): 2040. DOI:10.1109/JPROC.2008.2006138 |
| [9] |
YEPES J, HWANG I, ROTEA M. New algorithms for aircraft intent inference and trajectory prediction[J]. Journal of Guidance, Control, and Dynamics, 2007, 30(2): 370. DOI:10.2514/1.26750 |
| [10] |
PAIELLI R, ERZBERGER H, CHIU D, et al. Tactical conflict alerting aid for air traffic controllers[J]. Journal of Guidance, Control, and Dynamics, 2009, 32(1): 184. DOI:10.2514/1.36449 |
| [11] |
YANG Y, ZHANG J, CAI K, et al. Multi-aircraft conflict detection and resolution based on probabilistic reach sets[J]. IEEE Transactions on Control System Technology, 2017, 25(1): 309. DOI:10.1109/TCST.2016.2542046 |
| [12] |
GUAN X, ZHANG X, HAN D, et al. A strategic flight conflict avoidance approach based on a memetic algorithm[J]. Chinese Journal of Aeronautics, 2014, 27(1): 93. DOI:10.1016/j.cja.2013.12.002 |
| [13] |
YANG L, KUCHAR J. Prototype conflict alerting system for free flight[J]. Journal of Guidance, Control, and Dynamics, 1997, 20(4): 768. DOI:10.2514/2.4111 |
| [14] |
石磊, 吴仁彪. 预测位置空间离散化的多航路中期冲突探测算法[J]. 信号处理, 2012, 28(11): 1521. SHI Lei, WU Renbiao. Multi-route mid-term conflict detection algorithm based on discretization of predicted position space[J]. Signal Processing, 2012, 28(11): 1521. DOI:10.3969/j.issn.1003-0530.2012.11.005 |
| [15] |
石磊, 吴仁彪, 黄晓晓. 基于总体冲突概率和三维布朗运动的冲突探测算法[J]. 电子与信息学报, 2015, 37(2): 360. SHI Lei, WU Renbiao, HUANG Xiaoxiao. Conflict detection algorithm based on overall conflict probability and three dimensional brownian motion[J]. Journal of Electronics & Information Technology, 2015, 37(2): 360. |
| [16] |
Next generation air transportation system integrated plan[R]. Washington DC: Federal Aviation Administration Joint Planning and Development Office, 2004
|
| [17] |
张亚平, 廉冠, 邢志伟, 等. 飞机推出控制停机位等待惩罚策略[J]. 哈尔滨工业大学学报, 2018, 50(3): 39. ZHANG Yaping, LIAN Guan, XING Zhiwei, et al. Aircraft departure pushback control strategy based on gate-hold penalty[J]. Journal of Harbin Institute of Technology, 2018, 50(3): 39. |
| [18] |
NORMAN L, KOTZ S, BALAKRISHNAN N. Continuous Univariate Distributions[M]. 2nd ed. Ontario, Canada: John Wiley & Sons, 1994: 204.
|
| [19] |
HARVEY M. A measurement theory for time geography[J]. Geographical Analysis, 2005, 37(1): 17. DOI:10.1111/gean.2005.37.issue-1 |
| [20] |
HAO S, CHENG S, ZHANG Y. A multi-aircraft conflict detection and resolution method for 4-Dimensional trajectory-based operation[J]. Chinese Journal of Aeronautics, 2018, 31(7): 1579. DOI:10.1016/j.cja.2018.04.017 |
| [21] |
SONG Y, HARVEY M. Simulating visit probability distributions within planar space-time prisms[J]. International Journal of Geographical Information Science, 2014, 28: 104. DOI:10.1080/13658816.2013.830308 |
| [22] |
齐乃明, 孙小雷, 董程, 等. 航迹预测的多无人机任务规划方法[J]. 哈尔滨工业大学学报, 2016, 48(4): 32. QI Naiming, SUN Xiaolei, DONG Cheng, et al. Mission planning based on path prediction for multiple UAVs[J]. Journal of Harbin Institute of Technology, 2016, 48(4): 32. |
 2019, Vol. 51
2019, Vol. 51


