2. 昆明理工大学 交通工程学院,昆明 650500
2. School of Transportation Engineering, Kunming University of Science and Technology, Kunming 650500, China
高效、可靠的公交服务是解决城市交通拥堵问题、保障居民正常生活的关键,而目前普遍存在的公交串车问题导致公交车到站时刻往往与时刻表有所偏差,在很大程度上影响了公交系统的服务水平.为了解决该问题,公交运营者往往会采取在线路中设置时间控制点的措施,通过控制公交车到达各个控制点的准点率来提升线路整体的准点程度.因此,设置时间控制点对于提高公交线路服务可靠性具有重要意义.国内外学者在时间控制点设置方面的研究相对较少,大多是研究如何在控制点对公交车辆进行动态调度.如文献[1]提出了在控制站点对公交车辆离站时刻进行控制的滞站策略,以提高公交线路的准点程度;文献[2]认为应该将公交线路首末站默认为时间控制点;文献[3]提出了若干条原则作为设置时间控制点的前提条件;文献[4]研究发现,动态调度策略在公交车头时距的不稳定程度较大时,能够达到最佳的优化效果,因此建议把公交车头时距差异较大的站点设置为控制点;文献[5]认为时间控制点应该设置在客流量较大的站点;文献[6]提出在高需求路段或者靠近线路中间段的路段控制公交车是最有效的公交调度策略;文献[7]通过研究公交实时调度发现,将控制点设置在客流量较大的站点前方能够实现最优的控制效果;文献[8]根据公交定位数据对控制站的特征指标进行定量分析,基于层次分析法提出了控制站点的选择方法;文献[9]考虑了乘客上下车问题,并提出了多个控制点的控制策略法;文献[10]提出了服务状态指标及站点分散度指标,以对控制点设置原则进行量化,并建立了综合评价指标计算方法以及控制点选择流程,关键参数仍需要根据经验确定.
由以上叙述可知,国外的时间控制点设置仍然需要依赖专家经验,无法生成精确的最优方案.时间控制点的设置是公交规划中的重要环节,也是编制时刻表的基础.目前在我国各大城市中,公交调度方案的制定还不够精细、科学.大多城市只规定公交车驶离站点、到达终点的时刻,并未制定公交车到达中途各个站点的时刻,也未设置时间控制点.在这种情况下,公交司机很难把握在线路途中的运行状态,导致公交车在中途站点晚点或者早到现象普遍发生.个别城市虽然设置了时间控制点,但是并未对公众公布,所以无法查询到具体设置方法,也难以对其效果进行评价.在公交车载GPS日益普及的情况下,如何根据公交车GPS数据,从普通站点中优选出最佳的时间控制点,仍是一个亟待解决的问题.本文提出了时间控制点设置的原则,建立了两种时间控制点的优选流程,研究成果对于提高公交线路调度水平、缓解串车问题具有重要意义.
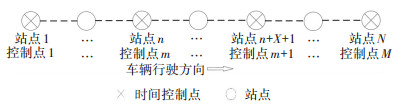
1 时间控制点设置原则对于一条有N个站点的公交线路,始发站的站点编号为1,终点站的站点编号为N,线路中一共设置M个时间控制点.根据文献[2]公交调度的研究成果,线路首末站应该首先被选择为时间控制点,即始发站设置为控制点1,终点站设置为控制点M.线路中站点n设置为控制点m,站点n+X+1设置为控制点m+1,即相邻两个控制点之间间隔的站点数为X.线路中时间控制点与站点的对应关系见图 1.
|
图 1 公交线路站点与控制点示意图 Fig. 1 Sketch of stops and control points of a bus route |
时间控制点的设置原则是选取控制点时必须满足的前提条件,主要有以下3点:1)设置在客流量大、战略位置重要的站点.在时间控制点的选择过程中,应当考虑大多数乘客的出行需求,将控制点设置在客流量大的站点或靠近商场、商业中心等战略位置重要的站点能够为更多的乘客提供有效、方便、可靠的公共交通服务. 2)公交在时间控制点间的行程时间变异程度较小.为了保证公交能够准时到达每一个时间控制点,必须确保公交在各控制点间的行程时间差异较小.若公交在控制点间的行程时间变异程度过大,则说明这一路段的路况较为复杂,公交运行状况不稳定且容易发生延误或提前到达,无法保证该站点的准点率,因此不适合选择该站点为时间控制点. 3)时间控制点间的距离应适度.首先,时间控制点间的距离不应过短,相邻的站点不能同时选择为控制点.设置时间控制点是为了使公交准点到达某些特定的站点,因此在运行过程中司机需要根据实际情况实时调整公交车的速度,如果控制点间的距离过短,司机可能无法在短时间内完成调整,不能保证准时到达下一个控制点.其次,时间控制点间的距离也不能过长,如果相邻两个控制点之间间隔的站点数过多,那么公交在这些中间路段的运行状况过于随机,无法对公交运行的整体过程进行有效约束.综合考虑,一条线路所设置的控制点个数M应为线路总站点数N的30%左右,相邻控制点之间间隔的站点数X应为N的10%~20%[11].
2 站点评价指标基于控制点设置的基本原则,可以初步筛选出满足限制条件的若干种控制点设置可行方案,为了在这些方案中找出最优解,需要确定一种可量化评价指标的控制点优选方法.从选择控制点的原则中选取若干个因素进行量化分析,便可建立公交站点选取的3个评价指标.
2.1 平均停站时间指标时间控制点应设置在线路中客流量大的站点,然而基于已有的GPS历史数据无法获取公交在各个站点的客流量数据,因此本文选择使用平均停站时间这一指标代替客流量指标进行评价,平均停站时间长说明该站点的客流量大,平均停站时间短说明该站点的客流量小.
为了能够对平均停站时间指标进行量化分析,为后面对时间控制点的优选作准备,需要对该指标进行归一化处理.停站时间等于公交车驶离站点的时刻减去到达该站点的时刻,根据GPS历史数据,可获取不同时间段内公交车在各个站点的停站时间.假设公交车在站点i的最短停站时间为tmin,最长停站时间为tmax,计算得到公交车在站点i的平均停站时间为ti,这3个指标的单位均为s.已知tmin≤ti≤tmax,以tmax作为平均停站时间的截止时间,可设平均停站时间的归一化指标为
行程时间指的是公交车辆在线路上从驶离一个站点至到达另一个站点所耗费的总时间,包括车辆的实际运行时间、停站时间以及由于交通状况而引起的延误时间等.时间控制点的设置是为了提高车辆的准点率以及公交服务的可靠性,因此在设置控制点的过程中应保证公交在各控制点间的行程时间差异较小.行程时间的差异可由行程时间变异系数来表示,其计算公式为
| $ {V_i} = \frac{{\sqrt {\frac{1}{{n - 1}} \cdot \sum\limits_{j = 1}^n {{{\left( {{T_{ij}} - \bar T} \right)}^2}} } }}{{\bar T}}. $ | (1) |
式中:Vi为站点i与距离站点i最近的上游相邻控制点间的行程时间变异系数;Tij为公交车次j在站点i与距离站点i最近的上游控制点间的行程时间,s;T为站点i与距离站点i最近的上游控制点间的平均行程时间,s.
变异系数等于标准差与平均值的比值,是衡量各观测值变异程度的一个统计量.在评价两组或多组数据的变异程度时,如果各组观测数据的平均数相等,则可以直接利用各组数据的标准差进行评价.如果平均数不相等,则需要采用标准差与平均数的比值来比较.在实际情况中,公交车在各个控制点间的平均行程时间显然并不相同,因此需要计算其变异系数以对控制点间的行程时间差异进行分析.
2.3 综合评价指标时间控制点应该设置在客流量大的站点,且公交在控制点间的行程时间差异应该尽量小,基于以上两个考虑因素可以提出时间控制点设置的综合评价指标Ki,其计算公式为
| $ {K_i} = \frac{{{V_i}}}{{{P_i}}} = \frac{{({t_{{\rm{max}}}} - {t_{{\rm{min}}}}) \cdot \sqrt {\frac{1}{{n - 1}} \cdot \sum\limits_{j = 1}^n {{{\left( {{T_{ij}} - \bar T} \right)}^2}} } }}{{\bar T\cdot({t_i} - {t_{{\rm{min}}}})}}. $ | (2) |
本文用停靠时间Pi间接反映站点的乘客流量. Pi越大,则站点i的乘客流量越大;而Vi越小,则各辆公交车在上一个控制点与站点i之间的行程时间的差异越小,它们在站点i偏离时刻表的程度越小.若此时将站点i设为时间控制点,不仅各辆公交车在站点i会具有较高的准点率,而且也能够服务更多的乘客、使更多乘客准点到达站点i.因此,式(2)中分母Pi越大、分子Vi越小,则Ki的值越小,代表站点i越适合被选择为时间控制点.
由于公交在始发站和终点站的停站时间均为0,导致该公式的分母为0,因此在计算综合评价指标时往往忽略这两个站点而只对线路的中间站点进行计算.此外,由于始发站和终点站在线路中的特殊性和重要性,这两个站点一般被默认为控制点,因此在计算时忽略这两个点, 对最终结果并没有影响.
3 时间控制点优选流程综合评价指标的建立为时间控制点的优选奠定了理论基础.本文基于该指标,从整体最优和局部最优两个方面提出两种时间控制点优选流程.
3.1 整体最优整体最优方法基本步骤如下:1)基于时间控制点的设置原则,枚举出所有可能的控制点设置方案.设一条公交线路包括N个站点,需要设置M个时间控制点.其中始发站与终点站默认为控制点,还需要在剩余的N-2个站点中选择M-2个合适的站点作为控制点.考虑相邻的站点不能同时作为时间控制点,则实际上可行的时间控制点备选方案数Z等于CN-M-1M-2,其中C为组合数符号. 2)根据公交GPS数据计算各个备选方案中除去首末站以外各控制点的平均停站时间ti,进一步得到其归一化指标Pi. 3)根据公交GPS数据计算各个备选方案中除去首末站以外各控制点与上游相邻控制点间公交行程时间变异系数Vi. 4)计算各个备选方案中除去首末站以外各控制点的综合评价指标Ki,并计算其平均值,则在所有备选方案中Ki平均值最小的方案为时间控制点设置的最优方案.
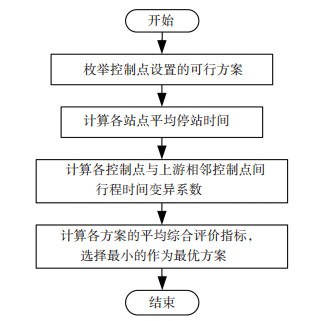
整体最优方法最终目的是从所有可行方案中选出Ki平均值最小的方案,以保证最终方案对全线路公交运行的优化效果最好.但是此方法存在着一些局限性,如在对多条线路进行规划控制时,由于每条线路的站点数及要设置的控制点数不同,需要对每条线路都进行枚举并计算枚举出的所有可行方案,在计算过程中所涉及的GPS数据量很大,处理起来人力及时间成本耗费较大.整体最优方法的流程图如图 2所示.
|
图 2 整体最优方法流程图 Fig. 2 Flow chart of the overall optimum method |
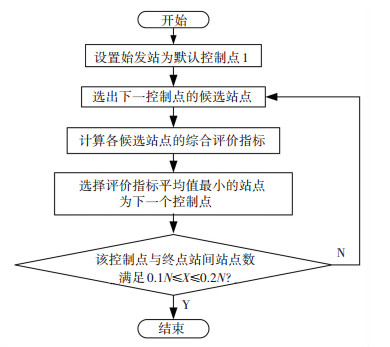
针对整体最优方法所存在的问题,本文提出了另一种局部最优的方法,其基本步骤如下:1)线路始发站作为默认时间控制点1被确定下来,根据设置控制点的原则,选出控制点2的候选站点并分别计算各站点综合评价指标Ki,从候选的站点中选择Ki值最小的站点作为控制点2.以苏州市102公交线路为例,该线路共有21个站点,站点1默认为控制点1.由于控制点不能相邻、且相邻控制点间的站点数应为总站点数的10%~20%,所以102线路每两个相邻控制点之间的站点数应满足2≤X≤4,则控制点2的候选站点为站点4、5、6. 2)从控制点2的下一站开始选出控制点3的候选站点,计算各候选站点的综合评价指标Ki,从候选站点中选择综合评价指标Ki值最小的一个站点作为控制点3. 3)用相同的方法依次选出后续的线路控制点,对于站点编号为n的控制点m,线路的站点总数为N,则该站点与终点站间的站点数为X=N-n-1,当X满足0.1N≤X≤0.2N时,停止计算,得出最终方案.局部最优方法的流程图如图 3所示.
|
图 3 局部最优方法流程图 Fig. 3 Flow chart of the local optimum method |
局部最优的优选方法是根据递推的思想,把控制点作为公交线路的节点,保证对于一个已确定的控制点来说,下一个控制点是下游站点中的最优选,进而确保对各相邻控制点间路段的优化效果最佳.此优选流程相对比较简单,选择出的最终方案未必是对线路整体优化效果最好的方案,但同样能够以分段控制的方式对公交在线路中的运行状况进行有效约束,以提供相对准确、可靠的公交运输服务.此外,当需要对多条公交线路进行控制点的设置时,采用这种方法能够避免重复的枚举和计算工作.
4 算例分析以苏州市102路公交为例,对第3节所建立的优选方法进行分析.
4.1 局部优选方法苏州市102路公交共设有21个站点,根据时间控制点设置的原则,拟选取6个站点作为时间控制点,相邻控制点间的站点数应满足2≤X≤4.由GPS历史数据可知,该线路公交在各个站点的停站时间基本分布在0~100 s内,因此这里取tmax=100,tmin=0,则综合评价指标Ki的计算公式为
| $ {K_i} = \frac{{{V_i}}}{{{P_i}}} = \frac{{100 \cdot \sqrt {\frac{1}{{n - 1}} \cdot \sum\limits_{j = 1}^n {{{\left( {{T_{ij}} - \bar T} \right)}^2}} } }}{{\bar T \cdot {t_{\rm{i}}}}}. $ | (3) |
线路始发站默认为控制点1,由于两个相邻控制点间的站点数必须满足2≤X≤4,则对线路中编号为4、5、6的站点进行计算,计算结果显示站点4、5、6的Ki值分别为1.413、0.371、0.302.在候选站点中站点6的综合评价指标最小,因此选择该站点为时间控制点2.
控制点2的站点编号为6,则对线路中编号为9、10、11的站点进行计算,计算结果显示站点9、10、11的Ki值分别为0.519、0.378、0.448.在候选站点中站点10的综合评价指标最小,因此选择该站点为时间控制点3.
控制点3的站点编号为10,则对线路中编号为13、14、15的站点进行计算,计算结果显示站点13、14、15的Ki值分别为0.737、0.502、0.625.在候选站点中站点14的综合评价指标最小,因此选择该站点为时间控制点4.
控制点4的站点编号为14,则对线路中编号为17、18、19的站点进行计算,计算结果显示站点17、18、19的Ki值分别为0.727、0.926、0.858.在候选站中站点17的综合评价指标最小,选择该站点为时间控制点5.
控制点5的站点编号为17,此时该控制点与线路终点站间的站点数为X=N-n-1=3,满足2≤X≤4,则计算结束.最终方案所选择的时间控制点:站点1、站点6、站点10、站点14、站点17、站点21.该方案的平均综合评价指标K为
| $ \bar K = \frac{{{K_6} + {K_{10}} + {K_{14}} + {K_{17}}}}{4} = 0.477. $ | (4) |
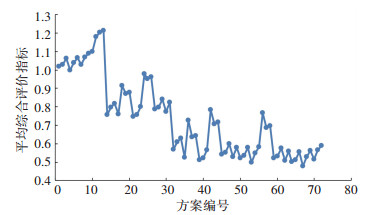
时间控制点设置的原则是可行方案所必须满足的前提,根据控制点设置的限制条件,本文使用C语言设计了对应的枚举程序,由程序运行结果可知,线路控制点选取的可行方案共有72种.为了批量计算各个方案的平均综合评价指标,本文将公交GPS历史数据以矩阵的形式导入MATLAB软件,通过编程处理得到了最终的计算结果,并根据计算结果绘制了各方案平均综合评价指标散点图,如图 4所示.由散点图可知,方案67的平均综合评价指标K值最小,该方案所选取控制点的站点编号为1、6、10、14、17、21,K67=0.477,最终方案与局部最优方法所得结果一致.
|
图 4 平均综合评价指标散点图 Fig. 4 Scatter plot of the average comprehensive evaluation index |
针对苏州市102路公交线路,两种方法最终得出了相同的控制点设置方案,主要原因是该线路站点及控制点的数量较少,导致备选的可行方案数量也较少.当线路情况发生变化时,局部最优方法可能无法得到这么理想的结果,如当线路站点数增加时,备选的可行方案可能有成百上千种,整体最优方法可以从庞大数量的方案中选择出最优解,然而采用局部优选方法时由于所考虑到的方案数较少,最终结果可能无法达到最佳的优化效果.
5 结论1) 以公交GPS数据为基础,建立了线路控制点选取的站点评价指标,并基于这3个指标提出了整体和局部两种不同的优选方法.
2) 在对单一公交线路进行优化时,采用整体优选方法可以选出优化效果最佳的控制点设置方案;在对某一区域的多条公交线路进行优化时,由于整体优选方法需要对每一条线路进行可行方案枚举,计算过程较为繁琐,而采用局部优选的方法可以在保证一定优化效果的前提下,节省大量时间和人力成本.
3) 针对公交线路的一个运行方向提出了时间控制点设置方法,而实际公交线路存在两个运行方向.同一条线路的两个运行方向往往存在差异,此时同样可以采用本文中的方法给两个方向分别设置控制点.由于目前我国各大城市的公交调度还不够精细,线路均未设置时间控制点,因此无法将本文的研究成果与工程实践方案进行对比分析.在将来有条件的情况下,完全可以将该方法应用于实践中,对其有效性进行科学评价.
| [1] |
HALL R, DESSOUKY M, LU Q. Optimal holding times at transfer stations[J]. Computer & Industrial Engineering, 2002, 40: 379. |
| [2] |
NEWELL G F. Control of pairing of vehicles on a public transportation route, two vehicles, one control point[J]. Transportation Science, 1974, 8(3): 248. DOI:10.1287/trsc.8.3.248 |
| [3] |
LIU G, WIRASINGHE S C. A simulation model of reliable schedule design for a fixed transit route[J]. Journal of Advanced Transportation, 2001, 35(2): 145. DOI:10.1002/atr.v35:2 |
| [4] |
TURNQUIST H, BLUME S W. Evaluating potential effectiveness of headway control strategies for transit systems[J]. Transportation Research Record, 1980, 746: 25. |
| [5] |
STRATHMAN J, DUEKER K, KIMPEL T, et al. Automated bus dispatching, operations control, and service reliability: baseline analysis[J]. Transportation Research Record: Journal of the Transportation Research Board, 1999, 1666: 28. DOI:10.3141/1666-04 |
| [6] |
FU L, YANG X. Design and implementation of bus-holding control strategies with real-time information[J]. Transportation Research Record, 2002, 1791: 6. DOI:10.3141/1791-02 |
| [7] |
ABKOWITZ M, EIGER A, ENGELSTEIN I. Optimal control of headway variation on transit routes[J]. Journal of Advanced Transportation, 1986(20): 73. |
| [8] |
张景, 沈吟东. 基于定位数据的公交时间站点自动选择方法[J]. 交通运输系统工程与信息, 2012, 12(6): 60. ZHANG Jing, SHEN Yindong. Automatic selection of time points based on AVL data[J]. Journal of Transportation Systems Engineering and Information Technology, 2012, 12(6): 60. DOI:10.3969/j.issn.1009-6744.2012.06.010 |
| [9] |
CHEN Q, ADIDA E, LIN J. Implementation of an iterative headway-based bus holding strategy with real-time information[J]. Public Transport, 2012, 4(3): 1. |
| [10] |
别一鸣, 程绍武, 黄晓雷. 基于综合评价指标的公交线路时间控制点优选方法[J]. 交通运输系统工程与信息, 2016, 16(2): 170. BIE Yiming, CHENG Shaowu, HUANG Xiaolei. A method for the selection of bus route time control points based on comprehensive evaluation index[J]. Journal of Transportation Systems Engineering and Information Technology, 2016, 16(2): 170. DOI:10.3969/j.issn.1009-6744.2016.02.027 |
| [11] |
DOU X, YAN Y, GUO X, et al. Time control point strategy coupled with transfer coordination in bus schedule design[J]. Journal of Advanced Transportation, 2016, 50(7): 1336. DOI:10.1002/atr.v50.7 |
 2019, Vol. 51
2019, Vol. 51


